| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201423648 | |
| Published online | 24 July 2014 | |
Online material
Appendix A: Geometric model for the computation of the effective stress
The geometric approach to the deformation theory of hot pressing and the conclusions for the plastic flow have been investigated by Kakar & Chaklader (1967) and Rao & Chaklader (1972). However, the detailed derivation of the formulae was not provided. Thus, we present the theory in detail and improve some aspects that were treated in a simplified manner in the studies mentioned above.
In the study by Kakar & Chaklader (1967) four basic systems of packing are considered, defined by the geometric arrangement of the grains and by the coordination number (this is the number Z of the contact points, an average value for equally sized spheres). In the simple cubic packing (SCP) every grain has four neighbours in a horizontal layer and two additional neighbours in the layers above and below. Orthorhombic (ORP) packing corresponds to six neighbours in a layer (plus two above and below). The rhombohedral packing (RHP) has coordination number 12 and the body-centred cubic packing (BCCP) 8. Although in a unidirectional force field the body-centred cubic packing is an unstable arrangement, we consider this case for the sake of completeness. Furthermore, although stability varies with the packing type, we assume that the symmetry is sustained throughout the whole compaction process. Assuming homogeneous and isotropic composition of the grains and symmetrical spread upon application of stress, for different packings the spheres will deform to polyhedra upon complete compaction, e.g. cubes for SCP, hexagonal prisms for ORP, rhombic dodecahedra for RHP, and tetrakaidecahedra for BCCP. During the deformation, necks develop at the contact points. The form of the grains will change, whereas the volume will remain constant.
For each kind of packing a specific unit cell of a certain form which is occupied by a
dust particle is considered. The form of a unit cell is defined by the polyhedra
mentioned above. From Figs. A.2–A.4, the volume V of such a unit cell can
be computed. For SCP, this is the volume of a cube, and, since
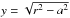 , we obtain
, we obtain 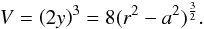 (A.1)For ORP, the volume of a hexagonal prism is
(A.1)For ORP, the volume of a hexagonal prism is
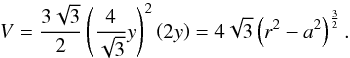 (A.2)For RHP we compute
(A.2)For RHP we compute 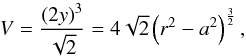 (A.3)and for BCCP
(A.3)and for BCCP 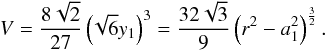 (A.4)Thus, the volume of the unit cell can be
expressed as the product of a constant β1 (the pre-factor of the bracket) and
the power
(A.4)Thus, the volume of the unit cell can be
expressed as the product of a constant β1 (the pre-factor of the bracket) and
the power 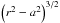 .
.
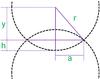 |
Fig. A.1
General deformation geometry at any contact point between two grains. |
| Open with DEXTER | |
The deformation of the BCC packing proceeds in two stages. For this reason we describe the theory for the other cases and the first stage of the BCCP deformation first, and then consider the second deformation stage of the BCC packing separately.
Prior to the hot pressing, the grain touches the surface of the unit cell at
Z points
where the neighbouring grains touch each other (Z1 for BCCP).
During compaction, the grains deform plastically at the contact points and develop
necks. The cross-section of such a neck between two grains has a circular form and is
called the face (the contact points have evolved to contact cross-sections). Still, the
volume of the particle needs to be kept constant. Thus, the current radius of the grain
is assumed to increase and the volume of those parts of the grain now lying outside of
the unit cell (the caps) need to be subtracted from the current sphere volume (we note
that the initial sphere volume is normalised to 1): 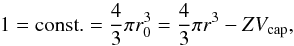 (A.5)where r is the current grain
radius and
(A.5)where r is the current grain
radius and 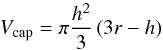 (A.6)is the volume of a cap. Using the relation
h = r −
y defined by the geometry of the packings (Fig.
A.1), we obtain the normalised volume of the
particle for the first three packings as
(A.6)is the volume of a cap. Using the relation
h = r −
y defined by the geometry of the packings (Fig.
A.1), we obtain the normalised volume of the
particle for the first three packings as 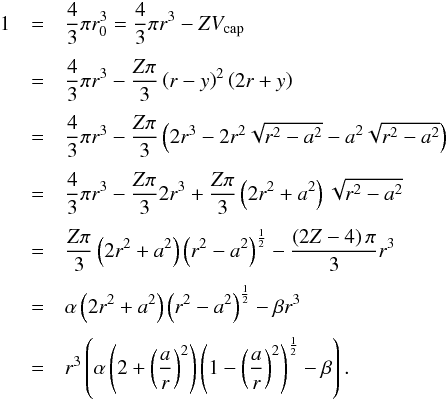 (A.7)This defines the geometric constants
α and
β from
Table 1 as α = Zπ/
3 and β =
(2Z − 4)π/ 3. From Eq. (A.7) the current radius of the particle is
computed:
(A.7)This defines the geometric constants
α and
β from
Table 1 as α = Zπ/
3 and β =
(2Z − 4)π/ 3. From Eq. (A.7) the current radius of the particle is
computed:
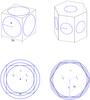 |
Fig. A.2
Unit cells and their intersections with an inscribed grain for the SCP and the ORP (top row from left to right) along with the top views of the unit cells and of the grain at its initial and critical (final) stages of deformation (bottom row). |
| Open with DEXTER | |
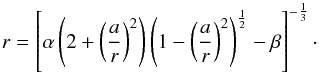 (A.8)Given the ratio a/r, the
current radius r of the sphere during deformation can be found (in
arbitrary units corresponding to unit volume of the sphere). The ratio a/r is
computed from the expression for the bulk density D, defined as the ratio
of the volume of the particle to the volume of the unit cell. This last value is
β1(r2 −
a2)3/2 (see Table 1). From the normalised grain volume 1 and the volume of the unit cell we
obtain
(A.8)Given the ratio a/r, the
current radius r of the sphere during deformation can be found (in
arbitrary units corresponding to unit volume of the sphere). The ratio a/r is
computed from the expression for the bulk density D, defined as the ratio
of the volume of the particle to the volume of the unit cell. This last value is
β1(r2 −
a2)3/2 (see Table 1). From the normalised grain volume 1 and the volume of the unit cell we
obtain 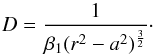 (A.9)Prior to compaction, i.e. for
a = 0,
the radius equals the initial radius (r = r0), hence
(A.9)Prior to compaction, i.e. for
a = 0,
the radius equals the initial radius (r = r0), hence
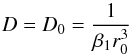 (A.10)holds, thus,
(A.10)holds, thus, 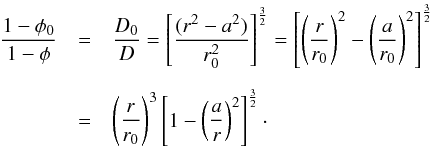 (A.11)This is solved for (a/r)2:
(A.11)This is solved for (a/r)2: 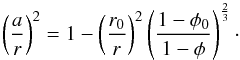 (A.12)For the computation of the effective
stress, we also need the area of the cross-section of the unit cell. In terms of the
geometries shown in Figs. A.2–A.4, the cross-section of a unit cell is the area of its projection
onto the horizontal plane. For SCP this is a square with the edge length 2y, for ORP a regular
hexagon with the edge length
(A.12)For the computation of the effective
stress, we also need the area of the cross-section of the unit cell. In terms of the
geometries shown in Figs. A.2–A.4, the cross-section of a unit cell is the area of its projection
onto the horizontal plane. For SCP this is a square with the edge length 2y, for ORP a regular
hexagon with the edge length 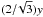 , for RHP a square with the edge length
2y, and
for BCCP an irregular octagon with four edges of the length
, for RHP a square with the edge length
2y, and
for BCCP an irregular octagon with four edges of the length
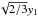 , four edges of the length
, four edges of the length
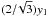 and the internal angle of
135 degrees. The areas of
those polygons can be written as γy2 (or as
and the internal angle of
135 degrees. The areas of
those polygons can be written as γy2 (or as
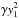 for BCCP; see Table 1 for the values of γ).
for BCCP; see Table 1 for the values of γ).
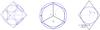 |
Fig. A.3
Unit cell of the RHP and its intersections with an inscribed grain (left panel), the top right view of the unit cell and of the grain at its initial and critical (final) stage of deformation (central panel), and a single face of the unit cell at the critical stage of the deformation (right panel). |
| Open with DEXTER | |
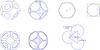 |
Fig. A.4
Unit cells and their intersections with an inscribed grain for the two deformation stages of the BCCP (top row, first and second panels); the faces of the unit cell at the second critical deformation stage (top row, third and fourth panels); topview of the unit cell before the first critical stage (bottom row, left panel) and after the first but before the second critical stage (bottom row, central panel); and the arrangement of the spheres at the first critical deformation stage as seen in the plane defined by the centres of the three spheres (bottom row, right panel). |
| Open with DEXTER | |
If a load m acts on a face then the stress on the face is
equal m/
(γy2). The total
stress on the sphere is Zm/
(γy2). In a
planetesimal, the applied stress is the lithostatic pressure σ0 and is
equal to the stress on the face:
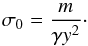 (A.13)From this the load acting on the
cross-section of the unit cell follows as m =
σ0γy2
and can be divided into two components. It is equal to the sum of the load acting on the
sphere through N non-vertical flat faces πa2cos(θ)σ1
lying above the equator of the unit cell and of the load acting on the void space
cσ2,
(A.13)From this the load acting on the
cross-section of the unit cell follows as m =
σ0γy2
and can be divided into two components. It is equal to the sum of the load acting on the
sphere through N non-vertical flat faces πa2cos(θ)σ1
lying above the equator of the unit cell and of the load acting on the void space
cσ2,  (A.14)where πa2 is the area of the
neck, θ is
the inclination angle of the faces, c is the cross-section of the porous part of the
unit cell, γ is a geometric constant which depends on the
packing (see Table 1), σ1 is the
stress acting along the z-axis through the neck, and σ2 = 0 is the
stress on the void space. The last equation is solved for σ1 to obtain
(A.14)where πa2 is the area of the
neck, θ is
the inclination angle of the faces, c is the cross-section of the porous part of the
unit cell, γ is a geometric constant which depends on the
packing (see Table 1), σ1 is the
stress acting along the z-axis through the neck, and σ2 = 0 is the
stress on the void space. The last equation is solved for σ1 to obtain
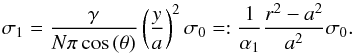 (A.15)Above we have shown
(A.15)Above we have shown
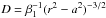 . From this we compute
. From this we compute 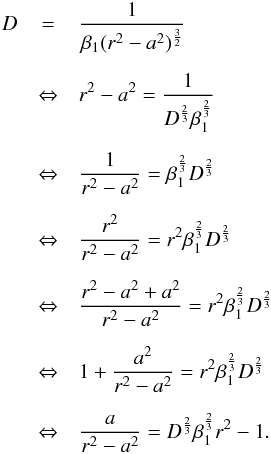 (A.16)Thus,
(A.16)Thus, 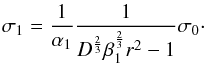 (A.17)To obtain the particle volume in the second
deformation stage of the BCCP, one needs to subtract Z1 = 8 caps of
the volume
(A.17)To obtain the particle volume in the second
deformation stage of the BCCP, one needs to subtract Z1 = 8 caps of
the volume 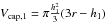 and additionally Z2 = 6 caps of
the volume
and additionally Z2 = 6 caps of
the volume 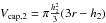 :
: 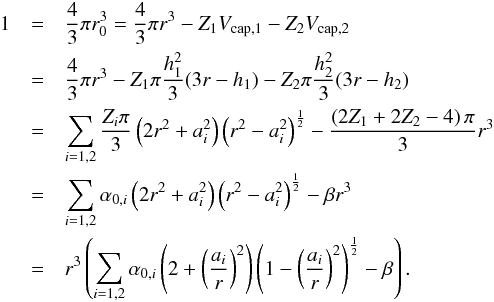 (A.18)This defines the geometric constants
(A.18)This defines the geometric constants
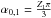 ,
, 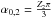 and
and
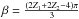 for BCCP. Similarly to the other cases,
Eq. (A.18) implies
for BCCP. Similarly to the other cases,
Eq. (A.18) implies 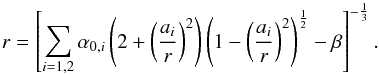 (A.19)The power (a1/r)2 is
computed analogously to Eq. (A.12):
(A.19)The power (a1/r)2 is
computed analogously to Eq. (A.12):
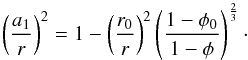 (A.20)For (a2/r)2 we
consider the first critical stage c1 when the cap of the second kind
with the radius a2 starts to form and express the
relative density in the terms of y2,
(A.20)For (a2/r)2 we
consider the first critical stage c1 when the cap of the second kind
with the radius a2 starts to form and express the
relative density in the terms of y2,
Additional parameter values for the derivation of the effective stress.
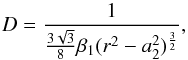 (A.21)because
(A.21)because
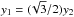 . Then
. Then
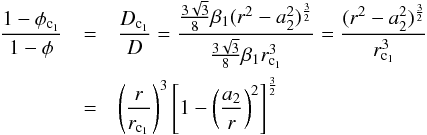 (A.22)and
(A.22)and 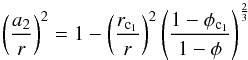 (A.23)follow. The relation between
a1 and a2 is obtained
from Eqs. (A.20) and (A.23) as
(A.23)follow. The relation between
a1 and a2 is obtained
from Eqs. (A.20) and (A.23) as
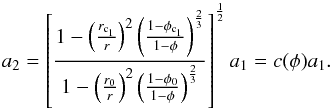 (A.24)The load on the octagonal cross-section of
the unit cell of the BCCP is
(A.24)The load on the octagonal cross-section of
the unit cell of the BCCP is 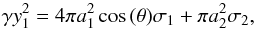 (A.25)where σ1 is the
effective stress on the faces of the first kind, σ2 on the
second kind, and
(A.25)where σ1 is the
effective stress on the faces of the first kind, σ2 on the
second kind, and 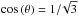 . Assuming equal load per face, we obtain
. Assuming equal load per face, we obtain
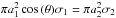 and from this
and from this
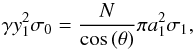 (A.26)where N = 5. Thus,
(A.26)where N = 5. Thus,
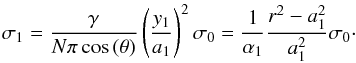 (A.27)The geometric relations described above are
valid from the beginning of the deformation until the faces start to touch each other.
In the beginning, for the normalised grain volume 1 the initial grain radius r0 is equal to
(3/4π)1 /
3. The stage when the equations lose their validity corresponds
to a certain particle radius rc, the critical radius. This can be
computed as
(A.27)The geometric relations described above are
valid from the beginning of the deformation until the faces start to touch each other.
In the beginning, for the normalised grain volume 1 the initial grain radius r0 is equal to
(3/4π)1 /
3. The stage when the equations lose their validity corresponds
to a certain particle radius rc, the critical radius. This can be
computed as
follows. For the first four cases, the critical face radius a can be expressed in
terms of the critical particle radius as ac =
δrc with the constants
δ (equal
to 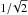 , 1/2, 1/2, and 1/2, respectively). Substituting this
into Eq. (A.8) we obtain
, 1/2, 1/2, and 1/2, respectively). Substituting this
into Eq. (A.8) we obtain 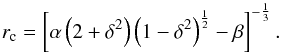 (A.28)From Eq. (A.10) we obtain the relative initial densities D0 (see Table
1). The critical density Dc is obtained
by substituting rc and ac =
δrc into Eq. (A.9):
(A.28)From Eq. (A.10) we obtain the relative initial densities D0 (see Table
1). The critical density Dc is obtained
by substituting rc and ac =
δrc into Eq. (A.9): 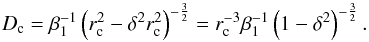 (A.29)At the transition from the first to the
second deformation stage of the BCC packing, contact points between the particle and the
six rectangular faces of the unit cell form. Using δ1 = 1/2,
the particle radius at this moment of deformation rc1
and the first critical density Dc1 follow from Eqs. (A.8) and (A.9), or using δ1 = 0.5 and a2 = 0, from
Eqs. (A.19) and (A.21), respectively. At the end of the
second stage, all fourteen faces come in contact. Here, with
(A.29)At the transition from the first to the
second deformation stage of the BCC packing, contact points between the particle and the
six rectangular faces of the unit cell form. Using δ1 = 1/2,
the particle radius at this moment of deformation rc1
and the first critical density Dc1 follow from Eqs. (A.8) and (A.9), or using δ1 = 0.5 and a2 = 0, from
Eqs. (A.19) and (A.21), respectively. At the end of the
second stage, all fourteen faces come in contact. Here, with
 and δ2 = 1/3,
the second critical radius rc2 and the second
critical density Dc2 follow from Eqs.
(A.19) and (A.21).
and δ2 = 1/3,
the second critical radius rc2 and the second
critical density Dc2 follow from Eqs.
(A.19) and (A.21).
After the respective critical density is reached, the geometric approach to the
computation of the effective stress σ1 can no longer be applied (i.e. for
D ≥
Dc or
 ). In this case we use a continuous
linear relationship between
). In this case we use a continuous
linear relationship between  and
and
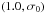 .
.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


