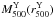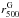| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322870 | |
| Published online | 17 April 2014 | |
Online material
Appendix A: Further scaling relations and tests
 |
Fig. A.1
Lensing mass – X-ray luminosity relation. The M–LX
relation is shown, for both |
| Open with DEXTER | |
Appendix A.1: The LX–M relation
To better assess the consistency of our weak lensing masses with the Vikhlinin et al. (2009a) results, we compare them
to the LX–MY-relation
derived by V09a using the 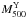 masses
of their low-z cluster sample. Figure A.1 inverts this relation by showing the
masses
of their low-z cluster sample. Figure A.1 inverts this relation by showing the
 masses as a function of the
0.5–2.0 keVChandra
luminosities measured by V09a. Statistical uncertainties in the
Chandra fluxes and, hence, luminosities are negligible for our
purposes. We calculate the expected 68 % confidence ranges in mass for a given luminosity by inverting
the scatter in LX at a fixed MY as given
in Eq. (22) of V09a. For two fiducial redshifts, z = 0.40 and
z =
0.80, spanning the unevenly populated redshift range of the eight
clusters, the M–LX relations and their expected
scatter are shown in Fig. A.1. Small filled
triangles in Fig. A.1 show the
masses as a function of the
0.5–2.0 keVChandra
luminosities measured by V09a. Statistical uncertainties in the
Chandra fluxes and, hence, luminosities are negligible for our
purposes. We calculate the expected 68 % confidence ranges in mass for a given luminosity by inverting
the scatter in LX at a fixed MY as given
in Eq. (22) of V09a. For two fiducial redshifts, z = 0.40 and
z =
0.80, spanning the unevenly populated redshift range of the eight
clusters, the M–LX relations and their expected
scatter are shown in Fig. A.1. Small filled
triangles in Fig. A.1 show the
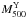 masses from
which V09a derived the LX–M relation. Our 8 MMT
clusters are nicely tracing the distribution of the overall sample of 36 clusters
(open triangles).
masses from
which V09a derived the LX–M relation. Our 8 MMT
clusters are nicely tracing the distribution of the overall sample of 36 clusters
(open triangles).
As an important step in the calculation of the mass function, these authors show that their procedure is able to correct for the Malmquist bias even in the presence of evolution in the LX–M
relation, which they include in the model. We emphasise that the Malmquist bias correction – which is not included here – applied by V09a moves the clusters upwards in Fig. A.1, such that the sample agrees with the best-fit from the low-z sample, as Fig. 12 in V09a demonstrates.
As already seen in Fig. 2, the Mwl (large symbols in Fig. A.1) and MY agree well. Thus we can conclude that the WL masses are consistent with the expectations from their LX. Finally, we remark that the higher X-ray luminosities for the some of the same clusters reported by Maughan et al. (2012) in their study of the LX–TX relation are not in disagreement with V09a, as Maughan et al. (2012) used bolometric luminosities.
Appendix A.2: Redshift scaling and cross-scaling of X-ray masses
Here we show further results mentioned in the main body of the article. Figure A.2 shows two examples of the X-ray/WL mass ratio as a function of redshift. Owing to the inhomegenous redshift coverage of our clusters, we cannot constrain a redshift evolution. All of our bias estimates are consistent with zero bias.
Table A.2 shows the fit results and bias estimates for various tests we performed modifying our default model, as well as for ancillary scaling relations. In particular, we probe the scaling behaviour of hydrostatic masses against the V09a estimates, for which we find a MY/Mhyd tentatively biased high by ~15%, while MT and MG do not show similar biases.
Appendix A.3: Choice of centre and fitting range
Weak lensing masses obtained from profile fitting have been shown to be sensitive to the choice of the fitting range (Becker & Kravtsov 2011; Hoekstra et al. 2011b; Oguri & Hamana 2011). Taking these results into account, we fitted the WL masses within a fixed physical mass range. Varying the fitting range by using rmin = 0 instead of 0.2 Mpc in one and rmax = 4.0 Mpc instead of 5.0 Mpc in another test, we find no evidence for a crucial influence on our results.
Both simulations and observations establish (e.g. Dietrich et al. 2012; George et al.
2012) that WL masses using lensing cluster centres are biased high due to
random noise with respect to those based on independently obtained cluster centres,
e.g. the ROSAT centres we employ. The fact that the
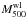 –
– relation
gives slightly milder difference between bMC for the high- and
low-Mwl bins when the peak of the
S-statistics is assumed as the cluster centre
(Table A.2) can be explained by the larger
relative Mwl “boost” for clusters with larger
offset between X-ray and lensing peaks. This affects the flat-profile clusters (Sect.
4.1) in particular, translating into a greater
effect for the cfit case than for cB13-based
masses. We find that WL cluster centres only slightly alleviate the observed
mass-dependence.
relation
gives slightly milder difference between bMC for the high- and
low-Mwl bins when the peak of the
S-statistics is assumed as the cluster centre
(Table A.2) can be explained by the larger
relative Mwl “boost” for clusters with larger
offset between X-ray and lensing peaks. This affects the flat-profile clusters (Sect.
4.1) in particular, translating into a greater
effect for the cfit case than for cB13-based
masses. We find that WL cluster centres only slightly alleviate the observed
mass-dependence.
 |
Fig. A.2
Continuation of Fig. 2. Panel A)
shows log (MT/Mwl)
within |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.