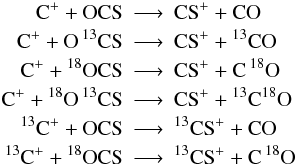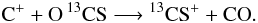| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220130 | |
| Published online | 24 January 2013 | |
Online material
Appendix A: Isotopization rules
Usually, only the main isotopes are considered in astrochemical databases, despite the fact that many isotopologues have been detected in astronomical observations so far. We will describe here our efforts to include 13C and 18O isotopes into the chemical database. However, in this paper we will only discuss the scientific implications of carbon fractionation not going into the details of the 18O chemistry.
Usually, in a reaction formula like H + O2 −→ OH + O it is not possible to identify which oxygen atom binds with hydrogen. Both atoms in O2 are indistinguishable. This changes by including an isotope into a molecule. Now both atoms in O18O are distinguishable and we get: 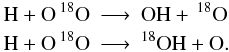 Unfortunately, this becomes more complicated if the isotope can be placed in more than one spot. The main isotope reaction
Unfortunately, this becomes more complicated if the isotope can be placed in more than one spot. The main isotope reaction  splits into 5 isotopic reactions
splits into 5 isotopic reactions 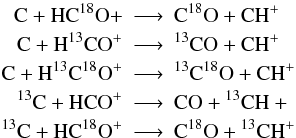 taking into account that the C=O binding is preserved (again we omit the isotopic superscript when denoting the main isotope). For more complex species the above scheme becomes much more complicated. Furthermore, the number of additional reactions is so large that it becomes difficult to perform the isotopization by hand, especially if one plans to update the chemical network regularly and manual isotopization is quite error-prone. We developed a software routine to automatically implement isotopic reactions into a given reaction set14. The routine features are:
taking into account that the C=O binding is preserved (again we omit the isotopic superscript when denoting the main isotope). For more complex species the above scheme becomes much more complicated. Furthermore, the number of additional reactions is so large that it becomes difficult to perform the isotopization by hand, especially if one plans to update the chemical network regularly and manual isotopization is quite error-prone. We developed a software routine to automatically implement isotopic reactions into a given reaction set14. The routine features are:
-
inclusion of a single 13C and a single 18O isotope (multiple isotopizations are neglected in this study);
UDfA often does not give structural information, for instance C2H3 does not distinguish between linear and circular configurations (l-C2H3 and c-C2H3). In such cases we consider all carbon atoms (denoted by Cn) as indistinguishable15, i.e.
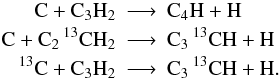 However, if structure information is provided we account for each possible isotopologue individually:
However, if structure information is provided we account for each possible isotopologue individually: 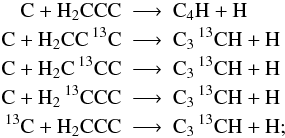
-
molecular symmetries are preserved, i.e. NC13CN = N13CCN, but HC18OOH ≠ HCO18OH;
functional groups like CHn are preserved (see also Woods & Willacy 2009), e.g.:
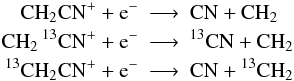 but not:
but not: 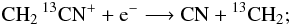
-
when the above assumptions are in conflict to each other we assume minimal scrambling, i.e. we choose reactions such, that the fewest possible number of particles switch partners. For example:
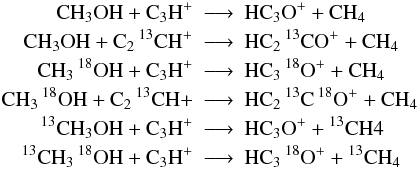 but not
but not 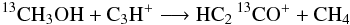 which would preserve the 13C=O bond but would require 5 particles to switch partners;
which would preserve the 13C=O bond but would require 5 particles to switch partners; we favor proton/H transfer over transfer of heavier atoms;
Appendix B: Rescaling of reaction rates
By introducing isotopologues into the chemistry we introduce many new reaction channels and we need to make sure that reaction rates are properly scaled. Unfortunately, not only the reaction rates for isotopologue reactions are unknown, we neither have information on branching ratios for reactions with several possible product channels. Thus, we assume equal probabilities for all branches, i.e. all isotopologue reactions possessing the same reactants but different products have their rate coefficient divided by the number of different product branches. For example: 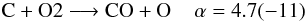 with α being the fit coefficient from UDfA06 at T = 300 K and the number in parentheses indicates the decimal power. Introducing 13C and 18O into this reactions opens up additional channels:
with α being the fit coefficient from UDfA06 at T = 300 K and the number in parentheses indicates the decimal power. Introducing 13C and 18O into this reactions opens up additional channels: 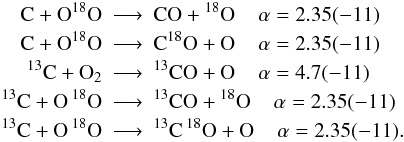 Assuming equal probabilities for different reaction branches is a strong assumption and the reader should keep in mind, that many of the introduced reactions might have different reaction rate coefficients with potentially strong impact on the solution of the chemical network. The isotope exchange reactions discussed in the following are a notable exception from this.
Assuming equal probabilities for different reaction branches is a strong assumption and the reader should keep in mind, that many of the introduced reactions might have different reaction rate coefficients with potentially strong impact on the solution of the chemical network. The isotope exchange reactions discussed in the following are a notable exception from this.
Appendix C: Influence of chemical data sets
To illustrate how the choice of the chemical data set affects the outcome of our astrochemical calculations we calculate our reference model for three different chemical sets: UDfA06 (Woodall et al. 2007), OSU (version osu_01_2009), and KIDA (version kida.uva.2011, Wakelam et al. 2012). To allow a consistent computation it was necessary to slightly alter the original data sets:
-
The formation of H2 on grain surfaces is calculated separately in KOSMA-τ and we removed the reaction H + H −→ H2 from OSU.
-
The same holds for the photo-dissociation of H2, we removed the reaction H2 + hν −→ H + H. KOSMA-τ explicitly calculates the H2 formation rate from the population of the (vibrational) v-levels (all rotational levels of one vibrational state summed, ground state v = 0 − 14, Lyman band 24 level + Werner band 10 level)
-
The unshielded CO photo-dissociation rate coefficient differs significantly among the three sets. We recomputed the unshielded photo-dissociation rate for a standard Draine FUV field using absorption cross sections available from http://home.strw.leidenuniv.nl/~ewine/photo/ and can confirm the value of 2 × 10-10 s-1 (van Dishoeck et al. 2006) from UDfA06. We replaced the corresponding α values in OSU and KIDA. For a discussion on differing photo-reaction rates see e.g. van Hemert & van Dishoeck (2008) and Röllig et al. (2013).
-
We replaced reactions with very large negative rate coefficients γ with a refitted expressions according to Röllig (2011).
-
KIDA uses the Su-Chesnavich capture approach to compute rate coefficients for unmeasured reactions between ions and neutral species with a dipole moment (Woon & Herbst 2009). Their formalism is incompatible with KOSMA-τ and we replace the corresponding 1877 reaction rate coefficients with a new set of rate coefficients α,β, and γ, suitable for the Arrhenius-Kooij formula α(T/300K)βexp(−γT), which are fitted such that they approximate the original rates between 10 and 1000 K.
-
For species where KOSMA-τ does not distinguish between linear and cyclic isomeric forms we consider all species only in terms of their molecular formula, e.g. C3H instead of l−C3H and c−C3H.
In Fig. C.1 we show the relative abundances of C+, C, and CO for model calculations with n = 105 cm-3, M = 1000 M⊙, and χ = 10 using different chemical data sets: UDfA06 (solid lines), OSU (dashed lines), KIDA (dotted lines) and the resulting range of gas temperatures. All three sets give the same chemical structure but with slight variations in the abundance profiles. The biggest difference is a higher CO abundance of OSU and KIDA at very low values of AV (factor 2 − 3 at AV = 0.01). This also leads to a carbon transition from C+ to CO at slightly lower values of AV compared to UDfA. Overall, the chemical structure of the main carbon species is comparable, particularly the effect on the total column density is small. The similar chemical structure and the almost identical gas temperatures around the carbon transition will result in a consistent fractionation behavior of the three species across all three chemical sets.
 |
Fig. C.1
Chemical structure of a model clump with the following model parameters: n0 = 105 cm-3, M = 100 M⊙, χ = 10 (UDfA06 (solid), OSU (dashed), KIDA (dotted). The gray shaded area shows the gas temperature spanned by the three models calculations. |
| Open with DEXTER | |
 |
Fig. C.2
Same as Fig. C.1 for HCO+, CH, and CH+. |
| Open with DEXTER | |
Figure C.2 shows how the different chemical sets influence the chemistry of HCO+, CH, and CH+. The differences are larger than those in Fig. C.1. UDfA06 produces a significantly higher CH abundance in the outer layer of the cloud, at some positions by a factor of 10 higher than OSU. However, we discussed earlier that fractionation of CH is the result of C+ fractionation. We do not expect any significant deviations in the fractionation ratio (FR) of C+) for the three chemical sets, hence the effect on the FR(CH) should be weak. The same should be the case for CH+ which shows even smaller differences for the three chemical sets. HCO+shows the same abundance in the cloud center, but some significant differences for AV < 1. This could lead to different fractionation behavior at these parts of the cloud when using different chemical sets. It is unlikely that this leads to observable effects because of the 100 times lower HCO+ abundance with respect to the center of the cloud and the respective weak influence on the total column density.
Appendix D: Spherical model context
D.1. Cloud radius
The model primarily computes radius dependent quantities. For a given density law, i.e., values α and fc = Rcore/Rtot, the total cloud radius Rtot (in cm) can be calculated from n0 (in cm-3) and M (in M⊙) using 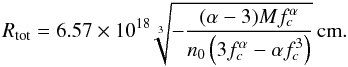 (D.1)For α = 3/2 and fc = 0.2 this reduces to
(D.1)For α = 3/2 and fc = 0.2 this reduces to 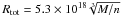 cm.
cm.
 |
Fig. C.3
Mean CH column density versus H2 column density (color/shape coding same as Fig. 9). Observational results are plotted as colored points (red: Sheffer et al. 2008; green: Rachford et al. 2002; olive: Magnani et al. 2005; black: Qin et al. 2010; brown: Magnani et al. 2006; orange Gerin et al. 2010; blue Suutarinen et al. 2011). The two lines are the CH − H2 relations from Mattila (1986) (red) and Qin et al. (2010) (black). |
| Open with DEXTER | |
D.2. Column density
The general expression for the maximum (radial) column density16 is 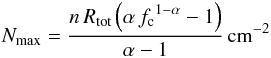 (D.2)that is Nmax = 4.7nR cm-2 for α = 3/2 and fc = 0.2.
(D.2)that is Nmax = 4.7nR cm-2 for α = 3/2 and fc = 0.2.
However, they are not observables. Observations always yield an projected, beam-convolved figure. We describe them in terms of measurable column densities.
In the framework of spherical model clouds, column densities differ depending on where we look at. To get a position-independent measure for the column density of a given species i, we calculate the average column density for the whole clump  (D.3)When referring to model column densities we always mean a clump averaged column density according to Eq. (D.3). This definition assumes that observations always cover whole clumps. This is equivalent to the traditional description of beam-filling factors for the observation of spatially unresolved clumps, i.e. we assume that we have (typically many) unresolved clumps within the telescope beam. In that sense, the fractionation of the column density is always the result of a convolution of the fractionation structure with the absolute abundance profile.
(D.3)When referring to model column densities we always mean a clump averaged column density according to Eq. (D.3). This definition assumes that observations always cover whole clumps. This is equivalent to the traditional description of beam-filling factors for the observation of spatially unresolved clumps, i.e. we assume that we have (typically many) unresolved clumps within the telescope beam. In that sense, the fractionation of the column density is always the result of a convolution of the fractionation structure with the absolute abundance profile.
D.3. CH column densities
Modelling the formation of the light hydrides, such as CH+ and CH, still poses a challenge to chemical models. In Fig. C.3 we plot the mean CH column density versus the total mean column density of the respective clump. The colored dots are observations from absorption and emission line measurements. The red and black lines are simple parametrized models to describe the column density (Mattila 1986; Qin et al. 2010). We note, that the column density splits into two distinct regimes with significantly different behavior. Diffuse clouds with total column densities below 1021 cm-2 show a steeper slope than denser clouds, where the CH column density appears to approach a limit of about 1015 cm-2. This behavior is approximately reproduced by the model calculations. The column densities in our model are consistent with values for TMC-1 given by Suutarinen et al. (2011) as well as with diffuse cloud observations presented by Gerin et al. (2010) which give N(CH) ≈ 1 − 26 × 1013 cm-2 for total H2 columns between 1021 − 1022 cm-2.
Sheffer et al. (2008) present column densities along 42 diffuse molecular Galactic sight lines. They find total columns between 1012 and 1014 cm-2 and a very strong correlation between column densities of CH and H2. Mattila (1986) confirms this trend for dark clouds. Magnani et al. (2005) derived CH column densities from 3335 MHz observations in the Galactic plane and used the linear relation given by Mattila (1986) to derive corresponding H2 column densities. They find 1013 ≤ N(CH) < 1015 cm-2.
Magnani et al. (2006) observed the CH2 Π1/2,J = 1/2,F = 1 − 1 transition toward the Galactic center. They find N(CH) ≈ 3 − 7 × 1015 cm-2. In addition to determining N(H2) from its linear correlation to N(CH) they also used a factor 1.8 × 1020 to derive N(H2) from integrated CO(1-0) line emission.
Qin et al. (2010) presented recent Herschel/HIFI observations against Sgr B2(M) which revealed that the linear relationship between CH and H2 flattens at higher visual extinctions. They give a log-log slope of 0.38 ± 0.07 for N(H2) ≥ 1021 cm-2. In Fig. C.3 we show our model results for N(CH) versus N(H2) together with the observational data (Rachford et al. 2002; Magnani et al. 2005, 2006; Sheffer et al. 2008; Qin et al. 2010; Gerin et al. 2010; Suutarinen et al. 2011).
We cannot reproduce the large column densities derived by Magnani et al. (2006). Their data is derived from emission line measurements, while all other studies used absorption lines, and consequently suffers from higher uncertainties due to its dependence on the assumed excitation temperature. To our knowledge 13CH has not yet been detected. The lack of 13CH observations makes it difficult to assess the model results. The total CH column densities that we find in our model results stay below 1015 cm-2. Nevertheless, the general behavior is well reproduced.
Appendix E: Fractionation plots of selected species
 |
Fig. E.1
C+ fractionation structure as function of relative clump radius r/Rtot for different values of n and M. Each sector corresponds to a different χ value. The FR is color coded, ratios within ± 10% of the ER are shown in green. Blue and violet denotes FR < ER, yellow and red denotes FR > ER. |
| Open with DEXTER | |
 |
Fig. E.2
Same as Fig. E.1 for C. |
| Open with DEXTER | |
 |
Fig. E.3
Same as Fig. E.1 for CO. |
| Open with DEXTER | |
 |
Fig. E.4
Same as Fig. E.1 for HCO+. |
| Open with DEXTER | |
 |
Fig. E.5
Same as Fig. E.1 for CH. |
| Open with DEXTER | |
 |
Fig. E.6
Same as Fig. E.1 for CH+. |
| Open with DEXTER | |
Here we show fractionation plots of selected species over a large portion of our model parameter space. We left out models with M = 103 M⊙ because they show very similar results as models with M = 102 M⊙. The fractionation plots are also available for download: http://www.astro.uni-koeln.de/kosma-tau.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.