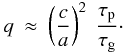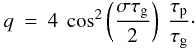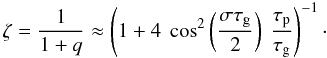| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220266 | |
| Published online | 21 December 2012 | |
Online material
Appendix A: Properties of eigenfunctions and mode inertia
A.1. Displacement eigenfunctions
 |
Fig. A.1
Displacement eigenfunctions as a function of the normalized radius r/R. In blue the horizontal component to the displacement eigenfunction z2 (Eq. (7)) and in red the radial component to the displacement eigenfunction z1 (Eq. (6)). From top to bottom ℓ = 1 modes 1 and 3 of Table 2. |
| Open with DEXTER | |
The displacement eigenfunctions computed for two modes of the selected pattern (see Table 2) for model M1 are shown as a function of the normalized radius r/R in Fig. A.1. They correspond to the modes with the largest and smallest maximum amplitudes in the pattern. The inner part is dominated by the horizontal displacement z2 and oscillates with a large number of nodes, as is typical of a high-order gravity mode. The largest maximum amplitude corresponds to the most g-dominated mode whereas the smallest maximum amplitudes arise for the p-m modes ν1 and ν6.
The maximum amplitude of z2 occurs deep in the g-cavity, at the same radius for all modes of the pattern. The region of non-negligible amplitude defines the radius of a seismic rotating core which is here found to be independent of the mode (r/R ~ 0.02) and far smaller than the upper turning radius of the inner gravity resonant cavity (x2 ~ 0.08, Table 3)
A.2. Behavior of β and βcore with ζ
For ℓ = 1 modes of red giants, the term
z2z1 in β
(Eq. (13)) plays almost no role
because 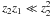 in the
core and
in the
core and 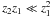 in the
envelope (see Fig. A.1). As a result, we have
in the
envelope (see Fig. A.1). As a result, we have
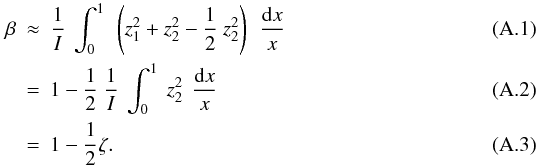 where
ζ is defined in Eq. (10). The linear dependence of β with ζ is
verified in Fig. A.2. Furthermore, for all
modes,
where
ζ is defined in Eq. (10). The linear dependence of β with ζ is
verified in Fig. A.2. Furthermore, for all
modes, 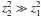 ,
2z1z2 in the g-cavity (see
Fig. A.1), then
βcore,nl ≈ βcore
where for l = 1 modes, we derive
,
2z1z2 in the g-cavity (see
Fig. A.1), then
βcore,nl ≈ βcore
where for l = 1 modes, we derive 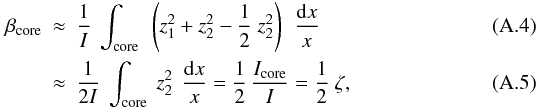 hence
hence
 (A.6)Numerical
values for model M1 confirm that βcore increases linearly
with ζ with a slope 1/2 (Fig. A.2). For g-m modes (ζ ~ 1),
βcore dominates with a nearly constant value of 0.5. P-m
modes correspond to the teeth of the saw-type variation in
βenv and the ratio
βenv/βcore ~ 0.25
(Fig. A.2).
(A.6)Numerical
values for model M1 confirm that βcore increases linearly
with ζ with a slope 1/2 (Fig. A.2). For g-m modes (ζ ~ 1),
βcore dominates with a nearly constant value of 0.5. P-m
modes correspond to the teeth of the saw-type variation in
βenv and the ratio
βenv/βcore ~ 0.25
(Fig. A.2).
 |
Fig. A.2
Top: βenv and βcore as a function of ν/Δν for model M1. Bottom: same as top for the ratio βcore as a function of ζ (black open dots). The approximation β = 1 − (1/2) ζ using the numerical values of ζ is represented with red crosses. |
| Open with DEXTER | |
A.3. An approximate expression for ζ
This section determines an approximate expression of ζ = Icore/I as a function of ν/Δν. The derivation is based on results of an asymptotic method developed by Shibahashi (1979) to which we refer for details (see also Unno et al. 1989).
-
The envelope (~p-propagative cavity) is characterized by
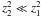 . Using
Eq. (16.47) from Unno et al., it is straightforward to derive the following
approximate expression
. Using
Eq. (16.47) from Unno et al., it is straightforward to derive the following
approximate expression 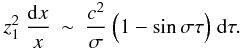 (A.7)The
constant c can be determined by the condition
ξr = 1 at the surface.
(A.7)The
constant c can be determined by the condition
ξr = 1 at the surface.
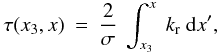 (A.8)with
(A.8)with
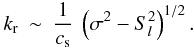 (A.9)where
we have assumed σ2 ≫ N2
in Eq. (27). In the process of
deriving the amplitude of
(A.9)where
we have assumed σ2 ≫ N2
in Eq. (27). In the process of
deriving the amplitude of 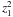 arising
in front of the sinusoidal term in Eq. (A.7), one can neglect
arising
in front of the sinusoidal term in Eq. (A.7), one can neglect 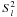 in
front of σ2 in the expression for
kr (i.e.
kr ~ σ/cs).
However this is not the case when kr is in the phase
of the sinusoidal term where we keep the expression Eq. (A.9). The inertia in the envelope
can then be approximated as
in
front of σ2 in the expression for
kr (i.e.
kr ~ σ/cs).
However this is not the case when kr is in the phase
of the sinusoidal term where we keep the expression Eq. (A.9). The inertia in the envelope
can then be approximated as 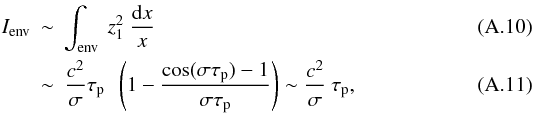 where
we have defined
where
we have defined 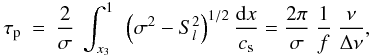 (A.12)and
the mean large separation is
(A.12)and
the mean large separation is
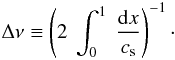 (A.13)The
factor f is of order unity and represents the difference
between the integration from x3 and from the center.
We take f = 1 unless specified otherwise. The last equality in
Eq. (A.10) is obtained
assuming στp ≫ 1.
(A.13)The
factor f is of order unity and represents the difference
between the integration from x3 and from the center.
We take f = 1 unless specified otherwise. The last equality in
Eq. (A.10) is obtained
assuming στp ≫ 1. -
The core (~g-propagative cavity) is characterized by
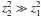 . Again,
the asymptotic results lead to the following expression
. Again,
the asymptotic results lead to the following expression
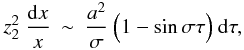 (A.14)where
a is a constant that is determined by the resonant frequency
condition between the p and g cavities, and
(A.14)where
a is a constant that is determined by the resonant frequency
condition between the p and g cavities, and
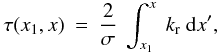 (A.15)and
we have used
(A.15)and
we have used 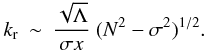 (A.16)Recalling
that στg ≫ 1, therefore the inertia
in the core can be approximated as
(A.16)Recalling
that στg ≫ 1, therefore the inertia
in the core can be approximated as
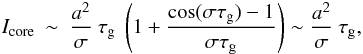 (A.17)where
we have defined
(A.17)where
we have defined 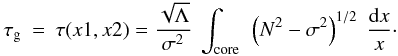 (A.18)
(A.18) -
We obtain the ratio c/a (from Eqs. (16.49) and (16.50) of Unno et al.) as
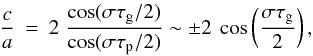 (A.20)where
we have used
στp ~ 2npπ.
A exponential term is present in the Unno et al expression with the argument
being an integral over the evanescent region between the p- and g-cavities. As
this region is quite narrow in our models for the considered modes, the
exponential is taken to be 1. Nevertheless the width of the evanescent region
depends on the considered mode, and in some cases, for accurate quantitative
results, it might be necessary to include effects of the evanescent zone with a
finite width.
(A.20)where
we have used
στp ~ 2npπ.
A exponential term is present in the Unno et al expression with the argument
being an integral over the evanescent region between the p- and g-cavities. As
this region is quite narrow in our models for the considered modes, the
exponential is taken to be 1. Nevertheless the width of the evanescent region
depends on the considered mode, and in some cases, for accurate quantitative
results, it might be necessary to include effects of the evanescent zone with a
finite width. -
We now use the approximate expressions Eqs. (A.12) and (A.18) in order to derive for the ratio τp/τg in terms of observable quantities
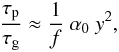 (A.23)where
for convenience we have defined
y = ν/Δν,
and
(A.23)where
for convenience we have defined
y = ν/Δν,
and 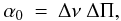 (A.24)with
the period spacing for g modes
(A.24)with
the period spacing for g modes
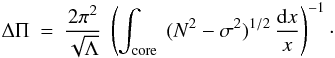 (A.25)We
also write
(A.25)We
also write 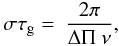 (A.26)so that we
obtain
(A.26)so that we
obtain 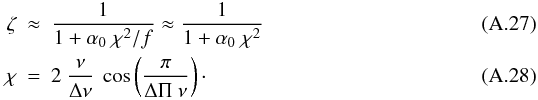
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.