| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219765 | |
| Published online | 25 October 2012 | |
Online material
Appendix A: V, (V – I) CMD
A colour–magnitude diagram allows an estimate of the dereddened magnitude and colour of the target, by comparison with the observed position of the RGC, if one assumes that both suffer the same amount of extinction. We retrieved stars within 2′ of the target in the OGLE-III photometric catalogue of field BLG 101.3, and constructed the calibrated CMD shown in Fig. A.1 (Szymański et al. 2011). From it, we measured the RGC centroid position, which is IRC = 15.940 ± 0.010 and (V − I)RC = 2.385 ± 0.005, and relative shifts in magnitude and colour of the three stars close to the target position, for which we found the values given in the last two columns of Table 2.
 |
Fig. A.1
Colour–magnitude diagram in I and V from calibrated OGLE-III photometry. The superimposed histograms show the position of the centroid of the RGC. |
| Open with DEXTER | |
Unlike in previous studies, we do not fix the absolute magnitude of the RGC at some standard value, because the population corrections to apply to the well determined local clump position are somewhat uncertain. For instance, Salaris & Girardi (2002) give corrections for Baade’s Window in V varying from 0.06 to 0.21 depending whether one adopts scaled-solar or α-enhanced metallicities. If one also changes the underlying adopted SFR (star formation rate) and AMR (age-metallicity relation), the corrections further vary, as shown in Girardi & Salaris (2001). We prefer using the same isochrone method as in the near-infrared to fit the RGC and giant branch positions. We adopt for this purpose the Marigo et al. (2008) set of isochrones, as given on their web site2.
Our parameters are now the extinction E(V − I) and the total-to-selective absorption ratio RI. An acceptable fit is shown in Fig. A.2. It uses E(V − I) = 1.30 and RI = 1.11. The first value is in good agreement with a similar determination at the target position in the OGLE-II BUL_SC3 field as reported by Sumi (2004), namely E(V − I) = 1.336. The agreement is not expected to be perfect, first because the OGLE-III transmission curves in I and V differ slightly from those of OGLE-II, and second because Sumi assumes an RGC intrinsic colour of 1.028, slightly different from the value we obtain. The second value is larger than the mean value adopted by Sumi (2004), which is 0.964, but in good agreement with an independent determination based on the recently released OGLE-III photometric catalogue of the Galactic bulge, which gives an average value of RI = 1.22 (Nataf et al. 2012). All these values are clearly lower than the standard value of this ratio, which is 1.5, justifying the so-called anomalous extinction law generally invoked when dealing with the Galactic bulge (see, e.g. Udalski 2003).
 |
Fig. A.2
The V and I colour–magnitude diagram similar to Fig. 3, but now with superimposed isochrones from Marigo et al. (2008) for solar metallicity and three different ages: 0.6 Gyr (blue), 5 Gyr (red) and 10 Gyr (green), assuming a distance modulus of 14.6, an extinction E(V − I) = 1.30 and RI = 1.11. The black star symbol marks the position of the source. |
| Open with DEXTER | |
From the adopted values of these two parameters, we derive absorption values for the field of AI = 1.44 and AV = 2.74. For the measured position of the RGC and our adopted distance modulus, the mean absolute magnitudes of the RGC are found to be MI = − 0.10 and MV = 0.98. The standard values for the RGC colour and magnitude adopted in Nataf et al. (2012) are (V − I)° = 1.06 ± 0.12 and MI = − 0.12 ± 0.09, in good agreement with our derivation.
Assuming once more that the source suffers the same amount of extinction as the RGC, and using the shifts in magnitude and colour listed in Table 2, the source is predicted to have 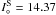 and (V − I)°S = 0.82. Using the previously derived values of the near-infared magnitudes of the source, we get a colour (V − K)° = 1.9. All these colours point to an early G giant spectral type.
and (V − I)°S = 0.82. Using the previously derived values of the near-infared magnitudes of the source, we get a colour (V − K)° = 1.9. All these colours point to an early G giant spectral type.
From the adopted dereddened magnitudes and colours, and using the revision of the surface brightness-colour relations in I°, (V − I)° published by Kervella & Fouqué (2008), we get an estimate of the angular source radius θ∗ in μas of 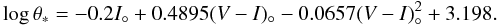 (A.1)The uncertainty of this estimate is 0.0238, so adding quadratically the uncertainty in magnitude (0.1) and colour (0.05) to this gives an accuracy of 9% on θ∗, i.e., θ∗ = 4.8 ± 0.4 μas. This confirms the previous result derived from the V°, (V − K)° surface brightness-colour relation.
(A.1)The uncertainty of this estimate is 0.0238, so adding quadratically the uncertainty in magnitude (0.1) and colour (0.05) to this gives an accuracy of 9% on θ∗, i.e., θ∗ = 4.8 ± 0.4 μas. This confirms the previous result derived from the V°, (V − K)° surface brightness-colour relation.
Note that, for this colour determination, we assumed that the star, OGLE-III-BLG-101.3 159762 in Table 2, is the source star. But in the MOA frames, the three stars in Table 2 are not fully resolved. The two OGLE stars close to the source, 160107 and 160108, can therefore contribute a blend flux in our models. In microlensing modelling we have to take this blend flux into account. Had we obtained calibrated data, we
could have predicted the blend and source fluxes using our models. Unfortunately, the reduction we used for our modelling is not calibrated. We therefore used the original reduction of MOA data, which is calibrated but of lower quality, to estimate the blend properties. We found that the colour and magnitude of this blend corresponds to the sum of the fluxes of the 160107 and the 160108 stars. This means that our identification of the three OGLE stars was correct. In any case, future adaptive optics observations would be useful to confirm our conclusions.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


