| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A190 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202347014 | |
| Published online | 24 October 2023 | |
Brown dwarf companions in binaries detected in the 2021 season high-cadence microlensing surveys
1
Department of Physics, Chungbuk National University, Cheongju 28644, Republic of Korea
e-mail: cheongho@astroph.chungbuk.ac.kr
2
Korea Astronomy and Space Science Institute, Daejon 34055, Republic of Korea
3
Korea University of Science and Technology (UST), 217 Gajeong-ro, Yuseong-gu, Daejeon 34113, Republic of Korea
4
Institute of Natural and Mathematical Science, Massey University, Auckland 0745, New Zealand
5
Center for Astrophysics | Harvard & Smithsonian, 60 Garden St., Cambridge, MA 02138, USA
6
University of Canterbury, Department of Physics and Astronomy, Private Bag 4800, Christchurch 8020, New Zealand
7
Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
8
Department of Astronomy, Ohio State University, 140 W. 18th Ave., Columbus, OH 43210, USA
9
Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Rehovot 76100, Israel
10
Department of Astronomy, Tsinghua University, Beijing 100084, PR China
11
School of Space Research, Kyung Hee University, Yongin, Kyeonggi 17104, Republic of Korea
12
Institute for Space-Earth Environmental Research, Nagoya University, Nagoya 464-8601, Japan
13
Code 667, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
14
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
15
Komaba Institute for Science, The University of Tokyo, 3-8-1 Komaba, Meguro, Tokyo 153-8902, Japan
16
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
17
Department of Earth and Space Science, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan
18
Institute of Astronomy, Graduate School of Science, The University of Tokyo, 2-21-1 Osawa, Mitaka, Tokyo 181-0015, Japan
19
Department of Physics, The Catholic University of America, Washington, DC 20064, USA
20
Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, 3-1-1 Yoshinodai, Chuo, Sagamihara, Kanagawa 252-5210, Japan
21
Sorbonne Université, CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98 bis bd Arago, 75014 Paris, France
22
Department of Physics, University of Auckland, Private Bag 92019, Auckland, New Zealand
23
University of Canterbury Mt. John Observatory, PO Box 56 Lake Tekapo 8770, New Zealand
Received:
26
May
2023
Accepted:
10
July
2023
Aims. As a part of the project aiming to build a homogeneous sample of binary-lens (2L1S) events containing brown dwarf (BD) companions, we investigate the 2021 season microlensing data collected by the Korea Microlensing Telescope Network (KMTNet) survey.
Methods. For this purpose, we first identified 2L1S events by conducting systematic analyses of anomalous lensing events. We then selected candidate BD companion events by applying the criterion that the mass ratio of the lens components is lower than qth ∼ 0.1.
Results. From this procedure, we find four events including KMT-2021-BLG-0588, KMT-2021-BLG-1110, KMT-2021-BLG-1643, and KMT-2021-BLG-1770, for which the estimated mass ratios are q ∼ 0.10, 0.07, 0.08, and 0.15, respectively. Event KMT-2021-BLG-1770 was selected as a candidate even though the mass ratio is slightly greater than qth because the lens mass expected from the measured short timescale of the event, tE ∼ 7.6 days, is low. From the Bayesian analyses, we estimate that the primary and companion masses are (M1/M⊙,M2/M⊙) = (0.54−0.24+0.31, 0.053−0.023+0.031) for KMT-2021-BLG-0588L, (0.74−0.35+0.27, 0.055−0.026+0.020) for KMT-2021-BLG-1110L, (0.73−0.17+0.24,0.061−0.014+0.020) for KMT-2021-BLG-1643L, and (0.13−0.07+0.18, 0.020−0.011+0.028) for KMT-2021-BLG-1770L. It is estimated that the probabilities that the lens companions are in the BD mass range are 82%, 85%, 91%, and 59% for the individual events. To confirm the BD nature of the lens companions found in this and previous works by directly imaging the lenses from future high-resolution adaptive-optics (AO) followup observations, we provide the lens-source separations expected in 2030, which is the approximate year of the first AO light on 30 m class telescopes.
Key words: gravitational lensing: micro
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Because it does not depend on the light of a lens, microlensing is suited for finding and studying faint and dark astronomical objects. One scientifically important object to which this microlensing trait has been successfully applied is an extrasolar planet. With the proposals of Mao & Paczyński (1991) and Gould & Loeb (1992), extensive searches for extrasolar planets using the microlensing method have been carried out since the 1990s. Starting with the first discovery of a giant planet in 2003 by Bond et al. (2004), 200 microlensing planets have been reported according to the NASA Exoplanet Archive1, which means that the third most planets are detected through microlensing, after the transit and radial velocity methods.
Brown dwarfs (BDs) are another population of astronomical objects that are well suited for detections with microlensing. Microlensing BDs can be detected through two channels. The first channel is via a single-lens single-source (1L1S) event with a short timescale tE. The event times is related to the lens mass M as
and thus short-timescale events may be produced by BDs with masses lower than those of stars. Here θE represents the angular Einstein radius, μ is the relative lens-source proper motion, κ = 4G/(c2AU), 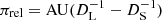 is the relative lens-source parallax, and DL and DS denote the distances to the lens and source, respectively. However, it is difficult to confirm the BD nature of a lens based on the event timescale alone because the timescale additionally depends on μ and πrel. The mass and distance to the lens can be unambiguously determined by measuring the additional observables of the Einstein radius θE and the microlens parallax πE from the relations
is the relative lens-source parallax, and DL and DS denote the distances to the lens and source, respectively. However, it is difficult to confirm the BD nature of a lens based on the event timescale alone because the timescale additionally depends on μ and πrel. The mass and distance to the lens can be unambiguously determined by measuring the additional observables of the Einstein radius θE and the microlens parallax πE from the relations
The microlens parallax is related to the relative lens-source parallax and Einstein radius by πE = πrel/θE (Gould 1992, 2000). For a 1L1S event, the probability of measuring the angular Einstein radius is very low because θE can be measured for only a very minor fraction of events in which the lens passes over the surface of the source, for example, the 1L1S events presented in Han et al. (2020), Gould et al. (2022b), and Koshimoto et al. (2023). The probability of measuring the microlens parallax, which is generally measured from the deviation of the lensing light curve caused by the departure of the relative lens-source motion from rectilinear induced by the orbital motion of Earth, is even lower because the parallax-induced deviation in the lensing light curve is generally too small to be measured for a short-timescale BD event. The microlens parallax for a short-timescale event can be measured under special observational environments, and only in three cases was the nature of the single BD lens confirmed from the mass determination by measuring the microlens parallax. The first case is OGLE-2007-BLG-224, for which πE was measured from the subtle differences among the light curves constructed from observations using telescopes stationed at multiple sites on Earth when the magnifications of the event were extremely high (Gould et al. 2009). For the other two cases of OGLE-2015-BLG-1268 (Zhu et al. 2016) and OGLE-2017-BLG-0896 (Shvartzvald et al. 2019), πE values were measured from simultaneous observations of the events using ground-based telescopes and the space-based Spitzer satellite. In the case of OGLE-2015-BLG-1482 (Chung et al. 2017), which was also simultaneously observed using the Spitzer and ground-based telescopes, the light curve was almost equally well explained by two solutions, in which the lens was a very low-mass star with a mass 0.10 ± 0.02 M⊙ according to one solution, and the lens is a BD with a mass 0.052 ± 0.008 MJ according to the other solution, and thus the BD nature of the lens could not be confirmed.
Another channel of detecting microlensing BDs is via a binary-lens single-source (2L1S) event. Compared to a 1L1S event, the analysis of a 2L1S event yields an additional constraint of the companion-to-primary mass ratio q. This constraint can be used to select candidate BD companions of binary lenses based on the fact that typical Galactic lensing events are produced by low-mass stars (Han & Gould 2003), and thus companions with mass ratios q ≲ 0.1 are very likely to be BDs. Furthermore, the probability of measuring the Einstein radii for these events is high because the light curves of these events usually exhibit anomaly features resulting from source crossings over or approaches very close to caustics. In these cases, the light curves are likely to be affected by finite-source effects, from which θE can be measured and the lens mass can be further constrained.
In order to find BDs through the second channel, Han et al. (2022), hereafter Paper I, investigated the microlensing data collected during the 2016–2018 period by the high-cadence surveys and reported six binaries with candidate BD companions, that is, OGLE-2016-BLG-0890LB, MOA-2017-BLG-477LB, OGLE-2017-BLG-0614LB, KMT-2018-BLG-0357LB, OGLE-2018-BLG-1489LB, and OGLE-2018-BLG-0360LB. From continued analyses of the lensing events found during the 2018–2020 period, Han et al. (2023), hereafter Paper II, reported another four binaries with candidate BD companions, that is, KMT-2018-BLG-0321LB, KMT-2018-BLG-0885LB, KMT-2019-BLG-0297LB, and KMT-2019-BLG-0335LB.
In this work, we report four additional candidate BD companions to binary lenses found from the inspection of the 2021 season microlensing data, which are KMT-2021-BLG-0588LB, KMT-2021-BLG-1110LB, KMT-2021-BLG-1643LB, and KMT-2021-BLG-1770LB. The main scientific purpose of this and previous works is building a homogeneous sample of 2L1S events containing BD companions found from the KMTNet survey by applying a consistent criterion. The sample will be useful for future statistical analyses of BDs, such as the distribution of mass ratios and separations, and the occurrence rate of star-BD binary pairs.
To present the findings and analyses of the BD events, we organize the paper as follows. In Sect. 2 we describe the procedure of selecting candidate events produced by binary lenses possessing BD companions. In Sect. 3 we describe the data used in the analyses and the observations carried out to obtain the data. In Sect. 4 we start by explaining the common procedure applied to analyze the events and detail the analyses of the individual events in the following subsections: KMT-2021-BLG-0588L in Sect. 4.1, KMT-2021-BLG-1110L in Sect. 4.2, KMT-2021-BLG-1643L in Sect. 4.3, and KMT-2021-BLG-1770L in Sect. 4.4. In Sect. 5 we describe the procedure of specifying the source stars and estimate the Einstein radii of the individual events. In Sect. 6 we explain the Bayesian analyses we conducted to estimate the physical lens parameters of the events and present the obtained parameters. In Sect. 7 we summarize the results from the analyses and discuss future followup observations that can confirm the BD natures of the lens companions reported in this work and those found from the previous analyses in Papers I and II.
2. Selections of BD candidates
The binary-lens events with BD companions were found by inspecting the microlensing events that were discovered in the 2021 season by the Korea Microlensing Telescope Network (KMTNet; Kim et al. 2016) survey. For a 2L1S event that includes a planetary lens companion, with a companion-to-primary mass ratio of about 10−3 or lower, the signal of the companion can in general be readily identified from its characteristic short-term anomaly feature in the lensing light curve (Gould & Loeb 1992). For a 2L1S event with a BD companion that has a mass ratio of about 10−2, however, it is difficult to promptly identify the BD nature of the companion because the lensing light curves in many cases are similar to those produced by binary lenses with approximately equal-mass components. In the searches for BD companions in binary lenses, we therefore conducted systematic analyses of all anomalous lensing events detected by the KMTNet survey.
We selected events with BD companions by imposing the criterion of q ≲ 0.1 among the 2L1S events identified from the first-round analyses. We note that the criterion is the same as the criterion that was adopted in Papers I and II, and thus the BD events presented in this and previous works constitute a uniform sample. From this procedure, we identified four candidate BD companion events, KMT-2021-BLG-0588, KMT-2021-BLG-1110, KMT-2021-BLG-1643, and KMT-2021-BLG-1770. In Table 1 we list the equatorial coordinates, (RA, Dec)J2000, of the individual events together with the corresponding Galactic coordinates, (l, b), and I-band extinction, AI, toward the field. Here the extinction values were adopted from the OGLE Internet archive (Nataf et al. 2013)2. The event KMT-2021-BLG-1770 was picked out even though the estimated mass ratio of the lens components, q ∼ 0.15, was slightly greater than the adopted threshold mass ratio qth ∼ 0.1, because the mass of the lens expected from the short timescale of the event, tE ∼ 7.6 days, was low, and thus the probability for the mass of the companion to be in the BD mass regime was high. For this reason, this event is not a part of the uniformly selected sample for future statistical studies, although the analysis is presented in this work. For the identified candidate events, we then checked whether the events were additionally observed by other lensing surveys to include the data in the analyses if they exist. We found that KMT-2021-BLG-0588 was additionally observed by the Microlensing Observations in Astrophysics (MOA; Bond et al. 2001) group, who referred to the event as MOA-2021-BLG-139, and the other events were observed solely by the KMTNet group. For KMT-2021-BLG-0588, we use the KMTNet ID reference because the KMTNet group found the event first.
Source positions and extinction.
3. Observations and data
The KMTNet group has carried out a high-cadence survey since 2016 by monitoring stars lying toward the Galactic bulge field in search of light variation of stars that is caused by microlensing. The survey group uses three wide-field telescopes that are distributed in three sites of the Southern Hemisphere for continuous and dense coverage of lensing events. The sites of the individual telescopes are the Siding Spring Observatory in Australia (KMTA), the Cerro Tololo inter-American Observatory in Chile (KMTC), and the South African Astronomical Observatory in South Africa (KMTS). The telescopes are identical, and each telescope with a 1.6 m aperture is equipped with a camera that yields a field of view of 4 deg2. KMTNet observations were mainly conducted in the I band, which is relatively little affected by extinction, and about one-tenth of the images were acquired in the V band for the source color measurements of the lensing events. Photometry of the events was conducted using the automatized pySIS pipeline (Albrow et al. 2009), which is based on the difference-image method (Tomaney & Crotts 1996; Alard & Lupton 1998). For the color measurements of the source stars, we additionally used the pyDIA code (Albrow 2017) to construct a set of the I- and V-band light curves and color-magnitude diagrams (CMDs) of stars that lie in the neighborhoods of the source stars. For the events analyzed in this work, we rereduced the data to obtain optimized photometry data after the events were selected as BD candidates. We normalized the error bars of the data to make them consistent with scatter of data and χ2 per degree of freedom (d.o.f.) for each data set to become unity. In the error-bar normalization process, we used the routine described in Yee et al. (2012).
Of the four analyzed events, the lensing event KMT-2021-BLG-0588 was additionally observed by the MOA survey. The observations of the event by the MOA survey were made with the use of the 1.8 m telescope of the Mt. John Observatory in New Zealand. The camera mounted on the telescope yields a field of view of 2.2 deg2. The MOA observations were mostly conducted in the customized MOA-R band, and the photometry was made using the MOA pipeline. The MOA data set was normalized using the same routine as was applied to the KMTNet data sets.
4. Analyses
The events were analyzed under the common interpretation of the lens-system configuration that the lenses are binaries because the light curves of all events exhibit caustic features that arise due to the multiplicity of the lens masses. Under the assumption of a rectilinear relative lens-source motion, the lensing light curve of a 2L1S event is described by seven basic lensing parameters. The first three of these parameters (t0, u0, tE) describe the lens-source approach, and the individual parameters represent the time of the closest lens-source approach, the lens-source separation at t0, and the event timescale, respectively. Another three parameters (s, q, α) describe the binarity of the lens, and the individual parameters describe the projected separation (scaled to θE) and mass ratio of the lens components, and the angle between the source trajectory and the axis connecting the binary lens components. The last parameter ρ represents the ratio of the angular source radius θ* to the Einstein radius, ρ = θ*/θE (normalized source radius), and it describes the deformation of the light curve during the caustic crossings of a source caused by finite-source effects.
A 2L1S lensing light curve can deviate from the standard form due to the departure of the relative lens-source motion from rectilinear. The first cause of this deviation is the microlens-parallax effects, which are caused by the positional change of the observer by the orbital motion of Earth around the Sun (Gould 1992). The second cause is the lens-orbital effects, which is caused by the change in the lens position by the orbital motion of the binary lens (Dominik 1998). These higher-order effects induce subtle deviations in the lensing light curve from the standard form, and a description of these deviations requires additional lensing parameters in the modeling. We checked these higher-order effects by conducting additional modeling, in which additional parameters were added in the modeling. The two parameters describing the parallax effect are (πE,N, πE,E), which represent the north and east components of the microlens-lens parallax vector πE = (πrel/θE)(μ/μ), respectively. Under the assumption that the positional change of the lens by the orbital motion is minor, the lens-orbital effect is described by two parameters (ds/dt, dα/dt) that denote the annual change rates of the binary separation and source trajectory angle, respectively. It was found that secure detections of the higher-order effects were difficult for KMT-2021-BLG-0588, KMT-2021-BLG-1110, and KMT-2021-BLG-1770, for which the event timescales are shorter than 40 days. For KMT-2021-BLG-1643 with tE ∼ 105 days, the higher-order effects are minor, but the amplitude of the parallax parameters yielded a useful constraint on the physical lens parameters. We refer to Sect. 6 for the detailed discussion of the parallax constraint.
In the 2L1S modeling, we searched for a lensing solution that refers to a set of the lensing parameters that best depict the observed lensing light curve. In the first round of modeling, we divided the lensing parameters into two groups, and found the binary parameters (s, q) of the first group via a grid approach with multiple initial values of α, and the other lensing parameters of the second group were searched for by minimizing χ2 using the Markov chain Monte Carlo (MCMC) method with an adaptive step-size Gaussian sampler (Doran & Mueller 2004). In the second round, we refined the local solutions identified from the first-round modeling by further reducing χ2 value using the MCMC method. We adopted this two-step approach because the change in the lensing magnification with the variation of the grid parameters is discontinuous, while the magnification changes smoothly with the variation of the downhill parameters. Furthermore, the Δχ2 map obtained from the first-round grid search enabled us to identify local solutions that are caused by various types of degeneracy. We considered the limb-darkening variation of the source surface brightness in the computation of finite magnifications by adopting the linear limb-darkening coefficients of Claret (2000), corresponding to the stellar type of the source stars. In the following subsections, we present the detailed analyses conducted for the individual events.
4.1. KMT-2021-BLG-0588
Figure 1 shows the lensing light curve of event KMT-2021-BLG-0588. The source with an I-band baseline magnitude Ibase ∼ 19.11 was in the KMT32 field, toward which observations were conducted with a 2.5 h cadence. The source flux magnification induced by lensing was first found by the KMTNet group on 2021 April 26, which corresponds to the abridged heliocentric Julian date HJD′ ≡ HJD − 2 450 000 = 9331, when the source was brighter than the baseline by ΔI ∼ 0.46 mag. The light curve exhibited a strong anomaly, which peaked at HJD′ ∼ 9354.25 with a strong deviation of ΔI ∼ 3 mag from the baseline 1L1S model. The MOA group independently found the event on 2021 May 22 (HJD′ = 9357), which was about three days after the strong peak. The zoom-in view of the strong peak, which was covered by the combination of the MOA and KMTA data sets, is shown in the top panel of Fig. 1. From the sharp rise and fall, the strong peak is likely to be produced by the source star’s crossing over the tip of a caustic formed by a binary lens.
 |
Fig. 1. Light curve of KMT-2021-BLG-0588. The bottom panel shows the whole view of the light curve, and the upper panels show the zoom-in view of the light curve, models, and residuals in the region around the strong peak. The dotted and solid curves drawn over the data points are the models of the close and wide solutions, respectively. The two insets in the bottom panel show the lens-system configurations of the close and wide models. |
In Table 2 we list the lensing parameters of the solutions found from the 2L1S modeling of the light curve together with the χ2 values of the fits and degrees of freedom (d.o.f.). We identified a pair of local solutions, in which one solution has a binary separation s < 1 (close solution) and the other solution has a separation s > 1 (wide solution). Although the solutions are designated as the “close” and “wide” solutions, we note that the similarity between the model curves of the two solutions is caused by an accidental degeneracy rather than the well-known close–wide degeneracy, which arises due to the similarity between the central caustics induced by a pair of solutions with separations s and 1/s (Griest & Safizadeh 1998; Dominik 1999; An 2005). We further discuss the cause of the degeneracy in the following paragraph. It is found that the wide solution with s ∼ 1.17 yields a better fit than the close solution with s ∼ 0.77 by Δχ2 = 71.8, and thus the degeneracy is resolved with strong statistical confidence.
Model parameters of KMT-2021-BLG-0588.
In Fig. 1 we draw the model curve of the wide solution in the bottom panel, which shows the whole view of the light curve, and plot the models curves and residuals of both the close and wide solutions in the upper panels, which show the zoom-in view of the region around the strong peak. According to the wide solution, the estimated event timescale and the mass ratio of the lens components are tE ∼ 39 days and q ∼ 0.10. Because the timescale is in the range of events produced by stellar lenses and because the mass ratio is low, the probability is high that the binary lens companion is a BD. The normalized source radius, ρ ∼ 0.7 × 10−3, was securely measured from the analysis of the strong peak, which was affected by finite-source effects
The lens-system configurations of the close and wide solutions are presented in the two insets of the bottom panel of Fig. 1. According to the wide solution, the binary lens forms a single six-sided resonant caustic, and the strong peak was produced by the source passage through the tip of the lower left cusp of the caustic. According to the close solution, on the other hand, the lens induces three sets of caustics, in which a single central caustic around the primary lens is detached from the two peripheral caustics, and the strong peak was generated by the source crossing over the slim cusp extending from the lower left cusp of the central caustic. The two sets of caustics of the close and wide solutions do not appear to be similar to each other, and this suggests that the degeneracy between the two solutions is accidental.
4.2. KMT-2021-BLG-1110
We present the light curve of the lensing event KMT-2021-BLG-1110 in Fig. 2. The lensing magnification of the source, which had a baseline magnitude Ibase ∼ 19.52 before lensing, was found by the KMTNet group on 2021 June 2 (HJD′ = 9367), when the source was brighter than the baseline by ΔI ∼ 0.5 mag. The source lies in the overlapping region of the KMTNet prime fields BLG01 and BLG41, toward which observations were made with a 0.5 h cadence for each field and with a 0.25 h cadence in combination. The light curve is characterized by the double spikes appearing at t1 ∼ 9370.85 and t2 ∼ 9371.56. The rising and falling sides of both spikes were densely and continuously resolved from the high-cadence observations conducted with the use of the three KMTNet telescopes. The first spike was resolved by the KMTC data, and the second one was covered by the combined data from KMTS and KMTC.
 |
Fig. 2. Lensing light curve of KMT-2021-BLG-1110. The layout and scheme of the plot are same as those in Fig. 1. |
The spike features are very likely to be produced by the caustic crossings of the source, and thus we modeled the light curve under the 2L1S interpretation. The modeling yielded two local solutions: one solution with s < 1 (close solution), and the other with s > 1 (wide solution). The wide solution is preferred over the close solution by Δχ2 = 33.8, which is large enough to resolve the degeneracy between the solutions. The model curve of the wide solution is drawn in the bottom panel of Fig. 2, and the model curves and residuals of both the close and wide solutions in the region around the two peaks are presented in the upper panels. The similarity between the models of the two solutions is caused by the classic close–wide degeneracy. The lensing parameters of the solutions are listed in Table 3 together with the values of χ2/d.o.f. The binary lensing parameters are (s, q)close ∼ (0.44, 0.07) for the close solution and (s, q)wide ∼ (2.43, 0.07) for the wide solution. Because the estimated mass ratio q ∼ 0.07 of the lens components is low and because the event timescale tE ∼ 27–29 days is a typical value of a stellar lens event, the companion of the lens is a strong BD candidate. The normalized source radius, ρ ∼ 0.79 × 10−3 for the wide solution, is precisely measured from the well-resolved spike features.
Model parameters of KMT-2021-BLG-1110.
In the two insets of the bottom panels of Fig. 2, we present the lens-system configurations of the close and wide solutions. Both solutions result in central caustics of similar shape, in which the caustic is elongated along the binary-lens axis. The source passed through the back-end side of the caustic at an acute source trajectory angle of ∼69° with respect to the binary axis. According to the model, the two spikes were produced by the successive passages of the source through the on-axis cusp and upper off-axis cusp of the caustic.
4.3. KMT-2021-BLG-1643
The lensing light curve of KMT-2021-BLG-1643 is presented in Fig. 3. The event was found in its early stage by the KMTNet survey on 2021 June 8 (HJD′ = 9374), at which time, the source was brighter than the baseline magnitude Ibase = 18.91 by ΔI ∼ 1.2 mag. The source lies in the KMTNet BLG04 field, toward which the event was monitored with a 1 h cadence. The event exhibited a pair of caustic spikes, which occurred at HJD′ ∼ 9401.1 and 9403.4, and a weak bump, which was centered at HJD′ ∼ 9409. The region between the two caustic spikes exhibited a characteristic U-shape pattern, indicating that the spikes occurred when the source entered and exited a caustic. The first caustic spike was not resolved because the sky at the KMTA site was clouded, but the second caustic was partially covered by the two KMTS and one KMTC data points.
 |
Fig. 3. Light curve of the lensing event KMT-2021-BLG-1643. The plot scheme and layout are same as those in Fig. 1. |
From the 2L1S modeling of the light curve, we found a pair of solutions resulting from the close–wide degeneracy. The binary lensing parameters are (s, q)close ∼ (0.69, 0.08) and (s, q)wide ∼ (1.52, 0.08) for the close and wide solutions, respectively. We list the full lensing parameters of the two solutions in Table 4, and the model curves and residuals are presented in Fig. 3. From the comparison of the fits, it is found that the wide solution is preferred over the close solution by Δχ2 = 38.3, indicating that the degeneracy is lifted with a fairly strong confidence level. Even though the caustic exit was partially covered by only a small number data points, the normalized source radius, ρ ∼ 0.3 × 10−3, could be constrained.
Model parameters of KMT-2021-BLG-1643.
The measured event timescale, tE ∼ 105 days, of the event comprises an important portion of a year, and thus it may be possible to constrain the microlens-parallax parameters. We conducted an additional modeling considering the higher-order effects. Figure 4 shows the scatter plot of the points in the MCMC chain on the πE,E–πE,N parameter plane. The improvement of model fit with the inclusion of the higher-order effects is very minor, but the amplitude of the scatter plot provided a constraint on the physical lens parameters.
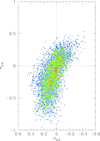 |
Fig. 4. Scatter plot of points in the MCMC chain on the πE,E–πE,N parameter plane obtained from modeling KMT-2021-BLG-1643 considering higher-order effects. The color-coding is set to represent points with Δχ2 ≤ 1 (red), ≤4 (yellow), ≤9 (green), ≤16 (cyan), and ≤25 (blue). |
We present the configurations of the close and wide lens systems in the two insets of the bottom panel of Fig. 3. Similar to the case of KMT-2021-BLG-1110, the source passed the back-end side of the caustic. The spike features were produced by the source passage through the lower left cusp of the caustic, and the weak bump was generated by the source approach close to the left on-axis cusp of the caustic.
4.4. KMT-2021-BLG-1770
Figure 5 shows the light curve of the lensing event KMT-2021-BLG-1770. The event was found by the KMTNet group on 2021 July 16 (HJD′ ∼ 9406). The source, which had a baseline magnitude Ibase = 19.06, was in the KMTNet prime field BLG03, for which images were taken with a 0.5 h cadence. Most region of this field overlaps with the region covered by the BLG43 field, but the event lies in the offset region that was not covered by the BLG43 field. In our analysis, we did not use the KMTA data set due to its low photometric quality. Similar to the event KMT-2021-BLG-1643, the light curve of KMT-2021-BLG-1770 is characterized by a pair of caustic spikes and a following weak bump. The first caustic spike, which occurred at HJD′ = 9412.2, was not covered, but the second spike, which occurred at HJD′ = 9412.4, and the U-shape region between the two spikes were resolved by the combination of the KMTS and KMTC data sets. The weak bump is centered at HJD′ ∼ 9414, which was about two days after the caustic spikes.
 |
Fig. 5. Light curve of KMT-2021-BLG-1770. The scheme and layout of the plot are same as those in Fig. 1. |
From the analyses of the light curve, we identified two local solutions, in which one solution has a binary separation s < 1 (close solution) and the other has a separation s > 1 (wide solution). The model curves of the solutions are drawn over the data points and residuals from the models are shown in Fig. 5. The binary lensing parameters of the individual solutions are (s, q)close ∼ (0.81, 0.15) and (s, q)wide ∼ (1.14, 0.19). We list the full lensing parameter of the models in Table 5. As stated, the event was chosen as a BD candidate even though the mass ratio of the lens components is slightly greater than the threshold mass ratio qth = 0.1 because the event timescale, tE ∼ 7 days, is substantially shorter than several-week time scale of typical lensing events. The normalized source radius, ρ ∼ (6 − 7)×10−3, was measured from analyzing the caustic-exit part of the light curve.
Model parameters of KMT-2021-BLG-1770.
The lens-system configurations of the close and wide solutions are presented in the two insets of the bottom panel of Fig. 5. The configurations of the close and wide solutions are very similar to those of the corresponding solutions of KMT-2021-BLG-0588. That is, the caustic spikes were generated by the passage of the source through the slim bridge part connecting the central and peripheral caustics according to the close solution, and by the source pass through the tip of the lower left cusp of the six-sided resonant caustic according to the wide solution. The difference between the solutions of the two events is that the close solution is preferred over the wide solution by Δχ2 = 8.9 in the case of KMT-2021-BLG-1770, while the wide solution yields a better fit than the close solution in the case of KMT-2021-BLG-0588. For the same reason mentioned in Sect. 4.1, the similarity between the model curves of the close and wide solutions is caused by an accidental degeneracy rather than a close–wide degeneracy.
5. Source stars and Einstein radii
In this section, we specify the source stars of the events. Specifying the source star of a caustic-crossing 2L1S event is important for estimating the angular Einstein radius from the relation
where the normalized source radius ρ is measured by analyzing the caustic-crossing parts of the light curve, and the angular source radius θ* can be deduced from the source type.
We specified the source stars of the individual events by measuring their dereddened colors and magnitudes. To estimate the dereddended color and magnitude, (V − I, I)0, from the instrumental values, (V − I, I)s, we applied the method of Yoo et al. (2004), in which the centroid of a red giant clump (RGC) is used as a reference for the calibration. Following the routine procedure of the method, we first estimated the instrumental I- and V-band magnitudes of the source by regressing the photometry data of the individual passbands processed using the pyDIA code, and placed the source in the instrumental CMD of stars around the source constructed using the same pyDIA code. We then measured the offsets in color and magnitude, Δ(V − I, I), of the source from the RGC centroid, and estimated dereddened color and magnitude as
where (V − I, I)RGC, 0 are the dereddened color and magnitude of the RGC centroid known from Bensby et al. (2013) and Nataf et al. (2013), respectively.
Figure 6 shows the positions of the source (blue dot) and RGC centroid (red dot) in the instrumental CMDs of the individual events. In Table 6 we list the values of (V − I, I)s, (V − I, I)RGC, (V − I, I)RGC, 0, and (V − I, I)s, 0 estimated from the procedure described in the previous paragraph. According to the estimated colors and magnitudes, the spectral types of the source stars are G0V, G9V, K3V, and G9V for KMT-2021-BLG-0588, KMT-2021-BLG-1110, KMT-2021-BLG-1643, and KMT-2021-BLG-1770, respectively. With the measured source color and magnitude, we estimated the angular radius of source star by first converting V − I color into V − K color using the Bessell & Brett (1988) relation, and then by deducing θ* from the Kervella et al. (2004) relation between (V − K, V) and θ*. With the measured source radii, the angular Einstein radii were estimated using the relation in Eq. (3). We list the estimated values of θ* and θE of the individual events in the bottom two lines of Table 6.
 |
Fig. 6. Source positions (blue dots) in the instrumental CMDs of stars lying near the source stars of the individual events. The red and green dots in each panel represent the centroid of the red giant clump and the position of the blend, respectively. |
Source properties and angular Einstein radii.
The positions of the blend (green dots) in the CMDs of the individual events are also marked in Fig. 6. We list the measured values of the color and magnitude of the blend, (V − I, I)b, in Table 6. Besides KMT-2021-BLG-0588, for which the blended light is similar to the flux of the source, the blended fluxes are substantially greater than the source fluxes. In order to determine whether the lens is the main origin of the blended flux, we measured the astrometric offset δθ between the centroid of the source measured at the peak time of the lensing magnification and that measured at the baseline. If the lens were the main origin of the blended flux, the offset would be very small because the relative lens-source proper motions are < 10 mas yr−1 for all events. If the origin of the blended flux were a nearby star, which is typically separated from the source by about 100 mas, the resulting astrometric offset would be substantially greater than the typical astrometric precision of about 10 mas. In Table 7 we list the measured centroid offsets of the individual events. For all events, the astrometric offsets are much greater than the measurement precision, and this indicates that the origins of the blended light are nearby stars rather than the lenses.
Astrometric centroid offsets.
6. Physical lens parameters
The mass M and distance DL to the lens can be constrained by measuring the lensing observables tE, θE, and πE. The event timescale is the basic observable that is measurable for general lensing events, and the angular Einstein radius is another observable that is measurable for events whose light curves are affected by finite-source effects. These two observables are related to the physical lens parameters by the relations in Eq. (1). With the measurement of the additional observable πE, the physical lens parameters would be uniquely determined from the relations in Eq. (2). For the analyzed events, the observables tE and θE were measured, but πE was not securely measured for any of the events. Without the constraint of πE, we estimated the physical lens parameters by conducting Bayesian analyses of the events using models of physical and dynamical distributions and mass function of objects in our Galaxy, together with the constraints provided by the measured blended flux.
In the first step of the Bayesian analysis, we conducted a Monte Carlo simulation to generate a large number of artificial lensing events. For each artificial event, the distances of the lens and source and their relative proper motion were assigned using a Galactic model, and the mass of the lens was assigned using a model mass function. In the simulation, we adopted the Galactic model of Jung et al. (2021) and the mass function model of Jung et al. (2018). In the mass function, we included white dwarf remnants, but excluded black holes and neuron stars. In the second step, we computed the lensing observables (tE, i, θE, i) corresponding to the assigned values (M, DL, DS, μ) of each artificial event using the relations in Eq. (1). In the final step, we constructed Bayesian posteriors of the lens mass and distance by imposing a weight wi = exp(−χ2/2) on each event. Here the χ2 value was calculated as
where [tE, σ(tE)] and [θE, σ(θE)] represent the measured values and uncertainties of the observables tE and θE, respectively. For the event KMT-2021-BLG-1643 with its long event timescale, we imposed the πE constraint by including an additional term 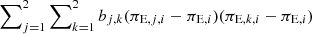 to the right side of Eq. (5).
to the right side of Eq. (5).
In addition to the constraints from the lensing observables, we imposed the blending constraint in the Bayesian analyses. This constraint is provided by the fact that the flux from the lens comprises a portion of the total blending flux, and thus the lens flux should be lower than the total blending flux. To impose this constraint, we calculated the lens brightness as
where MI, L denotes the absolute I-band magnitude corresponding to the lens mass, and AI, L is the extinction to the lens lying at a distance DL. The extinction was modeled as
where AI, tot denotes the total extinction toward the field, hz, dust = 100 pc is the adopted vertical scale height of dust, z = DL sin b + z0 and z0 = 15 pc represent the vertical positions of the lens and the Sun above the Galactic plane, respectively. The values AI, tot for the individual events are listed in Table 1. The blending constraint had strong effects on the determined physical parameters of events KMT-2012-BLG-0558 and KMT-2021-BLG-1643, for which the lenses are expected to be located relatively nearby to the Sun based on their large Einstein radii. Below, we discuss this issue in more detail.
In Figs. 7 and 8, we present the Bayesian posteriors of the mass of the binary lens companion and distance to the lens system, respectively. The estimated values of the primary (M1) and companion (M2) masses, distance, and projected separation between the lens components (a⊥ = sθEDL) are listed in Table 8. For each parameter, the median value was adopted as a representative value and the upper and lower ranges of the uncertainty were chosen as the 16% and 84% of the posterior distribution, respectively. Based on the estimated masses, the masses of the lens companions are well within the BD mass range 0.012 < M2/M⊙ ≤ 0.076 (or 13 < M2/MJ ≤ 80), although there is some variation in the primary masses, which lie in the mass range of main-sequence stars with spectral types from K to M. In Table 9 we list the probabilities for the companions of the individual lenses in the BD mass range, PBD. The probabilities are greater than 59% in all cases. For KMT-2021-BLG-1770L, the mass of the primary is so low that it can be a BD as well with a probability of PBD ∼ 35%. In this case, the lens is a BD binary like OGLE-2009-BLG-151L, OGLE-2011-BLG-0420L (Choi et al. 2013), OGLE-2016-BLG-1266L (Albrow et al. 2018), OGLE-2016-BLG-1469L (Han et al. 2017), MOA-2016-BLG-231L (Chung et al. 2019), and OGLE-2017-BLG-1038L (Malpas et al. 2022).
 |
Fig. 7. Bayesian posteriors for the companion mass of the lens. In each panel, the two vertical solid lines represent the mass range of the brown dwarf. The blue and red curves indicate the contributions by the disk and bulge lens populations, respectively. |
 |
Fig. 8. Bayesian posteriors for the distance to the lens. The layouts of the plots are same as those in Fig. 7. |
Physical lens parameters.
In Table 9 we list the probabilities that the lenses are in the disk, Pdisk, and bulge, Pbulge. For events KMT-2021-BLG-0588 and KMT-2021-BLG-1643, it is very likely that the lenses lie in the disk, while the lens of KMT-2021-BLG-1770 is likely to lie in the bulge. For KMT-2021-BLG-1110, on the other hand, the disk and bulge probabilities are approximately the same. The constraint on the lens location comes mainly from the estimated radius of the Einstein ring. For events KMT-2021-BLG-0588 and KMT-2021-BLG-1643, the respective Einstein radii are θE ∼ 0.90 mas and ∼1.08 mas, which are approximately two times larger than the typical Einstein radius of ∼0.5 mas for the event produced by a low-mass stellar lens with a mass M ∼ 0.3 M⊙ lying about halfway between the Sun and a bulge source. By contrast, the Einstein radius θE ∼ 0.16 mas of KMT-2022-BLG-1770 is substantially smaller than the typical value, and thus Pbulge is substantially higher than Pdisk. The Einstein radius θE ∼ 0.58 mas of KMT-2021-BLG-1110 is close to the typical value, and thus Pdisk and Pbulge are approximately the same. In the posterior distributions presented in Figs. 7 and 8, we mark the contributions of the disk and bulge lens populations by blue and red curves, respectively.
Brown dwarf, disk, and bulge lens probabilities.
7. Summary and discussion
Following the works in Papers I and II, we reported the BD companions in binary lenses found from inspecting the microlensing data collected in the 2021 season by the high-cadence surveys, that is, KMT-2021-BLG-0588LB, KMT-2021-BLG-1110LB, KMT-2021-BLG-1643LB, and KMT-2021-BLG-1770LB. Modeling the light curve of each event yielded a pair of solutions with projected separations smaller and greater than the Einstein radius, but the degeneracy between the solutions was resolved with a strong confidence level except for KMT-2021-BLG-1770, for which the resolution of the degeneracy was less clear than for the others. From the Bayesian analyses conducted with the constraints provided by the observables of the event timescale and Einstein radius together with the constraint from the blended light, it was estimated that the masses of the primary and companion of the individual events are 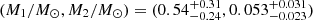 for KMT-2021-BLG-0588L,
for KMT-2021-BLG-0588L, 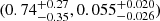 for KMT-2021-BLG-1110L,
for KMT-2021-BLG-1110L, 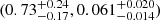 for KMT-2021-BLG-1643L, and
for KMT-2021-BLG-1643L, and 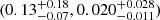 for KMT-2021-BLG-1770L. The estimated masses of the binary companions were well within the BD mass range, although there was some variation in the primary masses, which were in the mass range of main-sequence stars with spectral types from K to M. The probabilities that the lens companions were in the BD mass range were estimated as 82%, 85%, 91%, and 59% for the individual events.
for KMT-2021-BLG-1770L. The estimated masses of the binary companions were well within the BD mass range, although there was some variation in the primary masses, which were in the mass range of main-sequence stars with spectral types from K to M. The probabilities that the lens companions were in the BD mass range were estimated as 82%, 85%, 91%, and 59% for the individual events.
The BD nature of the lens companions presented in this work and Papers I and II can be confirmed by directly imaging the lenses from future high-resolution adaptive-optics (AO) follow-up observations when the lenses are separated from the source stars (Gould et al. 2022a). For these follow-up observations, we compute the lens-source separations Δθ2030 expected in 2030, which is the approximate year of the first AO light on 30 m class telescopes. In Table 10 we list the relative lens-source proper motions, expected lens-source separations, and K-band source magnitudes of the BD events reported in this work and in Papers I and II. The K-band source magnitude was estimated as K = Is, 0 + (V − I)0 − (V − K)0 + AI/7, and the separation is estimated as Δθ2030 = μΔt, where the relative lens-source proper motion is computed by μ = θE/tE and Δt indicates the time gap between the peak of the event and the year 2030. We note that Δθ2030 of the event OGLE-2017-BLG-0614 is not listed because the Einstein radius and the resulting proper motion could not be measured, and only the lower limits are listed for KMT-2018-BLG-0321 and KMT-2018-BLG-0885 because only the lower limits of θE were constrained for these events. The table shows that the separations are greater than 30 mas for all events with measured proper motions, and except for the two events KMT-2019-BLG-0335 and KMT-2021-BLG-1643, for which the separations are greater than ∼50 mas, which will be adequate for the clear resolution of the lens from the source. By comparing the relative lens-source proper motion estimated from the model with the value measured from follow-up AO observations, the solution can be confirmed. Furthermore, from the stellar type of the primary lens, which comprises most of the flux from the lens, the approximate mass of the lens can be estimated. Together with the estimated mass ratio, this enables us to confirm the BD nature of the lens companion. We note that this test of presented solutions will be most useful for events with a relative accuracy of the relative proper motion better than 10%.
Relative proper motion, angular separation in 2030, and K-band source magnitude.
Acknowledgments
Work by C.H. was supported by the grants of National Research Foundation of Korea (2019R1A2C2085965). This research has made use of the KMTNet system operated by the Korea Astronomy and Space Science Institute (KASI) at three host sites of CTIO in Chile, SAAO in South Africa, and SSO in Australia. Data transfer from the host site to KASI was supported by the Korea Research Environment Open NETwork (KREONET). This research was supported by the Korea Astronomy and Space Science Institute under the R&D program (Project No. 2023-1-832-03) supervised by the Ministry of Science and ICT. The MOA project is supported by JSPS KAKENHI Grant Number JP24253004, JP26247023, JP23340064, JP15H00781, JP16H06287, JP17H02871 and JP22H00153. J.C.Y., I.G.S., and S.J.C. acknowledge support from NSF Grant No. AST-2108414. Y.S. acknowledges support from BSF Grant No 2020740.
References
- Alard, C., & Lupton, R. H. 1998, ApJ, 503, 325 [Google Scholar]
- Albrow, M. 2017, https://doi.org/10.5281/zenodo.268049 [Google Scholar]
- Albrow, M., Horne, K., Bramich, D. M., et al. 2009, MNRAS, 397, 2099 [Google Scholar]
- Albrow, M. D., Yee, J. C., Udalski, A., et al. 2018, ApJ, 858, 107 [NASA ADS] [CrossRef] [Google Scholar]
- An, J. H. 2005, MNRAS, 356, 1409 [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [Google Scholar]
- Bond, I. A., Udalski, A., Jaroszyński, M., et al. 2004, ApJ, 606, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J.-Y., Han, C., Udalski, A., et al. 2013, ApJ, 768, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, S.-J., Zhu, W., Udalski, A., et al. 2017, ApJ, 838, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, S.-J., Gould, A., Skowron, J., et al. 2019, ApJ, 871, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Dominik, M. 1998, A&A, 329, 361 [NASA ADS] [Google Scholar]
- Dominik, M. 1999, A&A, 349, 108 [NASA ADS] [Google Scholar]
- Doran, M., & Mueller, C. M. 2004, JCAP, 09, 003 [CrossRef] [Google Scholar]
- Gould, A. 1992, ApJ, 392, 442 [Google Scholar]
- Gould, A. 2000, ApJ, 542, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., & Loeb, A. 1992, ApJ, 396, 104 [Google Scholar]
- Gould, A., Udalski, A., Monard, B., et al. 2009, ApJ, 698, L147 [Google Scholar]
- Gould, A., Jung, Y. K., Hwang, K.-H., et al. 2022a, JKAS, 55, 173 [NASA ADS] [Google Scholar]
- Gould, A., Han, C., Zang, W., et al. 2022b, A&A, 664, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griest, K., & Safizadeh, N. 1998, ApJ, 500, 37 [Google Scholar]
- Han, C., & Gould, A. 2003, ApJ, 592, 172 [Google Scholar]
- Han, C., Udalski, A., Sumi, T., et al. 2017, ApJ, 843, 59 [Google Scholar]
- Han, C., Lee, C.-U., Udalski, A., et al. 2020, AJ, 159, 134 [CrossRef] [Google Scholar]
- Han, C., Ryu, Y.-H., Shin, I.-G., et al. 2022, A&A, 667, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, C., Jung, Y. K., Kim, D., et al. 2023, A&A, 675, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jung, Y. K., Udalski, A., Gould, A., et al. 2018, AJ, 155, 219 [Google Scholar]
- Jung, Y. K., Han, C., Udalski, A., et al. 2021, AJ, 161, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 29 [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, JKAS, 49, 37 [Google Scholar]
- Koshimoto, N., Sumi, T., Bennett, D. P., et al. 2023, AJ, 166, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Malpas, A., Albrow, M. D., Yee, J. C., et al. 2022, AJ, 164, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S., & Paczyński, B. 1991, ApJ, 374, L37 [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [Google Scholar]
- Shvartzvald, Y., Yee, J. C., Skowron, J., et al. 2019, AJ, 157, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Tomaney, A. B., & Crotts, A. P. S. 1996, AJ, 112, 2872 [Google Scholar]
- Yee, J. C., Shvartzvald, Y., Gal-Yam, A., et al. 2012, ApJ, 755, 102 [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
- Zhu, W., Calchi Novati, S., Gould, A., et al. 2016, ApJ, 825, 60 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Relative proper motion, angular separation in 2030, and K-band source magnitude.
All Figures
 |
Fig. 1. Light curve of KMT-2021-BLG-0588. The bottom panel shows the whole view of the light curve, and the upper panels show the zoom-in view of the light curve, models, and residuals in the region around the strong peak. The dotted and solid curves drawn over the data points are the models of the close and wide solutions, respectively. The two insets in the bottom panel show the lens-system configurations of the close and wide models. |
| In the text | |
 |
Fig. 2. Lensing light curve of KMT-2021-BLG-1110. The layout and scheme of the plot are same as those in Fig. 1. |
| In the text | |
 |
Fig. 3. Light curve of the lensing event KMT-2021-BLG-1643. The plot scheme and layout are same as those in Fig. 1. |
| In the text | |
 |
Fig. 4. Scatter plot of points in the MCMC chain on the πE,E–πE,N parameter plane obtained from modeling KMT-2021-BLG-1643 considering higher-order effects. The color-coding is set to represent points with Δχ2 ≤ 1 (red), ≤4 (yellow), ≤9 (green), ≤16 (cyan), and ≤25 (blue). |
| In the text | |
 |
Fig. 5. Light curve of KMT-2021-BLG-1770. The scheme and layout of the plot are same as those in Fig. 1. |
| In the text | |
 |
Fig. 6. Source positions (blue dots) in the instrumental CMDs of stars lying near the source stars of the individual events. The red and green dots in each panel represent the centroid of the red giant clump and the position of the blend, respectively. |
| In the text | |
 |
Fig. 7. Bayesian posteriors for the companion mass of the lens. In each panel, the two vertical solid lines represent the mass range of the brown dwarf. The blue and red curves indicate the contributions by the disk and bulge lens populations, respectively. |
| In the text | |
 |
Fig. 8. Bayesian posteriors for the distance to the lens. The layouts of the plots are same as those in Fig. 7. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



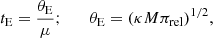
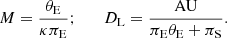
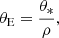
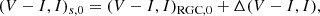
![$$ \begin{aligned} \chi _i^2 = \left[ {t_{\mathrm{E},i}-t_{\rm E}\over \sigma (t_{\rm E})}\right]^2 + \left[ {\theta _{\mathrm{E},i}-\theta _{\rm E}\over \sigma (\theta _{\rm E})}\right]^2, \end{aligned} $$](/articles/aa/full_html/2023/10/aa47014-23/aa47014-23-eq10.gif)
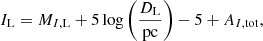
![$$ \begin{aligned} A_{I,\mathrm{L}} = A_{I,\mathrm{tot}} \left[ 1-\exp \left( -{|z|\over h_{z,\mathrm{dust}}}\right)\right], \end{aligned} $$](/articles/aa/full_html/2023/10/aa47014-23/aa47014-23-eq13.gif)