| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219765 | |
| Published online | 25 October 2012 | |
A brown dwarf orbiting an M-dwarf: MOA 2009–BLG–411L⋆
1
Probing Lensing Anomalies Network, http://planet.iap.fr
2
Microlensing Follow Up Network, http://www.astronomy.ohio-state.edu/~microfun
3
The Optical Gravitational Lensing Experiment, http://ogle.astrouw.edu.pl
4
Microlensing Observations in Astrophysics, http://www.phys.canterbury.ac.nz/moa
5
Robotic Telescope Network, http://robonet.lcogt.net
6
Microlensing Network for the Detection of Small Terrestrial Exoplanets,
http://www.mindstep-science.org
7
Department of Astronomy, Ohio State University,
140 West 18th Avenue,
Columbus, OH
43210,
USA
8
University of Canterbury, Department of Physics &
Astronomy, Private Bag
4800, Christchurch
8020, New
Zealand
9
European Southern Observatory (ESO), Casilla 19001, Vitacura 19, Santiago, Chile
10
European Southern Observatory, Karl-Schwarzschild-Stra β 2,
85748
Garching bei München,
Germany
11
Institut d’Astrophysique de Paris, CNRS, Université Pierre
& Marie Curie, 98bis Bd
Arago, 75014
Paris,
France
12
Astronomisches Rechen-Institut (ARI), Zentrum für Astronomie der
Universität Heidelberg (ZAH), Mönchhofstrasse 12ŋ-14, 69120
Heidelberg,
Germany
13
Scottish Universities Physics Alliance, School of Physics
& Astronomy, University of St Andrews, North Haugh, St Andrews, KY16
9SS, UK
14
University of Notre Dame, Department of Physics,
225 Nieuwland Science Hall,
Notre Dame, IN
46556,
USA
15
University of Texas, McDonald Observatory,
16120 St Hwy Spur 78,
Fort Davis
TX
79734,
USA
16
Institute of Geophysics and Planetary Physics (IGPP), L-413,
Lawrence Livermore National Laboratory, PO Box 808, Livermore, CA
94551,
USA
17
Physics Department, Faculty of Arts and Sciences, University of
Rijeka, Omladinska
14, 51000
Rijeka,
Croatia
18
Technical University of Vienna, Dept. of Computing, Wiedner Hauptstrasse 10,
Vienna,
Austria
19
School of Mathematics and Physics, University of
Tasmania, Private Bag 37,
Hobart, 7001
Tasmania,
Australia
20
NASA Exoplanet Science Institute, Caltech, MS 100-22, 770 South Wilson Avenue,
Pasadena, CA
91125,
USA
21
Perth Observatory, Walnut Road, Bickley, Perth
6076,
Australia
22
South African Astronomical Observatory,
PO Box 9, 7925
Observatory, South
Africa
23
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
24
Department of Physics, Institute for Basic Science Research,
Chungbuk National University, 361-763
Chongju,
Korea
25
Korea Astronomy and Space Science Institute,
61-1, Whaam-Dong, Youseong-Gu,
305-348
Daejeon,
Korea
26
Bronberg Observatory, Pretoria, South
Africa
27
Warsaw University Observatory. Al. Ujazdowskie 4,
00-478
Warszawa,
Poland
28
Universidad de Concepción, Departamento de Física, Astronomy Group,
Casilla 160-C,
Concepción,
Chile
29
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
30
Institute of Information and Mathematical Sciences, Massey
University, Private Bag 102-904,
North Shore Mail Centre, Auckland, New Zealand
31
Department of Earth and Space Science, Osaka
University, 560-0043
Osaka,
Japan
32
Jodrell Bank Centre for Astrophysics, University of
Manchester, Manchester
M13 9PL,
UK
33
Department of Physics, Konan University,
Nishiokamoto 8-9-1,
658-8501
Kobe,
Japan
34
Nagano National College of Technology,
381-8550
Nagano,
Japan
35
Department of Physics, University of Auckland,
Private Bag 92019, 1142
Auckland, New
Zealand
36
Tokyo Metropolitan College of Industrial Technology,
116-0003
Tokyo,
Japan
37
Department of Physics and Astrophysics, Faculty of Science, Nagoya
University, 464-8602
Nagoya,
Japan
38
Mount John Observatory, PO Box 56, 8770
Lake Tekapo, New
Zealand
39
Las Cumbres Observatory, 6740B Cortona Dr, suite 102, Goleta, CA
93117,
USA
40
Astrophysics Research Institute, Liverpool John Moores
University, Twelve Quays House,
Egerton Wharf, Birkenhead
CH41 1LD,
UK
41
School of Physics, University of Exeter,
Stocker Road, Exeter
EX4 4QL,
UK
42
Department of Physics, University of
Warwick, Coventry,
CV4 7AL,
UK
43
Department of Physics, Broida Hall, University of
California, Santa
Barbara
CA
93106-9530,
USA
44
IRAP, Université de Toulouse, CNRS, 14 avenue Edouard Belin, 31400
Toulouse,
France
45
Niels Bohr Institute and Centre for Star and Planet Formation,
University of Copenhagen, Juliane
Maries Vej 30, 2100
Copenhagen,
Denmark
46
University Observatory Munich, Scheinerstrasse 1, 81679
München,
Germany
47
Max Planck Institute for Astronomy, Königstuhl 17, 69117- Heidelberg, Germany
48
Institute of Theoretical Physics, Charles
University, V Holešovičkách
2, 18000
Prague, Czech
Republic
49
Bellatrix Observatory, via Madonna de Loco 47, 03023
Ceccano,
Italy
50
Dipartimento di Fisica, Università di Salerno, Fisciano, INFN,
sez. di Napoli,
IIASS, Vietri sul
Mare, Italy
51
Armagh Observatory, College Hill, Armagh, BT61
9DG, UK
52
Department of Physics, Sharif University of
Technology, PO Box
11155-9161, Tehran,
Iran
53
Institut für Astrophysik, Georg-August Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
54
Institut d’Astrophysique et de Géophysique,
Allée du 6 Août, Sart Tilman, Bât.
B5c, 4000
Liège,
Belgium
55
Astrophysics Group, Keele University, Newcastle-under-Lyme, ST5 5BG, UK
56
INAF, Osservatorio Astronomico di Brera,
23846
Merate ( LC), Italy
57
Deutsches SOFIA Institut, Universität Stuttgart,
Pfaffenwaldring 31,
70569
Stuttgart,
Germany
58
SOFIA Science Center, NASA Ames Research Center, Mail Stop
N211-3, Moffett Field
CA
94035,
USA
59
Department of Astronomy, Kyoto University,
606-8502
Kyoto,
Japan
60
School of Mathematical Sciences, Queen Mary University of
London, Mile End
Road, London
E1 4NS,
UK
61 The Wendelstein Calar Alto Pixellensing Project, http://www.usm.uni-muenchen.de/people/arri/wecapp.html
62
Possum Observatory, Patutahi, Gisbourne, New Zealand
e-mail: john_drummond@xtra.co.nz
63
School of Physics and Astronomy and Wise Observatory, Tel-Aviv
University, Tel-Aviv
69978,
Israel
e-mail: shai@wise.tau.ac.il; dani@wise.tau.ac.il; shporer@wise.tau.ac.il; david@wise.tau.ac.il
64
Auckland Observatory, Auckland, New
Zealand
e-mail: gwchristie@christie.org.nz
65
Farm Cove Observatory, Centre for Backyard
Astrophysics, Pakuranga, Auckland, New Zealand
e-mail: farmcoveobs@xtra.co.nz
66
Kiso Observatory, Institute of Astronomy, The University of
Tokyo, 10762-30, Mitake,
Kiso, 397-0101
Nagano,
Japan
67
Teide Observatory
68
The Graduate University for Advanced Studies
(Sokendai), 2-21-1 Oosawa,
Mitaka, 181-8588
Tokyo,
Japan
69
CALMIP, DTSI Université Paul Sabatier, Université de
Toulouse, 31062
Toulouse,
France
70
Perimeter Institute for Theoretical Physics,
31 Caroline Street North,
Waterloo, ON
N2L 2Y5,
Canada
71
Korea Astronomy and Space Science Institute, 776
Daedukdae-ro, Yuseong-gu, 305-348 Daejeon, Republic of Korea (South Korea)
72
International Institute for Advanced Scientific Studies, via G. Pellegrino 19,
84019 – Vietri sul Mare ( SA), Italy
73
Department of Physics, University of Salerno, via Ponte Don Melillo, 84084 –
Fisciano ( SA), Italy
74
Department of Physics & Astronomy, Aarhus
Universitet, Ny
Munkegade, 8000
Aarhus C,
Denmark
75
Molehill Astronomical Observatory, Auckland, New
Zealand
76
Departamento de Astronomía y Astrofísica, Universidad de
Valencia, 46100
Burjassot, Valencia, Spain
77
Dept. of Physics, Texas A&M University,
College Station, TX, USA
78
Institute for Advanced Study, Einstein Drive, Princeton, NJ
08540,
USA
79
AUT University, Auckland, New Zealand
80
Okayama Astrophysical Observatory, National Astronomical
Observatory of Japan, Asaguchi,
719-0232
Okayama,
Japan
Received: 6 June 2012
Accepted: 27 August 2012
Context. Caustic crossing is the clearest signature of binary lenses in microlensing. In the present context, this signature is diluted by the large source star but a detailed analysis has allowed the companion signal to be extracted.
Aims. MOA 2009-BLG-411 was detected on August 5, 2009 by the MOA-Collaboration. Alerted as a high-magnification event, it was sensitive to planets. Suspected anomalies in the light curve were not confirmed by a real-time model, but further analysis revealed small deviations from a single lens extended source fit.
Methods. Thanks to observations by all the collaborations, this event was well monitored. We first decided to characterize the source star properties by using a more refined method than the classical one: we measure the interstellar absorption along the line of sight in five different passbands (VIJHK). Secondly, we model the lightcurve by using the standard technique: make (s,q,α) grids to look for local minima and refine the results by using a downhill method (Markov chain Monte Carlo). Finally, we use a Galactic model to estimate the physical properties of the lens components.
Results. We find that the source star is a giant G star with radius 9 R⊙. The grid search gives two local minima, which correspond to the theoretical degeneracy s ≡ s-1. We find that the lens is composed of a brown dwarf secondary of mass MS = 0.05 M⊙ orbiting a primary M-star of mass MP = 0.18 M⊙. We also reveal a new mass-ratio degeneracy for the central caustics of close binaries.
Conclusions. As far as we are aware, this is the first detection using the microlensing technique of a binary system in our Galaxy composed of an M-star and a brown dwarf.
Key words: binaries: general / gravitational lensing: micro / stars: individual: MOA 2009-BLG-411L
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Gravitational microlensing has now become a robust and efficient way for detecting exoplanets very distant from the Sun that would not be detectable by other methods (Mao & Paczynski 1991; Gould & Loeb 1992; Sumi et al. 2010; Gould et al. 2010; Cassan et al. 2012). Moreover, this technique is uniquely very sensitive to planets orbiting far from their host stars (the majority of planets detected by microlensing are in this range). So, complementary to other techniques, microlensing detections are useful to better understand the planet formation mechanism. Microlensing provides very important statistics of planets around stars in our Galaxy, especially around M dwarfs, which form the majority of lenses (Dominik 2006). Some of them are binaries. It is well known that microlensing is sensitive only to companions orbiting in the “lensing zone” of their host stars, typically beyond the snowline. However, these limits can be extended, as discussed in Han (2009a,b) and Di Stefano (2012). Here, we present the detection of a low mass binary, with a classical s ≡ s-1 degeneracy, outside the classical lensing zone. In Sect. 2, we discuss the observations and the method of data reduction. In Sect. 3, we present a refined method for the extraction of the source properties, in particular a better determination of θ∗. Section 4 explains our error bar rescaling method, an important step before binary modelling as discussed in Sect. 5. The mass-ratio degeneracy for close binaries is presented in Sect. 6. Then, we determine the lens properties in Sect. 7 and conclude in Sect. 8.
2. Data sets: observations and data reductions
The MOA-II 1.8 m telescope at Mount John Observatory (New Zealand) issued an alert regarding the Bulge event MOA 2009–BLG–411 (α = 17h53m58.4s, 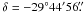 (J2000.0) and l = 0.237°, b = −1.979°) on August 5, 2009 (JD =2 455 048.5).
(J2000.0) and l = 0.237°, b = −1.979°) on August 5, 2009 (JD =2 455 048.5).
At this time, most telescopes of our networks were still busy with another promising event, MOA 2009–BLG–387, but this new event was bright, so we immediately started to follow it up.
Three nights later it was recognized as a potential high-magnification event so a larger number of telescopes from the various microlensing collaborations (MOA, PLANET, microFUN, RoboNet/LCOGT and MiNDSTEp) began to observe it more intensively. In total, 16 telescopes covered the event in different photometric bands: MOA-I 0.61 m (I-band) and MOA-II 1.8 m (wide MOA-red band) at Mount John (New Zealand), SAAO 1.0 m at Sutherland (South Africa) (V- and I-bands), Canopus 1.0 m at Hobart (Australia) (I-band), Perth/Lowell 0.61 m at Bickley (Australia) (I-band), a fleet of New Zealand amateur telescopes, namely Auckland 0.41 m (R-band), Farm Cove 0.36 m (unfiltered), Molehill 0.30 m (unfiltered), Possum 0.41 m (unfiltered), Bronberg 0.36 m at Pretoria (South Africa) (unfiltered), Wise 0.46 m at Mitzpe Ramon (Israel) (unfiltered), Teide IAC 0.82 m at Canary Islands (I-band), Faulkes North 2.0 m at Haleakala (Hawaii) (SDSS i-band), Faulkes South 2.0 m at Siding Spring (Australia) (SDSS i-band), Liverpool 2.0 m at La Palma (Spain) (SDSS i-band), and Danish 1.5 m at La Silla (Chile) (I-band). Unfortunately CTIO (Chile) was clouded out and could not observe this event.
Thanks to the public availability of data from the different groups, real-time modelling efforts showed that on August 9 the light curve was deviating from a normal Paczyński curve (Paczyński 1986), exhibiting evidence of extended source effects. The event peaked on the same night.
Data reduction was conducted using both point spread function (PSF) photometry based on a customized DoPhot package and image subtraction. The Danish images were reduced with an image subtraction package, namely DIAPL from Pych & Woźniak (Wozniak 2000), which models the convolution kernel for matching a reference image to a target image using a linear combination of a set of Gaussian basis functions of different widths further modified by polynomials, as pioneered by Alard’s ISIS package (Alard & Lupton 1998; Alard 2000). RoboNet/LCOGT images were reduced using a different image subtraction package, DanDIA, which works by solving for the kernel pixel values directly, imbuing the kernel solution with a flexibility that cannot be matched by the Gaussian expansion (Bramich 2008). PLANET telescopes also use image subtraction: at the telescope an on-line version called WISIS, based on Alard’s ISIS package, was used, while version 3.0 of pySIS (Albrow et al. 2009), based on the same numerical kernel as DanDIA, was employed for a final reduction. For consistency, we decided to reprocess the RoboNet/LCOGT images using pySIS. MOA images, both from MOA-I and from MOA-II telescopes, were reprocessed using the method described in a previous paper (Bachelet et al. 2012). In the MOA-II images, the target unfortunately falls close to a series of bad columns, which sometimes compromises photometric precision. All μFUN telescope images were first reduced using DoPhot then pySIS.
The final data set, with rejection of outliers, contains 1563 data points from 13 different telescopes (MOA-II: 521 after binning, Auckland R: 57, Farm Cove: 11, Faulkes South i: 299, Faulkes North i:40, SAAO I: 169, SAAO V: 11, Danish I: 30, Liverpool I: 100, Teide I: 50, Wise: 71, MOA-I I: 163, MOA-I V: 41). The lightcurve is shown in Fig. 1.
3. Source properties
The distance to the source and the amount of reddening along the line of sight are uncertainties which always affect the final determination of the properties of the lens-source system, as discussed in detail for instance in Fouqué et al. (2010).
Due to the geometry of the Galactic bulge with a bar embedded in it, the galactic coordinates of the target give an estimate of the relative position of the source with respect to the Galactic centre, if we assume that the source is at the same distance as the majority of the stars in the field. The Galactic centre distance itself is adopted as 8.0 ± 0.5 kpc, given the evolution of the best distance indicator, namely the orbits of stars revolving around the central black hole from DGC = 7.94 ± 0.42 kpc in Eisenhauer et al. (2003) to DGC = 7.62 ± 0.32 kpc in Eisenhauer et al. (2005) and ultimately 8.33 ± 0.35 kpc in Gillessen et al. (2009). The adopted value corresponds to a distance modulus of μGC = 14.52 ± 0.14.
We then use Rattenbury et al. (2007), who give the relative positions of the OGLE-II fields with respect to the field BUL_SC45, which contains Baade’s Window (l = 1.00°b = −3.88°). As assumed by Paczyński & Stanek (1998) and recently confirmed by Nataf et al. (2012), it is probably safe to assume that the mean distance of stars seen in Baade’s Window is similar to the Galactic centre distance. Our target’s position happens to fall in the OGLE-II field, BUL_SC3, which is claimed to be more distant by 0.07 ± 0.09 mag than BUL_SC45. We therefore adopt as the source distance modulus, μ = 14.6 ± 0.2.
 |
Fig. 1 Top: best single lens fit. Bottom: zoom close to the peak and residuals for single and best binary lens fits (close model). The geometry of caustic crossing is on the right (see inset), where the source star is represented by the blue circle. Note that the grey curve is for limb-darkening coefficient Γλ = 0.49 (R band) and the red curve is for Γλ = 0.67 (V band) in the middle panel. |
There are several estimates of the reddening in the KS band at positions near our target. They typically indicate about 0.2 mag of absorption in KS. However, given the patchiness of the dust structure, we need an estimate for our target’s position. This is based on IRSF/SIRIUS photometry of a 7.7′ × 7.7′ field containing our target. We use isochrones from Bonatto et al. (2004) based on Padova group models, but directly calibrated for the 2MASS bandpasses. We also calibrated the IRSF/SIRIUS photometry by using the 2MASS stars in the same field to ensure coherence.
We restrict the fitting region to 300 pixels around the target (2.25′ × 2.25′) to avoid too much differential extinction. This is large enough to form well-defined colour–magnitude diagrams (CMDs), where the red giant clump (RGC) is easily identified, which is not the case when using only 2MASS because its brighter limiting magnitude cuts off part of the clump. As can be seen from Fig. 2 and similar histograms for H and Ks, the mean magnitudes of the RGC are: J = 14.25, H = 13.5, and Ks = 13.2. The corresponding CMD is displayed in Fig. 3.
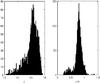 |
Fig. 2 Histograms of the RGC in J and J − H. The colour histogram has a symmetric distribution, while the magnitude histogram is pertubed by the first ascent giant branch. |
 |
Fig. 3 Colour–magnitude diagram in J and H from IRSF/SIRIUS stars in a 2.25′ × 2.25′ field around MOA 2009–BLG-411. Superimposed lines are isochrones from Bonatto et al. (2004) for three ages: 0.6 Gyr (blue), 5 Gyr (red), and 10 Gyr (green), assuming solar metallicity, a distance modulus of 14.6, and extinction coefficients of AJ = 0.57, AH = 0.32 and AKs = 0.19. The black star symbol marks the position of the source. |
Coordinates and magnitudes of the stars close to the target position in 2MASS PSC and IRSF photometric catalogue.
Coordinates and magnitudes of the stars close to the target position in MOA and OGLE-III catalogues, and relative shifts in magnitude with respect to the RGC centroid.
Although the mean observed magnitude of the clump could in principle give an estimate of its distance, in practice, variations of the absolute magnitudes of clump giants due to a range of ages and metallicities prevent us from deriving an accurate value. Assuming a 10 Gyr isochrone and solar metallicity, we get the following estimates of the near-infrared extinction and reddening law: ![\begin{eqnarray} \Aks &&= 0.19 \\[1.5mm] \label{eq:RL_HK} \Ah &&= 1.7 \times \Aks = 0.32 \\[1.5mm] \label{eq:RL_JK} \Aj &&= 3.0 \times \Aks = 0.57. \end{eqnarray}](/articles/aa/full_html/2012/11/aa19765-12/aa19765-12-eq60.png) These value are in good agreement with the reddening law of Nishiyama et al. (2009) and our value for E(J − K) (0.38) confirmed the extinction measured by the VVV telescope based in Chile (0.39) (Gonzalez et al. 2012). The PSF photometry obtained from IRSF images reveals two components at the target position. At the time when the images were taken (JD = 2 445 053.33929), the amplification of the source was 13.7 according to our model. So we have to add 2.842 mag to the IRSF measurements to find the unamplified magnitude of the source in each band. This magnitude shift is the same in all bands, as gravitational microlensing is an achromatic effect, except for the differential limb-darkening correction due to extended source effects, which are negligible in the near-infrared bands. However, the deblending of the two components may not be perfect, due to the huge amplification of the source at that time.
These value are in good agreement with the reddening law of Nishiyama et al. (2009) and our value for E(J − K) (0.38) confirmed the extinction measured by the VVV telescope based in Chile (0.39) (Gonzalez et al. 2012). The PSF photometry obtained from IRSF images reveals two components at the target position. At the time when the images were taken (JD = 2 445 053.33929), the amplification of the source was 13.7 according to our model. So we have to add 2.842 mag to the IRSF measurements to find the unamplified magnitude of the source in each band. This magnitude shift is the same in all bands, as gravitational microlensing is an achromatic effect, except for the differential limb-darkening correction due to extended source effects, which are negligible in the near-infrared bands. However, the deblending of the two components may not be perfect, due to the huge amplification of the source at that time.
 |
Fig. 4 A comparison of 2009 and 2010 observations at IRSF around the target position. North is up and east on the left side, and the horizontal line corresponds to 5 arcsec. The amplification of the source is obvious in the 2009 frame, while two stars are clearly separated in the 2010 frame: the westernmost star at the centre of the chart is our target. A third faint component north of the two other stars is also visible. |
For this reason, a new set of images was taken at the IRSF as soon as the target became visible in 2010, namely on March 3. A comparison of the two observations clearly illustrates the microlensing amplification, as can be seen in Fig. 4. On the 2010 image, two stars are clearly separated, our target being the westernmost component. A third faint star can be seen north of the other two, but it is not separated by DAOFIND in the final catalogue. In the following, we use the photometry from the 2010 observations, avoiding the need to correct for amplification and inaccurate deblending.
The target is also listed in the 2MASS PSC catalogue. However its photometry is rather imprecise, J and Ks being upper limits and H having a 0.1 mag uncertainty. This probably comes from the fact that the 2MASS “star” is in fact a blend of 3 stars. The accurate coordinates and magnitudes of the various objects at this position are given in Table 2 for OGLE and MOA, and in Table 1 for 2MASS and IRSF.
Although the 2MASS flags do not indicate any blending, the coordinates and magnitudes correspond well to the blend of the two IRSF stars. The microlensed source is the western component and the other IRSF star is a blend of the two other OGLE-III stars. However, as one of these stars is clearly bluer than the other, only the red one actually contributes to the near-infrared flux.
After converting IRSF magnitudes to the 2MASS photometric system using Kato et al. (2007), we get for the near-infrared magnitudes of the source: J = 14.328, H = 13.644 and Ks = 13.463. After correcting for our adopted values of absorption, this becomes J° = 13.76, H° = 13.32, and Ks° = 13.27. Finally, converting to the standard Bessell & Brett photometric system (Bessell & Brett 1988) using the revised version of the conversion equations originally published in Carpenter (2001), as given in the on-line version of the Explanatory Supplement to 2MASS1, we get K° = 13.31 and (J − K)° = 0.52. Using V° = 15.2 as derived in the Appendix, we get (V − K)° = 1.9.
From the adopted dereddened magnitudes and colours, and using the surface brightness – colour relations in K°, (V − K)° published by Groenewegen (2004), we get an estimate of the angular source radius θ∗ in μas of 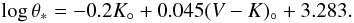 (4)The uncertainty of this estimate is 0.024, so adding quadratically the uncertainty in the magnitude (0.1) and estimated colour (0.07) gives an accuracy of 7% on θ∗, i.e., θ∗ = 4.8 ± 0.3 μas. At the adopted source distance, this translates into a linear radius of R∗ = 9 R⊙, typical of a G giant.
(4)The uncertainty of this estimate is 0.024, so adding quadratically the uncertainty in the magnitude (0.1) and estimated colour (0.07) gives an accuracy of 7% on θ∗, i.e., θ∗ = 4.8 ± 0.3 μas. At the adopted source distance, this translates into a linear radius of R∗ = 9 R⊙, typical of a G giant.
We repeated this procedure for the visible CMD, as reported in the appendix.
Using the dereddened colours and, for instance, the Houdashelt et al. (2000) tables, we estimate the effective temperature of the source star to be about 5250 K and the bolometric correction in K to be 1.7. Looking at Marigo et al. (2008) isochrones for a model star with similar characteristics to ours, our fits always tend to a star aged about 1.0 Gyr for solar metallicity, in other words, a giant of 2.1 M⊙ and log g = 3.0 on the first ascent giant branch. These are the blue isochrones in both Figs. 3 and A.2. This is very young for a Bulge star but Bensby et al. (2011) show that the age dispersion is large (1 to 13 Gyr) in the Bulge population. The star is clearly on the edge of this range but could support these previous observations. Another explanation is that the source star belongs to the disk of the Galaxy, which contains younger stars. A future high-resolution spectroscopic study would be useful to accurately measure Teff, log g and metallicity and see which scenario is preferred.
4. Data analysis: a noise model
From the original data set, we remove MOA data points earlier than HJD′ = 4850 (HJD′ = HJD-2 450 000). This corresponds to selecting only the 2009 observing season. We also binned the data outside of the peak. The reason for this cut is two-fold: the planetary deviation search is very demanding in terms of CPU time, so reducing the number of points helps; moreover, the number of data points in the baseline before HJD′ = 4850 is quite large, and any slight error in the photometric error estimate may bias the fit. We verified that this does not change the resulting fit parameters. We proceed to rescale photometric error bars in a consistent way. We first find a good single lens fit without rescaling. Then, we rescale error bars for this model. We avoid the classical approach (decrease the χ2/d.o.f. to one for each data set) which generally increases the error bars too much and, for our event, hides the caustic perturbation. We use two parameters (f, the classical rescaling factor and a minimal error emin which can reproduce the dispersion at high magnification) for rescaling as follows: 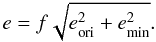 (5)We adjust those parameters as in Appendix C of Bachelet et al. (2012) and in Miyake et al. (2012) by using a standard cumulative distribution for Gaussian errors. If the dispersion of data is well represented by the original error bars, we set f = 1 and emin = 0. After some iteration, we find good pairs of parameters for each telescope and we keep them for the next step of the modelling. Results are shown in Table 3. We do not apply this procedure to data sets with fewer than ~30 points to ensure meaningful statistical results.
(5)We adjust those parameters as in Appendix C of Bachelet et al. (2012) and in Miyake et al. (2012) by using a standard cumulative distribution for Gaussian errors. If the dispersion of data is well represented by the original error bars, we set f = 1 and emin = 0. After some iteration, we find good pairs of parameters for each telescope and we keep them for the next step of the modelling. Results are shown in Table 3. We do not apply this procedure to data sets with fewer than ~30 points to ensure meaningful statistical results.
Adopted error rescaling and limb-darkening parameters.
Parameters for close and wide models.
5. Modelling
At first glance, this event looks like a single lens passing close enough to the source star to produce strong finite source effects in the lightcurve. We first perform a single-lens fit by using four single-lens parameters, namely tE, the Einstein time scale, u°, the lens-source minimal separation, t°, the corresponding time, and, to take account of finite source effects, the normalized angular source radius ρ∗. Our best single-lens fit gave χ2 = 2156.21 for 1563 data points and was unable to explain the deviations at peak, as we can see in Fig. 1. Different phenomena could explain these residuals: the presence of a companion, inadequate limb-darkening treatment or stellar variability. Two arguments suggest that the binary lens is the most reasonable solution. As previously emphasised by Dong et al. (2009), it is well known that gravitational lensing is achromatic. The residuals close to the peak have the same shape and amplitude in both SAAO-I and SAAO-V, showing the phenomenon was achromatic. The presence of anomalies only close to the peak, and their relative symmetry about it, rationally exclude stellar variability. Nevertheless, anomalies are clearly low amplitude for microlensing. A similar phenomenon has already been treated by Dong et al. (2009) and Janczak et al. (2010), who explain it as due to the low value of w/ρ∗ (comparable to or less than two), with w the “width” of the central caustic (Chung et al. 2005; Dong et al. 2009), which means that only a fraction of the source star is magnified by the caustic during the peak. As can be seen in Table 4, our single-lens parameter u° is small enough to ensure that we pass close to the central caustic, if it exists, and ρ∗ (see below) has a larger value than is typical for microlensing. All these considerations strongly suggest we have here a case as described above: a binary lens crossing a giant source. Then, we decided to investigate binary models by using the four parameters above and the three classical binary parameters: s, the projected separation between the two components in units of the Einstein radius, q, the mass ratio and α, the angle between the trajectory of the source and the binary axis. By convention, we define q as the mass ratio of the rightmost component over the leftmost one; therefore, q may take values larger than one.
Our exploration of parameter space first uses (q,s,α) grids to look for all minima in χ2 space. We use a Markov chain Monte Carlo (MCMC) algorithm for each pair of grid parameters to find the best solution for the other parameters. We start with a very large range for each parameter: 10-2 to 10 for s, 10-4 to 1 for q and 0 to 2π for α to explore all possible minima. We accelerate the calculation by using the “map making” technique first introduced by Dong et al. (2006) for the region close to the caustics and a Taylor development of source magnification, known as a “hexadecapole approximation” (Gould 2008; Pejcha & Heyrovský 2009), for more distant regions. We take account of the limb darkening by using a linear approximation, sufficient in our case, following Milne’s description (Milne 1921; An et al. 2002): ![\begin{equation} \Il = {{\Fl\over\pi\ThS^2}}\left[1 - \Gl \,\left(1-{3\over2} \cos\phi \right)\right] \label{eq:limbdarkening} \end{equation}](/articles/aa/full_html/2012/11/aa19765-12/aa19765-12-eq165.png) (6)where Γλ is the limb-darkening coefficient at wavelength λ, which is different for all telescopes, Fλ is the total flux from the star and φ is the angle between the line of sight and the normal to the stellar surface. The value of Γλ for each telescope (see Table 3) was found by an initial extended source single-lens fit with free limb-darkening coefficients for each colour. The resulting values are in good agreement with coefficients given in Claret (2000) for a giant star with an effective temperature of 5250 K and log g = 3.0.
(6)where Γλ is the limb-darkening coefficient at wavelength λ, which is different for all telescopes, Fλ is the total flux from the star and φ is the angle between the line of sight and the normal to the stellar surface. The value of Γλ for each telescope (see Table 3) was found by an initial extended source single-lens fit with free limb-darkening coefficients for each colour. The resulting values are in good agreement with coefficients given in Claret (2000) for a giant star with an effective temperature of 5250 K and log g = 3.0.
Finally, we found two local minima which correspond to the classical degeneracy of s ≡ s-1, as can be seen in Fig. 5. We investigated both, by using a MCMC algorithm for all parameters, to find the model parameters listed in Table 4 and the model lightcurves in Fig. 1.
 |
Fig. 5 χ2 landscape of mass ratio versus lens separation. Red, yellow, green, cyan, blue and purple colours show the one to six sigma regions away from the best model. The two crosses mark the positions of the final best fit models for the close and wide solutions. |
6. Study of deviations due to caustic crossing
Adding a companion to the lens greatly improves the fit. We find for both models that the ratio w/ρ∗ is smaller than two (in our case ~0.3), which indicates that the source star “smoothed” the light curve deviation induced by the caustic crossing near the peak. The same central caustic can be created by a close companion or a distant companion; this is the close/wide degeneracy (i.e., s ≡ s-1). Both cases were explored. It is well known that microlensing is sensitive to companions orbiting in the “lensing zone” of their host, i.e., s ∈ [0.6,1.6] . The majority of detected events are in this range but there can be exceptions. Griest & Safizadeh (1998) first showed that detection of companions with appropriate mass ratios and u° values is possible for s = 0.2. More recently, Han (2009a,b) and Han & Kim (2009) went into further details, especially for giant source stars. For a w/ρ∗ ratio close to 0.5, it is shown that the limits of the “lensing zone” become 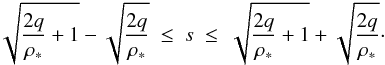 (7)In our case, for q ≡ 1 and ρ∗ ≡ 0.025, our values sclose = 0.11 and swide = 14.5 are in the range predicted above [0.056−17.9]. Nevertheless, experimental detection can be difficult because the magnification excess over a single-lens model can be as low as 5% (Han & Kim 2009). Our central caustic looks symmetric (diamond shape) and our models are degenerate modulo
(7)In our case, for q ≡ 1 and ρ∗ ≡ 0.025, our values sclose = 0.11 and swide = 14.5 are in the range predicted above [0.056−17.9]. Nevertheless, experimental detection can be difficult because the magnification excess over a single-lens model can be as low as 5% (Han & Kim 2009). Our central caustic looks symmetric (diamond shape) and our models are degenerate modulo 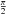 . The excess magnification for this kind of caustic (see Han 2009a) is also symmetric with respect to a rotation of
. The excess magnification for this kind of caustic (see Han 2009a) is also symmetric with respect to a rotation of 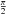 . However, the angle of the trajectory is not a “physical” parameter and we always find for these four values of α similar values for s and q as those given in Table 4. The theoretical anomalies predicted by Han (2009a) for a diamond-shaped central caustic are similar to ours (see his Fig. 3) and we can conclude that we have made the first experimental detection of this predicted effect. Figure 6 shows our MCMC exploration around our two best fit models. We can see a parabolic degeneracy in log q versus s for the close case. Following Chung et al. (2005), we did some algebra based on theory developed by An (2005), and found that the central caustic position is given by the following complex coordinate:
. However, the angle of the trajectory is not a “physical” parameter and we always find for these four values of α similar values for s and q as those given in Table 4. The theoretical anomalies predicted by Han (2009a) for a diamond-shaped central caustic are similar to ours (see his Fig. 3) and we can conclude that we have made the first experimental detection of this predicted effect. Figure 6 shows our MCMC exploration around our two best fit models. We can see a parabolic degeneracy in log q versus s for the close case. Following Chung et al. (2005), we did some algebra based on theory developed by An (2005), and found that the central caustic position is given by the following complex coordinate: 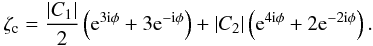 (8)This gives the following Cartesian coordinates:
(8)This gives the following Cartesian coordinates: ![\begin{eqnarray} \xi_{\rm c} &&= 2\left|C_1\right| \cos (\phi)^3 + 3\left|C_2\right|\left(2\cos(\phi)^4 - 1\right) \\[2mm] \eta_{\rm c} &&= -2\left|C_1\right| \sin(\phi)^3 - 8\left|C_2\right| \sin(\phi)^3\cos(\phi) \end{eqnarray}](/articles/aa/full_html/2012/11/aa19765-12/aa19765-12-eq181.png) with
with  (11)
(11)
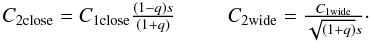 (12)(See Fig. 7 for the meaning of these variables.)
(12)(See Fig. 7 for the meaning of these variables.)
 |
Fig. 6 Scatter plots for our best models. The close model exploration is on the top and the wide one on bottom. For both case, the theoritical plot of Eq. (16) is visible on the right. The log q versus s parabolic degeneracy is cleary visible for the close model. |
The cusps are for values of φ which are solutions of 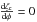 . They occur for φ = 0,
. They occur for φ = 0, 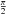 , π and
, π and 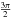 . Knowing that, we now define the horizontal and vertical width as Chung et al. (2005) and find
. Knowing that, we now define the horizontal and vertical width as Chung et al. (2005) and find  (13)which leads to
(13)which leads to 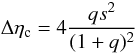 (14)for the close case and
(14)for the close case and  (15)for the wide case. This gives a width ratio Rc = 1, in perfect agreement with our experimental “diamond-shaped” central caustic for both cases. Then, we consider our experimental case with
(15)for the wide case. This gives a width ratio Rc = 1, in perfect agreement with our experimental “diamond-shaped” central caustic for both cases. Then, we consider our experimental case with  which gives
which gives 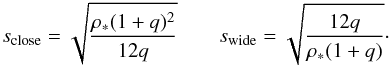 (16)Our theoretical plot of Eq. (16) can be seen in Fig. 6. These relations are in excellent agreement with our experimental results (MCMC search). We also checked its validity for a few other events (Choi et al. 2012). We conclude that, as far as we know, we have uncovered a new central caustic degeneracy, in terms of q, for extremely close binaries. This degeneracy is however not dramatic for microlensing studies in terms of physical parameters (lens mass and component separation), as is the case with the s ≡ s-1 degeneracy. Because of the near-exact symmetry of excess magnification (see Fig. 2 in Han 2009a), close models cannot be distinguished if the source passes the most massive component of the lens on its right/left, which explains the q ≡ q-1 degeneracy (see definition of q in Sect. 5). For wide models, this symmetry exists close to the central caustic, but the degeneracy is broken by the presence of the larger planetary caustic.
(16)Our theoretical plot of Eq. (16) can be seen in Fig. 6. These relations are in excellent agreement with our experimental results (MCMC search). We also checked its validity for a few other events (Choi et al. 2012). We conclude that, as far as we know, we have uncovered a new central caustic degeneracy, in terms of q, for extremely close binaries. This degeneracy is however not dramatic for microlensing studies in terms of physical parameters (lens mass and component separation), as is the case with the s ≡ s-1 degeneracy. Because of the near-exact symmetry of excess magnification (see Fig. 2 in Han 2009a), close models cannot be distinguished if the source passes the most massive component of the lens on its right/left, which explains the q ≡ q-1 degeneracy (see definition of q in Sect. 5). For wide models, this symmetry exists close to the central caustic, but the degeneracy is broken by the presence of the larger planetary caustic.
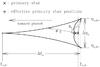 |
Fig. 7 Geometry of central caustic (from Chung et al. 2005). |
7. Results
In principle, a measurement of the source size in both Einstein radius and physical units, as well as the measurement of parallax parameters completely determines the lens location (given the source distance DS). As indicated before, standard models are not well enough constrained, so that modelling second-order effects (microlensing parallax, xallarap, or/and orbital motion), which will add more degeneracy, is clearly not possible and, more important, not reliable. Moreover, this event is of very short duration, so we can expect that these effects are quite small and, in practice, not measurable. That is why we did not explore this kind of modelling for this event.
With the angular Einstein radius being related to the angular source radius θ∗ as θE = θ∗/ρ∗, we find θE = 185 ± 20 μas for the close model. This value is lower than for typical microlensing events. This means that the lens is probably close to the Galactic bulge with a low mass. This enables us to calculate the relative lens-source proper motion, μrel = θE/tE = 6.3 ± 0.4 mas/yr. From the value of θE in mas and DS in kpc, we obtain a constraint on the lens mass ML in solar mass units as follows (Dominik 1998): 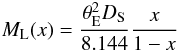 (17)where
(17)where 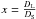 , which for DS = 8.5 kpc and θE = 0.185 mas gives
, which for DS = 8.5 kpc and θE = 0.185 mas gives 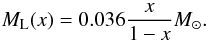 (18)We then use estimates of the physical parameters, following Dominik (2006) and assuming his adopted Galaxy model. For the close model, the event time-scale, tE = 10.7 days, and the angular Einstein radius, θE = 0.185 mas, provide us probability densities for the lens mass ML and lens distance DL as seen in Fig. 8. We find a median lens mass
(18)We then use estimates of the physical parameters, following Dominik (2006) and assuming his adopted Galaxy model. For the close model, the event time-scale, tE = 10.7 days, and the angular Einstein radius, θE = 0.185 mas, provide us probability densities for the lens mass ML and lens distance DL as seen in Fig. 8. We find a median lens mass 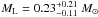 and distance
and distance  kpc. The wide model leads to similar values,
kpc. The wide model leads to similar values,  and
and 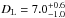 kpc.
kpc.
 |
Fig. 8 Probability densities for the lens mass |
8. Summary and conclusion
Dense photometric coverage made by all observational teams permitted a detailed study of MOA-2009-BLG-411. The maximum magnification was about Amax ≡ 80 and so was very sensitive to the presence of a central caustic. A caustic crossing signature did not appear clearly, because of a large normalized source radius ρ∗, but we found that considering a binary geometry increases the quality of the fit substantially. After exploration of the two local minima (s ≡ s-1 degeneracy), we found that the close model gives a slightly better fit. The model was highly degenerate for two major reasons: the peak was not sufficiently monitored and the theoretical degeneracy in q allows a large range of s values. Our study of the red giant clump, which gives a better estimation of extinction, leads to a source radius θ∗ = 4.8 ± 0.4 μas and so an Einstein ring radius θE = 0.185 mas. Finally, our Galactic and microlensing models lead to a binary system with an M-dwarf with mass, MP = 0.18 M⊙, and a brown dwarf with mass, MS = 0.05 M⊙, separated by a projected distance 0.15 AU (close model). This result is a new example of a brown dwarf in orbit around an M-dwarf, following the first results of Marley et al. (1996) and more recently of Irwin et al. (2010) and Johnson et al. (2011), based on transit-survey data.
Online material
Appendix A: V, (V – I) CMD
A colour–magnitude diagram allows an estimate of the dereddened magnitude and colour of the target, by comparison with the observed position of the RGC, if one assumes that both suffer the same amount of extinction. We retrieved stars within 2′ of the target in the OGLE-III photometric catalogue of field BLG 101.3, and constructed the calibrated CMD shown in Fig. A.1 (Szymański et al. 2011). From it, we measured the RGC centroid position, which is IRC = 15.940 ± 0.010 and (V − I)RC = 2.385 ± 0.005, and relative shifts in magnitude and colour of the three stars close to the target position, for which we found the values given in the last two columns of Table 2.
 |
Fig. A.1 Colour–magnitude diagram in I and V from calibrated OGLE-III photometry. The superimposed histograms show the position of the centroid of the RGC. |
Unlike in previous studies, we do not fix the absolute magnitude of the RGC at some standard value, because the population corrections to apply to the well determined local clump position are somewhat uncertain. For instance, Salaris & Girardi (2002) give corrections for Baade’s Window in V varying from 0.06 to 0.21 depending whether one adopts scaled-solar or α-enhanced metallicities. If one also changes the underlying adopted SFR (star formation rate) and AMR (age-metallicity relation), the corrections further vary, as shown in Girardi & Salaris (2001). We prefer using the same isochrone method as in the near-infrared to fit the RGC and giant branch positions. We adopt for this purpose the Marigo et al. (2008) set of isochrones, as given on their web site2.
Our parameters are now the extinction E(V − I) and the total-to-selective absorption ratio RI. An acceptable fit is shown in Fig. A.2. It uses E(V − I) = 1.30 and RI = 1.11. The first value is in good agreement with a similar determination at the target position in the OGLE-II BUL_SC3 field as reported by Sumi (2004), namely E(V − I) = 1.336. The agreement is not expected to be perfect, first because the OGLE-III transmission curves in I and V differ slightly from those of OGLE-II, and second because Sumi assumes an RGC intrinsic colour of 1.028, slightly different from the value we obtain. The second value is larger than the mean value adopted by Sumi (2004), which is 0.964, but in good agreement with an independent determination based on the recently released OGLE-III photometric catalogue of the Galactic bulge, which gives an average value of RI = 1.22 (Nataf et al. 2012). All these values are clearly lower than the standard value of this ratio, which is 1.5, justifying the so-called anomalous extinction law generally invoked when dealing with the Galactic bulge (see, e.g. Udalski 2003).
 |
Fig. A.2 The V and I colour–magnitude diagram similar to Fig. 3, but now with superimposed isochrones from Marigo et al. (2008) for solar metallicity and three different ages: 0.6 Gyr (blue), 5 Gyr (red) and 10 Gyr (green), assuming a distance modulus of 14.6, an extinction E(V − I) = 1.30 and RI = 1.11. The black star symbol marks the position of the source. |
From the adopted values of these two parameters, we derive absorption values for the field of AI = 1.44 and AV = 2.74. For the measured position of the RGC and our adopted distance modulus, the mean absolute magnitudes of the RGC are found to be MI = − 0.10 and MV = 0.98. The standard values for the RGC colour and magnitude adopted in Nataf et al. (2012) are (V − I)° = 1.06 ± 0.12 and MI = − 0.12 ± 0.09, in good agreement with our derivation.
Assuming once more that the source suffers the same amount of extinction as the RGC, and using the shifts in magnitude and colour listed in Table 2, the source is predicted to have  and (V − I)°S = 0.82. Using the previously derived values of the near-infared magnitudes of the source, we get a colour (V − K)° = 1.9. All these colours point to an early G giant spectral type.
and (V − I)°S = 0.82. Using the previously derived values of the near-infared magnitudes of the source, we get a colour (V − K)° = 1.9. All these colours point to an early G giant spectral type.
From the adopted dereddened magnitudes and colours, and using the revision of the surface brightness-colour relations in I°, (V − I)° published by Kervella & Fouqué (2008), we get an estimate of the angular source radius θ∗ in μas of 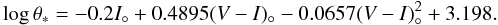 (A.1)The uncertainty of this estimate is 0.0238, so adding quadratically the uncertainty in magnitude (0.1) and colour (0.05) to this gives an accuracy of 9% on θ∗, i.e., θ∗ = 4.8 ± 0.4 μas. This confirms the previous result derived from the V°, (V − K)° surface brightness-colour relation.
(A.1)The uncertainty of this estimate is 0.0238, so adding quadratically the uncertainty in magnitude (0.1) and colour (0.05) to this gives an accuracy of 9% on θ∗, i.e., θ∗ = 4.8 ± 0.4 μas. This confirms the previous result derived from the V°, (V − K)° surface brightness-colour relation.
Note that, for this colour determination, we assumed that the star, OGLE-III-BLG-101.3 159762 in Table 2, is the source star. But in the MOA frames, the three stars in Table 2 are not fully resolved. The two OGLE stars close to the source, 160107 and 160108, can therefore contribute a blend flux in our models. In microlensing modelling we have to take this blend flux into account. Had we obtained calibrated data, we
could have predicted the blend and source fluxes using our models. Unfortunately, the reduction we used for our modelling is not calibrated. We therefore used the original reduction of MOA data, which is calibrated but of lower quality, to estimate the blend properties. We found that the colour and magnitude of this blend corresponds to the sum of the fluxes of the 160107 and the 160108 stars. This means that our identification of the three OGLE stars was correct. In any case, future adaptive optics observations would be useful to confirm our conclusions.
Acknowledgments
We are very grateful to the observatories that support our science (Bronberg, Canopus, CTIO, ESO, IRSF, LCOGT, Liverpool, LOAO, MOA, OGLE, Perth, SAAO, Skinakas) via the generous allocation of time that makes this work possible. The operation of Canopus Observatory is in part supported by a financial contribution from David Warren. Allocation of the Holmes grant from the French Agence Nationale de la Recherche has been indispensable to finance observing trips and travel costs for meetings, and is gratefully acknowledged here. D.H. was supported by Czech Science Foundation grant GACR 205/07/0824 and by the Czech Ministry of Education project MSM0021620860. C.H. was supported by the grant 2009-0081561 of National Research Foundation of Korea. T.C.H. was financed for his astronomical research at the Armagh Observatory by the Department for Culture, Arts and Leisure, Northern Ireland, UK and is now supported by the Korea Research Council for Fundamental Science and Technology (KRCF) via the Young Scientist Research Fellowship Program. MOA project was funded by JSPS18253002 and JSPS20340052. T.S. was funded by JSPS20740104. D.R. and J.S. acknowledge support from the Communauté française de Belgique – Actions de recherche concertées – Académie universitaire Wallonie-Europe. P.F. wishes to thank Noriyuki Matsunaga for discussions about the interplay between adopted distance and derived extinction. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (/FP7/2007-2013/) under grant agreement No 229517. A. Gould acknowledges support from NSF AST-1103471. B. S. Gaudi, A. Gould, and R. W. Pogge acknowledge support from NASA grant NNG04GL51G. Work by J. C. Yee is supported by a National Science Foundation Graduate Research Fellowship under Grant No. 2009068160. Work by S. Dong was performed under contract with the California Institute of Technology (Caltech) funded by NASA through the Sagan Fellowship Program. The RoboNet team is supported by the Qatar Foundation through QNRF grant NPRP-09-476-1-78. CUL acknowledges support by Korea Astronomy and Space Science Institute (KASI) grant 2012-1-410-02. This publication makes use of data products from the 2MASS project, as well as the SIMBAD database, Aladin and Vizier catalogue operation tools (CDS Strasbourg, France). The Two Micron All Sky Survey is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work was granted access to the HPC resources of CALMIP under the allocation 2012-[1131].
References
- Alard, C. 2000, A&AS, 144, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alard, C., & Lupton, R. H. 1998, ApJ, 503, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Albrow, M. D., Horne, K., Bramich, D. M., et al. 2009, MNRAS, 397, 2099 [NASA ADS] [CrossRef] [Google Scholar]
- An, J. H. 2005, MNRAS, 356, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- An, J. H., Albrow, M. D., Beaulieu, J.-P., et al. 2002, ApJ, 572, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Bachelet, E., Shin, I.-G., Han, C., et al. 2012, ApJ, 754, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., Bica, E., & Girardi, L. 2004, A&A, 415, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bramich, D. M. 2008, MNRAS, 386, L77 [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Cassan, A., Kubas, D., Beaulieu, J.-P., et al. 2012, Nature, 481, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J.-Y., Shin, I.-G., Han, C., et al. 2012, ApJ, 756, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, S.-J., Han, C., Park, B.-G., et al. 2005, ApJ, 630, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Di Stefano, R. 2012, ApJ, 752, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M. 1998, A&A, 329, 361 [NASA ADS] [Google Scholar]
- Dominik, M. 2006, MNRAS, 367, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., DePoy, D. L., Gaudi, B. S., et al. 2006, ApJ, 642, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., Bond, I. A., Gould, A., et al. 2009, ApJ, 698, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Schödel, R., Genzel, R., et al. 2003, ApJ, 597, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Genzel, R., Alexander, T., et al. 2005, ApJ, 628, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Fouqué, P., Heyrovský, D., Dong, S., et al. 2010, A&A, 518, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., & Salaris, M. 2001, MNRAS, 323, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A. 2008, ApJ, 681, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., & Loeb, A. 1992, ApJ, 396, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Dong, S., Gaudi, B. S., et al. 2010, ApJ, 720, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Griest, K., & Safizadeh, N. 1998, ApJ, 500, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2004, MNRAS, 353, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C. 2009a, ApJ, 691, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C. 2009b, ApJ, 691, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., & Kim, D. 2009, ApJ, 693, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Houdashelt, M. L., Bell, R. A., & Sweigart, A. V. 2000, AJ, 119, 1448 [Google Scholar]
- Irwin, J., Buchhave, L., Berta, Z. K., et al. 2010, ApJ, 718, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Janczak, J., Fukui, A., Dong, S., et al. 2010, ApJ, 711, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Apps, K., Gazak, J. Z., et al. 2011, ApJ, 730, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, D., Nagashima, C., Nagayama, T., et al. 2007, PASJ, 59, 615 [NASA ADS] [Google Scholar]
- Kervella, P., & Fouqué, P. 2008, A&A, 491, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mao, S., & Paczynski, B. 1991, ApJ, 374, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marley, M. S., Saumon, D., Guillot, T., et al. 1996, Science, 272, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Milne, E. A. 1921, MNRAS, 81, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Miyake, N., Udalski, A., Sumi, T., et al. 2012, ApJ, 752, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2012 [arXiv:1208.1263] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B., & Stanek, K. Z. 1998, ApJ, 494, L219 [NASA ADS] [CrossRef] [Google Scholar]
- Pejcha, O., & Heyrovský, D. 2009, ApJ, 690, 1772 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., Mao, S., Sumi, T., et al. 2007, MNRAS, 378, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Girardi, L. 2002, MNRAS, 337, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T. 2004, MNRAS, 349, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Bennett, D. P., Bond, I. A., et al. 2010, ApJ, 710, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Szymański, M. K., Udalski, A., Soszyński, I., et al. 2011, Acta Astron., 61, 83 [NASA ADS] [Google Scholar]
- Udalski, A. 2003, ApJ, 590, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, P. R. 2000, Acta Astron., 50, 421 [NASA ADS] [Google Scholar]
All Tables
Coordinates and magnitudes of the stars close to the target position in 2MASS PSC and IRSF photometric catalogue.
Coordinates and magnitudes of the stars close to the target position in MOA and OGLE-III catalogues, and relative shifts in magnitude with respect to the RGC centroid.
All Figures
 |
Fig. 1 Top: best single lens fit. Bottom: zoom close to the peak and residuals for single and best binary lens fits (close model). The geometry of caustic crossing is on the right (see inset), where the source star is represented by the blue circle. Note that the grey curve is for limb-darkening coefficient Γλ = 0.49 (R band) and the red curve is for Γλ = 0.67 (V band) in the middle panel. |
| In the text | |
 |
Fig. 2 Histograms of the RGC in J and J − H. The colour histogram has a symmetric distribution, while the magnitude histogram is pertubed by the first ascent giant branch. |
| In the text | |
 |
Fig. 3 Colour–magnitude diagram in J and H from IRSF/SIRIUS stars in a 2.25′ × 2.25′ field around MOA 2009–BLG-411. Superimposed lines are isochrones from Bonatto et al. (2004) for three ages: 0.6 Gyr (blue), 5 Gyr (red), and 10 Gyr (green), assuming solar metallicity, a distance modulus of 14.6, and extinction coefficients of AJ = 0.57, AH = 0.32 and AKs = 0.19. The black star symbol marks the position of the source. |
| In the text | |
 |
Fig. 4 A comparison of 2009 and 2010 observations at IRSF around the target position. North is up and east on the left side, and the horizontal line corresponds to 5 arcsec. The amplification of the source is obvious in the 2009 frame, while two stars are clearly separated in the 2010 frame: the westernmost star at the centre of the chart is our target. A third faint component north of the two other stars is also visible. |
| In the text | |
 |
Fig. 5 χ2 landscape of mass ratio versus lens separation. Red, yellow, green, cyan, blue and purple colours show the one to six sigma regions away from the best model. The two crosses mark the positions of the final best fit models for the close and wide solutions. |
| In the text | |
 |
Fig. 6 Scatter plots for our best models. The close model exploration is on the top and the wide one on bottom. For both case, the theoritical plot of Eq. (16) is visible on the right. The log q versus s parabolic degeneracy is cleary visible for the close model. |
| In the text | |
 |
Fig. 7 Geometry of central caustic (from Chung et al. 2005). |
| In the text | |
 |
Fig. 8 Probability densities for the lens mass |
| In the text | |
 |
Fig. A.1 Colour–magnitude diagram in I and V from calibrated OGLE-III photometry. The superimposed histograms show the position of the centroid of the RGC. |
| In the text | |
 |
Fig. A.2 The V and I colour–magnitude diagram similar to Fig. 3, but now with superimposed isochrones from Marigo et al. (2008) for solar metallicity and three different ages: 0.6 Gyr (blue), 5 Gyr (red) and 10 Gyr (green), assuming a distance modulus of 14.6, an extinction E(V − I) = 1.30 and RI = 1.11. The black star symbol marks the position of the source. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



