| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201118326 | |
| Published online | 13 June 2012 | |
Online material
Appendix A: Estimating the excess variance uncertainty
The uncertainty on the excess variance depends both on the measurement uncertainties (e.g. Poisson noise) in the light curve and on the stochastic nature of the variability. As shown by Vaughan et al. (2003) through MonteCarlo simulations, or Ponti et al. (2004) in the particular case of large number of photons, the former can be approximated by the formula (see Eq. (11) of Vaughan et al. 2003): 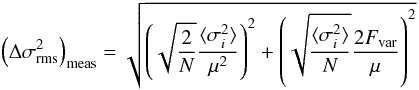 (A.1)where
(A.1)where 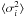 is the mean of the uncertainties squared and Fvar is the fractional variability.
is the mean of the uncertainties squared and Fvar is the fractional variability.
The uncertainty owing to the stochastic nature of the process is more difficult to estimate. Vaughan et al. (2003) showed that the uncertainty increases with the steepness of the power spectrum slope and it is large and highly non-Gaussian for steep Power Spectral Densities (PSD). A simple estimate of the uncertainty cannot be analytically derived, however two approaches can be pursued.
 |
Fig. A.1
Distribution of the observed excess variances computed for 10 ks intervals for 3C 273. The distribution of each of the other 6 sources with longer XMM-Newton exposures are displayed on the online version of the paper. The points above each distribution indicate the average excess variance and the “error bars” around this mean indicate the mean upper and lower 90% confidence limits on |
| Open with DEXTER | |
A.1. Estimating the “red noise” scatter: more than 10 intervals
The first approach is to estimate the uncertainty directly from the data, deriving the scatter from the distribution of the measured excess variances of the different intervals. Every excess variance measurement is an independent variable with identical distribution (unless the process is non-stationary). This is only approximately valid, because successive light curve parts may not be truly independent, if the “memory” of the system is longer than the segment’s length. Nevertheless, every time that more than 10 valid segments are available for the same source, we estimate the uncertainty on the mean excess variance computing the sigma of the mean of the different measurements. Furthermore, due to the central limit theorem, the distribution of the mean of all the excess variance estimates will become normally distributed for a large number of measurements. Obviously it is not easy to estimate how “large” the number of 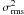 estimates should be but, following this line of reasoning, in the case of sources with more than 10 light curve intervals, we consider the error on the mean to be symmetric (as if its distribution were normal), and in order to estimate the 90% confidence level, this value is then multiplied by 1.6. Despite the numerous limitations, at least this approach allows us to estimate the uncertainty of our final estimate without the need to adopt any assumptions about the underlying variability process.
estimates should be but, following this line of reasoning, in the case of sources with more than 10 light curve intervals, we consider the error on the mean to be symmetric (as if its distribution were normal), and in order to estimate the 90% confidence level, this value is then multiplied by 1.6. Despite the numerous limitations, at least this approach allows us to estimate the uncertainty of our final estimate without the need to adopt any assumptions about the underlying variability process.
A.2. Estimating the “red noise” scatter: 1 interval
When the number of valid segments is just one, we estimated the uncertainty on 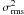 using the results from the Monte Carlo simulations of Vaughan et al. (2003) and assuming a PSD shape for each source. Detailed studies of PSD in AGN have shown an almost ubiquitous PSD shape characterised by a steep power law shape (α ~ 2) above a special frequency νbr and a flatter (α ~ 1) power law slope below (Uttley & McHardy 2005; but see also the case of ARK564; McHardy et al. 2007). In particular it has been observed that the characteristic break frequency (νbr) scales primarily with mass and with accretion rate (McHardy et al. 2006). We thus expect that the slope of the PSD, within the frequency range probed by our light curves (from 4 × 10-3 to either 10-4, 5 × 10-5 or 2.5 × 10-5 Hz, for the 10, 20 and 40 ks segments, respectively), may be different for the sources in the sample, depending on their MBH and accretion rate. Assuming that all AGN show the same PSD and that the PSD shape scales with mass and accretion rate as measured by McHardy et al. (2006), we can predict the position of the break frequency and the slope of the PSD in the frequency band which corresponds to 250 s binned light curves, of duration equal to 10, 20, 40 and 80 ks.
using the results from the Monte Carlo simulations of Vaughan et al. (2003) and assuming a PSD shape for each source. Detailed studies of PSD in AGN have shown an almost ubiquitous PSD shape characterised by a steep power law shape (α ~ 2) above a special frequency νbr and a flatter (α ~ 1) power law slope below (Uttley & McHardy 2005; but see also the case of ARK564; McHardy et al. 2007). In particular it has been observed that the characteristic break frequency (νbr) scales primarily with mass and with accretion rate (McHardy et al. 2006). We thus expect that the slope of the PSD, within the frequency range probed by our light curves (from 4 × 10-3 to either 10-4, 5 × 10-5 or 2.5 × 10-5 Hz, for the 10, 20 and 40 ks segments, respectively), may be different for the sources in the sample, depending on their MBH and accretion rate. Assuming that all AGN show the same PSD and that the PSD shape scales with mass and accretion rate as measured by McHardy et al. (2006), we can predict the position of the break frequency and the slope of the PSD in the frequency band which corresponds to 250 s binned light curves, of duration equal to 10, 20, 40 and 80 ks.
Using then the results listed in Table 1 of Vaughan et al. (2003), we assume a Δlog (S2) = + 0.45 and − 0.71, for the positive and negative error on 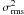 , respectively, if the break time-scale is longer than the length of the interval (this means that in the frequency window on which the excess variance is computed, the PSD has a slope of –2). We assumed Δlog (S2) = + 0.28 and − 0.36 if the break time-scale is shorter than the light curve time bin (in which case we would expect a PSD of a –1 slope in the frequency range sampled by each light curve segment). If the break time-scale falls within the frequency window, then we combine the errors with the formula:
, respectively, if the break time-scale is longer than the length of the interval (this means that in the frequency window on which the excess variance is computed, the PSD has a slope of –2). We assumed Δlog (S2) = + 0.28 and − 0.36 if the break time-scale is shorter than the light curve time bin (in which case we would expect a PSD of a –1 slope in the frequency range sampled by each light curve segment). If the break time-scale falls within the frequency window, then we combine the errors with the formula: 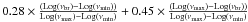 (and similarly for the negative error). When no MBH estimates are available, we are conservative and assume the largest uncertainties, associated with a PSD slope of –2. As computed by Vaughan et al. (2003) this scatter estimates the 90% confidence interval. In this way we are able to conservatively estimate the scatter in the excess variance measurements introduced by the red noise, in the case when we have just a single excess variance value.
(and similarly for the negative error). When no MBH estimates are available, we are conservative and assume the largest uncertainties, associated with a PSD slope of –2. As computed by Vaughan et al. (2003) this scatter estimates the 90% confidence interval. In this way we are able to conservatively estimate the scatter in the excess variance measurements introduced by the red noise, in the case when we have just a single excess variance value.
A.3. Estimating the “red noise” scatter: checking the approximations
In order to judge how accurate are our excess variance uncertainties, given the various assumptions that underlie the methods we described above, we performed the following test. We considered the 7 sources with the longest XMM-Newton observations in CAIXAvar. The number of 10 ks segments for each one of these objects is significantly larger than 10 (so the 10 ks excess variance measurement we list in Table 2 for these objects is the mean of all the individual measurements, and its error is based on the true scatter of the points around their mean, as explained above). Figure A.1 shows the distribution of the observed 10 ks excess variance values, for these objects. As expected, whenever we have a “signal” (i.e. the 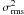 values are positive) the distributions are asymmetric with a tail at large values. In the case of 3C 273, due to its large MBH, we do not expect large amplitude variations on such short time scales. As a result, the distribution of the 10 ks
values are positive) the distributions are asymmetric with a tail at large values. In the case of 3C 273, due to its large MBH, we do not expect large amplitude variations on such short time scales. As a result, the distribution of the 10 ks 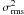 values is dominated by the uncertainties associated with the Poisson noise of the light curves, hence it is more symmetric.
values is dominated by the uncertainties associated with the Poisson noise of the light curves, hence it is more symmetric.
We then used the method described above to obtain the uncertainty of each individual 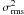 value, and we calculated the mean upper and lower 90% confidence limits on
value, and we calculated the mean upper and lower 90% confidence limits on 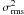 , for each object. The points on top of each sample distribution in Fig. A.1 indicate the average excess variance, and the “error bar” around this mean indicate the mean upper and lower 90% confidence limits on
, for each object. The points on top of each sample distribution in Fig. A.1 indicate the average excess variance, and the “error bar” around this mean indicate the mean upper and lower 90% confidence limits on 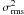 . A visual inspection shows that these confidence limits are compatible with the area where ~90% of the points are. In fact, we measure that the average 90% uncertainty estimated with our method actually contains 84, 92, 80, 93, 87, 97, 92% of the measured values of NGC 4051, 1H0707-495, MGC-6-30-15, MRK 766, MRK 335, NGC 3516 and 3C 273, respectively. Thus the typical difference between the estimated 90% uncertainty and the one measured from the observed distribution is less than 10%.
. A visual inspection shows that these confidence limits are compatible with the area where ~90% of the points are. In fact, we measure that the average 90% uncertainty estimated with our method actually contains 84, 92, 80, 93, 87, 97, 92% of the measured values of NGC 4051, 1H0707-495, MGC-6-30-15, MRK 766, MRK 335, NGC 3516 and 3C 273, respectively. Thus the typical difference between the estimated 90% uncertainty and the one measured from the observed distribution is less than 10%.
The 1-σ “error” has been estimated simply dividing the 90% uncertainties by 1.6. This approximation is valid for normal distributions, only. However, in the cases of NGC 4051, 1H0707-495, MGC-6-30-15, MRK 766, MRK 335, NGC 3516 and 3C 273, using the observed distribution, we can compare the 1-σ uncertainty computed in this way with the corresponding probabilities that are 73, 69, 51, 62, 58, 54 and 82%, respectively. We, thus, measure that the typical difference between the 1-σ computed in this way and the 1-σ measured from the observed distribution, is of the order of 10–15%, reaching maximum values of 25% for MCG-6-30-15.
Figure A.1, suggests that the method we have adopted to estimate the uncertainty on the excess variance in the case when there is just a single interval available results in an acceptable-conservative estimate of the true scatter of 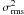 . The same figure also suggests that this result should be valid for AGN with different MBH and intrinsic excess variance values which spans almost four orders of magnitude.
. The same figure also suggests that this result should be valid for AGN with different MBH and intrinsic excess variance values which spans almost four orders of magnitude.
A.4. Estimating the “red noise” scatter: between 2 and 10 intervals
When the number of valid segments is higher than one and lower than 10, we estimated the stochastic scatter for each segment as detailed above, in the case of sources with just a single interval available. Then, following O’Neill et al. (2005), our final estimate of the mean excess variance is equal to the square root of the sum of the squared “error” of the individual segments, divided by the number of intervals. Finally, both in the case of
single and less than 10 intervals, we combined in quadrature the stochastic scatter and the one associated with the Poissonian noise (see Eq. (A.1)).
Appendix B: σ2rms computed in fixed length intervals and time dilation with redshift
Since CAIXAvar is composed mainly of local AGN (see Fig. 1), the impact of the differences in red-shift on the excess variance, if we estimate it using intervals with a fixed length in the observers frame, should be minimal. This is even more obvious in the case of the sources with at least one variable segment detected, whose redshift is less than 0.3 in all (but one) cases. For these objects, segments of fixed length in the observer’s frame should imply differences of less than ~30% in the rest frame segment’s length. Since the excess variance does depend on the maximum frequency sampled, we expect that the intrinsic excess variance should be different, depending on the source’s redshift. However we verified that, for power-spectra like the ones typically observed in AGN (see discussion in Sect. 6.1.3 below), the resulting differences in the intrinsic variance of the sources should be less than ~20% (for a large range in BH mass and accretion rates). This maximum difference is much smaller than the observed scatter in all the variability plots we study below. For this reason, we decided to work with the excess variance measurements that we estimated from the intervals we mentioned above, whose length is fixed, irrespective of the sources redshift. Regarding the highest redshift source (at z = 0.9) in the sample of “variable” objects, we always checked that its presence does not affect in anyway our results from the study of the correlations between the variability amplitude and the various physical parameters we present in this paper.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


