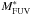| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201118010 | |
| Published online | 23 February 2012 | |
Online material
Appendix A: The weighting schemes
We refer the reader to Le Fèvre et al. (2005b) and Le Fèvre et al. (in prep.) for details on the quality flags assigned to redshift measurements in the VVDS Deep and Ultra-Deep surveys, respectively. We detail below the weighting schemes to be applied to our statistical analyses. They account for the selection function of the photometric sources targeted to acquire their spectrum (the Target Sampling Rate, TSR), and for the success to measure a reliable redshift from the spectrum (the Spectroscopic Success Rate, SSR). They are derived for the Deep survey, the Ultra-Deep survey, and for the merged Deep+Ultra-Deep sample.
To derive the weighting schemes, we made use of the photometric redshifts, zphot, computed as described in Ilbert et al. (2006), but using the more recent T0005 release of CFHTLS photometric data (u∗,g′,r′,i′,z′) and the latest near-infrared photometric data available from WIRDS (J, H and Ks, Bielby et al. 2011).
We emphasise that we correct the Deep and Ultra-Deep distributions of photometric redshifts, n(zphot), for their failure rate computing the ratio between the spectroscopic redshifts measured with a >97% confidence level (flags 3, 4), n(zf = 3,4) and their corresponding photometric redshifts, n(zphotf = 3,4).
A.1. Weights for the Deep survey
The Deep survey TSRd is defined as 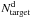 /
/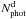 , where
, where 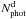 is the number of photometric sources in the Deep survey with 17.5 ≤ IAB ≤ 24.0, over ~2200 arcmin2 of sky area, and
is the number of photometric sources in the Deep survey with 17.5 ≤ IAB ≤ 24.0, over ~2200 arcmin2 of sky area, and 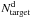 is the number of photometric sources targeted for spectroscopic observations. The TSRd depends on the projection of the angular size of each object on the x-axis of the image (“x-radius”, see also Ilbert et al. 2005). The weight associated to TSRd is
is the number of photometric sources targeted for spectroscopic observations. The TSRd depends on the projection of the angular size of each object on the x-axis of the image (“x-radius”, see also Ilbert et al. 2005). The weight associated to TSRd is 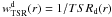 , where r is the x-radius defined above.
, where r is the x-radius defined above.
The Deep survey SSRd is defined as 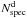 /
/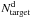 , where
, where 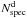 is the number of targets with a reliable spectroscopic redshift measurement in the Deep survey. The SSRd is a function of both selection magnitude and redshift (see Ilbert et al. 2005). As described in Le Fèvre et al. (in prep.), a fraction of low confidence level spectroscopic redshifts (flags 0, 1, 2) at z ≥ 1.4 from the Deep survey have been observed again, leading to a 100% confidence level in the redshift measurement. Comparing the old redshift distribution
is the number of targets with a reliable spectroscopic redshift measurement in the Deep survey. The SSRd is a function of both selection magnitude and redshift (see Ilbert et al. 2005). As described in Le Fèvre et al. (in prep.), a fraction of low confidence level spectroscopic redshifts (flags 0, 1, 2) at z ≥ 1.4 from the Deep survey have been observed again, leading to a 100% confidence level in the redshift measurement. Comparing the old redshift distribution 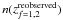 to the new one for this subsample, we have remodulated the full n(zf = 1,2) partially using the n(zphot) for z < 1.4 sources. We have also remodulated the single emission-line redshifts (flags 9) n(zf = 9) according to its n(zphotf = 9). This gives:
to the new one for this subsample, we have remodulated the full n(zf = 1,2) partially using the n(zphot) for z < 1.4 sources. We have also remodulated the single emission-line redshifts (flags 9) n(zf = 9) according to its n(zphotf = 9). This gives: 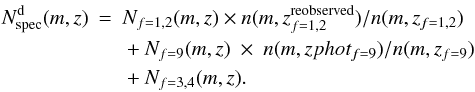 The weight associated to SSRd is
The weight associated to SSRd is 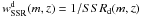 .
.
In summary, for the Deep survey, we have 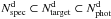 and we apply the weight
and we apply the weight 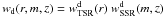 to each galaxy in
to each galaxy in 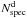 .
.
A.2. Weights for the Ultra-Deep survey
The Ultra-Deep survey covers a 576 arcmin2 sky area embedded in the Deep survey area. It is purely flux limited at 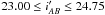 with
with 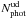 photometric sources. Several spectroscopic sources with 23 ≤ IAB ≤ 24 had already been observed in the VVDS Deep survey, when we started the Ultra-Deep observations. By excluding them, we obtained a reduced catalogue with
photometric sources. Several spectroscopic sources with 23 ≤ IAB ≤ 24 had already been observed in the VVDS Deep survey, when we started the Ultra-Deep observations. By excluding them, we obtained a reduced catalogue with 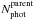 sources available for the Ultra-Deep spectroscopic target selection. The Ultra-Deep Photometric Sampling Rate (PSRud) is defined as
sources available for the Ultra-Deep spectroscopic target selection. The Ultra-Deep Photometric Sampling Rate (PSRud) is defined as 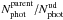 . The PSRud depends on the I-band apparent magnitude. The weight associated to PSRud is
. The PSRud depends on the I-band apparent magnitude. The weight associated to PSRud is 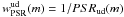 .
.
The Ultra-Deep survey TSRud is defined as 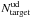 /
/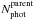 , where
, where 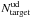 is the number of photometric sources targeted for Ultra-Deep spectroscopic observations. The TSRud does not depend on any parameter, it is a constant value (6.5%). The weight associated to TSRud is
is the number of photometric sources targeted for Ultra-Deep spectroscopic observations. The TSRud does not depend on any parameter, it is a constant value (6.5%). The weight associated to TSRud is 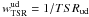 .
.
The Ultra-Deep SSRud is defined as 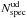 /
/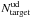 , where
, where 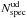 is the number of targets with a reliable spectroscopic redshift measurement in the Ultra-Deep survey. Here Nspec = Nf = 1.5,2,3,4,9, where flags 1.5 is a flag 1 with a photometric redshift in agreement with the spectroscopic redshift (Le Fèvre et al., in prep.). The SSRud is a function of both selection magnitude and redshift. The associated weight is
is the number of targets with a reliable spectroscopic redshift measurement in the Ultra-Deep survey. Here Nspec = Nf = 1.5,2,3,4,9, where flags 1.5 is a flag 1 with a photometric redshift in agreement with the spectroscopic redshift (Le Fèvre et al., in prep.). The SSRud is a function of both selection magnitude and redshift. The associated weight is 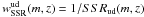 .
.
In summary, for the Ultra-Deep survey, we have 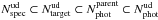 and we apply the weight
and we apply the weight 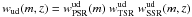 to each galaxy in
to each galaxy in 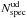 .
.
A.3. Weights for the combined Deep and Ultra-Deep surveys
We combine the two surveys and we derive an adapted weighting scheme to take advantage of both (i) the large magnitude range covered by the Deep survey (17.5 ≤ IAB ≤ 24.0) over a large sky area, and (ii) the depth reached by the Ultra-Deep survey (0.75 mag deeper than the Deep) over a smaller embedded sky area.
As a first step, we need to merge the two catalogues of galaxies in accounting for their different depth, especially for their different LF bias limit (see Sect. 3.1). Since the latter depends on the studied redshift bin, we merge the catalogues in each redshift bin in which we explore the LF, as follows. For the Ultra-Deep survey, we compute the LF bias limits with the method described in Sect. 3.1. For the Deep survey, we adopted more conservative limits with respect to those obtained with the above mentioned method, because of the magnitude range 23 ≤ IAB ≤ 24 common with the Ultra-Deep survey. In the Deep and Ultra-Deep samples we keep only galaxies brighter than the respective bias limit, and we merge the two sub-samples into a single catalogue. From now on, the merged catalogue is considered with flux limits within 17.50 ≤ IAB ≤ 24.75, over the Deep survey effective sky area.
As a second step, we need to slightly modify the TSR weighting scheme for the merged catalogue since the Ultra-Deep area is embedded in the Deep area. The Deep+Ultra-Deep TSRd+ud is 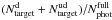 , where
, where 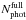 is the full photometric catalogue at 17.50 ≤ IAB ≤ 24.75 over ~ 2200 arcmin2. The TSRu+ud depends on the I-band apparent magnitude (see Fig. A.1). At 17.5 ≤ IAB < 23.0, it corresponds to TSRd when we compute it as a function of magnitude instead of angular size, while at 24.00 < IAB ≤ 24.75, it corresponds to the constant TSRud. At 23 ≤ IAB ≤ 24, it corresponds to the combination of both TSRs, i.e. at the numerator we have all targets of both the Deep and Ultra-Deep surveys. The weight associated to TSRd+ud is
is the full photometric catalogue at 17.50 ≤ IAB ≤ 24.75 over ~ 2200 arcmin2. The TSRu+ud depends on the I-band apparent magnitude (see Fig. A.1). At 17.5 ≤ IAB < 23.0, it corresponds to TSRd when we compute it as a function of magnitude instead of angular size, while at 24.00 < IAB ≤ 24.75, it corresponds to the constant TSRud. At 23 ≤ IAB ≤ 24, it corresponds to the combination of both TSRs, i.e. at the numerator we have all targets of both the Deep and Ultra-Deep surveys. The weight associated to TSRd+ud is 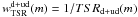 . We applied this weight according to the I-band apparent magnitude to all Deep survey galaxies and to Ultra-Deep galaxies which are brighter than the LF bias limits of the Deep survey. To the Ultra-Deep galaxies which are fainter than the Deep LF bias limits we applied the
. We applied this weight according to the I-band apparent magnitude to all Deep survey galaxies and to Ultra-Deep galaxies which are brighter than the LF bias limits of the Deep survey. To the Ultra-Deep galaxies which are fainter than the Deep LF bias limits we applied the 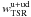 shown for IAB ≥ 24.
shown for IAB ≥ 24.
 |
Fig. A.1
Target Sampling Rate (TSR) for the merged Deep+Ultra-Deep catalogue as a function of the I-band apparent magnitude. Given the different flux limit of the two surveys (see text), this TSR is obtained using Deep data at IAB < 23, both Deep and Ultra-Deep data at 23 ≤ IAB ≤ 24, and Ultra-Deep data at IAB > 24. The last point is low because the Ultra-Deep survey TSR is much lower than the Deep survey TSR. |
| Open with DEXTER | |
In summary, for the merged Deep+Ultra-Deep catalogue, we apply the weight 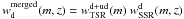 to
to 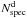 and the weight
and the weight 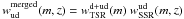 to
to 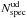 .
.
 |
Fig. A.2
Rest-frame FUV 1 / Vmax LF data points for the Deep survey (cyan empty squares) and the Ultra-Deep survey (blue filled triangles), from z = 0.05 to z = 4.50. There is no Ultra-Deep data in the lowest redshift bin. In each panel, the FUV absolute magnitude LF bias limit (see Sect. 3.1) is shown as a vertical cyan long-dashed line for the Deep survey and as a blue short-dashed line for the Ultra-Deep survey. The number quoted in parenthesis is the total number of used galaxies. We overplot the STY determinations of the merged Deep+Ultra-Deep sample, as illustrated in Fig. 1 and tabulated in Table B.1): (i) with free Schechter parameters (solid lines) and its associated error (shaded area), (ii) in setting the faint-end slope at z > 1.7 (dashed lines), and (iii) in setting |
| Open with DEXTER | |
A.4. The FUV-band LFs using the different weighting schemes
To verify the robustness of our weights, we separately derive the rest-frame FUV LF of the Deep and the Ultra-Deep surveys, using their independent weighting schemes, as described in Appendices A.1 and A.2. Figure A.2 shows the 1 / Vmax data points up to the respective LF bias limit (see Sect. 3.1) for the two surveys, together with the STY LFs of the combined Deep and Ultra-Deep surveys (see Sect. 3.2 and Fig. 1), using the merged weighting scheme, as described in Appendix A.3. On one side, the LF data points of the two surveys fully agree from z = 0.2 to z = 3.5 in their common range of luminosities. This is an a-posteriori check of the reliability of our individual weighting schemes. On the other side, the STY LFs estimated with the merged sample perfectly overlap the 1 / Vmax data points estimated with the two individual surveys. This confirms the reliability of the weighting scheme applied to our merged sample of individual surveys with different depth.
Appendix B: Verifying the robustness of our rest-frame FUV-band LF
Schechter parameters (M∗, α, φ∗) and total luminosity density LD for the rest-frame FUV- and NUV-band galaxy luminosity function for the VVDS Deep+Ultra-Deep sample with the cosmology (Ωm, ΩΛ, h) = (0.3, 0.7, 0.7).
In Sect. 3, we have presented our VVDS rest-frame FUV-band LF estimates from z = 0.05 up to z = 4.5 (see Fig. 1), and we have tabulated the corresponding best Schechter parameters in Table 1. Figure 2 summarises in one panel our best LF fits. In this Appendix, we give further details and tests we have performed to ensure the robustness of our best rest-frame FUV LF, in particular the flatness of the LF faint-end slope at z ≲ 1 and the low normalisation of the LF at z ≳ 3. Table B.1 gives our extensive computations of the Schechter parameters with the STY method, leaving the three Schechter parameters totally free. Obviously, we cannot constrain M∗ at z ≤ 0.2 nor α at z > 1.7. We fixed these two parameters as described in Sect. 3.2, and we also report the results in Table B.1. The entries labelled with a black dot are our final choices taken for our studies and also reported in Table 1.
As shown in Fig. 2, our FUV faint-end slope is quite flat (α ≃ −1) at z < 1.7, that is up to the highest redshift where we can constrain it. The compilation of the α values found in the literature (see Table B.2) shows very scattered values at 0 ≲ z ≲ 6. Nevertheless, it is a notable point that α has been generally found steeper (when estimated and not fixed) than our value. To strengthen the validity of our results against possible biases, we report below our LFs computed using photometric redshifts, using only starburst galaxies, and computed in the rest-frame NUV-band.
B.1. The rest-frame FUV LF with zphot
 |
Fig. B.1
Rest-frame FUV 1 / Vmax LF estimates from z = 0.05 to z = 4.5 derived with the VVDS zphot catalogue up to IAB = 26 (red open diamonds). They are plotted over a grey-scale version of Fig. 1, that is the rest-frame FUV LF of the VVDS Deep+Ultra-Deep spectroscopic sample up to IAB = 24.75. |
| Open with DEXTER | |
We derive the VVDS rest-frame FUV 1 / Vmax estimates using very deep photometric redshifts (zphot, see Appendix A for details). The zphot catalogue is complete up to IAB = 26 and it consists in ~43 000 photometric sources over the VVDS Deep area. In this case, the weighting scheme is obviously not used. The bias limit has been computed in each z bin as explained in Sect. 3.1, and at any z it is clearly fainter than the bias limit in the VVDS Deep+Ultra-Deep spectroscopic sample.
Results are shown in Fig. B.1, and globally overlap our best rest-frame FUV-band LF determinations using the VVDS Deep+Ultra-Deep spectroscopic sample up to IAB = 24.75. Thus, our spectroscopic sample (brighter 1.25 mag in IAB than the zphot sample) does not significantly miss any faint galaxies, which strengthens the reliability of our flat faint-end slope. One small discrepancy occurs at z ≤ 0.2, where the photometric 1 / Vmax points have an higher normalisation with a slightly steeper slope. It is due to the well known degeneracy in the computation of photometric redshifts, i.e., some objects end up with a wrong too low (zphot ≲ 0.3) photometric redshift (see e.g. Ilbert et al. 2009). Furthermore, it confirms once more that our weighting scheme is adequate. This strengthens also the reliability of our low φ∗ value at 3.5 < z ≤ 4.5, which is neither caused by the cut at IAB = 24.75 nor by an incomplete weighting scheme. We refer the reader to Sect. 3.3.2 and to McCracken et al. (2003) for a discussion about photometric completeness with respect to IAB-band magnitude and surface brightness.
B.2. The rest-frame FUV LF of starburst galaxies
 |
Fig. B.2
Rest-frame FUV 1 / Vmax LF estimates from z = 0.05 to z = 4.5 for our intrinsically bluest galaxies (red open circles, VVDS Type 4, see text) in the VVDS Deep+Ultra-Deep spectroscopic sample. They are plotted over a grey-scale version of Fig. 1, that is the rest-frame FUV LF of the total VVDS Deep+Ultra-Deep spectroscopic sample. |
| Open with DEXTER | |
We are interested to check whether the flatness of our slope at z < 1.7 could be due to a very low density of intrinsically reddish galaxies, which could have hidden, in the total sample, very high densities of faint intrinsically blue galaxies. Indeed an I-band selection does not select only starbursting galaxies, in contrast with UV-band selected samples like GALEX (Arnouts et al. 2005).
We have classified our galaxies of the VVDS Deep+Ultra-Deep spectroscopic redshift sample according the VVDS scheme of four photometric types, as described in Zucca et al. (2006). Here, we consider the “Type 4” galaxies, corresponding to galaxies for which the best template fit over the u∗g′r′i′z′JHKs broad bands is among the bluest galaxy templates, i.e., a starburst or irregular galaxy template. The Type 4 rest-frame FUV-band 1 / Vmax LF estimates are shown in Fig. B.2. At z < 1.7, their normalisation is obviously lower with respect to the total sample, because the fraction of Type 4 galaxies in our sample goes from ~40% at z ~ 0.1 up to ~85% at z ~ 4 (when considering galaxies brighter than the bias limit). The faint-end LF slope for Type 4 galaxies is very similar to the one found for the total sample. Our flat slope is obviously not due to very low densities of faint intrinsically red galaxies, which could have overcompensate very high densities of faint intrinsically blue galaxies. Thus, it reinforces the flatness of our slope.
B.3. The rest-frame NUV LF
 |
Fig. B.3
Rest-frame NUV-band LFs from z = 0.05 to z = 4.5 of the VVDS Deep+Ultra-Deep sample, in 10 redshift bins as indicated in each panel. Red circles represent the 1 / Vmax data points up to the LF bias limit and the corresponding number of galaxies are given in parenthesis. The vertical cyan long-dashed and blue short-dashed lines correspond to the LF bias limits for the Deep and Ultra-Deep surveys, respectively. The black solid curve and the associated shaded area is the STY LF estimate assuming free Schechter parameters and its associated error. The dot-dashed curve is the same in each panel, and it corresponds to the solid curve in the 0.2 < z < 0.4 redshift bin, as reference. All Schechter parameters are given in Table B.1. For the NUV-band, we were not interested in fixing either M∗ nor α. We note that in the last redshift bin the STY fit is unconstrained, so there is no solid curve overplotted. |
| Open with DEXTER | |
The last point to test is the fact that our rest-frame FUV magnitudes are based on template extrapolations at z ≤ 1, which could have an impact on the faint-end LF slope. Our bluest photometric information is in the u∗-381 CFHTLS filter, and thus the rest-frame FUV emission is directly observed from z ≥ 1. Nevertheless, the rest-frame NUV emission is directly observed at z ≥ 0.4. Thus we report our results from the rest-frame NUV-band LF of the Deep+Ultra-Deep spectroscopic sample. We list the Schechter parameters derived with the STY method, in Table B.1, and plot the LFs in Fig. B.3. We note that we were not interested in trying to fix M ∗ at low z, nor to fix α at very high z. These estimates enable us to measure the faint-end slope at 0.4 ≲ z ≲ 1, that is where the FUV intrinsic luminosity is extrapolated but not the NUV intrinsic luminosity. Again, we do not find a steeper faint-end slope in the rest-frame NUV-band LFs. As our aim is to derive the SFRD from the rest-frame ultraviolet continuum spanning from FUV to the NUV using the relation of Kennicutt (1998), we can affirm that the extrapolation of the FUV-band luminosities does not change our SFRD results since the faint-end slope stays flat.
Non exhaustive list of the faint-end slope values, α, of the rest-frame FUV-band luminosity functions at 0 < z < 6, as found in the literature.
Appendix C: FUV number counts and luminosity functions at z ~ 3
At 2.7 ≤ z ≤ 3.4, Le Fèvre et al. (2005a) and Le Fèvre et al. (in prep.) show that the VVDS presents number counts per 0.5 mag interval of IAB apparent magnitude per unit surface area (i.e., dN/0.5 mag/arcmin2) at least 2 times larger than those quoted by Steidel et al. (1999) within the same redshift range. This is particularly evident for bright galaxies (IAB ≲ 23.5). In contrast, the VVDS rest-frame FUV LF is only ~50% higher than the one found by Steidel et al. (1999), as illustrated in the left panel of our Fig. C.1, and this holds only for MFUV < −22.5. Here, we demonstrate that these two results are not in conflict. We remark that throughout the paper we compute our VVDS FUV absolute magnitudes using a filter centred at 1500 Å, while Steidel et al. (1999) use a FUV-band filter centred at 1700 Å. To compare our results with their work, in this section we compute our VVDS FUV absolute magnitudes using the same filter as Steidel et al. (1999), even though our VVDS FUV-150 and VVDS-1700 LFs are very similar.
 |
Fig. C.1
Left panel. Comoving luminosity densities as a function of FUV (1700 Å) absolute luminosities at 2.7 ≤ z ≤ 3.4: 1 / Vmax estimates of our VVDS Deep+Ultra-Deep sample fitted with a Schechter function (red circles and dashed curve, respectively); our mST = (r + i) / 2 number counts per volume density for the Deep and Ultra-Deep surveys converted into FUV absolute magnitudes with a rigid shift (see text), and fitted with a Schechter function (blue diamonds and triangles, and solid line, respectively); the mST = ℛ number counts per volume density of Steidel et al. (1999) converted into FUV absolute magnitudes with their rigid shift (see text), and fitted with a Schechter function by them (orange squares and solid line, respectively). Right panel. Number counts per unit volume of galaxies as a function of mST apparent magnitudes at 2.7 ≤ z ≤ 3.4: our number counts from the VVDS Deep and Ultra-Deep surveys (blue diamonds and triangles, respectively); our VVDS number counts derived from our VVDS 1 / Vmax LF (see right panel) shifted rigidly in magnitude (red circles, see text); number counts from Steidel et al. (1999) (orange squares; see text for conversion details). The three curves correspond to the same curves in the left panel, shifted rigidly (see text). Note that the CFHTLS (r + i) / 2 photometric system mimics the ℛ one used by Steidel et al. (1999). |
| Open with DEXTER | |
As Steidel et al. (1999) begin their analysis from galaxy number counts as a function of ℛ apparent magnitude, we overplot the same for the VVDS Deep and Ultra-Deep surveys in the right panel of Fig. C.1. We remark that in this figure we plot the number of galaxies per unit magnitude and per unit volume (i.e., dN/mag/Mpc3), while Steidel et al. (1999) cite in their Table 3 the surface density number counts for 0.5 mag intervals (dN/0.5 mag/arcmin2). To convert their values in dN/mag/Mpc3 units, we multiplied them × 2 to obtain the correct magnitude interval, and we divided for the effective volume of each arcmin2, quoted in their Table 3 (with the same cosmology that we adopt, Ωm = 0.3, ΩΛ = 0.7). Our number counts are weighted as described in Appendices A.1 and A.2, and they are realized as a function of mST = (r + i) / 2 apparent magnitude, i.e., the mean value of the r- and i-CFHTLS broadband filters, because it mimics the ℛ-broadband filter used by Steidel et al. (1999). We observe that the VVDS counts are clearly higher than those from Steidel et al. (1999), at least at the brightest magnitudes.
Next, from their number counts, Steidel et al. (1999) derive their rest-frame FUV LF (shown in the left panel of Fig. C.1), translating apparent magnitudes into absolute magnitudes with the following rigid shift: 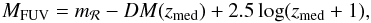 (C.1)where DM(zmed) is the distance modulus defined as 5 × log (DL(zmed) / 10 pc), with DL(zmed) the luminosity distance at zmed, and zmed the median redshift of the studied sample. For their sample at 2.7 ≤ z ≤ 3.4 (zmed = 3.04), it gives:
(C.1)where DM(zmed) is the distance modulus defined as 5 × log (DL(zmed) / 10 pc), with DL(zmed) the luminosity distance at zmed, and zmed the median redshift of the studied sample. For their sample at 2.7 ≤ z ≤ 3.4 (zmed = 3.04), it gives: 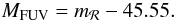 (C.2)For the VVDS Deep+Ultra-Deep sample, at 2.7 ≤ z ≤ 3.4 we have zmed = 2.92. With the same method, starting from our observed number counts (see right panel of Fig. C.1), we obtain the rest-frame FUV LF data points, as illustrated in the left panel of Fig. C.1, and we fitted them with a Schechter function. The result is that our dN-derived LF is higher at the bright end than our direct 1 / Vmax LF data points, as derived in Sect. 3.2, and here fitted also with a Schechter function. We conclude that our N-derived LF presents a different shape than our 1 / Vmax-derived LF.
(C.2)For the VVDS Deep+Ultra-Deep sample, at 2.7 ≤ z ≤ 3.4 we have zmed = 2.92. With the same method, starting from our observed number counts (see right panel of Fig. C.1), we obtain the rest-frame FUV LF data points, as illustrated in the left panel of Fig. C.1, and we fitted them with a Schechter function. The result is that our dN-derived LF is higher at the bright end than our direct 1 / Vmax LF data points, as derived in Sect. 3.2, and here fitted also with a Schechter function. We conclude that our N-derived LF presents a different shape than our 1 / Vmax-derived LF.
Below we verify that, as expected, it is not correct to use a simple, rigid shift to transform our apparent magnitudes to absolute ones, as done with Eq. (C.1), to obtain correct dN-derived LFs. The main reasons are the following.
1) The n(z) shape.: In the range 2.7 ≤ z ≤ 3.4, the redshift distribution n(z) of an I-band selected survey as observed by the VVDS decreases as a function of z as shown in Le Fèvre et al. (in prep.), in particular in a faster way for brighter galaxies. In contrast, due to the colour selection function used to find Lyman-break galaxies, the n(z) in Steidel et al. (1999) peaks around its median value within the same redshift range. The shapes of the different n(z) are shown in the inset of Fig. C.2. If the n(z) is skewed, it is crucial to use the correct redshift distribution in Eq. (C.1), and not simply the median redshift value.
2) The K- and colour corrections.: Steidel et al. (1999) restrict the (K+colour) term to 2.5log(1 + z), as in Eq. (C.1), because they work with the observed ℛ-band, corresponding to the FUV light emitted at z ~ 3. Nevertheless, this is correct for z ~ 3.0 galaxies only.
We made a simple simulation to illustrate these two aspects. We started with a set of 3 × 106 galaxies distributed in FUV absolute magnitude like the Schechter fit of our 1 / Vmax-derived FUV LF. We want to know whether, with a selection function as the VVDS, we recover our observed galaxy number counts as a function of mST apparent magnitude at 2.7 ≤ z ≤ 3.4. Using Eq. (C.1), we operate a rigid shift to transform our FUV absolute magnitudes into mST apparent magnitudes, and to obtain a LF-derived number counts as illustrated in the right panel of Fig. C.1. We call this LF-derived distribution n(mST,LF). We see that these LF-derived number counts are not in agreement with our observed number counts which are at least twice higher at mST < 23. We illustrate in Fig. C.2 the ratio of our observed number counts to our n(mST,LF) as a function of mST. |
Fig. C.2
As a function of mST, ratio of the directly observed VVDS FUV number counts at 2.7 ≤ z ≤ 3.4 to the number counts derived in various ways from the FUV luminosity function in the same z range. The black dotted line (ratio = 1) is the ideal case where both counts are identical. The black solid line represents the ratio of the observed VVDS to the VVDS LF derived counts using Eq. (C.1), n(mST,LF) (i.e. blue solid line to the red dashed line of Fig. C.1, right panel). The other lines represent the ratio of the observed VVDS number counts (the above mentioned blue line) to the following various simulated distributions: n(mST,z) (blue long-dash curve), n(mST,z,K,col) (green short-dash curve) and n(mST,ΔM) (red dot-dash curve). See text for details about these simulated distributions. In the inset, we plot the global shape of the redshift distributions in Steidel et al. (1999) (dashed line) and in our work, separately for faint and bright galaxies (thin and thick solid lines, respectively). The normalisation on the y-axis is consistent between the two solid lines, while the normalisation of the dashed line has been arbitrarily chosen to better illustrate the different shapes. |
| Open with DEXTER | |
We will now test the n(z) and the (K+colour) corrections, respectively. We fit separately the n(z) of VVDS galaxies with mST ≤ 23 and with mST > 23, to account for the steeper n(z) decrease for bright magnitudes (see inset in Fig. C.2). Given the monotonic (even if scattered) relation between observed and absolute magnitudes, mST ~ 23 corresponds to MFUV ~ −21.1. Thus, for each previously simulated galaxy, we assign a redshift in respecting the different n(z) distributions for galaxies brighter or fainter than MFUV = −21.1, that is we do not anymore assume a single median redshift. We now compute the observed mST magnitudes of our simulated sample using Eq. (C.1), where we substitute zmed with the particular redshift that has been assigned to each galaxy. We obtain a mST distribution that we call n(mST,z). The ratio of our observed number counts to the n(mST,z) is shown in Fig. C.2. The n(mST,z) distribution is now closer to our observed number counts than the n(mST,LF) distribution.
As a further step, we account for the (K+colour) terms for each previously simulated galaxy, that is: 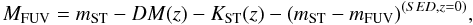 (C.3)
where KST(z) is the K-correction at z and (mST − mFUV) is the colour term at z = 0, both derived from the best SED fitting template. We have modelled the best fitting template distribution in the VVDS sample, which gives us the VVDS distributions of KST(z) and (mST − mFUV)(SED,z = 0) terms. Also in this case we assumed the two n(z) distributions (for faint and bright galaxies) described above. Using the specific distribution of all the terms in Eq. (C.3), we computed a new set of mST starting from our sample of absolute magnitudes, and obtained their distribution (n(mST,z,K,col)). We show in Fig. C.2 the ratio of our observed number counts to the n(mST,z,K,col) distribution. We observe that the modelisation of the K+colour term further improves the match with the observed number counts. Still, the ratio is not equal to unity, which demonstrates that the reality is more complex than a simple simulated recipe.
(C.3)
where KST(z) is the K-correction at z and (mST − mFUV) is the colour term at z = 0, both derived from the best SED fitting template. We have modelled the best fitting template distribution in the VVDS sample, which gives us the VVDS distributions of KST(z) and (mST − mFUV)(SED,z = 0) terms. Also in this case we assumed the two n(z) distributions (for faint and bright galaxies) described above. Using the specific distribution of all the terms in Eq. (C.3), we computed a new set of mST starting from our sample of absolute magnitudes, and obtained their distribution (n(mST,z,K,col)). We show in Fig. C.2 the ratio of our observed number counts to the n(mST,z,K,col) distribution. We observe that the modelisation of the K+colour term further improves the match with the observed number counts. Still, the ratio is not equal to unity, which demonstrates that the reality is more complex than a simple simulated recipe.
To mimic the VVDS observed data, but still with a very simple test, we have fitted with a Gaussian function the distribution of ΔM = MFUV − mST in the VVDS sample. Subtracting from each simulated MFUV a value of ΔM extracted randomly from the distribution, we obtained a new mST distribution, that we called n(mST,ΔM). It is clear that this last distribution (see Fig. C.2) mimics better than the others the real observed number counts distribution at bright magnitudes, but then the match for fainter galaxies is slightly worse.
In summary, this simple exercise confirms that it is very dangerous to transform number counts within a given redshift range to a luminosity function in the case of a skewed n(z) within the redshift interval considered, and/or in the case of dissimilar n(z) for different galaxy populations. The fact that the n(z) of colour-selected samples is very different from the n(z) of magnitude limited samples, implies that number counts when using colour-selected samples are not representative of the number counts for the complete galaxy population. We refer the reader to Le Fèvre et al. (2005a) and Le Fèvre et al. (in prep.) for more details on number counts and sample selections.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.