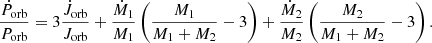| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | A178 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202554603 | |
| Published online | 07 July 2025 | |
Reverse mass transfer and rejuvenation in the massive contact system
1
College of Physics, Guizhou University, Guiyang city, Guizhou Province, 550025
PR China
2
Geneva Observatory, Geneva University, CH-1290
Sauverny, Switzerland
3
College of Physics, Henan Normal University, Xinxiang, Henan Province, 453007
PR China
4
Department of Physics, Anhui Normal University, Wuhu city, Anhui Province, 241000
PR China
⋆ Corresponding authors: hfsong@gzu.edu.cn, georges.meynet@unige.ch
Received:
18
March
2025
Accepted:
26
May
2025
Context. Numerous studies have established that in main-sequence binary systems, mass transfer generally proceeds from the initially more massive star to its less massive companion, thereby inducing rejuvenation in the latter. However, in certain massive close binary systems with orbital periods on the order of a few days, a reversed mass transfer scenario emerges: mass flows from the initially less massive component to the more massive one, during which the two stars simultaneously overflow their Roche lobes. This configuration potentially facilitates stellar rejuvenation in both members of the binary system.
Aims. The phenomenon of reverse mass transfer in binary systems is closely linked to the efficiency of stellar rejuvenation in the mass accretor. However, the physical mechanism driving the rejuvenation of the accretor remains poorly understood. In this work, we employ the Schwarzschild criterion to define the boundaries of convective regions at the solar metallicity, as opposed to the Ledoux criterion typically used for convective conditions at low metallicities. Our study aims to investigate how mass transfer significantly influences the rejuvenation process of the mass-accreting star. Furthermore, we aim to systematically investigate how initial binary parameters (particularly the mass ratio and orbital period) regulate the initiation of reverse mass transfer from the secondary to the primary component.
Methods. We constructed a new set of detailed, grid-based binary evolution models, systematically varying initial orbital periods and mass ratios, q, within a parameter space.
Results. Our results show that for systems with initial primary masses of 16 M⊙ and initial mass ratios of qini= M2M1 ≥ 0.4, those with shorter initial orbital periods, Porb < 1.8 days, are statistically more prone to evolving into contact binaries that exhibit reverse mass transfer. The results further demonstrate that stellar rejuvenation significantly influences the overall evolution of binary systems, notably extending the main-sequence lifetime of the mass-gaining star. Specifically, rejuvenation can induce increases in both the radius and luminosity of the accretor, potentially triggering reverse mass transfer. The transfer causes the mass of accretor’s convective core to increase, facilitating the mixing of fresh fuel from outer layers into the central nuclear-burning region. Following mass transfer, the evolutionary state of the accretor is closer to the zero age main sequence. Due to the high efficiency of rejuvenation, the mass-gaining star can even outpace the mass-losing star in terms of evolution. Meanwhile, the initially more massive star can also undergo rejuvenation via reverse mass transfer, as it must rapidly adapt to its newly increased mass.
Key words: convection / stars: abundances / binaries: close / stars: massive / stars: mass-loss
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In recent years, numerous stellar evolution codes have been employed to investigate the evolution of close binary systems. It is well established that the initially more massive star in such systems undergoes faster evolution than its less massive companion, typically being the first to fill its Roche lobe. In general, binary systems with shorter orbital periods have smaller Roche lobes, leading to an earlier onset of mass transfer via Roche lobe overflow (RLOF). Theoretical binary models demonstrate that any material exceeding the Roche lobe boundary will accrete onto the companion star.
When the more massive star donates mass to its less massive companion, the orbital separation decreases as a result of angular momentum conservation. This scenario can lead to a semidetached configuration and trigger unstable mass transfer occurring on a thermal timescale, where material is transferred at a rate governed by the donor star’s thermal evolution. Case A mass transfer–where the star first fills its Roche lobe during the main-sequence phase–typically comprises a rapid transfer phase (governed by the primary’s thermal timescale) and a slow transfer phase (governed by the nuclear timescale). In such systems, mass transfer typically proceeds from the initially more massive star to its less massive companion. Notably, while the mass-losing (originally more massive) component has been extensively studied, the mass-gaining (originally less massive) star has received comparatively less attention. Some studies have assumed the mass accretor remains inert, passively accumulating all transferred mass and angular momentum Matese & Whitmire (1983), Sepinsky et al. (2007) and Menon et al. (2021) without significant internal redistribution. When the mass ratio of a binary system deviates significantly from unity, the secondary’s response to accretion involves rapid expansion. In close binary systems with orbital periods of several days, the mass-gaining component can exceed its Roche lobe Eggleton (1983). Consequently, a common-envelope binary forms Flannery & Ulrich (1977), Benson (1970) and Ulrich & Burger (1976). In particular, for Case A binaries, the contact state becomes inevitable owing to the initial closeness of the two components. The evolution of low-mass contact binaries has been thoroughly investigated Webbink (1976b), Robertson & Eggleton (1977) and Song et al. (2020). In the contact state, mass transfer ensures that the two components have the same Roche potential.
Recently, Sen et al. (2023) explicitly investigated reverse mass transfer in Algols, which are Case A binaries. Marchant et al. (2016) found that massive binary systems exhibit multiple episodes of alternating mass transfer during contact, including transfer from the initially less massive star to the initially more massive one. Menon et al. (2021) also report an episode of reverse mass transfer that occurred during the contact phase under similar condition, where the initial secondary (or initially less massive star) donates mass to the initial primary. However, the parameter regions that give rise to reverse mass transfer have not yet been explored.
Extensive studies of massive contact binaries have been conducted by Sybesma (1985) and Nakamura & Nakamura (1982), Nakamura & Nakamura (1984). In a complementary line of research, De Loore & De Greve (1992) investigated massive contact binaries with initial masses in the range 9–40 M⊙ and wider orbital periods, 3.95 days < Porb < 25 days, following their evolution through Case B mass transfer until the end of core helium burning in the primary component. Earlier works such as Webbink (1976a) and Robertson & Eggleton (1977) explored the simultaneous evolution of the two components in the contact state. A significant fraction of massive binary systems can ultimately undergo a merger to form new stellar objects de Mink et al. (2013), processes that can give rise to intriguing phenomena such as peculiar supernovae–astrophysical events challenging to reproduce in single-star models. Menon & Heger (2017) and Menon et al. (2019) modeled peculiar Type II supernovae originating from stellar mergers.
Menon et al. (2021) conducted a pioneering systematic investigation of massive contact binaries through extensive binary evolution modeling. Using the Modules for Experiments in Stellar Astrophysics (MESA) code, they computed 5580 evolutionary models, covering a comprehensive range of initial binary parameters for both the Large and Small Magellanic Clouds. Their study revealed that binary systems maintaining prolonged contact phases undergo significant mass exchange, driving the component stars toward mass equalization. Notably, Menon et al. (2021) excluded heat transfer between components in their models, as the surface temperature differences typically remain below 20 percent. In accordance with this approach, we similarly neglected energy transfer between components in our contact binary models for consistency.
This study aims to investigate two key aspects of massive binary evolution: (1) the significant role of mass transfer in rejuvenating the hydrogen-burning core of the mass-accreting component, and (2) the influence of initial system parameters–particularly orbital periods and mass ratios–on binary evolution toward contact phases and subsequent reverse mass transfer scenarios.
The paper is organized as follows: Section 2 outlines the computational methods and initial parameter selection. Section 3 presents the results of our evolutionary calculations. Finally, Section 4 provides comprehensive conclusions and a discussion of the implications of these findings.
2. The initial parameters and model descriptions
We performed stellar evolution calculations using MESA (version r10398; Paxton et al. (2011, 2013, 2015, 2018))
We modeled a binary system with a primary star of 16 M⊙, exploring a parameter space of initial orbital periods ranging from 1.2 days to 2.4 days. Systems with shorter initial periods (i.e., Porb < 1.2 days) come into contact before reaching the zero-age main sequence (ZAMS). Additionally, we investigated initial mass ratios, 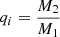 , spanning from 0.1 to 0.9, which allowed us to study how mass transfer and contact evolution depend on the secondary star’s initial mass. We tracked the coupled evolution of both stellar components in detail. The initial chemical composition follows the heavy element mixture of Asplund et al. (2005) with the exception of neon abundance, which adopts the revised values from Cunha et al. (2006). For nuclear reaction rates, we utilized those generated by the NetGen tool1, ensuring up-to-date physics in our stellar evolution calculations. Some nuclear reaction rates have been redetermined and updated (see Ekström et al. (2012) and Angulo et al. (1999) for more details).
, spanning from 0.1 to 0.9, which allowed us to study how mass transfer and contact evolution depend on the secondary star’s initial mass. We tracked the coupled evolution of both stellar components in detail. The initial chemical composition follows the heavy element mixture of Asplund et al. (2005) with the exception of neon abundance, which adopts the revised values from Cunha et al. (2006). For nuclear reaction rates, we utilized those generated by the NetGen tool1, ensuring up-to-date physics in our stellar evolution calculations. Some nuclear reaction rates have been redetermined and updated (see Ekström et al. (2012) and Angulo et al. (1999) for more details).
We assumed synchronous rotation (corotation) for the two stars and neglected secondary spin-up effects, as tidal synchronization is expected to dominate in these close binary systems. We implicitly followed the Ritter scheme (Ritter 1988) to treat the mass transfer process during RLOF, switching to the contact prescription from Marchant et al. (2016) upon RLOF by both components. We disregarded accretion stream kinetic energy and imposed on entropy equilibrium between accreted matter and the gainer’s surface Ulrich & Burger (1976) and Paxton et al. (2015).
The following summarizes the key characteristics of contact phase implementation in MESA, following the methods detailed in Marchant et al. (2018) and Marchant et al. (2016). When the binary mass ratio significantly deviates from unity, the secondary star responds to accretion with rapid expansion, leading to contact or common-envelope binary formation Flannery & Ulrich (1977). In contact binaries, stellar material is not spatially separated. Due to the mass transfer between components, the two stellar surfaces remain on the same equipotential surface Webbink (1976a) and Robertson & Eggleton (1977).
The precise quantification of mass transfer follows the detailed formulation presented in Marchant et al. (2018). We adopted the assumptions that: (1) the mass gainer fully incorporates all transferred material, and (2) the RLOF process remains conservative (see Table 1 for parameters). In the semidetached configuration, the mass transfer stream impacts the secondary directly without forming an accretion disk. The potential energy of the infalling matter is entirely radiated away at the impact location on the stellar surface.
Initial parameters in the computational models.
During the contact phase, we assumed that both stellar surfaces remain on a common equipotential surface. The mass transfer rate between components was dynamically adjusted to maintain the following equilibrium condition:
where Φ represents the common equipotential surface shared by the two stars, Rj and RRL, j denote the volume-equivalent stellar radius and Roche lobe radius, respectively, for each component (j = 1, 2), and q = M2/M1 is the mass ratio with M2 representing the initially less massive star in the binary system.
The function F(q, x), where 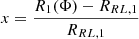 , was determined by numerically integrating the equipotential volumes of both stars through the inner Lagrangian point L1 across various mass ratios. F(q, x) is approximated as F(q, x) = q0.52x for x > 0 with the boundary conditions: F(q, x) = 0 when x = 0 and F(q, x) = 0 when q = 1 (i.e.corresponding to equal-radius stars at equal masses).
, was determined by numerically integrating the equipotential volumes of both stars through the inner Lagrangian point L1 across various mass ratios. F(q, x) is approximated as F(q, x) = q0.52x for x > 0 with the boundary conditions: F(q, x) = 0 when x = 0 and F(q, x) = 0 when q = 1 (i.e.corresponding to equal-radius stars at equal masses).
The volume-equivalent radius corresponding to the outer Lagrangian point L2 (denoted as RL2, 2) is determined by both the Roche lobe radius of the less massive star (RRL, 2) and the instantaneous mass ratio, q, calculated as:
Note that throughout this subsection (and exclusively in this subsection), we adhere to the notation convention established by Marchant et al. (2016) where subscript 1 consistently denotes the currently more massive component at any given evolutionary stage. This designation corresponds to either: (1) the original primary (initially more massive star), or (2) the original secondary (initially less massive star) in cases where mass transfer has reversed the mass ratio.
This study employs several initial parameters and modeling approaches that differ from recent comparable calculations Menon et al. (2021) and Marchant et al. (2016). The key distinctions between our implementation and previous works are systematically compared below.
The occurrence of reverse mass transfer may be closely linked to the efficiency of semi-convective mixing Wellstein et al. (2001). In their study, Menon et al. (2021) implemented the Ledoux criterion for determining convective stability. Their model incorporated additional mixing beyond formally unstable regions through an overshooting parameter αover = 0.335 following the calibration by Brott et al. (2011).
Menon et al. (2021) incorporated semi-convection with an efficiency parameter αsc = 1.0 following the prescription of Langer et al. (1983). This parameter choice critically influences the evolutionary pathways of accreting binary components Braun & Langer (1995). Previous studies have generated extensive grids of binary evolution models for Large and Small Magellanic Cloud metallicities under the assumption of conservative mass transfer. Notably, Marchant et al. (2016) explored four distinct metallicity regimes in their analysis, 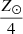 ,
, 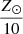 ,
, 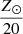 , and
, and 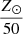 , with Z⊙ = 0.017.
, with Z⊙ = 0.017.
In our study, we employed the Schwarzschild criterion to define convective boundaries. During both hydrogen- and helium-burning phases, we applied convective core overshooting with an extent of αover = 0.25 Hp. The overshooting parameter was constrained by matching the main-sequence band width for stellar clusters with turn-off masses below 15 M⊙ Mermilliod & Maeder (1986). Previous nonrotating models by Mermilliod & Maeder (1986) and Maeder & Meynet (1987) established an optimal overshooting parameter range of 0.25 and 0.3. consistent with the results of Napiwotzki et al. (1991). Our initial composition is set to X = 0.720 (hydrogen), Y = 0.266 (helium), and Z = 0.014 (metals).
The radiative wind mass-loss rate is from Langer (2012). The mass-loss prescription for the hot part of the evolutionary tracks is that of de Jager et al. (1988) for the initial masses 9 M⊙ and 15 M⊙ and for log(Teff/K) > 3.7. For log(Teff/K) < 3.7, we used a fit to the data from Sylvester et al. (1998) and van Loon et al. (1999), as suggested by Crowther (2001).
The orbital angular momentum of a binary system is expressed as
where M1 and M2 are the masses of two components and M1 > M2. This yields the familiar formula
The complete set of initial parameters implemented in our models is systematically presented in Table 1.
3. Results of numerical calculations
3.1. Evolution before the RLOF
Figure 1 shows that the binary parameters of the model with the initial orbital period Porb = 1.2 days change with time. The binary system consists of a 16 M⊙ primary and a 8 M⊙ secondary star. From the onset of the evolution, two components in the binary system expand steadily until they fill in its Roche lobes. During this period of evolution, the central temperature of two components decreases first and then gradually increases. The mean molecular weight (μ) of the core experiences an increase as a consequence of central hydrogen burning. As demonstrated by Pols et al. (2009), for hydrogen burning processes in which the CNO cycle plays a dominant role, the radius follows the scaling law R ∝ μ0.67M0.81. From this equation, it is evident that the radius exhibits a proportional relationship with the 0.67 power of the mean molecular weight μ. Stellar radii increase during main sequence until they fill in Roche lobe. The core temperature remains about constant at the phase of main sequence. The convective core of two components gradually reduces because of the reduced electron-scattering opacity. The orbital separation and period maintain approximately constant values due to the weak stellar wind (see Fig. 1a).
 |
Fig. 1. Evolution of detailed system parameters in the model. Panel (a):Variations in the orbital period and mass ratio with evolutionary time. Other panels: Roche lobe mass transfer rate evolution (b), radii of both components and their corresponding Roche lobe radii (c), central temperature evolution (d), mass changes of both components (e), and convective core mass variations for both components (f). The right panels mirror the left panels but magnify the first episode of rapid mass transfer. The light gray area marks the contact phase in the conservation case. The “r1” denotes the first reverse mass transfer episode (from the initially less massive to the more massive star), while “f1” indicates the first forward mass transfer episode (from the initially more massive to the less massive star). |
3.2. Evolution during the RLOF
A defining characteristic of mass transfer through RLOF is the decline in the orbital period until a mass ratio of 1.0 is achieved (see the red line in the right of Fig. 1a). At the commencement of mass transfer via RLOF, the transfer rate remains low prior to reaching a narrow peak. This provides sufficient time for both components to adjust, thereby maintaining both hydrostatic and thermal equilibrium. As depicted in the right panel Fig. 1b, the mass transfer rate experiences a sharp increase at the left hand side of the narrow peak. This rapid mass transfer phase occurs approximately on the Kelvin–Helmholtz timescale, τKH, of the primary star. The initially more massive star rapidly loses mass and contracts in radius, while the initially less massive star exhibits the opposite behavior (see Fig. 1e). This dynamic process significantly modifies the nuclear and thermal timescales of the two stars.
The mass transfer rate reaches the maximum value when the orbit shrinks. The orbital period reaches a minimum value when the mass ratio of the two components 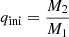 attains 1.0. The shrinking Roche lobe of the primary star indicates that the enhanced rate of mass transfer attains a peak transfer rate of ∼10−4 M⊙/yr (see the right panel of Fig. 1b). At such a high rate, the primary star is driven out of thermal equilibrium. The maximum mass transfer rate is typically well approximated by
attains 1.0. The shrinking Roche lobe of the primary star indicates that the enhanced rate of mass transfer attains a peak transfer rate of ∼10−4 M⊙/yr (see the right panel of Fig. 1b). At such a high rate, the primary star is driven out of thermal equilibrium. The maximum mass transfer rate is typically well approximated by 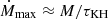 for the primary star Paczyński (1971) see also our Fig. 1b). The maximum mass-transfer rate Ṁmax increases with stellar radius due to the corresponding decrease in the Kelvin-Helmholtz timescale as the primary star expands. Additionally, Ṁmax decreases with the initial mass ratio of the binary system,
for the primary star Paczyński (1971) see also our Fig. 1b). The maximum mass-transfer rate Ṁmax increases with stellar radius due to the corresponding decrease in the Kelvin-Helmholtz timescale as the primary star expands. Additionally, Ṁmax decreases with the initial mass ratio of the binary system, 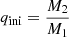 because a higher qini reduces the Roche lobe radius of the mass-losing star.
because a higher qini reduces the Roche lobe radius of the mass-losing star.
Furthermore, a greater amount of mass can be transferred during the rapid mass-transfer phase for systems with smaller initial mass ratios qini. The orbital separation follows a trend similar to the orbital period, consistent with Kepler’s third law a3 ∝ P2 under conservative mass transfer (see the dashed lines in Fig. 1a). As the mass ratio q reverses, the orbital period begins to recover due to the conservation of total angular momentum. The separation increases again. In an initial tighter binary system, the enhanced mass transfer allows the mass-gaining star to accrete more total mass. This leads to a higher central temperature and a higher convective core mass (see Fig. 1e-f).
The rapid mass transfer phase terminates when thermal equilibrium is reestablished in the primary star. If the secondary star does not expand to fill its Roche lobe, mass transfer in the subsequent stage proceeds on a nuclear timescale. However, such systems eventually evolve into contact configurations, making them potentially observable in the universe. The duration of the contact phase strongly depends on the mass transfer timescale, as orbital period variations are closely related to the mass transfer rate (see Ziółkowski & Zdziarski 2018).
The rapid mass transfer leads the secondary to quickly refill its Roche lobe in the binary system with an initial orbital period Porb < 1.6 days. During this rapid mass transfer phase, only one contact phase occurs, located at the position marked in Fig. 1b. Notably, the mass transfer rate during the contact stage remains lower than that of the semidetached stage. This is because the surface potential of the mass gainer star in the semidetached stage is consistently lower than that in the contact stage.
The accretor exhibits immediate rejuvenation during the first episode of mass transfer. As shown in Fig. 1f, The mass gainer’s convective core grows to nearly match the mass loser’s original core mass before RLOF. Specifically, the secondary star’s convective core expands from 2.5 M⊙ to 7.5 M⊙, while its composition is enriched by the less processed material from the overlying layers (see Fig. 3). Concurrently, the central hydrogen mass fraction rises from 0.672 to 0.688, whereas the central helium abundance in the core decreases from 0.311 to 0.289 due to dilution by nuclear matter (Figs. 3c and 3d). Further analysis reveals that the central oxygen abundance increases as fresh oxygen is supplied from the outer envelope, while central carbon decreases owing to the rapid CN cycle (Fig. 3). In contrast, the convective core mass of the mass-losing star demonstrates an opposing trend (Figs. 2 and 3). A significant inverse correlation is observed between the central oxygen abundance and the initial mass ratio 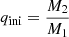 . This relationship arises because systems with smaller
. This relationship arises because systems with smaller 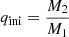 experience higher mass transfer rates during RLOF, driven by rapid orbital separation shrinkage at low mass ratios.
experience higher mass transfer rates during RLOF, driven by rapid orbital separation shrinkage at low mass ratios.
 |
Fig. 2. Evolution of central chemical elements in binary systems with different initial orbital periods and mass ratios for both components. Panel (a): Central hydrogen evolution for systems with initial orbital periods ranging from 1.2 to 1.6 days. Panel (b): Central hydrogen evolution for systems with companion masses between 8.0 M⊙ and 12 M⊙. Panel (c): Same as panel (a) but for helium evolution. Panel (d):Same as panel (b) but for helium evolution. The “RMT” denotes reverse mass transfer from the initially less massive to the initially more massive star. |
 |
Fig. 3. Evolution of central chemical elements in binary systems with different initial orbital periods and component mass ratios. Panel (a): Central oxygen evolution for systems with orbital periods of 1.2–1.6 days. Panel (b): Central oxygen evolution for systems with companion masses of 8.0 M⊙ to 12 M⊙. Panel (c): Same as panel (a) but for carbon evolution. Panel (d): Same as panel (b) but for carbon evolution. |
The mass transfer rate also increases with the initial orbital period. However, a tighter initial orbit results in more extensive stripping of the hydrogen envelope via RLOF. In fact, systems with both a small initial mass ratio (qini) and a short orbital period tend to experience a greater total mass transfer during RLOF. Consequently, the degree of stellar rejuvenation is strongly influenced by the total transferred mass.
The rejuvenation effect has three key implications:
(1): The mass gainer’s radius increases, raising the likelihood of contact formation and subsequent reverse mass transfer.
(2): The influx of fresh hydrogen into the convective core prolongs the mass gainer’s main-sequence phase (see Fig. 2).
(3): The radiative temperature gradient (∇rad) increases, leading to an increase in the convective core.
Notably, rejuvenation is highly dependent on the evolutionary stage of the accreting star. During the main sequence, efficient core-envelope coupling allows for significant rejuvenation. However, after the main sequence, core-envelope decoupling prevents rejuvenation from occurring.
However, as the stellar material accumulates, nuclear burning in core of the mass gainer accelerates. Consequently, the central hydrogen content in its core depletes at an increasing rate, counteracting and ultimately diminishing the rejuvenation effect. Meanwhile, the mass loser’s convective core shrinks due to mass transfer via RLOF, leading to a slight reduction in central carbon abundance as the convective region gradually contracts.
3.3. Thermal readjustment due to mass transfer via the RLOF
When accretion proceeds on a timescale shorter than the accretor’s Kelvin-Helmholtz timescale, the mass-receiving star must undergo rapid structural adjustments to accommodate the incoming material. This rapid accretion primarily compresses the underlying stellar layers, releasing substantial gravitational energy. If the energy release surpasses the star’s radiative capacity, the system is forced out of thermal equilibrium. The excess energy that cannot be efficiently radiated is subsequently diverted into expanding the stellar envelope.
At sufficiently high accretion rates, this mechanism can cause the accretor to expand well beyond its main-sequence radius. Although much of the surplus energy is expended in driving this expansion–thereby diminishing both the temperature gradient and radiative flux–the increased core luminosity eventually outweighs the gravitational energy required for expansion. Consequently, the star can exhibit significantly enhanced luminosity compared to predictions from standard mass-luminosity relations, L ∝ M3.5. This dramatic expansion can have significant consequences: if the accretor (secondary star) possesses a radiative envelope, it can swell until it fills its Roche lobe, potentially triggering the formation of a contact binary system.
When a star experiences sudden mass loss, both its hydrostatic and thermal equilibrium are disrupted. In response, the star undergoes structural readjustment, modifying its radius to restore thermal equilibrium. An immediate pressure drop occurs throughout its interior. This happens because the gravitational force exerted by the removed mass on the stellar surface is eliminated. Consequently, mass transfer has a tendency to suppress internal nuclear burning, which is highly sensitive to temperature fluctuations. In these regions, energy losses due to radiation or convection are no longer replenished by nuclear reactions. As a result, the affected regions are compressed under the weight of the overlying layers until the compression restores nuclear burning, reestablishing a balance with energy losses and enabling the star to reach a new state of thermal equilibrium. Consistent with the mass-radius correlation, the present radius of the donor star is reduced relative to its pre-mass-transfer value.
Correspondingly, the luminosity of the donor star decreases, whereas the secondary star becomes more luminous. For each of the five models presented in Table 1, the first episode of mass transfer occurs on the thermal timescale of the primary star. The luminosity of the primary star decreases significantly due to a larger amount of the transferred mass (see panel b1 in Fig. 4).
 |
Fig. 4. Evolution of detailed binary parameters during the rapid Case A mass transfer episode. Panel (a1): Entropy profile versus mass coordinate for the mass-losing star. Panel (a2): Corresponding profile for the mass-gaining star. panels (b1) and (b2): Luminosity profiles for both components. Panels (c1) and (c2): Temperature profiles. Panels (d1) and (d2): Density profiles. Panels (e1) and (e2): Mean molecular weight profiles. Panels (f1) and (f2): Hydrogen energy production rate, ϵH, profiles for both components. |
Radiative envelopes, characterized by higher central concentration and lower outer-layer density than convective envelopes, respond distinctively to abrupt mass loss. When the outermost layers are rapidly stripped away, the underlying layers decompress and expand adiabatically to reestablish pressure balance. Because radiative envelopes initially exhibit a steeper density gradient, the newly exposed layers following mass loss originate from deeper within the star. As a result, once hydrostatic equilibrium is regained, a star with a radiative envelope contracts to a more compact configuration, achieving a significantly reduced radius.
The core hydrogen depletion rate of the mass-losing star slows down as expected due to mass transfer via RLOF. Following the rapid mass transfer phase, both the luminosity and the size of the primary star’s convective core decrease. The net effect is an extension of the remaining main-sequence lifetime compared to an unperturbed star. The earlier mass transfer begins in a binary system, the more significantly the main-sequence lifetime is prolonged. This mechanism provides a potential pathway for producing blue stragglers, making these stars appear younger than their host cluster.
3.4. The internal profile of some thermodynamic quantities
Figure 4 illustrates the evolution of various physical quantities during mass transfer via RLOF. The temperature profile of the primary (mass-losing) star decreases due to mass loss, while that of the secondary (mass-gaining) star increases (see panels c1 and c2 in Figs. 4 and 5). Consequently, the gainer star rejuvenates toward a ZAMS state, whereas the loser star evolves toward lower temperatures (see Fig. 5).
 |
Fig. 5. Evolutionary tracks of both components in the Hertzsprung-Russell diagram for the 16 M⊙primary binary system. Point A marks the ZAMS. Point B indicates the onset of mass transfer. Point C denotes the peak mass transfer rate. Point D represents the termination of mass transfer. |
This behavior arises because the central temperature scales with stellar mass as 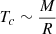 . The quantity M is the stellar mass and R is the stellar radius. Similarly, the central pressure follows
. The quantity M is the stellar mass and R is the stellar radius. Similarly, the central pressure follows 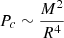 , causing the internal pressure to mirror the temperature trend. Accordingly, the core density decreases in the gainer star but increases in the loser star (see panels d1 and d2 in Fig. 4). The CNO nuclear energy generation rate ϵCNO, being highly temperature-sensitive (i.e., ϵCNO ∝ ε0ρTν with ν ≈ 17 at T ≈ 2.5 × 107 K), exhibits trends similar to the temperature profile (see panels f1 and f2 in Fig. 4).
, causing the internal pressure to mirror the temperature trend. Accordingly, the core density decreases in the gainer star but increases in the loser star (see panels d1 and d2 in Fig. 4). The CNO nuclear energy generation rate ϵCNO, being highly temperature-sensitive (i.e., ϵCNO ∝ ε0ρTν with ν ≈ 17 at T ≈ 2.5 × 107 K), exhibits trends similar to the temperature profile (see panels f1 and f2 in Fig. 4).
The stellar luminosity (L) follows the well-established mass-luminosity relation L ∼ Mα, where α = 3.5 depends on the mass range considered. The mass-luminosity relation is strictly applicable only to main-sequence stars. While stellar luminosity generally increases with mass, the surface luminosity evolution in binary systems exhibits more complex behavior during mass transfer. Specifically, the donor star’s surface luminosity decreases due to its reduced radius and effective temperature, whereas the accretor’s surface luminosity increases as a consequence of its expanded radius and elevated temperature (see panels b1 and b2 in Fig. 4).
During RLOF mass transfer, the core mean molecular weight decreases in the accretor star while increasing in the donor star (see panels e1 and e2 in Fig. 4). This phenomenon is linked to concurrent changes in the convective core structure–specifically, its amplification in the accretor and narrowing in the donor.
The expansion of the convective core in the accretor leads to a reduction in the core mean molecular weight, as it mixes the material with lower core mean molecular weight from the envelope into the core. Conversely, the contraction of the donor’s convective core concentrates the material with higher mean molecular weight produced by nuclear reactions. This dichotomy arises because the accretor’s outer envelope contains the material with a lower mean molecular weight (primarily hydrogen), while the donor’s inner core accumulates elements with a higher mean molecular weight (e.g., helium) from hydrogen burning.
The mean molecular weight at the surface of the mass gainer star increases due to the higher mean molecular weight of the accreted material. This increase is likely to induce thermohaline mixing at the mass gainer’s surface. We find that the entropy profile increases with the mass coordinate. (cf., a1 and a2 in Fig. 4). In the outer radiative layer, the specific entropy gradient follows 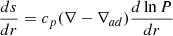 . Hydrostatic equilibrium requires that
. Hydrostatic equilibrium requires that 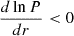 , and ∇ < ∇ad, the condition ds/dr > 0 holds, indicating an outward increase in specific entropy. For the mass-losing star, the specific entropy decreases with mass transfer. This reduction arises from the combined increase in mean molecular weight and density, coupled with the core’s decreasing T3/2. The entropy profile variation is primarily governed by the evolution of T3/2/ρ. Conversely, the mass gainer exhibits an opposing trend. The mean molecular weight and density in the core reduce whereas the quantity T3/2/ρ increases due to the rejuvenation effect. its core experiences a reduction in mean molecular weight and density, while T3/2/ρ increases due to rejuvenation. Consequently, the entropy profile shifts in the opposite direction.
, and ∇ < ∇ad, the condition ds/dr > 0 holds, indicating an outward increase in specific entropy. For the mass-losing star, the specific entropy decreases with mass transfer. This reduction arises from the combined increase in mean molecular weight and density, coupled with the core’s decreasing T3/2. The entropy profile variation is primarily governed by the evolution of T3/2/ρ. Conversely, the mass gainer exhibits an opposing trend. The mean molecular weight and density in the core reduce whereas the quantity T3/2/ρ increases due to the rejuvenation effect. its core experiences a reduction in mean molecular weight and density, while T3/2/ρ increases due to rejuvenation. Consequently, the entropy profile shifts in the opposite direction.
3.5. Contact configuration and the reverse mass transfer
In the mass gainer stars, the residual composition gradient from the contracting convective core is erased following mass transfer (see panel e2 in Fig. 4). The secondary star departs from thermal equilibrium during rapid mass transfer, as the accretion timescale (i.e., the Kelvin-Helmholtz timescale of the donor star) becomes shorter than its own thermal timescale. When this timescale disparity is sufficiently large, the secondary can fill its Roche lobe upon accreting a critical mass. The secondary becomes overluminous relative to its mass and undergoes significant expansion, exceeding its main-sequence radius. Shorter initial orbital periods result in the mass gainer’s radius approaching closer to its Roche lobe. Consequently, initially tight binary systems are more likely to evolve into contact configurations. Pols (1994). Therefore, the contact configuration strongly depends on the orbital evolution and the response to mass accretion (see Fig. 6).
 |
Fig. 6. Diagram of the initial mass ratio, q (ranging from 0.1 to 0.9) versus the initial orbital period, Porb (in days) for binary systems with primary mass M1 = 16 M⊙. The timescale for reverse mass transfer in contact configuration corresponds to the nuclear timescale. The semidetached binary region (shaded) indicates systems that bypass the contact phase, where mass transfer occurs from the initially more massive component to the initially less massive one. |
Figure 6 presents the variation of initial mass ratio qini as a function of initial orbital period Porb for binary systems with an initial primary mass M1 = 16 M⊙. Based on evolutionary calculations, we mapped the parameter space of initial mass ratios qini and orbital periods Porb for massive close binaries, identifying distinct evolutionary outcomes. Our results demonstrate that systems with an initial primary mass of M1 = 16 M⊙ and low mass ratios (qini ≤ 0.4) preferentially form contact binaries through a forward mass transfer (i.e., transfer from the initially more massive component to its less massive companion).
These results demonstrate that when the stellar radius expands sufficiently slowly, the surface potential energy of the mass gainer remains below that of the mass donor throughout the process of mass transfer. However, systems with initial mass ratios (q ≥ 0.4) exhibit markedly different behavior. For close binaries with Porb < 1.6 days, we observe preferential formation of contact binaries through reverse mass transfer (from the initially less massive component to its more massive companion). In these systems, the mass gainer undergoes rapid radial expansion, causing its surface potential to readily surpass that of the mass donor. Notably, higher initial mass ratios (q ≥ 0.7) in wider systems (Porb > 1.8 days) favor the development of semidetached configurations through standard forward mass transfer (from the more massive to less massive star).
Following the initial brief contact phase, the mass gainer evolves into the more massive component with a nuclear timescale shorter than the donor’s after 5.33 Myr. The system transitions to a detached configuration, persisting from 5.34 Myr to 10.1 Myr (Fig. 1b), during which the donor star reestablishes thermal equilibrium. Subsequent mass transfer, driven by stellar expansion, proceeds on nuclear timescales from approximately 10.2 Myr to 15.5 Myr. For systems with initial orbital periods Pini, orb = 1.2 days, the mass gainer continues accreting material during the second mass transfer episode. Our calculations reveal that the secondary’s mass increases gradually during this slow transfer phase (∼10−6 M⊙/yr), characteristic of semidetached, Algol-type binaries. Several observed systems exhibit similar properties, such as V Pup (B1+B2; 17+9 M⊙; 1.45 days; Popper 1980). The accelerated evolution of the initially less massive component (now the more evolved star) leads to secular expansion that may produce RLOF, potentially forming a contact binary. In this subsequent contact phase, reverse mass transfer occurs on thermal timescales.
Binary systems characterized by initially compact orbits (small Porb) and low mass ratios (qini) exhibit a higher probability of establishing contact during rapid mass transfer phases. Our analysis reveals an inverse correlation between the initial orbital period and contact binary formation timescale–systems with shorter initial periods achieve contact configurations earlier in their evolution.
The contact phase establishes itself through dynamically unstable mass transfer. This configuration triggers reverse mass transfer (from the originally less massive component to its initially more massive companion), operating on the thermal timescale of the donor star. This process effectively inverts the system’s mass ratio for the second time. The initially more massive star can be rejuvenated by this reverse mass transfer, as fresh hydrogen is mixed into its core Xc, increasing the central hydrogen abundance and extending its main-sequence lifetime (see Fig. 2). Following this phase, the reinvigorated (now more massive) accretor evolves along accelerated evolutionary tracks, ultimately refilling its Roche lobe. The subsequent contact phase typically persists for significantly longer durations compared to earlier stages. As illustrated in Fig. 8, this extended contact epoch facilitates yet another mass ratio inversion.
3.6. Evolution of the stellar mass and the orbital period
Figure 6 presents the orbital period evolution for five binary systems spanning different initial orbital periods and mass ratios. The orbital period increases significantly after mass reverse due to the mass transfer from the current less massive star to the more massive star) (see Fig. 6). In the subsequent slow mass transfer phase, in systems with an initial Porb = 1.2 days, matter is transferred from the current less massive star to the current more massive star, further increasing the orbital period. Figure 8 also shows that the inverse mass transfer causes the orbit to shrink, highlighting the strong dependence of orbital evolution on mass transfer between the two components.
In fact, the evolution of the orbital period is highly dependent on the mass ratio of the two components and how the mass ratio, q, changes throughout the mass transfer process (e.g., Pribulla 1998). As shown in Fig. 8, the shorter initial orbital periods result in shorter final orbital periods. The shorter initial orbital period also increases the likelihood of reverse mass transfer, indicating that more material is transferred from the initially less massive star to the initially more massive star during reverse mass transfer. Panel (a) of Fig. 7 reveals that the smaller initial orbital period lead to a higher number of reverse mass transfer event and longer durations of these events. Similar trends are observed for the mass ratio: larger initial mass ratios 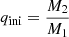 result in more mass being transferred during the rapid Case A mass transfer episode (see Fig. 8), and longer contact phases. Smaller initial mass ratios lead to smaller final orbital periods, making the binary system more likely to merge (see right panel of Fig. 8). Binary systems with large initial orbital periods are unfavorable for reverse mass transfer. For example, a system with an initial orbital period Porb = 1.6 days does not exhibit reverse mass transfer. Over time, the binary systems with small initial orbital periods and mass ratios tend to merge.
result in more mass being transferred during the rapid Case A mass transfer episode (see Fig. 8), and longer contact phases. Smaller initial mass ratios lead to smaller final orbital periods, making the binary system more likely to merge (see right panel of Fig. 8). Binary systems with large initial orbital periods are unfavorable for reverse mass transfer. For example, a system with an initial orbital period Porb = 1.6 days does not exhibit reverse mass transfer. Over time, the binary systems with small initial orbital periods and mass ratios tend to merge.
 |
Fig. 7. Left: Stellar mass evolution for three binary systems with different initial orbital periods. Right: Stellar mass evolution for three binary systems with different initial mass ratios. |
 |
Fig. 8. Left: Orbital period evolution for three systems with different initial orbital periods. Right: Orbital period evolution for three systems with different initial mass ratios. |
The positions of the outer Lagrangian points L2 or L3 relative to the center of mass are proportional to the binary separation. It is well known that the principal mechanism that causes orbital changes is mass transfer between two components. Contact binaries form when the accretor star fills its Roche lobe during a mass transfer phase. Our models predict that Case-A binaries mainly get into contact and merges because of runaway mass transfer and the expansion of the accretion on a thermal timescale. Because the secondary is initially less massive than the primary, the secondary’s Roche lobe initially shrinks as a result of mass transfer (the minimum orbital separation is reached when the masses are equal). Furthermore, the secondary deviates from thermal equilibrium in response to rapid mass transfer, because the accretion timescale (i.e., the thermal timescale of the primary) is shorter than the thermal timescale of the secondary. Whether or not contact is reached is mostly determined by the reaction of the secondary star to the accretion. The mass gainer becomes overluminous for its mass, when the difference in timescales is very large. It expands significantly beyond its main-sequence radius. Consequently, the secondary can fill its Roche lobe after the transfer of a certain amount of mass. The tighter systems with initial orbital period about Porb < 1.6 days attain the contact state, with a merger as the likely outcome in the contact state. The smaller the initial period, the closer the secondary radius approaches the outer Lagrangian point L2. The closest system with initial orbital period Porb = 1.2 days almost touches its the outer Lagrangian point L2. The moment of the outer Lagrangian point L2-overflow is a stopping condition once the radii of the components are compared to the outer Lagrangian point L2 volume-equivalent radii from Marchant et al. (2016).
If the expansion happens on the accretor’s thermal timescale, two things can happen. If the thermal expansion of the accretor continues, the contact binary will be unstable and likely merge. If the thermal expansion halts upon reaching contact, the contact phase tends to be relatively short-lived since the accretor typically shrinks again after regaining thermal equilibrium.
During runaway (unstable) mass transfer, the primary star increasingly overfills its Roche lobe, and the secondary’s expansion timescale becomes orders of magnitude lower than its thermal timescale. When the primary star is a main sequence or Hertzsprung-gap star, a contact binary forms and merge on a timescale shorter than the primary’s thermal timescale because of the runaway expansion of both components.
When the common envelope of a stable contact binary increasingly overfills the Roche lobe (e.g. because of the expansion of the components or orbital shrinkage), it can fill the outer Lagrangian point L2-lobe. Expansion beyond this point leads to mass loss though the outer Lagrangian L2 point (L2-overflow). Mass loss from the outer Lagrangian L2 point will take away a significant amount of specific angular momentum from the system, which can lead to rapid orbital shrinkage and a subsequent merger. The rate of orbital shrinkage and hence the time until the merging event depends on the mass-loss rate and the outflow velocity through the outer Lagrangian point L2.
4. Summary and conclusion
For systems with an initial high mass ratio (q ≥ 0.4) and a primary mass of 16 M⊙, tight orbital configurations (Porb < 1.6) preferentially evolve into contact binaries that undergo reverse mass transfer. These binary systems ultimately lead to a merger of the two components. Conversely, systems with initially low mass ratios (qini ≤ 0.4) tend to form contact binaries via forward mass transfer. A wider binary system is more likely to evolve into a semidetached system where mass transfer proceeds in the forward direction (i.e., mass transfer typically occurs from the initially more massive component to its less massive counterpart).
Stellar rejuvenation is strongly dependent on the mass transfer efficiency through RLOF, making it intrinsically linked to both the initial mass ratio and orbital period. This rejuvenation process has significant effects: (1) The expansion of the mass gainer’s radius enhances the probability of reverse mass transfer initiation. (2) The secondary’s main-sequence lifetime extends due to increased hydrogen mixing into its convective core. (3) The radiative temperature gradient (∇rad) elevation leads to convective core expansion.
When mass is transferred from the initially more massive star to its companion, the primary star’s central hydrogen depletion rate slows. Following the rapid mass transfer phase, the mass-losing star has a reduced luminosity and a smaller convective core. Consequently, its remaining main-sequence lifetime becomes longer than that of an isolated star. The earlier the mass transfer begins in a binary system, the more significantly the main-sequence lifetime of the initially more massive star is extended. Additionally, due to the contraction of the convective core, the resulting central carbon abundance becomes slightly lower.
The lifetime of the initially less massive star can be significantly extented due to stellar rejuvenation. Mass transfer via RLOF erases the weak composition gradient left by the contracting convective core. The accreted material enlarges the star’s convective core, mixing fresh hydrogen from outer layers into the central burning region. As a result, the star becomes more luminous than expected for its mass on the main sequence, and its radius expands significantly.
During the rapid mass transfer phase, the thermal timescale of the accretor significantly exceeds the accretion timescale, causing the secondary to expand rapidly and fill its Roche lobe. The formation of a contact configuration is highly sensitive to the initial orbital period, mass ratio, and the accretor’s response to mass transfer. Due to mass accretion, the nuclear timescale of the mass gainer (which scales roughly as τnuc ∼ M−2.8) is substantially reduced. As a result, the mass gainer evolves faster than the mass donor, leading to both a contact state and potential reverse mass transfer. However, if the initial orbital period is sufficiently long, reverse mass transfer can be avoided.
Acknowledgments
This work was sponsored by the National Natural Science Foundation of China (Grant Nos. 11863003, 12173010), Swiss National Science Foundation (project number 200020-172505), Science and technology plan projects of Guizhou province (Grant No. [2018]5781). Dr. Y. Qin acknowledges support from the Anhui Provincial Natural Science Foundation (grant No. 2308085MA29), and the National Natural Science Foundation of China (grant No. 12473036), and the Anhui Province Graduate Education Quality Engineering Project (grant No. 2024qyw/sysfkc012).
References
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. I. Barnes, G. Thomas, & F. N. Bash, ASP Conf. Ser., 336, 25 [NASA ADS] [Google Scholar]
- Benson, R. S. 1970, BAAS, 2, 295 [Google Scholar]
- Braun, H., & Langer, N. 1995, A&A, 297, 483 [NASA ADS] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A. 2001, in The Influence of Binaries on Stellar Population Studies, ed. D. Vanbeveren, Astrophys. Space Sci. Lib., 264, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Hubeny, I., & Lanz, T. 2006, ApJ, 647, L143 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- De Loore, C., & De Greve, J. P. 1992, A&AS, 94, 453 [NASA ADS] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- Flannery, B. P., & Ulrich, R. K. 1977, ApJ, 212, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
- Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 1987, A&A, 182, 243 [NASA ADS] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchant, R., Richer, S., Boles, O., et al. 2018, Earth Sci. Rev., 178, 322 [Google Scholar]
- Matese, J. J., & Whitmire, D. P. 1983, ApJ, 266, 776 [Google Scholar]
- Menon, A., & Heger, A. 2017, MNRAS, 469, 4649 [NASA ADS] [Google Scholar]
- Menon, A., Utrobin, V., & Heger, A. 2019, MNRAS, 482, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, A., Langer, N., de Mink, S. E., et al. 2021, MNRAS, 507, 5013 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J. C., & Maeder, A. 1986, A&A, 158, 45 [Google Scholar]
- Nakamura, M., & Nakamura, Y. 1982, Ap&SS, 83, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, M., & Nakamura, Y. 1984, Ap&SS, 104, 367 [Google Scholar]
- Napiwotzki, R., Schoenberner, D., & Weidemann, V. 1991, A&A, 243, L5 [NASA ADS] [Google Scholar]
- Paczyński, B. 1971, ARA&A, 9, 183 [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R. 1994, A&A, 290, 119 [Google Scholar]
- Pols, O. R., Izzard, R. G., Glebbeek, E., & Stancliffe, R. J. 2009, PASA, 26, 327 [Google Scholar]
- Popper, D. M. 1980, ARA&A, 18, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Pribulla, T. 1998, Contrib. Astron. Obs. Skalnate Pleso, 28, 101 [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Robertson, J. A., & Eggleton, P. P. 1977, MNRAS, 179, 359 [NASA ADS] [Google Scholar]
- Sen, K., Langer, N., Pauli, D., et al. 2023, A&A, 672, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sepinsky, J. F., Willems, B., Kalogera, V., & Rasio, F. A. 2007, ApJ, 667, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Song, H., Meynet, G., Maeder, A., et al. 2020, ApJ, 905, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Sybesma, C. H. B. 1985, A&A, 142, 171 [NASA ADS] [Google Scholar]
- Sylvester, R. J., Skinner, C. J., & Barlow, M. J. 1998, MNRAS, 301, 1083 [Google Scholar]
- Ulrich, R. K., & Burger, H. L. 1976, ApJ, 206, 509 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- Webbink, R. F. 1976a, ApJ, 209, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1976b, ApJS, 32, 583 [Google Scholar]
- Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ziółkowski, J., & Zdziarski, A. A. 2018, MNRAS, 480, 1580 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Evolution of detailed system parameters in the model. Panel (a):Variations in the orbital period and mass ratio with evolutionary time. Other panels: Roche lobe mass transfer rate evolution (b), radii of both components and their corresponding Roche lobe radii (c), central temperature evolution (d), mass changes of both components (e), and convective core mass variations for both components (f). The right panels mirror the left panels but magnify the first episode of rapid mass transfer. The light gray area marks the contact phase in the conservation case. The “r1” denotes the first reverse mass transfer episode (from the initially less massive to the more massive star), while “f1” indicates the first forward mass transfer episode (from the initially more massive to the less massive star). |
| In the text | |
 |
Fig. 2. Evolution of central chemical elements in binary systems with different initial orbital periods and mass ratios for both components. Panel (a): Central hydrogen evolution for systems with initial orbital periods ranging from 1.2 to 1.6 days. Panel (b): Central hydrogen evolution for systems with companion masses between 8.0 M⊙ and 12 M⊙. Panel (c): Same as panel (a) but for helium evolution. Panel (d):Same as panel (b) but for helium evolution. The “RMT” denotes reverse mass transfer from the initially less massive to the initially more massive star. |
| In the text | |
 |
Fig. 3. Evolution of central chemical elements in binary systems with different initial orbital periods and component mass ratios. Panel (a): Central oxygen evolution for systems with orbital periods of 1.2–1.6 days. Panel (b): Central oxygen evolution for systems with companion masses of 8.0 M⊙ to 12 M⊙. Panel (c): Same as panel (a) but for carbon evolution. Panel (d): Same as panel (b) but for carbon evolution. |
| In the text | |
 |
Fig. 4. Evolution of detailed binary parameters during the rapid Case A mass transfer episode. Panel (a1): Entropy profile versus mass coordinate for the mass-losing star. Panel (a2): Corresponding profile for the mass-gaining star. panels (b1) and (b2): Luminosity profiles for both components. Panels (c1) and (c2): Temperature profiles. Panels (d1) and (d2): Density profiles. Panels (e1) and (e2): Mean molecular weight profiles. Panels (f1) and (f2): Hydrogen energy production rate, ϵH, profiles for both components. |
| In the text | |
 |
Fig. 5. Evolutionary tracks of both components in the Hertzsprung-Russell diagram for the 16 M⊙primary binary system. Point A marks the ZAMS. Point B indicates the onset of mass transfer. Point C denotes the peak mass transfer rate. Point D represents the termination of mass transfer. |
| In the text | |
 |
Fig. 6. Diagram of the initial mass ratio, q (ranging from 0.1 to 0.9) versus the initial orbital period, Porb (in days) for binary systems with primary mass M1 = 16 M⊙. The timescale for reverse mass transfer in contact configuration corresponds to the nuclear timescale. The semidetached binary region (shaded) indicates systems that bypass the contact phase, where mass transfer occurs from the initially more massive component to the initially less massive one. |
| In the text | |
 |
Fig. 7. Left: Stellar mass evolution for three binary systems with different initial orbital periods. Right: Stellar mass evolution for three binary systems with different initial mass ratios. |
| In the text | |
 |
Fig. 8. Left: Orbital period evolution for three systems with different initial orbital periods. Right: Orbital period evolution for three systems with different initial mass ratios. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



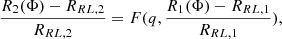
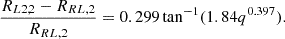
![$$ \begin{aligned} J_{\rm orb}=\frac{M_{1}M_{2}(G^{2}P_{\rm orb})^{1/3}}{[2\pi (M_{1}+M_{2})]^{1/3}}, \end{aligned} $$](/articles/aa/full_html/2025/07/aa54603-25/aa54603-25-eq11.gif)