Dark skies of the slightly eccentric WASP-18 b from its optical-to-infrared dayside emission

Open Access

Table I.1

Values of the systematic parameters for CHEOPS.

Background	a _bkg [ppm] 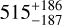$515_{- 187}^{+ 186}$ ${515}_{-{187}}^{+{186}}$	b _bkg [ppm] 695 ± 96
Roll angle	σ_GP [ppm] 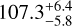${107.3}_{- 5.8}^{+ 6.4}$ ${107.3}_{-{5.8}}^{+{6.4}}$	ρ_GP [deg] 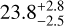${23.8}_{- 2.5}^{+ 2.8}$ ${23.8}_{-{2.5}}^{+{2.8}}$
	σ_w [ppm]	f ₀	c ₁ [day⁻¹]
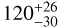
Visit 01	$120_{- 30}^{+ 26}$ ${120}_{-{30}}^{+{26}}$	{0.999843 ± 0.000054}	–
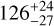
Visit 02	$126_{- 27}^{+ 24}$ ${126}_{-{27}}^{+{24}}$	0.999802 ± 0.000053	–
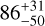
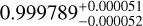
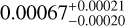
Visit 03	$86_{- 50}^{+ 31}$ ${86}_{-{50}}^{+{31}}$	${0.999789}_{- 0.000052}^{+ 0.000051}$ ${0.999789}_{-{0.000052}}^{+{0.000051}}$	${0.00067}_{- 0.00020}^{+ 0.00021}$ ${0.00067}_{-{0.00020}}^{+{0.00021}}$
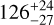
Visit 04	$126_{- 27}^{+ 24}$ ${126}_{-{27}}^{+{24}}$	0.999791 ± 0.000050	–
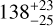
Visit 05	$138_{- 25}^{+ 23}$ ${138}_{-{25}}^{+{23}}$	0.999806 ± 0.000051	–
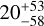
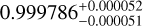
Visit 06	$20_{- 58}^{+ 53}$ ${20}_{-{58}}^{+{53}}$	${0.999786}_{- 0.000051}^{+ 0.000052}$ ${0.999786}_{-{0.000051}}^{+{0.000052}}$	–
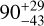
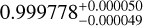
Visit 07	$90_{- 43}^{+ 29}$ ${90}_{-{43}}^{+{29}}$	${0.999778}_{- 0.000049}^{+ 0.000050}$ ${0.999778}_{-{0.000049}}^{+{0.000050}}$	–
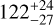
Visit 08	$122_{- 27}^{+ 24}$ ${122}_{-{27}}^{+{24}}$	0.999775 ± 0.000050	–
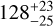
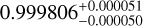
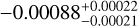
Visit 09	$128_{- 25}^{+ 23}$ ${128}_{-{25}}^{+{23}}$	${0.999806}_{- 0.000050}^{+ 0.000051}$ ${0.999806}_{-{0.000050}}^{+{0.000051}}$	${- 0.00088}_{- 0.00021}^{+ 0.00022}$ ${-0.00088}_{-{0.00021}}^{+{0.00022}}$
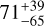
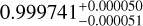
Visit 10	$71_{- 65}^{+ 39}$ ${71}_{-{65}}^{+{39}}$	${0.999741}_{- 0.000051}^{+ 0.000050}$ ${0.999741}_{-{0.000051}}^{+{0.000050}}$	–
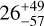
Visit 11	$26_{- 57}^{+ 49}$ ${26}_{-{57}}^{+{49}}$	0.999764 ± 0.000049	–
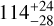
Visit 12	$114_{- 28}^{+ 24}$ ${114}_{-{28}}^{+{24}}$	0.999808 ± 0.000049	–
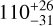
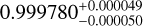
Visit 13	$110_{- 31}^{+ 26}$ ${110}_{-{31}}^{+{26}}$	${0.999780}_{- 0.000050}^{+ 0.000049}$ ${0.999780}_{-{0.000050}}^{+{0.000049}}$	–
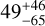
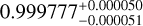
Visit 14	$49_{- 65}^{+ 46}$ ${49}_{-{65}}^{+{46}}$	${0.999777}_{- 0.000051}^{+ 0.000050}$ ${0.999777}_{-{0.000051}}^{+{0.000050}}$	–
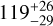
Visit 15	$119_{- 29}^{+ 26}$ ${119}_{-{29}}^{+{26}}$	1.000084 ± 0.000055	–
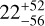
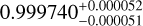
Visit 16	$22_{- 56}^{+ 52}$ ${22}_{-{56}}^{+{52}}$	${0.999740}_{- 0.000051}^{+ 0.000052}$ ${0.999740}_{-{0.000051}}^{+{0.000052}}$	–
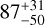
Visit 17	$87_{- 50}^{+ 31}$ ${87}_{-{50}}^{+{31}}$	0.999772 ± 0.000051	–
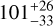
Visit 18	$101_{- 33}^{+ 26}$ ${101}_{-{33}}^{+{26}}$	1.000101 ± 0.000051	–
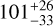
Visit 19	$101_{- 33}^{+ 26}$ ${101}_{-{33}}^{+{26}}$	1.000062 ± 0.000050	–
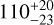
Visit 20	$110_{- 23}^{+ 20}$ ${110}_{-{23}}^{+{20}}$	0.999665 ± 0.000049	–
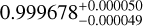
Visit 21	145 ± 18	${0.999678}_{- 0.000049}^{+ 0.000050}$ ${0.999678}_{-{0.000049}}^{+{0.000050}}$	–
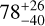
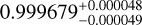
Visit 22	$78_{- 40}^{+ 26}$ ${78}_{-{40}}^{+{26}}$	${0.999679}_{- 0.000049}^{+ 0.000048}$ ${0.999679}_{-{0.000049}}^{+{0.000048}}$	–
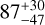
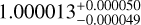
Visit 23	$87_{- 47}^{+ 30}$ ${87}_{-{47}}^{+{30}}$	${1.000013}_{- 0.000049}^{+ 0.000050}$ ${1.000013}_{-{0.000049}}^{+{0.000050}}$	–
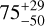
Visit 24	$75_{- 50}^{+ 29}$ ${75}_{-{50}}^{+{29}}$	0.999891 ± 0.000049	–
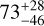
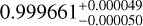
Visit 25	$73_{- 46}^{+ 28}$ ${73}_{-{46}}^{+{28}}$	${0.999661}_{- 0.000050}^{+ 0.000049}$ ${0.999661}_{-{0.000050}}^{+{0.000049}}$	–
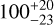
Visit 26	$100_{- 23}^{+ 20}$ ${100}_{-{23}}^{+{20}}$	0.999664 ± 0.000049	–
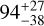
Visit 27	$94_{- 38}^{+ 27}$ ${94}_{-{38}}^{+{27}}$	1.000069 ± 0.000049	–
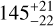
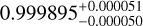
Visit 28	$145_{- 22}^{+ 21}$ ${145}_{-{22}}^{+{21}}$	${0.999895}_{- 0.000050}^{+ 0.000051}$ ${0.999895}_{-{0.000050}}^{+{0.000051}}$	–
Visit 29	176 ± 17	0.999659 ± 0.000049	–
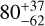
Visit 30	$80_{- 62}^{+ 37}$ ${80}_{-{62}}^{+{37}}$	0.999937 ± 0.000056	–
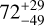
Visit 31	$72_{- 49}^{+ 29}$ ${72}_{-{49}}^{+{29}}$	0.999928 ± 0.000049	0.00037 ± 0.00012
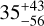
Visit 32	$35_{- 56}^{+ 43}$ ${35}_{-{56}}^{+{43}}$	0.999888 ± 0.000050	${0.00101}_{- 0.00014}^{+ 0.00015}$ ${0.00101}_{-{0.00014}}^{+{0.00015}}$
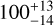
Visit 33	$100_{- 14}^{+ 13}$ ${100}_{-{14}}^{+{13}}$	0.999643 ± 0.000048	0.00012 ± 0.00002
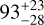
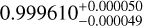
Visit 34	$93_{- 28}^{+ 23}$ ${93}_{-{28}}^{+{23}}$	${0.999610}_{- 0.000049}^{+ 0.000050}$ ${0.999610}_{-{0.000049}}^{+{0.000050}}$	–
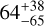
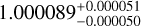
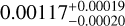
Visit 35	$64_{- 65}^{+ 38}$ ${64}_{-{65}}^{+{38}}$	${1.000089}_{- 0.000050}^{+ 0.000051}$ ${1.000089}_{-{0.000050}}^{+{0.000051}}$	${0.00117}_{- 0.00020}^{+ 0.00019}$ ${0.00117}_{-{0.00020}}^{+{0.00019}}$
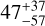
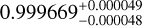
Visit 36	$47_{- 57}^{+ 37}$ ${47}_{-{57}}^{+{37}}$	${0.999669}_{- 0.000048}^{+ 0.000049}$ ${0.999669}_{-{0.000048}}^{+{0.000049}}$	–
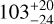
Visit 37	$103_{- 24}^{+ 20}$ ${103}_{-{24}}^{+{20}}$	0.999605 ± 0.000050	–

Notes. The background parameters a _bkg and b _bkg are the ones defined in Eq. 1. The roll-angle GP hyperparameters σ_GP and ρ_GP are the standard deviation of the process and the correlation scale in roll-angle unit (deg), respectively (see Section 4.1). The parameters σ _w, f₀ and c ₁ are the additive noise jitter term, the flux normalisation factor and the flux linear slope, respectively. σ_w is expressed in parts-per-million (ppm) and is added to all error bars quadratically. A negative value of σ _w means that the error bars are shrunk. Each f ₀ value is fitted after the corresponding data set has been normalised by its median value (i.e. all flux values are close to 1 and without units). The linear slope c ₁ is expressed in normalised flux units per day.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.