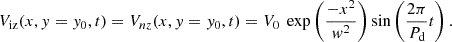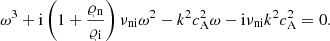| Issue |
A&A
Volume 698, May 2025
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 6 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202554085 | |
| Published online | 28 May 2025 | |
Driven two-fluid Alfvén waves in a solar magnetic flux tube with a realistic ionization rate
Institute of Physics, University of M. Curie-Skłodowska, Pl. M. Curie-Skłodowskiej 1, 20-031 Lublin, Poland
⋆ Corresponding author.
Received:
9
February
2025
Accepted:
23
April
2025
Context. This study was performed in the context of the chromosphere and low corona heating.
Aims. We considered the evolution of driven Alfvén waves in the solar atmosphere, whose initial state was modeled with a realistic ionization profile. We discuss their potential role in plasma heating.
Methods. Two- and half-dimensional (2.5 D) numerical simulations of the solar atmosphere were performed with the use of the code JOANNA. The dynamics of the atmosphere was described by the two-fluid equations (and ionization and recombination terms were taken into account) for ions (protons) combined with electrons and neutrals (hydrogen atoms). The initial atmosphere was described by a hydrostatic background supplemented by the Saha equation and embedded in a magnetic flux tube. This background was perturbed by a monochromatic driver that operated in the transversal components of the ion and neutral velocities.
Results. We demonstrated that as a result of ion-neutral collisions, Alfvén waves are damped. The damping length grows with the wave period. This is anticipated based on the linear theory for a homogeneous medium. The developed flux-tube model results at higher temperatures rise for shorter periods of the driving wave, and the effect is stronger than for the pure hydrostatic state.
Conclusions. We highlight the importance of taking the realistic background plasma into account in the evolution of two-fluid Alfvén waves that participate in the thermal energy release and in the heating in the solar chromosphere and low corona.
Key words: Sun: activity / Sun: atmosphere / Sun: chromosphere
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
It is well established that as a result of their low temperatures, neutrals dominate the photosphere, and the chromosphere is weakly ionized. The abundance of neutral atoms in these atmosphere layers leads to a modest two-fluid model in which ions combined with electrons and neutrals are described by magnetohydrodynamic (MHD) equations and hydrodynamic equations, respectively, and they are coupled by means of the collisional terms (e.g. Ballester et al. 2018). Based on these coupled equations, deviations from MHD were found both analytically (e.g. Kumar & Roberts 2003; Zaqarashvili et al. 2011; Soler et al. 2019) and numerically (e.g. Maneva et al. 2017; Kuźma et al. 2020). These non-MHD effects are important in the context of the heating of the chromosphere because the relative motions between ions and neutrals cause the collisional damping of Alfvén waves and the release of thermal energy (e.g. Vranjes et al. 2008).
One of the most outstanding issues of the solar atmosphere is the problem of energy transfer from the photosphere to the higher layers and the heating of the plasma. Alfvén waves are thought to play an important role in this transfer. They were described by Alfvén (1942) as waves that propagate along the magnetic lines and are driven by magnetic tension. An analytical approach to Alfvén waves in the two-fluid approximation can be found in Soler (2024), who presented the dispersion relation for linear Alfvén waves and confirmed that Alfvén waves are damped by neutral-ion collisions.
Recently, Kraśkiewicz et al. (2023) showed that driven two-fluid Alfvén waves exhibit the potential to heat the chromosphere. However, these studies were performed for magnetohydrostatic equilibrium with a straight vertical magnetic field. We study driven two-fluid Alfvén waves in a solar magnetic flux tube with diverging magnetic field lines with height and consider the magnetohydrostatic background supplemented by the Saha equation, which implies a realistic ionization profile in the solar atmosphere (Saha 1920).
The organization of the remainder of this paper is as follows. Sect. 2 describes the two-fluid equations, the background plasma models of the solar atmosphere, and the driven perturbations that were applied in the numerical simulations. Sect. 3 presents the results of the numerical simulations, and Sect. 4 contains a discussion and summary of the numerical results, together with the conclusions that we draw from them.
2. Numerical models of the solar atmosphere
The solar atmosphere is assumed to consist of hydrogen plasma, that is, of neutrals (hydrogen atoms) and ions (protons) + electrons, which are treated as two separate fluids. These fluids interact with each other through collisions described by ion-neutral drag force. The neutrals are governed by the following equations:
where the total energy density
The ions + electrons are described by
where
In Eqs. (1)–(9), the subscripts i, e, and n correspond to ions, electrons, and neutrals, respectively. The symbols 𝜚i, n denote the mass densities, Vi, n = [Vi, n x, Vi, n y, Vi, n z] are the velocities, pe = pi and pn the gas pressures, B = [Bx, By, Bz] is the magnetic field, and Ti, n are the temperatures, specified by the ideal gas laws,
with mn ≃ mi = mH being the masses, and mH is the hydrogen (proton) mass. Here,  and
and  are coefficients of ionization and recombination (Murawski et al. 2022) and the collisional momentum, Sm, and energy, Qi, n, source terms are given as (Draine 1986)
are coefficients of ionization and recombination (Murawski et al. 2022) and the collisional momentum, Sm, and energy, Qi, n, source terms are given as (Draine 1986)
with collisional heating,
and thermal energy exchange,
terms. The gravitational acceleration vector g = [0, −g, 0] has a magnitude g = 274.78 m s−2 on the Sun. The symbol kB denotes the Boltzmann constant, γ = 5/3 is the ratio of specific heats, and μ means the magnetic permeability of the medium.
The coefficient of collisions between ions and neutrals is given by (Oliver et al. 2016)
where σin is the collisional cross-section, here taken as 1.4 × 10−19 m2 (Vranjes & Krstic 2013). The Cartesian coordinate system was used with the x-axis horizontal, the y-axis vertical, and the z-axis lying along the ignorable direction with ∂/∂z = 0, and Vi, nz and Bz being non-identically zero. In this system, the equilibrium quantities depend on x and y. The other symbols have their standard meaning (Murawski et al. 2022).
2.1. Static background
The solar atmosphere is a highly dynamical medium (e.g. Wedemeyer et al. 2004). However, we assumed that the solar atmosphere is initially in a static state, that is, all quantities are invariant of time, ∂/∂t = 0, and the atmosphere is still, Vi = Vn = 0.
The hydrostatic background was supplemented by the Saha equation (Saha 1920), from which realistic vertical profiles were obtained (Niedziela et al. 2024).
The background temperature, specified here by the semi-empirical model of Avrett & Loeser (2008), is shown in Fig. 1 (top). At the bottom of the photosphere, the top boundary of which is located at y = 0.5 Mm, T(y = 0)≈5800 K. Higher up, the temperature declines with height (y) in the photosphere and reaches its minimum of 4341 K in the low chromosphere, at y ≈ 0.6 Mm. Then, T grows with y to about 106 K at y = 30 Mm in the corona, which occupies the region above the transition region, located at y = 2.1 Mm.
 |
Fig. 1. Top: Background temperature. Middle: 𝜚n (dashed line) and 𝜚i (solid line). Bottom: Neutral-ion τni (solid line) and ion-neutral τin (dashed line) collision times vs. height y. |
The background ion (solid line) and neutral (dashed line) mass densities are displayed in Fig. 1 (middle). 𝜚n is much larger than 𝜚i in the photosphere and in the low chromosphere. In the corona, the opposite relation takes place. Mainly, 𝜚n is much smaller than 𝜚i there.
Figure 1 (bottom) displays the neutral-ion collision time, τni = 𝜚n/αin, (solid line), and the ion-neutral collision time, τin = 𝜚i/αin, (dashed line) versus height. In the photosphere, 10−3 s ≲ τni ≲ 10−1 s. The local maximum of τni is about 0.2 s and takes place in the low chromosphere at y ≈ 0.6 Mm, where T(y) attains its minimum. The local minimum of about 2 ⋅ 10−3 s can be found at y ≈ 1 Mm and τni > 0.1 s in the low corona. In addition, τin is much smaller than τni, which means that ion-neutral collisions are more frequent than neutral-ion collisions.
2.2. Flux-tube model
The hydrostatic background is overlaid by a current- and thus force-free magnetic field in the form of a magnetic arcade, given as
where B0 is the flux-tube magnetic field at y = 0 Mm, Bv is the vertical magnetic field, chosen here to be equal to −10 G (unless otherwise stated), ΛB = 2L/π is the magnetic scale height, with L being the arcade half-width, taken here as 1.28 Mm. The magnetic field lines, which diverge with height, are shown in Fig. 2 (top). The corresponding total Alfvén speed, 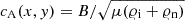 , is illustrated in a color map. cA achieves values of about 2 km s−1 in the low photosphere. Higher up, it grows with y and takes the following values: cA(x = 0, y = 2 Mm)≈500 km s−1 up to its maximum value of about 2300 km s−1 at y = 2.4 Mm. In the higher corona, cA decreases to about 700 km s−1 at y ≈ 6 Mm (Fig. 2, top).
, is illustrated in a color map. cA achieves values of about 2 km s−1 in the low photosphere. Higher up, it grows with y and takes the following values: cA(x = 0, y = 2 Mm)≈500 km s−1 up to its maximum value of about 2300 km s−1 at y = 2.4 Mm. In the higher corona, cA decreases to about 700 km s−1 at y ≈ 6 Mm (Fig. 2, top).
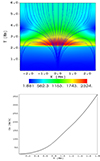 |
Fig. 2. Initial (at t = 0 s) magnetic field lines overlaid with the Alfvén speed cA(x, y) in km s−1, (color map) (top) and cA(x = 0, y) (bottom). |
2.3. Monochromatic driver
The magnetohydrostatic background described above is perturbed by a monochromatic driver specified in the transversal (z) components of the ion and neutral velocities as
Here, y0 is the operation height, V0 is the amplitude of the driver, w = 100 km denotes its width, and Pd stands for its period.
3. Numerical results
In this section, we present the results for 2.5 D numerical simulations performed using the code JOANNA (Wójcik et al. 2020). In the developed model, all plasma quantities were assumed to be invariant of z (∂/∂z = 0), but the transversal components of ion (Viz) and neutral (Vnz) velocities and the magnetic field (Bz) were not identically zero. Prior to considering the flux-tube model, we show the numerical results for two simplified atmosphere models. In the first model, presented in Sect. 3.1, the solar gravity was set to 0 and all background quantities were assumed to be independent of x and y. This model serves for comparison purposes with the linear wave theory, and thus, for testing the code. In the second model, discussed in Sect. 3.2, the gravity was switched on, but the physical system was assumed to be invariant of x (∂/∂x = 0). In these two models, B0 = 0 G and Bv = 10 G were set in Eq. (15). Finally, the flux-tube model was considered with B0 = 500 G and Bv = −10 G (see Sect. 3.3).
3.1. A test for the gravity-free and homogeneous medium
We considered a gravity-free (g = 0) medium with constant values of the background quantities, mainly 𝜚i = 10−9 kg m3, 𝜚n = 10−8 kg m3, and T = 6676 K, and the magnetic field was taken to be vertical with B0 = 0 and Bv = 10 G in Eq. (15). These values correspond to conditions in the upper chromosphere or low corona. For these conditions, τni ≈ 10−2 s. The two-fluid equations were solved numerically within the regions that are covered by the grid of 1024 cells with their vertical size, Δy, depending on Pd and varying from Δy = 0.01 km for Pd = 0.01 s to Δy = 0.1 km for Pd = 0.1 s. The simulation region also depends on Pd and was larger for larger Pd, and it varied from 10 km to 100 km.
Figure 3 displays the time-distance plot for Viz for the driver, which is given by Eq. (16) with y0 = 1 Mm, V0 = 1 km s−1, and Pd = 0.02 s. this is approximately ten times longer than neutral-ion collision time, τni(y = 1 Mm), (Fig. 1, bottom). The Alfvén waves are damped while they propagate up from the driver.
 |
Fig. 3. Time-distance plots for Viz(y, t) for the driver with Pd = 0.02 s in Eq. (16) operating in a gravity-free and homogeneous medium that mimics the chromosphere with a vertical magnetic field of Bv = 10 G. |
To estimate the damping length of Alfvén waves, we adopted the following dispersion relation (Zaqarashvili et al. 2011):
Here, ω = 2π/Pd and νni = αin/𝜚n, are cyclic and neutral-ion collision frequencies, respectively, i2 = −1, and k = kr + iki denotes the complex wave number from which the wavelength is λ = 2π/kr, and the damping length is λd = 2π/ki.
Fig. 4 illustrates λd versus Pd obtained from the dispersion relation of Eq. (17) (solid line) and numerically by solving the two-fluid equations (dashed line). We infer that λd grows with Pd, meaning that waves with longer periods experience less attenuation than waves with shorter periods, and the trend is non-linear. For Pd = 0.01 s, the Alfvén waves are strongly damped with λd = 5 km. For Pd = 0.1 s, the Alfvén waves are less strongly damped with λd = 500 km. The numerical and analytical values of λd converge and reach similar values for all the selected values of Pd.
 |
Fig. 4. Damping length, λd, obtained from the dispersion relation of Eq. (17) (solid line) and numerically (dashed line) for the driver with V0 = 1 km s−1 operating at y0 = 1 Mm in a gravity-free homogeneous background. |
3.2. The gravitationally stratified solar atmosphere model with a vertical magnetic field
In this part of the paper, we present the numerical results for the gravitationally stratified solar atmosphere model, with x being the invariant coordinate (∂/∂x = 0). In Eq. (15), B0 was set to 0 G and Bv = 10 G. The numerical simulations were performed in the region y0 ≤ y ≤ y0 + 2.56 Mm with the grid resolution Δy = 0.625 km. Several values of y0 were considered, such as y0 = 0.6 Mm, y0 = 0.8 Mm, and y0 = 1 Mm. The driver operates at y = y0 with an amplitude V0 = 1 km s−1 and a period Pd = 2.5 s.
Figure 5 illustrates time-distance plots for Viz and y0 = 0.8 Mm. The Alfvén waves are clearly damped. Parametric studies made for various values of y0 revealed that the damping length, λd, decreases with y0 < 0.8 Mm, and it grows higher up with y0 (Fig. 6, dots). This behavior may result from the specific dependence of the ion and neutral mass densities on the height in the vicinity of y = 0.8 Mm (Fig. 1, middle). In particular, for y0 = 0.6 Mm and y0 = 1.0 Mm, the values of λd are 40 km and 100 km, respectively, which is close to the range of values of λd derived for the homogeneous atmosphere model (Fig. 4), which were obtained for Pd ≤ 0.05 s. However, for Pd = 2.5 s from the dispersion relation of Eq. (17) and for 𝜚i, 𝜚n, and T corresponding to y0 = 0.8 Mm, we obtain that λd ≈ 7 km, which is lower by more than three times than the numerical value of λd ≈ 25 km. At the other heights, the difference between λd, calculated numerically and from the dispersion relation, is also significant (Fig. 6). The dispersion relation is strictly valid for a homogeneous medium, and therefore, it is a crude description for the low chromosphere, which is a strongly stratified medium. Therefore, the dispersion relation was only used here for reference purposes and should be taken with caution. As the numerical values of λd are lower than 100 km for y0 < 1 Mm, we infer that Alfvén waves deposit their kinetic energy in the form of thermal energy in the chromosphere, and for higher values of y0, the Alfvén waves experience weaker damping (Fig. 6).
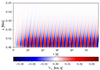 |
Fig. 5. Time-distance plots for Viz(y, t) for the driver located at y0 = y0 = 0.8 Mm with Pd = 2.5 s in Eq. (16) for a solar chromosphere with ∂/∂x = 0, g ≠ 0, and a vertical magnetic field Bv = 10 G. |
 |
Fig. 6. Damping length of Alfvén waves vs. the position of the driver with Pd = 2.5 s and V0 = 1 km s−1 in Eq. (16) (dots) for the solar chromosphere with Bv = 10 G and obtained from the dispersion relation of Eq. (17) (asterisks). |
The values of y0 listed above are close to the height at which the neutral-ion collision time reaches its local extrema: the maximum at y ≈ 0.6 Mm and the minimum at y ≈ 1 Mm (Fig. 1, bottom, solid line). The presence of this maximum results in strong damping of Alfvén waves, which was much weaker in the case of the hydrostatic equilibrium recently studied by Kraśkiewicz et al. (2023).
3.3. The solar atmosphere with a flux tube
In this part of the paper, we present the numerical results for the solar atmosphere with a flux tube. For the flux tube, a fine grid, which was used in the cases of the vertical magnetic field, would lead to too costly numerical simulations. Therefore, a uniform grid with its vertical size Δy = 2.5 km was set (except for Pd = 2.5 s where Δy = 1 km), which extends over the region 0 ≤ y ≤ 2.56 Mm. For higher values of y, the computational box was covered by 64 grid points up to y = 20 Mm. Along the x-direction, which is given as |x|≤2.56 Mm, the size of a numerical cell was set to Δx = 5 km. The monochromatic driver operates at the bottom of the photosphere, given by y0 = 0 Mm, with its amplitude V0 = 1 km s−1 in Eq. (16).
Figure 7 (top) displays time-distance plots for Viz(x = 0, y, t) for the driver with Pd = 2.5 s (left) and Pd = 10 s (right). For Pd = 2.5 s, the Alfvén waves are attenuated with significant amplitude that decreases with height. For Pd = 10 s, the amplitude of the Alfvén waves decreases weakly with height for y < 0.2 Mm. However, higher up, their amplitude starts to grow, and in effect, the waves reach the transition region and the corona.
 |
Fig. 7. Time-distance plots for Viz(x = 0, y, t) (top), |Viz − Vnz| (middle), and δTi (bottom) for a solar atmosphere with a flux tube for the driver with Pd = 2.5 s (left) and Pd = 10 s (right). |
As the transverse velocity drift, ΔVz ≡ |Viz − Vnz|, reaches finite numbers (Fig. 7, middle), it results in plasma heating by Alfvén waves. For Pd = 2.5 s, a magnitude of ΔVz reaches its maximum of about 0.4 m s−1 above y = 0 Mm, and higher up, it decreases along with the attenuation of the Alfvén waves. For Pd = 10 s, max(ΔVz) ≈ 1.5 m s−1 and it takes place at y ≈ 0.7 Mm which is at a higher altitude than in the case of Pd = 2.5 s.
As a result of ΔVz > 0, the Alfvén waves thermalize their kinetic energy and warm the atmosphere while they are damped by ion-neutral collisions. Fig. 7 (bottom) illustrates the relative perturbed ion temperature, defined as δTi = 100% (Ti − T)/T. Here, T(y) is the temperature at t = 0 (Fig. 1, top). For Pd = 2.5 s and Pd = 10 s, δTi reaches a value of about 4% at y ≈ 0.01 Mm and y ≈ 0.04 Mm, respectively. Hence, we infer that for Pd = 2.5 s, Alfvén waves result in plasma heating at a lower height than for Pd = 10 s.
Figure 8 shows how the numerically estimated damping length, λd, depends on Pd. For Pd = 2.5 s, λd ≈ 50 km, and for higher values of Pd, λd grows, achieving for Pd = 5 s and Pd = 10 s values of λd ≈ 70 km and λd ≈ 200 km, respectively. Even though these values of λd correspond to a damping of Alfvén waves in the photosphere, they have similar magnitudes as λd evaluated in the chromosphere (compare the values of λd in Figs. 4, 6, and 8).
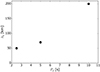 |
Fig. 8. Damping length λd vs. Pd obtained numerically for Alfvén waves propagating along the flux tube. |
4. Summary and conclusions
We constructed a model of a solar magnetic flux tube with a background state that was governed by the magnetohydrostatic conditions supplemented by the Saha equation. This model is an extension of the model discussed by Kraśkiewicz et al. (2023), who studied driven Alfvén waves in a purely hydrostatic atmosphere with a vertical magnetic field. In both models, the solar atmosphere was described by two-fluid equations for ions (protons) + electrons and neutrals (hydrogen atoms), which were treated as two separate fluids. However, in the model we developed, a realistic ionization profile and ionization and recombination were additionally implied. These equations were solved numerically with the use of the code JOANNA (Wójcik et al. 2020). Two-fluid Alfvén waves were excited in this atmosphere by a monochromatic driver. To test the code and for comparison purposes, two simplified models of the solar atmosphere were constructed that either corresponded to a gravity-free and homogeneous chromosphere or to a gravitationally stratified but horizontally invariant atmosphere. A straight vertical magnetic field was implemented in both models. The test for the gravity-free atmosphere model revealed that the values of the numerically estimated damping length of Alfvén waves were close to the analytical data that were obtained from the dispersion relation.
From the numerical results for the model of the solar atmosphere, which is gravitationally stratified, we inferred that Alfvén waves experience damping by ion-neutral collisions, with stronger effects corresponding to waves with shorter periods, and this damping is stronger than in the purely hydrostatic case considered by Kraśkiewicz et al. (2023). As a result, we claim that the presence of the realistic ionization profile and ionization and recombination plays an important role in Alfvén waves damping and thus in the thermalization of their energy, which contributes to the heating of the solar atomosphere.
Acknowledgments
The authors express their thanks to Dr. Fan Zhang for a few discussions during the initial phase of this project evolution. KM’s work was done within the framework of the project from the Polish Science Center (NCN) Grant No. 2020/37/B/ST9/00184. The Saha equation-based hydrostatic background was implemented into the code JOANNA by Dr. Luis Kadowaki during his research funded by the grant. All numerical simulations was run on the LUNAR cluster at the Institute of Mathematics at M. Curie-Sklodowska University in Lublin, Poland. The simulation data was visualized using the ViSIt software package (Childs et al. 2012) and Python scripts.
References
- Alfvén, H. 1942, Nature, 150, 405 [Google Scholar]
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [Google Scholar]
- Ballester, J. L., Alexeev, I., Collados, M., et al. 2018, Space Sci. Rev., 214, 58 [Google Scholar]
- Childs, H., Brugger, E., Whitlock, B., et al. 2012, VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data (Chapman and Hall/CRC), 357 [Google Scholar]
- Draine, B. T. 1986, MNRAS, 220, 133 [NASA ADS] [Google Scholar]
- Kraśkiewicz, J., Murawski, K., Zhang, F., & Poedts, S. 2023, Sol. Phys., 298, 11 [CrossRef] [Google Scholar]
- Kumar, N., & Roberts, B. 2003, Sol. Phys., 214, 241 [Google Scholar]
- Kuźma, B., Wójcik, D., Murawski, K., Yuan, D., & Poedts, S. 2020, A&A, 639, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maneva, Y. G., Alvarez Laguna, A., Lani, A., & Poedts, S. 2017, ApJ, 836, 197 [Google Scholar]
- Murawski, K., Musielak, Z. E., Poedts, S., Srivastava, A. K., & Kadowaki, L. 2022, Ap&SS, 367, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Niedziela, R., Murawski, K., & Poedts, S. 2024, A&A, 691, A254 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, R., Soler, R., Terradas, J., & Zaqarashvili, T. V. 2016, ApJ, 818, 128 [Google Scholar]
- Saha, M. N. 1920, Nature, 105, 232 [CrossRef] [Google Scholar]
- Soler, R. 2024, Philos. Trans. R. Soc. Lond. Ser. A, 382, 20230223 [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., & Ballester, J. L. 2019, ApJ, 871, 3 [Google Scholar]
- Vranjes, J., & Krstic, P. S. 2013, A&A, 554, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vranjes, J., Poedts, S., Pandey, B. P., & De Pontieu, B. 2008, A&A, 478, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wójcik, D., Kuźma, B., Murawski, K., & Musielak, Z. E. 2020, A&A, 635, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Khodachenko, M. L., & Rucker, H. O. 2011, A&A, 534, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Top: Background temperature. Middle: 𝜚n (dashed line) and 𝜚i (solid line). Bottom: Neutral-ion τni (solid line) and ion-neutral τin (dashed line) collision times vs. height y. |
| In the text | |
 |
Fig. 2. Initial (at t = 0 s) magnetic field lines overlaid with the Alfvén speed cA(x, y) in km s−1, (color map) (top) and cA(x = 0, y) (bottom). |
| In the text | |
 |
Fig. 3. Time-distance plots for Viz(y, t) for the driver with Pd = 0.02 s in Eq. (16) operating in a gravity-free and homogeneous medium that mimics the chromosphere with a vertical magnetic field of Bv = 10 G. |
| In the text | |
 |
Fig. 4. Damping length, λd, obtained from the dispersion relation of Eq. (17) (solid line) and numerically (dashed line) for the driver with V0 = 1 km s−1 operating at y0 = 1 Mm in a gravity-free homogeneous background. |
| In the text | |
 |
Fig. 5. Time-distance plots for Viz(y, t) for the driver located at y0 = y0 = 0.8 Mm with Pd = 2.5 s in Eq. (16) for a solar chromosphere with ∂/∂x = 0, g ≠ 0, and a vertical magnetic field Bv = 10 G. |
| In the text | |
 |
Fig. 6. Damping length of Alfvén waves vs. the position of the driver with Pd = 2.5 s and V0 = 1 km s−1 in Eq. (16) (dots) for the solar chromosphere with Bv = 10 G and obtained from the dispersion relation of Eq. (17) (asterisks). |
| In the text | |
 |
Fig. 7. Time-distance plots for Viz(x = 0, y, t) (top), |Viz − Vnz| (middle), and δTi (bottom) for a solar atmosphere with a flux tube for the driver with Pd = 2.5 s (left) and Pd = 10 s (right). |
| In the text | |
 |
Fig. 8. Damping length λd vs. Pd obtained numerically for Alfvén waves propagating along the flux tube. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



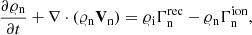
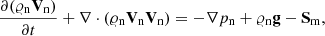
![$$ \begin{aligned} \frac{\partial E_{\rm {n}}}{\partial t}+\nabla \cdot [(E_{\rm {n}}+p_{\rm {n}})\mathbf{V }_{\rm {n}}]&= (\varrho _{\rm {n}} \mathbf{g } -\mathbf{S }_{\rm m} ) \cdot \mathbf{V }_{\rm n} + Q_{\rm n}, \end{aligned} $$](/articles/aa/full_html/2025/06/aa54085-25/aa54085-25-eq3.gif)
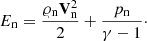
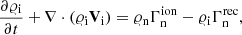
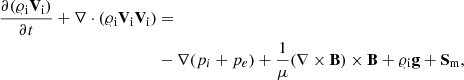
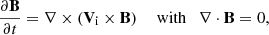
![$$ \begin{aligned} \frac{\partial E_{\rm i}}{\partial t}+&\nabla \cdot \left[\left(E_{\rm i}+p_{\rm i} + p_{\rm e} + \frac{\mathbf{B }^2}{2\mu } \right)\mathbf{V }_{\rm i}-\frac{\mathbf{B }}{\mu }(\mathbf{V }_{\rm i}\cdot {\mathbf{B }})\right]\nonumber \\&=(\varrho _{\rm i} \mathbf{g }+{{\mathbf{S }}_{\rm m}}) \cdot \mathbf{V }_{\rm i} + Q_{\rm i}, \end{aligned} $$](/articles/aa/full_html/2025/06/aa54085-25/aa54085-25-eq8.gif)
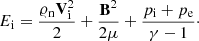
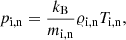
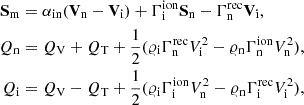
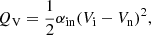
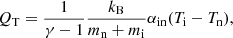
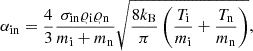
![$$ \begin{aligned} \mathbf{B }&=[B_{\rm x}, B_{\rm y}, 0]= \nonumber \\&B_0 \exp \left({\frac{-y}{\Lambda _{\rm B}}}\right)\left[\cos \left(\frac{x}{\Lambda _{\rm B}}\right), -\sin \left(\frac{x}{\Lambda _{\rm B}}\right),0\right]+[0, B_{\rm v}, 0], \end{aligned} $$](/articles/aa/full_html/2025/06/aa54085-25/aa54085-25-eq17.gif)