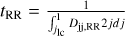The S stars’ zone of avoidance in the Galactic center

Aleksey Generozov; Hagai B. Perets; Matteo S. Bordoni; Guillaume Bourdarot; Antonia Drescher; Frank Eisenhauer; Reinhard Genzel; Stefan Gillessen; Felix Mang; Thomas Ott; Diogo C. Ribeiro; Rainer Schödel

doi:10.1051/0004-6361/202453272

Home

All issues

Volume 696 (April 2025)

A&A, 696 (2025) A68

Full HTML

Open Access

Issue		A&A Volume 696, April 2025


Article Number		A68
Number of page(s)		14
Section		Galactic structure, stellar clusters and populations
DOI		https://doi.org/10.1051/0004-6361/202453272
Published online		04 April 2025

A&A, 696, A68 (2025)

The S stars’ zone of avoidance in the Galactic center

Aleksey Generozov¹^★, Hagai B. Perets¹^,2, Matteo S. Bordoni³, Guillaume Bourdarot³, Antonia Drescher³, Frank Eisenhauer³^,4, Reinhard Genzel³^,5, Stefan Gillessen³, Felix Mang³, Thomas Ott³, Diogo C. Ribeiro³ and Rainer Schödel⁶

¹ Physics Department, Technion – Israel Institute of Technology, 3200003 Haifa, Israel
² Astrophysics Research Center of the Open University (ARCO), 4353701 Raanana, Israel
³ Max-Planck-Institut für Extraterrestrische Physik, 85748 Garching, Germany
⁴ Department of Physics, Technical University of Munich, 85748 Garching, Germany
⁵ Departments of Physics & Astronomy, University of California, Berkeley, CA 94720, USA
⁶ Instituto de Astrofísica de Andalucía, 18008 Granada, Spain

^★ Corresponding author; aleksey.generozov@gmail.com

Received: 3 December 2024
Accepted: 5 February 2025

Abstract

This paper investigates the origin and orbital evolution of S stars in the Galactic center using models of binary disruption and relaxation processes. We focus on explaining the recently discovered “zone of avoidance” in S-star orbital parameters, defined as a region where no S stars are observed with pericenters of log(r_p/AU) ≤ 1.57 + 2.6(1 − e) pc. We demonstrate that the observed S-star orbital distributions, including this zone of avoidance and their thermal eccentricity distribution, can be largely explained by the continuous disruption of binaries near the central supermassive black hole, followed by orbital relaxation. Our models consider binaries originating from large scales (5–100 pc) and incorporate empirical distributions of binary properties. We simulate close encounters between binaries and the black hole, tracking the remnant stars’ orbits. The initially highly eccentric orbits of disrupted binary remnants evolve due to nonresonant and resonant relaxation in the Galactic center potential. While our results provide insights into the formation mechanism of S stars, there are limitations, such as uncertainties in the initial binary population and mass function and simplifications in our relaxation models. Despite these caveats, our study demonstrates the power of using S-star distributions to probe the dynamical history and environment of the central parsec of our Galaxy.

Key words: black hole physics / Galaxy: center

© The Authors 2025

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The Galactic center’s proximity allows for the direct measurement of stellar orbits within the central parsec. There are distinct structures within this region: multiple young stellar disks with O and Wolf–Rayet stars (Levin & Beloborodov 2003; Paumard et al. 2006; Bartko et al. 2009; Yelda et al. 2014; von Fellenberg et al. 2022), as well as the isotropic S-star cluster with many B-and later-type stars (Gillessen et al. 2017).

These stars have been the subject of intense, decades-long studies. They have established the presence of the central super- massive black hole (SMBH) in the Galactic center (Genzel et al. 1996, 1997; Ghez et al. 1998), and the closest S stars can be used for stringent tests of general relativity (GRAVITY Collaboration 2018, 2020; Do et al. 2019). The S stars can also be used to probe the extended mass distribution in the Galactic center (GRAVITY Collaboration 2020, 2022).

The origin of the S stars is a long-standing puzzle, considering that strong tides from Sgr A* are expected to suppress star formation in the S-star region (Sanders 1992; Ghez et al. 2003). Instead, the S stars may have migrated inward from larger scales via tidal disruption of binary stars (Hills 1988; Gould & Quillen 2003). Binaries may either come from relatively large scales (~ tens of parsecs; Perets et al. 2007; Hamers & Perets 2017) or from one of the young disks (Madigan et al. 2009; Generozov & Madigan 2020; Rantala & Naab 2023). Remnants from binary stars would initially be on highly eccentric (e ≳ 0.98; Hills 1988) orbits. In contrast, the observed S stars have a thermal eccentricity distribution. However, other stars or remnants can perturb the stars’ orbits following binary disruptions. The stars’ energy only evolves due to uncorrelated two-body encounters (nonresonant relaxation). The star’s angular momentum can evolve on much faster timescales due to coherent torques (resonant relaxation; Rauch & Tremaine 1996; Hopman & Alexander 2006a; Perets et al. 2009; Kocsis & Tremaine 2011; Antonini & Merritt 2013). The S stars can easily isotropize within their lifetime via vector resonant relaxation (Hopman & Alexander 2006a), but the eccentricity distribution relaxes on the slower scalar resonant relaxation time. Many papers have studied whether this process can reproduce the observed eccentricities within the stars’ lifetimes.

For example, Merritt et al. (2009) and Perets et al. (2009) used N-body simulations to provide the first detailed theoretical study of the S stars’ eccentricity evolution due to an intermediate-mass black hole (IMBH) and stellar-mass black holes, respectively. Antonini & Merritt (2013) were the first to study resonant relaxation in the Galactic center with both relativistic and Newtonian precession. Initial studies used approximate treatments for resonant relaxation. Subsequently, a self- consistent formalism was developed (Bar-Or & Alexander 2014; Sridhar & Touma 2016; Fouvry et al. 2017; Bar-Or & Fouvry 2018) and applied to the S stars by Generozov & Madigan (2020) and Tep et al. (2021).

Generally, these studies find that a population of stellar-mass black holes is needed to reproduce the S stars’ eccentricity within their lifetimes. The exact number and mass required depend on the modeling assumptions, the observational dataset, and the uncertain ages of the S stars. The other orbital elements provide complementary constraints on the S stars’ origin. For example, Perets & Gualandris (2010) found that many theoretical models have difficulty explaining the populations of B stars on small and large scales.

We revisit the problem of the S stars’ orbital evolution, in light of the most recent S-star observations and constraints on the background mass distribution. For example, recently it was shown that there is a dearth of S stars with pericenters of 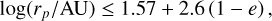$\log (r_{p} / AU) \leq 1.57 + 2.6 (1 - e),$ $\log \left( {{r_p}/{\rm{AU}}} \right) \le 1.57 + 2.6(1 - e),$ (1)

even though they would be observable (Burkert et al. 2024). The S stars’ eccentricity distribution in the latest GRAVITY data is thermal, within observational uncertainties. The zone of avoidance constrains the semimajor axis distribution of the progenitor binaries, which depends on their intrinsic distribution and the rate of loss cone refilling. The eccentricity distribution of the S stars is sensitive to the properties of the background population, including the mass distribution of stellar-mass black holes.

We show that these orbital distributions can be explained via a combination of binary disruptions and relaxation in the Galactic center. If binaries are continuously disrupted in the Galactic center, the observed eccentricity distribution can be reproduced with a population of ~10 M_⊙ black holes in the S- star cluster. In the case of impulsive injection, as is expected in the young disk scenario, the background black holes would have to be at least ~30 M_⊙, considering existing constraints on the total enclosed mass in the Galactic center.

Our model accounts for many processes that to our knowledge have never been studied together in the literature. In particular, we have (i) an observationally motivated progenitor binary population, (ii) self-consistent diffusion coefficients for resonant relaxation, (iii) both eccentricity and semimajor axis evolution, (iv) stellar evolution, and (v) a loss cone. We also model the K-band luminosity function (KLF) of the S stars and incorporate this into our observational comparisons.

The remainder of this paper is organized as follows. In Sect. 2, we discuss our methods and the relevant physical processes. In Sect. 3, we show that most S-star observables can be reproduced by continuous disruption of binaries in the Galactic center. In Sect. 4, we discuss additional effects that are not accounted for in our fiducial models. In Sect. 5, we discuss models where binaries are all disrupted at a fixed lookback time. We summarize our main results in Sect. 6.

2 Relevant physical processes and methods

2.1 Binary disruptions

We assume that all the S stars are initially sourced by the disruption of binaries that come near their tidal radius: 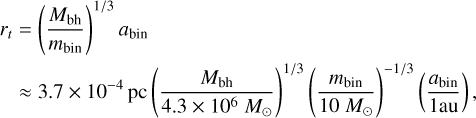$\begin{array}{l} r_{t} = {(\frac{M_{bh}}{m_{bin}})}^{1 / 3} a_{bin} \\ \approx 3.7 \times 10^{- 4} pc {(\frac{M_{bh}}{4.3 \times 10^{6} M_{⊙}})}^{1 / 3} {(\frac{m_{bin}}{10 M_{⊙}})}^{- 1 / 3} (\frac{a_{bin}}{1 au}), \end{array}$ $\eqalign{ & {r_t} = {\left( {{{{M_{{\rm{bh}}}}} \over {{m_{{\rm{bin}}}}}}} \right)^{1/3}}{a_{{\rm{bin}}}} \cr & \approx 3.7 \times {10^{ - 4}}{\rm{pc}}{\left( {{{{M_{{\rm{bh}}}}} \over {4.3 \times {{10}^6}{M_ \odot }}}} \right)^{1/3}}{\left( {{{{m_{{\rm{bin}}}}} \over {10{M_ \odot }}}} \right)^{ - 1/3}}\left( {{{{a_{{\rm{bin}}}}} \over {1\,{\rm{au}}}}} \right), \cr}$ (2)

where M_bh and m_bin are the mass of the black hole and binary, and a_bin is the binary semimajor axis. During a tidal interaction with an SMBH, a binary can (i) collide, (ii) survive (with some change to the orbital elements), or (iii) disrupt (Hills 1991; Ginsburg & Loeb 2007; Antonini et al. 2010; Bradnick et al. 2017). In the latter case, the binary is split into two stars. In the limit of a parabolic center-of-mass orbit, one of the stars is always bound to the SMBH, while the other is unbound. The semimajor axis of the remnant star is (e.g., Sari et al. 2010) $\begin{array}{l} a_{s} = χ {(\frac{M_{BH}}{m_{bin}})}^{2 / 3} (\frac{m_{bin}}{m_{ej}}) a_{bin}, \\ \approx 0.028 pc {(\frac{M_{bh}}{4.3 \times 10^{6} M_{⊙}})}^{2 / 3} {(\frac{m_{bin}}{10 M_{⊙}})}^{- 2 / 3} (\frac{m_{bin}}{m_{ej}}) (\frac{a_{bin}}{1 au}), \end{array}$ $\eqalign{ & {a_s} = \chi {\left( {{{{M_{{\rm{BH}}}}} \over {{m_{{\rm{bin}}}}}}} \right)^{2/3}}\left( {{{{m_{{\rm{bin}}}}} \over {{m_{{\rm{ej}}}}}}} \right){a_{{\rm{bin}}}}, \cr & \,\,\,\,\, \approx 0.028{\rm{pc}}{\left( {{{{M_{{\rm{bh}}}}} \over {4.3 \times {{10}^6}{M_ \odot }}}} \right)^{2/3}}{\left( {{{{m_{{\rm{bin}}}}} \over {10{M_ \odot }}}} \right)^{ - 2/3}}\left( {{{{m_{{\rm{bin}}}}} \over {{m_{{\rm{ej}}}}}}} \right)\left( {{{{a_{{\rm{bin}}}}} \over {1\,{\rm{au}}}}} \right), \cr}$ (3)

where m_ej is the mass of the ejected star and χ is typically a factor of order unity. The pericenter of the remnant star, r_p,s, is comparable to that of the progenitor binary. Thus, r_p,s ≲ r_t. The eccentricity of the remnant star, e_s, is close to one. More precisely, 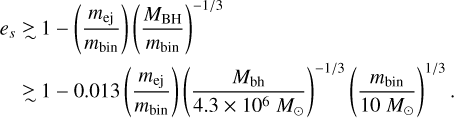$\begin{array}{l} e_{s} ≳ 1 - (\frac{m_{ej}}{m_{bin}}) {(\frac{M_{BH}}{m_{bin}})}^{- 1 / 3} \\ ≳ 1 - 0.013 (\frac{m_{ej}}{m_{bin}}) {(\frac{M_{bh}}{4.3 \times 10^{6} M_{⊙}})}^{- 1 / 3} {(\frac{m_{bin}}{10 M_{⊙}})}^{1 / 3} . \end{array}$ $\eqalign{ & {e_s} \mathbin{\lower.3ex\hbox{\buildrel>\over {\smash{\scriptstyle\sim}\vphantom{_x}}}} 1 - \left( {{{{m_{{\rm{ej}}}}} \over {{m_{{\rm{bin}}}}}}} \right){\left( {{{{M_{{\rm{BH}}}}} \over {{m_{{\rm{bin}}}}}}} \right)^{ - 1/3}} \cr & \,\,\,\,\, \mathbin{\lower.3ex\hbox{\buildrel>\over {\smash{\scriptstyle\sim}\vphantom{_x}}}} 1 - 0.013\left( {{{{m_{{\rm{ej}}}}} \over {{m_{{\rm{bin}}}}}}} \right){\left( {{{{M_{{\rm{bh}}}}} \over {4.3 \times {{10}^6}{M_ \odot }}}} \right)^{ - 1/3}}{\left( {{{{m_{{\rm{bin}}}}} \over {10{M_ \odot }}}} \right)^{1/3}}. \cr}$ (4)

Binaries can have a few different sources: the clockwise disk (Madigan et al. 2009; Generozov & Madigan 2020; Rantala & Naab 2023), scattering from massive perturbers such as large- scale molecular clouds or stellar clusters ~5 − 100 pc away from the Galactic center (Perets et al. 2007), or large-scale gaseous spiral arms at similar scales Hamers & Perets (2017). We focus on the massive perturbers’ origin here.

To model binary disruptions in the Galactic center, we first constructed a model field-like binary population such that

The primary mass distribution follows a Kroupa mass function 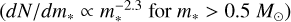$(d N / d m_{*} \propto m_{*}^{- 2.3} for m_{*} > 0.5 M_{⊙})$ $\left( {dN/d{m_*} \propto m_*^{ - 2.3}{\rm{for }}{m_*} > 0.5{M_ \odot }} \right)$ (Kroupa 2001).
The binary properties (semimajor axis, eccentricity, and mass ratio) follow the empirical distributions in Moe & Di Stefano (2017). We only considered mass ratios above 0.1, considering the distribution is unconstrained for smaller mass ratios. The higher multiplicity fraction of massive stars is accounted for.

In principle, dynamical processes such as binary evaporation can affect the binary distribution. In practice, this is not relevant for binaries that would populate the S-star region. Specifically, binaries would disrupt prior to evaporating or hardening (see Appendix A).

For each binary, we simulated a close encounter with a pericenter drawn from a uniform distribution (up to three times the maximum tidal radius of the binary population), implicitly assuming binaries are in the full loss cone regime as might be expected for the massive perturbers scenario. Furthermore, the S stars imply high rates of disruptions that are difficult to reproduce in the empty loss-cone regime (Perets et al. 2007; Perets & Gualandris 2010). If the pericenter of the encounter is greater than three times the binary tidal radius, the binary is unlikely to be disrupted (see Sari et al. 2010 and Fig. 5 in Generozov & Madigan 2020), and thus unlikely to deposit stars in the S-star region. Such binaries were excluded from further analysis. Otherwise, we simulated a close encounter between the binary and the central SMBH with the Fewb ody code (Fregeau et al. 2004).

For simplicity, we assumed a constant disruption rate. Model binaries were disrupted at a random look-back time between 10⁹ years ago and the present day. Furthermore, the binary was disrupted at a random point along the main sequence of the primary star. We discuss the implications of a disruption rate rising toward the present day in Sect. 4, motivated by recent observational results on the star formation history in the Galactic center. Such models may be able to better reproduce the age distribution and the KLF of the S stars. However, more massive background black holes may be required to reproduce the S stars’ eccentricity distribution. Finally, we collected the remnants of all disrupted binaries with semimajor axes <0.05 pc, as S-star progenitors, and modeled their subsequent orbital relaxation.

2.2 Relaxation

Binary disruptions deposit stars onto highly eccentric orbits (see Equation (4)), and cannot account for the nearly thermal S-star eccentricity distribution Perets et al. (2009). However, the orbits of remnant stars can evolve due to nonresonant and resonant relaxation (Hopman & Alexander 2006a; Perets et al. 2009). In the former, stars change their energy and angular momenta due to uncorrelated two-body encounters. In the latter, stars change their angular momenta due to coherent torques in potentials with a high degree of symmetry (like the nearly Keplerian potential in the Galactic center).

The nonresonant relaxation time at Galactocentric radius r is 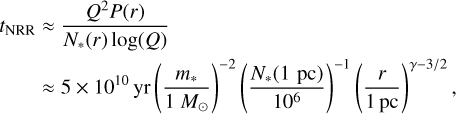$\begin{array}{l} t_{NRR} \approx \frac{Q^{2} P (r)}{N_{*} (r) \log (Q)} \\ \approx 5 \times 10^{10} yr {(\frac{m_{*}}{1 M_{⊙}})}^{- 2} {(\frac{N_{*} (1 pc)}{10^{6}})}^{- 1} {(\frac{r}{1 pc})}^{γ - 3 / 2}, \end{array}$ $\eqalign{ & {t_{{\rm{NRR}}}} \approx {{{Q^2}P(r)} \over {{N_*}(r)\log (Q)}} \cr & \,\,\,\,\,\,\,\,\, \approx 5 \times {10^{10}}{\rm{yr}}{\left( {{{{m_*}} \over {1{M_ \odot }}}} \right)^{ - 2}}{\left( {{{{N_*}(1{\rm{pc}})} \over {{{10}^6}}}} \right)^{ - 1}}{\left( {{r \over {1{\rm{pc}}}}} \right)^{\gamma - 3/2}}, \cr}$ (5)

where P(r) is the orbital period, N_* (r) is the number of stars enclosed within r, Q is the ratio of the SMBH mass to a characteristic stellar mass, and γ is the power law index of the 3D density profile. It should be noted that the presence of stellar- mass black holes or other massive objects can significantly reduce the relaxation timescale (see review by Alexander 2017).

In the limit in which the precession is dominated by extended stellar mass, the resonant relaxation time is 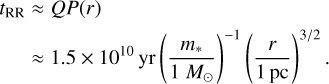$\begin{array}{l} t_{RR} \approx Q P (r) \\ \approx 1.5 \times 10^{10} yr {(\frac{m_{*}}{1 M_{⊙}})}^{- 1} {(\frac{r}{1 pc})}^{3 / 2} . \end{array}$ $\eqalign{ & {t_{{\rm{RR}}}} \approx QP(r) \cr & \,\,\,\,\,\,\, \approx 1.5 \times {10^{10}}{\rm{yr}}{\left( {{{{m_*}} \over {1{M_ \odot }}}} \right)^{ - 1}}{\left( {{r \over {1{\rm{pc}}}}} \right)^{3/2}}. \cr}$ (6)

For highly eccentric orbits, general relativistic precession dominates and resonant relaxation is suppressed (Merritt et al. 2011).

These timescales depend on the background density profile of stars and remnants. We modeled the background with two components: (i) low-mass stars and remnants (~1 M_⊙), and (ii) stellar-mass black holes (~10 M_⊙). This is a reasonable approximation for modeling relaxation in an evolved galactic nucleus, and has been used extensively in the literature (Merritt 2013). In principle, the high-eccentricity S stars should also contribute to the background density. In practice, we assume that the enclosed mass is dominated by the older, relaxed population that dominates the central 10″ (Schödel et al. 2020).

Well inside the sphere of influence, a relaxed stellar profile will be between r^−1.5 and r^−1.75, depending on the relative abundance of stellar-mass black holes (Bahcall & Wolf 1976; Alexander & Hopman 2009). The black hole profile will be steeper than r⁻² on larger scales, and flatten to r^−1.75 in the innermost parts of the Galactic center (Freitag et al. 2006a; Hopman & Alexander 2006b; Alexander & Hopman 2009; Preto & Amaro-Seoane 2010; Aharon & Perets 2015; Vasiliev 2017; Zhang & Amaro Seoane 2024)¹. We used the following power law approximations for the density profiles of stars and black holes: 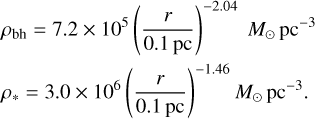$\begin{array}{l} ρ_{bh} = 7.2 \times 10^{5} {(\frac{r}{0.1 pc})}^{- 2.04} M_{⊙} {pc}^{- 3} \\ ρ_{*} = 3.0 \times 10^{6} {(\frac{r}{0.1 pc})}^{- 1.46} M_{⊙} {pc}^{- 3} . \end{array}$ $\eqalign{ & {\rho _{{\rm{bh }}}} = 7.2 \times {10^5}{\left( {{r \over {0.1{\rm{pc}}}}} \right)^{ - 2.04}}{M_ \odot }{\rm{p}}{{\rm{c}}^{ - 3}} \cr & {\rho _*} = 3.0 \times {10^6}{\left( {{r \over {0.1{\rm{pc}}}}} \right)^{ - 1.46}}{M_ \odot }{\rm{p}}{{\rm{c}}^{ - 3}}. \cr}$ (7)

This is a reasonable approximation for different Galactic center models. Equation (7) is within ~10% of the density profiles from the Fokker-Planck models Vasiliev (2017) and within ~40% of the ‘Fiducial’ model in Generozov et al. (2018) between 0.01 and 0.1 pc after 10 Gyr of evolution. The final density profiles of these models are similar, despite differences in the initial conditions. In Vasiliev (2017), the stars and black holes all form together in the distant past. In Generozov et al. (2018), the black holes are completely sourced by ongoing star formation at the present-day location of the clockwise disk. Recent measurements of the diffuse starlight and resolved stars in the Galactic center indicate a stellar density profile between r^−1.1 and r^−1.4 (Schödel et al. 2018; Gallego-Cano et al. 2018). There is some evidence for stellar-mass black holes in the central parsec from observations of X-ray transients in this region (Mori et al. 2019). There is also a population of quiescent black hole X-ray binary candidates (Hailey et al. 2018; Mori et al. 2021, though the identification of these sources as black holes is controversial Maccarone et al. 2022).

In this model, the total mass enclosed within the apocenter of S2 is ~1.5 × 103 M_⊙, comparable to the 1-σ upper limit from the GRAVITY collaboration (~ 1000 M_⊙; GRAVITY Collaboration 2024). We note that, in principle, the present-day upper limit does not rule out a larger number of black holes in the past.

We calculated angular momentum diffusion coefficients for this model, using JuDOKA (Tep et al. 2021). Then we evolved the remnants’ orbital elements forward in time, using the Monte Carlo procedure described in Bar-Or & Alexander (2016). For every timestep, Δt, the reduced angular momentum, j², and the semimajor axis, a, are incremented by 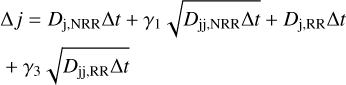$\begin{array}{l} Δ j = D_{j, NRR} Δ t + γ_{1} \sqrt{D_{jj, NRR} Δ t} + D_{j, RR} Δ t \\ + γ_{3} \sqrt{D_{jj, RR} Δ t} \end{array}$ $\eqalign{ & \Delta j = {D_{{\rm{j}},{\rm{NRR}}}}\Delta t + {\gamma _1}\sqrt {{D_{{\rm{ij}},{\rm{NRR}}}}\Delta t} + {D_{{\rm{j}},{\rm{RR}}}}\Delta t \cr & \, + {\gamma _3}\sqrt {{D_{{\rm{ij}},{\rm{RR}}}}\Delta t} \cr}$ (8) $Δ a = D_{a, NR} Δ t + γ_{2}^{'} (γ_{1}, γ_{2}) D_{aa, NRR},$ $\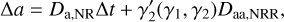Delta a = {D_{{\rm{a}},{\rm{NR}}}}\Delta t + \gamma _2^\prime \left( {{\gamma _1},{\gamma _2}} \right){D_{{\rm{aa}},{\rm{NRR}}}},$ (9)

respectively, where D_j, D_jj, D_a, and D_aa are the diffusion coefficients, and the subscripts RR and NRR denote resonant and nonresonant relaxation, respectively. The unprimed γ coefficients were independently drawn from a Gaussian distribution of unit variance, and 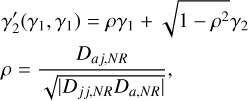$\begin{array}{l} γ_{2}^{'} (γ_{1}, γ_{1}) = ρ γ_{1} + \sqrt{1 - ρ^{2}} γ_{2} \\ ρ = \frac{D_{a j, N R}}{\sqrt{| D_{j j, N R} D_{a, N R} |}}, \end{array}$ $\eqalign{ & \gamma _2^\prime \left( {{\gamma _1},{\gamma _1}} \right) = \rho {\gamma _1} + \sqrt {1 - {\rho ^2}} {\gamma _2} \cr & \rho = {{{D_{aj,NR}}} \over {\sqrt {\left| {{D_{jj,NR}}{D_{a,NR}}} \right|} }}, \cr}$ (10)

accounting for the covariance between energy and angular momentum diffusion. We used an adaptive timestep for the evolution: 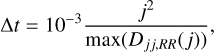$Δ t = 10^{- 3} \frac{j^{2}}{\max (D_{j j, R R} (j))},$ $\Delta t = {10^{ - 3}}{{{j^2}} \over {\max \left( {{D_{jj,RR}}(j)} \right)}},$ (11)

where max(D jj,_RR(j)) is the maximum of D_jj,RR at fixed energy. Gravitational wave emission was included, following Peters (1964), but was negligible except for a small minority of stars (e.g., for 99% of stars, the semimajor axis changes by less than 1% with the semimajor axis diffusion artificially turned off). To speed up our calculations, we computed the diffusion coefficients for a predefined grid of semimajor axes and angular momenta.

At each step, we linearly interpolated the resonant diffusion coefficients in a and j. The nonresonant diffusion coefficients also depend on the S-star masses. More precisely, they are a linear combination of integrals of the background distribution function, with mass-dependent coefficients. We linearly interpolated each integral term in a and j and combined them. Our interpolation tables extend between j = 0.001 and j = 0.999 and between a = 7 × 10⁻⁴ pc and 0.5 pc. These are the boundaries of our integration domain.

The outer boundaries are purely reflective. The inner semimajor axis is purely absorptive.

At the inner j boundary, stars can be disrupted if their pericenter falls below the stellar tidal radius (Rees 1988), 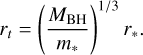$r_{t} = {(\frac{M_{BH}}{m_{*}})}^{1 / 3} r_{*} \cdot$ ${r_t} = {\left( {{{{M_{{\rm{BH}}}}} \over {{m_*}}}} \right)^{1/3}}{r_*} \cdot$ (12)

Here, m_* and r_* are the stellar mass and radius, respectively. These were evolved as is described in Sect. 2.3, so that the inner boundary depends on stellar properties³. To avoid stars overshooting and crossing into negative angular momenta, we implemented a second, reflective inner boundary at j = 10⁻³.

The true tidal radius may differ by a factor of order unity from Equation (12), based on the results of hydrodynamic simulations (Ryu et al. 2020a). We used Equation (2) in any case, as there is currently no fitting formula for the tidal radius of evolved stars that is calibrated to hydrodynamic simulations.

2.3 Stellar evolution

As time progresses, the stars evolve. We used both PARS EC isochrones (Bressan et al. 2012; Chen et al. 2014, 2015; Tang et al. 2014; Marigo et al. 2017; Pastorelli et al. 2019, 2020) and MIST (Dotter 2016; Choi et al. 2016; Paxton et al. 2011, 2013, 2015) stellar evolution tracks⁴ to evolve the stellar masses, radii, and types. We find similar results with both approaches. For conciseness, we only present the results from MIST.

We present results for solar metallicity, though we find similar results for [Fe/H]=0.5. There are no existing metallicity constraints for the young stars in the Galactic center.

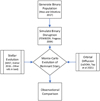Fig. 1

Key steps in our model for the production of S stars, including references and software used.

2.4 Summary of model

We now summarize our forward model for the formation of the S-star cluster, starting from binary disruptions. The key steps are (see Fig. 1):

Generate model binaries following the assumptions in Sect. 2.1.
- (a)
  We only consider binaries with semimajor axes up to 15 au, as wider binaries are unlikely to deposit stars into the S-star region (see Equation (3)).
- (b)
  The primary mass is between 1 and 100 M_⊙. Lower-mass binaries would not produce the presently observed S stars.
Generate close encounters with the SMBH following a Monte Carlo procedure:
- (a)
  The look-back time for the encounter is sampled uniformly between 10⁹ yr ago and the present day.
- (b)
  The pericenter of the encounter is sampled uniformly between 16 gravitational radii (~ the tidal radius of a single star) and three times the maximum tidal radius of the binary population (Equation (2)). Thus, we implicitly assume binaries are in the full loss cone regime, such that the pericenter of the center-of-mass orbit is uniformly distributed (see Merritt 2013 for a discussion of loss cone physics).
- (c)
  If the pericenter of the encounter exceeds three times the binary tidal radius (Equation (2)), the binary is unlikely to disrupt, and we proceed to the next one (Sari et al. 2010; Generozov & Madigan 2020).
We simulate tidal encounters between each binary and the SMBH using the FEWBODY code (Fregeau et al. 2004). In these encounters, the binary is initialized at 50 tidal radii on a nearly parabolic orbit with respect to the SMBH. The binary is generally split into low angular momentum bound and unbound stars (see Sect. 2.1).
- (a)
  We discard cases where the binary stars collide. This happens only ~1% of the time.
We collect all bound remnant stars with semimajor axes <0.05 pc, and follow their angular momentum and energy relaxation in a fixed background, as is described in Sect. 2.2. The effect of the remnant stars on the background density profile is neglected (Fragione & Sari 2018).
Stars are allowed to evolve and die (see Sect. 2.3). Furthermore, stars may be tidally disrupted by the central SMBH (see Equation (12)).
We collect the properties of all surviving stars with semimajor axes <0.05 pc and K-band magnitudes <18, and compare them to observations.
For each model star, we compute the probability to measure its orbital elements according to Equation (1) in Burkert et al. (2024). To account for observational bias, we exclude stars according to this probability.

Fig. 2

Initial (top) and final (bottom) pericenters and eccentricities for a subsample of model stars. (Note the different x scales in the two panels.) The top panel shows all stars, independently of when they are deposited in the Galactic center. The bottom panel shows the 71 model stars surviving to the present day with K ≤ 18 and a ≤ 0.05 pc. Early (late) stars are shown in purple (red). Model stars initially have high eccentricities and evolve toward lower ones. For comparison, we show the observed S stars in the bottom panel using blue squares for early- type stars and orange circles for late-type stars. The upper boundary of the zone of avoidance from Burkert et al. (2024) is shown as a solid gray line. The dashed gray line shows an adjusted zone of avoidance so that all S stars are outside it.

3 Results

The initial conditions of bound stars with semimajor axes of a_s ≤ 0.05 pc are shown in the top panel of Fig. 2. As was expected, all stars start on highly eccentric orbits. The semimajor axis distribution is close to uniform, due to the approximately log-uniform semimajor axis distribution of the progenitor binaries, and our assumption of a full loss cone (see also Perets & Gualandris 2010). The minimum semimajor axis is ~5 × 10−4 pc, corresponding to remnants of near-contact binaries (see Equation (3)). After ~200 Myr, a quasi-steady state is reached in the S-star region. The final pericenters and eccentricities of surviving stars are shown in the bottom panel of Fig. 2. Purple and red stars correspond to early- and late-type stars, respectively⁵. We also show the observed orbits of early and late-type S stars with blue squares and orange circles, respectively. We group observed stars of unknown type with early stars. If they were late-type stars, they would likely have been identified as such, considering CO absorption lines are prominent, and therefore easily observed with current instruments. Unless otherwise specified, here and in other observational comparisons, we exclude (i) disk S stars⁶, (ii) unbound S stars, and (iii) S stars with semimajor axes greater than 1.25″. The disk and the rest of the S stars differ in their eccentricity distribution, suggesting these are distinct populations that formed separately. The presence of O and WR stars in the disk also supports this. We exclude stars at large semimajor axes, as they will be strongly affected by completeness effects, complicating any comparisons to our model. Furthermore, our assumption of a full loss cone will break down at large radii (see Fig. 1 in Perets & Gualandris 2010), further complicating the comparison.

Overall, we find a reasonable agreement with the zone of avoidance. Approximately ~14% of model stars are in the zone of avoidance, as it is defined in Burkert et al. (2024). Similarly, in the latest orbital data, 3 of the ~40 observed stars are in the zone of avoidance (S14, S18, and S23). If we adjust the zone of avoidance so that all observed stars are outside (dashed gray line in Fig. 2), then only ~3.9% of model stars are inside the modified zone. For 40 stars, this would correspond to a ~20% probability of no stars being in the zone of avoidance.

Fig. 3 shows the one-dimensional pericenter and eccentricity of our model stars, compared to the observed S stars. Both distributions are consistent with the observations.

Fig. 4 shows the orbital properties of early S stars with K ≤ 16 and K > 16. This magnitude roughly divides the observed sample in half. The model eccentricity and pericenter distributions of each group are consistent with observations, though the bright stars have a somewhat superthermal eccentricity distribution. The faint stars’ semimajor axis distribution is too skewed toward large semimajor axes, compared to observations. In part, this is due to the assumed model for the progenitor binaries: as the primary mass decreases, the period distribution gradually shifts from approximately log-uniform to log-normal (with a peak near 10⁵ days). We also note that faint stars at large semimajor axes are the most difficult to detect, and this comparison is subject to observational bias.

We now compare the stellar properties of model stars with observations. In the model, ~20% of stars are late-type. This is consistent (within Poisson uncertainties) with the observed fraction of ~26%. However, we note that we have not included disruptions of old (≳10¹⁰) stars that make up the bulk of the nuclear stellar disk, and that can increase the population of evolved stars in the S-star region.

We also compare the K-band magnitudes of our model stars to observations (Fig. 5). In practice, we used the JWST F210M magnitude from MIST isochrones (Dotter 2016; Choi et al. 2016; Paxton et al. 2011, 2013, 2015) to approximate the K-band magnitude of our model stars. We also assumed an extinction of 2.42 (Fritz et al. 2011) and a Galactocentric distance of 8.3 kpc (GRAVITY Collaboration 2021). We neglected corrections from differential extinction (~0.3 mag; Schödel et al. 2010; Do et al. 2013).

The top panel of Fig. 5 compares the overall KLFs from theory and observations. We rescaled the luminosity functions to match at K = 16.2. There are significant discrepancies between the model and observed S-star KLF at both the faint and bright ends. The former can plausibly be explained by completeness effects. The latter is due to ~3 bright giants with K < 14 that are not observed, and is of marginal significance. We note that collisions with black holes cannot remove these bright giants (see Sect. 4.2).

The bottom panel of Fig. 5 compares the model and observed KLF of early-type stars (blue and orange). Here, there are no large differences at the bright end, while the model has many more stars with K > 16. This discrepancy may again be due to completeness effects. Unfortunately, this is difficult to quantify, as the observational selection function is highly nontrivial (the orange KLF only includes stars with measured orbits). The model more closely matches overall KLF from Schödel et al. (2020) (light red points; see Appendix B for details), which should be more complete, as even stars without orbits are included.

However, the progenitor binaries are more likely to follow a present-day mass function than an initial mass function (as assumed here). A present-day mass function would steepen the model KLF, and exacerbate the tension with observations (see Sect. 4).

The top panel of Fig. 6 shows the K-band magnitude as a function of age for the eight bright (K ≤ 15.5) S stars from Habibi et al. (2017) and for our model stars, which appear significantly older. To better compare the age distributions, we selected a subset of model stars with comparable K magnitudes. First, we selected all model stars within 0.1 mag for each of the Habibi et al. (2017) stars. Then, we sampled 100 stars (with replacement) from each of these subsets. The gray line in the bottom panel of Fig. 6 shows the stacked age distribution of the selected stars. On average, model stars are significantly older, even after accounting for the observational bias toward bright stars. This may suggest that the brightest S stars have a distinct origin or that the star formation rate (and delay time distribution between star formation and disruption) is nonuniform. Finally, there is a degeneracy between the age and metallicity (see Appendix C), such that the S stars may in fact have subsolar metallicity and be significantly older. Currently, there are no measurements of metallicity for the S stars, but future observations of the S stars with ERIS and NIRSpec will constrain this. A priori, this explanation is less likely, considering the nuclear stellar disk and nuclear star cluster are mostly metal-rich with small metal-poor populations (Do et al. 2015; Feldmeier-Krause et al. 2017; Rich et al. 2017; Nandakumar et al. 2018; Schultheis et al. 2019; Schödel et al. 2020; Schultheis et al. 2021; Nieuwmunster et al. 2024; Nogueras-Lara et al. 2024).

Finally, Fig. 7 shows a corner plot of a, e, and K. Once again, we see a good agreement between the observed and theoretical eccentricity distributions. At the same time, the model produces too many faint stars, and too many stars at large semimajor axes (though again we caution that faint stars at large semimajor axes are the most difficult to detect, and the latter discrepancy may be due to observational bias). In the observations, many of the lowest-eccentricity stars are in a narrow band of semimajor axes (3.3 ≲ log(a/au) ≲ 3.55). This feature is not apparent in the model. However, there are not enough stars to conclude that this is a statistically significant difference. Furthermore, the absence of this feature may simply reflect the differences in the one-dimensional semimajor axis distributions. To test this, we selected the model star with the closest semimajor axis for each observed S star. The structure of these model stars in the a – e space is more similar to the observed one, as is shown in the bottom panel of Fig. 7. Interestingly, there is a band of low- eccentricity stars near the Galactocentric radius where the scalar resonant relaxation time⁷ is minimized (log(a/au) ≈ 3.24). This is where angular momentum relaxation is most efficient.

Fig. 3

Left panel: cumulative eccentricity distribution from the model (solid blue line), compared to the observed S-star eccentricity distribution (dashed orange line). For reference, we also show a thermal eccentricity distribution (dash-dotted green line). Right panel: cumulative pericenter distribution from our model and observations. The numbers in the legend are the p values from a two-sample KS test with the model and observed distributions.

Fig. 4

Cumulative eccentricity, pericenter, and semimajor axis distributions for bright (K ≤ 16, left panels) and faint (K > 16, right panels) early S stars.

Fig. 5

Top panel: KLF of all model (blue) and observed (dashed orange) S stars. Bottom panel: KLFs for model (blue) and observed (dashed orange) early S stars (with orbits). The red line is the KLF of early stars in the central 0.5″ from Schödel et al. (2020) (see Appendix B for details). The luminosity functions are normalized to match at a K-band magnitude of 16.2.

Fig. 6

Top panel: age versus K-band magnitude for eight bright S stars (red; Habibi et al. 2017), compared to early model stars (gray). Bottom: Age distribution of Habibi et al. (2017) stars and model stars with comparable magnitudes (see text for details).

Fig. 7

Top panel: corner plot showing distributions of semimajor axis (a), eccentricity (e), and K magnitude from theory (orange) and observations (blue). Bottom panel: eccentricity versus semimajor axis for the observed S stars, and for the model stars that are closest in the semimajor axis.

Fig. 8

K-band luminosity function accounting for the dependence of the binary disruption probability on stellar lifetime (light green line). Effectively, this means that the progenitor binaries are drawn from a present-day mass function rather than an initial mass function. The other lines are the same as in Fig. 5.

4 Critical discussion of model assumptions

Here, we critically examine a few assumptions about the progenitor binary population, and how they affect observational comparisons. Firstly, the primary mass of each binary is drawn from an initial mass function. However, a steeper present-day mass function is more realistic, considering the shorter lifetimes of massive stars. Secondly, binaries disrupt at a constant rate and are allowed to disrupt immediately after formation. In reality, binaries may need some time to reach disruption, especially if they form on circular orbits. As is discussed below, delays and a present-day mass function exacerbate the tension with the observed KLF.

We also discuss the effect of stellar collisions and repeated, individually nondisruptive tidal encounters between the stars and the central SMBH. These effects are not included in our base model, but do not affect the results.

4.1 Mass function and disruption times

In our base model, the primary mass of each binary is drawn from a Kroupa initial mass function. However, the mass function of disrupting binaries will likely be more bottom-heavy, due to the longer lifetimes of low-mass stars.

Here, we account for this effect by re-weighting probability distributions. In particular, each remnant star is weighted by the main-sequence lifetime of the primary star in the progenitor binary. This causes the KLF to steepen, in tension with observations, as is shown in Fig. 8.

This result depends on the star formation history in the Galactic center, particularly within the region of the nuclear stellar disk, where disrupting binaries likely originate (see Fig. 3 in Perets et al. 2007). Schödel et al. (2023) recently showed that the star formation history in the nuclear stellar disk is highly nonuniform: ≳70% of the stars formed more than 10 Gyr ago, ∼15% formed ∼1 Gyr ago, and up to 10% formed in the last tens to hundreds of millions of years. This suggests a star formation rate rising toward the present day (since a comparable number of stars were formed within the last ∼10⁸ yr and ∼10⁹ yr). Furthermore, the star formation rate is likely correlated with the binary disruption rate, since both are correlated with the molecular gas density.

Motivated by these observations, we discarded stars that formed more than 10⁸ yr ago to see the effect of a star formation history rising to the present day. Fig. 9 shows the KLF after this cut, with and without re-weighting for stellar lifetimes. In the former case, massive stars receive a weight equal to their main-sequence lifetime divided by 10⁸ yr. Stars with main- sequence lifetimes longer than 10⁸ yr receive a weight of unity. This ameliorates, but does not entirely remove, the tension with observations, as is shown in Fig. 9. Furthermore, the model eccentricity distribution is in tension with observations, though this can be resolved if the background black holes are each 20 M_⊙ instead of 10 M_⊙.

The results also depend on the delay time distribution between star formation and disruptions. In the base model, binaries can be disrupted immediately after formation. More realistically, binaries will take some time to reach the loss cone, especially if they form on circular orbits. Imposing a minimum age at disruption tends to steepen the KLF, as is illustrated in Fig. 10. This shows the KLF after (i) discarding stars older 10⁸ yr and (ii) discarding stars injected into the Galactic center less than 10⁷ yr after formation.

The better agreement between theory and observation in Fig. 9 suggests that the early S stars are primarily sourced by binaries formed within the last ∼100 Myr. Nonetheless, a slight tension remains, especially for realistic delay times between star formation and disruption, as in Fig. 10. In this case, there is a ~2σ tension between the observed (orange) and theoretical (turquoise) KLF between K = 14 and K = 16⁸. Potentially, this tension could be resolved via a bursty star formation rate that is more skewed toward the present day. This may also help with the tension between model and observed ages among the bright S stars (see Fig. 6).

Alternatively, the tension with the observed KLF may be resolved with a top-heavy initial mass function. The mass function required itself depends on the binary injection history. In the last case (Fig. 10), an initial mass function of dN/dm ∝ m^−0.2 reduces the tension to 1σ.

Fig. 9

K-band luminosity functions, after discarding stars formed more than 10⁸ yr ago. The blue (light green) line corresponds to binaries drawn from an initial (present-day) mass function.

Fig. 10

Same as Fig. 9, except we discarded stars that were less than 10⁷ yr old at the moment of binary disruption.

4.2 Collisions

In principle, stars may suffer mass loss or destruction via collisions with other stars or compact objects. Alternatively, star-star collisions can lead to mergers and the buildup of massive stars (Spitzer & Saslaw 1966; Duncan & Shapiro 1983; Murphy et al. 1991; Genzel et al. 1996; Davies et al. 1998; Portegies Zwart et al. 1999; Gürkan et al. 2004; Freitag et al. 2006b; Dale et al. 2009; Rose et al. 2023).

We estimated the impact of destructive black-hole star collisions. In particular, we computed the orbit-averaged collision rate between the remnant stars and black holes in our Monte Carlo models: 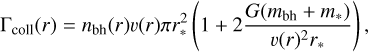$Γ_{coll} (r) = n_{bh} (r) v (r) π r_{*}^{2} (1 + 2 \frac{G (m_{bh} + m_{*})}{v {(r)}^{2} r_{*}}),$ ${\Gamma _{{\rm{coll}}}}(r) = {n_{{\rm{bh}}}}(r)v(r)\pi r_*^2\left( {1 + 2{{G\left( {{m_{{\rm{bh}}}} + {m_*}} \right)} \over {v{{(r)}^2}{r_*}}}} \right),$ (13)

where m_∗ and mbh are the stellar and BH masses, respectively, r_* is the stellar radius, 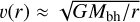$v (r) \approx \sqrt{G M_{bh} / r}$ $\v (r) \approx \sqrt {G{M_{{\rm{bh}}}}/r}$ is the local velocity dispersion, and n_bh(r) is the BH density (see Eq. (7)). The orbit average was calculated from 10⁴ points along the orbit, equally spaced in eccentricity anomaly (EA). Each point is weighted by (1 − e cos( EA)) in the average.

For each Monte Carlo timestep, δt, we generated a random number between 0 and 1, and recorded a collision if it was less than the expected number of collisions, <Γ_coll > δt.

Removing stars that experience collisions has a minor impact on the results. Most notably, the fraction of late-type S stars decreases from ∼20% to ∼16%. In fact, the impact of collisions may be overestimated, considering that deeply penetrating encounters are necessary to significantly dim giant stars (Dale et al. 2009).

Rose et al. (2023) have shown that star-star collisions in the S-star region can lead to the buildup of massive stars (but this would require nondisruptive collisions). We leave this effect to future studies, though it may have a major impact on the comparisons to the observed KLF and ages. Additionally, stellar collisions can lead to transients that look like tidal disruption events or supernovae (Balberg et al. 2013; Amaro Seoane 2023; Ryu et al. 2024; Dessart et al. 2024).

4.3 Repeated tidal encounters with the SMBH

So far, we have only considered the removal of stars due to full tidal disruptions by the central SMBH. However, stars can also be removed due to multiple partial tidal disruptions. Furthermore, stars can become swollen and disrupted due to tidal heating (Alexander & Morris 2003). To experience such effects, the star needs to pass within a factor of a few of the central SMBH (Guillochon & Ramirez-Ruiz 2013; Li & Loeb 2013; Mainetti et al. 2017; Ryu et al. 2020b; Lu et al. 2021; Generozov 2021). To test how these effects would change the results, we multiplied the tidal radius of each star by two. We found that this has no significant effect on the comparisons previously discussed.

5 Fixed age model (eccentric disk)

So far, we have considered models in which stellar ages and disruption times can vary freely. We now discuss models in which all stars are injected at similar times in the recent past. Such an impulsive burst of disruptions may be triggered by a secular gravitational instability in the ~2.5–8 Myr old (Levin & Beloborodov 2003; Paumard et al. 2006; Bartko et al. 2009; Lu et al. 2013; Yelda et al. 2014) clockwise disk if it starts in a lopsided, eccentric configuration (Madigan et al. 2009; Generozov & Madigan 2020; Rantala & Naab 2023). This configuration can arise from the tidal disruption of a molecular cloud (Bonnell & Rice 2008; Gualandris et al. 2012; Generozov et al. 2022), or via an SMBH merger in the Galactic center (Akiba et al. 2024)⁹. Interactions between the misaligned young disks can also trigger a burst of binary disruptions (Löckmann et al. 2008).

Previously, Generozov & Madigan (2020) and Tep et al. (2021) analyzed the relaxation of the S-stars in such scenarios. The former found that 10 M_⊙ BHs would be able to reproduce the observed S-star eccentricity distribution, by modeling angular momentum relaxation at a fixed semimajor axis of 0.01 pc. However, the resonant relaxation time will be significantly longer in the outer part of the S-star cluster. Tep et al. (2021) accounted for the S stars’ semimajor axis distribution and found that reproducing the observed S-star eccentricity distribution requires black holes above 100 M_⊙ at 2σ confidence, though this constraint depends on the S-star sample (i.e., this is the constraint including late-type and disk S stars).

We performed a similar analysis, assuming that stars are injected into the Galactic center all at once. First, for consistency with Tep et al. (2021), we turned off (i) the loss cone, (ii) stellar evolution, and (iii) semimajor axis diffusion. Effects (i) and (ii) will be negligible for the S stars over million-year timescales. However, we show that the loss cone can affect black hole mass constraints by a factor of ~2.

We also matched the initial conditions in Tep et al. (2021), assuming that all stars were injected into the Galactic center 7.1 Myr ago, the mean age of eight bright S stars from Habibi et al. (2017)¹⁰. The initial angular momentum distribution is a Gaussian with a mean of 0.2 (e = 0.98) and a standard deviation of 0.02.

We present results for both the density profiles in Tep et al. (2021): 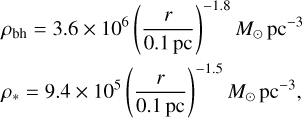$\begin{array}{l} ρ_{bh} = 3.6 \times 10^{6} {(\frac{r}{0.1 pc})}^{- 1.8} M_{⊙} {pc}^{- 3} \\ ρ_{*} = 9.4 \times 10^{5} {(\frac{r}{0.1 pc})}^{- 1.5} M_{⊙} {pc}^{- 3}, \end{array}$ $\eqalign{ & {\rho _{{\rm{bh}}}} = 3.6 \times {10^6}{\left( {{r \over {0.1{\rm{pc}}}}} \right)^{ - 1.8}}{M_ \odot }{\rm{p}}{{\rm{c}}^{ - 3}} \cr & {\rho _*} = 9.4 \times {10^5}{\left( {{r \over {0.1{\rm{pc}}}}} \right)^{ - 1.5}}{M_ \odot }{\rm{p}}{{\rm{c}}^{ - 3}}, \cr}$ (14)

and our fiducial density profile (Eq. (7)), which is in better agreement with the latest constraints from GRAVITY (GRAVITY Collaboration 2024) and which has a factor of 3 fewer BHs within 0.05 pc.

Using the same S-star sample and background profile as Tep et al. (2021), we find good agreement with their results: black hole masses <100 M_⊙ can be ruled out. However, the full sample includes late-type stars and stars at larger scales that may be unrelated to binary disruptions. For example, eight of the S stars are members of the clockwise disk. For the 25 early, non-disk S stars with semimajor axes within 0.05 pc, only black holes with masses <17 M_⊙ can be ruled out. For the same subsample and our fiducial density profile, masses <50 M_⊙ can be ruled out. Finally, the lower limit is reduced to ~24 M_⊙, with a loss cone.

Overall, explaining the entire S-star population via binaries from the young clockwise disk requires a background with more massive black holes. There is also tension between the mass functions of the disk and S stars that may require an unusual mass ratio distribution within the disk to reconcile (Generozov 2021). Moreover, it is not clear whether the conditions for the eccentric disk instability could arise with steep background density profiles (e.g., Eq. (7); see the discussions in Madigan et al. 2009 and Generozov et al. 2022). On the other hand, efficient angular momentum relaxation of the S stars likely requires a steep black hole cusp. Detailed modeling of disk binary disruptions suggests that they can reproduce the zone of avoidance, but remnant stars will be skewed toward large semimajor axes compared to the observations¹¹.

6 Summary and discussion

We show that many properties of the observed S-star cluster in the Galactic center, including the recently discovered zone of avoidance, can be explained by a combination of isotropic binary disruptions, and relaxation in the Galactic center. Our focus is on explaining the classic, isotropic S-star cluster. In our model, the young disks would have a different origin that we leave to future work.

Our main conclusions are summarized as follows:

In the full-loss-cone regime, the remnant stars from massive binary disruptions will have an approximately uniform semimajor axis distribution. This naturally explains the lack of S stars in the zone of avoidance. Empty loss cone models would place too many stars in this region;
The overall orbital eccentricity and pericenter distribution of the S-star cluster is well reproduced in our models, via relaxation processes. We have only considered nonresonant and resonant relaxation from a background population of stars and 10 M_⊙ black holes. Potentially, an AGN disk may also perturb the S-star orbits, dramatically reducing the angular momentum relaxation time (Chen & Amaro-Seoane 2014);
There is a slight tension with the observed semimajor axis distribution of fainter S stars (K < 16), potentially indicating the progenitor binary population is more skewed to small separations than in Moe & Di Stefano (2017);
The model KLF is in tension with observations, particularly with a Kroupa present-day mass function and realistic delay times between star formation and disruption. Potentially, this tension may be resolved with a top-heavy initial mass function or with a bursty star formation rate that is skewed toward the present day. However, reproducing the observed thermal eccentricity distribution would be more challenging in such scenarios;
There is also tension with the measured ages of the bright S stars, with the model predicting older ages. Again, this may point to a bursty star formation rate. Alternatively, the measured ages may be underestimated if the S stars have subsolar metallicities.

Acknowledgements

We thank the anonymous referee for helpful comments. We are very grateful to our funding agencies. AG was supported at the Technion by a Zuckerman Fellowship. RS acknowledges financial support from the Severo Ochoa grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033, grant EUR2022-134031 funded by MCIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR, and grant PID2022-136640NB- C21 funded by MCIN/AEI 10.13039/501100011033 and by the European Union. We thank Pau Amaro Seoane, Andreas Burkert, Sebastiano von Fellenberg, Jean-Baptiste Fouvry, Karamveer Kaur, Fabrice Martins, Nicholas Stone, Odelia Teboul, and Kerwann Tep for helpful comments and discussions. This work made use of the following software packages: Astropy (Astropy Collaboration 2013; The Astropy Collaboration 2018; Astropy Collaboration 2022), Fewbody (Fregeau et al. 2004), JuDOKA (Tep et al. 2021), Jupyter (Kluyver et al. 2016), Matplotlib (Hunter 2007), MIST (Paxton et al. 2011, 2013, 2015; Dotter 2016; Choi et al. 2016), NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), PARSEC (Bressan et al. 2012; Chen et al. 2014, 2015; Tang et al. 2014; Marigo et al. 2017; Pastorelli et al. 2019, 2020), seaborn (Waskom 2021).

Appendix A Binary evaporation

In principle, the binary population in the Galactic center region may be shaped by dynamical processes. For example, soft binaries can be evaporated by encounters with other stars. Here we quantify this effect and show that in our models binaries are more likely to disrupt rather than evaporate, and thus binary evaporation may be neglected.

The local evaporation timescale is (see Alexander & Pfuhl 2014) 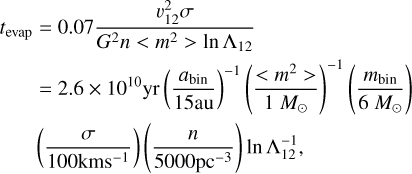$\begin{array}{l} t_{evap} = 0.07 \frac{v_{12}^{2} σ}{G^{2} n < m^{2} > ln Λ_{12}} \\ = 2.6 \times 10^{10} yr {(\frac{a_{bin}}{15 au})}^{- 1} {(\frac{< m^{2} >}{1 M_{⊙}})}^{- 1} (\frac{m_{bin}}{6 M_{⊙}}) \\ (\frac{σ}{100 {kms}^{- 1}}) (\frac{n}{5000 {pc}^{- 3}}) ln Λ_{12}^{- 1}, \end{array}$ $\eqalign{ & {t_{{\rm{evap }}}} = 0.07{{\v _{12}^2\sigma } \over {{G^2}n < {m^2} > \ln {\Lambda _{12}}}} \cr & \,\,\,\,\,\,\,\,\, = 2.6 \times {10^{10}}{\rm{yr}}{\left( {{{{a_{{\rm{bin }}}}} \over {15{\rm{au}}}}} \right)^{ - 1}}{\left( {{{ < {m^2} > } \over {1{M_ \odot }}}} \right)^{ - 1}}\left( {{{{m_{{\rm{bin }}}}} \over {6{M_ \odot }}}} \right) \cr & \,\,\,\,\,\,\,\,\left( {{\sigma \over {100{\rm{km}}{{\rm{s}}^{ - 1}}}}} \right)\left( {{n \over {5000{\rm{p}}{{\rm{c}}^{ - 3}}}}} \right)\ln \Lambda _{12}^{ - 1}, \cr}$ (A.1)

where υ₁₂ is the internal velocity of the binary, n, σ, and <m² > are the number density, velocity dispersion of the perturbing population, and 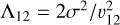$Λ_{12} = 2 σ^{2} / v_{12}^{2}$ ${{\rm{\Lambda }}_{12}} = 2{\sigma ^2}/\v _{12}^2$ . In our model, binaries come from outside the central 5 pc, where n ≈ 5 × 10³ pc⁻³, and σ ≈ 100 km s⁻¹. For binaries with semimajor axes ≤ 15 au in this region, the evaporation timescale is of order 10 Gyr or more.

In comparison, the timescale for binaries to disrupt is 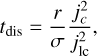$t_{dis} = \frac{r}{σ} \frac{j_{c}^{2}}{j_{lc}^{2}},$ ${t_{{\rm{dis}}}} = {r \over \sigma }{{j_c^2} \over {j_{{\rm{lc}}}^2}},$ (A.2)

where 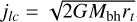$j_{l c} = \sqrt{2 G M_{bh} r_{t}}$ ${j_{lc}} = \sqrt {2G{M_{{\rm{bh}}}}{r_t}}$ . For an enclosed mass of 10⁷ M_⊙ inside 5 pc, 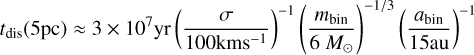$t_{dis} (5 pc) \approx 3 \times 10^{7} yr {(\frac{σ}{100 {kms}^{- 1}})}^{- 1} {(\frac{m_{bin}}{6 M_{⊙}})}^{- 1 / 3} {(\frac{a_{bin}}{15 au})}^{- 1}$ ${t_{{\rm{dis}}}}(5{\rm{pc}}) \approx 3 \times {10^7}{\rm{yr}}{\left( {{\sigma \over {100{\rm{km}}{{\rm{s}}^{ - 1}}}}} \right)^{ - 1}}{\left( {{{{m_{{\rm{bin}}}}} \over {6{M_ \odot }}}} \right)^{ - 1/3}}{\left( {{{{a_{{\rm{bin }}}}} \over {15{\rm{au}}}}} \right)^{ - 1}}$ (A.3)

Binaries on eccentric orbits will cross the central region, where the evaporation timescale is shorter. In particular, the evaporation timescale will be between r^1.3 − r ^1·5.¹² The average evaporation time over the binary population is 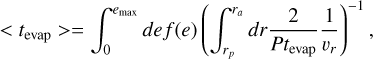$< t_{evap} > = \int_{0}^{e_{\max}} d e f (e) {(\int_{r_{p}}^{r_{a}} d r \frac{2}{P t_{evap}} \frac{1}{v_{r}})}^{- 1},$ $< {t_{{\rm{evap}}}} > = \int_0^{{e_{\max }}} {def} (e){\left( {\int_{{r_p}}^{{r_a}} d r{2 \over {P{t_{{\rm{evap}}}}}}{1 \over {{\v _r}}}} \right)^{ - 1}},$ (A.4)

where r_p, r_a, υ_r, P, e, and f (e) are the pericenter, apocenter, radial velocity, orbital period, eccentricity, and eccentricity distribution respectively. Note that the inner integral corresponds to a harmonic average.

In steady state f (e) is expected to be thermal. Also, since we are considering binaries that are not too far outside the SMBH sphere of influence, we assume Keplerian scalings with radius for all the dynamical quantities. Overall, we find eccentric orbits give a ~10% correction to the evaporation time.

Although we have focused on soft binaries, the hardening rate of hard binaries has a similar dependence on cluster and binary properties (Heggie 1975; Hills 1983). Therefore, we also expect hard binaries to disrupt before they can significantly harden.

Appendix B K-band luminosity function

Here, we describe how we derive the KLF of early stars inside 0.5” (the red line in Figure 5) from the data in Schödel et al. (2020).

First, we compute the KLF in two radial rings with r_proj < 0·5″ and 4″ < r_proj < 5″. These KLFs include contribution from both early and late stars, with surface density profiles r^0±0·⁰⁸ and r^0±0·⁰⁸, respectively (Table 6 in Gallego-Cano et al. 2024). The surface densities are equal at ~0·7″, such that late (early) stars dominate on larger (smaller) scales.

The KLF of early stars within 0·5″ is 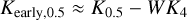$K_{early, 0.5} \approx K_{0.5} - W K_{4}$ ${K_{{\rm{early }},0.5}} \approx {K_{0.5}} - W{K_4}$ (B.1)

where K_0.5 is the total KLF inside 0·5″ and K₄ is the KLF between 4″ and 5", which is dominated by late stars. The weight, W, is chosen to reproduce the ratio of late to all stars inside 0·5″, X. From the surface density profiles in Gallego-Cano et al. (2024), X ≈ 0·3 and 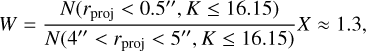$W = \frac{N (r_{proj} < {0.5}^{''}, K \leq 16.15)}{N (4^{''} < r_{proj} < 5^{''}, K \leq 16.15)} X \approx 1.3,$ $W = {{N\left( {{r_{{\rm{proj }}}} < {{0.5}^{\prime \prime }},K \le 16.15} \right)} \over {N\left( {{4^{\prime \prime }} < {r_{{\rm{proj }}}} < {5^{\prime \prime }},K \le 16.15} \right)}}X \approx 1.3,$ (B.2)

where the numerator is the number of stars with projected radius, r_proj less than 0.5″ and K ≤ 16. Similarly, the denominator is the number of stars with 4″ < r_proj < 5″ and K ≤ 16.15. The cut near K = 16.15 is motivated by exclusion of fainter stars from the surface density fits in Gallego-Cano et al. (2024).

From equations (B.1) and (B.2), we obtain the K_early,0.5, the red line in Figure 5. The uncertainty is calculated by adding the uncertainties from K_0.5 and K₄ in quadrature. The results change by less than the uncertainty, if we use the KLF from 2–3″ or 3–4″ in lieu of K₄. In fact, the difference between K_0.5 and K_early,0.5 are smaller than the uncertainties for K ≲ 19.

Appendix C S-star ages versus metallicity

Here we show that the S-star ages are degenerate with metallicity. Figure C.1 shows a comparison of MIST isochrones of log(g) versus log(T_eff) for two different metallicities. Qualitatively, the S stars can either be younger and metal-rich or older and metal-poor. For each star, we estimate the age by identifying the closest main-sequence isochrone point.¹³ We summarize these estimates in Table C.1, along with the fits from Habibi et al (2017) We em hasize that our a es are merel estimates to illustrate the trend with metallicity, rather than detailed fits

Fig. C.1

log(g) versus log(T_eff) for the eight bright S stars from Habibi et al. (2017) compared to MIST isochrones (v1.2, υ/υ_crit = 0.4). The solid (dashed) lines correspond to [Fe/H] = 0 ([Fe/H] = −0.5).

Table C.1

Ages for eight bright S stars from Habibi et al. (2017), and from MIST isochrones at different metallicities.

References

Aharon, D., & Perets, H. B. 2015, ApJ, 799, 185 [NASA ADS] [CrossRef] [Google Scholar]
Akiba, T., Naoz, S., & Madigan, A.-M. 2024, ApJ submitted, [arXiv:2410.19881] [Google Scholar]
Alexander, T. 2017, arXiv e-prints [arXiv:1701.04762] [Google Scholar]
Alexander, T., & Hopman, C. 2009, ApJ, 697, 1861 [NASA ADS] [CrossRef] [Google Scholar]
Alexander, T., & Morris, M. 2003, ApJ, 590, L25 [NASA ADS] [Google Scholar]
Alexander, T., & Pfuhl, O. 2014, ApJ, 780, 148 [Google Scholar]
Amaro Seoane, P. 2023, ApJ, 947, 8 [CrossRef] [Google Scholar]
Antonini, F., & Merritt, D. 2013, ApJ, 763, L10 [NASA ADS] [Google Scholar]
Antonini, F., Faber, J., Gualandris, A., & Merritt, D. 2010, ApJ, 713, 90 [NASA ADS] [Google Scholar]
Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
Bahcall, J. N., & Wolf, R. A. 1976, ApJ, 209, 214 [NASA ADS] [CrossRef] [Google Scholar]
Balberg, S., Sari, R., & Loeb, A. 2013, MNRAS, 434, L26 [CrossRef] [Google Scholar]
Bar-Or, B., & Alexander, T. 2014, Class. Quant. Grav., 31, 244003 [NASA ADS] [CrossRef] [Google Scholar]
Bar-Or, B., & Alexander, T. 2016, ApJ, 820, 129 [NASA ADS] [CrossRef] [Google Scholar]
Bar-Or, B., & Fouvry, J.-B. 2018, ApJ, 860, L23 [NASA ADS] [CrossRef] [Google Scholar]
Bartko, H., Martins, F., Fritz, T. K., et al. 2009, ApJ, 697, 1741 [Google Scholar]
Baumgardt, H., Amaro-Seoane, P., & Schödel, R. 2018, A&A, 609, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonnell, I. A., & Rice, W. K. M. 2008, Science, 321, 1060 [NASA ADS] [CrossRef] [Google Scholar]
Bradnick, B., Mandel, I., & Levin, Y. 2017, MNRAS, 469, 2042 [Google Scholar]
Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
Burkert, A., Gillessen, S., Lin, D. N. C., et al. 2024, ApJ, 962, 81 [NASA ADS] [CrossRef] [Google Scholar]
Cao, C. Y., Liu, F. K., Li, S., Chen, X., & Wang, K. 2024, arXiv e-prints [arXiv:2411.09278] [Google Scholar]
Chen, X., & Amaro-Seoane, P. 2014, ApJ, 786, L14 [NASA ADS] [CrossRef] [Google Scholar]
Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [Google Scholar]
Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [Google Scholar]
Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
Dale, J. E., Davies, M. B., Church, R. P., & Freitag, M. 2009, MNRAS, 393, 1016 [Google Scholar]
Davies, M. B., Blackwell, R., Bailey, V. C., & Sigurdsson, S. 1998, MNRAS, 301, 745 [NASA ADS] [Google Scholar]
Dessart, L., Ryu, T., Amaro Seoane, P., & Taylor, A. M. 2024, A&A, 682, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Do, T., Lu, J. R., Ghez, A. M., et al. 2013, ApJ, 764, 154 [NASA ADS] [CrossRef] [Google Scholar]
Do, T., Kerzendorf, W., Winsor, N., et al. 2015, ApJ, 809, 143 [Google Scholar]
Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [Google Scholar]
Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
Duncan, M. J., & Shapiro, S. L. 1983, ApJ, 268, 565 [NASA ADS] [Google Scholar]
Feldmeier-Krause, A., Kerzendorf, W., Neumayer, N., et al. 2017, MNRAS, 464, 194 [Google Scholar]
Fouvry, J. B., Pichon, C., & Magorrian, J. 2017, A&A, 598, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fragione, G., & Sari, R. 2018, ApJ, 852, 51 [NASA ADS] [CrossRef] [Google Scholar]
Fragione, G., Capuzzo-Dolcetta, R., & Kroupa, P. 2017, MNRAS, 467, 451 [Google Scholar]
Fregeau, J. M., Cheung, P., Portegies Zwart, S. F., & Rasio, F. A. 2004, MNRAS, 352, 1 [CrossRef] [Google Scholar]
Freitag, M., Amaro-Seoane, P., & Kalogera, V. 2006a, ApJ, 649, 91 [NASA ADS] [CrossRef] [Google Scholar]
Freitag, M., Gürkan, M. A., & Rasio, F. A. 2006b, MNRAS, 368, 141 [NASA ADS] [Google Scholar]
Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [Google Scholar]
Gallego-Cano, E., Schödel, R., Dong, H., et al. 2018, A&A, 609, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gallego-Cano, E., Fritz, T., Schödel, R., et al. 2024, A&A, 689, A190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Generozov, A. 2021, MNRAS, 501, 3088 [Google Scholar]
Generozov, A., & Madigan, A.-M. 2020, ApJ, 896, 137 [NASA ADS] [CrossRef] [Google Scholar]
Generozov, A., Stone, N. C., Metzger, B. D., & Ostriker, J. P. 2018, MNRAS, 478, 4030 [Google Scholar]
Generozov, A., Nayakshin, S., & Madigan, A. M. 2022, MNRAS, 512, 4100 [NASA ADS] [CrossRef] [Google Scholar]
Genzel, R., Thatte, N., Krabbe, A., Kroker, H., & Tacconi-Garman, L. E. 1996, ApJ, 472, 153 [NASA ADS] [CrossRef] [Google Scholar]
Genzel, R., Eckart, A., Ott, T., & Eisenhauer, F. 1997, MNRAS, 291, 219 [NASA ADS] [CrossRef] [Google Scholar]
Ghez, A. M., Klein, B. L., Morris, M., & Becklin, E. E. 1998, ApJ, 509, 678 [NASA ADS] [CrossRef] [Google Scholar]
Ghez, A. M., Duchêne, G., Matthews, K., et al. 2003, ApJ, 586, L127 [Google Scholar]
Gillessen, S., Plewa, P. M., Eisenhauer, F., et al. 2017, ApJ, 837, 30 [Google Scholar]
Ginsburg, I., & Loeb, A. 2007, MNRAS, 376, 492 [NASA ADS] [Google Scholar]
Gould, A., & Quillen, A. C. 2003, ApJ, 592, 935 [NASA ADS] [Google Scholar]
GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
GRAVITY Collaboration (Abuter, R., et al.) 2020, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
GRAVITY Collaboration (Abuter, R., et al.) 2021, A&A, 647, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
GRAVITY Collaboration (Abuter, R., et al.) 2022, A&A, 657, L12 [NASA ADS] [CrossRef] [Google Scholar]
GRAVITY Collaboration (Abd El Dayem, K., et al.) 2024, A&A, 692, A242 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gualandris, A., Mapelli, M., & Perets, H. B. 2012, MNRAS, 427, 1793 [Google Scholar]
Guillochon, J., & Ramirez-Ruiz, E. 2013, ApJ, 767, 25 [NASA ADS] [CrossRef] [Google Scholar]
Gürkan, M. A., Freitag, M., & Rasio, F. A. 2004, ApJ, 604, 632 [NASA ADS] [CrossRef] [Google Scholar]
Habibi, M., Gillessen, S., Martins, F., et al. 2017, ApJ, 847, 120 [Google Scholar]
Hailey, C. J., Mori, K., Bauer, F. E., et al. 2018, Nature, 556, 70 [Google Scholar]
Hamers, A. S., & Perets, H. B. 2017, ApJ, 846, 123 [NASA ADS] [CrossRef] [Google Scholar]
Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
Hills, J. G. 1983, AJ, 88, 1269 [NASA ADS] [CrossRef] [Google Scholar]
Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]
Hills, J. G. 1991, AJ, 102, 704 [Google Scholar]
Hopman, C., & Alexander, T. 2006a, ApJ, 645, 1152 [NASA ADS] [CrossRef] [Google Scholar]
Hopman, C., & Alexander, T. 2006b, ApJ, 645, L133 [NASA ADS] [CrossRef] [Google Scholar]
Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
Kim, S. S., Figer, D. F., & Morris, M. 2004, ApJ, 607, L123 [NASA ADS] [Google Scholar]
Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt (IOS Press), 87 [Google Scholar]
Kocsis, B., & Tremaine, S. 2011, MNRAS, 412, 187 [NASA ADS] [CrossRef] [Google Scholar]
Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
Levin, Y., & Beloborodov, A. M. 2003, ApJ, 590, L33 [NASA ADS] [CrossRef] [Google Scholar]
Li, G., & Loeb, A. 2013, MNRAS, 429, 3040 [Google Scholar]
Löckmann, U., Baumgardt, H., & Kroupa, P. 2008, ApJ, 683, L151 [Google Scholar]
Lu, J. R., Do, T., Ghez, A. M., et al. 2013, ApJ, 764, 155 [NASA ADS] [CrossRef] [Google Scholar]
Lu, W., Fuller, J., Raveh, Y., et al. 2021, MNRAS, 503, 603 [Google Scholar]
Maccarone, T. J., Degenaar, N., Tetarenko, B. E., et al. 2022, MNRAS, 512, 2365 [NASA ADS] [Google Scholar]
Madigan, A.-M., Levin, Y., & Hopman, C. 2009, ApJ, 697, L44 [NASA ADS] [Google Scholar]
Mainetti, D., Lupi, A., Campana, S., et al. 2017, A&A, 600 [Google Scholar]
Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
Merritt, D. 2013, Dynamics and Evolution of Galactic Nuclei (Princeton University Press) [Google Scholar]
Merritt, D., Gualandris, A., & Mikkola, S. 2009, ApJ, 693, L35 [NASA ADS] [CrossRef] [Google Scholar]
Merritt, D., Alexander, T., Mikkola, S., & Will, C. M. 2011, Phys. Rev. D, 84, 044024 [CrossRef] [Google Scholar]
Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
Mori, K., Hailey, C. J., Mandel, S., et al. 2019, ApJ, 885, 142 [NASA ADS] [CrossRef] [Google Scholar]
Mori, K., Hailey, C. J., Schutt, T. Y. E., et al. 2021, ApJ, 921, 148 [NASA ADS] [CrossRef] [Google Scholar]
Murphy, B. W., Cohn, H. N., & Durisen, R. H. 1991, ApJ, 370, 60 [NASA ADS] [Google Scholar]
Nandakumar, G., Ryde, N., Schultheis, M., et al. 2018, MNRAS, 478, 4374 [Google Scholar]
Nieuwmunster, N., Schultheis, M., Sormani, M., et al. 2024, A&A, 685, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Nogueras-Lara, F., Nieuwmunster, N., Schultheis, M., et al. 2024, A&A, 690, A313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pastorelli, G., Marigo, P., Girardi, L., et al. 2019, MNRAS, 485, 5666 [Google Scholar]
Pastorelli, G., Marigo, P., Girardi, L., et al. 2020, MNRAS, 498, 3283 [Google Scholar]
Paumard, T., Genzel, R., Martins, F., et al. 2006, ApJ, 643, 1011 [NASA ADS] [CrossRef] [Google Scholar]
Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
Perets, H. B., & Gualandris, A. 2010, ApJ, 719, 220 [NASA ADS] [Google Scholar]
Perets, H. B., Hopman, C., & Alexander, T. 2007, ApJ, 656, 709 [CrossRef] [Google Scholar]
Perets, H. B., Gualandris, A., Kupi, G., Merritt, D., & Alexander, T. 2009, ApJ, 702, 884 [NASA ADS] [CrossRef] [Google Scholar]
Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
Portegies Zwart, S. F., Makino, J., McMillan, S. L. W., & Hut, P. 1999, A&A, 348, 117 [NASA ADS] [Google Scholar]
Preto, M., & Amaro-Seoane, P. 2010, ApJ, 708, L42 [NASA ADS] [CrossRef] [Google Scholar]
Rantala, A., & Naab, T. 2023, MNRAS, 527, 11458 [NASA ADS] [CrossRef] [Google Scholar]
Rauch, K. P., & Tremaine, S. 1996, New A, 1, 149 [NASA ADS] [CrossRef] [Google Scholar]
Rees, M. J. 1988, Nature, 333, 523 [Google Scholar]
Rich, R. M., Ryde, N., Thorsbro, B., et al. 2017, AJ, 154, 239 [NASA ADS] [CrossRef] [Google Scholar]
Rose, S. C., Naoz, S., Sari, R., & Linial, I. 2023, ApJ, 955, 30 [NASA ADS] [CrossRef] [Google Scholar]
Ryu, T., Krolik, J., Piran, T., & Noble, S. C. 2020a, ApJ, 904, 98 [NASA ADS] [CrossRef] [Google Scholar]
Ryu, T., Krolik, J., Piran, T., & Noble, S. C. 2020b, ApJ, 904, 100 [NASA ADS] [CrossRef] [Google Scholar]
Ryu, T., Amaro Seoane, P., Taylor, A. M., & Ohlmann, S. T. 2024, MNRAS, 528, 6193 [NASA ADS] [CrossRef] [Google Scholar]
Sanders, R. H. 1992, Nature, 359, 131 [Google Scholar]
Sari, R., Kobayashi, S., & Rossi, E. M. 2010, ApJ, 708, 605 [NASA ADS] [Google Scholar]
Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [Google Scholar]
Schödel, R., Gallego-Cano, E., Dong, H., et al. 2018, A&A, 609, A27 [Google Scholar]
Schödel, R., Nogueras-Lara, F., Gallego-Cano, E., et al. 2020, A&A, 641, A102 [Google Scholar]
Schödel, R., Nogueras-Lara, F., Hosek, M., et al. 2023, A&A, 672, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schultheis, M., Rich, R. M., Origlia, L., et al. 2019, A&A, 627, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schultheis, M., Fritz, T. K., Nandakumar, G., et al. 2021, A&A, 650, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Spitzer, Lyman, J., & Saslaw, W. C. 1966, ApJ, 143, 400 [NASA ADS] [Google Scholar]
Sridhar, S., & Touma, J. R. 2016, MNRAS, 458, 4143 [CrossRef] [Google Scholar]
Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287 [NASA ADS] [CrossRef] [Google Scholar]
Tep, K., Fouvry, J.-B., Pichon, C., et al. 2021, MNRAS, 506, 4289 [NASA ADS] [CrossRef] [Google Scholar]
The Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
Vasiliev, E. 2017, ApJ, 848, 10 [NASA ADS] [CrossRef] [Google Scholar]
Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
von Fellenberg, S. D., Gillessen, S., Stadler, J., et al. 2022, ApJ, 932, L6 [NASA ADS] [CrossRef] [Google Scholar]
Waskom, M. L. 2021, J. Open Source Softw., 6, 3021 [CrossRef] [Google Scholar]
Yelda, S., Ghez, A. M., Lu, J. R., et al. 2014, ApJ, 783, 131 [Google Scholar]
Zhang, F., & Amaro Seoane, P. 2024, ApJ, 961, 232 [NASA ADS] [CrossRef] [Google Scholar]

¹

For radii of r ≳ 0.1 pc, the BH profile can be somewhat flatter (e.g., Baumgardt et al. 2018 find r^−1.55 in N -body simulations). However, this is outside the S-star cluster.

²

The angular momentum divided by the circular angular momentum.

³

In our base simulations, stars are required to spend at least one orbit within the loss cone before being removed. We also ran simulations in which stars were removed immediately once the pericenter dropped below r_t, and found the results to be unaffected. This was expected, since remnant stars are in the empty loss cone regime.

⁴

We used MIST Version 1.2 tracks with Ω/Ω_crit = 0.4.

⁵

In the model, the late S stars are those with T_eff ≤ 5000 K.

⁶

These are stars with angular momentum that is comparable to the clockwise disk (see Fig. 12 in Gillessen et al. 2017).

⁷

$t_{R R} = \frac{1}{\int_{j_{l c}}^{1} D_{i j, RR} 2 j d j}$ ${t_{RR}} = {1 \over {\mathop \smallint \nolimits_{{j_{lc}}}^1 {D_{ij,RR}}2jdj}}$ (Bar-Or & Fouvry 2018).

⁸

We have not included fainter stars in this comparison, as the observations may be incomplete. In fact, we find that at faint magnitudes the theoretical KLF agrees better with the KLF from Schödel et al. (2020), which is less sensitive to completeness effects (see the discussion in Sect. 3).

⁹

Mergers of clusters and IMBHs and/or SMBHs with the Galactic center may also form or shape the S-star cluster via other processes (e.g., scattering, dynamical friction) (Kim et al. 2004; Fragione et al. 2017; Cao et al. 2024).

¹⁰

Tep et al. (2021) used the age measurements in Habibi et al. (2017) for the eight bright S stars, and 7.1 Myr otherwise.

¹¹

Generozov & Madigan (2020) reproduced the S-star semimajor axis distribution but considered only a single disruptive encounter per binary and focused on the region within 0.03 pc. They also used a different approach for generating binaries, sampling first a thermal eccentricity and then a semimajor axis from a log-uniform distribution, resulting in an overall binary semimajor distribution that is flatter than log-uniform and likely less realistic than the empirically motivated model here. Finally, we caution that alternative disk initial conditions (e.g., a larger inner edge) may better reproduce the observed S-star semimajor axis distribution.

¹²

For black hole density profiles between r^−1.8 and r⁻².

¹³

We minimize (log(Lobs) – log(L_iso))² + (log(T_eff,obs) − log(T_eff,iso))² + (log(ɡ_obs) − log(ɡ_iso))², where the subscripts “obs” and “iso” indicate observed (from Habibi et al. 2017) and isochrone values respectively.

All Tables

Table C.1

Ages for eight bright S stars from Habibi et al. (2017), and from MIST isochrones at different metallicities.

In the text

All Figures

	Fig. 1 Key steps in our model for the production of S stars, including references and software used.
In the text

Fig. 2

Initial (top) and final (bottom) pericenters and eccentricities for a subsample of model stars. (Note the different x scales in the two panels.) The top panel shows all stars, independently of when they are deposited in the Galactic center. The bottom panel shows the 71 model stars surviving to the present day with K ≤ 18 and a ≤ 0.05 pc. Early (late) stars are shown in purple (red). Model stars initially have high eccentricities and evolve toward lower ones. For comparison, we show the observed S stars in the bottom panel using blue squares for early- type stars and orange circles for late-type stars. The upper boundary of the zone of avoidance from Burkert et al. (2024) is shown as a solid gray line. The dashed gray line shows an adjusted zone of avoidance so that all S stars are outside it.

In the text

Fig. 3

Left panel: cumulative eccentricity distribution from the model (solid blue line), compared to the observed S-star eccentricity distribution (dashed orange line). For reference, we also show a thermal eccentricity distribution (dash-dotted green line). Right panel: cumulative pericenter distribution from our model and observations. The numbers in the legend are the p values from a two-sample KS test with the model and observed distributions.

In the text

	Fig. 4 Cumulative eccentricity, pericenter, and semimajor axis distributions for bright (K ≤ 16, left panels) and faint (K > 16, right panels) early S stars.
In the text

	Fig. 5 Top panel: KLF of all model (blue) and observed (dashed orange) S stars. Bottom panel: KLFs for model (blue) and observed (dashed orange) early S stars (with orbits). The red line is the KLF of early stars in the central 0.5″ from Schödel et al. (2020) (see Appendix B for details). The luminosity functions are normalized to match at a K-band magnitude of 16.2.
In the text

	Fig. 6 Top panel: age versus K-band magnitude for eight bright S stars (red; Habibi et al. 2017), compared to early model stars (gray). Bottom: Age distribution of Habibi et al. (2017) stars and model stars with comparable magnitudes (see text for details).
In the text

	Fig. 7 Top panel: corner plot showing distributions of semimajor axis (a), eccentricity (e), and K magnitude from theory (orange) and observations (blue). Bottom panel: eccentricity versus semimajor axis for the observed S stars, and for the model stars that are closest in the semimajor axis.
In the text

	Fig. 8 K-band luminosity function accounting for the dependence of the binary disruption probability on stellar lifetime (light green line). Effectively, this means that the progenitor binaries are drawn from a present-day mass function rather than an initial mass function. The other lines are the same as in Fig. 5.
In the text

	Fig. 9 K-band luminosity functions, after discarding stars formed more than 10⁸ yr ago. The blue (light green) line corresponds to binaries drawn from an initial (present-day) mass function.
In the text

	Fig. 10 Same as Fig. 9, except we discarded stars that were less than 10⁷ yr old at the moment of binary disruption.
In the text

	Fig. C.1 log(g) versus log(T_eff) for the eight bright S stars from Habibi et al. (2017) compared to MIST isochrones (v1.2, υ/υ_crit = 0.4). The solid (dashed) lines correspond to [Fe/H] = 0 ([Fe/H] = −0.5).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Aharon, D., & Perets, H. B. 2015, ApJ, 799, 185 [NASA ADS] [CrossRef] [Google Scholar]

[2] Akiba, T., Naoz, S., & Madigan, A.-M. 2024, ApJ submitted, [arXiv:2410.19881] [Google Scholar]

[3] Alexander, T. 2017, arXiv e-prints [arXiv:1701.04762] [Google Scholar]

[4] Alexander, T., & Hopman, C. 2009, ApJ, 697, 1861 [NASA ADS] [CrossRef] [Google Scholar]

[5] Alexander, T., & Morris, M. 2003, ApJ, 590, L25 [NASA ADS] [Google Scholar]

[6] Alexander, T., & Pfuhl, O. 2014, ApJ, 780, 148 [Google Scholar]

[7] Amaro Seoane, P. 2023, ApJ, 947, 8 [CrossRef] [Google Scholar]

[8] Antonini, F., & Merritt, D. 2013, ApJ, 763, L10 [NASA ADS] [Google Scholar]

[9] Antonini, F., Faber, J., Gualandris, A., & Merritt, D. 2010, ApJ, 713, 90 [NASA ADS] [Google Scholar]

[10] Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[11] Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]

[12] Bahcall, J. N., & Wolf, R. A. 1976, ApJ, 209, 214 [NASA ADS] [CrossRef] [Google Scholar]

[13] Balberg, S., Sari, R., & Loeb, A. 2013, MNRAS, 434, L26 [CrossRef] [Google Scholar]

[14] Bar-Or, B., & Alexander, T. 2014, Class. Quant. Grav., 31, 244003 [NASA ADS] [CrossRef] [Google Scholar]

[15] Bar-Or, B., & Alexander, T. 2016, ApJ, 820, 129 [NASA ADS] [CrossRef] [Google Scholar]

[16] Bar-Or, B., & Fouvry, J.-B. 2018, ApJ, 860, L23 [NASA ADS] [CrossRef] [Google Scholar]

[17] Bartko, H., Martins, F., Fritz, T. K., et al. 2009, ApJ, 697, 1741 [Google Scholar]

[18] Baumgardt, H., Amaro-Seoane, P., & Schödel, R. 2018, A&A, 609, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[19] Bonnell, I. A., & Rice, W. K. M. 2008, Science, 321, 1060 [NASA ADS] [CrossRef] [Google Scholar]

[20] Bradnick, B., Mandel, I., & Levin, Y. 2017, MNRAS, 469, 2042 [Google Scholar]

[21] Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]

[22] Burkert, A., Gillessen, S., Lin, D. N. C., et al. 2024, ApJ, 962, 81 [NASA ADS] [CrossRef] [Google Scholar]

[23] Cao, C. Y., Liu, F. K., Li, S., Chen, X., & Wang, K. 2024, arXiv e-prints [arXiv:2411.09278] [Google Scholar]

[24] Chen, X., & Amaro-Seoane, P. 2014, ApJ, 786, L14 [NASA ADS] [CrossRef] [Google Scholar]

[25] Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [Google Scholar]

[26] Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [Google Scholar]

[27] Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]

[28] Dale, J. E., Davies, M. B., Church, R. P., & Freitag, M. 2009, MNRAS, 393, 1016 [Google Scholar]

[29] Davies, M. B., Blackwell, R., Bailey, V. C., & Sigurdsson, S. 1998, MNRAS, 301, 745 [NASA ADS] [Google Scholar]

[30] Dessart, L., Ryu, T., Amaro Seoane, P., & Taylor, A. M. 2024, A&A, 682, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[31] Do, T., Lu, J. R., Ghez, A. M., et al. 2013, ApJ, 764, 154 [NASA ADS] [CrossRef] [Google Scholar]

[32] Do, T., Kerzendorf, W., Winsor, N., et al. 2015, ApJ, 809, 143 [Google Scholar]

[33] Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [Google Scholar]

[34] Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]

[35] Duncan, M. J., & Shapiro, S. L. 1983, ApJ, 268, 565 [NASA ADS] [Google Scholar]

[36] Feldmeier-Krause, A., Kerzendorf, W., Neumayer, N., et al. 2017, MNRAS, 464, 194 [Google Scholar]

[37] Fouvry, J. B., Pichon, C., & Magorrian, J. 2017, A&A, 598, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[38] Fragione, G., & Sari, R. 2018, ApJ, 852, 51 [NASA ADS] [CrossRef] [Google Scholar]

[39] Fragione, G., Capuzzo-Dolcetta, R., & Kroupa, P. 2017, MNRAS, 467, 451 [Google Scholar]

[40] Fregeau, J. M., Cheung, P., Portegies Zwart, S. F., & Rasio, F. A. 2004, MNRAS, 352, 1 [CrossRef] [Google Scholar]

[41] Freitag, M., Amaro-Seoane, P., & Kalogera, V. 2006a, ApJ, 649, 91 [NASA ADS] [CrossRef] [Google Scholar]

[42] Freitag, M., Gürkan, M. A., & Rasio, F. A. 2006b, MNRAS, 368, 141 [NASA ADS] [Google Scholar]

[43] Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [Google Scholar]

[44] Gallego-Cano, E., Schödel, R., Dong, H., et al. 2018, A&A, 609, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[45] Gallego-Cano, E., Fritz, T., Schödel, R., et al. 2024, A&A, 689, A190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[46] Generozov, A. 2021, MNRAS, 501, 3088 [Google Scholar]

[47] Generozov, A., & Madigan, A.-M. 2020, ApJ, 896, 137 [NASA ADS] [CrossRef] [Google Scholar]

[48] Generozov, A., Stone, N. C., Metzger, B. D., & Ostriker, J. P. 2018, MNRAS, 478, 4030 [Google Scholar]

[49] Generozov, A., Nayakshin, S., & Madigan, A. M. 2022, MNRAS, 512, 4100 [NASA ADS] [CrossRef] [Google Scholar]

[50] Genzel, R., Thatte, N., Krabbe, A., Kroker, H., & Tacconi-Garman, L. E. 1996, ApJ, 472, 153 [NASA ADS] [CrossRef] [Google Scholar]

[51] Genzel, R., Eckart, A., Ott, T., & Eisenhauer, F. 1997, MNRAS, 291, 219 [NASA ADS] [CrossRef] [Google Scholar]

[52] Ghez, A. M., Klein, B. L., Morris, M., & Becklin, E. E. 1998, ApJ, 509, 678 [NASA ADS] [CrossRef] [Google Scholar]

[53] Ghez, A. M., Duchêne, G., Matthews, K., et al. 2003, ApJ, 586, L127 [Google Scholar]

[54] Gillessen, S., Plewa, P. M., Eisenhauer, F., et al. 2017, ApJ, 837, 30 [Google Scholar]

[55] Ginsburg, I., & Loeb, A. 2007, MNRAS, 376, 492 [NASA ADS] [Google Scholar]

[56] Gould, A., & Quillen, A. C. 2003, ApJ, 592, 935 [NASA ADS] [Google Scholar]

[57] GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[58] GRAVITY Collaboration (Abuter, R., et al.) 2020, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[59] GRAVITY Collaboration (Abuter, R., et al.) 2021, A&A, 647, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[60] GRAVITY Collaboration (Abuter, R., et al.) 2022, A&A, 657, L12 [NASA ADS] [CrossRef] [Google Scholar]

[61] GRAVITY Collaboration (Abd El Dayem, K., et al.) 2024, A&A, 692, A242 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[62] Gualandris, A., Mapelli, M., & Perets, H. B. 2012, MNRAS, 427, 1793 [Google Scholar]

[63] Guillochon, J., & Ramirez-Ruiz, E. 2013, ApJ, 767, 25 [NASA ADS] [CrossRef] [Google Scholar]

[64] Gürkan, M. A., Freitag, M., & Rasio, F. A. 2004, ApJ, 604, 632 [NASA ADS] [CrossRef] [Google Scholar]

[65] Habibi, M., Gillessen, S., Martins, F., et al. 2017, ApJ, 847, 120 [Google Scholar]

[66] Hailey, C. J., Mori, K., Bauer, F. E., et al. 2018, Nature, 556, 70 [Google Scholar]

[67] Hamers, A. S., & Perets, H. B. 2017, ApJ, 846, 123 [NASA ADS] [CrossRef] [Google Scholar]

[68] Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]

[69] Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]

[70] Hills, J. G. 1983, AJ, 88, 1269 [NASA ADS] [CrossRef] [Google Scholar]

[71] Hills, J. G. 1988, Nature, 331, 687 [Google Scholar]

[72] Hills, J. G. 1991, AJ, 102, 704 [Google Scholar]

[73] Hopman, C., & Alexander, T. 2006a, ApJ, 645, 1152 [NASA ADS] [CrossRef] [Google Scholar]

[74] Hopman, C., & Alexander, T. 2006b, ApJ, 645, L133 [NASA ADS] [CrossRef] [Google Scholar]

[75] Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]

[76] Kim, S. S., Figer, D. F., & Morris, M. 2004, ApJ, 607, L123 [NASA ADS] [Google Scholar]

[77] Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt (IOS Press), 87 [Google Scholar]

[78] Kocsis, B., & Tremaine, S. 2011, MNRAS, 412, 187 [NASA ADS] [CrossRef] [Google Scholar]

[79] Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]

[80] Levin, Y., & Beloborodov, A. M. 2003, ApJ, 590, L33 [NASA ADS] [CrossRef] [Google Scholar]

[81] Li, G., & Loeb, A. 2013, MNRAS, 429, 3040 [Google Scholar]

[82] Löckmann, U., Baumgardt, H., & Kroupa, P. 2008, ApJ, 683, L151 [Google Scholar]

[83] Lu, J. R., Do, T., Ghez, A. M., et al. 2013, ApJ, 764, 155 [NASA ADS] [CrossRef] [Google Scholar]

[84] Lu, W., Fuller, J., Raveh, Y., et al. 2021, MNRAS, 503, 603 [Google Scholar]

[85] Maccarone, T. J., Degenaar, N., Tetarenko, B. E., et al. 2022, MNRAS, 512, 2365 [NASA ADS] [Google Scholar]

[86] Madigan, A.-M., Levin, Y., & Hopman, C. 2009, ApJ, 697, L44 [NASA ADS] [Google Scholar]

[87] Mainetti, D., Lupi, A., Campana, S., et al. 2017, A&A, 600 [Google Scholar]

[88] Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]

[89] Merritt, D. 2013, Dynamics and Evolution of Galactic Nuclei (Princeton University Press) [Google Scholar]

[90] Merritt, D., Gualandris, A., & Mikkola, S. 2009, ApJ, 693, L35 [NASA ADS] [CrossRef] [Google Scholar]

[91] Merritt, D., Alexander, T., Mikkola, S., & Will, C. M. 2011, Phys. Rev. D, 84, 044024 [CrossRef] [Google Scholar]

[92] Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]

[93] Mori, K., Hailey, C. J., Mandel, S., et al. 2019, ApJ, 885, 142 [NASA ADS] [CrossRef] [Google Scholar]

[94] Mori, K., Hailey, C. J., Schutt, T. Y. E., et al. 2021, ApJ, 921, 148 [NASA ADS] [CrossRef] [Google Scholar]

[95] Murphy, B. W., Cohn, H. N., & Durisen, R. H. 1991, ApJ, 370, 60 [NASA ADS] [Google Scholar]

[96] Nandakumar, G., Ryde, N., Schultheis, M., et al. 2018, MNRAS, 478, 4374 [Google Scholar]

[97] Nieuwmunster, N., Schultheis, M., Sormani, M., et al. 2024, A&A, 685, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[98] Nogueras-Lara, F., Nieuwmunster, N., Schultheis, M., et al. 2024, A&A, 690, A313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[99] Pastorelli, G., Marigo, P., Girardi, L., et al. 2019, MNRAS, 485, 5666 [Google Scholar]

[100] Pastorelli, G., Marigo, P., Girardi, L., et al. 2020, MNRAS, 498, 3283 [Google Scholar]

[101] Paumard, T., Genzel, R., Martins, F., et al. 2006, ApJ, 643, 1011 [NASA ADS] [CrossRef] [Google Scholar]

[102] Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]

[103] Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]

[104] Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]

[105] Perets, H. B., & Gualandris, A. 2010, ApJ, 719, 220 [NASA ADS] [Google Scholar]

[106] Perets, H. B., Hopman, C., & Alexander, T. 2007, ApJ, 656, 709 [CrossRef] [Google Scholar]

[107] Perets, H. B., Gualandris, A., Kupi, G., Merritt, D., & Alexander, T. 2009, ApJ, 702, 884 [NASA ADS] [CrossRef] [Google Scholar]

[108] Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]

[109] Portegies Zwart, S. F., Makino, J., McMillan, S. L. W., & Hut, P. 1999, A&A, 348, 117 [NASA ADS] [Google Scholar]

[110] Preto, M., & Amaro-Seoane, P. 2010, ApJ, 708, L42 [NASA ADS] [CrossRef] [Google Scholar]

[111] Rantala, A., & Naab, T. 2023, MNRAS, 527, 11458 [NASA ADS] [CrossRef] [Google Scholar]

[112] Rauch, K. P., & Tremaine, S. 1996, New A, 1, 149 [NASA ADS] [CrossRef] [Google Scholar]

[113] Rees, M. J. 1988, Nature, 333, 523 [Google Scholar]

[114] Rich, R. M., Ryde, N., Thorsbro, B., et al. 2017, AJ, 154, 239 [NASA ADS] [CrossRef] [Google Scholar]

[115] Rose, S. C., Naoz, S., Sari, R., & Linial, I. 2023, ApJ, 955, 30 [NASA ADS] [CrossRef] [Google Scholar]

[116] Ryu, T., Krolik, J., Piran, T., & Noble, S. C. 2020a, ApJ, 904, 98 [NASA ADS] [CrossRef] [Google Scholar]

[117] Ryu, T., Krolik, J., Piran, T., & Noble, S. C. 2020b, ApJ, 904, 100 [NASA ADS] [CrossRef] [Google Scholar]

[118] Ryu, T., Amaro Seoane, P., Taylor, A. M., & Ohlmann, S. T. 2024, MNRAS, 528, 6193 [NASA ADS] [CrossRef] [Google Scholar]

[119] Sanders, R. H. 1992, Nature, 359, 131 [Google Scholar]

[120] Sari, R., Kobayashi, S., & Rossi, E. M. 2010, ApJ, 708, 605 [NASA ADS] [Google Scholar]

[121] Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [Google Scholar]

[122] Schödel, R., Gallego-Cano, E., Dong, H., et al. 2018, A&A, 609, A27 [Google Scholar]

[123] Schödel, R., Nogueras-Lara, F., Gallego-Cano, E., et al. 2020, A&A, 641, A102 [Google Scholar]

[124] Schödel, R., Nogueras-Lara, F., Hosek, M., et al. 2023, A&A, 672, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[125] Schultheis, M., Rich, R. M., Origlia, L., et al. 2019, A&A, 627, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[126] Schultheis, M., Fritz, T. K., Nandakumar, G., et al. 2021, A&A, 650, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[127] Spitzer, Lyman, J., & Saslaw, W. C. 1966, ApJ, 143, 400 [NASA ADS] [Google Scholar]

[128] Sridhar, S., & Touma, J. R. 2016, MNRAS, 458, 4143 [CrossRef] [Google Scholar]

[129] Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287 [NASA ADS] [CrossRef] [Google Scholar]

[130] Tep, K., Fouvry, J.-B., Pichon, C., et al. 2021, MNRAS, 506, 4289 [NASA ADS] [CrossRef] [Google Scholar]

[131] The Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]

[132] Vasiliev, E. 2017, ApJ, 848, 10 [NASA ADS] [CrossRef] [Google Scholar]

[133] Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]

[134] von Fellenberg, S. D., Gillessen, S., Stadler, J., et al. 2022, ApJ, 932, L6 [NASA ADS] [CrossRef] [Google Scholar]

[135] Waskom, M. L. 2021, J. Open Source Softw., 6, 3021 [CrossRef] [Google Scholar]

[136] Yelda, S., Ghez, A. M., Lu, J. R., et al. 2014, ApJ, 783, 131 [Google Scholar]

[137] Zhang, F., & Amaro Seoane, P. 2024, ApJ, 961, 232 [NASA ADS] [CrossRef] [Google Scholar]