EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 696 (April 2025) A&A, 696 (2025) L9 Full HTML
Open Access
Issue
A&A
Volume 696, April 2025
Article Number L9
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202452991
Published online 08 April 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Pulsars are rapidly rotating, highly magnetized neutron stars. The most plausible scenario for their formation involves core-collapse supernova explosions, which occur at the end of a massive star’s life. In particular, stars with an initial mass in the range of 8−25 M⊙, as well as those with higher initial masses and a high metallicity, are more likely to be progenitors of neutron stars (Woosley et al. 2002; Heger et al. 2003). Massive stars emit powerful winds throughout their lifetimes, which significantly influence their environment by shaping the surroundings and depositing large amounts of stellar material and energy into the interstellar medium (ISM; Weaver et al. 1977). When a massive star explodes as a supernova, the young supernova ejecta propagates through the circumstellar medium (CSM) created by the progenitor star (Meyer et al. 2015). This interaction decelerates the supernova ejecta, extracting both momentum and energy (Dessart 2024). In some cases, it can even confine or reshape it (Meyer & Meliani 2022).

If a pulsar forms after a supernova explosion, it generates a pulsar wind nebula (PWN) or plerion. The pulsar wind is extremely powerful and relativistic, reaching up to 1038 erg s−1 with speeds close to the speed of light. This wind first interacts with the core-collapse supernova ejecta, and subsequently with the CSM of the massive progenitor star (Bühler & Blandford 2014). The interaction between the pulsar wind nebula and the reverse shock of the supernova remnant (SNR) initiates the phase known as reverberation (see Bandiera et al. 2023a,b). Simulations have shown that the encounter between an anisotropic pulsar wind nebula and the reverse shock of the SNR can also induce instabilities and turbulence within the SNR, resulting in a significant mixing of materials (Orlando et al. 2021, 2022; Meyer et al. 2023).

These regions of multiple shocks and discontinuities become important sites for cosmic ray production through particle acceleration (Das et al. 2024), as well as non-thermal emission Orlando et al. (2019). Studying plerionic SNRs in detail offers insights into the history of massive stars and helps constrain stellar evolution models, along with the physics of the ISM (Langer 2012). The geometry of pulsar wind nebulae, at least for young pulsars, is intrinsically linked to the morphology of the medium, where the progenitor star evolved and eventually died (Blondin et al. 2001; Bucciantini 2014; Kargaltsev et al. 2015). This connection becomes particularly significant when the progenitor star becomes a runaway star moving supersonically through the ISM prior to its explosion (Hoogerwerf et al. 2000), transforming its pre-supernova CSM into a stellar wind bow shock (Wilkin 1996). Additionally, the pulsar can receive a birth kick during the explosion, imparting a proper motion with velocities of several hundred kilometers per second (Igoshev 2020). The pulsar then moves first through the supernova ejecta, then the CSM, and eventually into the ISM. As a result, the shape and appearance of PWNe become a complex problem governed by multiple physical processes and influenced by a wide range of parameters. Understanding this geometry requires considering not only the motion of the pulsar and environment but also the dynamic evolution of the surrounding medium over time. Recent observations from the James Webb Space Telescope (JWST) in the infrared offer a new opportunity to investigate young SNRs and the environments where young kicked pulsars evolve (Milisavljevic et al. 2024).

In recent decades, the community has made extensive efforts to investigate PWNe numerically. However, the high complexity of this problem often necessitates numerous simplifying assumptions to facilitate analysis. Various models, motivated by the study of the Crab Nebula, have been performed in 1D, 2D, and 3D and focusing on the expansion of pulsar wind nebulae into uniform media, (Komissarov & Lyubarsky 2004; Del Zanna et al. 2006; Del Zanna & Olmi 2017; Porth et al. 2013; Olmi et al. 2014; Porth et al. 2014). The consideration of the natal kick received by the pulsar has also generated a body of literature involving 2D and 3D simulations that encompass the entire structure where the pulsar wind interacts with the ISM (Bucciantini & Bandiera 2001) and (Bucciantini 2018; Olmi & Bucciantini 2019). Non-magnetized 3D models have been developed to investigate interactions between the winds of moving pulsars and expanding supernova ejecta (Temim et al. 2015; Kolb et al. 2017; Temim et al. 2017, 2022). Additionally, 2D magnetized models for static pulsars that include the progenitor’s past history have been presented by Meyer & Meliani (2022). In this work, we extend these numerical efforts by presenting a 3D magnetized model for a runaway pulsar, which accounts for both the supernova ejecta and the complex CSM of its progenitor.

2. Numerical setup

A global classical magneto-hydrodynamics simulation of the CSM around a runaway massive star in the warm ISM of the Milky Way’s galactic plane is performed, following its evolution up to the plerionic SNR phase using the PLUTO code (Mignone et al. 2007, 2012). The classical approximation for pulsar wind follows, for instance, Blondin et al. (2001) and Temim et al. (2017).

We first investigated a model of a runaway star with an initial mass of 20 M⊙, which is entering its final evolutionary phase as a red supergiant. The star moves with velocity v⋆ = 40 km s−1 through the warm phase of the galactic plane in the Milky Way (Blaauw 1993), where the temperature is 8000 K and the number density is 0.79 cm−3 (Wolfire et al. 2003; Meyer et al. 2014). The magnetic field in the ISM, with a strength of 7 μG, is assumed to be aligned with the star’s direction of motion (Meyer et al. 2017). For the thermal processes in the wind nebula, we applied optically thin cooling and heating appropriate for fully ionized gas (Wiersma et al. 2009), assuming solar metallicity (Asplund et al. 2009), as described in Meyer et al. (2014). Stellar surface parameters, including wind velocity, effective temperature, and mass-loss rate as a function of time, are derived from the non-rotating zero-age main-sequence model of 20 M⊙, interpolated from the GENEVA evolutionary track library (Ekström et al. 2012). The terminal wind velocities were derived using the method described in Eldridge et al. (2006). The simulation for the CSM surrounding the massive star is conducted in a 2.5D cylindrical coordinate system (2D plus an additional toroidal component for the vectors), utilizing a uniform grid that spans [0,150] × [−50,50] pc consisting of 7500 × 5000 grid zones.

The supernova explosion phase is initially simulated in 1D spherical symmetry, since during this initial phase, the SNR propagates through an isotropic medium. Specifically, the supernova blast wave is set within the red supergiant stellar wind in 1D. For this purpose, we employ a radial grid spanning [0, 2.0] pc, mapped with 50 000 uniform grid zones. We adopted the core-collapse explosion model from Whalen et al. (2008) and Truelove & McKee (1999), using an ejecta mass of Mej = 6.96 M⊙ and a canonical explosion energy of Eej = 1 foe. The 1D simulation runs until the supernova blast wave reaches a distance of 1.2 pc from the progenitor star. The results from the 1D simulation are then mapped onto a 3D Cartesian coordinate system spanning [ − 20, 20]3 pc, consisting of 10243 grid zones, which is pre-filled with the 2.5D CSM, assuming rotational symmetry and introducing a 30 degrees shift between the cylindrical axis of symmetry and the Cartesian Oz axis, avoiding grid effects. We ensure that no information is lost in the wind-ISM interaction when modeling the pulsar wind nebula by using a CSM distribution with a higher spatial resolution than that of the SNR. The latter is chosen to properly resolve the termination shock of the pulsar’s bow shock, preventing boundary effects that could introduce numerical artifacts, such as those seen in Fig. 2 of Temim et al. (2017).

About 20 years after the supernova explosion, the pulsar wind is set at the surface of a sphere with a radius of ∼ 0.4 pc (corresponding to 20 cells in the simulation box). We followed the prescriptions given by Komissarov & Lyubarsky (2004) for the pulsar wind. Moreover, the pulsar wind is set with a mechanical power luminosity of Ėo = 1038 erg s−1, a velocity up to 1% of the speed of light and a magnetisation of σ = 10−3 (Slane 2017). It should be noted that in this paper, we use a non-relativistic pulsar wind. The initial pulsar spin is set to Po = 0.3 s, with a time variation of Ṗo = 10−17 s s−1 and a braking index of n = 3 (Pacini & Salvati 1973; Slane 2017), following the model used in Meyer & Meliani (2022); Meyer et al. (2024a). We considered the pulsar’s velocity as vpsr = 300 km s−1 along the Ox axis, perpendicularly to the initial direction of motion of the runaway progenitor star, also introducing small arbitrary angles (< few degrees) between it and the Cartesian characteristic directions, to get rid of grid effects. The simulation grid is set in the reference frame of the pulsar, and the ISM is given a velocity of −vpsr (Verbunt et al. 2017; Igoshev 2020). The simulation parameters were chosen to match those of the most common galactic SNRs associated with runaway massive progenitors (see the discussion in Meyer et al. 2024b). Further explorations of this problem ae highly desirable, for instance, with regard to variations in the initial progenitor star mass, velocity, and supernova energy.

In this work, the radiative transfer calculations were performed using the RADMC-3D code (Dullemond 2012) on the results of the MHD simulations. The synthetic radio waveband observables resulting from synchrotron emission are generated (Meyer et al. 2024b). Two simulations were conducted: one with the CSM of the core-collapse progenitor prior to the supernova and the other without.

3. Results

3.1. Without the pre-supernova CSM

To constrain the influence of the progenitor star’s CSM on the PWN, we first modeled that of a kicked-off pulsar within an isotropic SNR surrounded by a static ISM (Fig. 1a). In that figure, the orange surfaces represent the isodensity contours highlighting the forward shock of the blast wave propagating through the uniform ISM. Approximately 15 kyr after the supernova explosion, the pulsar moves through the low-density bubble created by the expanding SNR before it begins interacting with the reverse shock and, later, with the contact discontinuity of the SNR. Due to the anisotropy of the PWN, these interactions with the SNR’s reverse shock trigger the development of Richtmyer-Meshkov instabilities at the contact discontinuity, as described by Kane et al. (1999). These instabilities are visible in Fig. 1a, where the SNR tracer is shown in cyan. The magnetic field, illustrated in Fig. 1a with white tubes, becomes turbulent in the unstable regions of the SNR. As the PWN propagates through the SNR, the magnetic field of the SNR is compressed and connects to the structured magnetic field of the PWN. The PWN also bends laterally as the pulsar moves within the SNR. This bending effect can be observed by an observer situated perpendicular to both the jet’s propagation direction and its axis. Indeed, the jet is inclined backward by an angle of approximately 35 degrees.

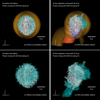thumbnail Fig. 1.

Rendering of the 3D MHD pulsar wind nebula models, considered without (a,c) and with (b,d) their complex environments. The orange surfaces trace the constant density regions of the stellar wind bubble. The remaining color coding is as follows: red traces the supergiant wind, blue traces the WR wind, cyan traces the supernova ejecta, and white tubes trace the magnetic field lines in the pulsar wind. The 3D figures are cut with two planes, allowing for a visualization of the internal structure of the plerionic supernova remnants.

3.2. With the pre-supernova CSM

In this simulation, we first allow the CSM of the runaway 20 M⊙ massive star to evolve until it explodes as a supernova, approximately 15 kyr after the explosion, as shown in Fig. 1b,d,c. In these figures, the red surfaces trace the red supergiant wind, while the blue surfaces represent the Wolf-Rayet (WR) wind. The supernova ejecta expands within the CSM and is deformed by it, resulting in the SNR adopting a Cygnus-loop-like morphology (Meyer et al. 2024b). The ejecta forms a strongly elongated region, with an extended cavity to the south and a northern outflow that sweeps up the CSM and ISM. This behavior aligns with the mechanism described by Meyer et al. (2023), where post-main sequence material is channeled into the stellar wind cavity (represented by the red and blue contours in Fig. 1b), which, in turn, causes deviations from sphericity in the expanding supernova ejecta (cyan surface). The material from the stellar wind becomes confined between the SNR and the PWN, which expands and moves laterally with the pulsar. The higher density and temperature of the channeled CSM and supernova material (compared to the previous simulation) increase the thermal pressure, leading to a stronger confinement of the PWN’s jet. This results in a more bent and collimated jet than in the first case.

4. Discussion and conclusion

Using classical magneto-hydrodynamics, we simulated the propagation of a kicked-off young pulsar through the CSM of its progenitor star for the first time in 3D. By incorporating the detailed history of the progenitor star, magnetic field effects, and higher spatial resolution, our model provides a more accurate profile of the SNR hydrodynamic simulations, such as those by Temim et al. (2017) in their modeling of the SNR MSH 15-56. The anisotropic PWN interacts with the SNR, enhancing the development of instabilities. Simultaneously, the SNR and backflow of older CSM, converging toward the center of the CSM, further confining the PWN. As the pulsar moves outward, this material bends the jet within the nebula at an angle of approximately 40−50 degrees. Furthermore, because the CSM of the moving progenitor star has a dense bow shock at the front and a lower density tail, the jet propagating toward the tail experiences less bending. As this side of the jet reaches the CSM’s tail, it begins to propagate more linearly along the tail’s axis. However, as the pulsar continues to move, this side of the jet also gradually bends.

To better quantify the effect of the CSM on the morphology of the PWN, we plot the ram pressure nv2, where n is the gas number density and v the velocity field in the SNR in the frame of reference of the moving pulsar (see Fig. 2). This figure shows the ram pressure distribution in the y = 0 plane, including the pulsar’s motion along the Ox axis, with the pulsar located at the origin. The structure of the stellar wind bow shock is evident in this figure, along with the high ram pressure regions corresponding to the free-streaming pulsar wind and the bent vertical jets. The post-shock region at the forward shock of the supernova blastwave interacting with the unperturbed ISM also exhibits significant ram pressure, particularly in the southern region of the SNR, where localized areas apply pressure on the pulsar’s polar jets. These regions result from the reflection of the supernova blastwave’s termination shock against the CSM, altering the morphology of the PWN (as seen in Fig. 1a-d).

thumbnail Fig. 2.

Ram pressure in the y = 0 plane of the models, without (a) and with (b) the CSM.

Emission maps are calculated using the emission coefficients of Meyer et al. (2024b). It is assumed that the radiative emission is synchrotron radiation emitted by a population of relativistic electrons, with an energy distribution following a power law proportional to γ−p, where γ is the Lorentz factor and p = 2.2. In our approach, we assume that 1% of the gas number density consists of electrons and that 1% of the thermal energy of the gas is transferred to the electron population. Our calculations are limited to radio frequencies, specifically, ν = 1.4 GHz. Furthermore, for the sake of simplicity, we have chosen to neglect the effects of self-absorption and a simplified electron energy distribution in the integration of the radiative transfer equation along the line of sight. These assumptions may influence maps interpretation, particularly in dense CSM or high optical depths, as those factors might lead to overestimating emission at frequencies much lower than 1.4 GHz, as it alters spectral shapes in compact PWN (Gelfand et al. 2009). Additionally, adopting a simplified power-law electron distribution may overlook the spectral variations observed in real systems (Slane 2017).

The resulting synthetic images were viewed from different angles (with θobs = 0° and θobs = 45° from the Oy axis, which is perpendicular to both the progenitor star’s motion and that of the kicked pulsar). The movement of the CSM is illustrated in Fig. 3a,b for the model without CSM and in Fig. 3c,d for the model with CSM. In both models, the emission is dominated by the supernova blast wave and the PWN. It exhibits an arc-like morphology with filamentary structures trailing behind the moving pulsar. The apparent morphology of the PWN is dependent on the observation angle. At an observation angle of 0°, the jet within the PWN appears more elongated and thinner than it does at an observation angle of 45°, where the jet appears broader. Our study proposes a novel scenario to produce bending of runaway pulsar’s tails as a direct results of the dense CSM material encountered by the polar material in the pulsar wind, naturally explaining north-south asymmetries, such as those observed around young pulsars still moving in their host remnant; for instance, PSR J1509–5850 (Bordas & Zhang 2020) and Gemina (Posselt et al. 2017).

thumbnail Fig. 3.

Nonthermal 1.4 GHz radio synchrotron emission maps (in erg s1 cm2 sr1 Hz1) for the pulsar wind nebulae and their host SNR, without (a,b) and with (c,d) CSM. The maps are displayed with a viewing angle of θincl = 0° (a,c) and θincl = 45° (b,d). The dark color marks the regions of strong emission intensity, while the pale color marks the regions of fainter radio emission intensity, respectively.

The controlling effect of the runaway pulsar bow shock on the radio appearance of the SNR – governed by the pulsar properties (relativistic wind velocity and wind power luminosity) and by the local conditions – provides insights into the age of the SNR, its direction of motion, and the past evolution of its progenitor. This effect also influences the distribution of the various chemical species involved in the problem; namely, the ejecta and the different stellar winds blown during the red supergiant and WR evolutionary phases, respectively. Our setup can be used in the future to perform models tailored to specific objects.

Acknowledgments

The author acknowledges RES resources provided by BSC in MareNostrum to AECT-2025-1-0004. The authors also acknowledge computing time on the high-performance computer “Lise” at the NHR Center NHR@ZIB. This center is jointly supported by the Federal Ministry of Education and Research and the state governments participating in the NHR (https://www.nhr-verein.de/unsere-partner). This work has been supported by the grant PID2021-124581OB-I00 funded by MCIU/AEI/10.13039/501100011033 and 2021SGR00426 of the Generalitat de Catalunya. This work was also supported by the Spanish program Unidad de Excelencia María de Maeztu CEX2020-001058-M with funding from European Union NextGeneration EU (PRTR-C17.I1).

References

  1. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bandiera, R., Bucciantini, N., Martín, J., Olmi, B., & Torres, D. F. 2023a, MNRAS, submitted [arXiv:2301.04056] [Google Scholar]
  3. Bandiera, R., Bucciantini, N., Olmi, B., & Torres, D. F. 2023b, MNRAS, 525, 2839 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blaauw, A. 1993, ASP Conf. Ser., 35, 207 [Google Scholar]
  5. Blondin, J. M., Chevalier, R. A., & Frierson, D. M. 2001, ApJ, 563, 806 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bordas, P., & Zhang, X. 2020, A&A, 644, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bucciantini, N. 2014, Astron. Nachr., 335, 234 [NASA ADS] [Google Scholar]
  8. Bucciantini, N. 2018, MNRAS, 478, 2074 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bucciantini, N., & Bandiera, R. 2001, A&A, 375, 1032 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bühler, R., & Blandford, R. 2014, Rep. Prog. Phys., 77, 066901 [NASA ADS] [CrossRef] [Google Scholar]
  11. Das, S., Brose, R., Pohl, M., Meyer, D. M. A., & Sushch, I. 2024, A&A, 689, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Del Zanna, L., & Olmi, B. 2017, Astrophys. Space Sci. Lib., 446, 215 [NASA ADS] [Google Scholar]
  13. Del Zanna, L., Volpi, D., Amato, E., & Bucciantini, N. 2006, A&A, 453, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dessart, L. 2024, arXiv e-prints [arXiv:2405.04259] [Google Scholar]
  15. Dullemond, C. P. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
  16. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
  17. Eldridge, J. J., Genet, F., Daigne, F., & Mochkovitch, R. 2006, MNRAS, 367, 186 [CrossRef] [Google Scholar]
  18. Gelfand, J. D., Slane, P. O., & Zhang, W. 2009, ApJ, 703, 2051 [NASA ADS] [CrossRef] [Google Scholar]
  19. Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [CrossRef] [Google Scholar]
  20. Hoogerwerf, R., de Bruijne, J. H. J., & de Zeeuw, P. T. 2000, ApJ, 544, L133 [NASA ADS] [CrossRef] [Google Scholar]
  21. Igoshev, A. P. 2020, MNRAS, 494, 3663 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kane, J., Drake, R. P., & Remington, B. A. 1999, ApJ, 511, 335 [Google Scholar]
  23. Kargaltsev, O., Cerutti, B., Lyubarsky, Y., & Striani, E. 2015, Space Sci. Rev., 191, 391 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kolb, C., Blondin, J., Slane, P., & Temim, T. 2017, ApJ, 844, 1 [CrossRef] [Google Scholar]
  25. Komissarov, S. S., & Lyubarsky, Y. E. 2004, MNRAS, 349, 779 [NASA ADS] [CrossRef] [Google Scholar]
  26. Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
  27. Meyer, D. M. A., & Meliani, Z. 2022, MNRAS, 515, L29 [NASA ADS] [CrossRef] [Google Scholar]
  28. Meyer, D. M.-A., Mackey, J., Langer, N., et al. 2014, MNRAS, 444, 2754 [NASA ADS] [CrossRef] [Google Scholar]
  29. Meyer, D. M.-A., Langer, N., Mackey, J., Velázquez, P. F., & Gusdorf, A. 2015, MNRAS, 450, 3080 [NASA ADS] [CrossRef] [Google Scholar]
  30. Meyer, D. M.-A., Vorobyov, E. I., Kuiper, R., & Kley, W. 2017, MNRAS, 464, L90 [NASA ADS] [CrossRef] [Google Scholar]
  31. Meyer, D. M. A., Pohl, M., Petrov, M., & Egberts, K. 2023, MNRAS, 521, 5354 [NASA ADS] [CrossRef] [Google Scholar]
  32. Meyer, D. M. A., Meliani, Z., Velázquez, P. F., Pohl, M., & Torres, D. F. 2024a, MNRAS, 527, 5514 [Google Scholar]
  33. Meyer, D. M. A., Velázquez, P. F., Pohl, M., et al. 2024b, A&A, 687, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
  35. Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
  36. Milisavljevic, D., Temim, T., De Looze, I., et al. 2024, ApJ, 965, L27 [CrossRef] [Google Scholar]
  37. Olmi, B., & Bucciantini, N. 2019, MNRAS, 484, 5755 [NASA ADS] [CrossRef] [Google Scholar]
  38. Olmi, B., Del Zanna, L., Amato, E., Bandiera, R., & Bucciantini, N. 2014, MNRAS, 438, 1518 [NASA ADS] [CrossRef] [Google Scholar]
  39. Orlando, S., Miceli, M., Petruk, O., et al. 2019, A&A, 622, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Orlando, S., Wongwathanarat, A., Janka, H. T., et al. 2021, A&A, 645, A66 [EDP Sciences] [Google Scholar]
  41. Orlando, S., Wongwathanarat, A., Janka, H. T., et al. 2022, A&A, 666, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Pacini, F., & Salvati, M. 1973, ApJ, 186, 249 [NASA ADS] [CrossRef] [Google Scholar]
  43. Porth, O., Komissarov, S. S., & Keppens, R. 2013, MNRAS, 431, L48 [NASA ADS] [CrossRef] [Google Scholar]
  44. Porth, O., Komissarov, S. S., & Keppens, R. 2014, MNRAS, 438, 278 [Google Scholar]
  45. Posselt, B., Pavlov, G. G., Slane, P. O., et al. 2017, ApJ, 835, 66 [CrossRef] [Google Scholar]
  46. Slane, P. 2017, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin, 2159 [CrossRef] [Google Scholar]
  47. Temim, T., Slane, P., Kolb, C., et al. 2015, ApJ, 808, 100 [CrossRef] [Google Scholar]
  48. Temim, T., Slane, P., Plucinsky, P. P., et al. 2017, ApJ, 851, 128 [Google Scholar]
  49. Temim, T., Slane, P., Raymond, J. C., et al. 2022, ApJ, 932, 26 [Google Scholar]
  50. Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [Google Scholar]
  51. Verbunt, F., Igoshev, A., & Cator, E. 2017, A&A, 608, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [Google Scholar]
  53. Whalen, D., van Veelen, B., O’Shea, B. W., & Norman, M. L. 2008, ApJ, 682, 49 [Google Scholar]
  54. Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wilkin, F. P. 1996, ApJ, 459, L31 [Google Scholar]
  56. Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [Google Scholar]
  57. Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Rendering of the 3D MHD pulsar wind nebula models, considered without (a,c) and with (b,d) their complex environments. The orange surfaces trace the constant density regions of the stellar wind bubble. The remaining color coding is as follows: red traces the supergiant wind, blue traces the WR wind, cyan traces the supernova ejecta, and white tubes trace the magnetic field lines in the pulsar wind. The 3D figures are cut with two planes, allowing for a visualization of the internal structure of the plerionic supernova remnants.
In the text
thumbnail Fig. 2.

Ram pressure in the y = 0 plane of the models, without (a) and with (b) the CSM.
In the text
thumbnail Fig. 3.

Nonthermal 1.4 GHz radio synchrotron emission maps (in erg s1 cm2 sr1 Hz1) for the pulsar wind nebulae and their host SNR, without (a,b) and with (c,d) CSM. The maps are displayed with a viewing angle of θincl = 0° (a,c) and θincl = 45° (b,d). The dark color marks the regions of strong emission intensity, while the pale color marks the regions of fainter radio emission intensity, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.