| Issue |
A&A
Volume 694, February 2025
|
|
|---|---|---|
| Article Number | A281 | |
| Number of page(s) | 9 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202453088 | |
| Published online | 19 February 2025 | |
Mutual gravitational potential of two solid bodies revisited
Application to Mars and Phobos orbit perturbations in the context of mission MMX
CNES – Centre spatial de Toulouse,
18 avenue Edouard Belin,
31401
Toulouse Cedex 9,
France
★ Corresponding author; julien.laurent-varin@cnes.fr
Received:
20
November
2024
Accepted:
24
January
2025
Context. The discovery in the Solar System of more and more binary asteroids, or even triple asteroids with odd shapes, has triggered studies and new space missions to these bodies related to their dynamical behavior. The Martian moons, due to their characteristics, are the focus of similar interest.
Aims. In this context, the aims of this paper are to revisit the mutual gravitational potential of two celestial bodies, and evaluate the dynamical effects on their orbit of terms, which are often neglected. The rotational dynamics of the bodies is not addressed here.
Methods. The method uses complex gravity spherical harmonic coefficients of each body and takes into account their exact orientation in space. These coefficients are usually estimated from the spherical harmonic representation of the shape and assuming constant density. The analytical derivation of the potential is achieved by using the rotation and translation formulas for the spherical harmonic functions and coefficients. The different components of the potential function are categorized into central direct, indirect, and coupling terms.
Results. Application to the Didymos–Dimorphos pair shows the importance of indirect and coupling terms, for which accelerations reach, respectively, 5% and 1% of the direct terms. This approach was then applied to the Mars-Phobos system, for which the effects on the Phobos orbit due to its gravity field coupling with Mars field were numerically evaluated; effects can reach several tens of meters, as is shown after orbit adjustment on currently adopted Phobos reference ephemeris. The analysis of the radio science data from the coming MMX mission (Martian Moons eXploration) may ultimately require such refinement.
Key words: gravitation / celestial mechanics / planets and satellites: general
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Space missions, for which rendezvous with Solar System bodies and sometimes landing demand the highest possible accuracy in the navigation of spacecraft, also require increased accuracy in the ephemerides of the targeted body(ies). It is therefore necessary to model as well as possible all forces acting on these bodies, which may include improvements in the orbit of natural satellites such as Phobos in the case of the Martian Moons eXploration (MMX) mission (Kuramoto et al. 2022). Among the model uncertainties are those related to coupling between the complex shapes, and gravitational attractions of a satellite and its parent planet. The Mars-Phobos case was studied analytically by Borderies and Yoder (Borderies & Yoder 1990), especially in relation to Phobos libration, taking into account the satellite gravity harmonic coefficients to the degree and order two. Jacobson and Lainey (Jacobson & Lainey 2014), and more recently Yang et al. (Yang et al. 2024), have also studied this problem, but without the coupling terms (CoT) between Mars and Phobos. Our goal has been to revisit the general expression of the mutual gravitational field of two bodies, and first to apply it and quantify the orbital effects on the Didymos–Dimorphos system, which is unusual in terms of shape and relative distance. Then, we numerically assess the effect of the full gravitational CoT on the Phobos orbit with respect to other small perturbations such as the tidal forces. In this paper, we neither work out the dynamical equations for the rotational (attitude) dynamics of the bodies involved, nor do we propagate those dynamics.
2 General formulation
The mutual gravitational potential of two bodies (B) and (B’) is a function, U, which simply depends on the shape and mass distribution of both bodies interacting on each other. Its general expression is
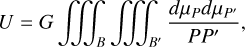 (1)
(1)
where G is the Newtonian gravitational constant, and dµP and dµ′P are the infinitesimal mass densities of the two bodies at any couple of points, P, P′. As is usual in celestial mechanics, we note that U is a force potential function (the opposite of the potential energy).
For a single body, its gravitational potential is usually represented as a (truncated) spherical harmonics series in a reference frame, [R], fixed relative to it. At any point of spherical coordinates, r, ϕ, λ (radius vector, latitude, longitude), the body gravitational potential can be written as (Balmino & Borderies 1978; Balmino 1994)
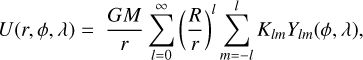 (2)
(2)
where M is the mass of the body, G is the Newton constant, and R is a reference equatorial radius. Klm are the complex gravitational harmonics coefficients of degree l and order m, and Ylm the corresponding complex harmonics functions with the following definition:
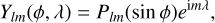 (3)
(3)
where Plm (m > 0) is the usual Legendre associated function, extended to negative orders by
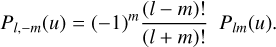 (4)
(4)
The complex Klm coefficients are related to the usual real coefficients, Clm and Slm (m > 0), by
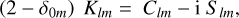 (5)
(5)
where δ0m is the Dirac delta (equal to 1 if m = 0 and 0 else),
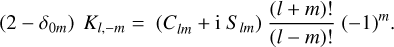 (6)
(6)
In the following, we use non-normalized functions and coefficients, which is appropriate from a numerical point of view, since we do not go to a high degree and order in this work.
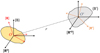 |
Fig. 1 Two bodies, (B) and (B′), and their body-fixed reference systems, [R] and [R′], respectively. [R0] and [R′0] are two other reference frames that have the same orientation in space. |
2.1 Mutual potential
For two bodies, (B) and (B′), we considered reference frames [R0] for (B) and [R′0] for (B′), whose origins, O, O′, are distant from r and whose axes have the same orientations (Fig. 1).
We let 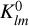 and
and 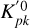 be the complex gravity harmonics of (B) and (B′) in the reference frames [R0] and [R′0], respectively. The mutual gravitational potential can be expanded as (Borderies 1978)
be the complex gravity harmonics of (B) and (B′) in the reference frames [R0] and [R′0], respectively. The mutual gravitational potential can be expanded as (Borderies 1978)
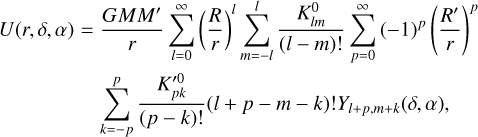 (7)
(7)
where M′, and R′ are, for (B′), analogous to M and R, and α and δ are, respectively, the right ascension and declination of O′ in [R0]. In this formula, we can identify certain terms that correspond to usual simplifications. In order to distinguish them, we shall refer to them in the remainder of this article using the conventions of Table 1.
For calculation purposes, we must refer the  coefficients of (B) to its harmonics, Kjn, in its proper body fixed system, [R], and also refer the
coefficients of (B) to its harmonics, Kjn, in its proper body fixed system, [R], and also refer the  coefficients of (B') to its harmonics,
coefficients of (B') to its harmonics, 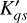 , in its body fixed system, [R']. To do so, we introduced the Euler angles, Ψ, Θ, Φ, of [R] with respect to [R0], as is defined in Fig. 2, and similarly the “3-1-3” Euler angles, Ψ′, Θ′, Φ′, of [R′] with respect to [R′0].
, in its body fixed system, [R']. To do so, we introduced the Euler angles, Ψ, Θ, Φ, of [R] with respect to [R0], as is defined in Fig. 2, and similarly the “3-1-3” Euler angles, Ψ′, Θ′, Φ′, of [R′] with respect to [R′0].
We used the spherical harmonics rotation theorem (Wigner & Fano 1960) in its dual form, which yields
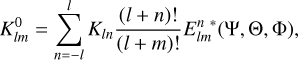 (8)
(8)
are the Clifford polynomials. The conjugate of the 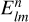 functions that enter in Eqs. (8) and (9) verify that
functions that enter in Eqs. (8) and (9) verify that
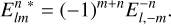 (12)
(12)
In formulas (8) and (9), we note that the degree of the spherical harmonics is preserved. For comparison purposes with other simplified expressions of U found in the literature, we give in the appendix formulas for the case in which spherical harmonics are limited to the degree and order two for each body and when Ψ = Ψ′ = Θ = Θ′ = 0.
Naming convention for terms of U in spherical harmonics.
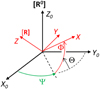 |
Fig. 2 Going from reference system [R0] to another one, [R], by means of the Euler angles, Ψ, Θ, and Φ. |
2.2 Dynamical equations
The motion of O′ relative to O is described by the equation
![$\vec \Gamma \left( {{O^\prime }/\left[ {{{\rm{R}}^0}} \right]} \right) = {{{d^2}} \over {d{t^2}}}\left( {\overrightarrow {O{O^\prime }} } \right) = {{M + {M^\prime }} \over {M{M^\prime }}}{\vec \nabla _{{O^\prime }}}U.$](/articles/aa/full_html/2025/02/aa53088-24/aa53088-24-eq19.png) (13)
(13)
Then we have to compute the components of the mutual gravitational potential gradient U defined in Eq. (7). Xs being the components of 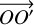 in [R0], these gradient components are
in [R0], these gradient components are 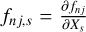 , where fnj is defined ∀n ∊ 〚1, lmax + pmax〛 and ∀ j ∊ 〚−n, n〛 by the equation:
, where fnj is defined ∀n ∊ 〚1, lmax + pmax〛 and ∀ j ∊ 〚−n, n〛 by the equation:
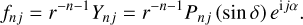 (14)
(14)
These terms originate from formula (7), where n = l + p and j = m + k. It should be noted that the coefficients of such terms capture all of the dependence on the attitudes of both bodies and have no dependence on the relative position of the bodies, in a separable fashion. We followed an approach whereby we wrote Pnj(sin δ) = cosj δ Hnj(sin δ), Hnj being the Helmholtz polynomials, here non-normalized (the degree and order remain small, as was said above). They were computed by recursive formulas with a fixed order, j, as well as their derivatives. Introducing the direction cosines (ε1, ε2, ε3) of 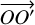 in [R0], we have for j > 0:
in [R0], we have for j > 0:
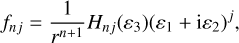 (15)
(15)
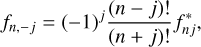 (16)
(16)
from which nonsingular expressions (valid when cos δ = 0) for fnj,s can be derived (Balmino et al. 1990).
3 Example: Didymos and Dimorphos
We present a simplified case of the Didymos and Dimorphos binary, which was visited by the DART mission (Daly et al. 2023) and which is targeted by the Hera mission (ESA 2022). This example consists of taking the known physical parameters of this binary system, propagating a Keplerian orbit of Dimorphos around Didymos, and evaluating over one revolution the value of the different terms of the acceleration induced by the mutual potential – according to definitions in Table 1.
3.1 Data assumptions
As the precise shape of each of these bodies is not precisely known, we carried out the calculation using ellipsoidal models with the parameters given in Table 2 (Daly et al. 2023); the semimajor axes are those in the X, Y, Z directions of the [R] system for Didymos and similarly in the [R′] system for Dimorphos. For each body, defining: p = a2 − b2, q = c2 − (a2 + b2)/2, one can compute the nonzero gravity spherical harmonics according to (Balmino 1994; Boyce 1997)
![$\matrix{ {{K_{2l,2m}} = {3 \over {{{\rm{a}}^{2l}}}}{{l!(2l - 2m)!} \over {{2^{2m}}(2l + 3)(2l + 1)!}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathop \sum \limits_{i = 0}^{[(l - m)/2]} {{{p^{m + 2i}}{q^{l - m - 2i}}} \over {{{16}^i}i!(m + i)!(l - m - 2i)!}},} \hfill \cr } $](/articles/aa/full_html/2025/02/aa53088-24/aa53088-24-eq26.png) (17)
(17)
where the a2l term corresponds to a scaling factor (Brillouin sphere radius) equal to a. The resulting coefficients (unnormalized) are given up to the degree and order six in Table 3 for the two bodies.
The mean orbital parameters used in the computation are listed in Table 4. Finally, we fixed the Euler angles (rotational elements) at the following values:
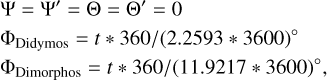
where 360/(11.9217 * 3600) is the mean motion (n) of Dimorphos (before the DART impact) and t is the time in seconds.
Didymos and Dimorphos data: a, b, and c are semimajor axes.
Gravity harmonic coefficients of Didymos and Dimorphos.
Orbital elements of Dimorphos.
Accelerations of Dimorphos along one orbit.
 |
Fig. 3 Acceleration magnitudes of Dimorphos over one orbit for the direct term (DT). |
 |
Fig. 4 Acceleration magnitudes of Dimorphos over one orbit for IT. |
3.2 Numerical results
The maximum and minimum accelerations along one orbit are given in Table 5 for the different classes of terms: central, direct, indirect, and coupling. Indirect accelerations are smaller though close to the direct terms; the CoT amount to about 1% of the direct ones, which is significant for the system dynamics.
Figures 3, 4, and 5 more precisely show the behaviour of the different terms (apart from the central one). In addition to once-per-revolution variations in the direct and indirect radial and normal accelerations, higher-frequency variations due to direct and CoT are clearly visible, especially in the tangential and radial directions; the direct perturbations dominate due to the much higher mass and C20 of Didymos.
 |
Fig. 5 Acceleration magnitudes of Dimorphos over one orbit for CoT. |
4 Application to Mars-Phobos
To see the impact of the mutual potential on a well-known orbit, we chose the Mars-Phobos system. Phobos has a rather unusual gravitational configuration with Mars, being relatively close and not spherical in shape.
We focus on the effects of the gravitational CoT compared to other forces at work in the system, the tidal effects of Mars (i.e., the k2 Love number contribution), the third-body perturbations mainly due to the Sun and Jupiter, and relativistic effects.
4.1 Orbit models and assumptions
4.1.1 Mars and Phobos orientation
For the body orientation and rotation, the models in the IAU 2015 standards (Archinal et al. 2018) were used. For Phobos, the correction (Archinal et al. 2019) has been taken into account in this study, even though its impact remains small.
4.1.2 Gravity model
The Martian gravity model used is the Konopliv model (Konopliv et al. 2016) developed to degree 120. The version used is MRO120d, but only the first eight degrees were retained.
The Phobos gravity model was derived from the transformation of the most accurate body shape (Ernst et al. 2023) into gravitational spherical harmonics under the assumption of uniform mass distribution. This model is given in Appendix B. We assumed a GM value of 708 700 m3/s2 (consistent with Jacobson & Lainey 2014) and a translation was done to make the center of mass, O, and the center of figure, C, coincide. Thanks to this translation, 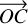 , of (82.194, 521.606, 31.433) (m), the degree one coefficients vanish.
, of (82.194, 521.606, 31.433) (m), the degree one coefficients vanish.
4.1.3 Other forces
Third body and tidal forces were taken into account in accordance with current knowledge and state-of-the-art algorithms (see the GINS software documentation; Space Geodesy 2018). The third bodies taken into account are: the Sun, Jupiter, Saturn, Uranus, and the Earth. It should be noted that only the contributions of the Sun and Jupiter are significant, the other planets contributing only marginally. The Solar System ephemeris data are consistent with the de430bdlf file (Folkner et al. 2014). It is not the last updated ephemeris (Park et al. 2021), but it is consistent with the Phobos mar097.bsp model.
Phobos and Deimos distort Mars’ gravity field, the effect of which is modeled by the Love number k2, whose adopted value is: 0.152 + i 0.00183. The imaginary part corresponds to the delayed effect of gravity deformation. This value is consistent with Jacobson (2010).
Finally, the effect of relativity can be modeled by several terms: the Schwarzschild term, the relativistic Coriolis term, and the Lense-Thirring term (see, for instance, Huang & Liu 1992). In our case, only the Schwarzschild effect is taken into account; this term is already very small, and the others are even smaller,
![${F_{S{\rm{ }}chwarschild{\rm{ }}}} = {\mu \over {{c^2}{r^3}}}\left[ {\left[ {4{\mu \over r} - {\v ^2}} \right]r + 4(\v \cdot r)\v } \right].$](/articles/aa/full_html/2025/02/aa53088-24/aa53088-24-eq29.png) (18)
(18)
In Eq. (18), c is the light velocity, µ the standard gravitational parameter (GM) of the central attracting body, r the vector position of Phobos, and υ its velocity vector.
 |
Fig. 6 Acceleration magnitude over one orbit for each term. |
 |
Fig. 7 Difference between the Jacobson model (Eq. (19)) and the IT+CoT term of full mutual potential model. |
4.1.4 Reference orbit
PDS (Planetary Data System) archives (Acton 1996; Acton et al. 2018) provide the up-to-date Phobos ephemeris in the file mar097.bsp. This was selected as the reference for comparison with all other orbits, since this reference is determined from observations that are astrometric in nature and that thus reflect precisely where Phobos is and how the body shape is oriented at all of the observation epochs. As is described in the orbit file documentation, it models Mars’ gravity, third body, and tides, although the implementation may differ from ours.
The main difference lies in the account of the Mars-Phobos mutual gravity: it is limited to a so-called libration term force and written as (Jacobson 2010)
![${F_1} = - {3 \over 2}\mu \left( {{{{R^{\prime 2}}} \over {{r^4}}}} \right)\left[ {\left( { - C_{20}^\prime + 6C_{22}^\prime \cos 2\beta '} \right)\mathord{\buildrel{\lower3pt\hbox{\scriptscriptstyle\frown}}\over r} + 4C_{22}^\prime \sin 2\beta '\mathord{\buildrel{\lower3pt\hbox{\scriptscriptstyle\frown}}\over t} } \right],$](/articles/aa/full_html/2025/02/aa53088-24/aa53088-24-eq30.png) (19)
(19)
where µ is the GM of Mars, R′ the equatorial radius of Phobos, r the distance from Phobos to Mars, C′20 the second degree zonal harmonic of Phobos, and C′22 its second degree and order tesseral term. β′ equals 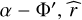 is the unit vector directed from Mars toward Phobos, and
is the unit vector directed from Mars toward Phobos, and 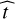 is the unit vector in the Phobos orbit plane normal to
is the unit vector in the Phobos orbit plane normal to 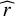 and in the direction of Phobos’s orbital motion. This agrees with the degree two model presented in Appendix A, with some simplifications: it retains only one part of the indirect terms (IT) and none of the CoT due to assuming S′22 = 0, and δ = 0.
and in the direction of Phobos’s orbital motion. This agrees with the degree two model presented in Appendix A, with some simplifications: it retains only one part of the indirect terms (IT) and none of the CoT due to assuming S′22 = 0, and δ = 0.
Adjustment on the Jacobson orbit of the Phobos trajectory without full mutual potential.
Adjustment on the Jacobson orbit of the Phobos trajectory with full mutual potential.
4.2 Numerical results
4.2.1 Comparison of accelerations
Figure 6 shows the amplitudes of the total accelerations involved in the dynamics of Phobos over one revolution. The central and direct terms are the dominant ones but do not exhibit any particularity and are not shown; only accelerations between 10−6 and 10−12 are presented.
The term “Jacobson model” represents the contribution of the mutual potential that Jacobson uses (Eq. (19)). This contribution is very close to the IT of our mutual potential model.
The CoT acceleration is of the same order as the effect of the Martian tide but larger. The contribution is therefore relatively small in the orbit of Phobos, though not negligible.
The smallest accelerations in Fig. 6 are the relativistic Schwarzschild effect and the contribution of the third body, Jupiter. Both are less than 10−10 m/s2.
4.2.2 Jacobson model and full mutual potential impact
Figure 7 shows the difference in the RTN axis between the Jacobson acceleration, which assumes an equatorial and circular orbit and neglects terms of a degree greater than two, and the acceleration induced by the full mutual potential; that is, the complete IT and CoT terms.
In order to quantify the impact of the mutual potential, the numerically integrated trajectory of Phobos was compared with the Jacobson reference trajectory described in Sect. 4.1.4. The calculations were carried out over 3 days (72 hours). Firstly, the orbit generation and adjustment were made using the same dynamics as for the Jacobson trajectory. A second case was run with our full mutual potential model, followed by a similar adjustment on Jacobson orbit. The least-squares fit seeks to minimize the 3D residuals from the reference orbit, so in terms of orbital parameters we can observe a secular trend for certain parameters, which is due to the fit in the Cartesian domain over a relatively short period (3 days).
In the first case, a 3D RMS of less than 7 m over 3 days is obtained, which means the dynamical models are fairly consistent with the Jacobson ones. However, in the second case in which the full mutual potential is included, the 3D RMS rises to greater than 27 m.
Tables 6 and 7 respectively show the trajectory difference statistics in the RTN axes after the adjustment. As was expected, the impact of the difference in dynamical models is mainly on the tangential axis. The graphs in Fig. 8 show the evolution of the difference between the two adjusted trajectories, in terms of orbital parameters.
Figure 9 shows the differences in position (in R,T,N) between the Jacobson reference trajectory and our adjusted trajectories, without and with the full mutual potential modeling. On the butterfly shape inherent to the least squares adjustment, and on the once-per-revolution terms expected from the dynamics differences, was superimposed an along-track secular effect. This deviation from the Jacobson reference orbit was an order of magnitude smaller than the translation of the Phobos shape model in order to make the center of mass coincide with the shape’s center of figure (see Sect. 4.1.2). Therefore, it seems that the present uncertainty in Phobos’ internal mass distribution swamps the effects of including or not including the additional parts of the IT terms and the CoT terms that Jacobson did not include. Nevertheless, for future modeling of Phobos gravity field and mass distribution, we recommend including such terms, which otherwise would induce (additional) errors in any density model.
 |
Fig. 8 Difference between orbital parameters for case 1 and case 2. The X axis represents the number of Julian days since January 1, 1950 (day 27 709 = 12/11/2025). |
 |
Fig. 9 Position differences in tangential, normal, and radial between Jacobson Phobos orbit and our adjusted orbits: with a simplified model for the mutual potential (left) consistent with Table 6, and with a full mutual potential (right) consistent with Table 7 The X axis represents the number of Julian days since January 1, 1950 (day 27 709 = 12/11/2025). |
5 Conclusion
We have shown that usually neglected terms in the expression of the mutual gravitational potential of two celestial bodies of an odd shape can have a significant dynamical effect on their relative orbit. In particular, the MMX mission at the Mars-Phobos system, to be launched in 2026, will bring a wealth of data, including new tracking measurements that will be used to improve our knowledge of Phobos and especially its ephemeris and gravity field model. Their determination process should take into account the indirect and coupling gravitational terms of the Mars–Phobos pair, as we do here.
Acknowledgements
Supports of CNES (Centre National d’Etudes Spatiales) and of OMP (Observatoire Midi-Pyrénées) are gratefully acknowledged. We thank the reviewers for very sharp remarks which greatly helped improving the paper.
Appendix A Case of degree and order-two coefficients in a simplified geometry
A special case is considered when the equatorial planes of the two bodies remain parallel to the [R0] reference system equator (Fig. A.1) and when the spherical harmonics are limited to degree and order two for each body. Direct formulas using un-normalized real spherical harmonic coefficients (Clm, Slm, C′lm, S′lm) can be derived and allow comparison with other authors’ results as well as numerical verification with the more general formulas applied to this case.
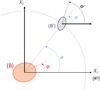 |
Fig. A.1 Particular case (viewed from X3 > 0): Ψ= Ψ′ = Θ = Θ′ =0, and harmonic coefficients are limited to degree and order two for each body. |
and with β =α − Φ; β’ = α − Φ’
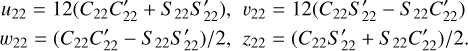
As an example, note that Jacobson (2010) considered the term T20 and only the portion of T02 without S′22 (with P20(0) = −1/2, Pշշ(0) = 3)
Appendix B Phobos gravity model
The Phobos gravity field was calculated by transforming the body shape into gravity spherical harmonics, assuming a uniform mass distribution.
The algorithm involved calculating the gravity field modeled from the polyhedral shape on a sphere containing all the masses. The calculation was performed on a 0.1° grid in longitude and latitude using the “polyhedral-gravity-model” tool of Tsoulis (Tsoulis 2012; Tsoulis & Gavriilidou 2021). The projection on the spherical harmonics basis was then carried out using an internal tool.
The whole process was compared to another method (Balmino 1994) and gave consistent results. Table B.1 gives the normalized derived Phobos gravity field spherical harmonics. We have set the coefficients of degree 1 to 0.0 to align the center of the figure with the center of gravity, and the coefficients C21 and S21 to 0 also to align the main axis of inertia of the body with the Z axis of the frame of reference attached to the body.
Phobos normalized spherical harmonics coefficient.
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [Google Scholar]
- Acton, C., Bachman, N., Semenov, B., & Wright, E. 2018, Planet. Space Sci., 150, 9 [Google Scholar]
- Archinal, B. A., Acton, C. H., A’Hearn, M. F., et al. 2018, Celest. Mech. Dyn. Astron., 130, 22 [Google Scholar]
- Archinal, B. A., Acton, C. H., Conrad, A., et al. 2019, Celest. Mech. Dyn. Astron., 131, 61 [Google Scholar]
- Balmino, G. 1994, Celest. Mech. Dyn. Astron., 60, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Balmino, G., & Borderies, N. 1978, Celest. Mech., 17, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Balmino, G., Barriot, J. P., & Valès, N. 1990, Manuscr. Geod., 15, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Borderies, N. 1978, Celest. Mech., 18, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Borderies, N., & Yoder, C. F. 1990, A&A, 233, 235 [NASA ADS] [Google Scholar]
- Boyce, W. 1997, Celest. Mech. Dyn. Astron., 67, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Daly, R. T., Ernst, C. M., Barnouin, O. S., et al. 2023, Nature, 616, 443 [CrossRef] [Google Scholar]
- Ernst, C. M., Daly, R. T., Gaskell, R. W., et al. 2023, Earth Planets Space, 75, 103 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 2022, https://www.heramission.space [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., & Kuchynka, P. 2014, Interplanetary Network Progress Report, 42-196, 1 [Google Scholar]
- Huang, C., & Liu, L. 1992, Celest. Mech. Dyn. Astron., 53, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. A. 2010, AJ, 139, 668 [Google Scholar]
- Jacobson, R. A., & Lainey, V. 2014, Planet. Space Sci., 102, 35 [CrossRef] [Google Scholar]
- Konopliv, A. S., Park, R. S., & Folkner, W. M. 2016, Icarus, 274, 253 [Google Scholar]
- Kuramoto, K., Kawakatsu, Y., Fujimoto, M., et al. 2022, Earth Planets Space, 74, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Park, R. S., Folkner, W. M., Williams, J. G., & Boggs, D. H. 2021, AJ, 161, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Space Geodesy, C. s. 2018, Algorithmic documentation of the GINS software, Tech. rep., CNES [Google Scholar]
- Tsoulis, D. 2012, Geophysics, 77, F1 [NASA ADS] [CrossRef] [Google Scholar]
- Tsoulis, D., & Gavriilidou, G. 2021, Geophys. Prospect., 69, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Wigner, E. P., & Fano, U. 1960, Am. J. Phys., 28, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Yan, J., Jian, N., Matsumoto, K., & Barriot, J.-P. 2024, A&A, 685, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Adjustment on the Jacobson orbit of the Phobos trajectory without full mutual potential.
Adjustment on the Jacobson orbit of the Phobos trajectory with full mutual potential.
All Figures
 |
Fig. 1 Two bodies, (B) and (B′), and their body-fixed reference systems, [R] and [R′], respectively. [R0] and [R′0] are two other reference frames that have the same orientation in space. |
| In the text | |
 |
Fig. 2 Going from reference system [R0] to another one, [R], by means of the Euler angles, Ψ, Θ, and Φ. |
| In the text | |
 |
Fig. 3 Acceleration magnitudes of Dimorphos over one orbit for the direct term (DT). |
| In the text | |
 |
Fig. 4 Acceleration magnitudes of Dimorphos over one orbit for IT. |
| In the text | |
 |
Fig. 5 Acceleration magnitudes of Dimorphos over one orbit for CoT. |
| In the text | |
 |
Fig. 6 Acceleration magnitude over one orbit for each term. |
| In the text | |
 |
Fig. 7 Difference between the Jacobson model (Eq. (19)) and the IT+CoT term of full mutual potential model. |
| In the text | |
 |
Fig. 8 Difference between orbital parameters for case 1 and case 2. The X axis represents the number of Julian days since January 1, 1950 (day 27 709 = 12/11/2025). |
| In the text | |
 |
Fig. 9 Position differences in tangential, normal, and radial between Jacobson Phobos orbit and our adjusted orbits: with a simplified model for the mutual potential (left) consistent with Table 6, and with a full mutual potential (right) consistent with Table 7 The X axis represents the number of Julian days since January 1, 1950 (day 27 709 = 12/11/2025). |
| In the text | |
 |
Fig. A.1 Particular case (viewed from X3 > 0): Ψ= Ψ′ = Θ = Θ′ =0, and harmonic coefficients are limited to degree and order two for each body. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



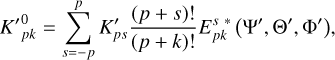
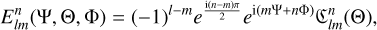
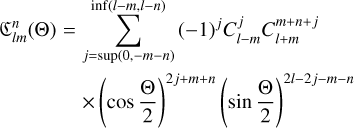
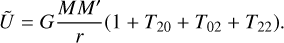
![$\eqalign{ & \matrix{ {{T_{20}} = {{\left( {{R \over r}} \right)}^2}\left[ {{C_{20}}{P_{20}}(\sin \delta ) + \left\{ {{C_{22}}\cos 2\beta + {S_{22}}\sin 2\beta } \right\}{P_{22}}(\sin \delta )} \right]} \cr {{T_{02}} = {{\left( {{{R'} \over r}} \right)}^2}\left[ {C_{20}^\prime {P_{20}}(\sin \delta )} \right.} \cr } \cr & \matrix{ {\left. { + \left\{ {C_{22}^\prime \cos 2\beta ' + S_{22}^\prime \sin 2\beta '} \right\}{P_{22}}(\sin \delta )} \right]} \cr {{T_{22}} = {{\left( {{R \over r}} \right)}^2}{{\left( {{{R'} \over r}} \right)}^2}\left[ {Q_{22}^0 + Q_{22}^{ \pm 2}} \right],} \cr } \cr} $](/articles/aa/full_html/2025/02/aa53088-24/aa53088-24-eq35.png)
![$\eqalign{ & \matrix{ {Q_{22}^0 = {C_{20}}\left[ {6C_{20}^\prime {P_{40}}(\sin \delta ) + \left\{ {C_{22}^\prime \cos 2\beta ' + S_{22}^\prime \sin 2\beta '} \right\}{P_{42}}(\sin \delta )} \right]} \cr {Q_{22}^{ \pm 2} = \left[ {{u_{22}}\cos 2\left( {{\rm{\Phi }} - {\rm{\Phi '}}} \right) + {\v _{22}}\sin 2\left( {{\rm{\Phi }} - {\rm{\Phi '}}} \right)} \right]{P_{40}}(\sin \delta )} \cr } \cr & \matrix{ { + C_{20}^\prime \left[ {{C_{22}}\cos 2\beta + {S_{22}}\sin 2\beta } \right]{P_{42}}(\sin \delta )} \cr { + \left[ {{w_{22}}\cos \left[ {4\alpha - 2\left( {{\rm{\Phi }} + {\rm{\Phi '}}} \right)} \right]} \right.} \cr {\left. {\quad + {_{22}}\sin \left[ {4\alpha - 2\left( {{\rm{\Phi }} + {\rm{\Phi '}}} \right)} \right]} \right]{P_{44}}(\sin \delta )} \cr } \cr} $](/articles/aa/full_html/2025/02/aa53088-24/aa53088-24-eq36.png)