| Issue |
A&A
Volume 688, August 2024
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 9 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202450246 | |
| Published online | 09 August 2024 | |
Apsidal precession in binary asteroids
Smead Department of Aerospace Engineering, University of Colorado Boulder,
3775 Discover Dr,
Boulder,
CO
80303,
USA
e-mail: alex.meyer@colorado.edu
Received:
4
April
2024
Accepted:
6
June
2024
While the secondary in a binary asteroid plays an important role in the precession of the mutual orbit, this role has not been thoroughly studied. Given the complex spin-orbit-coupled dynamics in binary asteroids, we used a numerical approach to study the relationship between the secondary’s shape and spin and the apsidal precession rate of the orbit. Using this approach in conjunction with observations of Didymos, we find it is likely that Dimorphos was significantly reshaped as a result of the DART impact, with its new shape more elongated than the pre-impact shape. Finally, we show that non-principal axis rotation of the secondary can lead to a chaotic evolution of the longitude of the periapsis.
Key words: methods: numerical / celestial mechanics / minor planets, asteroids: general / minor planets, asteroids: individual: Didymos
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The secular precession rate of an orbit is an important quantity driven by the physical characteristics of the system. It is well understood that the oblateness of the primary body plays a major role in the precession rate (Murray & Dermott 1999). This fact has been used to estimate mass distributions within the body given an observed orbital precession rate. However, the typical assumption in these problems is that the secondary body is small and massless in comparison to the primary. This is not the case for binary asteroids, in which the secondary can be a significant fraction of the total mass of the system. Furthermore, the secondary is typically elongated, and its nonspherical shape can have an important influence on the system dynamics, especially in a perturbed system (Meyer et al. 2023).
The topic of orbital precession in systems with irregular satellites has been previously discussed in the literature. Borderies & Yoder (1990) examined how the shape of Phobos influences its orbit and libration. However, they did not account for free libration in the system, instead focusing only on the libration caused by the orbit’s eccentricity (i.e., forced libration). Furthermore, Phobos’s mass fraction is very small, around 7 orders of magnitude smaller than that of Mars.
Specific to binary asteroids, Fahnestock & Scheeres (2008) identified a relationship between the secondary’s shape and its orbit precession rate in their analysis of the dynamics of (66391) Moshup (known as 1999 KW4 at the time of their publication). However, several assumptions were made in the derivation of this expression that do not hold in general. Meyer et al. (2023) show that for librating, elongated secondaries, the expression is inaccurate.
Meyer et al. (2021) explored how the secondary shape can affect the observed orbit period in a binary asteroid, which experiences fluctuations due to the precession rate. This begins to connect the physical parameters of the secondary to the precession rate, but they did not explicitly study this relationship. Here we take a more formal approach to understanding how the secondary parameters are manifested in observations of the precession rate.
Perhaps the best understanding of the secondary’s effect on the precession rate is given by Ćuk & Nesvornỳ (2010). While this work explicitly relates the apsidal precession rate to the physical parameters of the secondary, it does not fully investigate how observations can constrain estimates of the secondary’s shape and dynamics. Here we use the relationship defined in Ćuk & Nesvornỳ (2010) to inform a numerical investigation in which we relate observations to the physical and dynamical properties of the secondary.
The primary motivation for this study is the recent impact of the Double Asteroid Redirection Test (DART). The DART impact into Dimorphos, the secondary in the Didymos binary asteroid system, perturbed the orbit, resulting in an apsidal precession signal in observations. The estimated precession rate cannot be explained by the primary’s oblateness alone, and after performing a formal fit to the Didymos data, Naidu et al. (2024) find that a more elongated Dimorphos can explain the observed precession rate. In this work, we performed a deeper study of the role played by the secondary in the orbital precession rate within a binary asteroid. We then used this relationship to place constraints on the physical and dynamical properties of Dimorphos.
Additional analysis of the Didymos data suggests that Dimor-phos is currently in a state of non-principal axis (NPA) rotation (Pravec et al. 2024). Due to the spin-orbit-coupled nature of binary asteroid dynamics, this rotation state would have an effect on the orbit’s precession rate. We also investigated this relationship.
We first outline the dynamical model we used in Sect. 2 and summarize the analytic work done by Ćuk & Nesvornỳ (2010) in Sect. 3. We then present our general numerical study in Sect. 4. In Sect. 5 we apply this approach to Didymos to place constraints on the shape and libration amplitude of Dimorphos. In Sect. 6, we explore how the presence of NPA rotation changes the precession rate. Finally, we provide a discussion in Sect. 7 and our conclusions in Sect. 8.
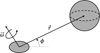 |
Fig. 1 Diagram of our dynamical model, the sphere-restricted full two-body problem. This shows the relative position and angular velocity vectors centered in the secondary’s body-fixed frame. The libration angle is labeled. |
2 Dynamical model
Since we are interested in the role played by the elongation and spin of the secondary in the precession rate of binary asteroids, we chose the simplest dynamical model that preserves those quantities. This is the sphere-ellipsoid model, where the primary is modeled as a sphere and the secondary as a triaxial ellipsoid. This will allow us to investigate the effects of only the secondary’s shape and dynamics on the precession, eliminating the well-understood role played by the primary’s oblateness.
The diagram of our dynamical model presented in Fig. 1 shows the prolate secondary and spherical primary. This model permits full three-dimensional rotation and translation. The equations of motion for the sphere-restricted full two-body problem were derived in Scheeres (2006), which take the secondary as the central body:
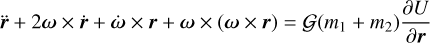 (1)
(1)
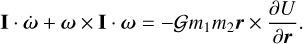 (2)
(2)
Here, r is the position of the primary relative to the secondary and ω is the spin rate of the secondary. 𝒢 is the universal gravitational constant, m1 and m2 are the mass of the primary and secondary, respectively. U is the gravitational potential; with the secondary modeled as a triaxial ellipsoid, we calculated the second-order potential using MacCullagh’s formula (Murray & Dermott 1999). The libration angle is an important quantity, which we defined as the angle between the secondary’s long axis and the relative position of the primary in the secondary’s body-fixed frame. This is labeled as ϕ on Fig. 1.
We note the equations of motion, written in Eqs. (1) and (2), are written in the body-fixed frame of the secondary. However, we are interested in the apsidal precession rate of the orbit, which is defined relative to an inertial frame. To account for this, we also integrated a simple set of quaternions in parallel with the equations of motion, which allowed us to track the secondary’s attitude relative to an inertial frame and perform a coordinate transformation between these two frames. The quaternions have the added benefit of having time derivatives that are a linear function of the spin vector (Schaub & Junkins 2003).
3 Analytical approach
The groundwork for an analytic expression of the apsidal precession rate around an elongated body was done by Burns (1976, 1977) through an application of the classical Gauss Planetary Equations. The radial and tangential accelerations due to the perturbation of the elongated body were derived in Scheeres (2009). Using these, the time derivative of the longitude of periapsis, or equivalently the apsidal precession rate, as applied to binary asteroids was then finalized in Ćuk & Nesvornỳ (2010). The apsidal precession resulting from the body’s oblateness is a classical result (Murray & Dermott 1999), so here we focused only on the effect of the body’s prolateness. For convenience we repeat the expression here, with corrections to minor errors in the original derivation. We also point out that this equation is only defined for planar motion. Our numerical model allows for out-of-plane motion as well, so this expression should only be used if the dynamics are guaranteed to remain planar. The equation is non-dimensionalized; the radius of the primary is used as the unit of length and the total system mass as the mass unit, leading to the unit of time equal to 1/2π of the orbit period at the equator of the primary (Ćuk & Nesvornỳ 2010):
![$\eqalign{ & \dot \varpi = {{\sqrt {a(1 - {e^2})} } \over e}{{B - A} \over {{r^4}}}[{9 \over 4}\cos 2\phi \cos f \cr & & & & & + {3 \over 2}\sin 2\phi \sin f{{2 + e\cos f} \over {1 + e\sin f}}]. \cr} $](/articles/aa/full_html/2024/08/aa50246-24/aa50246-24-eq3.png) (3)
(3)
Apart from the classical precession rate driven by oblate-ness, this expression shows the driving quantities in apsidal precession. Beyond the semimajor axis, a, eccentricity, e, and separation, r, we also see the precession rate depends on the C22 gravity term (here equivalently written as B − A, where A < B < C are the mass-normalized principal moments of inertia), the libration angle, φ, and the orbital position, measured by true anomaly, f. Here we can directly observe increasing the secondary’s C22 increases the apsidal precession rate. The libra-tion angle is the angle between the longest axis and the position vector, also written mathematically as
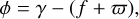 (4)
(4)
where γ is the elongated body’s orientation in inertial space and ϖ is the longitude of periapsis.
Interestingly, Eq. (3) includes the relative orientation of the prolate body. This orientation will depend on the spin state of the body, meaning perturbations to the body’s spin will have an effect on the precession rate. This can be used to our advantage; if the precession rate of the orbit is measured, it can help constrain the spin rate and libration amplitude of the secondary in a binary asteroid. Here, we defined our libration amplitude as the maximum of the libration angle.
Another point of interest is the role the true anomaly plays in the precession rate. Scheeres (2009) established that in the synchronous equilibrium of binary asteroids, the true anomaly is equal to zero and the secondary is trapped at periapsis, with the longitude of periapsis precessing at the orbit rate. This issue can be circumvented by using a set of orbit elements that account for the primary’s oblateness, for example the geometric elements (Borderies-Rappaport & Longaretti 1994). Within the Keplerian elements, this phenomenon is also reflected in Eq. (3), where if the true anomaly and libration angle are equal to zero the apsidal precession rate is rapid. For small perturbations, the true anomaly and libration angle both oscillate about 0°. In this case, the precession rate is not constant, but is still rapid, since the longitude of periapsis is still circulating while the true anomaly oscillates. The critical point where the true anomaly switches from oscillation to circulation was derived in Meyer et al. (2023), who also briefly discuss the relationship between the true anomaly and apsidal precession rate.
Unfortunately, this expression relies on both ϕ and f, which are not independent and lack an explicit relationship between the two. Thus, they must be integrated together using proper equations of motion, for example the model in Scheeres (2009) or Ćuk & Nesvornỳ (2010). Furthermore, the semimajor axis, eccentricity, and separation all also depend on these two quantities, and the semimajor axis and eccentricity in particular are not constant. We illustrate the relationships between these parameters in Fig. 2, which shows complex dependences between the true anomaly, libration, separation distance, semimajor axis, and eccentricity.
One can attempt to average Eq. (3) over one orbit period. However, as demonstrated in Fig. 2, and also discussed in Meyer et al. (2021), there are in reality several frequencies, specifically the frequency of the true anomaly and the frequency of libration. Thus, averaging over one orbit period will not capture the true secular behavior, except for the specific case where the libration frequency is resonant with the orbit mean motion (for a synchronous secondary, this is the case of only forced libration). Alternatively, one could average over one precession period. However, in a purely analytical approach we still run into the problem of the complex relationships between f and ϕ.
From Fig. 2, it is clear there are several underlying frequencies driving the evolution of the system. These frequencies can be obtained through the linearization of our equations of motion. Specifically, in a system undergoing planar dynamics, it is limited to three degrees of freedom, one of which can be eliminated via the angular momentum integral. This linearization was carried out in Fahnestock & Scheeres (2008), who report the two natural frequencies for a planar system as
![$\eqalign{ & \omega _a^2,\omega _b^2 = \left[ {{{ - 12A + 3B + 9C} \over 4} - {1 \over 2} - {3 \over 2}\nu \kappa } \right]{9 \over 4} \cr & & \,\,\,\, \pm \left[ {{9 \over 4}{{\left( {{{12A - 7B - 5C} \over 2}\nu \kappa } \right)}^2}} \right] \cr & & \,\,\,\, + {3 \over 4}( - 20A + 17B + 3I) - {3 \over 2}\nu \kappa + {1 \over 4}{]^{{1 \over 2}}}, \cr} $](/articles/aa/full_html/2024/08/aa50246-24/aa50246-24-eq5.png) (5)
(5)
where 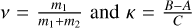 . We can use these frequencies to write an approximation for the true anomaly and libration angle over time. For example, the libration angle can be defined as
. We can use these frequencies to write an approximation for the true anomaly and libration angle over time. For example, the libration angle can be defined as
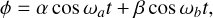 (6)
(6)
where α and β are scalars dependent on the physical parameters of the system. However, as seen in Fig. 3, this analytical definition diverges from the numerical solution after only a few days. Thus, for even moderate perturbations from the equilibrium, a linear approximation is inaccurate.
Despite this shortfall, the linearization suggests higher-order approximations will be more accurate in describing the motion within the system. This shows a possible path toward obtaining an analytic averaged expression for the apsidal precession rate in elongated systems. However, even the substitution of the linearized approximation into Eq. (3) yields an unwieldy expression containing embedded trigonometric functions, and the derivation is beyond the topic of this work. Thus, we used a numerical approach, leaving a potential derivation of an accurate, analytically averaged expression to future work.
For a purely analytical approach, we turned to a separate expression for the apsidal precession rate, derived in Jacobson (2010). This model also includes the effects of secondary elongation and libration, but only considers the forced libration within the system. The benefit of reducing the model to only incorporating the forced libration is the relationship between ϕ and f becomes much simpler, and we can average over 1 orbit period. However, unfortunately we cannot use this equation when free libration is present in the system.
For now, we restricted our dynamics to perfectly planar, so the angular momentum of the secondary and orbit are aligned. Because we do not analytically solve Eq. (3), we used our dynamical model to calculate the orbital elements and the libra-tion angle. We approximated the apsidal precession rate using a linear fit of the numerically obtained longitude of periapsis. In our dynamics, we started the secondary aligned with the primary (ϕ(0) = 0°) and perturbed the velocity to add a small amount of eccentricity to the system. This is similar to the effect of the DART impact in the Didymos binary asteroid system. We tested different initial values of 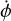 by adding a spin perturbation,
by adding a spin perturbation, 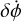 , away from the unperturbed secondary spin rate.
, away from the unperturbed secondary spin rate.
 |
Fig. 2 Panel a: the libration as a function of the true anomaly. Panel b: the separation as a function of the libration. Panel c: the semimajor axis as a function of the libration. Panel d: the eccentricity as a function of the libration. This illustrates the complicated relationships between these quantities, in particular the importance of the libration angle. |
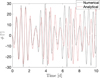 |
Fig. 3 Time history of the libration angle. The analytical definition diverges from the numerical solution after a few days. |
4 Numerical approach
We used a Didymos-like system to investigate how the apsi-dal precession rate depends on the system parameters. From the orbital fit derived in Naidu et al. (2024), we started our system in a mutual circular orbit with a separation distance of r = 1.19 km. The secondary has a volume-equivalent diameter of 150 m, with semiaxes a > b > c determined by a/b = 1.3 and b/c = 1.1. We assumed an equal uniform density of 2.8 g cm−3 between the primary and secondary, and a primary diameter of 710 m. The system equilibrium orbit rate, 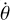 , was calculated using the expression derived in Scheeres (2009):
, was calculated using the expression derived in Scheeres (2009):
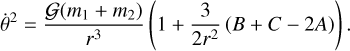 (7)
(7)
We set the secondary spin rate equal to this orbit rate for the equilibrium state.
We applied a Δv of −3 mm s−1 to the secondary (tangential and retrograde to the orbital motion), similar to the value caused by the DART impact (Cheng et al. 2023; Naidu et al. 2024). Along with this velocity perturbation, we also applied a perturbation to the secondary’s spin rate, 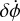 , which again is consistent with the results in Naidu et al. (2024), who estimate a spin perturbation to Dimorphos. We then integrated the system forward in time for 60 days and calculated the precession rate by linearly fitting to the secular drift in the longitude of periapsis over this time.
, which again is consistent with the results in Naidu et al. (2024), who estimate a spin perturbation to Dimorphos. We then integrated the system forward in time for 60 days and calculated the precession rate by linearly fitting to the secular drift in the longitude of periapsis over this time.
Figure 4 shows the results of these simulations. Panel a plots the precession rate as a function of the spin perturbation, while panel b shows the precession rate as a function of the libration amplitude Φ. The relationship between the libration amplitude and the spin perturbation is shown in panel c. Finally, panel d shows the eccentricity as a function of the spin perturbation. This demonstrates how the precession rate does depend on the secondary’s spin, and is not only driven by the changing eccentricity.
From Fig. 4, we see that there is a critical spin perturbation that results in the largest apsidal regression rate. This occurs at the perturbation that minimizes the libration amplitude, meaning that this is the secondary spin rate which eliminates the free libration and leaves only the forced libration. Increasing libration amplitude, or equivalently perturbing the secondary spin away from this value, results in decreasing the apsidal regression rate (increasing the precession rate closer to zero). We also see how the secondary’s spin perturbation has a small effect on the eccentricity. Increasing the secondary’s spin rate results in a higher eccentricity.
In Fig. 4, we see some discontinuities in the precession rate for a spin perturbation around 16° h−1, and to a lesser extent also around −6° h−1. These appear to be due to a resonance between the average orbit period and the average secondary spin period, but they only have a small effect on the dynamics.
Next we compared these results with the analytic equations for apsidal precession rate. To calculate the precession rate using Eq. (3), we integrated our equations of motion to get a time history for true anomaly and libration angle, then averaged the time history of 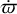 to determine an average apsidal precession rate. For the forced libration model in Jacobson (2010), we calculated the libration amplitude as the maximum libration angle.
to determine an average apsidal precession rate. For the forced libration model in Jacobson (2010), we calculated the libration amplitude as the maximum libration angle.
The comparison between these three approaches is shown in Fig. 5. We see excellent agreement when averaging Eq. (3). The forced libration solution from Jacobson (2010) diverges sharply from the numerical solution. This is expected, since this equation only considers the forced libration. When the numerical solution only has forced libration, then the model in Jacobson (2010) matches the numerical solution closely. In this system, a spin perturbation around 7° h−1 eliminates free libration from the system, only leaving the forced libration. Around this point, all three models have a close match for the precession rate.
 |
Fig. 4 Panel a: the precession rate as a function of the spin perturbation. Panel b: the precession rate as a function of the libration amplitude. Panel c: the libration amplitude as a function of the spin perturbation. Panel d: the eccentricity as a function of the spin perturbation. |
5 Application to Didymos
Next, we applied this analysis to the Didymos system. Using the estimated apsidal precession rate (Naidu et al. 2024), we were able to place constraints on the secondary shape and libration.
We now included the oblateness of the primary, which for Didy-mos is estimated to be J2 = 0·09 (Naidu et al. 2024). The estimated apsidal precession rate in Didymos is  . The separation of the orbit at the time of the DART impact was 1.189 km, and we assumed Dimorphos was in a circular orbit about Didymos prior to the perturbation. We also fixed the Dimorphos b/c = 1.2.
. The separation of the orbit at the time of the DART impact was 1.189 km, and we assumed Dimorphos was in a circular orbit about Didymos prior to the perturbation. We also fixed the Dimorphos b/c = 1.2.
In our algorithm, we iterated a tangential and instantaneous Δv on the orbital speed of Dimorphos until our post-impact system matches the measured post-DART orbital period of 11.37 h. Once this was achieved, we performed a second iteration to the secondary’s rotation rate: we added a 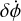 to correctly achieve the estimated apsidal precession rate.
to correctly achieve the estimated apsidal precession rate.
In this work, we are exploring the relationship between the secondary shape and spin and the orbit’s apsidal precession rate. As a result, we do not account for uncertainties in the size of the two asteroids or in the separation distance at the time of impact. The mass of the asteroids are calculated by inverting Eq. (7) using the pre-impact orbit period of 11.92 h, and assuming equal and uniform densities between Didymos and Dimorphos.
In the system dynamics, the secular apsidal rate is governed by the oblateness of Didymos and Dimorphos, as well as the prolateness of Dimorphos (assuming Didymos to be axially symmetric). The effect of the oblateness is a classical and well-understood result. In this work, we focus only on the role of the prolateness.
In Fig. 6a, we plot curves that represent combinations of secondary elongation and spin perturbation that replicate the apsidal precession rate in Didymos. In Fig. 6b, we plot the same curves but for libration amplitude. For a given Dimorphos C22, or equiv-alently an a/b value, there are two values of spin perturbation, 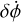 , that can reproduce the observed precession rate. Thus, some knowledge of the perturbation’s geometry is required to resolve the ambiguity between the two curves. For the geometry of the DART impact, we likely have a negative value of
, that can reproduce the observed precession rate. Thus, some knowledge of the perturbation’s geometry is required to resolve the ambiguity between the two curves. For the geometry of the DART impact, we likely have a negative value of 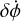 (Naidu et al. 2024), corresponding to the lower of the two curves in Figs. 6a and 6b.
(Naidu et al. 2024), corresponding to the lower of the two curves in Figs. 6a and 6b.
These curves demonstrate that for the nominal system (ignoring uncertainties on the shape of Didymos and the orbit geometry), we are required to have an a/b > 1.25, equivalent to having C22 ≳ 0.018. This is a purely dynamical constraint indicating likely significant reshaping in Dimorphos as a result of the DART impact, which complements the physical argument for the same phenomenon by Raducan et al. (2024). This is also consistent with the estimation of the system parameters by Naidu et al. (2024).
However, we only used the nominal system parameters. In reality, smaller values of a/b are permitted, for example if the primary’s J2 term is in reality smaller than the best estimate. Taking into account all uncertainties, it is possible for the pre-impact and post-impact shape of Dimorphos to be essentially the same and still produce the measured precession rate. However, this case requires extreme values for the Didymos J2 and the separation distance, which is a fringe case. Thus, we argue it is very likely Dimorphos experienced some degree of reshaping, with its new shape more elongated than the pre-impact shape.
We can also use this approach to investigate the allowable libration amplitude in the system. Here we see uniformly increasing libration amplitude with increasing C22. The minimum C22 results in a libration amplitude of around 10°, indicating the nominal system has at least this libration amplitude. Again, smaller values are permissible given the uncertainties in the system, but most combinations of parameters will result in a libration amplitude larger than this value.
As we have already seen, the eccentricity is also affected by the spin perturbation. In Fig. 6c, we see increasing eccentricity with increasing 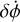 . This illustrates the spin-orbit coupling inherent to binary asteroids: as the angular momentum of the secondary changes, this is reflected in the angular momentum of the orbit as well.
. This illustrates the spin-orbit coupling inherent to binary asteroids: as the angular momentum of the secondary changes, this is reflected in the angular momentum of the orbit as well.
 |
Fig. 5 Comparison between the numerically calculated apsidal precession rate and the analytic expressions. The Cuk model corresponds to Eq. (3), and the Jacobson model corresponds to the result in Jacobson (2010). |
6 Out-of-plane rotation
Next we examined the role played by out-of-plane rotation on the orbital precession. We recall that our dynamical model permits out-of-plane rotation by the secondary. It has been well established that resonances within the binary asteroid system can induce attitude instabilities in the secondary (Agrusa et al. 2021). Typically, the attitude of the secondary is reported as a set of 1–2–3 Euler angles corresponding to its roll, pitch, and yaw, relative to a rotating hill frame (Meyer & Scheeres 2021; Agrusa et al. 2021; Richardson et al. 2022), and we adopted this convention as well.
We are interested in how the apsidal precession rate is affected by NPA rotation, particularly applied to Didymos. Thus, we kept the algorithm as described in Sect. 5, but now also perturbed the secondary’s out-of-plane rotation. When we calculated the spin perturbation about the major principal axis to achieve the estimated precession rate in the planar case, we applied an additional perturbation no larger than this value to the other axes as well.
In their work, Pravec et al. (2024) break up NPA rotation of the binary secondary into three regimes: No tumbling, epicyclic tumbling, and constant tumbling. We show an example from each of these regimes, demonstrating the effect of NPA rotation on the apsidal precession rate.
When NPA rotation is very minimal, we essentially have no tumbling in the secondary. In this regime, the out-of-plane Euler angles are small and quasiperiodic, and the system behaves nearly identically to principal axis rotation. An example of NPA rotation with no tumbling is shown in Fig. 7. We see generally well-behaved dynamics. The NPA rotation is small, and as a result we see nearly constant semimajor axis and eccentricity, and an on-average constant apsidal precession.
Figure 7 also shows the power spectrum of e cos ϖ. We see the influence of the natural frequencies (now also including the two additional natural frequencies from Fahnestock & Scheeres 2008). Beating between these natural frequencies is also important as illustrated in Fig. 7. The dominance of these natural frequencies within the power spectrum indicates the motion is still quasiperiodic despite the presence of NPA rotation in the no tumbling regime. If high fidelity measurements are able to detect these frequencies within the data, they can provide information about the physical parameters of the system.
In epicyclic tumbling, the dynamics become more complicated as out-of-plane rotation angles can become large, and the secondary frequently enters the barrel instability (Ćuk et al. 2021). However, generally the secondary remains on-average synchronous, where its long axis points toward or away from the primary. In this regime, the libration amplitude varies as angular momentum is exchanged between the secondary and the orbit, and as a result the apsidal precession rate can vary as well. An example of epicyclic tumbling is shown in Fig. 8. The barrel instability begins around 20 days into the simulation and is shown by a “flipping” of the roll angle. As angular momentum is exchanged between the secondary and orbit, we see a corresponding drop in eccentricity, as explained in Meyer et al. (2023). The semimajor axis sees a small amount of variation, and the apsidal precession rate can fluctuate significantly away from the average rate, even reversing occasionally. Since the eccentricity is not constant, we see corresponding changes to the apsidal precession rate as expected.
The power spectrum for epicyclic tumbling is also shown in Fig. 8. Now we see the loss of prominence for the natural frequencies within the system, with the exception of the mean motion. Thus, the motion in epicyclic tumbling is no longer quasiperiodic and becomes chaotic. Connecting the frequencies to physical parameters in the system becomes impossible once tumbling has begun.
Finally, Pravec et al. (2024) define constant tumbling as a fully asynchronous chaotic rotation of the secondary. An example of this is shown in Fig. 9. Here we see no real structure to the Euler angles, and all three have significant amplitudes. This corresponds to fully chaotic secondary rotation. The semimajor axis sees more variation, along with the eccentricity. Interestingly, the longitude of periapsis does not have much of a secular drift, but varies with the eccentricity. Again, the power spectrum in Fig. 9 reveals chaotic motion within the system, as the natural frequencies do not have a strong influence on the power spectrum outside the mean motion.
From these examples, it is evident that NPA rotation of the secondary has a substantial impact on the apsidal precession of the orbit. While rotation within the no tumbling regime does not have much of an effect, epicyclic tumbling can cause significant departures from the expected precession rate, and constant tumbling can destroy this secular drift altogether. Thus, the extant estimate of Didymos’s precession rate over the first ~70 days after the DART impact suggests Dimorphos was in planar rotation during this time period. However, after this time, NPA rotation is likely as detailed in Pravec et al. (2024).
 |
Fig. 6 Panel a: the required spin perturbation as a function of pro-lateness necessary to reach the measured precession rate. Panel b: the required libration amplitude as a function of the Dimorphos prolateness. Panel c: the resulting eccentricity as a function of the spin perturbation at the measured precession rate. |
 |
Fig. 7 Illustration of no tumbling in NPA rotation (stable), characterized by small out-of-plane Euler angles seen, a constant precession rate, and relatively constant eccentricity. The power spectrum shows the influence of the natural frequencies, as well as several beating frequencies. This demonstrates the motion is quasiperiodic. |
 |
Fig. 8 Illustration of epicyclic tumbling in NPA rotation (synchronous tumbling), characterized by large out-of-plane Euler angles with θ3 rotating around 0 or 180°, occasional rapid increases in the precession rate, and rapid changes in the eccentricity. The power spectrum shows the motion is no longer quasiperiodic, as the natural frequencies no longer dominate. |
 |
Fig. 9 Illustration of constant tumbling in NPA rotation (chaotic tumbling) characterized by large and uncorrelated out-of-plane Euler angles and relatively constant precession rates and eccentricities. The power spectrum shows the motion is no longer quasiperiodic, as the natural frequencies no longer dominate. |
7 Discussion
In this work, we have investigated the role played by the secondary in the secular evolution of the orbit in a binary asteroid. The apsidal precession rate of the orbit is driven by the elongation and spin rate of the secondary, as well as the orbit geometry and mean motion. Thus, unravelling the relationship between observations of the apsidal precession rate and the physical system parameters is a complicated problem and we are limited to numerical investigation.
We find a critical spin rate of the secondary results in eliminating free libration in the system. This is an expected result, but has not been investigated in binary asteroids previously. This critical spin rate places restrictions on the physical parameters of the system given an estimated precession rate. For the nominal estimates of primary J2, separation distance, and apsidal precession rate in Didymos after the DART impact, we can constrain Dimorphos’s elongation to a/b ≳ 1.25, with a corresponding minimum libration amplitude of about 10°. Furthermore, a negative spin perturbation serves to decrease the eccentricity of the orbit after the DART impact. This can explain the difference between the eccentricity estimates obtained by Meyer et al. (2023) who did not account for this parameter and the smaller estimate given in Naidu et al. (2024).
Our constraint on Dimorphos’s nominal elongation is more restrictive than the values obtained in the analysis by Pravec et al. (2024), who find possible secondary elongations as low as a/b = 1.1 . In this work, we only focused on the nominal system parameters, and did not account for uncertainties in the orbit semimajor axis, Didymos J2, the apsidal precession rate, or Dimorphos b/c. Thus, smaller elongations and libration amplitudes are in reality possible when accounting for uncertainty in J2 and the semimajor axis. However, we are mainly concerned with unravelling the relationship between different observable parameters within the binary asteroid. But from the nominal system parameters, we expect significant reshaping in Dimorphos, consistent with results obtained from impact simulations (Raducan et al. 2024). These results are also all consistent with the best fit of the post-impact dynamical state of Didymos obtained by Naidu et al. (2024).
Given the dynamically coupled nature of binary asteroids, NPA rotation in the secondary can also affect the orbital precession rate. While a small amount of NPA rotation does not have an appreciable effect, larger amplitudes of out-of-plane rotation can remove the secular trend in the longitude of periapsis altogether. Power spectrum decompositions of our simulations demonstrate that if a system is not tumbling, the natural frequencies within the system dominate and we can use these to constrain the physical parameters within the system. For Didy-mos, this is how we are able to argue reshaping has occurred in Dimorphos. However, once NPA rotation becomes significant the natural frequencies within the data no longer drive the evolution of the system. The benefit of this is that the loss of these signals indicates the presence of tumbling in the secondary. Thus, the loss of the precession signal around 70 days after the DART impact as reported in Scheirich et al. (2024) is an indication of tumbling in Dimorphos. Unfortunately, this means leveraging the natural frequencies or precession period becomes impossible once tumbling has begun.
So far, we have only used the apsidal precession signal, but the direct detection of the natural frequencies could provide further constraints to the system. Unfortunately, these short-period frequencies are difficult to detect, and could possibly be dominated by the mean motion. It would require very high quality data to detect and separate these frequencies, likely impossible using ground-based observations.
We have demonstrated that the apsidal precession rate is an important observable within binary asteroids that can help constrain the physical parameters of the system. However, the relationship between these is complicated and can be ambiguous. There are a range of combinations between J2, a/b, b/c, and 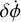 that can produce a measured precession rate. Furthermore, the problem is made more complicated by the presence of NPA rotation, which can have a significant effect on the orbital precession rate.
that can produce a measured precession rate. Furthermore, the problem is made more complicated by the presence of NPA rotation, which can have a significant effect on the orbital precession rate.
8 Conclusion
We have investigated how the physical and dynamical properties of a binary asteroid secondary affect the apsidal precession rate of its mutual orbit. Due to complex relationships in these spin-orbit-coupled systems, we relied primarily on numerical simulations. They demonstrate how spin perturbations to the secondary have a significant effect on the precession rate. When applied to Didymos and the DART impact, we find a lower limit on the possible elongation of Dimorphos that is consistent with the estimated precession rate, suggesting a significant reshaping of the asteroid. This places constraints on the post-impact shape and spin state of the secondary, suggesting the libration amplitude is likely larger than 10°. Finally, we find that NPA rotation in the secondary has a major impact on the orbit’s precession rate.
References
- Agrusa, H. F., Gkolias, I., Tsiganis, K., et al. 2021, Icarus, 370, 114624 [NASA ADS] [CrossRef] [Google Scholar]
- Borderies, N., & Yoder, C. 1990, A&A, 233, 235 [NASA ADS] [Google Scholar]
- Borderies-Rappaport, N., & Longaretti, P.-Y. 1994, Icarus, 107, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A. 1976, Am. J. Phys., 44, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A. 1977, Am. J. Phys., 45, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, A. F., Agrusa, H. F., Barbee, B. W., et al. 2023, Nature, 616, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Ćuk, M., & Nesvornỳ, D. 2010, Icarus, 207, 732 [CrossRef] [Google Scholar]
- Ćuk, M., Jacobson, S. A., & Walsh, K. J. 2021, Planet. Sci. J., 2, 231 [CrossRef] [Google Scholar]
- Fahnestock, E. G., & Scheeres, D. J. 2008, Icarus, 194, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, R. 2010, AJ, 139, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, A. J., & Scheeres, D. J. 2021, Icarus, 367, 114554 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, A. J., Gkolias, I., Gaitanas, M., et al. 2021, Planet. Sci. J., 2, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, A. J., Agrusa, H. F., Richardson, D. C., et al. 2023, Planet. Sci. J., 4, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge University Press) [Google Scholar]
- Naidu, S. P., Chesley, S. R., Moskovitz, N., et al. 2024, Planet. Sci. J., 5, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Meyer, A. J., Scheirich, P., et al. 2024, Icarus, submitted [Google Scholar]
- Raducan, S., Jutzi, M., Cheng, A., et al. 2024, Nat. Astron., 1 [Google Scholar]
- Richardson, D. C., Agrusa, H. F., Barbee, B., et al. 2022, Planet. Sci. J., 3, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Schaub, H., & Junkins, J. L. 2003, Analytical Mechanics of Space Systems (AIAA) [CrossRef] [Google Scholar]
- Scheeres, D. J. 2006, Celest. Mech. Dyn. Astron., 94, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J. 2009, Celest. Mech. Dyn. Astron., 104, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Scheirich, P., Pravec, P., Meyer, A. J., et al. 2024, Planet. Sci. J., 5, 17 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Diagram of our dynamical model, the sphere-restricted full two-body problem. This shows the relative position and angular velocity vectors centered in the secondary’s body-fixed frame. The libration angle is labeled. |
| In the text | |
 |
Fig. 2 Panel a: the libration as a function of the true anomaly. Panel b: the separation as a function of the libration. Panel c: the semimajor axis as a function of the libration. Panel d: the eccentricity as a function of the libration. This illustrates the complicated relationships between these quantities, in particular the importance of the libration angle. |
| In the text | |
 |
Fig. 3 Time history of the libration angle. The analytical definition diverges from the numerical solution after a few days. |
| In the text | |
 |
Fig. 4 Panel a: the precession rate as a function of the spin perturbation. Panel b: the precession rate as a function of the libration amplitude. Panel c: the libration amplitude as a function of the spin perturbation. Panel d: the eccentricity as a function of the spin perturbation. |
| In the text | |
 |
Fig. 5 Comparison between the numerically calculated apsidal precession rate and the analytic expressions. The Cuk model corresponds to Eq. (3), and the Jacobson model corresponds to the result in Jacobson (2010). |
| In the text | |
 |
Fig. 6 Panel a: the required spin perturbation as a function of pro-lateness necessary to reach the measured precession rate. Panel b: the required libration amplitude as a function of the Dimorphos prolateness. Panel c: the resulting eccentricity as a function of the spin perturbation at the measured precession rate. |
| In the text | |
 |
Fig. 7 Illustration of no tumbling in NPA rotation (stable), characterized by small out-of-plane Euler angles seen, a constant precession rate, and relatively constant eccentricity. The power spectrum shows the influence of the natural frequencies, as well as several beating frequencies. This demonstrates the motion is quasiperiodic. |
| In the text | |
 |
Fig. 8 Illustration of epicyclic tumbling in NPA rotation (synchronous tumbling), characterized by large out-of-plane Euler angles with θ3 rotating around 0 or 180°, occasional rapid increases in the precession rate, and rapid changes in the eccentricity. The power spectrum shows the motion is no longer quasiperiodic, as the natural frequencies no longer dominate. |
| In the text | |
 |
Fig. 9 Illustration of constant tumbling in NPA rotation (chaotic tumbling) characterized by large and uncorrelated out-of-plane Euler angles and relatively constant precession rates and eccentricities. The power spectrum shows the motion is no longer quasiperiodic, as the natural frequencies no longer dominate. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


