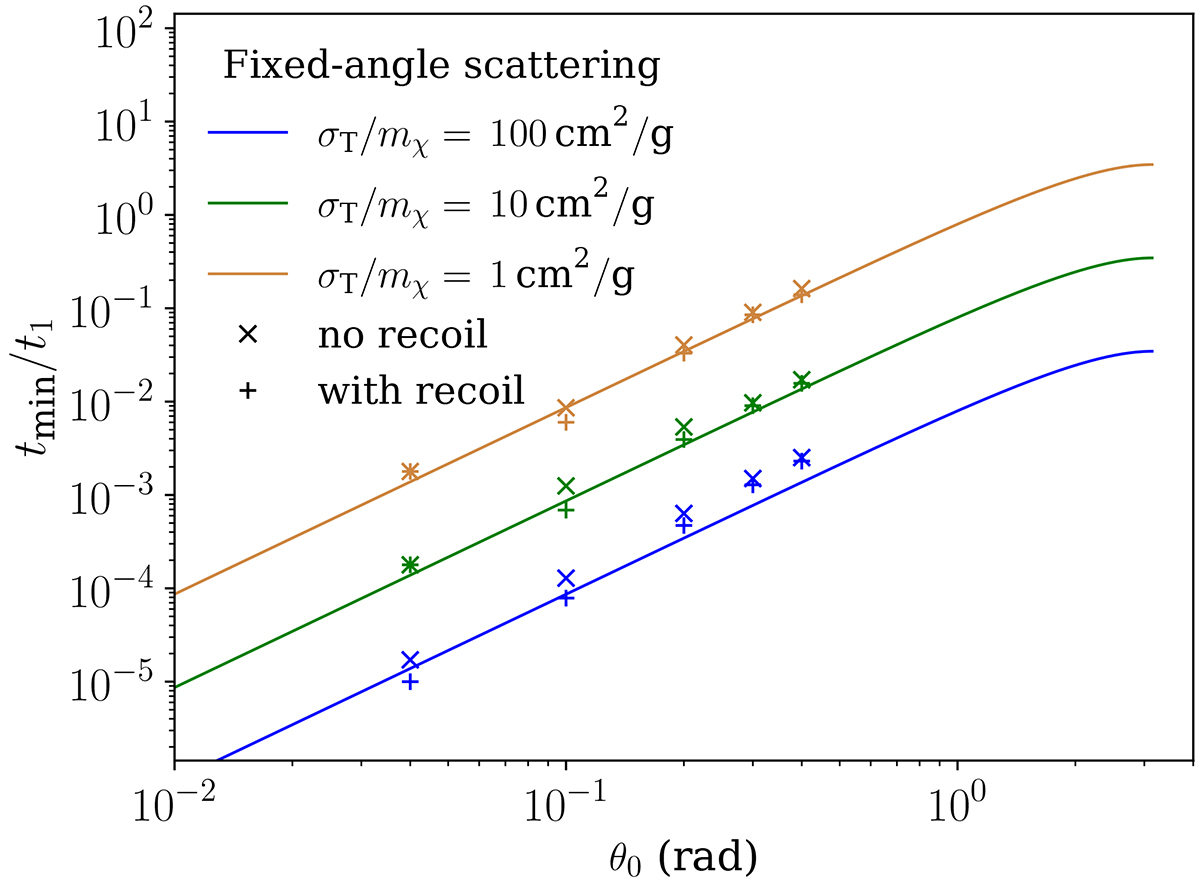
Validity check of the effective small-angle approach (fSIDM, scheme b) as compared to an explicit treatment of angle dependence (rSIDM, scheme c). Shown is the minimal timescale t_min after which the angular distributions obtained for the deflection test problem solved with the fSIDM and the rSIDM method agree with each other. Cross symbols show the numerically determined minimal agreement time t_min, for three values of σ_T/m_χ and for the set-up with and without recoil in beam-target scattering, respectively. Lines show the analytical prediction for t_min from Eq. (32). Here we assume a differential cross section for which all individual scatterings occur with a fixed angle θ₀ (shown on the x-axis). The numerically more efficient effective small-angle approach is advantageous if t_min is much smaller than the typical dynamical scale of the system, given by t_dyn = (1, 0.1, 0.01)⋅t₁ for σ_T/m_χ = (1, 10, 100) cm² g⁻¹, respectively. This is safely the case for scatterings with θ ≲ 1. Details on the fixed-angle scattering are presented in Appendix I.