| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 20 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201935042 | |
| Published online | 17 October 2019 | |
Inner dark matter distribution of the Cosmic Horseshoe (J1148+1930) with gravitational lensing and dynamics⋆
1
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Str. 1, 85741 Garching, Germany
e-mail: schuldt@mpa-garching.mpg.de
2
Physik Department, Technische Universität München, James-Franck Str. 1, 85741 Garching, Germany
e-mail: stefan.schuldt@tum.de
3
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of ASMAB, No.1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
4
Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
5
Kavli Institute for the Physics and Mathematics of the Universe, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 277-8583, Japan
6
Pyörrekuja 5 A, 04300 Tuusula, Finland
7
Sydney Institute for Astronomy, School of Physics, A28, The University of Sydney, Sydney, NSW 2006, Australia
Received:
10
January
2019
Accepted:
19
August
2019
We present a detailed analysis of the inner mass structure of the Cosmic Horseshoe (J1148+1930) strong gravitational lens system observed with the Hubble Space Telescope (HST) Wide Field Camera 3 (WFC3). In addition to the spectacular Einstein ring, this systems shows a radial arc. We obtained the redshift of the radial arc counterimage zs, r = 1.961 ± 0.001 from Gemini observations. To disentangle the dark and luminous matter, we considered three different profiles for the dark matter (DM) distribution: a power law profile, the Navarro, Frenk, and White (NFW) profile, and a generalized version of the NFW profile. For the luminous matter distribution, we based the model on the observed light distribution that is fitted with three components: a point mass for the central light component resembling an active galactic nucleus, and the remaining two extended light components scaled by a constant mass-to-light ratio (M/L). To constrain the model further, we included published velocity dispersion measurements of the lens galaxy and performed a self-consistent lensing and axisymmetric Jeans dynamical modeling. Our model fits well to the observations including the radial arc, independent of the DM profile. Depending on the DM profile, we get a DM fraction between 60% and 70%. With our composite mass model we find that the radial arc helps to constrain the inner DM distribution of the Cosmic Horseshoe independently of the DM profile.
Key words: gravitational lensing: strong / dark matter / Galaxy: structure / Galaxy: kinematics and dynamics / Galaxy: halo
The reduced spectrum is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A40
© S. Schuldt et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
In the standard cold dark matter (CDM) model, the structure of dark matter (DM) halos is well understood through large numerical simulations based only on gravity (e.g., Dubinski & Carlberg 1991; Navarro et al. 1996a,b; Ghigna et al. 2000; Diemand et al. 2005; Graham et al. 2006a; Gao et al. 2012). From these N-body DM only simulations it appears that halos are well described by the NFW profile (Navarro et al. 1997). This profile has characteristic slopes; it falls at large radii as ρr≫rs ∝ r−3, while, for small radii, it goes as ρr≪rs ∝ r−1 and thus forms a central density cusp. The so-called scale radius rs is the radius where the slope changes. Nowadays, simulations with higher resolution predict shallower behavior for the density slope at very small radii and thus a deviation from this simple profile (e.g., Golse & Kneib 2002; Graham et al. 2006b; Navarro et al. 2010; Gao et al. 2012). Thus, the distribution is more cored than cuspy (e.g., Collett et al. 2017; Dekel et al. 2017). These simulations also show that DM halos are not strictly self-similar as first expected for a CDM universe (e.g., Ryden 1991; Moutarde et al. 1995; Chuzhoy 2006; Lapi & Cavaliere 2011).
In realistic models for halos the baryonic component must be included and that modifies the distribution and the amount of dark matter. The distribution of stars, dark matter, and gas depends on processes such as gas cooling, which allows baryons to condense toward the center (e.g., Blumenthal et al. 1986; Gnedin et al. 2004; Sellwood & McGaugh 2005; Gustafsson et al. 2006; Pedrosa et al. 2009; Abadi et al. 2010; Sommer-Larsen & Limousin 2010), active galactic nuclei (AGNs) feedback (e.g., Peirani et al. 2008, 2017; Martizzi et al. 2013; Li et al. 2017), dynamical heating in the central cuspy region due to infalling satellites and mergers (e.g., El-Zant et al. 2001, 2004; Nipoti et al. 2004; Romano-Díaz et al. 2008; Tonini et al. 2006; Laporte & White 2015), and thermal and mechanical feedback from supernovae (e.g., Navarro et al. 1996b; Governato et al. 2010; Pontzen & Governato 2012).
Therefore, detailed observations of the mass distribution include important information of these complex baryonic processes. Of particular interest is the radial density profile of DM on small scales. In addition, at small radii we expect to have the densest regions of DM particles, therefore these regions are ideal to learn more about their interactions and nature (Spergel & Steinhardt 2000; Abazajian et al. 2001; Kaplinghat 2005; Peter et al. 2010).
Strong gravitational lensing has arisen as a good technique to obtain the mass distribution for a wide range of systems. Gravitational lensing provides a measurement of the total mass within the Einstein ring since the gravitational force is independent of the mass nature (e.g., Treu 2010; Treu & Ellis 2015). Dye & Warren (2005) showed that strong lens systems with a nearly full Einstein ring are better than those observations for which the source is lensed into multiple point-like images with the aim of constructing a composite profile of baryons and DM. With such observations, we can very well fit the profile near the region of the Einstein ring, but the inner part cannot be well constrained because of the typical absence of lensing data in the inner region. The presence of a radial arc, even though seldom observed in galaxy-scale lenses, can help break the lensing degeneracies and put constraints on the inner mass distribution. Another possibility is to combine lensing and dynamics, which is now a well-established probe to get for instance the density profile for early-type galaxies (ETGs; e.g., Mortlock & Webster 2000; Treu & Koopmans 2002, 2004; Gavazzi et al. 2007; Barnabè et al. 2009, 2011; Auger et al. 2010; van de Ven et al. 2010; Grillo et al. 2013).
In this paper, we present a detailed study of the inner mass structure of the Cosmic Horseshoe lens through lensing and combine these information with those coming from dynamical modeling. The Cosmic Horseshoe, discovered by Belokurov et al. (2007), is ideal for such a study. The huge amount of mass of the deflector galaxy results in a spectacular and large Einstein ring, and near the center of the lens a radial arc exists, which helps to constrain the mass distribution in the inner part of the Einstein ring. To include the radial arc and our association for its counterimage in the models, we have spectroscopy measurements for the counterimage to get its redshift.
The outline of the paper is as follows. In Sect. 2 we introduce the imaging and spectroscopic observations with their characteristics and describe the data reduction and redshift measurement for the radial arc counterimage. Then we revisit briefly in Sect. 3 the multiple-lens-plane theory. In Sect. 4 we present our results of the composite mass model of baryons and DM using lensing-only, while in Sect. 5 we present the results of our models based on dynamics-only. In Sect. 6 we combine lensing and dynamics and present our final models. Sect. 7 summarizes and concludes our results.
Throughout this work, we assume a flat ΛCDM cosmology with Hubble constant H0 = 72 km s−1 Mpc−1 (Bonvin et al. 2017) and ΩM = 1 − ΩΛ = 0.32 whose values correspond to the updated Planck data (Planck Collaboration XIII 2016). Unless specified otherwise, each quoted parameter estimate is the median of its 1D marginalized posterior probability density function, and the quoted uncertainties show the 16th and 84th percentiles (that is, the bounds of a 68% credible interval).
2. Cosmic Horseshoe (J1148+1930)
The Cosmic Horseshoe, also known as SDSS J1148+1930, was discovered by Belokurov et al. (2007) within the Sloan Digital Sky Survey (SDSS). A color image of this gravitational-lensed image is shown in Fig. 1. The center of the lens galaxy G, at a redshift of zd = 0.444, lies at (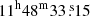 ;
; 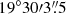 ) of the epoch J2000 (Belokurov et al. 2007). The tangential arc is a star-forming galaxy at redshift zs, t = 2.381 (Quider et al. 2009), which is strongly lensed into a nearly full Einstein ring (≈300°), whose radius is around 5″ and thus one of the largest Einstein rings observed up to now. This large size shows that this lens galaxy must be very massive. A first estimate of the enclosed mass within the Einstein ring is ≈5 × 1012 M⊙ (Dye et al. 2008) and thus the lens galaxy, a luminous red galaxy (LRG), is one of the most massive galaxies ever observed. Apart from the nearly full Einstein ring and the huge amount of mass within the Einstein ring, which already makes this observation unique, the Cosmic Horseshoe observations reveal a radial arc. This radial arc is in the west of the lens, as indicated in the green solid box in Fig. 1. We include this radial arc in our models as well as our association of its counterimage, delineated with a green dashed box in Fig. 1. We have Gemini measurements (see Sect. 2.2) to yield a redshift of zs, r = 1.961 ± 0.001 for this counterimage. A summary of various properties about the Cosmic Horseshoe is given in Table 1.
) of the epoch J2000 (Belokurov et al. 2007). The tangential arc is a star-forming galaxy at redshift zs, t = 2.381 (Quider et al. 2009), which is strongly lensed into a nearly full Einstein ring (≈300°), whose radius is around 5″ and thus one of the largest Einstein rings observed up to now. This large size shows that this lens galaxy must be very massive. A first estimate of the enclosed mass within the Einstein ring is ≈5 × 1012 M⊙ (Dye et al. 2008) and thus the lens galaxy, a luminous red galaxy (LRG), is one of the most massive galaxies ever observed. Apart from the nearly full Einstein ring and the huge amount of mass within the Einstein ring, which already makes this observation unique, the Cosmic Horseshoe observations reveal a radial arc. This radial arc is in the west of the lens, as indicated in the green solid box in Fig. 1. We include this radial arc in our models as well as our association of its counterimage, delineated with a green dashed box in Fig. 1. We have Gemini measurements (see Sect. 2.2) to yield a redshift of zs, r = 1.961 ± 0.001 for this counterimage. A summary of various properties about the Cosmic Horseshoe is given in Table 1.
 |
Fig. 1. Color image of the Cosmic Horseshoe obtained through a combination of the F475W, F606W, and F814W filter images from the HST WFC3. The size of this image is 20″ × 20″. We can see the ≈300° wide blue Einstein ring of the Cosmic Horseshoe. In addition, the Cosmic Horseshoe observation includes a radial arc that is indicated with a green solid box. This is shown in detail in the bottom panel, in color (left) and from the F475W filter (right). We associate this radial arc to its counterimage, indicated in the main figure with a dashed green box and located around 8″ on the east side of the lens galaxy G. Both the radial arc and its counterimage correspond to a source at redshift zs, r = 1.961 (see Sect. 2.2). The three star-like objects in the field of view, which we include in our light model, are circled in yellow. The figures are oriented such that north is up and east is left. |
Properties of the Cosmic Horseshoe (J1148+1930).
2.1. Hubble Space Telescope imaging
The data we analyse in this work come from the Hubble Space Telescope (HST) Wide Field Camera 3 (WFC3) and can be downloaded from the Mikulski Archive for Space Telescopes1. The observations with filters F475W, F606W, F814W, F110W, and F160W were obtained in May 2010 (PI: Sahar Allam) and the observations with the F275W filter in November 2011 (PI: Anna Quider).
We used HST DrizzlePac2 for the data reduction. The size of a pixel after reduction is 0.04″ for WFC3 UVIS (i.e., the F275W F475W, F814W, and F606W band) and 0.13″ for the WFC3 IR (i.e., the F160W and F110W band), respectively. The software includes a sky background subtraction. In our case the subtracted background appears to be overestimated since many of the pixels have negative value, possibly because of the presence of a very bright and saturated star in the lower right corner of the WFC3 field of view (≈160″ × 160″). Since negative intensity is unphysical and we fit the surface brightness (SB) of the pixels, we subtracted the median of an empty patch of sky that we picked to be around 25″ N-E to the Cosmic Horseshoe from all pixels of the reduced F160W band image. After our background correction, around 300 pixels (≈1.3% of the full cutout) of the corrected image still have negative values, which is consistent with the number given by background noise fluctuations. We proceeded in a similar way with the F475W band, where the number of negative pixel is still high but in the range of background fluctuations.
To align the images of the different filters we use in this paper, we modeled the light distribution of the star-like objects O2 and O3 (see Fig. 1) in the F475W band, masking out all the remaining light components (such as arc, lens and object O1). We did not include object O1 in the alignment since we did not model the light distribution of the lens in this band and the lens has significant flux in the region of O1 that could affect the light distribution of O1. From this model and our lens light model in the F160W band, which we present in Sect. 4.2.1, we get the coordinates of the centers of both objects in the two considered bands. Under the assumption these coordinates should match, we are able to align the F475W and F160W images.
2.2. Spectroscopy: redshift of the counterimage of radial arc
We obtained a spectrum of the counterimage to the radial arc using the Gemini Near-InfraRed Spectrograph (GNIRS; Elias et al. 2006) on the Gemini North Telescope (Program ID: GN-2012B-Q-42, PI Sonnenfeld). We chose the counterimage since the radial arc image is too faint to obtain a redshift directly. We used GNIRS in cross-dispersed mode with the 32 l mm grating, the short cross-dispersing (SXD) prism, the short blue camera (0.15″ pix), and a 7″ × 0.675″ slit. This configuration allowed us to achieve continuous spectral coverage in the range 9000−25 000 Å with a spectral resolution R ∼ 900. We obtained 18 × 300 s exposures, nodding along the slit with an ABBA template.
We reduced the data using the Gemini Image Reduction and Analysis Facility (IRAF) package. We identified two emission lines in the 2D spectrum, plotted in Fig. 2: these are Hα and [OIII] 5007 Å at a redshift zs, r = 1.961 ± 0.001. From here on, we take this to be the redshift of the radial arc and its counterimage.
 |
Fig. 2. Top (bottom): two-dimensional and 1D spectrum around the Hα ([OIII] 5007 Å) emission line from the counterimage to the radial arc, obtained from GNIRS observations. The 1D spectrum is extracted from a 5 pixel, corresponding to 0.75″, aperture around each line. The secondary peak redward of [OII] visible in the 1D spectrum is due to a cosmic ray that was not properly removed in the data reduction process. |
3. Multiplane lensing
In this work we employ multiplane gravitational lensing, given the presence of two sources at different redshifts (corresponding to the tangential and radial arcs, respectively). We therefore briefly revisit in this section the single plane and generalized multiplane gravitational lens formalism. In the single plane formalism a light ray of a background source is deflected by one single lens whereas in the multiplane case the same light ray is deflected several times by different deflectors at different redshifts (e.g., Blandford & Narayan 1986; Schneider et al. 2006; Gavazzi et al. 2008). The lens equation of the multiplane lens theory, which gives the relation between the angular position θj of a light ray in the jth lens plane and the angular position in the j = 1 plane, which is the observed image plane, is given by
where θN = β corresponds to the source plane if N is the number of planes, θk is the image position on the kth plane, 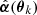 is the deflection angle on the kth plane, Dkj is the angular diameter distance between the kth and jth plane, and Dj is the angular diameter distance between us and the jth plane. The total deflection angle αtot is then the sum over all deflection angles on all planes
is the deflection angle on the kth plane, Dkj is the angular diameter distance between the kth and jth plane, and Dj is the angular diameter distance between us and the jth plane. The total deflection angle αtot is then the sum over all deflection angles on all planes
In the case of N = 2 the general formula reduces to the well-known lens equation for the single plane formalism, namely,
In this equation the only lens is at θ = θ1, the source at β = θ2, 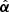 is the (total) deflection angle, and Dds, Ds, and Dd the distances between deflector (lens) and source, observer and source, and observer and deflector, respectively (e.g., Schneider et al. 2006).
is the (total) deflection angle, and Dds, Ds, and Dd the distances between deflector (lens) and source, observer and source, and observer and deflector, respectively (e.g., Schneider et al. 2006).
The magnification μ is in the multiplane formalism defined in the same way as in the single plane formalism, namely,
with the Jacobian matrix
For the surface mass density Σ(R) we need the convergence κ, sometimes also called the dimensionless surface mass density. In the single-lens plane case, the convergence is
where 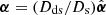 . This can then be multiplied with
. This can then be multiplied with
to derive Σ(R) using the definition of convergence
We can then compute the average surface mass density with the formula
These general equations hold in the single plane case, but for the multiplane case we define similar, so-called effective, quantities. To calculate the effective convergence κeff we replace in Eq. (6) the deflection angle α with the total deflection angle αtot from Eq. (2). In analogy to the case above we compute the effective average surface mass density Σeff(<R), now using κeff instead of κ. The consequence is that this quantity Σeff(<R) is the gradient of the total deflection angle αtot instead of a physical surface density.
4. Lens mass models
Since the position of an observed gravitationally lensed image depends on both baryonic and DM, we can use gravitational lensing as a probe for the total mass, i.e., baryonic and DM together. We started with a model of the lensed source positions, i.e., SB peaks in the observed Einstein ring, with a single power law plus external shear for the total mass. In addition to the main arc, which is the tangential arc, this model includes the radial arc and its counterimage and is presented in Sect. 4.1. Based on this, we constructed a composite mass model to describe the total mass. To disentangle the visible (baryonic) matter from the DM, we modeled the lens light distribution (see Sect. 4.2.1), which is then scaled by a constant mass-to-light ratio, M/L, for the baryonic mass. Combining the total mass and the baryonic mass, as described in Sect. 4.2.2, we constructed a composite mass model of baryons and DM assuming a power law (Barkana 1998), a NFW profile (Navarro et al. 1997), or a generalized NFW profile for DM distribution. We then used a model based on the full HST images (Sect. 4.3) to refine our image positions (Sect. 4.4). In these models we always include the radial arc and our assumption for its counterimage. In the last section with the redefined image positions we explicited treat models with and without the radial arc as constraints. This allows us to quantify the additional constraint on the inner DM distribution of the Cosmic Horseshoe from the radial arc, which is the primary goal of this paper.
For the modeling, we used Gravitational Lens Efficient Explorer (GLEE), a gravitational lensing software developed by Suyu & Halkola (2010) and Suyu et al. (2012). This software contains several types of lens and light profiles and uses Bayesian analysis such as simulated annealing and Markov Chain Monte Carlo (MCMC) to infer the parameter values of the profiles. The software also employs the EMCEE package developed by Foreman-Mackey et al. (2013) for sampling the model parameters.
4.1. Power law model for total mass distribution
In this section, we consider a simple power law model for the total lens mass distribution, which has been shown by previous studies to describe well the observed tangential arc (e.g., Chae et al. 1998; Keeton 2001; Belokurov et al. 2007; Dye et al. 2008; Quider et al. 2009; Bellagamba et al. 2017). This allows us to compare our model, which includes the radial arc, with previous models. We visually identified and used as constraints six sets of multiple image positions, where each set comes from a distinct source component. For modeling the lensed source positions, we chose the image of the F475W band, since we can distinguish better between the different parts of the Einstein ring and since the arc is bluer than the lens galaxy. This is an indicator that the lens galaxy is fainter and therefore we can better identify multiple images in F475W. We used a singular power law elliptical mass distribution (SPEMD; Barkana 1998) with slope γ′ = 2g + 1 for the lens (where the convergence κ(θ)∝θγ′ − 1) with an external shear. We infer the best-fit parameters of this model by minimizing
with GLEE. In this equation, Npt is the number of data points, 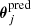 the predicted, and
the predicted, and 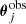 the observed image position, where σj is the corresponding uncertainty of point j.
the observed image position, where σj is the corresponding uncertainty of point j.
This model contains six sets of multiple images in addition to the radial arc and its counterimage (see Fig. 6 with refined identifications that are described in Sect. 4.4). This model has a χ2 of 12.6 for the image positions and the best-fit parameter and median values with 1σ uncertainties are given in Table 2. The obtained marginalized and best-fit values for the total mass model are in agreement with models from previous studies (e.g., Dye et al. 2008; Spiniello et al. 2011). The external shear is relatively high and might be due to the nearby cluster RMJ114847.5+193115.1 (Rykoff et al. 2014). From the number of known members, which might include the Cosmic Horseshoe lens galaxy, we infer a mass of a few times 1014 M⊙ (Murata et al. 2018). We estimate the corresponding peculiar velocity for the Cosmic Horseshoe lens as approximately 1200 km s−1, which is consistent with typical peculiar velocities in a cluster (Harrison 1974). Dye et al. (2008) already mentioned a loose cluster but assume a relatively small influence to the Cosmic Horseshoe configuration.
Best-fit and marginalized parameter values for the model assuming a power law profile plus external shear.
4.2. Components for composite mass model
Since the light deflection depends on both the baryonic and dark matter, we can construct a composite mass model. For the baryonic component, we need a model of the lens light to scale it by a M/L (Sect. 4.2.1). Since we do not have other information to infer the DM component, we fit to the data using different types of mass profiles (Sect. 4.2.2).
4.2.1. Lens light distribution for baryonic mass
To disentangle the baryonic matter from the DM, we need a model of the lens light distribution. For this we masked out all flux from other components such as stars and the Einstein ring in the image of the F160W filter. We then fit the parameters to the observed intensity value by minimizing the 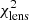 , which is defined as
, which is defined as
In this equation, Np is the number of pixels; σtot, j the total noise, i.e., background and Poisson noise (see below for details), of pixel j; and ⊗ represents the convolution of the point spread function (PSF) and the predicted intensity. It is necessary to take the convolution with the PSF into account because of telescope effects. We used a normalized bright star ≈40″ S-W of the Cosmic Horseshoe lens as the PSF. We also subtracted from the PSF a constant to counterbalance the background coming from a very bright object in the field of view, which scatters light over the image.
We approximated the background noise σbkgd as a constant that is set to the standard deviation computed from an empty region. We also included the contribution of the astrophysical Poisson noise (Hasinoff 2012), which is expressed as a count rate for pixel i
where ti is the exposure time, di the observed intensity of pixel i (in e−-counts per second), and 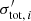 is the total Poisson noise (labeled with an apostrophe as it is not a rate like σpoisson, i). We only included the contribution of the astrophysical Poisson noise if it is larger than the background noise. We summed the background noise and astrophysical noise in quadrature such that
is the total Poisson noise (labeled with an apostrophe as it is not a rate like σpoisson, i). We only included the contribution of the astrophysical Poisson noise if it is larger than the background noise. We summed the background noise and astrophysical noise in quadrature such that 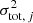 in Eq. (11) is
in Eq. (11) is
Sersic. To describe the SB of the Cosmic Horseshoe lens galaxy, we used the commonly adopted Sersic profile (Sérsic 1963), which is the generalization of the de Vaucouleurs law (also called r1/4 profile, De Vaucouleurs 1948). To model the lens light distribution, we chose the observation in the F160W band, since the lens is brighter in F160W than in the other bands and infrared bands trace better the stellar mass of the lens galaxy.
The best-fit model obtained by using two Sersic profiles and two stellar profiles (in this model we included two star-like objects, labeled object O1 and object O2 in Fig. 1) has χ2 = 2.73 × 104 (corresponding to a reduced χ2 of 1.74).
Chameleon. In addition to our lens light distribution model with the Sersic profile, we also modeled with another type of profile that mimics the Sersic profile well and allows analytic computations of lensing quantities (e.g., Maller et al. 2000; Dutton et al. 2011; Suyu et al. 2014). It is often called chameleon and is composed by a difference of two isothermal profiles, i.e.,
In this equation, qL is the axis ratio and wt and wc are parameters of the profile with wt > wc to keep L > 0.
By modeling with the chameleon profile we assumed the same background noise as using the Sersic profile (see Sect. 4.2.1). The model including two isothermal profile sets and two stellar profiles for the two objects, as used above with the Sersic profile, has a χ2 of around two times the Sersic χ2. Therefore, we added a third chameleon profile and get a χ2 of 2.89 × 104, which corresponds to a reduced χ2 of 1.85. In this model we also included objects O1, O2, and O3 (numbering follows Fig. 1), since we want to use the coordinates for the alignment of the two considered bands, F160W and F475W.
We use both filters in the extended source modeling (see Sect. 4.3) while in the models using identified image positions we only use the F160W band for the lens light fitting. The parameter values of this best-fit model are used for the mass modeling (given in Table 3) and the corresponding image is shown in Fig. 3. The left image shows the observed intensity and the middle image shows the modeled intensity. In the right panel we can see the normalized residuals of this model in a range (−7σ, +7σ). The constant gray regions are the masked-out areas (containing lensed arcs and neighboring galaxies) in order to fit only to the flux of the lens. Although there are significant image residuals visible in the right panel, the typical baryonic mass residuals (corresponding to the light residuals scaled by M/L) would lead to a change in the deflection angle that is smaller than the image pixel size of 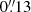 at the locations of the radial arc.
at the locations of the radial arc.
Best-fit and marginalized parameter values for the lens light component of the mass model obtained by reconstructing the source SB.
 |
Fig. 3. Best-fit model for the lens light distribution. Left image: observation of the Cosmic Horseshoe in the F160W band, whereas central panel: predicted light distribution. This model includes three chameleon profiles (see Eq. (14)), two PSF profiles, and one de Vaucouleurs profile for the three objects. The right image shows, in the range between −7σ and +7σ, the normalized residuals of this model. The constant gray regions are the masked-out areas (containing lensed arcs and neighboring galaxies) to fit only to the flux of the lens The figures are oriented such that north is up and east is left. |
In Fig. 4 we show the contributions of the different components, plotted along the x-axis of the cutout in units of solar luminosities for comparison of the contribution of the different light profiles. To compare those component widths to that of the PSF, in the same figure we show the latter (black dotted line) scaled to the lens light of the central component (plotted in red).
 |
Fig. 4. Left: different components of the chameleon profiles shown in units of solar luminosity in red (“inner”), blue (“medium”), and green (“outer” component), respectively. The total light observed from the Cosmic Horseshoe lens galaxy in the HST filter F160W is described by the sum of all three components. To compare the width of the components, scaled PSF is plotted with a black dotted line. Right: radially averaged total light of the model (red) and observed (blue) in solar luminosities, plotted as a function of radius. The Einstein radius is indicated with the black dotted line and the vertical gray band marks the range with substantial light from the lensed arcs. |
To convert the fitted light distribution into the baryonic mass, we assumed at first a constant M/L. This means we scaled all three light components by the same M/L value. Additionally, we explored models with different M/L values for the different components, either two ratios with M/Lcentral = M/Lmedium or M/Lmedium = M/Louter and the remaining different, or with three different M/L values, namely, one for each component. These baryonic mass models are considered in the Sects. 4.3 and 4.4.1. Furthermore, since the width of the central component, shown in red in Fig 4, is comparably to the width of the PSF, and based on our modeling results in Sect. 4.4.1, we model in Sect. 6 this central component by a point mass with Einstein radius described by
where the Einstein radius is defined for a source at redshift infinity, superseding the model that scales the central component with an M/L. The value G is the gravitational constant, M the point mass, c the speed of light, and Dd the distance to the deflector. For the remaining two components (blue and green in Fig. 4) we assumed either one or two different M/L ratios to scale the light to a mass.
4.2.2. Dark matter halo mass distribution
In the previous section we derived the baryonic component by modeling the light distribution. To disentangle the baryonic mass from the dark component, we modeled the DM distribution using three different profiles. At first we used a NFW (Navarro et al. 1997) profile but, since newer simulations predict deviations from this simple profile, we present in addition the best-fit mass model obtained assuming a power law profile (Barkana 1998, SPEMD), with parameters q as axis ratio, θE as Einstein radius, and rc as core radius, and a generalized version of the NFW profile, given by
where γg is the inner DM slope. The generalized NFW profile reduces to the standard NFW profile in the case γg = 1.
We assumed an axisymmetric lens mass distribution (axisymmetric in three dimensions) and imposed the projected orientation of the DM profile to be 0° or 90° rotated with respect to that of the projected light distribution. We find that the 90° orientation gives a better χ2, and thus the DM halo seems to be prolate for an axisymmetric system that has its rotation axis along the minor axis of the projected light distribution. Since strong lensing is only sensitive on scales of the Einstein radius, we assumed four different values for the scale radius in the NFW and gNFW profile, namely rs ≡ 18.11″, 36.22″, 90.54″, and 181.08″. These values correspond to 100 kpc, 200 kpc, 500 kpc, and 1000 kpc, respectively, for the lens redshift in the considered cosmology. We included the mass of the radial arc source in the model, using a singular isothermal sphere (SIS) profile, as the mass of this source galaxy deflects the light coming from the background tangential arc source. The center of this profile is set to the coordinates for the radial arc source, which we obtained from the multiplane lensing, calculated by the weighted mean of the mapped positions of the radial arc and its counterimage on the redshift plane of the radial arc.
4.3. Extended source modeling
In the next stage of our composite mass model, we reconstructed the source SB distribution and fit to the observed lensed source light, i.e., the main arc and the radial arc with its counterimage. This helped us to refine our image positions afterward. To accomplish this, we started with the mass model obtained in Sect. 4.2.2, which includes the lens light distribution described by the three chameleon profiles scaled with a constant M/L as baryonic mass and a power law profile for the DM halo. We then allowed the mass parameters to vary and, for a given set of mass parameter values, GLEE reconstructed the source SB on a grid of pixels (Suyu et al. 2006). This source is then mapped back to the image plane to get the predicted arc. To infer the best-fit parameters, we optimized with GLEE the posterior probability distribution, which is proportional to the product of the likelihood and the prior of the lens mass parameters; we refer to Suyu et al. (2006) and Suyu & Halkola (2010) for more details. The fitting of the SB distribution has
where d = dlens + darc is the intensity values dj of pixel j written as a vector with length Nd, the number of image pixels, and CD is the image covariance matrix. In the pixellated source SB reconstruction, we imposed a curvature form of regularization on the source SB pixels (Suyu et al. 2006).
Since we used the observed intensity of the arc to constrain our mass model and the F475W band has the brightest arc relative to the lens light, we included the F475W band in addition to the F160W, which is used for the lens light model. For simplicity we assumed the same structural parameters of the lens light profiles in the two bands (such as axis ratio q, center, and orientation θ) and model only the amplitude of the three chameleon profiles and of the three objects included. Explicitly, we modeled the light of the lens galaxy in both filters and reconstructed the observed intensity of the Einstein ring in both. We also specified and modeled the radial arc and its counterimage separately owing to their different redshift from the tangential arc. This was done only in the F475W filter. The light component parameter values of this model, with a 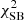 of 7.2 × 104 for the F160W filter and 3.1 × 105 for the F475W filter (the corresponding reduced
of 7.2 × 104 for the F160W filter and 3.1 × 105 for the F475W filter (the corresponding reduced  for the total model is 1.37), are presented in Table 3. In the same table we also give the median values with 1σ uncertainty. The corresponding images of the best-fit model are presented in Fig. 5. In the top row images of the F160W band are shown, in the middle row the images of the tangential arc and lens light in the F475W band, and in the bottom row the images of the radial arc in the F475W band, respectively. The images are ordered, for each row from left to right, as follows: the first image shows the observed data, the second the predicted, the third image shows the normalized residuals and the fourth image represents the reconstructed source. Despite visible residuals in the reconstruction, some of which are due to finite source pixel size, we reproduce the global features of the tangential arcs (compare panels a to b, and e to f) to allow us to refine our multiple image positions.
for the total model is 1.37), are presented in Table 3. In the same table we also give the median values with 1σ uncertainty. The corresponding images of the best-fit model are presented in Fig. 5. In the top row images of the F160W band are shown, in the middle row the images of the tangential arc and lens light in the F475W band, and in the bottom row the images of the radial arc in the F475W band, respectively. The images are ordered, for each row from left to right, as follows: the first image shows the observed data, the second the predicted, the third image shows the normalized residuals and the fourth image represents the reconstructed source. Despite visible residuals in the reconstruction, some of which are due to finite source pixel size, we reproduce the global features of the tangential arcs (compare panels a to b, and e to f) to allow us to refine our multiple image positions.
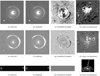 |
Fig. 5. Images for the best-fit model that includes the source SB reconstruction. In top row images are shown of the F160W band, and in the middle (tangential arc with lens) and bottom (radial arc) rows the images of the F475W band, respectively. It is necessary to separate the radial arc and the tangential arc since they lie at a different redshift. The images are ordered from left to right as follows: observed data, predicted model, normalized residuals in the range from −7σ to +7σ, and the reconstructed source SB on a grid of pixels. |
We also modeled the Cosmic Horseshoe observation with source SB reconstruction assuming the NFW or gNFW for the DM halo mass. The fits give for the NFW based model a  of 3.76 × 105 (corresponding to a reduced
of 3.76 × 105 (corresponding to a reduced  ) and very similar values for the gNFW model. From this, it seems that the gNFW fits almost as well as the NFW profile. Compared with the power law extended source model, the χ2 is slightly higher, but still comparable. The images reproduce the observations comparably well assuming the power law profile, as shown in Fig. 5.
) and very similar values for the gNFW model. From this, it seems that the gNFW fits almost as well as the NFW profile. Compared with the power law extended source model, the χ2 is slightly higher, but still comparable. The images reproduce the observations comparably well assuming the power law profile, as shown in Fig. 5.
4.4. Image position modeling
Finally, we refined multiple image systems using the extended SB modeling results of the last section. This time we find, similar to what was done in Sect. 4.1, eight sets of multiple images systems, in addition to the radial arc and its counterimage.
4.4.1. Three chameleon profiles
If we assume a constant M/L for all three chameleon profiles to scale the light to the baryonic mass, our model predicts the positions very well, with a χ2 of 20.23, which corresponds to a reduced χ2 of 1.07 (in Eq. (10)). In this section we use the best-fit model obtained in Sect. 4.3, which adopts the power law profile, now with core radius set to 10−4, for the DM distribution. This is done since the value is always very small and we want to focus on constraining the slope. Another reason is that we need to fix one parameter for our dynamics-only model, which is explained more in Sect. 6. The model with the selected multiple image systems is shown in Fig. 6. The figure also shows the critical curves and caustics for both redshifts, zs, r = 1.961 and zs, t = 2.381, as well as the predicted image positions from GLEE. The filled squares and circles correspond to the model source position, which is the magnification-weighted mean of the mapped source position of each image.
 |
Fig. 6. Best-fit model of the lensed source positions of the Cosmic Horseshoe, which are identified using our best-fit mass model with source SB reconstruction. This model assumes a power law profile for the DM distribution. It is obtained using, as constraints, eight multiple image systems for the Einstein ring (circles) and the radial arc and its counterimage (squares). We delineate the predicted image positions with a cross. We can see that all predicted images are very close to the selected images. The blue lines correspond to the critical curves (solid) and caustics (dashed) computed for the redshift of the radial arc, i.e., zs, r = 1.961, and the red line to the critical curves (solid) and caustics (dashed) computed for the redshift of the tangential arc, i.e., zs, t = 2.381. The lens position is denoted with a blue star. The small additional red features near the radial arc source position, shown in the lower left corner in detail and on the right-hand side, are probably due to the presence of radial arc source, i.e., as a result of multiplane lensing. Indeed, these features do not appear in the single-plane case (blue line). The filled squares and circles correspond to the weighted mean positions of the predicted source position, which are shown in more detail in the zoom in the upper and lower left corner. The figure is oriented such that north is up and east is left. |
To compare how much constraint we get from the radial arc, we also treated a model based on these image positions excluding the radial arc and its counterimage. In this case we had to remove the SIS profile that we adopted for the radial arc source mass. With this model we get a best-fit χ2 of 18.87, which corresponds to a reduced χ2 of 1.18.
As before, we test how well we can fit the same multiple image systems, i.e., these eight sets for the tangential arc and the radial arc with its counterimage as shown in Fig. 6, with our model by assuming a NFW or gNFW DM distribution. It turns out that our model based on the NFW profile gives a χ2 of 35.48 (reduced χ2 = 1.87) whereas the model based on the gNFW profile gives a χ2 of 35.19 (reduced χ2 = 1.96). This means that we do not fit the refined multiple image systems with the NFW or gNFW DM distribution as well as with the power law. We see a big difference in χ2 compared to the models where we exclude the radial arc and its counterimage. Explicitly, the χ2 values are 25.44 (reduced χ2 = 1.59) and 25.40 (reduced χ2 = 1.70) without radial arc for the NFW and gNFW profiles, respectively.
While the power law halo model fits well to the image positions, it yields a M/L of around 0.4 M⊙/L⊙ that is unphysically low. On the other hand, the NFW and gNFW with a common M/L for all three light components cannot fit well to the image positions, particularly those of the radial arc. Since newer publications (e.g., Samurović 2016; Sonnenfeld et al. 2018; Bernardi et al. 2018) have predicted variations in the stellar M/L of massive galaxies, we treated our model of the refined image position models with different M/L ratios for each chameleon profile. Different ratios result in a similar effect as a radial-varying ratio. We treated this variation of different M/L for all our models, which means both with and without radial arc as well as for all three different DM profiles NFW, gNFW, and power law. This is considered further in Sect. 6.
4.4.2. Central point mass with constant M/L of extended chameleon profiles
Since (1) we get a very small M/L for the central component (compare red line in Fig. 4) in the previous model, (2) this component is very peaky that the width is smaller as the PSF width, and (3) the Cosmic Horseshoe galaxy is known to be radio active, we infer that the central component is a luminous point component like an AGN. Thus we cannot assume an M/L for the central component to scale to the baryonic matter. Therefore we also treated models where we assumed a point mass instead of the central light component. The mass range is restricted to be between 108 M⊙ and 1010 M⊙ as these are the known limits of black hole masses (e.g., Thomas et al. 2016; Rantala et al. 2018). This range is in agreement with current MBH-σ relations (van den Bosch 2016), which give a value of around 109.5 M⊙ for the central black hole. For the two other, extended chameleon profiles, we assumed a M/L to scale them to the baryonic mass. Under this assumption we were able to reproduce a good, physical meaningful model for all three adopted DM profiles. Since our final model also includes the kinematic information of the lens galaxy, we discuss the details for this model in Sect. 6.
5. Kinematics and dynamics
In Sect. 4 we constructed a composite mass model of the Cosmic Horseshoe lens galaxy using lensing alone. In this section we present the kinematic data of the Cosmic Horseshoe lens galaxy taken from Spiniello et al. (2011) and a model based on dynamics-only (e.g., Yıldırım et al. 2016, 2017; Nguyen 2017; Wang et al. 2018).
For the dynamical modeling we used a software that has been further developed by Yıldırım et al. (in prep.) and is based on the code from Cappellari & Copin (2003) and Cappellari (2008). For an overview of the Jeans ansatz and the considered parameterization, the multi-Gaussian-expansion (MGE) method, see Appendix B. We infer the best-fit parameters again using EMCEE as already done for the lensing part.
5.1. Lens stellar kinematic data
Following the discovery of the famous Cosmic Horseshoe by Belokurov et al. (2007), several follow-up observations were done. In particular, Spiniello et al. (2011) obtained long-slit kinematic data for the lens galaxy G in March 2010. This was part of their X-shooter program (PI: Koopmans). The observations covered a wavelength range from 300 Å to 25 000 Å simultaneously with a slit centered on the galaxy, a length of 11″, and a width of 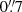 .
.
To spatially resolve the kinematic data, these authors defined seven apertures along the slit and summed up the signal within each aperture. The size of each aperture was chosen to be bigger than the seeing of 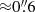 , such that independent kinematic measurement for each aperture were obtained. These data are listed in Table 4, together with the uncertainties. The obtained weighted average value of the velocity dispersion is 344 ± 25 km s−1. This is within the uncertainty of the measurements. As a consquence of the small number of available data and the huge errors we consider the symmetrized values and uncertainties as given in Table 4. For further details on the measurement process or the data of the stellar lens kinematics, see Spiniello et al. (2011).
, such that independent kinematic measurement for each aperture were obtained. These data are listed in Table 4, together with the uncertainties. The obtained weighted average value of the velocity dispersion is 344 ± 25 km s−1. This is within the uncertainty of the measurements. As a consquence of the small number of available data and the huge errors we consider the symmetrized values and uncertainties as given in Table 4. For further details on the measurement process or the data of the stellar lens kinematics, see Spiniello et al. (2011).
Stellar kinematic data of the Cosmic Horseshoe lens galaxy.
5.2. Dynamics-only modeling
Before we combine all available data to constrain maximally the mass of the Cosmic Horseshoe lens galaxy, we modeled the stellar kinematic data alone. We started from the best-fit model from lensing and included the parameters anisotropy β and inclination i. Since we have only seven data points (see Table 4), we could vary at most six parameters. Thus we set the core radius rc of the power law, which turned out to be very small in our lensing models, to 10−4. For a correct comparison to the refined lensing models (see Sect. 4.4) we fixed the core radius there as well. For dynamics we only adopted the power law and the NFW DM distribution, i.e., no longer the generalization of the NFW profile. This is because of the small improvement compared to the NFW profile. Another reason for this is that otherwise we have to fix one parameter to vary fewer parameters than the available data points. In other words, to consider the generalized NFW profile we have to fix one parameter such that the number of free parameters is smaller than the number of data points. In analogy to the case of the power law profile where we fix the core radius, we would set for the generalized NFW profile the slope γg ≡ 1. This would result in the NFW profile.
The power law DM distribution gives a dynamics-only best-fit model with χ2 = 0.25. The big uncertainties are the reason that our model has a χ2 much smaller than 1. The data points are shown in Fig. 7 (blue) with our dynamics-only model assuming power law (solid) or NFW (dashed) dark matter distribution. Since we can easily fit to these seven data points in the given range, we also treated the same model with forecasted 5% uncertainties for every measurement. The obtained best-fit dynamics-only model has a χ2 of 4.95, which is clearly much higher than for the full error. The best-fit parameter and median values with 1σ uncertainty are given in Table 5 for the model assuming the actual measured errors. As expected, most parameters are within the 1σ range and the M/L is in a good range. The relatively large errors on the parameters are due to the small number of data points we used as constraints.
 |
Fig. 7. Values for the second velocity moments vrms obtained by adopting the power law DM distribution (solid gray) or NFW (dashed blue) for dynamics-only. The measured data points with the full error bars are shown in brown. |
Best-fit parameter values for our model based on the power law DM distribution with dynamics-only.
For the NFW DM distribution we fit comparably well as with the power law model (χ2 = 0.25 compared to χ2 = 0.26), when using the full kinematic uncertainty, while the χ2 is slightly higher for the reduced (forecasted 5%) uncertainty on the kinematic data (χ2 = 4.95 compared to χ2 = 5.61). Comparing the power law and NFW profiles, we do not find a remarkable difference, apart from the radius, which appears to be lower in the NFW forecasted case. This, however, is in agreement with the higher χ2 of the NFW since the predicted vrms values are lower than the measurement in both the power law and NFW profile versions. For a further detailed analysis based on dynamics-only spatially, resolved kinematic measurements would be helpful.
6. Dynamical and lensing modeling
After modeling the inner mass distribution of the Cosmic Horseshoe lens galaxy based on lensing-only (Sect. 4) and dynamics-only (Sect. 5), we now combine both approaches. In recent years a huge effort has been spent to combine lensing and dynamics for strongly lensed observations to get a more robust mass model (e.g., Treu & Koopmans 2002, 2004; Mortlock & Webster 2000; Gavazzi et al. 2007; Barnabè et al. 2009, 2011; Auger et al. 2010; Sonnenfeld et al. 2012; Grillo et al. 2013; Lyskova et al. 2018). Since strong lensing normally has the constraints at the Einstein radius r ≈ θE, which is in our case ≈5″, and kinematic measurements are normally in the central region around the effective radius (here r ≲ 2″), we combined information at different radii with these two approaches. This results in a better constrained model and we might break parameter degeneracies because these two approaches are complementary. However, in our particular lens system, we also used the radial arc as lensing constraints in the inner regions.
Although using the HST SB observations would provide more lensing constraints, we only considered the refined image positions presented in Sect. 4.4. The reason for this choice is that we would otherwise overwhelm the seven data points from dynamics with more than 105 SB pixel from the images. The data points coming from the identified image positions are still higher, but at the same order of magnitude. Moreover, with this method we were able to weight the contribution of the radial arc and its counterimage more.
When we combined dynamics and lensing, we again considered models with and without radial arc, each adopting power law or NFW DM distribution; we also considered all four versions with the full uncertainty of the kinematic data as well as with 5% as a forecast. Additionally, we treated all models with one single M/L as well as with different M/L ratios as already done for lensing-only (see Sect. 4.2.1 for details). Based on the same arguments as for the lensing-only, we also treated models by replacing the PSF-like central component (shown in red in Fig. 4) by a point mass.
6.1. Three chameleon mass profiles
By combining lensing and dynamics we considered different composite mass models. As first, we used the lens light, which is composed by three chameleon profiles as obtained in Sect. 4.2.1, scaled by a constant M/L as baryonic component. Under this assumption, we find the best fit when using a power law DM mass distribution, i.e., a χ2 of 25.08, and, when using a NFW DM distribution, i.e., a χ2 of 71.54. The χ2 values reveal that the NFW is not as good at describing the observation as the power law profile. However, assuming a power law DM distribution, the M/L value for scaling all three light components is around 0.1 M⊙/L⊙. This is unphysically low and results in a very high DM fraction.
The next step to model the baryonic component is to allow different M/L ratios for the different light components shown in Fig. 4. This allows us to fit remarkably better with the NFW profile, while we do not get much improvement adopting a power law DM distribution. However, this method does not allow us to obtain meaningful models, as the central component needs an unphysically low M/L. Therefore, we infer that we cannot assume a M/L for the central component, irrespective of the DM distribution.
6.2. Point mass and two chameleon mass profiles
As noted in Sect. 4.4.2, the central component is probably associated with an AGN, since its light profile width is similar to the width of the PSF (see Fig. 4) and its M/L was very low from the previous model in Sect. 6.1. Thus, assuming a M/L for this component would not be physically meaningful and we supersede it by a point mass in the range of a black hole mass. From our previous models and from the fact that the lens galaxy is very massive, we expect this point mass to be comparable to that of a supermassive black hole. For the two other light components we still assume the two fitted chameleon profiles scaled by a M/L, either the same M/L for both components, or a different M/L for each component. Moreover, we test the effect of relaxing the scale parameter rs of the NFW profile. It turns out to be very similar to the model by assuming a fixed value, as expected, such that we present only plots of the model with free rs.
We see by comparing the different models with the point mass that both DM profiles result in a similar χ2 value (see Table 6). Both DM distributions seem to fit the observation with an acceptable DM fraction between 60% and 70%, whose value is slightly higher as predicted by Spiniello et al. (2011), but within their 1σ range. These values are difficult to compare to general studies of the DM fraction of galaxies because the Cosmic Horseshoe lens galaxy is very massive. Adopting the relation found by Cappellari et al. (2013) based on galaxies between the mass range 1010 M⊙ and 1011.5 M⊙ would give a DM fraction fDM of around 0.75. We assume this relation is overestimating the fraction for very low and very high galaxy masses. The corresponding plot is shown in Fig. 8 for the following final models:
-
lensing & dynamics, power law DM, without radial arc
-
lensing & dynamics, power law DM, with radial arc
-
lensing & dynamics, NFW DM, without radial arc
-
lensing & dynamics, NFW DM, with radial arc.
 |
Fig. 8. Enclosed DM fraction, i.e., DM divided by the sum of baryonic matter from the scaled lens light and dark matter enclosed in radius r, of the models adopting a power law (bottom) or NFW (top) DM distribution. All models include the point mass in the lens center, which is not considered among the baryonic mass and thus not shown in this plot. For comparison, the value of the DM fraction within one effective radius of Spiniello et al. (2011) is shown by the horizontal solid line (for the value) and dashed lines (for 1σ uncertainties). |
The DM fraction is defined in this work as the DM divided by the sum of baryonic matter from the scaled lens light and DM enclosed in the radius r. To be noted is that the point mass is not assumed to be pure baryonic matter, and thus not included in the baryonic component in the calculation. This results in the profile of DM fraction having a concave curve in the very central region. Including the point mass with less than 1010 M⊙ would shift the fraction insignificantly to lower values. The best-fit parameter values for these four models are given with the corresponding median values with 1σ uncertainties in Table 7 (adopting power law DM distribution) and Table 8 (adopting NFW with free scale radius rs).
As already mentioned in Sect. 4.1, the external shear can be explained with a mass concentration in the direction of the cluster RMJ114847.5+193115.1 (Rykoff et al. 2014), which lies in the north-west direction from the Cosmic Horseshoe.
Allowing two independent M/L seems not to decrease the χ2 notably, and we see from the sampling that the outer M/L is not well constrained and highly degenerate with the other mass components. This might come from the flatness of the profile (see green line in Fig. 4) and less constraints on the outer part where the profile is dominant.
In all models, we can fit very well to the kinematic data with a dynamics-χ2 of around 0.5. This can be seen in Fig. 9 and is expected because of the large uncertainties and small number of data points available. According to that, we see from Tables 7 and 8 that we cannot well constrain the anisotropy β and inclination i given a prior range of β ∈ [−0.3, 0.3] and i ∈ [0, 0.3] (e.g., Cappellari et al. 2007; Thomas et al. 2009; Chae et al. 2019). Moreover, from those two tables we see that the radial arc definitely helps to constrain the model better based on the 1σ values. Especially, parameters that are associated with the central region (e.g., the point mass) are much better constrained using the radial arc.
 |
Fig. 9. Values for the second velocity moments vrms obtained by adopting the power law DM distribution (bottom) or NFW (top) for dynamics and lensing. The full uncertainties on the kinematic measurements and the point mass are shown instead of the central component of the fitted light. The measured data points with the error bars are shown in brown. |
Additionally we compared the mean convergence 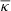 curves of our different models. In Fig. 10 we show the effect of including the radial arc among the constraints in the case of the power law DM distribution (bottom) or NFW DM distribution (top) for the DM component and in Fig. 11 for both baryonic and DM components. In the plot of NFW
curves of our different models. In Fig. 10 we show the effect of including the radial arc among the constraints in the case of the power law DM distribution (bottom) or NFW DM distribution (top) for the DM component and in Fig. 11 for both baryonic and DM components. In the plot of NFW 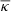 we show for comparison green lines for a concentration of cNFW = 5 and different M200 masses. We can see that the
we show for comparison green lines for a concentration of cNFW = 5 and different M200 masses. We can see that the 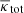 are very similar in both cases. In both plots we see good improvement if we include the radial arc. However, if we compare the NFW and the power law for the DM component, we can see a slight difference in the inner regions. The NFW profile looks less steep.
are very similar in both cases. In both plots we see good improvement if we include the radial arc. However, if we compare the NFW and the power law for the DM component, we can see a slight difference in the inner regions. The NFW profile looks less steep.
 |
Fig. 10. Mean convergence |
 |
Fig. 11. Mean convergence |
Indeed, Fig. 12 shows the logarithm of the slope of the DM profile 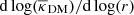 . On the bottom panel, we compare the NFW and power law models including the radial arc while the top panel shows those excluding the radial arc as constraint. We see that the inferred slope at the Einstein ring is well constrained and independent of the adopted profile. Including the radial arc, we are able to constrain the slope near the radial arc better to a range between ∼−0.3 and ∼−0.15 at the radial arc radius, covering the spread between the two models. More information in the central region (of ∼1″), such as spatially resolved kinematics, would be required to break further the model degeneracies in measuring the DM profile slope in this region.
. On the bottom panel, we compare the NFW and power law models including the radial arc while the top panel shows those excluding the radial arc as constraint. We see that the inferred slope at the Einstein ring is well constrained and independent of the adopted profile. Including the radial arc, we are able to constrain the slope near the radial arc better to a range between ∼−0.3 and ∼−0.15 at the radial arc radius, covering the spread between the two models. More information in the central region (of ∼1″), such as spatially resolved kinematics, would be required to break further the model degeneracies in measuring the DM profile slope in this region.
 |
Fig. 12. Radial slope of DM profile, |
Finally, to see the contribution of the radial arc further, we show the probability density distribution of our final best-fit models. In particular, Fig. 13 shows the power law models, while Fig. 14 shows the NFW models. From those figures we also see that parameters are much better constrained when radial arc is included, especially the point mass parameter, which is understandable as it is only present in the central region where the radial arc is observed. The prior range of the point mass strength is the same for all models as we restrict this range to 108–1010 M⊙ as the known mass range of black holes. This corresponds to log(θE, point) between −4 and −1. We see from this distribution that the radial arc forces the point mass to its upper limit. Since the lens galaxy is very massive, a supermassive black hole is realistic. Interestingly, the M/L is also better constrained by including the radial arc. This confirms the importance of including the radial arc as constraint. We also see that the contribution of the constraints coming from dynamics is very small, probably due to the small amount of data and the large uncertainties.
 |
Fig. 13. Probability density distribution for our best-fit models, adopting a power law DM profile. Along the diagonal, the 1D histograms for the corresponding parameter given on the x-axis (and independent of the label in the y-axis) are shown, while below in the triangle the joint 2D probability distributions corresponding to the parameters given on x- and y-axis are shown. The different opacities in the 2D plots indicate the different sigma ranges. In general, the model with the radial arc is much better constrained than without. The parameters are the anisotropy β, inclination i, shear magnitude, and its orientation counterclockwise to the x-axis, for the DM profile the axis ratio q, Einstein angle θE, and the slope γ′. Additionally, we show the M/L, which is used to scale the two light components, and the logarithm of the strength of the point mass θE, point. The prior range for the point mass is set to 108−1010 M⊙ as the known limits of black holes, corresponding to log(θE, point) between −4 and −1. |
 |
Fig. 14. Probability density distribution for our best-fit models, adopting a NFW DM profile. Along the diagonal, the 1D histograms for the corresponding parameter given on the x-axis (and independent of the label in the y-axis) are shown, while below in the triangle the joint 2D probability distributions corresponding to the parameters given on x- and y-axis are shown. The different opacities in the 2D plots indicate the different sigma ranges. In general, the model with radial arc is much better constrained than without. The parameters are the anisotropy β, inclination i, shear magnitude, and its orientation counterclockwise to the x-axis for the DM profile the axis ratio q, strength (right) θE, and the scale radius rs. Additionally, we show the M/L, which is used to scale the two light components, and the logarithm of the strength of the point mass θE, point. The prior range for the point mass is set to 108−1010 M⊙ as the known limits of black holes, corresponding to log(θE, point) between −4 and −1. |
Our derived scale radius based on our final model adopting the NFW profile for the DM is around 180″, which is relatively large. The given rs value and the normalization of our model translate into a large halo mass, M200 ≈ 1.1 × 1015 M⊙ (equivalent to r200 ≈1.7 Mpc), typical of massive clusters, and a concentration cNFW ≈ 1.8, which is low compared to the typical values measured in groups and clusters (Newman et al. 2015). The large M200 value could come from the extrapolation of the NFW density profile to much larger radii than our data are probing. Another reason for the increase of the DM inside the Einstein ring of the Cosmic Horseshoe is the loose cluster RMJ114847.5+193115.1 around 3 arcmin away (Rykoff et al. 2014) as mentioned already earlier in Sect. 4.1.
We also considered all models under the assumption of 5% uncertainty as the current errors are very huge. Comparing to the figure obtained with the real uncertainties, we do not see a remarkable difference. The uncertainties do not seem to reduce the parameter space substantially, even though the χ2 is higher. Therefore, to further improve the mass modeling through dynamics, spatially resolved kinematic measurements would likely be needed in the future.
7. Summary and conclusions
While in the standard CDM model the structure of DM is well understood through large numerical DM only simulations (e.g., Dubinski & Carlberg 1991; Navarro et al. 1996a,b), we have to include the baryonic component to reach more complex, but realistic models. Since the deflection of light depends on the total matter, strong gravitational lensing provides a good opportunity to obtain the distribution of the mass of the lens. In this paper we study the matter distribution of a unique strong lensing observation, known as the Cosmic Horseshoe (J1148+1930). This observation shows a radial arc at a redshift of zs, r = 1.961 inside the huge Einstein ring, whose redshift we measured based on spectroscopic observations presented in this paper. Including that radial arc in our models helps to improve our model as it gives lensing constraints in the central region. To obtain a self-consistent mass model, we include kinematic measurements of the lens galaxy in our final model.
Before disentangling DM and baryonic mass, we first construct a model of the total lens mass. Based on this model, we create a composite model with baryonic and DM components separately. We adopt different DM profiles, namely, a power law profile, a NFW profile, or a generalization of the NFW profile. For the baryonic component we adopt the lens light distribution, which is described by three components, scaled by a M/L. As one component is very peaky and thus AGN-like, we suggest in our final model to supersede this component by a point mass as we cannot assume a physical meaningful M/L value. The other two components are still scaled by a M/L. We then include stellar kinematic information of the lens and consequently we are able to construct a self-consistent mass model. As we are also interested in seeing the improvement coming from the radial arc; we always model with and without radial arc and compare those models. From our study of the matter distribution we obtain the following key results:
-
Since the width of the central component of the fitted lens light is comparable with the PSF width (compare Fig. 4) and the lens galaxy emits in the radio wavelengths, our modeling results support a mass model for the Cosmic Horseshoe lens galaxy with a point component in the center instead of a luminous component scaled by a M/L. The two outer components are scaled with a M/L to account for the baryonic mass. The DM component could follow either a power law or a NFW profile, since both profiles could adequately fit to the current data.
-
We can construct a better mass model thanks to the contribution of radial arc and its counterimage. Thus we infer the radial arc is part of the full Cosmic Horseshoe system. It turns out that the radial arc improves the DM halo parameter constraints independently of the adopted DM distribution.
-
When adding the contribution of dynamical modeling, we find that actually this method is not able to constrain the possible parameter range significantly better. We suspect this might be due to the lack of data points and large uncertainties. When using the forecasted 5% uncertainties on the kinematic measurements, we constrain the parameter ranges slightly better.
-
When trying to model the baryonic matter independently of the DM, we consider two scenarios: the matter aligned with the lens light or 90° offset. We find that the model with the 90° rotated orientation fits better. Thus, the major axis of the projected halo mass distribution seem to be perpendicular to the major axis of the baryonic mass distribution.
-
For all the tested models, we obtain a mass of around 5.2 × 1012 M⊙ enclosed in the Einstein ring. This is in agreement with previous studies of the Cosmic Horseshoe, for example, Dye et al. (2008). We predict the DM fraction at one effective radius to be 0.65, whose value is slightly higher as predicted by Spiniello et al. (2011), but within their 1σ range. The exact fraction also depends on the specific model. A general comparison to other galaxies is difficult as there are not many known galaxies in the same mass range as the Cosmic Horseshoe.
-
During our modeling we do not find a notable improvement in fitting the data by allowing for freedom in the NFW DM profile slope, i.e., adopting the generalized NFW instead of the normal NFW profile (compare Eq. (16)). This suggests that the profile slope is not significantly steeper or shallower than that of the NFW profile even in the presence of the baryons.
From this work, we demonstrate the utility of having a radial arc in constraining the DM profile, particularly in the inner regions. This is important for the future, when we might discover more lenses in current and future surveys. New single-galaxy lens systems with radial arcs would provide great opportunities to model the inner DM distributions and probe galaxy formation scenarios. This would also give a more general statement rather than from one anecdotal example.
Moreover, we see that combining lensing and kinematic data helps to constrain the model better, even though current kinematic data of the Cosmic Horseshoe are limited. Thus further kinematic measurements, particularly if spatially resolved, of such strong lens observations would help to construct a better mass model.
Acknowledgments
We thank M. Auger for useful discussions. SS, GC, SHS, and AY thank the Max Planck Society for support through the Max Planck Research Group for SHS. This research was supported in part by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development and by the Province of Ontario through the Ministry of Research, Innovation and Science. The analysis is based on the following: (1) observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations were done in May 2010 with Proposal ID 11602 and in November 2011 with Proposal ID 12266; (2) observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina), and Ministério da Ciência, Tecnologia e Inovação (Brazil).
References
- Abadi, M. G., Navarro, J. F., Fardal, M., Babul, A., & Steinmetz, M. 2010, MNRAS, 407, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Abazajian, K., Fuller, G. M., & Patel, M. 2001, Phys. Rev. D, 64, 023501 [NASA ADS] [CrossRef] [Google Scholar]
- Auger, M. W., Treu, T., Bolton, A. S., et al. 2010, ApJ, 724, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Barkana, R. 1998, ApJ, 502, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Barnabè, M., Czoske, O., Koopmans, L. V. E., et al. 2009, MNRAS, 399, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Barnabè, M., Czoske, O., Koopmans, L. V. E., Treu, T., & Bolton, A. S. 2011, MNRAS, 415, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Bellagamba, F., Tessore, N., & Metcalf, R. B. 2017, MNRAS, 464, 4823 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Evans, N. W., Moiseev, A., et al. 2007, ApJ, 671, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bendinelli, O. 1991, ApJ, 366, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Sheth, R. K., Dominguez-Sanchez, H., et al. 2018, MNRAS, 477, 2560 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Mamon, G. A. 1982, MNRAS, 200, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. J., Davies, R. L., & Illingworth, G. D. 1990, ApJ, 361, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., & Narayan, R. 1986, ApJ, 310, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., Faber, S. M., Flores, R., & Primack, J. R. 1986, ApJ, 301, 27 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bonvin, V., Courbin, F., Suyu, S. H., et al. 2017, MNRAS, 465, 4914 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2002, MNRAS, 333, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, K.-H., Khersonsky, V. K., & Turnshek, D. A. 1998, ApJ, 506, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, K., Bernardi, M., & Sheth, R. 2019, ApJ, 874, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Chuzhoy, L. 2006, ArXiv e-prints [arXiv:astro-ph/0608637] [Google Scholar]
- Collett, T. E., Buckley-Geer, E., Lin, H., et al. 2017, ApJ, 843, A148 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Ishai, G., Dutton, A. A., & Maccio, A. V. 2017, MNRAS, 468, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- De Vaucouleurs, G. 1948, Comptes Rendus Acad. Sci, 227, 586 [Google Scholar]
- Diemand, J., Zemp, M., Moore, B., Stadel, J., & Carollo, C. M. 2005, MNRAS, 364, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., & Carlberg, R. G. 1991, ApJ, 378, 496 [Google Scholar]
- Dutton, A. A., Brewer, B. J., Marshall, P. J., et al. 2011, MNRAS, 417, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., & Warren, S. J. 2005, ApJ, 623, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., Evans, N. W., Belokurov, V., Warren, S. J., & Hewett, P. 2008, MNRAS, 388, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Elias, J. H., Joyce, R. R., Liang, M., et al. 2006, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Proc. SPIE, 6269, 62694C [Google Scholar]
- El-Zant, A., Shlosman, I., & Hoffman, Y. 2001, ApJ, 560, 636 [NASA ADS] [CrossRef] [Google Scholar]
- El-Zant, A. A., Hoffman, Y., Primack, J., Combes, F., & Shlosman, I. 2004, ApJ, 607, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gao, L., Navarro, J. F., Frenk, C. S., et al. 2012, MNRAS, 425, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R., Treu, T., Koopmans, L. V. E., et al. 2008, ApJ, 677, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Ghigna, S., Moore, B., Governato, F., et al. 2000, ApJ, 544, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, O. Y., Kravtsov, A. V., Klypin, A. A., & Nagai, D. 2004, ApJ, 616, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Golse, G., & Kneib, J.-P. 2002, A&A, 390, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Governato, F., Brook, C., Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Graham, A. W., Merritt, D., Moore, B., Diemand, J., & Terzić, B. 2006a, AJ, 132, 2711 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Merritt, D., Moore, B., Diemand, J., & Terzić, B. 2006b, AJ, 132, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Grillo, C., Christensen, L., Gallazzi, A., & Rasmussen, J. 2013, MNRAS, 433, 2604 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, M., Fairbairn, M., & Sommer-Larsen, J. 2006, Phys. Rev. D, 74, 123522 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, E. R. 1974, ApJ, 191, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinoff, S. W. 2012, Photon, Poisson noise [Google Scholar]
- Jeans, J. H. 1922, MNRAS, 82, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplinghat, M. 2005, Phys. Rev. D, 72, 063510 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R. 2001, ArXiv e-prints [arXiv:astro-ph/0102341] [Google Scholar]
- Kochanek, C. S., & Rybicki, G. B. 1996, MNRAS, 280, 1257 [NASA ADS] [Google Scholar]
- Lapi, A., & Cavaliere, A. 2011, ApJ, 743, 127 [Google Scholar]
- Laporte, C. F. P., & White, S. D. M. 2015, MNRAS, 451, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Ruszkowski, M., & Bryan, G. L. 2017, ApJ, 847, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Lyskova, N., Churazov, E., & Naab, T. 2018, MNRAS, 475, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Maller, A. H., Simard, L., Guhathakurta, P., et al. 2000, ApJ, 533, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Martizzi, D., Teyssier, R., & Moore, B. 2013, MNRAS, 432, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Monnet, G., Bacon, R., & Emsellem, E. 1992, A&A, 253, 366 [NASA ADS] [Google Scholar]
- Mortlock, D. J., & Webster, R. L. 2000, ArXiv e-prints [arXiv:astro-ph/0011235] [Google Scholar]
- Moutarde, F., Alimi, J.-M., Bouchet, F. R., & Pellat, R. 1995, ApJ, 441, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Murata, R., Nishimichi, T., Takada, M., et al. 2018, ApJ, 854, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, R., & Miyamoto, M. 1976, PASJ, 28, 1 [NASA ADS] [Google Scholar]
- Navarro, J. F., Eke, V. R., & Frenk, C. S. 1996a, MNRAS, 283, L72 [NASA ADS] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996b, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Ludlow, A., Springel, V., et al. 2010, MNRAS, 402, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Ellis, R. S., & Treu, T. 2015, ApJ, 814, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, D. D. 2017, ArXiv e-prints [arXiv:1712.02470] [Google Scholar]
- Nipoti, C., Treu, T., Ciotti, L., & Stiavelli, M. 2004, MNRAS, 355, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Pedrosa, S., Tissera, P. B., & Scannapieco, C. 2009, MNRAS, 395, L57 [NASA ADS] [Google Scholar]
- Peirani, S., Kay, S., & Silk, J. 2008, A&A, 479, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peirani, S., Dubois, Y., Volonteri, M., et al. 2017, MNRAS, 472, 2153 [CrossRef] [Google Scholar]
- Peter, A. H. G., Moody, C. E., & Kamionkowski, M. 2010, Phys. Rev. D, 81, 103501 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A., & Governato, F. 2012, MNRAS, 421, 3464 [NASA ADS] [CrossRef] [Google Scholar]
- Quider, A. M., Pettini, M., Shapley, A. E., & Steidel, C. C. 2009, MNRAS, 398, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Rantala, A., Johansson, P. H., Naab, T., Thomas, J., & Frigo, M. 2018, ApJ, 864, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Romano-Díaz, E., Shlosman, I., Hoffman, Y., & Heller, C. 2008, ApJ, 685, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B. 1987, in Structure and Dynamics of Elliptical Galaxies, ed. P. T. de Zeeuw, IAU Symp., 127, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Ryden, B. S. 1991, ApJ, 370, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Samurović, S. 2016, Bulg. Astron. J., 24, 12 [Google Scholar]
- Satoh, C. 1980, PASJ, 32, 41 [NASA ADS] [Google Scholar]
- Schneider, P., Kochanek, C., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro – Saas-Fee Advanced Course 33 (Berlin, Heidelberg: Springer Science& Business Media) [Google Scholar]
- Sellwood, J. A., & McGaugh, S. S. 2005, ApJ, 634, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1963, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 6, 41 [Google Scholar]
- Sommer-Larsen, J., & Limousin, M. 2010, MNRAS, 408, 1998 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnenfeld, A., Treu, T., Gavazzi, R., et al. 2012, ApJ, 752, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnenfeld, A., Leauthaud, A., Auger, M. W., et al. 2018, MNRAS, 481, 164 [Google Scholar]
- Spergel, D. N., & Steinhardt, P. J. 2000, Phys. Rev. Lett., 84, 3760 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spiniello, C., Koopmans, L. V. E., Trager, S. C., Czoske, O., & Treu, T. 2011, MNRAS, 417, 3000 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., & Halkola, A. 2010, A&A, 524, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suyu, S. H., Marshall, P. J., Hobson, M. P., & Blandford, R. D. 2006, MNRAS, 371, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Hensel, S. W., McKean, J. P., et al. 2012, ApJ, 750, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J., Saglia, R. P., Bender, R., et al. 2009, ApJ, 691, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J., Ma, C.-P., McConnell, N. J., et al. 2016, Nature, 532, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Tonini, C., Lapi, A., & Salucci, P. 2006, ApJ, 649, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T. 2010, ARA&A, 48, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Ellis, R. S. 2015, Contemp. Phys., 56, 17 [NASA ADS] [Google Scholar]
- Treu, T., & Koopmans, L. V. E. 2002, ApJ, 575, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Koopmans, L. V. E. 2004, ApJ, 611, 739 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R. C. E. 2016, ApJ, 831, 134 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Binney, J., & Davies, R. L. 1990, MNRAS, 245, 582 [NASA ADS] [Google Scholar]
- van de Ven, G., Falcón-Barroso, J., McDermid, R. M., et al. 2010, ApJ, 719, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W., Han, J., Cole, S., et al. 2018, MNRAS, 476, 5669 [NASA ADS] [CrossRef] [Google Scholar]
- Yıldırım, A., van den Bosch, R. C. E., van de Ven, G., et al. 2016, MNRAS, 456, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Yıldırım, A., van den Bosch, R. C. E., van de Ven, G., et al. 2017, MNRAS, 468, 4216 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Sersic model details
Since the Sersic profile is commonly used for the light distribution of a galaxy, we also modeled the Horseshoe main lens with two Sersic profiles as noted in Sect. 4.2.1. For completeness we give the obtained parameter values in Table A.1.
Marginalized parameter values with 1σ (68% CI) uncertainties for the light distribution of the Cosmic Horseshoe lens.
Appendix B: Dynamical modeling using MGE parameterization and Jeans ansatz
We briefly introduce the Jeans formalism that we use for dynamical modeling in our mass model of the Cosmic Horseshoe. Since we assume an axisymmetric model, we only consider this specific case and for details and the general case refer to Cappellari (2008).
We start from the general axisymmetric Jeans equations (Jeans 1922)
which are only two equations since the third reduces to zero in the axisymmetric case. The quantity Φ is the gravitational potential, (R, z, ϕ) standard cylindrical coordinates,  an abbreviation for ∫ vkvjfd3v with f(x, v) the distribution function at position x and with velocity v and μ the luminosity density (not ν as in Cappellari 2008 to distinguish better from the velocity v). We can reduce these two equations to
an abbreviation for ∫ vkvjfd3v with f(x, v) the distribution function at position x and with velocity v and μ the luminosity density (not ν as in Cappellari 2008 to distinguish better from the velocity v). We can reduce these two equations to
by assuming that the velocity ellipsoid is aligned with the cylindrical coordinate system (R, z, ϕ) and that the anisotropy b is constant and given by
The situation b = 1 is the so-called semi-isotropic or two-integral case.
For the stellar density and the total density we adopt MGE parameterization (Bendinelli 1991; Monnet et al. 1992) as described in Cappellari (2002) because of its accuracy in reproducing the SB and because of its robustness. By assuming that the x-axis is aligned with the photometric major axis, the SB Σ is given by
at the position (x′,y′) of the plane of sky. The parameter N is the number of adopted Gauissians with luminosity Lk, observed axis ratio  between 0 and 1, and dispersion σk along the major axis.
between 0 and 1, and dispersion σk along the major axis.
Since the galaxies have an unknown inclination i, we need a deprojection of the SB to get the intrinsic luminosity density. This is not unique unless we considers edge-on (i = 90°) oriented galaxies (Rybicki 1987; Kochanek & Rybicki 1996). As described in Cappellari (2008), one advantage of the MGE method is that we can relatively well include the roundness of the model to get realistic densities and fulfill the morphological criterion, which is described in detail in Cappellari & Copin (2003). Thereafter we can write the deprojected MGE oblate axisymmetric luminous density μ as
where the intrinsic axial ratio of each Gaussian component is written as
As we said, we adopt for the total density ρ an MGE parameterization as well, such that we can write it as a sum of M Gaussians, i.e.,
After applying the MGE formalism to the solution of axisymmetric anisotropic Jeans Eqs. (B.3) and (B.4), i.e., we substitute Eq. (B.7) and the gravitational potential obtained from Eq. (B.9) into Eqs. (B.3) and (B.4), then we can perform the integral analytically. With that, we can integrate along the line of sight (LOS) to obtain the observables, which we then compare to the galaxy kinematics. These are the total observed second moment and the first moment. For the latter, we need additional assumptions because we have to decide how the second moment separates into the contribution of ordered and random motion, which is defined by
or in simplified, but often used notation
In this equation vrms is the second velocity moment, v the rotation, and σ the velocity dispersion. These necessary additional assumptions are the reason why we often consider the second velocity moment, which is the more general formula. However, the first moment are very useful to quantify the amount of rotation in galaxies and are thus sometimes used (e.g., Nagai & Miyamoto 1976; Satoh 1980; Binney et al. 1990; van der Marel et al. 1990).
In the case that the anisotropy bk is different for each Gaussian, the total luminosity-weighted anisotropy of an MGE model, under the assumptions noted above, is given by the definition (Binney & Mamon 1982; Cappellari 2008)
Further theoretical discussions are provided in Cappellari (2008).
All Tables
Best-fit and marginalized parameter values for the model assuming a power law profile plus external shear.
Best-fit and marginalized parameter values for the lens light component of the mass model obtained by reconstructing the source SB.
Best-fit parameter values for our model based on the power law DM distribution with dynamics-only.
Marginalized parameter values with 1σ (68% CI) uncertainties for the light distribution of the Cosmic Horseshoe lens.
All Figures
 |
Fig. 1. Color image of the Cosmic Horseshoe obtained through a combination of the F475W, F606W, and F814W filter images from the HST WFC3. The size of this image is 20″ × 20″. We can see the ≈300° wide blue Einstein ring of the Cosmic Horseshoe. In addition, the Cosmic Horseshoe observation includes a radial arc that is indicated with a green solid box. This is shown in detail in the bottom panel, in color (left) and from the F475W filter (right). We associate this radial arc to its counterimage, indicated in the main figure with a dashed green box and located around 8″ on the east side of the lens galaxy G. Both the radial arc and its counterimage correspond to a source at redshift zs, r = 1.961 (see Sect. 2.2). The three star-like objects in the field of view, which we include in our light model, are circled in yellow. The figures are oriented such that north is up and east is left. |
| In the text | |
 |
Fig. 2. Top (bottom): two-dimensional and 1D spectrum around the Hα ([OIII] 5007 Å) emission line from the counterimage to the radial arc, obtained from GNIRS observations. The 1D spectrum is extracted from a 5 pixel, corresponding to 0.75″, aperture around each line. The secondary peak redward of [OII] visible in the 1D spectrum is due to a cosmic ray that was not properly removed in the data reduction process. |
| In the text | |
 |
Fig. 3. Best-fit model for the lens light distribution. Left image: observation of the Cosmic Horseshoe in the F160W band, whereas central panel: predicted light distribution. This model includes three chameleon profiles (see Eq. (14)), two PSF profiles, and one de Vaucouleurs profile for the three objects. The right image shows, in the range between −7σ and +7σ, the normalized residuals of this model. The constant gray regions are the masked-out areas (containing lensed arcs and neighboring galaxies) to fit only to the flux of the lens The figures are oriented such that north is up and east is left. |
| In the text | |
 |
Fig. 4. Left: different components of the chameleon profiles shown in units of solar luminosity in red (“inner”), blue (“medium”), and green (“outer” component), respectively. The total light observed from the Cosmic Horseshoe lens galaxy in the HST filter F160W is described by the sum of all three components. To compare the width of the components, scaled PSF is plotted with a black dotted line. Right: radially averaged total light of the model (red) and observed (blue) in solar luminosities, plotted as a function of radius. The Einstein radius is indicated with the black dotted line and the vertical gray band marks the range with substantial light from the lensed arcs. |
| In the text | |
 |
Fig. 5. Images for the best-fit model that includes the source SB reconstruction. In top row images are shown of the F160W band, and in the middle (tangential arc with lens) and bottom (radial arc) rows the images of the F475W band, respectively. It is necessary to separate the radial arc and the tangential arc since they lie at a different redshift. The images are ordered from left to right as follows: observed data, predicted model, normalized residuals in the range from −7σ to +7σ, and the reconstructed source SB on a grid of pixels. |
| In the text | |
 |
Fig. 6. Best-fit model of the lensed source positions of the Cosmic Horseshoe, which are identified using our best-fit mass model with source SB reconstruction. This model assumes a power law profile for the DM distribution. It is obtained using, as constraints, eight multiple image systems for the Einstein ring (circles) and the radial arc and its counterimage (squares). We delineate the predicted image positions with a cross. We can see that all predicted images are very close to the selected images. The blue lines correspond to the critical curves (solid) and caustics (dashed) computed for the redshift of the radial arc, i.e., zs, r = 1.961, and the red line to the critical curves (solid) and caustics (dashed) computed for the redshift of the tangential arc, i.e., zs, t = 2.381. The lens position is denoted with a blue star. The small additional red features near the radial arc source position, shown in the lower left corner in detail and on the right-hand side, are probably due to the presence of radial arc source, i.e., as a result of multiplane lensing. Indeed, these features do not appear in the single-plane case (blue line). The filled squares and circles correspond to the weighted mean positions of the predicted source position, which are shown in more detail in the zoom in the upper and lower left corner. The figure is oriented such that north is up and east is left. |
| In the text | |
 |
Fig. 7. Values for the second velocity moments vrms obtained by adopting the power law DM distribution (solid gray) or NFW (dashed blue) for dynamics-only. The measured data points with the full error bars are shown in brown. |
| In the text | |
 |
Fig. 8. Enclosed DM fraction, i.e., DM divided by the sum of baryonic matter from the scaled lens light and dark matter enclosed in radius r, of the models adopting a power law (bottom) or NFW (top) DM distribution. All models include the point mass in the lens center, which is not considered among the baryonic mass and thus not shown in this plot. For comparison, the value of the DM fraction within one effective radius of Spiniello et al. (2011) is shown by the horizontal solid line (for the value) and dashed lines (for 1σ uncertainties). |
| In the text | |
 |
Fig. 9. Values for the second velocity moments vrms obtained by adopting the power law DM distribution (bottom) or NFW (top) for dynamics and lensing. The full uncertainties on the kinematic measurements and the point mass are shown instead of the central component of the fitted light. The measured data points with the error bars are shown in brown. |
| In the text | |
 |
Fig. 10. Mean convergence |
| In the text | |
 |
Fig. 11. Mean convergence |
| In the text | |
 |
Fig. 12. Radial slope of DM profile, |
| In the text | |
 |
Fig. 13. Probability density distribution for our best-fit models, adopting a power law DM profile. Along the diagonal, the 1D histograms for the corresponding parameter given on the x-axis (and independent of the label in the y-axis) are shown, while below in the triangle the joint 2D probability distributions corresponding to the parameters given on x- and y-axis are shown. The different opacities in the 2D plots indicate the different sigma ranges. In general, the model with the radial arc is much better constrained than without. The parameters are the anisotropy β, inclination i, shear magnitude, and its orientation counterclockwise to the x-axis, for the DM profile the axis ratio q, Einstein angle θE, and the slope γ′. Additionally, we show the M/L, which is used to scale the two light components, and the logarithm of the strength of the point mass θE, point. The prior range for the point mass is set to 108−1010 M⊙ as the known limits of black holes, corresponding to log(θE, point) between −4 and −1. |
| In the text | |
 |
Fig. 14. Probability density distribution for our best-fit models, adopting a NFW DM profile. Along the diagonal, the 1D histograms for the corresponding parameter given on the x-axis (and independent of the label in the y-axis) are shown, while below in the triangle the joint 2D probability distributions corresponding to the parameters given on x- and y-axis are shown. The different opacities in the 2D plots indicate the different sigma ranges. In general, the model with radial arc is much better constrained than without. The parameters are the anisotropy β, inclination i, shear magnitude, and its orientation counterclockwise to the x-axis for the DM profile the axis ratio q, strength (right) θE, and the scale radius rs. Additionally, we show the M/L, which is used to scale the two light components, and the logarithm of the strength of the point mass θE, point. The prior range for the point mass is set to 108−1010 M⊙ as the known limits of black holes, corresponding to log(θE, point) between −4 and −1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



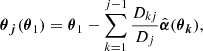
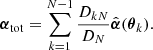
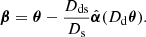
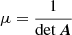
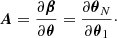
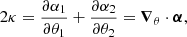
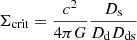
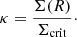
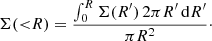
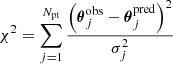
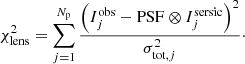
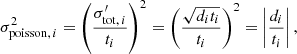
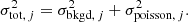
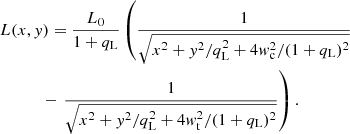
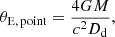
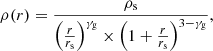
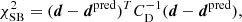
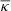
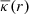
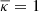
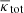

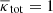
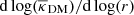
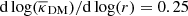
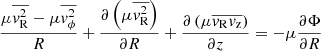
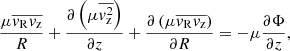
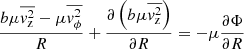
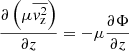
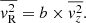
![$$ \begin{aligned} \Sigma (x\prime ,{ y}\prime ) = \sum _{k=1}^{N} \frac{L_k}{2 \pi \sigma ^2_k q\prime _k} \, \exp \left[ - \frac{1}{2 \sigma _k^2} \, \left(x^{\prime 2} + \frac{{ y}^{\prime 2}}{q^{\prime 2}_k} \right) \right] \end{aligned} $$](/articles/aa/full_html/2019/11/aa35042-19/aa35042-19-eq140.gif)
![$$ \begin{aligned} \mu (R,z) = \sum _{k=1}^{N} \frac{L_k}{(2 \pi )^{3/2} \sigma _k^3 q_k} \, \exp \left[ - \frac{1}{2 \sigma _k^2} \left( R^2 + \frac{z^2}{q_k^2} \right) \right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35042-19/aa35042-19-eq142.gif)
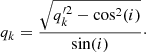
![$$ \begin{aligned} \rho (R,z) = \sum _{j=1}^M \frac{M_j }{(2 \pi )^{3/2} \sigma _j^3 q_j} \exp \left[ - \frac{1}{2 \sigma _j^2} \left( R^2 + \frac{z^2}{q_j^2} \right) \right] . \end{aligned} $$](/articles/aa/full_html/2019/11/aa35042-19/aa35042-19-eq144.gif)
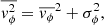
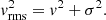
![$$ \begin{aligned} \beta _z (R,z) \equiv 1 - \frac{\overline{{ v}^2_z}}{\overline{{ v}^2_R}} = 1 - \frac{ \sum _{k=1}^N [\mu \overline{{ v}^2_z}]_k}{\sum _{k=1}^{N} b_k [\mu \overline{{ v}^2_z}]_k }\cdot \end{aligned} $$](/articles/aa/full_html/2019/11/aa35042-19/aa35042-19-eq147.gif)