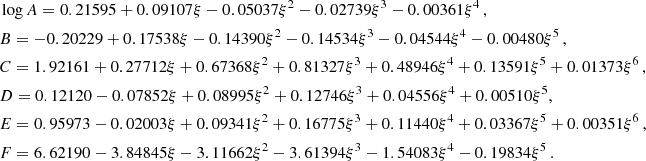| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202451798 | |
| Published online | 03 January 2025 | |
A simplified approach for reproducing fully relativistic spectra in X-ray binary systems: Application to Cygnus X-1
1
Department of Physics, University of Ioannina, GR-45110 Ioannina, Greece
2
Department of Informatics, University of Western Macedonia, GR-52100 Kastoria, Greece
⋆ Corresponding authors; th.papavasileiou@uowm.gr; hkosmas@uoi.gr
Received:
5
August
2024
Accepted:
22
November
2024
Context. General relativistic effects are strong near the black hole of an X-ray binary and significantly impact the total energy released in the innermost accretion disk’s region. The simple pseudo-Newtonian solution in the standard disk model cannot replenish for effects such as light-bending, gravitational redshift, and Doppler boost. These can heavily affect the observed spectra depending on the rotation of the black hole and the disk’s inclination.
Aims. A proper relativistic treatment would be troublesome, unappealing, or require more advanced computational tools (e.g., the kerrbb code). Our goal is to fully incorporate the black hole’s spin and all the general relativistic effects on the observed spectra coming from X-ray binary systems while maintaining the simplicity of the standard Shakura-Sunyaev disk model.
Methods. We propose a way to replicate general relativistic spectra as predicted by the Novikov-Thorne model and the kerrbb numerical code by assuming a standard accretion disk with a shifted inner boundary that depends on the black hole spin and the source’s viewing angle. An essential aspect in employing this approach for a broader range of disk inclinations is the derivation of spin-dependent temperature profiles for the accretion disk, obtained from some of the most efficient pseudo-Newtonian potentials around Kerr black holes. We then applied this method to Cygnus X-1, fitting the observational data obtained during its soft and hard spectral states.
Results. The fully relativistic spectra are reproduced to an excellent approximation, with an error margin of 0.03–4%, by a standard disk model with a modified innermost radius within the range Rin = (0.2 − 2)RISCO, depending on the source’s viewing angle and black hole spin. This approach produces observed spectra as predicted by general relativity without the need for the ray-tracing method and complex numerical calculations. Thus, it emerges as a more straightforward alternative way of estimating black hole spins through the continuum-fitting method by successfully blending the general relativity properties with the Newtonian simplicity in a more complete way than the pseudo-Newtonian solutions. Relativistic effects near the black hole make an otherwise standard accretion disk with inclination θ < 60° seem truncated to larger radii to a distant observer. On the other hand, an edge-on view of the disk gives the perspective of being pulled closer to the central object than the respective innermost radius of the stable circular orbit. In addition, we show that the observational data of Cygnus X-1 can be satisfactorily fitted by employing a reasonably simple lepto-hadronic jet model and a hybrid thermal–nonthermal corona along with the relativistic-equivalent standard thin accretion disk.
Key words: accretion, accretion disks / black hole physics / gravitation / radiation mechanisms: non-thermal / radiation mechanisms: thermal / relativistic processes
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Black hole X-ray binaries (XRBs) feature an accretion disk of gas and matter extracted from the stellar companion and twin relativistic jets propagating in the interstellar medium. These systems constitute constant and prominent sources of detectable multiwavelength emission reaching the Earth, which is measured by prominent space telescopes, such as INTEGRAL, the Cherenkov Telescope Array (CTA), MAGIC, H.E.S.S, and Fermi-LAT (Albert et al. 2007; Bodaghee et al. 2013; Ahnen et al. 2017, 2018; Malizia et al. 2023).
Many studies focus on modeling the broadband emission from XRB systems, such as Cygnus X-1 and SS 433. Such studies provide new insights into the jet collimation and acceleration mechanisms, the accretion process, the transition between different spectral states, and the disk-corona dynamics (Gierliński et al. 1999; Fender et al. 2004; Bosch-Ramon et al. 2006; Romero et al. 2007; Zdziarski et al. 2012; Zhang et al. 2014; Kantzas et al. 2020; Papavasileiou et al. 2021, 2023a,b; Mastichiadis et al. 2022). In particular, fitting the accretion disk spectra can provide valuable information about the black hole itself, such as the mass and spin and their evolution with time (Sun & Malkan 1989; Ghisellini & Tavecchio 2009; Calderone et al. 2013; Capellupo et al. 2016).
Adapting pseudo-Newtonian (PN) potentials in the standard disk model is a simple way to replenish some of the emission output emerging due to the geometric properties of general relativity (Yang & Kafatos 1995; Hawley & Krolik 2001; Sarkar & Das 2016; Dihingia et al. 2017). However, this plain solution is not free of a substantial error margin, especially for rapidly rotating black holes (Artemova et al. 1996; Semerak & Karas 1999; Mukhopadhyay 2002; Chakrabarti & Mondal 2006; Dihingia et al. 2018).
Pseudo-potentials also lack the necessary information about how the viewing angle affects the observed spectra due to effects such as gravitational redshift or the bending of light near the event horizon. The latter causes a partial reheating of the accretion disk or a decrease in the angular momentum of the compact object due to the returning radiation from the disk (Novikov & Thorne 1973; Li et al. 2005).
The numerical code kerrbb integrates all the relativistic effects following the Novikov-Thorne thin disk model (Novikov & Thorne 1973), including the disk’s self-irradiation caused by light deflection (Li et al. 2005). It is employed as part of the xspec package (Arnaud 1996) for fitting accretion disk spectra through a ray-tracing method and provides a blackbody emission continuum. Nonetheless, finding a straightforward and simpler way to estimate the fully relativistic spectra from a standard accretion disk is necessary for constructing relativistic-equivalent models to the Shakura-Sunyaev prototype.
In this work we aim to reproduce the fully relativistic disk spectra and their dependence on the black hole spin and disk inclination by appropriately modifying the disk’s innermost boundary. This is achieved using the emission pattern, as determined by the observed radiative efficiency of Kerr black holes following the kerrbb model (Campitiello et al. 2018). A necessary condition is the implementation of efficient PN gravitational potentials that are applicable even at radii smaller than the innermost stable circular orbit (ISCO) limit. Hence, we need to derive valid temperature profiles that depend on the black hole’s angular momentum.
Moreover, with this process we avoid the complexities of a complete general relativistic treatment akin to that of Novikov & Thorne (1973). Additionally, it solidifies a method for fully integrating general relativity in fitting the observed spectra from XRBs while upholding the fundamental assumptions and simplicity of the Shakura-Sunyaev model.
We adopted this method to fit the spectra from Cygnus X-1 in both its hard/low and high/soft spectral states. Toward this aim, we employed the recently revised values for the distance and the mass of the black hole associated with Cygnus X-1 (Miller-Jones et al. 2021). We also considered an angle to the line of sight that exceeds 45° based on recent findings on the system’s high polarization degree (Krawczynski et al. 2022).
Cygnus X-1 is one of the most well-studied and well-observed XRBs in our Galaxy. Measurements of its spectral distribution in the soft state by RXTE, ASCA, and OSSE in 1996 (Ling et al. 1997; Dotani et al. 1997) and more recently by XMM-Newton, NuSTAR, NICER, and IXPE (Duro et al. 2011; Walton et al. 2016; König et al. 2024; Steiner et al. 2024) indicate a thermal component from the accretion disk and a hard tail up to the MeV scale. The latter is assumed to originate from the up-scattering of seed photons from the disk in a thermal–nonthermal corona hybrid.
Observations of Cygnus X-1 in its hard/low state dictate various nonthermal emission mechanisms associated with the relativistic jet and the corona. They include the IR photometry from 0.1–0.5 eV by Persi et al. (1980) and the radio detection by Mirabel et al. (1996) and Fender et al. (2000). Soft and hard X-ray emission was detected by BeppoSAX and INTEGRAL (Di Salvo et al. 2001; Zdziarski et al. 2012), while COMPTEL measurements occupy a soft gamma-ray tail (McConnell et al. 2002). Higher-energy detection attempts and upper limits were carried out by the Fermi-LAT and MAGIC telescopes (Malyshev et al. 2013; Ahnen et al. 2017).
In the remainder of this work, we discuss the disk geometry and the radial temperature obtained from the two PN solutions for rotating black holes in Sect. 2. In Sect. 3 we discuss the radiative efficiency perceived by an observer and how it can be employed to acquire an expression for the location of the disk’s inner edge as a function of the spin and the viewing angle. Then, in Sect. 4 we compare our approach to general relativistic results and apply this method to the multiwavelength spectra detected from Cygnus X-1 in its two primary spectral states. Finally, we conclude in Sect. 5.
2. Spin incorporation in the dynamics of the standard disk model
2.1. Marginally stable orbits around rotating black holes
The stellar black holes in XRBs introduce some fundamental general relativity properties, challenging the validity of the Newtonian hydrodynamic treatment of the standard model. Those properties involve the locations of the marginally bound orbits (i.e., Rmb) and the marginally stable circular orbits (i.e., Rms or RISCO). The first case refers to particles barely resisting the gravitational pull beyond the event horizon, while the latter constitutes the innermost boundary of the accretion disk.
Static black holes are characterized by an ISCO radius of 6Rg, with Rg = GMbh/c2 being the gravitational radius. However, most black holes display a rotational motion, providing orbiting particles with the energy required to resist the gravitational pull at smaller radii. Therefore, the accretion disk begins at a radius determined by the black hole spin as (Bardeen et al. 1972)
where it is
The dimensionless spin parameter 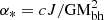 varies between 0 and 1. Moreover, the maximum possible value is considered to be α* ≈ 0.998, although indications suggest a higher limit considering a geometrically thick accretion flow (Benson & Babul 2009). In Eq. (1), the plus sign corresponds to the disk’s retrograde orbit (i.e., the opposite rotational direction) around the black hole, while the minus sign to the prograde one (i.e., corotation), which is the case for most binary systems.
varies between 0 and 1. Moreover, the maximum possible value is considered to be α* ≈ 0.998, although indications suggest a higher limit considering a geometrically thick accretion flow (Benson & Babul 2009). In Eq. (1), the plus sign corresponds to the disk’s retrograde orbit (i.e., the opposite rotational direction) around the black hole, while the minus sign to the prograde one (i.e., corotation), which is the case for most binary systems.
The ISCO radius varies between Rg and 9Rg depending on the rotational velocity and direction. Regarding prograde orbits, a significant increase in α* leads to a disk augmentation up to the gravitational radius, as seen in Fig. 1. On the other hand, maximum counter-rotation leads to a truncated accretion disk with a maximized inner boundary at 9Rg.
 |
Fig. 1. ISCO radius as a function of the black hole’s spin corresponding to prograde and retrograde orbits of the accretion flow. |
2.2. The pseudo-Newtonian solution to the standard accretion disk
Regarding static black holes, a pretty successful treatment employs the PN potential proposed by Paczyński and Wiita (Paczyńsky & Wiita 1980; Abramowicz 2009). Calculating the disk’s angular velocity using the potential ΦPW = −GMbh/(R − 2Rg) yields the fixed disk temperature profile, assuming a torque-free boundary condition (Gierliński et al. 1999). This condition is a pretty usual assumption, which is even more valid for rotating central objects since nonzero torque effects are less significant. Moreover, this treatment is often employed for rotating black holes, neglecting its limitations regarding the frame-dragging caused by the Lense-Thirring effect (Pfister 2007).
Accounting for the black hole’s angular momentum in the standard model requires a new, convenient solution in the same manner as the Paczyński-Wiita, introducing a generalized radial temperature. One of the most well-known and most successful Kerr pseudo-potentials is the one derived by Artemova et al. (1996). The corresponding gravitational force is given by
where r = R/Rg, 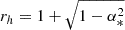 is the event horizon in the Kerr metric, and β = rin/rh − 1 denotes a dimensionless constant for a given specific black hole angular momentum. The corresponding potential reproduces pretty accurately the location of the marginally stable orbit and the disk radiative efficiency as predicted by general relativity.
is the event horizon in the Kerr metric, and β = rin/rh − 1 denotes a dimensionless constant for a given specific black hole angular momentum. The corresponding potential reproduces pretty accurately the location of the marginally stable orbit and the disk radiative efficiency as predicted by general relativity.
Another PN solution derived directly from the Kerr metric was proposed by Mukhopadhyay (2002) as
This expression refers to the equatorial plane and reproduces Rmb within 5% of error and the mechanical energy at RISCO with a 10% maximum deviation from the theoretical predictions. Hence, it produces a slightly increased luminosity in comparison. The energy dissipation distribution exhibits a less than 10% error for extreme spin values. Negative values of α* correspond to a counter-rotating accretion flow relative to the black hole. Both Eqs. (4) and (5) reduce to the Paczyński-Wiita formula for α* = 0.
The Mukhopadhyay solution has limited use due to its complex and troublesome analytical expression of the potential. However, we can still derive valid temperature profiles for the accretion disk using the force expression. To confirm our results, we used numerical integration of the gravitational force.
More recently, Dihingia et al. (2018) improved upon the attempt of Chakrabarti & Mondal (2006) to study accretion flows around rotating black holes with α* < 0.8. They nullify the spin limitation since most observational data incline toward extreme rotating stellar objects. However, the proposed effective potential is not as convenient or accurate in its predictions compared to the ones discussed above.
2.3. Spin-dependent disk temperature profiles
The radial temperature of an accretion disk around a Kerr black hole employing the pseudo-potential of Eq. (4) is derived as
where we have
The constant T0 depends on the black hole accretion rate and mass as
The mathematical expressions used to derive T(r) can be found in Appendix A. In a similar way, the modified temperature profile that corresponds to the Mukhopadhyay potential is written as
The spin contribution is inserted through the following functions:
In comparison, Eq. (6) produces negligibly larger disk luminosity across the spectrum below 1 keV that drops slightly more abruptly for higher energies. The deviation is marginal for large α* in the corotation case, while they coincide for the rest of the spin values. Both expressions reduce to the temperature function of Gierliński et al. (1999) adopting the Paczyński-Wiita potential.
Figure 2 demonstrates the disk surface temperature of Eq. (9) for varying positive and negative spins. As described in the previous subsection, the inner disk edge rin (in units of Rg) is given by the assumption of locally nonrotating frames in the Kerr geometry. We can see a significant increase in temperature for α* > 0.9. It should be noted that this is the value range in which the PN solution is more likely to deviate from a thorough general relativistic treatment.
 |
Fig. 2. Temperature dependence on the disk’s radius for different values of the black hole spin. |
The total energy radiated from the accretion disk equals the loss of mechanical energy at its innermost boundary,
where the specific energy is defined as
In Fig. 3 we can clearly see how the brightness of the disk is determined by the rotation of the black hole. The abrupt increase with higher spin is attributed to the accretion flow near the gravitational radius.
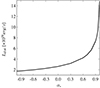 |
Fig. 3. Black hole spin impact on the total energy emitted by the accretion disk. |
Extreme Kerr black holes (i.e., α* > 0.9), governed by frame-dragging effects near their event horizon, are verified as central objects for an increasing number of well-known XRBs (McClintock et al. 2006; Stuchlík & Kološ 2016; Zhao et al. 2021). Therefore, the spin-dependent profiles given by Eqs. (6) and (9) yield a more realistic measurement of the energy released near those sources.
3. Spectral angular distribution via disk surface fluctuations
The detectable spectra from accretion disks are heavily dependent on the observer’s viewing angle. Ignoring all relativistic effects, the observed radiative efficiency is 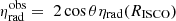 , where
, where 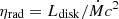 . Regardless, frame-dragging, gravitational redshift, Doppler boost, and light-bending effects significantly alter the angular dependence of the perceived emission near the black hole. Thus, the emission pattern following the relativistic kerrbb model is determined by an analytic expression derived by Campitiello et al. (2018) as
. Regardless, frame-dragging, gravitational redshift, Doppler boost, and light-bending effects significantly alter the angular dependence of the perceived emission near the black hole. Thus, the emission pattern following the relativistic kerrbb model is determined by an analytic expression derived by Campitiello et al. (2018) as 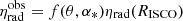 . The function f(θ, α*) is given in the Appendix B.
. The function f(θ, α*) is given in the Appendix B.
The associated observed total luminosity normalized by Ṁc2 is plotted for varying values of α* in Fig. 4. We also include the radiative efficiency produced with both pseudo-potentials discussed in this work and the respective theoretical predictions of Novikov-Thorne. The comparison between the PN adaptation and general relativity reveals an increasing deviation for highly rotating black holes.
 |
Fig. 4. Comparison of the energy radiated from Novikov-Thorne and Shakura-Sunyaev disks. The solid lines correspond to the radiative efficiency given by the analytic counterpart of the kerrbb model as observed for different disk inclinations and black hole spin values (Campitiello et al. 2018 is referred to as C18). The dashed purple line showcases the angular dependence according to the Shakura-Sunyaev model for a static black hole, neglecting all relativistic contributions. The colored dotted lines for each spin value depict the respective theoretical predictions of Novikov & Thorne (1973). For comparison, the respective black and dotted orange lines represent the Kerr PN treatment of this work. |
Concerning nonrotating central objects, the angular distribution, according to the standard model, follows a similar pattern to that of the relativistic case. Higher angular momentum yields an abrupt drop in the total emission output for accretion disks inclined beyond 60°, a viewing angle less affected by light-bending effects. However, extreme rotation triggers a resurgence between 50° and 70° in the radiation escaping from the black hole’s gravitational field.
The radiative efficiency is independent of the accretion rate and the spectral hardening factor fcol. It depends negligibly on the black hole’s stellar mass Mbh and the disk’s inner radius Rin, as long as the outer radius is large enough, Rout > 1011 cm, akin to the default value set in kerrbb. Figure 5 illustrates this correlation, which is established by employing Eqs. (6) and (9) in calculating the thermal spectra from the disk. In this work, we fit the power-law form of the Artemova solution (black dotted lines in Fig. 5) with the following expression:
 |
Fig. 5. Radiative efficiency for different α* as a function of the disk’s inner radius, given in terms of the RISCO. The total disk luminosity is calculated using the Artemova (A96; solid black lines) and the Mukhopadhyay (M02; solid orange lines) potentials. The dotted black lines correspond to Eq. (14), while the orange ones fit a similar expression with a power-law index of p = 0.75. |
The respective orange solid lines of the Mukhopadhyay potential are fitted using a power-law index of p = 0.75 instead. A noticeable deviation for all spin values, especially near the ISCO radius, deter us from further exploiting the Mukhopadhyay pseudo-force. Also, the fact that the Artemova potential works for radii significantly smaller than RISCO makes it a very suitable tool for matching the fully relativistic spectrum for a given angle of view.
Furthermore, including all the effects of general relativity and incorporating the correct angular distribution urges the equivalence between Eq. (14) and the observed efficiency given by the analytic function of Campitiello et al. (2018, see our Appendix B). By doing so, we find an expression for the modified inner boundary of the accretion disk, which is given by
This way, energy distributions equivalent to the fully relativistic spectra are reproduced by a standard disk model with the temperature profile of Eq. (6) and an innermost radius given by Eq. (15). The latter is plotted in Fig. 6 and depends on the inclination and angular momentum of the accreting compact object. Basically, when we modify the disk inner radius in order to achieve the kerrbb observed radiative efficiency, we produce spectra that depend on the angle θ in the same way as dictated by general relativity.
 |
Fig. 6. The innermost radius of a standard accretion disk as a function of the source’s viewing angle and the black hole’s rotation. This adjustment leads to spectra similar to those obtained with the kerrbb model when Rin = RISCO. |
Figure 6 shows that, independently of the rotation, the physical processes associated with an accretion disk observed from an angle of approximately θ = 60 − 65° identify with the Newtonian-like dynamics of the Shakura-Sunyaev model. Consequently, the boundary-modification approach is exceptionally accurate regarding this angle range.
Relativistic effects near the black hole make an otherwise standard accretion disk viewed with an angle of θ < 60° seem truncated to larger radii to a distant observer. On the other hand, an edge-on view of the disk gives the perspective of being pulled closer to the central object than the respective ISCO radius. That is a focal point in fabricating fully relativistic counterparts to simple standard disks using Eq. (15).
4. Results and discussion
4.1. Comparison to general relativity
There are three primary sources of error concerning the approach presented in this work for calculating relativistic spectra. The first is the intrinsic error margin of the analytic function f(θ, α*), which is relatively small and does not exceed 1% (Campitiello et al. 2018). The second one is due to the PN-potential adoption, which can reach 8–9% in the case of the Artemova solution. Lastly, the error introduced in the context of this work is due to the deviation between the PN-generated ηrad(Rin) and Eq. (14), with the choice of the p = 1.17 index, which is also evident in Fig. 5.
By adjusting the disk’s inner radius, we eradicate the most significant part of the PN-induced error entering the calculations. That holds for every choice of parameterization. The only deviation remaining concerns the radiative efficiency at the ISCO radius, ηrad(RISCO), which is still slightly overestimated. A fitting solution involves a subtle redefinition of the RISCO according to the factor k = R′ISCO/RISCO, which on average is k ≈ 1.075, covering the spin value range. The resulting spectra are slightly shifted to lower energies, as shown in Fig. 7 for a sample of spin values with their respective shifting factors. For comparison, we also demonstrate the disk emission (dotted lines) assuming the RISCO given in Eq. (1).
 |
Fig. 7. Modified disk spectra that correspond to the correct radiative efficiencies for different α*. They are produced by slightly shifting the ISCO radius as R′ISCO = kRISCO while the rest of the free parameters remain unchanged. The unaltered spectra are also shown (dotted lines) for comparison. |
The error introduced due to the index p = 1.17 in Eq. (14) ranges between 0.03 and 2.5% for θ < 60° regardless how fast the black hole is rotating, as demonstrated in the heat map of Fig. 8. Moreover, there is a slight general increase in the deviation for viewing angles close to 80° (i.e., the kerrbb code operates in the 0–85° range) when the spin does not belong in the α* = 0.4 − 0.7 regime.
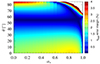 |
Fig. 8. The ηrad error heat map depending on the viewing angle and black hole spin. The observed radiative efficiency is obtained via the boundary-shifting method for approximating the fully relativistic spectra from standard accretion disks. |
The applicability of this work’s approach to highly inclined accretion disks around corotating black holes with α* > 0.8 is constrained due to the limitations of the temperature of Eq. (4). That is also obvious from the abruptly broken power law in Fig. 5. Furthermore, relativistic spectra can be attained for θ ≤ 65° when α* ≥ 0.998. That is somewhat restrictive but falls within the parameter range of many well-known XRBs in our galaxy, while the rest of the sources would require the kerrbb model.
In Fig. 8, the dark red contour around the restricted white area signifies a substantial increase in the ηrad error that reaches 10–12%. Nonetheless, a better-suited index in Eq. (14) in the p = 1.05 − 1.2 range for a specific spin-inclination combination could significantly reduce the deviation from the actual relativistic results. That is one of our targets in future projects.
In the left panel of Fig. 9, we compare the observed disk spectra corresponding to the Artemova PN solution with the spectra obtained through this work’s boundary-shifting approach following Eq. (15). We assume a static (α* = 0), and a rapidly rotating black hole (α* = 0.998) for greater variety. We can see that the two different approaches are rather close for both spin values when the disk is viewed with an angle of θ = 60°, a result also verified by Fig. 6 where Rin ≈ RISCO. However, the significant deviation is obvious when θ = 0°, especially in the maximum spin case where the disk’s inner edge is closer to the black hole and general relativistic effects are very important.
 |
Fig. 9. Comparison between the disk spectra produced through the boundary-shifting method of this work and: the Artemova PN potential (left panel) and the general relativistic treatment of the kerrbb model (right panel). The parameters used are Mbh = 10 M⊙, Ṁ = 1018 g/s, and fcol = 1. |
The PN potential clearly overestimates the total disk luminosity for θ ≲ 60°, while it underestimates it when θ ≳ 60°. Besides its intrinsic error, the main reason is that while it offers a very good measurement of the additional energy radiated away by the disk, it cannot offer any information on the spectra a distant observer receives depending on θ. Instead, the PN solution adopts the angular dependence of the classic Shakura-Sunyaev model, 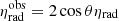 .
.
Our results show an excellent agreement with the fully relativistic formalism of Novikov and Thorne incorporated in the kerrbb model, as seen in the right panel of Fig. 9. The deviation, partially due to the ηrad error margin of Fig. 8, is minimal even for highly inclined accretion disks around rapidly rotating central objects.
Furthermore, the approach of this work presents a direct alternative solution in obtaining the observed fully relativistic disk spectra without any complex mathematical formalism and the need for a ray-tracing method. Given that the Novikov-Thorne model has been proven very efficient by general relativity magnetohydrodynamic simulations (Kulkarni et al. 2011), our approach could provide a very suitable and straightforward way for estimating black hole spins via the continuum-fitting method.
4.2. Cygnus X-1: High/soft spectral state
Using Eqs. (6) and (15) and the recently redefined Cygnus X-1 parameters of Table 1, we showcase the spin-dependent disk spectra while the system is going through the soft state in Fig. 10. It should be mentioned that those results were obtained for a fixed mass accretion rate of Ṁ = 8.5 × 10−8 M⊙/yr, which, in most cases, is a free model parameter. In addition, we estimate the radiative efficiency of an extreme rotating black hole to be ηrad ≈ 0.35, which agrees with the theoretical predictions. Moreover, employing this work’s approach allows us to constrain more accurately the black hole’s accretion rate as long as we have a precise value of the spin or vice versa.
Cygnus X-1 parameters employed in this work.
 |
Fig. 10. Spectral energy distribution emitted from the accretion disk for varying black hole spins. The solid lines correspond to the alignment between the black hole and accretion disk rotational directions. |
The spectrum’s shift to higher energies in Fig. 10 is attributed to a substantially hotter inner disk layer that contributes heavily to the harder X-ray thermal component. On the other hand, the soft thermal emission is associated with the extended disk region far from the ISCO radius (i.e., R ≫ 6Rg).
In Fig. 11 we outline the data obtained during observations of the soft spectral state of Cygnus X-1 (Ling et al. 1997; Dotani et al. 1997; Walton et al. 2016). The thermal emission at lower energies is fitted by a blackbody spectrum emitted by the inner disk regions. The respective spin is found to be α* = 0.97, satisfying the lower limit α* > 0.9696 set by Miller-Jones et al. (2021) for the slightly misaligned spin-orbit case. This value is close to the limits set by the continuum-fitting method as α* > 0.983 (Gou et al. 2014) and the relativistic reflection modeling as 0.93 ≳ α* ≲ 0.96 (Walton et al. 2016). The high spin yields an accretion disk close to the compact object (i.e., Rin ≈ Rg), a primary characteristic of the high/soft state.
 |
Fig. 11. High/soft spectral state of Cygnus X-1 as observed by RXTE, ASCA, and NuSTAR (Ling et al. 1997; Dotani et al. 1997; Walton et al. 2016). The observational data are fitted by a blackbody spectrum emitted by the inner disk region and an IC-scattered component of the disk emission off a combination of thermal and nonthermal corona electrons. |
Non-blackbody effects are incorporated through a spectral hardening factor fcol ≈ 1 − 2 in multicolor disk models (Merloni et al. 2000; Li et al. 2005). It constitutes a color correction of the disk temperature. This adjustment, paired with an appropriate accretion rate, accounts for the intense electron scattering corresponding to disk temperatures around 106 − 107 K, the nonzero torque near the inner disk edge associated with strong accretion flow magnetization, and returning radiation effects. Fitting the Cygnus X-1 observational data using the radial temperature of Eq. (6) yields a color correction factor of fcol ≈ 1 and a substantially lower mass accretion rate than what would be otherwise necessary to produce the disk photons above 1 keV.
Moreover, the hard tail above 5 keV is reproduced by the inverse-Compton (IC) scattered disk emission off a thermal–nonthermal corona hybrid described by the parameters of Table 2. In this case, the corona is much more weakly present compared to the hard/low state. The power-law spectrum indicates an electron (or positron) distribution injection, differentiating the two leading emission mechanisms near 10 keV. The injected distribution could be a product of an intense photon annihilation process above the disk level that softens by gradually losing energy due to IC scattering. The resulting power law has an index of p > 3 since pinj > 2. We neglected Compton reflection of the scattered spectrum and irradiation effects beyond those integrated into the kerrbb model as they go beyond the scope of this work. As a result, there is a slight deviation near 6–7 keV in Fig. 11 where the iron K line is detected (Walton et al. 2016).
Model parameterization of Cygnus X-1 that fits the observational data.
We assumed the injection of 50 nonthermal electrons blending in a thousand thermal ones. Those particles preserve their initial power-law shape, while the rest are described by a Maxwell–Jüttner distribution, which dominates for energies below γ = 1.8. The optical depth in Table 2 corresponds to the thermal counterpart of the corona hybrid. Assuming a fixed spherical region, injecting power-law particles increases corona’s opacity by a factor of 1 + h, where h is the fraction of accelerated to thermal electrons (or positrons; i.e., τcorh = τcor(1 + h)≈0.3 in our case).
4.3. Jet emission model
We adopted a simple jet model that assumes partial acceleration of hadrons and leptons due to shock-wave propagation within a conic slice of the jet frame. A power-law energy dependence with an index of p = 2 describes the nonthermal particle distribution (Bosch-Ramon et al. 2006; Reynoso & Carulli 2019). The model is explicitly described in previous works (Reynoso & Romero 2009; Romero et al. 2007; Papavasileiou et al. 2021, 2022; Kosmas et al. 2023). The transport equation shaping the energy-dependent particle distributions within the jet is in a steady-state form as
The particle injection function is denoted as Qinj(E, z) and the rate at which the particles lose energy is given by 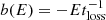 .
.
The accelerated electrons and protons inside the jet are cooled down primarily via synchrotron emission, which covers the regime from radio to soft gamma-ray wavelengths. On the other hand, the hadronic emission mechanism involves collisions between the relativistic protons and thermal ones, which produce pions and muons that decay to high-energy neutrinos and gamma rays.
As described in the previous subsection, we considered an IC spectrum component to explain the MeV tail observed from Cygnus X-1. We employed the mathematical formalism described in Rybicki & Lightman (2008) for those calculations, assuming both the Compton and IC cases. We adopted the conclusions of Blumenthal & Gould (1970) to estimate the scattered spectrum caused by an electron distribution with γe ≫ 1 while considering both the Thomson and the Klein-Nishina limits.
4.4. Cygnus X-1: Hard/low spectral state
The hard/low state is characterized by the intense presence of the relativistic jet and a strong coronal activity. The accretion disk experiences a truncation to larger radii, leaving behind a radiatively inefficient advection-dominated accretion flow (Takahashi 2007; Narayan & McClintock 2008; Li & Qiao 2023). Therefore, relativistic effects are expected to be less significant compared to the soft state.
In Fig. 12, we present the total disk spectra for various spin values of the black hole. They comprise a blackbody component and the respective IC emission due to a purely thermal corona. For the case of a rapidly counter-rotating black hole, we also include the scattered emission flux due to a nonthermal corona component described by the parameter h, which is the number density ratio of the nonthermal to thermal particles. The corona parameterization is listed in Table 2. In this case, we assume an accretion rate of Ṁ ≈ 10−8 M⊙/yr.
The slump between the two emission peaks in Fig. 12 is smoothed out for extreme spin values. At the same time, the incident disk spectrum covers a broader energy range, allowing for up-scattering even to the gamma-ray regime. Nonetheless, this outcome heavily relies on the assumed truncation radius, which we consider to be equal to 3RISCO in this case. Thus, the hard state signifies the growing irrelevance of the relativistic effects on the detected emission flows due to the disk retreating to distances further away from the black hole.
 |
Fig. 12. Thermal disk emission based on the dimensionless spin parameter. The spectrum produced when seed photons from the disk are IC-scattered off the purely thermal corona is also included. The dotted brown curves correspond to the injection of nonthermal particles in the corona, assuming a maximum counter-rotating black hole. Their number density is written as a fraction, h, of the thermal electrons. |
The IR measurements of Cygnus X-1 (Persi et al. 1980), as demonstrated in Fig. 13, are fitted by the thermal emission of the system’s blue supergiant, whose effective temperature and luminosity are listed in Table 1. Synchrotron emission by magnetically accelerated leptons and hadrons inside the jet frame reproduce the radio emission flux below 0.01 eV. Nevertheless, the employed jet emission model is relatively simple and would require some modifications to replicate the softer radio data accurately.
 |
Fig. 13. Spectral energy distribution associated with the hard/low state of Cygnus X-1. The plotted observational data include the IR and radio emission points up to 1 eV Persi et al. (1980) as P80, Fender et al. (2000) as F00), the soft and hard X-ray emission detected by BeppoSAX and INTEGRAL (Di Salvo et al. 2001; Zdziarski et al. 2012), and the gamma-ray measurements and upper limits by COMPTEL, Fermi-LAT, and MAGIC (McConnell et al. 2002; Malyshev et al. 2013; Ahnen et al. 2017). |
The soft and hard X-ray measurements by BeppoSAX and INTEGRAL (Di Salvo et al. 2001; Zdziarski et al. 2012) fit an IC spectrum caused by the corona’s intervention on the incident disk spectrum. The corona parameterization for the hard state is given in Table 2. It is significantly hotter, larger, and optically thicker than the one attributed to the soft state. Moreover, the thermal electrons dominate the distribution over energies up to γ = 1.7.
So far, we have adopted a maximally rotating compact object. Matching the observations with a static black hole (i.e., α* = 0) would require a considerably higher accretion rate and the adoption of a color-corrected disk. In addition, the corona electrons would have to achieve energies above γ = 40, as indicated in Fig. 13.
The intersection between the high-energy tail of the synchrotron spectrum and the IC-scattered flux matches the MeV measurements by COMPTEL (McConnell et al. 2002). Without the particle injection in the corona, the thermal distribution would have to reach a temperature of a few hundred keV to replicate the data.
The synchrotron component due to highly relativistic electrons and protons (the latter achieve energies up to Emax ≈ 107 GeV) confirms the Fermi-LAT gamma-ray measurements and upper limits, as seen in Fig. 13. At last, the proton-proton mechanism is too weak in our lepton-dominated jet model (i.e., Lp/Le = 0.009) to reach the upper limits set by the MAGIC collaboration for the high-energy gamma-ray regime (Ahnen et al. 2017). Nevertheless, photo-absorption caused by the disk is dominant near the lower-jet emitting regions. Hence, detected gamma-ray fluxes above 10 GeV are more likely to originate inside the expanded jet frame (Zanin et al. 2016; Papavasileiou et al. 2023a).
5. Summary and conclusions
We propose a simple and effective approach for including relativistic effects in the spectra observed from standard accretion disks. That is possible by integrating the emission pattern of the kerrbb model, found in Campitiello et al. (2018), via modification of the disk’s boundary, through which most of the gravitational energy is released. Hence, it is necessary to implement spin-dependent temperature profiles derived from PN potentials that account for the Kerr metric’s fundamental properties. Furthermore, we employed this approach to fit the observed spectra from Cygnus X-1 from when it went through its (i) high/soft and (ii) hard/low spectral states.
The energy distribution radiated away from a thin accretion disk described by the Novikov-Thorne and kerrbb models is equivalent to that emitted by a Shakura-Sunyaev disk with a modified innermost radius, which depends on the system’s spin and viewing angle. It is crucial to use the spin-dependent PN potential. Otherwise, the modified boundary cannot be applied to XRBs inclined by θ > 60° regardless of the black hole’s rotation. The best-suited potential is the one suggested by Artemova et al. (1996) because it produces valid results for small radii, even more so than the RISCO. Hence, the boundary transition is within the Rin/RISCO = 0.2 − 1.0 range when θ ≥ 60°, and Rin/RISCO = 1.0 − 2.0 otherwise.
The thermal emission from Cygnus X-1 in the high/soft state is reproduced by a blackbody spectrum associated with the inner disk surface. The nonthermal tail at higher energies fits the IC-scattered emission of the incident disk photons due to a thermal–nonthermal corona hybrid. Regarding the hard/low state, the synchrotron emission from a fairly simple lepto-hadronic jet is sufficient to match the radio and soft gamma-ray measurements. The soft X-ray emission approximates the blackbody spectrum from a truncated accretion disk. A harder IC component accompanies it due to a more extensive, hotter, and optically thicker corona compared to the one in the soft state. Regarding higher energies, the collisions of protons inside the jet are insufficient in generating detectable high-energy gamma rays.
Our results show a very good agreement with the fully relativistic treatment of the Novikov-Thorne model incorporated in the kerrbb code, with a deviation within 0.03–4%. The intrinsic error of the pseudo-potential, which leads to an overestimation of the radiated luminosity, is minimized by the consistent boundary transition to fit the relativistic predictions. However, the radiative efficiency deviation at RISCO remains. Therefore, we propose a fixing factor of k ≈ 1.075 that marginally shifts the RISCO to match the theoretical predictions.
References
- Abramowicz, M. A. 2009, A&A, 500, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahnen, M., Ansoldi, S., Antonelli, L., & Arcaro, C. 2017, MNRAS, 472, 3474 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2018, A&A, 612, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 665, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Artemova, I. V., Bjoernsson, G., & Novikov, I. D. 1996, ApJ, 461, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [Google Scholar]
- Benson, A. J., & Babul, A. 2009, MNRAS, 397, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [Google Scholar]
- Bodaghee, A., Tomsick, J. A., Pottschmidt, K., et al. 2013, ApJ, 775, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Romero, G. E., & Paredes, J. M. 2006, A&A, 447, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brocksopp, C., Fender, R. P., Larionov, V., et al. 1999, MNRAS, 309, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., & Dotti, M. 2013, MNRAS, 431, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Campitiello, S., Ghisellini, G., Sbarrato, T., & Calderone, G. 2018, A&A, 612, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capellupo, D. M., Netzer, H., Lira, P., Trakhtenbrot, B., & Mejía-Restrepo, J. 2016, MNRAS, 460, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., & Mondal, S. 2006, MNRAS, 369, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Dihingia, I. K., Das, S., & Mandal, S. 2017, MNRAS, 475, 2164 [Google Scholar]
- Dihingia, I. K., Das, S., Maity, D., & Chakrabarti, S. 2018, Phys. Rev. D, 98, 083004 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., Done, C., Życki, P. T., Burderi, L., & Robba, N. R. 2001, ApJ, 547, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Dotani, T., Inoue, H., Mitsuda, K., et al. 1997, ApJ, 485, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Duro, R., Dauser, T., Wilms, J., et al. 2011, A&A, 533, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fender, R. P., Pooley, G. G., Durouchoux, P., Tilanus, R. P. J., & Brocksopp, C. 2000, MNRAS, 312, 853 [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [Google Scholar]
- Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [CrossRef] [Google Scholar]
- Gou, L., McClintock, J. E., Remillard, R. A., et al. 2014, ApJ, 790, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., & Krolik, J. H. 2001, ApJ, 548, 348 [CrossRef] [Google Scholar]
- Kantzas, D., Markoff, S., Beuchert, T., et al. 2020, MNRAS, 500, 2112 [CrossRef] [Google Scholar]
- König, O., Mastroserio, G., Dauser, T., et al. 2024, A&A, 687, A284 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosmas, O., Papavasileiou, T., & Kosmas, T. 2023, Universe, 9, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczynski, H., Muleri, F., Dovčiak, M., et al. 2022, Science, 378, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, A. K., Penna, R. F., Shcherbakov, R. V., et al. 2011, MNRAS, 414, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., & Qiao, E. 2023, MNRAS, 521, 3237 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., Zimmerman, E. R., Narayan, R., & McClintock, J. E. 2005, ApJS, 157, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ling, J. C., Wheaton, W. A., Wallyn, P., et al. 1997, ApJ, 484, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Malizia, A., Bassani, L., Landi, R., et al. 2023, A&A, 671, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malyshev, D., Zdziarski, A. A., & Chernyakova, M. 2013, MNRAS, 434, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Mastichiadis, A., Petropoulou, M., & Kylafis, N. D. 2022, A&A, 662, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClintock, J. E., Shafee, R., Narayan, R., et al. 2006, ApJ, 652, 518 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, M. L., Zdziarski, A. A., Bennett, K., et al. 2002, ApJ, 572, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Fabian, A. C., & Ross, R. R. 2000, MNRAS, 313, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
- Mirabel, I. F., Claret, A., Cesarsky, C. J., Boulade, O., & Cesarsky, D. A. 1996, A&A, 315, L113 [NASA ADS] [Google Scholar]
- Mukhopadhyay, B. 2002, ApJ, 581, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & McClintock, J. E. 2008, New Astron. Rev., 51, 733, jean-Pierre Lasota, X-ray Binaries, Accretion Disks and Compact Stars [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, Astrophysics of Black Holes (United States: Gordon and Breach, Science Publishers, Inc) [Google Scholar]
- Paczyńsky, B., & Wiita, P. J. 1980, A&A, 88, 23 [NASA ADS] [Google Scholar]
- Papavasileiou, T., Kosmas, O., & Sinatkas, I. 2021, Galaxies, 9, 67 [CrossRef] [Google Scholar]
- Papavasileiou, T., Kosmas, O., & Sinatkas, I. 2022, Symmetry, 14, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Papavasileiou, T. V., Kosmas, O. T., & Sinatkas, I. 2023a, A&A, 673, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papavasileiou, T., Kosmas, O., & Sinatkas, I. 2023b, Universe, 9, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Persi, P., Ferrari-Toniolo, M., Grasdalen, G. L., & Spada, G. 1980, A&A, 92, 238 [NASA ADS] [Google Scholar]
- Pfister, H. 2007, Gen. Relat. Grav., 39, 1735 [CrossRef] [Google Scholar]
- Reynoso, M. M., & Carulli, A. M. 2019, Astropart. Phys., 109, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, M. M., & Romero, G. E. 2009, A&A, 493, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 2008, Radiative Processes in Astrophysics (New York: John Wiley& Sons) [Google Scholar]
- Sarkar, B., & Das, S. 2016, MNRAS, 461, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Semerak, O., & Karas, V. 1999, A&A, 343, 325 [NASA ADS] [Google Scholar]
- Steiner, J. F., Nathan, E., Hu, K., et al. 2024, ApJ, 969, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Stirling, A., Spencer, R., de La Force, C., et al. 2001, MNRAS, 327, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., & Kološ, M. 2016, ApJ, 825, 13 [CrossRef] [Google Scholar]
- Sun, W.-H., & Malkan, M. A. 1989, ApJ, 346, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, R. 2007, A&A, 461, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tetarenko, A. J., Casella, P., Miller-Jones, J. C. A., et al. 2019, MNRAS, 484, 2987 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Tomsick, J. A., Madsen, K. K., et al. 2016, ApJ, 826, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, R., & Kafatos, M. 1995, A&A, 295, 238 [NASA ADS] [Google Scholar]
- Zanin, R., Fernández-Barral, A., de Oña Wilhelmi, E., et al. 2016, A&A, 596, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Lubiński, P., & Sikora, M. 2012, MNRAS, 423, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Xu, B., & Lu, J. 2014, ApJ, 788, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, X., Gou, L., Dong, Y., et al. 2021, ApJ, 908, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Ziółkowski, J. 2005, MNRAS, 358, 851 [CrossRef] [Google Scholar]
Appendix A: Derivation of the temperature corresponding to each disk’s surface area
The temperature corresponding to the blackbody spectrum emitted by a single surface area of the accretion disk, according to the Stefan-Boltzmann law, is given by
where σ is the well-known Stefan-Boltzmann constant and Q(R) is the energy flux generated per unit of time and area of the disk side that faces the Earth. The latter is defined as
where jin is the specific angular momentum at the innermost disk regions and ω is the angular velocity, which is determined as
Replacing the angular velocity and momentum per unit mass yields the following definition of the disk’s surface brightness
where F(R) is the gravitational force.
Appendix B: Radiative efficiency configuration due to general relativistic effects
The analytic function integrating all the effects of general relativity is presented in Campitiello et al. (2018) as
The parameters in the above expression depend on the spin. Posing ξ = log(1 − α*) yields the following best-fitting functions for the numerical results of kerrbb:
All Tables
All Figures
 |
Fig. 1. ISCO radius as a function of the black hole’s spin corresponding to prograde and retrograde orbits of the accretion flow. |
| In the text | |
 |
Fig. 2. Temperature dependence on the disk’s radius for different values of the black hole spin. |
| In the text | |
 |
Fig. 3. Black hole spin impact on the total energy emitted by the accretion disk. |
| In the text | |
 |
Fig. 4. Comparison of the energy radiated from Novikov-Thorne and Shakura-Sunyaev disks. The solid lines correspond to the radiative efficiency given by the analytic counterpart of the kerrbb model as observed for different disk inclinations and black hole spin values (Campitiello et al. 2018 is referred to as C18). The dashed purple line showcases the angular dependence according to the Shakura-Sunyaev model for a static black hole, neglecting all relativistic contributions. The colored dotted lines for each spin value depict the respective theoretical predictions of Novikov & Thorne (1973). For comparison, the respective black and dotted orange lines represent the Kerr PN treatment of this work. |
| In the text | |
 |
Fig. 5. Radiative efficiency for different α* as a function of the disk’s inner radius, given in terms of the RISCO. The total disk luminosity is calculated using the Artemova (A96; solid black lines) and the Mukhopadhyay (M02; solid orange lines) potentials. The dotted black lines correspond to Eq. (14), while the orange ones fit a similar expression with a power-law index of p = 0.75. |
| In the text | |
 |
Fig. 6. The innermost radius of a standard accretion disk as a function of the source’s viewing angle and the black hole’s rotation. This adjustment leads to spectra similar to those obtained with the kerrbb model when Rin = RISCO. |
| In the text | |
 |
Fig. 7. Modified disk spectra that correspond to the correct radiative efficiencies for different α*. They are produced by slightly shifting the ISCO radius as R′ISCO = kRISCO while the rest of the free parameters remain unchanged. The unaltered spectra are also shown (dotted lines) for comparison. |
| In the text | |
 |
Fig. 8. The ηrad error heat map depending on the viewing angle and black hole spin. The observed radiative efficiency is obtained via the boundary-shifting method for approximating the fully relativistic spectra from standard accretion disks. |
| In the text | |
 |
Fig. 9. Comparison between the disk spectra produced through the boundary-shifting method of this work and: the Artemova PN potential (left panel) and the general relativistic treatment of the kerrbb model (right panel). The parameters used are Mbh = 10 M⊙, Ṁ = 1018 g/s, and fcol = 1. |
| In the text | |
 |
Fig. 10. Spectral energy distribution emitted from the accretion disk for varying black hole spins. The solid lines correspond to the alignment between the black hole and accretion disk rotational directions. |
| In the text | |
 |
Fig. 11. High/soft spectral state of Cygnus X-1 as observed by RXTE, ASCA, and NuSTAR (Ling et al. 1997; Dotani et al. 1997; Walton et al. 2016). The observational data are fitted by a blackbody spectrum emitted by the inner disk region and an IC-scattered component of the disk emission off a combination of thermal and nonthermal corona electrons. |
| In the text | |
 |
Fig. 12. Thermal disk emission based on the dimensionless spin parameter. The spectrum produced when seed photons from the disk are IC-scattered off the purely thermal corona is also included. The dotted brown curves correspond to the injection of nonthermal particles in the corona, assuming a maximum counter-rotating black hole. Their number density is written as a fraction, h, of the thermal electrons. |
| In the text | |
 |
Fig. 13. Spectral energy distribution associated with the hard/low state of Cygnus X-1. The plotted observational data include the IR and radio emission points up to 1 eV Persi et al. (1980) as P80, Fender et al. (2000) as F00), the soft and hard X-ray emission detected by BeppoSAX and INTEGRAL (Di Salvo et al. 2001; Zdziarski et al. 2012), and the gamma-ray measurements and upper limits by COMPTEL, Fermi-LAT, and MAGIC (McConnell et al. 2002; Malyshev et al. 2013; Ahnen et al. 2017). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



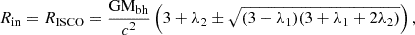
![$$ \begin{aligned} \lambda _{1}&= 1+\left(1-\alpha _{*}^{2}\right)^{1/3}\left[\left(1+\alpha _{*}\right)^{1/3}+\left(1-\alpha _{*}\right)^{1/3}\right], \end{aligned} $$](/articles/aa/full_html/2025/01/aa51798-24/aa51798-24-eq2.gif)
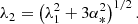
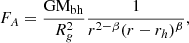
![$$ \begin{aligned} F_M= \frac{\mathrm{GM}_{\rm bh}}{R_{g}^2}\frac{\left(r^2-2\alpha _{*}\sqrt{r}+\alpha _{*}^2\right)^2}{r^3\left[\sqrt{r}(r-2)+\alpha _{*}\right]^2}\cdot \end{aligned} $$](/articles/aa/full_html/2025/01/aa51798-24/aa51798-24-eq7.gif)
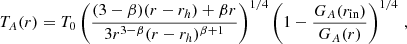
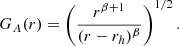
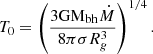
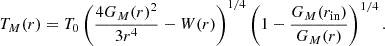
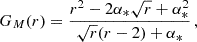
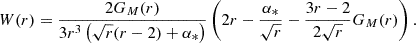
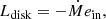
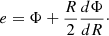
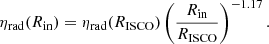
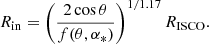
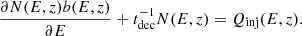
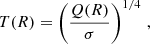
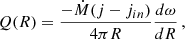
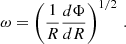
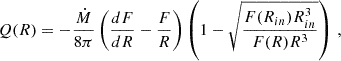
![$$ \begin{aligned} f(\theta , \alpha _*)= A\cos \theta \left[1-(\sin \theta )^C\right]^B\left[1-E(\sin \theta )^F\right]^D \, . \end{aligned} $$](/articles/aa/full_html/2025/01/aa51798-24/aa51798-24-eq28.gif)