| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202451657 | |
| Published online | 29 October 2024 | |
Diffuse interstellar bands as dust indicators: The contribution from 3D maps
1
GEPI, Observatoire de Paris, PSL University, CNRS,
5 Place Jules Janssen,
92190
Meudon,
France
2
ACRI-ST,
260 Route du Pin Montard, BP234,
06904
Sophia-Antipolis,
France
3
ACRI-ST, Centre d’Etudes et de Recherche de Grasse (CERGA),
10 Av. Nicolas Copernic,
06130
Grasse,
France
★ Corresponding author; rosine.lallement@obspm.fr
Received:
25
July
2024
Accepted:
3
September
2024
Context. Three-dimensional (3D) distributions of the 862 nm diffuse interstellar band (DIB) carrier have been computed based on Gaia parallaxes and DIB catalogues, in parallel with 3D maps of dust extinction density. Three-dimensional maps provide local diagnostics and information on the distribution of structures in addition to line-of-sight (LOS) integrated quantities, and allow us to focus on poorly studied low-extinction areas. They make cross-matching with other catalogues possible through estimates of the DIB and extinction along any given path.
Aims. We re-examined the relationships between the density of DIB carriers and the absorption and emission properties of spatially co-located dust. Along with laboratory identifications of carriers, these properties may shed light on the formation and evolution of this organic matter. They may also help to model dust emission and absorption properties in a more detailed way.
Methods. We used the 3D maps of 862 nm DIBs and of dust extinction, as well as available DIB equivalent width (EW) catalogues and published measurements of parameters characterizing the dust extinction law and the dust emission. We studied the relationships between the extinction-normalized 862 nm DIB EW and the extinction level, the total-to-selective extinction ratio RV, and the dust far-IR emission spectral index β. We re-visited the link between several DIBs and the UV absorption bump at 220 nm.
Results. The ratio of the 862 nm DIB carrier density to the optical extinction density (DIBnorm862) is increasing in low-density clouds, confirming with local values the trend seen in the LOS data. In both cases, the coefficients of a fitted power law fall within the range of those measured towards SDSS high-latitude targets for 20 different bands, ranking this DIB among those with a high increase, above that of the broad 4430 Å DIB. This is consistent with the recent measurement of a larger scale height above the Plane for the 862 nm DIB compared to that of the 4430 Å DIB. Using map-integrated 862 nm DIB EWs and extinctions along the paths to APOGEE targets with published proxies R′V for the total-to-selective extinction ratio, we found that, despite a large scatter, DIBnorm862 is positively correlated with R′V for those stars with low to moderate extinctions (AV = 0.2 to 2–3 mag). Independently, using stars from the 862 nm DIB catalogue located outside the disk and for the same regime of extinction, DIBnorm862 is found to be globally anti-correlated with the Planck opacity spectral index β. This is consistent with the observed anti-correlation between β and R′V. In the light of a recent result on the variability of the carbon/silicate ratio in dust grains as a source of this anti-correlation, it suggests that DIBnorm862 increases with the fraction of carbonaceous to silicate grains in the co-located dust, in agreement with the carbonaceous nature of DIB carriers and recent evidences for a spatial correlation between DIBnorm862 and the fluxes of carbon-rich ejecta of asymptotic giant branch (AGB) stars. At higher extinction both trends disappear, and there is evidence for a trend reversal. Regarding the link between the height of the 220 nm UV absorption bump and extinction-normalized EWs of DIBs, we found that two factors explain the absence of previous clear results: the correlation disappears when we move from σ-type to ζ-type DIBs and/or from single-cloud LOSs to paths crossing multiple clouds distant from each other; ζ-type bands can be used to predict low and high values of the bump height, provided one adds a correcting factor linked to the ambient radiation field (e.g. the 5780/5797 DIB ratio). We show examples of simple models of the bump height based on the 5780 Å band, the 5850 Å band and the 5780/5797 DIB ratio. We also found an anti-correlation between DIBnorm and the width of the bump, which similarly disappears from σ-type to ζ-type DIBs. This suggests that a fraction of the bump is generated outside the dense molecular clouds.
Conclusions. There are complex relationships between DIBs and dust; however, massive measurements of DIBs and extinction and the derived 3D maps may provide some constraints on the density, the nature, and the contribution to extinction and emission of the co-located dust. This requires large stellar spectroscopic surveys and space-based measurements of UV extinction.
Key words: ISM: abundances / ISM: clouds / dust, extinction / ISM: general / ISM: lines and bands / ISM: molecules
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Diffuse interstellar bands (DIBs) have already fascinated (and sometimes discouraged) two generations of specialists of the interstellar medium and astrochemists. These weak irregular absorptions are imprinted in the spectra of all astrophysical sources located behind interstellar clouds. About 600 of these features of various intensities and widths have been observed in the visible and near-infrared (NIR), and discoveries of new bands are continuously made, especially for faint or very broad bands (Ebenbichler et al. 2024; Maíz Apellániz et al. 2021), and in the NIR (Hamano et al. 2016). Their width, shape, and strength strongly vary from one band to another (for catalogues and recent reviews, see Jenniskens & Desert 1994; Hobbs et al. 2008; Geballe et al. 2011; Cox et al. 2014; Hamano et al. 2016; Cox et al. 2017; Fan et al. 2019). Their multiple-peak substructure favours large carbonaceous molecules or molecular ions (Sarre et al. 1995), but only one of these carriers could be identified, the buckminsterfullerene cation ![$\[\mathrm{C}_{60}^{+}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq9.png) (Foing & Ehrenfreund 1994; Campbell et al. 2015; Cordiner et al. 2019).
(Foing & Ehrenfreund 1994; Campbell et al. 2015; Cordiner et al. 2019).
For all DIBs, there is a strong link between the DIB strength and the extinction along the line of sight (LOS), as well as the total amount of gas. However, there is a significant scatter on these relations. At least two influencing factors have been identified. Firstly, the intensity of the radiation field (Vos et al. 2011; Friedman et al. 2011) acts on almost all carriers, and in a different way from one to another. Secondly, there is a significant decrease in the DIB strength relative to the amount of dust for LOSs crossing the most opaque regions of the clouds (Krelowski & Westerlund 1988; Herbig 1995; Cami et al. 1997; Vos et al. 2011; Elyajouri et al. 2017), called the skin effect, but other factors certainly play a role, as shown by Ensor et al. (2017). Although they probably constitute a large reservoir of interstellar organic matter, little is known about their formation, thought to be either gradual around evolved stars together with dust and other carbonaceous complex particles such as polycyclic aromatic hydrocarbons (PAHs) (see e.g. Kwok 2023), or in dense molecular clouds along with other identified complex molecules. In support of the former mechanism, C60 and C70 have been detected in emission in planetary nebulae (PNe; first detections by Cami et al. 2010). However, enhancements of DIBs (![$\[\mathrm{C}_{60}^{+}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq10.png) or others) along LOSs towards PNe and attributable to the PN itself have been too scarce to establish a link between DIB carriers and PNe. More recently, evidence has been reported of the enhanced density of 862 nm DIB1 carriers in regions of the Milky Way harbouring asymptotic giant branch (AGB) stars with strong carbon-rich dust emission (Cox et al. 2024). Because C-rich AGB ejecta enriches the ISM in carbonaceous matter, favouring the formation of carbonaceous macromolecules, while O-rich ejecta favours the formation of silicates, such a link may appear natural. However, it does not necessarily imply the formation of the DIB carrier within the ejecta. It may simply enhance the carbon abundance in the region, which in turn impacts all types of molecular processes.
or others) along LOSs towards PNe and attributable to the PN itself have been too scarce to establish a link between DIB carriers and PNe. More recently, evidence has been reported of the enhanced density of 862 nm DIB1 carriers in regions of the Milky Way harbouring asymptotic giant branch (AGB) stars with strong carbon-rich dust emission (Cox et al. 2024). Because C-rich AGB ejecta enriches the ISM in carbonaceous matter, favouring the formation of carbonaceous macromolecules, while O-rich ejecta favours the formation of silicates, such a link may appear natural. However, it does not necessarily imply the formation of the DIB carrier within the ejecta. It may simply enhance the carbon abundance in the region, which in turn impacts all types of molecular processes.
One may expect some continuity between the macro-molecules at the origin of DIBs and the smallest dust grains (see Jones 2016, for a review). This is why links between DIBs and other phenomena potentially related to carbonaceous matter, free-flying molecules, or grains have been searched for, such as the 220 nm bump feature, the extended red emission (ERE), and the unidentified infrared emission (UIE). Unfortunately, tight relationships between DIB equivalent widths (EWs) and dust extinction parameters could not be found because there are very few stars for which the path from the Sun to the target is strongly dominated by a unique homogeneous cloud. The situation is even worse for links with dust emission data because, as an additional limitation, only stars located beyond the Galactic dust layer are appropriate targets. Links between DIB carriers and the UV bump have been sought for decades and in different ways (see Xiang et al. 2011 for an exhaustive review of the many attempts). Among the positive results, Krelowski et al. (1992) suggested a dependence of the normalized DIB on the bump, based on six early-type highly reddened stars. Later on, in a full spectral analysis of 28 stars, Desert et al. (1995) found a positive correlation between the DIB-to-reddening ratio of a few strong DIBs and the height of the 220 nm bump, as well as, in parallel, an anti-correlation with the width of the bump and with the far-UV rise assigned to nanograins. More recently, Xiang et al. (2011) disfavoured dependences on the basis of too weak correlation coefficients, and Xiang et al. (2017) confirmed this negative result. Xiang et al. (2017) also did not find any correlation between DIBs and the far-UV rise of the extinction curve. As part of a study of the potential relationships between the DIB carriers and cometary material, and based on the compilation of the Xiang et al. (2017) data, Bertaux & Lallement (2017) argued that high values of the well-known ratio of DIB 5797 Å to DIB 5780 Å (also called the radiation-shielding ratio) have some link with the steep far-UV rise of the LOS extinction law. They interpreted this trend as a coincidence between the increase in ultra-small grains in dense cloud cores and the disappearance of the radiation-resilient 5780 Å DIB. More recently, Ramírez-Tannus et al. (2018) and Li et al. (2019) investigated the link between several DIBs and the total-to-selective extinction ratio RV = AV / E(B-V), based on the same high-extinction LOSs towards M17 (AV ≥ 4). Ramírez-Tannus et al. (2018) found a negative correlation between the DIB EW normalized to the reddening E(B-V) and RV (they also included the peculiar or extreme LOS towards Herschel 36), while Li et al. (2019) found no correlation between the DIB EW normalized to the extinction AV (instead of the reddening) and RV. In summary, the link between DIB strengths and the extinction law is far from clear. Regarding the dust continuum emission, to our knowledge nothing has appeared in the literature linking DIBs to emission parameters. Potential relationships are more difficult to establish, DIB being distance-limited quantities, while emission parameters characterize entire LOSs.
As already mentioned, tight relationships between DIBs and dust extinction or emission parameters cannot be found, and only trends may be detected. However, we believe that such trends may contain valuable information. The goal of the present work is to search for these trends using new Gaia data and 3D maps based on this data. In particular, the availability of DIB equivalent width measurements for massive numbers of stars distributed in 3D space has allowed us to perform their inversion to derive local values (i.e. quantities proportional to the volume densities of the carriers). This was recently done by Cox et al. (2024) using the extended 862 nm DIB catalogue of Gaia Collaboration (2023b) based on RVS spectra. In parallel, and importantly for our present work, Cox et al. (2024) performed a specific inversion of extinctions based on the same LOSs as those used for the DIB inversion, and for the same parameters of the inversion code. This way, the two 3D DIB and extinction maps are suitable for optimal comparisons.
The existence of 3D density maps brings several new possibilities. Firstly, it allows the comparison between local values of DIB carriers and of other interstellar constituents (in particular the dust grains responsible for the extinction). Such relationships are more direct diagnostics than those based on Sun-star integrated values. They may reveal links with the environment, the radiation field, or the presence of specific types of stars. As an example, the above-mentioned evidence for a link between the 862 nm DIB-to-extinction ratio ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq11.png) on the one hand, and the presence of carbon-rich AGB stars (AGBs) on the other hand, was found based on the 3D maps. Secondly, the maps allow us to focus on dust-poor areas, overlooked in studies based on LOS data. A third advantage of a 3D map is that it constitutes a tool for estimates of integrated quantities along the LOS to any target, including those which were not part of the inverted catalogue used to produce the map, and have been observed for various purposes. Finally, a fourth advantage is the possibility of a documented selection of regions and directions appropriate to a specific study (e.g. selections of single-cloud LOSs or targets beyond the layer of dust). For this work we made use of all these advantages.
on the one hand, and the presence of carbon-rich AGB stars (AGBs) on the other hand, was found based on the 3D maps. Secondly, the maps allow us to focus on dust-poor areas, overlooked in studies based on LOS data. A third advantage of a 3D map is that it constitutes a tool for estimates of integrated quantities along the LOS to any target, including those which were not part of the inverted catalogue used to produce the map, and have been observed for various purposes. Finally, a fourth advantage is the possibility of a documented selection of regions and directions appropriate to a specific study (e.g. selections of single-cloud LOSs or targets beyond the layer of dust). For this work we made use of all these advantages.
The 862 nm DIB is a broad (≃0.4 nm wide) DIB. It is not particularly strong; however, being spectrally close to ionized calcium (CaII) lines commonly used to constrain the stellar parameters, its study benefits from stellar spectroscopic surveys. It was intensively studied based on the spectra of the RAVE survey and was found to be well correlated with the reddening (Munari et al. 2008; Kos et al. 2013, 2014). This was also confirmed by data from the Gaia-ESO and GIBS surveys (Puspitarini et al. 2015; Zhao et al. 2021), and the 862 nm DIB was found useful as a tracer of the arms and of their dynamical properties. It was shown to be well correlated with the NIR DIB at 1.5273 μm (Zhao et al. 2021). It did not show any particular characteristics that set it apart from other bands, and, as a result, it is probably representative of most other DIBs.
Section 2 is devoted to the relationship between the 862 nm DIB and the extinction, and to the comparison with DIB-extinction relationships found for other DIBs. In Sect. 3, we detail the search for a link between the total-to-extinction ratio RV and the DIB strength normalized to the extinction (![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq12.png) ). In Sec. 4 we similarly detail the search for a link between
). In Sec. 4 we similarly detail the search for a link between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq13.png) (for the 862 nm DIB) and the dust opacity spectral index β measured by Planck. In Sec. 5, we revisit the studies between DIBs and the 220 nm bump of the extinction law. Section 6 discusses the various types of relationships, their limitations, and their potential use. We also discuss some implications.
(for the 862 nm DIB) and the dust opacity spectral index β measured by Planck. In Sec. 5, we revisit the studies between DIBs and the 220 nm bump of the extinction law. Section 6 discusses the various types of relationships, their limitations, and their potential use. We also discuss some implications.
 |
Fig. 1 862 nm DIB carrier and extinction volume densities. All voxels of the Cox et al. (2024) 3D maps have been used. Left: DIB density averaged in voxels with equal extinction density. An adjusted power law limited to the low-extinction regime is superimposed (see text). Right: ratio of the DIB EW density to the extinction density for the same voxels, and superimposed power law. |
2 Extinction-normalized DIB and extinction
Significant attention has been given to DIB variability in star-forming regions and, in particular, to DIB carrier depletion in dense UV-protected parts of dense clouds (the skin effect). It is due, in large part, to the observation preference for highly extinguished target stars. Conversely, much less attention has been given to the low-extinction part of the DIB dependence on dust opacity. The 3D maps of the 862 nm DIB (Cox et al. 2024) are not of high enough spatial resolution to address the skin effect for individual clouds. However, for the first time, it is possible to use the maps to investigate the relationship between the local value of the DIB carrier density ρDIB, measured as the spatial gradient of the DIB EW, and the local value of the extinction density ρAV in wide low-dust areas, or similarly the relationship between the extinction-normalized DIB density ![$\[\rho \mathrm{DIB}_{\text {norm }}^{862}{=}\rho \mathrm{DIB} / \rho A_V\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq14.png) and the extinction density ρAV.
and the extinction density ρAV.
To do so, we selected all 10 × 10 × 10 pc3 voxels of both DIB and extinction 3D maps containing enough target stars to perform the local inversion of DIB EWs (see details in Cox et al. 2024). We distributed the DIB densities ρDIB in these voxels in bins of similar local extinction density ρAV, and computed their average in each bin. We note that densities ρAV are lower than actual densities in moderate- or high-density clouds because the spatial resolution of the 3D maps used is poor, including that of the dust map that was especially computed based on the same series of LOS as those of the DIB catalogue, and there is a dilution of clumpy structures in the map voxels. We did the same sampling for the ratios ρDIB / ρAV. Figure 1 displays the two distributions of bin-averaged DIB density ρDIB on the one hand, and bin-averaged ratio ρDIB / ρAV (i.e. the averaged extinction-normalized DIB density ρ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq15.png) ) as a function of the local extinction density ρAV. Superimposed are fitted power laws:
) as a function of the local extinction density ρAV. Superimposed are fitted power laws:
![$\[\begin{aligned}\rho \mathrm{DIB} & =K\left(\rho A_V\right)^\gamma, \\\rho \mathrm{DIB}_{\text {norm }} & =\frac{\rho \mathrm{DIB}}{\rho A_V}=K\left(\rho A_V\right)^{\gamma-1}=K\left(\rho A_V\right)^\alpha .\end{aligned}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq16.png) (1)
(1)
We restricted the adjustment to the extinction density interval 0.00018 < ρAV < 0.0044 mag pc−1. The lower limit ensures the exclusion of uncertain ratios corresponding to low statistics, while the upper limit excludes voxels containing dense clouds. The power-law coefficients γ are found to be γ = +0.74 for the DIB versus extinction dependence and, accordingly, α = γ − 1 = −0.26 for the normalized DIB dependence.
In addition to local values, we also used directly measured LOS-integrated EW values from two catalogues: the catalogue of individual LOSs (Gaia Collaboration 2023b) and the catalogue of averaged EWs among stars belonging to the same spatial bin (Gaia Collaboration 2023a). For both datasets, we used the EXPLORE 3D extinction density maps (Vergely et al. 2022) to compute the corresponding integrated extinctions, from the Sun to each target star in the first case, and from the Sun to each centre of the spatial bin in the second case. Figure 2 displays the EW measurements for individual targets of the first catalogue (left), and for spatial bins from the second catalogue (right), both as a function of the corresponding integrated extinction. An adjusted power law is superimposed for the two datasets. We restricted the fit to the low-moderate extinction interval 0.12 ≤ AV ≤ 1.5 mag. The γ coefficients were found to be 0.57 and 0.62, respectively, for the two catalogues. The two coefficients are similar, and are slightly lower than that found from the 3D maps (0.74). Taken as a whole, these results provide an order of magnitude of the uncertainty on the coefficients for such a simple relationship. One can see that they depend on the DIB extraction method and that they also differ depending on the use of direct or inverted measurements. However, the existence of similar trends for integrated values and for local values confirms that the increase, for lower values of the dust extinction density, in the extinction-normalized DIB strength is well established. In particular, the result based on local values, taken from 3D distributions, confirms that it is not due to an existing bias in the measurements of weak extinctions, or low-DIB EWs.
An interesting aspect of this exercise is the comparison with the results obtained by Lan et al. (2015) for a series of different DIBs. The authors used Sloane Digital Sky Survey (SDSS) spectra of halo stars, galaxies, and quasars at high Galactic latitudes, and extracted 20 different DIBs from stacked spectra in a large fraction of the high-latitude sky. They adjusted power-law functions to the DIB EWs as a function of the reddening, for the same extinction interval as the one we used above in the case of the Gaia catalogue (namely 0.12 ≤ AV ≤ 1.5 mag). Their Table 3 lists power-law coefficients γ for the DIB dependence on E(B-V). The whole set of γ coefficients is in the range from 0.51 to 1.13 and six of the DIBs have a low γ between 0.51 and 0.74. This demonstrates that the 862 nm DIB behaves as several other DIBs do, but is part of those bands with the highest relative increase with respect to extinction in dust-poor regions (i.e. the lowest γ). By comparison, for the strong 5780 Å DIB Lan et al. (2015) derived a γ coefficient close to 1, which explains the linear correlation between its EW and the extinction in the regimes of low to moderate extinction. A comparison can also be made with the 9577 and 9632 Å ![$\[\mathrm{C}_{60}^{+}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq17.png) DIBs. Schlarmann et al. (2021) inferred from published data a strong decrease (more than a factor of three) in the DIB/reddening ratio when the E(B-V) reddening increases from 0.1 mag to 0.6 mag (quantities derived from their Fig. 3c). This would correspond roughly to a power-law coefficient γ ≃ 0.4, which is lower than the lowest from the Lan et al. (2015) series (0.51). The stability of the C60 structure may explain why it can persist in low-density, generally UV-permeated clouds.
DIBs. Schlarmann et al. (2021) inferred from published data a strong decrease (more than a factor of three) in the DIB/reddening ratio when the E(B-V) reddening increases from 0.1 mag to 0.6 mag (quantities derived from their Fig. 3c). This would correspond roughly to a power-law coefficient γ ≃ 0.4, which is lower than the lowest from the Lan et al. (2015) series (0.51). The stability of the C60 structure may explain why it can persist in low-density, generally UV-permeated clouds.
Since the density of dust decreases with the distance to the Plane, the γ coefficient is expected to have some link with the DIB carrier scale height: the lower the γ, the larger the scale height. A recent study by Zhao et al. (2023) derives a significant difference in scale heights for two DIBs, namely the 4430 Å DIB and the 862 nm DIB; the 862 nm DIB scale height is larger than that of the 4430 Å DIB. The Lan et al. (2015) γ coefficient for the 4430 Å DIB is 0.89, above our three estimates of γ for the 862 nm DIB, all three below 0.74. This is consistent with the heights measured by Zhao et al. (2023). Further measurements of DIB scale heights should help to confirm (or not) their direct link with the γ coefficient. We note that the hierarchy of DIBs with respect to these Lan et al. (2015) γ coefficients does not seem to correspond to the hierarchy of ζ to σ DIBs, related to the UV radiation field (see e.g. the work of Ensor et al. 2017). This means that the phenomenon responsible for the increase in carrier density in low-dust clouds is not directly or simply related to the ζ versus σ classification. This deserves further study, being, instead, a likely indication of the carrier formation process and site.
 |
Fig. 2 862 nm DIB EW and LOS-integrated extinction. Top: DIB EW from the Gaia DR3 catalogue as a function of the extinction Av integrated from the Sun to the target star. A power law is fitted to the data from Av=0 to Av=1.5 mag. Isocontours of target number densities have been drawn to illustrate the various contributions. Bottom: same as top, but for the second catalogue of averaged EWs in spatial bins. |
3 Extinction-normalized DIB and total-to-selective extinction ratio Rv
Schlafly et al. (2016, 2017) published a large catalogue of measurements of a proxy ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq18.png) for the total-to-selective extinction ratio RV = AV/E(B-V), estimated for the LOSs to SDSS/APOGEE target stars. To do so, they combined accurate stellar atmospheric parameters derived from APOGEE spectra with available photometric data. They found wide-area variations in
for the total-to-selective extinction ratio RV = AV/E(B-V), estimated for the LOSs to SDSS/APOGEE target stars. To do so, they combined accurate stellar atmospheric parameters derived from APOGEE spectra with available photometric data. They found wide-area variations in ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq19.png) on large angular scales (≥30°). The lack of a link of these variations with the interstellar (IS) matter column density led the authors to conclude that they are not governed by grain size changes in dense clouds, and are due to other effects acting on large scales. They also found that
on large angular scales (≥30°). The lack of a link of these variations with the interstellar (IS) matter column density led the authors to conclude that they are not governed by grain size changes in dense clouds, and are due to other effects acting on large scales. They also found that ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq20.png) is globally higher outside the solar circle (at galactocentric distances larger than that of the Sun). Interestingly, a global increase in the extinction-normalized 862 nm DIB with the galactocentric radius is also one of the results of the 3D mapping presented in Cox et al. (2024), a radial increase potentially attributed to the increased prevalence of ejecta from C-rich AGBs over ejecta from O-rich stars. If the two phenomena were linked, it would imply the existence of a positive correlation between the extinction-normalized 862 nm DIB EW
is globally higher outside the solar circle (at galactocentric distances larger than that of the Sun). Interestingly, a global increase in the extinction-normalized 862 nm DIB with the galactocentric radius is also one of the results of the 3D mapping presented in Cox et al. (2024), a radial increase potentially attributed to the increased prevalence of ejecta from C-rich AGBs over ejecta from O-rich stars. If the two phenomena were linked, it would imply the existence of a positive correlation between the extinction-normalized 862 nm DIB EW ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq21.png) and
and ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq22.png) , which motivated the following study.
, which motivated the following study.
We used the catalogue of Schlafly et al. (2016), and for all LOSs to the APOGEE targets, we integrated along these paths within the 3D distribution of DIB density from Cox et al. (2024) and within the 3D distributions of extinction density from Vergely et al. (2022) to get estimates of the 862 nm DIB cumulative EW on the one hand and of the extinction Av of the target on the other hand. Their ratio ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq24.png) was then computed. Since the spatial extent of the Vergely et al. (2022) 3D maps is resolution-dependent, we used the series of extinction maps in a hierarchical mode. We started the integration in the highest resolution map and, if the map boundary is reached before the target star location, we continued to integrate in the second-best resolution map, and so on. Targets outside the 3D DIB density map, of smaller extent than the widest extinction map (+/− 4 kpc instead of +/−5 kpc), were eliminated. As said in Sect. 1, this is one of the potential uses of 3D maps, namely the computation of DIB and extinction estimates for any target star that is not part of the inverted catalogue. The APOGEE catalogue is appropriate for our study for the following reasons: it is massive; it is homogeneously obtained; and most of the targets are distant, but the extinction is limited (i.e. very dense cloud cores are generally avoided). The last aspect is important since the resolution of the 3D maps is too poor to reconstruct very small structures. Instead, they are appropriate for the study of large-scale characteristics.
was then computed. Since the spatial extent of the Vergely et al. (2022) 3D maps is resolution-dependent, we used the series of extinction maps in a hierarchical mode. We started the integration in the highest resolution map and, if the map boundary is reached before the target star location, we continued to integrate in the second-best resolution map, and so on. Targets outside the 3D DIB density map, of smaller extent than the widest extinction map (+/− 4 kpc instead of +/−5 kpc), were eliminated. As said in Sect. 1, this is one of the potential uses of 3D maps, namely the computation of DIB and extinction estimates for any target star that is not part of the inverted catalogue. The APOGEE catalogue is appropriate for our study for the following reasons: it is massive; it is homogeneously obtained; and most of the targets are distant, but the extinction is limited (i.e. very dense cloud cores are generally avoided). The last aspect is important since the resolution of the 3D maps is too poor to reconstruct very small structures. Instead, they are appropriate for the study of large-scale characteristics.
We made a first visual comparison of distributions over the sky of ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq25.png) measurements and computed extinction-normalized DIB EWS
measurements and computed extinction-normalized DIB EWS ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq26.png) . Figure 3 shows the locations of the APOGEE LOSs in Galactic coordinates, colour-coded according to
. Figure 3 shows the locations of the APOGEE LOSs in Galactic coordinates, colour-coded according to ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq27.png) from Schlafly et al. (2016) (top) and to the normalized 862 nm DIB (bottom). There are some large-scale similarities, for example in the third quadrant where both quantities are particularly high. There are also discrepancies, especially in the highly opaque directions above the Galactic centre, or in the Taurus area where
from Schlafly et al. (2016) (top) and to the normalized 862 nm DIB (bottom). There are some large-scale similarities, for example in the third quadrant where both quantities are particularly high. There are also discrepancies, especially in the highly opaque directions above the Galactic centre, or in the Taurus area where ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq28.png) is high, but the DIB-to-extinction ratio is notably low. As a result, these sky distributions suggest a link between the two quantities, but certainly different regimes must exist according to the extinction. We note that the
is high, but the DIB-to-extinction ratio is notably low. As a result, these sky distributions suggest a link between the two quantities, but certainly different regimes must exist according to the extinction. We note that the ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq29.png) values from Schlafly et al. (2016) vary between 3.0 and 3.7, while
values from Schlafly et al. (2016) vary between 3.0 and 3.7, while ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq30.png) changes by a much larger factor, of the order of three.
changes by a much larger factor, of the order of three.
A more direct comparison is presented in Fig. 4, where the extinction-normalized DIB for each star located within the 3D DIB map is displayed as a function of the inverse of the total-to-selective extinction ratio proxy ![$\[R_V^{\prime-1}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq31.png) . Since all extinctions that have been inverted to produce the 3D extinction maps were estimated under the assumption of a unique fixed RV=3.1 parameter, to avoid a bias and take into account the actual variability of RV we multiplied each individual extinction by a factor of RV/3.1 before computing the DIB-to-extinction ratio. Despite the very large scatter, there is a clear decrease in
. Since all extinctions that have been inverted to produce the 3D extinction maps were estimated under the assumption of a unique fixed RV=3.1 parameter, to avoid a bias and take into account the actual variability of RV we multiplied each individual extinction by a factor of RV/3.1 before computing the DIB-to-extinction ratio. Despite the very large scatter, there is a clear decrease in ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq32.png) versus
versus ![$\[R_V^{\prime-1}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq33.png) (i.e. an increase with
(i.e. an increase with ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq34.png) ). This decrease occurs in the low- to moderate-extinction regime AV ⪅ 3 mag (extinctions are colour-coded), which is the range for most APOGEE targets used by Schlafly et al. (2016). Apart from the largest group of data points, one can distinguish several higher extinction data points at the lower left of the graph (
). This decrease occurs in the low- to moderate-extinction regime AV ⪅ 3 mag (extinctions are colour-coded), which is the range for most APOGEE targets used by Schlafly et al. (2016). Apart from the largest group of data points, one can distinguish several higher extinction data points at the lower left of the graph (![$\[R_V^{\prime-1}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq35.png) between 0.2 and 0.26) that strongly depart from the general trend. This suggests that the trend disappears for some directions characterized by a high extinction. The decrease versus
between 0.2 and 0.26) that strongly depart from the general trend. This suggests that the trend disappears for some directions characterized by a high extinction. The decrease versus ![$\[R_V^{\prime-1}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq36.png) observed at low to moderate extinction, is opposite to what was found by Ramírez-Tannus et al. (2018) for RV based on targets of the M17 open cluster. However, the regime of extinction for the M17 stars considered by the authors is clearly above that of the APOGEE targets (AV varies between 5 and 9 mag for the M17 targets). We have superimposed their results in Fig. 4, using the same colour-coding representing the extinction as used for the APOGEE data. The M17 data points depart from the main distribution of the APOGEE data points to reach lower RV−1 and lower
observed at low to moderate extinction, is opposite to what was found by Ramírez-Tannus et al. (2018) for RV based on targets of the M17 open cluster. However, the regime of extinction for the M17 stars considered by the authors is clearly above that of the APOGEE targets (AV varies between 5 and 9 mag for the M17 targets). We have superimposed their results in Fig. 4, using the same colour-coding representing the extinction as used for the APOGEE data. The M17 data points depart from the main distribution of the APOGEE data points to reach lower RV−1 and lower ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq37.png) values. From the combination of the two results, it appears that the DIB-RV positive relationship is suppressed when the extinction reaches levels of the order of ≃3 mag, with the appearance of the negative trend noted by Ramírez-Tannus et al. (2018). High RV values are generally associated with large grains formed by accretion or coagulation in UV-shielded molecular clouds, with high extinctions and DIB depletion. This is the trend observed by Ramírez-Tannus et al. (2018) above AV = 3 mag. On the other hand, the opposite trend appearing at lower extinction is a different phenomenon.
values. From the combination of the two results, it appears that the DIB-RV positive relationship is suppressed when the extinction reaches levels of the order of ≃3 mag, with the appearance of the negative trend noted by Ramírez-Tannus et al. (2018). High RV values are generally associated with large grains formed by accretion or coagulation in UV-shielded molecular clouds, with high extinctions and DIB depletion. This is the trend observed by Ramírez-Tannus et al. (2018) above AV = 3 mag. On the other hand, the opposite trend appearing at lower extinction is a different phenomenon.
 |
Fig. 3
|
 |
Fig. 4 Relationship between the extinction-normalized 862 nm DIB and the Schlafly et al. (2016) total to selective extinction R′V for APOGEE LOSs (dots). For low to moderate extinctions, despite the large scatter, |
4 Extinction-normalized DIB and dust emission spectral index from Planck
In the frame of their study, Schlafly et al. (2016) discovered a tight inverse relationship between ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq42.png) and the dust opacity spectral index β, the parameter used in the modified black-body representation of the Galactic dust far-IR emission. Properties or mechanisms at the origin of this trend have been searched for and, more recently, Zelko & Finkbeiner (2020) found that increasing the carbon-to-silicate ratio in dust grains may explain the simultaneous increase in RV and decrease in β. This effect comes in addition to the known increase in RV in opaque clouds, attributed to the increased size of the grains. Such a result on the influence of the dust composition has important consequences in the context of extinction laws and also cosmological observations, through dust effects on the CMB spectral distortion (Zelko & Finkbeiner 2021). If the above positive correlation between
and the dust opacity spectral index β, the parameter used in the modified black-body representation of the Galactic dust far-IR emission. Properties or mechanisms at the origin of this trend have been searched for and, more recently, Zelko & Finkbeiner (2020) found that increasing the carbon-to-silicate ratio in dust grains may explain the simultaneous increase in RV and decrease in β. This effect comes in addition to the known increase in RV in opaque clouds, attributed to the increased size of the grains. Such a result on the influence of the dust composition has important consequences in the context of extinction laws and also cosmological observations, through dust effects on the CMB spectral distortion (Zelko & Finkbeiner 2021). If the above positive correlation between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq43.png) and
and ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq44.png) for low- to moderate-extinction APOGEE LOSs is due to the existence of a physical link between the DIB carrier density and the grain composition, it should, in turn, be accompanied by a negative correlation between
for low- to moderate-extinction APOGEE LOSs is due to the existence of a physical link between the DIB carrier density and the grain composition, it should, in turn, be accompanied by a negative correlation between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq45.png) and the far-IR dust emission spectral index β. This expectation motivated the following study.
and the far-IR dust emission spectral index β. This expectation motivated the following study.
As already mentioned, contrary to RV, β is not a distance-limited quantity and target stars or locations in the 3D maps must be carefully selected to ensure that most of the IS matter in their direction is located in front of them, and there is negligible IS matter beyond. Here we used the first catalogue of individual 862 nm DIBs of Gaia Collaboration (2023b) due to the more extended distribution of directions and selected DIB data for which the quality flag is 0. For each direction we estimated the spectral index β by interpolation in the high-resolution Planck map (Planck Collaboration Int. XLVIII 2016). We also used, in parallel, the more recent map of Casandjian et al. (2022). For each target, we computed the extinction AV by integrating in the highest resolution dust extinction density maps from Vergely et al. (2022), available from the EXPLORE facility. Similarly to the comparison with RV, we first show, for a preliminary visual comparison, the distributions over the sky of the DIB-to-extinction ratio ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq46.png) and the two interpolated β values (Fig. 5). We masked the Galactic latitudes lower than 6° since in those directions β is too strongly influenced by dust beyond the limits of the extinction maps. We tuned the colour-coding of the β maps in order to obtain about the same contrast in β and
and the two interpolated β values (Fig. 5). We masked the Galactic latitudes lower than 6° since in those directions β is too strongly influenced by dust beyond the limits of the extinction maps. We tuned the colour-coding of the β maps in order to obtain about the same contrast in β and ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq47.png) . There are obvious similarities of the patterns at large angular scale. We note that the optimal similarity is somewhat higher in the case of the Casandjian et al. (2022) estimates of β. In both cases, there are also obvious discrepancies, for example at ≃5–10° Galactic longitude and ≃20°−30° Galactic latitude in the Aquila Rift region.
. There are obvious similarities of the patterns at large angular scale. We note that the optimal similarity is somewhat higher in the case of the Casandjian et al. (2022) estimates of β. In both cases, there are also obvious discrepancies, for example at ≃5–10° Galactic longitude and ≃20°−30° Galactic latitude in the Aquila Rift region.
Figure 6 illustrates the complex dependence on β of the extinction-normalized DIB, and especially the variability of this dependence according to the extinction regime. Here we used data from the second catalogue of Gaia Collaboration (2023a) for its reduced uncertainties on the EWs and selected flag=0 data. The extinction was computed by integration in the 3D maps from the Sun to the centre of the spatial bins. The figure displays ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq49.png) as a function of the LOS opacity. For each LOS the dust emission spectral index β interpolated from the Planck maps for the corresponding direction of each DIB bin centre is colour-coded. For Av values below ~3 mag, a decrease in the normalized DIB (going down along vertical lines in the figure) corresponds to an increase in β (colour variation from red to green). Above Av at ~3–4 mag, this trend is no longer visible, and there seems to be a weak reversed trend, namely β is decreasing (colours from violet to blue); however, the number of LOSs becomes low, something expected from the rare cases of high extinction and high Galactic latitude. This bi-modal behaviour, namely an anti-correlation between
as a function of the LOS opacity. For each LOS the dust emission spectral index β interpolated from the Planck maps for the corresponding direction of each DIB bin centre is colour-coded. For Av values below ~3 mag, a decrease in the normalized DIB (going down along vertical lines in the figure) corresponds to an increase in β (colour variation from red to green). Above Av at ~3–4 mag, this trend is no longer visible, and there seems to be a weak reversed trend, namely β is decreasing (colours from violet to blue); however, the number of LOSs becomes low, something expected from the rare cases of high extinction and high Galactic latitude. This bi-modal behaviour, namely an anti-correlation between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq50.png) and β for low to moderate extinctions, and a null-positive correlation with β in the high-opacity regime, is reminiscent of what we found for the relationship between the normalized DIB and RV. Since the RV and β data sources are completely independent, and since, as noted above, it has been shown that RV and beta are anticorrelated (Schlafly et al. 2016), this reinforces the two detected trends.
and β for low to moderate extinctions, and a null-positive correlation with β in the high-opacity regime, is reminiscent of what we found for the relationship between the normalized DIB and RV. Since the RV and β data sources are completely independent, and since, as noted above, it has been shown that RV and beta are anticorrelated (Schlafly et al. 2016), this reinforces the two detected trends.
Given the complexity of the dependence on β, we performed comparisons in selected limited regimes of Galactic latitude and opacity. As an example of the various comparisons, Fig. 7 shows the dependence on β of the DIB-to-extinction ratio for Galactic latitudes between 10° and 20° and again for selected data (flag zero in the catalogue). The negative trend is clearly seen. Figure 8 shows another example of the dependence on β of the DIB-to-extinction ratio for a restricted range of opacity values, namely extinctions AV comprised between 1.5 and 2.5 mag. There is a significant negative slope for the ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq51.png) −β relationship in this regime of extinction. An orthogonal distance regression linear fit is superimposed. It assumes errors of 0.01 Å mag−1 on
−β relationship in this regime of extinction. An orthogonal distance regression linear fit is superimposed. It assumes errors of 0.01 Å mag−1 on ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq52.png) and of 0.02 on β.
and of 0.02 on β.
Finally, Fig. 9 summarizes a series of results of the type shown in Fig. 8, here for 0.3 mag extinction intervals distributed between AV = 0.5 and AV = 4.5 mag, for the two DIB catalogues, and for the two β maps. At high extinction, the slope becomes very uncertain due to scarce data. At low extinction, the difference between individual LOSs and spatial bins has a strong effect. Between 1 and 3 magnitudes of extinction, the different determinations are all compatible and show a negative slope of the ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq53.png) versus β relationship. In summary, our results suggest that, despite a wide dispersion around the general trend, the as-yet-little-studied regime of low to moderate extinction is characterized by opposite dependences between
versus β relationship. In summary, our results suggest that, despite a wide dispersion around the general trend, the as-yet-little-studied regime of low to moderate extinction is characterized by opposite dependences between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq54.png) and RV and between
and RV and between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq55.png) and β. Due to the very strong variability of the DIB-to-extinction ratio associated with the extinction density (Sec. 2), these trends are hard to detect unless massive datasets are available.
and β. Due to the very strong variability of the DIB-to-extinction ratio associated with the extinction density (Sec. 2), these trends are hard to detect unless massive datasets are available.
 |
Fig. 5 Images of 862 nm |
5 DIBs and 220 nm UV absorption bump
As mentioned in Sect. 1, contradictory conclusions were drawn on the relationship between the DIBs and the UV bump. We used the compilation of Xiang et al. (2017) and the 3D extinction maps in an attempt to re-examine this point. The compilation was initiated by Xiang et al. (2011), who concluded on the absence of a correlation between reddening-normalized DIBs and the reddening-normalized bump strength, based on poor Pearson correlation coefficients Pr. The strength of the bump was defined as the area above the linear profile in the classical description of Fitzpatrick & Massa (1990), namely πc3γ−1, where c3 and γ are strength and width coefficients of the Drude profile fitted to the bump. The authors used the E(Λ-V)/E(B-V) formulation of the extinction law, in the same way as Desert et al. (1995). Later on, and based on an augmented compilation of DIBs and extinction law parameters, Xiang et al. (2017) used the A(Λ)/A(V) form of the extinction law and defined a new decomposition of the law. Based on this new definition, the authors confirmed the absence of correlation between extinction-normalized DIBs and the newly defined bump area. Here we re-examined the dependences on the bump in two parallel ways, using reddening-normalized DIBs and the E(λ-V)/E(B-V) formulation of the extinction law on the one hand (hereafter FORM1), and extinction-normalized DIBs and the A(λ)/A(V) form of the extinction law on the other hand (hereafter FORM2). The bump height is proportional to c3γ−2 in both cases, but c3 is not defined in the same way.
As we already discussed, LOS-integrated data cannot give rise to tight correlations, due to cloud multiplicity. Our goal was to use the LOS structure as it shows up in the 3D dust map to infer the potential level of degradation of a DIB-bump dependence due to the existence of clouds with different properties. For all targets from the Xiang et al. (2017) compilation, we inspected visually the series of clouds along the LOS, using the image of the extinction in a vertical plane containing the Sun and the target, computed from the 3D extinction distribution of Vergely et al. (2022). Admittedly somewhat arbitrarily, we defined a flag F according to the cloud distribution between the Sun and the star. If most of the extinction is produced by a single compact cloud or by a cloud group with limited extension (e.g. smaller than ≃ 100 pc), then F = 1. If, on the contrary, the extinction is produced by series of clouds distributed over long distances or to two groups separated by a large distance (e.g. more than ≃500 pc), F = 0. This produces two groups of LOSs of about the same size. The series of targets and their attributed flags is listed in Table 1. Two examples are shown in Fig. 10 for the target star HD 192216 (l = 88.92°, b = 3.02°, d = 1100 pc) as an example of a flag F = 0, and for HD 143567 (l = 350.87°, b = 22.68°, d = 135 pc) as an example of a flag F = 1.
 |
Fig. 6 Illustration of the dependence on the extinction regime of the relationship between the normalized DIB and β. Plotted are the normalized ratios as a function of the LOS extinction, color-coded for the β value for each LOS. Marker sizes increase with target location distance to the Plane. The two estimates for β are shown (left and right). Below Av≃3 mag (left part of the graphs), decreasing |
Line-of-sight flags F adopted for stars from the Xiang et al. (2017) catalogue.
5.1 Bump height
We first selected the strong 5780 Å DIB. In Fig. 11 the reddening-normalized (respectively extinction-normalized) EWs are displayed as a function of the bump height in the FORM1 (respectively FORM2) representations of the extinction law. Adjusted linear fits are shown for all stars (top), flag F = 1 stars (middle), and flag F=0 stars (bottom). Uncertainties on the DIB equivalent widths from Xiang et al. (2017) are shown at the top. The displayed fitted line does not take any error bars into account, errors on the reddening (or on the extinction) being too uncertain. Instead, the dispersion around the fitted line is used as an estimate of the mean prevailing uncertainty. For this particular DIB, the Pearson correlation coefficients are 0.54 ± 0.09, 0.67 ± 0.10, and 0.01 ± 0.17 respectively for 94, 59, and 35 stars for the first formalism. The estimated errors on the correlation coefficient are based on Student’s t-distributions (i.e. assuming normal distributions for input data). In the case of the second formalism, these coefficients become 0.51 ± 0.09, 0.69 ± 0.10, and −0.14 ± 0.17. The slopes and 1σ uncertainties are 2.0 ± 0.3 × 10−3, 2.7 ± 0.4 × 10−3, and 0.02 ± 0.4 × 10−3 mag Å−1, respectively, for formalism 1, and 2.0 ± 0.3 × 10−3, 2.6 ± 0.4 × 10−3, and −0.5 ± 0.6 × 10−3 mag Å−1, respectively, for formalism 2. These results demonstrate that, in both cases, the selection of LOSs closer to the ideal case of a mono-cloud situation has a strong effect. For a LOS characterized by cloud multiplicity (F = 0), the UV bump height is about constant, and there is a reduced dispersion around the linear fit, which we interpret as a consequence of the averaging of the cloud properties. This series of data produces the central plateau in the figure displaying all the assembled data. On the contrary, restricting the data to those LOSs closer to the mono-cloud situation, there is a pronounced positive slope and a large variability around the linear fit. This shows the actual existence of a positive correlation between the strength of this particular DIB and the bump height.
While re-examining in the same way the potential relationships with the bump height for other DIBs than the 5780 Å band, we were surprised to find a decreasing correlation strength from the σ-type DIBs (e.g. like the 5780 Å DIB and the 6284 Å DIB) to ζ-type DIBs (e.g. like the 5797 Å DIB or the 5850 Å DIB). The former (σ) bands are well known for being significantly reduced in dense, molecular clouds, while the latter are not. The σ-to-ζ ratio 5780/5797 is often used as an indicator of this difference, and is shown to increase with the UV radiation field prevailing in diffuse clouds (e.g. Krelowski & Walker 1987; Cami et al. 1997).
We show in Fig. 12, as an example, the results for the ζ-type 5850 Å DIB. The relationship between the reddening-normalized DIB EW and the bump height is dramatically different from that of the 5780 Å DIB, since no trend is detectable, whatever the LOS selection, in formalism 1, and a very weak trend is detected for formalism2 (not shown here). Tables 2 and 3 list the correlation coefficients of the adjusted linear fits for the dependence of the bump height on reddening-normalized and extinction-normalized DIB EW. We limited the choice of DIBs to those with more than 12 LOSs. Coefficients are also listed for flag F=1 only and flag F=0 only. The estimated standard error on the correlation coefficient based on a Student’s t-distribution (i.e. assuming normal distributions) is also listed. The DIBs are listed by decreasing Pearson correlation coefficient computed for all flags F=1 and F=0 LOS and formalism1 (i.e. from 0.54 down to 0.07). We also see that the improvement (respectively degradation or total disappearance) of the correlation when considering only flag F=+1 (respectively flag F=0) we found for the 5780 Å DIB is also found for all other DIBs, which reinforces the case for actual correlations. We note that all correlations are stronger for formalism 2. However, for both formalisms, the sequence of DIBs for decreasing trends shares similarities with the hierarchy of DIBs associated with the σ to ζ types, or to the PC2 components of Ensor et al. (2017), found by the authors to represent the UV-field and is taken from their Fig. 7.
 |
Fig. 7 Extinction-normalized 862 nm DIB EWs as a function of the spectral index β from Casandjian et al. (2022), for DIB with quality flag 0 data from the second catalogue of Gaia Collaboration (2023a), and Galactic latitudes between 10° and 20°. Superimposed is a linear fit for this catalogue selection. |
 |
Fig. 8 Extinction-normalized 862 nm DIB EW for selected data from the second catalogue (Gaia Collaboration 2023a) as a function of the sky-interpolated Planck spectral index β (see text for selection). The colour scale refers to the distance to the Plane of the spatial bin, and excludes distances below 200 pc. Extinction values are restricted to the 1.5 to 2.5 mag interval. An orthogonal distance regression linear fit is superimposed (see text). |
 |
Fig. 9 Ranges of gradients for extinction-normalized DIB EWs as a function of β for data from the two catalogues and in various regimes of LOS extinctions. Errors are 1σ uncertainties on the slopes. There are differences at low extinctions due to the very different types of data (individual LOSs vs spatial bins) and at high extinctions due to the small number of data points. Between 1 and 3 magnitudes of extinction, all determinations are compatible and show a negative slope. |
 |
Fig. 10 Illustration of the attribution of a flag F to a given star from the Xiang et al. (2017) list. Shown are images of the dust distribution in vertical planes containing the Sun and the star. The dark areas correspond to high dust opacity. The LOS to the target (green marker) is shown as a green dotted line. HD 143567 (top) is attributed a flag F=1 since most of the extinction is generated in a single very dense nearby cloud. The more distant HD 192216 (bottom) is attributed a flag F=0 since at least two dense clouds separated by a large distance contribute to the extinction. |
 |
Fig. 11 Comparisons between the σ-type 5780 Å DIB EW and the UV bump height, under formalism 1 of the extinction law (a-c) and formalism 2 (d-f). Data are from the compilation of Xiang et al. (2017). (a) and (d) show the bump height vs the reddening-normalized EW for all targets and the adjusted linear fit. The colour-coding refers to the extinction (from yellow for the lowest extinctions to black for the highest ones). Errors bars on EWs are indicated. (b and e) Same as (a) and (d), for flag F=1 stars only. (c and f) Same as (a) and (d) for flag F=0 only. The F=0 LOSs show no dependence, and lower the correlation based on all data. F=1 targets show a clearer positive correlation. |
Reddening-normalized DIB EW and bump height (formalism 1).
Extinction-normalized DIB EW and bump height (formalism 2).
5.2 Estimates of bump height based on DIBs
The above results suggest that the response of a particular DIB to environmental conditions (here the strength of the UV radiation field) modifies the link with the bump height. We introduced a UV factor defined by the classical EW(DIB 5780)/EW(DIB 5797) ratio as an additional factor of the relationship between the bump and the reddening-normalized DIB. We show in Fig. 13a the relationship between the bump height and this UV factor. For flag F=0 stars there is no trend. For flag F=1 stars there may be some link, visible for extreme low and high values of the height; however, obviously a link far from a linear relationship. We then fitted the UV bump height (i.e. the c3γ−2 coefficient taken from the Xiang et al. 2017, Table 1) to the product of two power laws, one on the reddening-normalized DIB and the other on the UV factor (i.e. the λ5780/λ5797 ratio):
![$\[\text {Height}(\text {model})=c_3 / \gamma^2{=}K~\left(\mathrm{DIB}_{\text {norm}}\right)^{A 1} \cdot(E W 5780 / E W 5797)^{A 2} .\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq58.png) (2)
(2)
Figure 13 shows the fitted model bump height for the case of the 5850 Å DIB, based on the use of all 5850 Å data with flags F=0 and F=1 (part b), and based on flag F=1 stars only (part c). The K, A1, and A2 coefficients are 0.35, 0.16, and 1.3 and 0.45, 0.23, and 0.88, respectively. Although this is certainly a far from perfect representation, we can see that this simplistic model reproduces the high and low values of the bump.
We pursued this exercise for other DIBs, namely the 5780, 5797, 6196, and 6614 Å DIBs. The results were approximately the same. We also tested combinations of power laws for several DIBs. The advantage is to increase the number of targets for the fitting and the comparison since EWs are not available for all bands. Finally, what we discovered from these various attempts is that σ DIBs, such as 5780 Å, can be used directly and are a kind of reference; instead ζ DIBs, while corrected for their specific UV ratio (σ/ζ), may also provide some estimates of the bump height. As an example, Fig. 13d shows the adjusted model based on a combination of the 5780 Å and 5850 Å DIBs. Its formulation is
![$\[\begin{aligned}\text { Height(model)}= & 0.58 \cdot\left(\operatorname{DIB}(5780)_{\text {norm }}\right)^{0.27} \cdot(5780 / 5797)^{0.073} \\& \cdot\left(\operatorname{DIB}(5850)_{\text {norm }}\right)^{0.026} .\end{aligned}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq59.png) (3)
(3)
This simplistic model reproduces the high and low values of the bump, and may provide a prior coefficient for the bump height. The 1σ deviation from the model is 0.5, compared with height values ranging from 2 to 5. Further extinction law measurements would help to refine and to correct this approach purely based on DIBs.
5.3 Bump width and bump area
We made the same comparisons and linear fits, this time as a function of the bump width and the bump area. The correlations with the bump width are displayed in Fig. 14 for the strong 5780 Å DIB. The Pr factors vary from −0.46 ± 0.09 to −0.42 ± 0.12 and reduced χ2 values vary from 8.9 to 7.4, before and after the LOS selection for formalism 1. The Pr factors are almost constant at −0.42 ± 0.09 and −0.38 ± 0.12 and reduced χ2 constant at 7.4 for formalism 2. The slopes and their 1σ uncertainties are respectively −3.2 ± 0.6 × 10−4, −3.1 ± 0.9 × 10−4, and −3.6 ± 0.8 × 10−4 μm−1 mag A−1 for 94, 59, and 35 targets with flags F=0 and F=1, only F=1, and only F=0 for formalism 1. The numbers become −9 ± 2 × 10−4, −8.4 ± 3 × 10−4, and −12.2 ± 3 × 10−4 μm−1 mag A−1 for formalism 2. The uncertainties on the slopes are larger than in the case of the bump height, but all results favour an inverse trend between the reddening normalized DIB and the width. Results for correlation factors and uncertainties, for the same DIBs and in the same order as in Table 2 for the height, are listed in Table 4. We listed the results for formalism 1 only. Results for formalism 2 are similar. There is again a net decrease in the correlation strengths (here anti-correlation strengths) from σ to ζ DIBs. However, at variance with the case of the height, the strength of the correlation for the width does not seem to be linked to the LOS type.
The results for the bump area are shown in the case of formalism 1 in Fig. 15. The slopes and their 1σ uncertainties are 7.6 ± 3.7 × 10−4, 14 ± 5 × 10−4, −13 ± 5 × 10−4 mag μm−1 Å−1 respectively for 94, 59, 35 targets with flags F=0 and 1, F=1, and F=0 for formalism 1. The Pearson correlation coefficients are 0.21 ± 0.10, +0.39 ± 0.12, and −0.44 ± 0.16 respectively for the 94, 59, and 35 targets. The uncertainties on the slopes of the linear fits are much larger than in the case of the bump height and are still significantly larger than for the bump width. At variance with the case of the bump height and the bump width, there is no constancy of the slope sign since there are two opposite trends for flag F=1 and flag F=0, and the links are unclear. Results for correlation factors and uncertainties, for the same DIBs and in the same order as in Table 2 for the height are listed in Table 5.
All together, the results are in agreement with those from Desert et al. (1995) for reddening-normalized DIBs, namely a positive correlation with the bump height and a negative correlation with the bump width, provided one uses σ-type DIBs and mono-cloud-type LOSs. They also agree with the absence of a clear global trend for the bump area found by Xiang et al. (2017) for extinction-normalized DIBs, and by Xiang et al. (2011) for reddening-normalized DIBs. This is consistent with the fact that the area is close to the product of the width and the height. At variance with the results of Xiang et al. (2017), we obtain some positive correlations for the area, although weaker than for the height, when we restrict to flag F=1 and if we use σ-type DIBs. We note that the area and the width are more difficult to measure than the height; in particular, they depend on the choice of the underlying linear part of the extinction law, and this may partly explain the results.
 |
Fig. 12 Same as Fig. 11 (a-c) but for the ζ-type 5850 Å DIB and formalism 1. Top: all flags. Middle: flag F=1. Bottom: flag F=0. No trend is detected, neither for all stars, nor for F=1 stars only. |
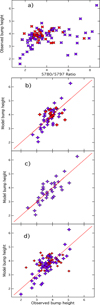 |
Fig. 13 Illustration of a composite model of the bump height based on DIBs and the UV ratio EW(5780)/EW(5797). (a) Bump height and UV ratio 5780/5797. (b) Composite power-law model (Eq. (2)) based on the 5850 Å DIB and the UV ratio, for all stars with DIB 5850 Å data (55 targets). (c) Same as panel b, for a model based on flag F=1 stars only. (d) Composite power-law model (Eq. (2)) based on DIB 5780, DIB 5850, and the UV ratio, adjusted on flag F=1 stars (89 targets). Flag F=0 stars are in red, Flag F=1 stars in violet. In panels b, c, and d, the y = x curves are superimposed. |
Reddening-normalized DIB EW and bump width.
Reddening-normalized DIB EW and bump area.
6 Summary and discussion
The existence of links between DIBs and dust properties has been the subject of numerous works, mainly based on spectra of hot strongly reddened stars. The results have been limited, and sometimes apparently contradictory. Several new kinds of studies are now permitted by the availability of 3D maps and massive datasets from Gaia for the 862 nm DIB, a diffuse band likely representative of most other DIBs: (i) the use of local diagnostics instead of LOS-integrated diagnostics, (ii) the use of massive information on LOSs with low extinction and on dust-poor areas, and (iii) the cross-match of the information contained in 3D maps with independent information from different surveys by means of integration in the 3D maps along any LOS. Moreover, for any DIB, the existence of 3D dust extinction density maps permits (iv) the use of the LOS structure to weigh correlative studies. We used these four new possibilities and, over the course of searches for correlations, we obtained several new results.
In Sec. 2, we used (i) and (ii) and examined the relative increase in the 862 nm DIB density with respect to the extinction density occurring in low-extinction clouds, a trend detected in the 3D maps (Cox et al. 2024). We extended the study to LOS-integrated data of the two 862 nm DIB catalogues. We fitted the ratio of local (respectively LOS-integrated) DIB and extinction to a power law of the local (respectively integrated extinction) in the low-extinction regime (AV between 0.12 and 1.5 mag). The fitted power-law coefficients, comprised between 0.57 and 0.74 for LOS data from the two catalogues and for local (3D map) data, were compared with those found by Lan et al. (2015) for a series of 20 DIBs and for the same range of extinctions, based on SDSS stacked spectra for high-latitude directions. We found them in agreement with the coefficients of several other DIBs. This implies that the 862 nm DIB behaves similarly to several other DIBs in the low-extinction regime, with a power-law coefficient at the lower end of the Lan et al. (2015) series (i.e. presenting one of the highest relative increases with respect to extinction in dust-poor clouds, the lowest values of γ). This study, based on local values and massive data, validates the behaviour found with SDSS. The variability of the power-law γ coefficients found by Lan et al. (2015), to date poorly discussed, contains information on the presence of the carriers far from the dense clouds. We note that the hierarchy of DIBs associated with these coefficients is significantly different from that associated with component 2 of the principal component analysis (PCA) of Ensor et al. (2017), assumed to represent the influence of the radiation field. It may be the manifestation of one of the unidentified components in their PCA analysis. Interestingly, the ranking of the 862 nm DIB, based on our results, among the 20 DIBs from the Lan et al. (2015) study, includes a comparison with the broad 4430 Å DIB. This comparison implies that the 4430 Å DIB density increases more moderately in dust-poor clouds compared to the 862 nm DIB. This is consistent with the recent results of Zhao et al. (2023), who show a smaller extension of the 4430 Å DIB carriers at a large distance from the Plane in comparison with the 862 nm DIB carriers. This opens the possibility of using the Lan et al. (2015) coefficients to rank the scale heights of the various DIB carriers.
In Sect. 3, we used (iii), and investigated the link between the 862 nm DIB strength normalized to the extinction on the one hand, and the proxy ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq60.png) for the total-to-selective extinction ratio RV = AV/E(B-V) derived by Schlafly et al. (2016) for a large number of SDSS/APOGEE target stars. One of the results from this work is the existence of large-scale variations of RV over the sky. For all the targets from the Schlafly et al. (2016) catalogue, we integrated from the Sun to the target within the 3D map of 862 nm DIB carrier density on the one hand, and within the corresponding 3D map of extinction density on the other hand (maps from Cox et al. 2024). The results were combined to obtain estimates of the extinction-normalized
for the total-to-selective extinction ratio RV = AV/E(B-V) derived by Schlafly et al. (2016) for a large number of SDSS/APOGEE target stars. One of the results from this work is the existence of large-scale variations of RV over the sky. For all the targets from the Schlafly et al. (2016) catalogue, we integrated from the Sun to the target within the 3D map of 862 nm DIB carrier density on the one hand, and within the corresponding 3D map of extinction density on the other hand (maps from Cox et al. 2024). The results were combined to obtain estimates of the extinction-normalized ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq61.png) . Based on this dataset, and despite a large scatter due to the poor resolution of the 3D DIB map, we detected a positive correlation between
. Based on this dataset, and despite a large scatter due to the poor resolution of the 3D DIB map, we detected a positive correlation between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq62.png) and
and ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq63.png) for the low- to moderate-reddening regime AV ⪅ 2.5 mag. Combining with measurements of Ramírez-Tannus et al. (2018) and their estimates of RV for stars in the M17 cloud with AV ≥ ≃4 mag, it appears that at higher extinctions the trend is suppressed and reversed. This type of bi-modal regime may explain the absence of previous clear results on the DIB-RV relationship when data from the two regimes are mixed together.
for the low- to moderate-reddening regime AV ⪅ 2.5 mag. Combining with measurements of Ramírez-Tannus et al. (2018) and their estimates of RV for stars in the M17 cloud with AV ≥ ≃4 mag, it appears that at higher extinctions the trend is suppressed and reversed. This type of bi-modal regime may explain the absence of previous clear results on the DIB-RV relationship when data from the two regimes are mixed together.
In Sect. 4, we also used (iii), and investigated the link between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq64.png) and the dust emission spectral index β. To do so, we used Planck β sky maps and selected targets from the two 862 nm DIB catalogues located outside the dust layer (i.e. with negligible interstellar dust beyond the star). This is necessary since the spectral index β refers to the totality of the dust in the chosen direction. Such targets are preferentially found at high latitude. We integrated in the best resolution 3D extinction maps to estimate the extinction of the targets. Despite a large scatter, we found a negative correlation between
and the dust emission spectral index β. To do so, we used Planck β sky maps and selected targets from the two 862 nm DIB catalogues located outside the dust layer (i.e. with negligible interstellar dust beyond the star). This is necessary since the spectral index β refers to the totality of the dust in the chosen direction. Such targets are preferentially found at high latitude. We integrated in the best resolution 3D extinction maps to estimate the extinction of the targets. Despite a large scatter, we found a negative correlation between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq65.png) and β for AV ≤≃2.5 mag, and a disappearance of the trend above this threshold (i.e. for high extinctions). There may be a hint for reversal; however, the number of appropriate targets with high extinctions and located beyond the dust layer becomes very small. The trend at low-moderate AV is more apparent when using recent estimates of β by Casandjian et al. (2022).
and β for AV ≤≃2.5 mag, and a disappearance of the trend above this threshold (i.e. for high extinctions). There may be a hint for reversal; however, the number of appropriate targets with high extinctions and located beyond the dust layer becomes very small. The trend at low-moderate AV is more apparent when using recent estimates of β by Casandjian et al. (2022).
The two trends, for ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq66.png) and β, in the low- to moderate-extinction regime, are found to be fully consistent with the anti-correlation between β and
and β, in the low- to moderate-extinction regime, are found to be fully consistent with the anti-correlation between β and ![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq67.png) found by Schlafly et al. (2016), which reinforces the likeliness of these two independent results. The opposite trends we have derived are particularly interesting in view of the models and results of Zelko & Finkbeiner (2020), namely that the β and RV anti-correlation is induced by variations of the relative fractions of carbonaceous and silicate dust grains, with a higher RV (and lower β) being associated with a higher fraction of carbonaceous grains. In this case, because it is now generally admitted that DIB carriers are carbonaceous macro-molecules, their density relatively to the total dust content, measured by
found by Schlafly et al. (2016), which reinforces the likeliness of these two independent results. The opposite trends we have derived are particularly interesting in view of the models and results of Zelko & Finkbeiner (2020), namely that the β and RV anti-correlation is induced by variations of the relative fractions of carbonaceous and silicate dust grains, with a higher RV (and lower β) being associated with a higher fraction of carbonaceous grains. In this case, because it is now generally admitted that DIB carriers are carbonaceous macro-molecules, their density relatively to the total dust content, measured by ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq68.png) , is naturally expected to correlate with RV and anti-correlate with β, which is what we derive. The trends are no longer valid for LOSs crossing opaque clouds, where accretion onto grains and grain coagulation dominate, and the skin effect for the DIB carriers starts to play a role. Regarding the carbon to silicon abundance, we note that Cox et al. (2024) found evidence from the 3D maps that higher
, is naturally expected to correlate with RV and anti-correlate with β, which is what we derive. The trends are no longer valid for LOSs crossing opaque clouds, where accretion onto grains and grain coagulation dominate, and the skin effect for the DIB carriers starts to play a role. Regarding the carbon to silicon abundance, we note that Cox et al. (2024) found evidence from the 3D maps that higher ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq69.png) values are spatially associated with regions where C-rich ejecta from AGBs increase relative to the O-rich fluxes. From the point of view of extinction and emission laws, this shows that useful predictions on the dust composition may be obtained based on DIB measurements.
values are spatially associated with regions where C-rich ejecta from AGBs increase relative to the O-rich fluxes. From the point of view of extinction and emission laws, this shows that useful predictions on the dust composition may be obtained based on DIB measurements.
In Sec. 5, we used (iv) and re-examined the link between the 220 nm UV bump and the DIBs, using data from the intensive compilation of Xiang et al. (2017). The results, so far, have been contradictory regarding the existence of a link. One of the reasons for the difficulty of such a study is the cloud multiplicity and the resulting mixing of the cloud (and DIB carrier) properties along the LOS of the target star, especially in the case of distant, highly reddened hot stars generally used for UV extinction law measurements and DIB extraction. Here we added to the previous searches an additional criterion based on the 3D dust maps and reflecting the cloud singleness (item iv in the above list). If the LOS is characterized by a unique dense cloud or group of clouds at short distance from each other, the flag is set to F=1. If, on the contrary, there are two or more groups of clouds contributing to the extinction (and to the DIB EW) separated by distances of the order of several hundred parsecs or more, one may expect different properties of the IS matter and the flag is set to F=0. This criterion is defined visually, and it should be used with limited ambition. However, our goal was to detect (or not) an improvement in the link between DIBs and the bump when selecting flag F=1 LOS by comparison with the full dataset or with flag F=0 LOS. This approach allowed us to demonstrate the existence of a positive relationship between the reddening-normalized (or extinction-normalized) DIB EWs and the height of the bump for those DIBs that are of σ type, known to be favoured in UV-irradiated regions and to decrease in cloud cores (the UV field here is estimated by the 5780/5797 ratio). It confirmed, based on the larger number of LOSs from the Xiang et al. (2017) compilation, the previous conclusions drawn by Desert et al. (1995). The relationship disappears for DIBs such as λ5797 or λ5850 (i.e. of ζ type). This may explain the negative conclusion of Xiang et al. (2011) and Xiang et al. (2017) regarding a global DIB-bump relationship associating all DIBs. We tested a simplistic predictive model of the bump height based on a combination of reddening-normalized DIBs and the 5780/5797 ratio. It provided some estimates of the bump height, especially in the case of particularly low, or particularly high bumps. On the other hand, we found a negative relationship between the reddening-normalized 5780 Å DIB EW and the bump width, similarly to Desert et al. (1995), although this trend is characterized by a larger scatter and a higher uncertainty on the slope compared to the case of the bump height. Finally, no general trend emerges from the comparisons between DIBs and the bump area, in agreement with the results of Xiang et al. (2017), although a weak positive trend is found for σ-type DIBs.
These results on the UV bump are surprising, in particular the fact that direct positive correlations between the bump height and DIBs, and direct anti-correlations between bump widths and DIBs, are found only for the DIBs that are the most prone to the skin effect (or σ DIBs), the decrease in the carriers relative to the extinction in the dense cloud cores. Correlations may also be found in the case of ζ DIBs, but only after application of a corrective factor whose effect is to increase their strengths in LOS characterized by a high 5780 Å-to-5797 Å DIB ratio (or σ-to-ζ ratio). There may be evidence here for the building of the bump outside of the densest cores, and this point deserves further observations and modelling. In this respect, it is interesting to recall the result obtained by Fitzpatrick & Massa (1986) on the bump width. The authors inferred that the 220 nm bump is narrower in the diffuse ISM, and broader in dense quiescent clouds. Given that for σ-type DIBs, such as the 5780 Å DIB, the ratio ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq70.png) is found to increase when the bump width decreases (Fig. 14), the Fitzpatrick & Massa (1986) trend predicts, in turn, that
is found to increase when the bump width decreases (Fig. 14), the Fitzpatrick & Massa (1986) trend predicts, in turn, that ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq71.png) should increase from dense clouds to regions of lower density. This is what is statistically found based on 3D maps, and mono-cloud type LOSs, as discussed in Sec. 2, and adds a consistent link between the trends found between
should increase from dense clouds to regions of lower density. This is what is statistically found based on 3D maps, and mono-cloud type LOSs, as discussed in Sec. 2, and adds a consistent link between the trends found between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq72.png) and the bump on the one hand, and between
and the bump on the one hand, and between ![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq73.png) and the ISM type on the other hand.
and the ISM type on the other hand.
It is beyond the scope of this observational work to discuss the implications in terms of the DIB carriers and species responsible for the UV bump. Our unique remark is that, despite the limited strength of all correlations, as expected from the integration along the LOSs, the results on bump height and width may be hints of a partial contribution to the bump of some specific molecular species and their specific lines, in addition to the global contribution of a large variety of species (e.g. PAHs). In this respect, it is interesting to note that recent works point to high densities of two-ring polycyclic aromatic hydrocarbons, their formation around AGBs, and their potential contribution to the bump. Stockett et al. (2023) found a mechanism that explains why cyanonaphthalene (C10H7N) can be orders of magnitude higher than predicted by models, following the discovery of quantities of this species and of indene in the Taurus Molecular Cloud with quantities orders of magnitude higher than expected (McGuire et al. 2021; Burkhardt et al. 2021). According to Stockett et al. (2023), their results challenge the widely accepted picture of rapid destruction of small PAHs in space. As a result of their advanced models, Krasnoukhov et al. (2022) found that under the conditions prevailing in the circumstellar envelopes of the asymptotic giant branch stars (AGBs), the formation of two-ring polycyclic aromatic hydrocarbons is favoured. On the other hand, based on a state-of-the-art laboratory experimental set-up, Fréreux et al. (2023) found that substituted naphthalene units, such as substructures of hydrogenated amorphous carbons, are favoured in combustion processes and produce spectral signatures around 217.5 nm. Further measurements of the bump central wavelength and its potential association with the LOS type may bring support to the existence of such contributions.
All together, these results based on 3D maps and surveys reveal complex, but real relationships between the DIB carrier densities and some dust extinction and emission parameters. They suggest that future precise, massive measurements of various DIBs and of extinction, as well as massive measurements of the UV part of the extinction law, may provide constraints on the interplay between the carbonaceous macro-molecules at the origin of DIBs and the size distribution of grains, on the spatial variability of the dust composition, and in turn on the variability of extinction and emission law parameters. DIBs are easy to measure and their EWs are calibration-free measurements, which are strong advantages. They are no longer restricted to early-type stars, but extended to the far more numerous cool targets (e.g. Kos et al. 2013; Puspitarini et al. 2015; Zasowski et al. 2015), thanks to the huge progresses made over recent years on stellar models and on their adjustments to data from recent surveys and Gaia. Being distance-limited data, the use of distributed targets provides local measurements, allowing us in turn to understand where and how the extinction and emission are built, and to make predictions.
 |
Fig. 14 Same as Fig. 11, but for the dependence on the bump width, for formalism 1 and 2. Top: all targets. Middle: Flag F=1 targets. Bottom: flag F=0 targets. |
 |
Fig. 15 Same as Fig. 11, but for the dependence on the bump area and formalism 1. Top: all flags. Middle: F=1. Bottom: F=0. |
Acknowledgements
We thank our reviewer for his/her careful reading and helpful suggestions. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101004214 (EXPLORE project – https://explore-platform.eu). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France (DOI: 10.26093/cds/vizier). The original description of the VizieR service is published in 2000, A&AS 143, 23.
References
- Bertaux, J.-L., & Lallement, R. 2017, MNRAS, 469, S646 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhardt, A. M., Long Kelvin Lee, K., Bryan Changala, P., et al. 2021, ApJ, 913, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Cami, J., Sonnentrucker, P., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 326, 822 [NASA ADS] [Google Scholar]
- Cami, J., Bernard-Salas, J., Peeters, E., & Malek, S. E. 2010, Science, 329, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Casandjian, J.-M., Ballet, J., Grenier, I., & Remy, Q. 2022, ApJ, 940, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Cordiner, M. A., Linnartz, H., Cox, N. L. J., et al. 2019, ApJ, 875, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Cami, J., Kaper, L., et al. 2014, A&A, 569, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Cami, J., Farhang, A., et al. 2017, A&A, 606, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Vergely, J. L., & Lallement, R. 2024, A&A, 689, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desert, F. X., Jenniskens, P., & Dennefeld, M. 1995, A&A, 303, 223 [Google Scholar]
- Ebenbichler, A., Smoker, J. V., Lallement, R., et al. 2024, A&A, 686, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elyajouri, M., Lallement, R., Monreal-Ibero, A., Capitanio, L., & Cox, N. L. J. 2017, arXiv e-prints [arXiv:1702.00223] [Google Scholar]
- Ensor, T., Cami, J., Bhatt, N. H., & Soddu, A. 2017, ApJ, 836, 162 [Google Scholar]
- Fan, H., Hobbs, L. M., Dahlstrom, J. A., et al. 2019, ApJ, 878, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1986, ApJ, 307, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1990, ApJS, 72, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1994, Nature, 369, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Fréreux, J. N., Godard, M., Dartois, E., & Pino, T. 2023, A&A, 677, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedman, S. D., York, D. G., McCall, B. J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Schultheis, M., et al.) 2023a, A&A, 680, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Schultheis, M., et al.) 2023b, A&A, 674, A40 [CrossRef] [EDP Sciences] [Google Scholar]
- Geballe, T. R., Najarro, F., Figer, D. F., Schlegelmilch, B. W., & de La Fuente, D. 2011, Nature, 479, 200 [Google Scholar]
- Hamano, S., Kobayashi, N., Kondo, S., et al. 2016, ApJ, 821, 42 [Google Scholar]
- Herbig, G. H. 1995, ARA&A, 33, 19 [Google Scholar]
- Hobbs, L. M., York, D. G., Snow, T. P., et al. 2008, ApJ, 680, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., & Desert, F.-X. 1994, A&As, 106 [Google Scholar]
- Jones, A. P. 2016, Roy. Soc. Open Sci., 3, 160223 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Grebel, E. K., et al. 2013, ApJ, 778, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Wyse, R., et al. 2014, Science, 345, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnoukhov, V. S., Pivovarov, P. S., Zagidullin, M. V., et al. 2022, Astron. Rep., 66, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Krelowski, J., & Walker, G. A. H. 1987, ApJ, 312, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Krelowski, J., & Westerlund, B. E. 1988, A&A, 190, 339 [NASA ADS] [Google Scholar]
- Krelowski, J., Snow, T. P., Seab, C. G., & Papaj, J. 1992, MNRAS, 258, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Kwok, S. 2023, Galaxies, 11, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Lan, T.-W., Ménard, B., & Zhu, G. 2015, MNRAS, 452, 3629 [Google Scholar]
- Li, K., Li, A., & Xiang, F. Y. 2019, MNRAS, 489, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Caballero, J. A., Bohlin, R. C., & Fariña, C. 2021, MNRAS, 501, 2487 [CrossRef] [Google Scholar]
- McGuire, B. A., Loomis, R. A., Burkhardt, A. M., et al. 2021, Science, 371, 1265 [Google Scholar]
- Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVIII. 2016, A&A, 596, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Tannus, M. C., Cox, N. L. J., Kaper, L., & de Koter, A. 2018, A&A, 620, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarre, P. J., Miles, J. R., Kerr, T. H., et al. 1995, MNRAS, 277, L41 [NASA ADS] [Google Scholar]
- Schlafly, E. F., Meisner, A. M., Stutz, A. M., et al. 2016, ApJ, 821, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Peek, J. E. G., Finkbeiner, D. P., & Green, G. M. 2017, ApJ, 838, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Schlarmann, L., Foing, B., Cami, J., & Fan, H. 2021, A&A, 656, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stockett, M. H., Bull, J. N., Cederquist, H., et al. 2023, Nat. Commun., 14, 395 [CrossRef] [Google Scholar]
- Vergely, J. L., Lallement, R., & Cox, N. L. J. 2022, A&A, 664, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vos, D. A. I., Cox, N. L. J., Kaper, L., Spaans, M., & Ehrenfreund, P. 2011, A&A, 533, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiang, F. Y., Li, A., & Zhong, J. X. 2011, ApJ, 733, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Xiang, F. Y., Li, A., & Zhong, J. X. 2017, ApJ, 835, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Ménard, B., Bizyaev, D., et al. 2015, ApJ, 798, 35 [Google Scholar]
- Zelko, I. A., & Finkbeiner, D. P. 2020, ApJ, 904, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Zelko, I. A., & Finkbeiner, D. P. 2021, ApJ, 914, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., Schultheis, M., Rojas-Arriagada, A., et al. 2021, A&A, 654, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, H., Schultheis, M., Arentsen, A., et al. 2023, MNRAS, 519, 754 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 862 nm DIB carrier and extinction volume densities. All voxels of the Cox et al. (2024) 3D maps have been used. Left: DIB density averaged in voxels with equal extinction density. An adjusted power law limited to the low-extinction regime is superimposed (see text). Right: ratio of the DIB EW density to the extinction density for the same voxels, and superimposed power law. |
| In the text | |
 |
Fig. 2 862 nm DIB EW and LOS-integrated extinction. Top: DIB EW from the Gaia DR3 catalogue as a function of the extinction Av integrated from the Sun to the target star. A power law is fitted to the data from Av=0 to Av=1.5 mag. Isocontours of target number densities have been drawn to illustrate the various contributions. Bottom: same as top, but for the second catalogue of averaged EWs in spatial bins. |
| In the text | |
 |
Fig. 3
|
| In the text | |
 |
Fig. 4 Relationship between the extinction-normalized 862 nm DIB and the Schlafly et al. (2016) total to selective extinction R′V for APOGEE LOSs (dots). For low to moderate extinctions, despite the large scatter, |
| In the text | |
 |
Fig. 5 Images of 862 nm |
| In the text | |
 |
Fig. 6 Illustration of the dependence on the extinction regime of the relationship between the normalized DIB and β. Plotted are the normalized ratios as a function of the LOS extinction, color-coded for the β value for each LOS. Marker sizes increase with target location distance to the Plane. The two estimates for β are shown (left and right). Below Av≃3 mag (left part of the graphs), decreasing |
| In the text | |
 |
Fig. 7 Extinction-normalized 862 nm DIB EWs as a function of the spectral index β from Casandjian et al. (2022), for DIB with quality flag 0 data from the second catalogue of Gaia Collaboration (2023a), and Galactic latitudes between 10° and 20°. Superimposed is a linear fit for this catalogue selection. |
| In the text | |
 |
Fig. 8 Extinction-normalized 862 nm DIB EW for selected data from the second catalogue (Gaia Collaboration 2023a) as a function of the sky-interpolated Planck spectral index β (see text for selection). The colour scale refers to the distance to the Plane of the spatial bin, and excludes distances below 200 pc. Extinction values are restricted to the 1.5 to 2.5 mag interval. An orthogonal distance regression linear fit is superimposed (see text). |
| In the text | |
 |
Fig. 9 Ranges of gradients for extinction-normalized DIB EWs as a function of β for data from the two catalogues and in various regimes of LOS extinctions. Errors are 1σ uncertainties on the slopes. There are differences at low extinctions due to the very different types of data (individual LOSs vs spatial bins) and at high extinctions due to the small number of data points. Between 1 and 3 magnitudes of extinction, all determinations are compatible and show a negative slope. |
| In the text | |
 |
Fig. 10 Illustration of the attribution of a flag F to a given star from the Xiang et al. (2017) list. Shown are images of the dust distribution in vertical planes containing the Sun and the star. The dark areas correspond to high dust opacity. The LOS to the target (green marker) is shown as a green dotted line. HD 143567 (top) is attributed a flag F=1 since most of the extinction is generated in a single very dense nearby cloud. The more distant HD 192216 (bottom) is attributed a flag F=0 since at least two dense clouds separated by a large distance contribute to the extinction. |
| In the text | |
 |
Fig. 11 Comparisons between the σ-type 5780 Å DIB EW and the UV bump height, under formalism 1 of the extinction law (a-c) and formalism 2 (d-f). Data are from the compilation of Xiang et al. (2017). (a) and (d) show the bump height vs the reddening-normalized EW for all targets and the adjusted linear fit. The colour-coding refers to the extinction (from yellow for the lowest extinctions to black for the highest ones). Errors bars on EWs are indicated. (b and e) Same as (a) and (d), for flag F=1 stars only. (c and f) Same as (a) and (d) for flag F=0 only. The F=0 LOSs show no dependence, and lower the correlation based on all data. F=1 targets show a clearer positive correlation. |
| In the text | |
 |
Fig. 12 Same as Fig. 11 (a-c) but for the ζ-type 5850 Å DIB and formalism 1. Top: all flags. Middle: flag F=1. Bottom: flag F=0. No trend is detected, neither for all stars, nor for F=1 stars only. |
| In the text | |
 |
Fig. 13 Illustration of a composite model of the bump height based on DIBs and the UV ratio EW(5780)/EW(5797). (a) Bump height and UV ratio 5780/5797. (b) Composite power-law model (Eq. (2)) based on the 5850 Å DIB and the UV ratio, for all stars with DIB 5850 Å data (55 targets). (c) Same as panel b, for a model based on flag F=1 stars only. (d) Composite power-law model (Eq. (2)) based on DIB 5780, DIB 5850, and the UV ratio, adjusted on flag F=1 stars (89 targets). Flag F=0 stars are in red, Flag F=1 stars in violet. In panels b, c, and d, the y = x curves are superimposed. |
| In the text | |
 |
Fig. 14 Same as Fig. 11, but for the dependence on the bump width, for formalism 1 and 2. Top: all targets. Middle: Flag F=1 targets. Bottom: flag F=0 targets. |
| In the text | |
 |
Fig. 15 Same as Fig. 11, but for the dependence on the bump area and formalism 1. Top: all flags. Middle: F=1. Bottom: F=0. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\[R_V^{\prime}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq23.png)
![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq38.png)
![$\[R_V^{\prime-1}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq39.png)
![$\[R_V^{\prime-1}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq40.png)
![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq41.png)
![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq48.png)
![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq56.png)
![$\[\mathrm{DIB}_{\text {norm }}^{862}\]$](/articles/aa/full_html/2024/11/aa51657-24/aa51657-24-eq57.png)