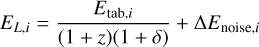| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A317 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202451736 | |
| Published online | 18 October 2024 | |
jaxspec: A fast and robust Python library for X-ray spectral fitting
1
IRAP, Université de Toulouse, CNRS, CNES,
UT3-PS,
Toulouse, France
Corresponding author; sdupourque@irap.omp.eu
2
European Space Agency (ESA), European Space Astronomy Centre (ESAC),
Camino Bajo del Castillo s/n,
28692
Villanueva de la Cañada, Madrid, Spain
Received:
31
July
2024
Accepted:
9
September
2024
Context. Inferring spectral parameters from X-ray data is one of the cornerstones of high-energy astrophysics, and is achieved using software stacks that have been developed over the last 20 years and more. However, as models get more complex and spectra are obtained with higher resolutions, these established software solutions become more feature-heavy, difficult to maintain and less efficient.
Aims. We present jaxspec, a Python package for performing this task quickly and robustly in a fully Bayesian framework. Based on the JAX ecosystem, jaxspec allows the generation of differentiable likelihood functions compilable on core or graphical process units (GPUs), enabling the use of robust algorithms for Bayesian inference.
Methods. We demonstrate the effectiveness of jaxspec samplers, in particular the no U-turn sampler, using a composite model and comparing what we obtain with the existing frameworks. We also demonstrate its ability to process high-resolution spectroscopy data using original methods by reproducing the results of the Hitomi collaboration on the Perseus cluster, while solving the inference problem using variational inference on a GPU.
Results. We obtain identical results when compared to other software and approaches, meaning that jaxspec provides reliable results while being ~10 times faster than existing alternatives. In addition, we show that variational inference can produce convincing results even on high-resolution data in less than 10 minutes on a GPU.
Conclusions. With this package, we aim to pursue the goal of opening up X-ray spectroscopy to the existing ecosystem of machine learning and Bayesian inference, enabling researchers to apply new methods to solve increasingly complex problems in the best possible way. Our long-term ambition is the scientific exploitation of the data from the newAthena X-ray Integral Field Unit (X-IFU).
Key words: methods: data analysis / methods: statistical / X-rays: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Spectral fitting is one of the cornerstones of X-ray astrophysics and has been widely used and developed since the 1990s as the number of X-ray instruments has increased. An X-ray spectrum, represented by a number of counts in energy bins, can be reduced to meaningful parameters using an appropriate physical model. Constraining the plausible values of these parameters given an X-ray spectrum is usually achieved using publicly available software, such as xspec (Arnaud 1996), SPEX (Kaastra et al. 1996), sherpa (Freeman et al. 2001; Doe et al. 2007), or ISIS (Houck & Denicola 2000).
The typical approach is to define a fit statistic (e.g. χ2 or C-stat; see Cash 1979) and optimise it using gradient-free minimisation algorithms. This type of approach is efficient if the initial parameter estimates are close to their optimal values, but is highly dependent on the dimensionality and smoothness of the parameter space. In general, there is no guarantee that these algorithms will not get stuck in local minima, which would ultimately lead to incorrect physical interpretations. Moreover, deriving a meaningful error budget in this situation is not trivial and often requires an exhaustive evaluation of the fit statistic in an N-dimensional lattice in the neighbourhood of the best fit, which is not efficient as the number of parameters, N, increases.
On the other hand, Bayesian approaches provide a sample of parameters that are distributed according to the likelihood. The sample of posterior parameters carries information about the dispersion and is less likely to get stuck in a local minimum (e.g. Bonson & Gallo 2016; Choudhury et al. 2017; Barret & Cappi 2019). This type of approach requires orders of magnitude more computation time than direct minimisation. Posterior samples can also be generated using Markov chain Monte Carlo (MCMC) approaches, or other algorithms such as the nested sampling (Ns) implemented in BXA (Buchner et al. 2014; Buchner 2021), which can efficiently check their convergence. We recently proposed a new approach using neural networks to directly learn the posterior distribution, given a set of simulated spectra (see SIXSA, Barret & Dupourqué 2024). This simulation-based inference approach showed a similar performance compared to the existing solutions, while being much faster.
As a more general trend, we have seen major advances in the field of machine learning over the last decade, mainly due to the use of back-propagation algorithms (Rumelhart et al. 1986). Today’s neural networks can be parameterised with up to billions of parameters, and finding the best parameters to achieve a given task is unthinkable using classical minimisation algorithms. The back-propagation algorithm allows the gradient of any function to be estimated as long as it can be represented by a computational graph of differentiable components. This additional gradient information allows the use of powerful minimisation algorithms, such as the adam algorithm (Kingma & Ba 2017), which can find optimal values for parameters in high-dimensional spaces. Modern frameworks such as tensorflow (Abadi et al. 2015a,b), PyTorch (Paszke et al. 2019) and JAX (Bradbury et al. 2018) can provide this gradient information automatically. In particular, JAX is already used in the astrophysics community to facilitate the inference of cosmological parameters (e.g. Campagne et al. 2023; Piras & Mancini 2023; Balkenhol et al. 2024) by providing differentiable likelihood functions.
In this article we present jaxspec, a JAX-based X-ray spectral fitting package written in pure Python. Using differentiable programming, gradient-based MCMC samplers and variational inference (VI) algorithms, jaxspec quickly and efficiently provides distributions for the spectral model parameters. We describe the design of jaxspec and we benchmark it against existing packages to demonstrate the benefits of just-in-time compilation and auto-differentiability. By studying Hitomi/Soft X-ray Spectrometer (SXS) observations of the core of the Perseus cluster and constraining the gas motions using a Bayesian hierarchical model, we demonstrate the feasibility of VI for high-resolution X-ray spectral fitting. Finally, we discuss the philosophy behind the development of jaxspec and our desire to provide software that is modern, flexible, open source, and driven by the community.
2 Description of jaxspec
We have designed jaxspec as a software package written entirely in Python. By leveraging key packages from the data science ecosystem, the source code itself is greatly simplified compared to other existing solutions and some sustainability is ensured over time. In particular, jaxspec relies on two widely used and maintained dependences. The first is JAX (Bradbury et al. 2018), a library similar to tensorflow and pytorch for writing automatically differentiable code that can be compiled at runtime. JAX is widely used in the machine learning community and allows code to be executed transparently on core, graphical or tensor process units (CPUs, GPUs and TPUs, respectively) to achieve significant speed-up. The second is numpyro (Phan et al. 2019), a probabilistic programming library that implements the construction of hierarchical Bayesian models and the tools needed to perform the associated inference. In particular, numpyro includes a JAX implementation of the no U-turn sampler (Hoffman & Gelman 2014) and an interface for applying VI methods. We are distributing jaxspec to the community as a Python package that can be downloaded and installed directly from the pypi portal. The codebase is open source, publicly available in a GitHub repository1 and documented2.
Spectral models in jaxspec can be built in the same way as one would expect from xspec, namely, by organically nesting model components. We have already implemented some commonly used and analytically computable model components3 (e.g. blackbody spectra and power-law spectra) and tabulated absorption models, such as the Tübingen-Boulder interstellar medium absorption model tbabs (Wilms et al. 2000). jaxspec does not (yet) implement many of the models available in xspec, and porting legacy Fortran / C models to pure JAX is neither a quick nor an easy task. However, models that are interpolated on rectangular grids are readily implementable in jaxspec, such as the nsatmos neutron star atmosphere model (Heinke et al. 2006). As described in Sect. 5, we are counting on the community to update, maintain and share models, and we will do our best to help model developers integrate their work into this codebase.
Each spectral model is parameterised by a subset of the parameters θ. These models are folded into the instrumental response using matrix multiplications, which allow the expected number of counts in each instrumental bin, λi, to be estimated given a set of parameters and for a particular observing setup. Finding the best set of parameters to describe the observed data requires a metric to define how good a model is. In the case of X-ray spectral fitting, the detection of photons within instrumental bins can be described as a counting process, which means it can be modelled as a Poisson random variable. The corresponding log-likelihood4 for the expected photons, λ(θ), according to the model and the observed values, c, is written as
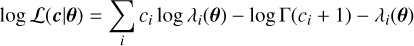 (1)
(1)
where 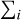 denotes the summation over the instrument bins. This Poisson likelihood is directly related to the well-known Cash statistic (Cash 1979), which is actually a transformation of the Poisson likelihood that corresponds to the χ2 statistic at high counts.jaxspec implement only on the Poisson likelihood, as the χ2 likelihood has historically been used to study high-count spectra and to simplify error calculations, and is biased at lower counts (see, e.g. Humphrey et al. 2009; Kaastra 2017; Buchner & Boorman 2023). Finding the best set of parameters that maximises this likelihood and its associated variance can be achieved using Bayesian inference approaches.
denotes the summation over the instrument bins. This Poisson likelihood is directly related to the well-known Cash statistic (Cash 1979), which is actually a transformation of the Poisson likelihood that corresponds to the χ2 statistic at high counts.jaxspec implement only on the Poisson likelihood, as the χ2 likelihood has historically been used to study high-count spectra and to simplify error calculations, and is biased at lower counts (see, e.g. Humphrey et al. 2009; Kaastra 2017; Buchner & Boorman 2023). Finding the best set of parameters that maximises this likelihood and its associated variance can be achieved using Bayesian inference approaches.
3 Benchmarking Bayesian inference in jaxspec
Solving an inference problem with Bayesian approaches requires inverting this likelihood into a posterior distribution of θ constrained to the observed number of counts c. This requires defining prior distributions for θ that encapsulate our (lack of) knowledge about the expected values of our model parameters. Once the Bayesian inference problem is set up, the easiest way to solve it is to sample the parameter values {θ}i from the posterior distribution. There are many methods for doing this, such as MCMC or NS.
3.1 Quality of the MCMC samples
Markov chain Monte Carlo sampling has been one of the most widely used approaches to obtaining parameter samples that are distributed according to the posterior distribution of a Bayesian inference problem since the Metropolis-Hastings algorithm was proposed (Hastings 1970). MCMC algorithms generate chains of samples by moving gradually through the parameter space, making small, local changes at each step. They are designed so that the stationary distribution of these chains is the posterior distribution of the parameters. As such, reaching the stationary distribution requires a sufficiently large number of iterations, which is not trivial to quantify. Many solutions based on MCMC sampling can provide posterior samples. The affine invariant ensemble sampler (AIES, Goodman & Weare 2010) uses multiple chains that are not independent (often referred to as walkers) to shift the proposal distribution towards optimal regions of the parameter space. This is the sampler implemented in the well-known emcee package (Foreman-Mackey et al. 2013), and also the default sampler implemented in xspec. While the traditional MCMC sampling algorithm requires numerous steps to achieve stationarity, gradient-based samplers can significantly reduce the number of steps required. Hamiltonian Monte Carlo (e.g. Betancourt & Girolami 2013) uses the gradient of the likelihood to perform ‘energy saving’ steps in the parameter space, allowing much better exploration and faster convergence. In particular, NUTS (Hoffman & Gelnian 2014) uses this dynamic to adoptively explore the likelihood, setting the step size depending on the local curvature. Since jaxspec provides auto-differentiable likelihoods, we set the numpyro implementation of NUTS as the default sampler, and compared the numpyro and xspec implementations of AIES.
To compare the performance of jaxspec with existing solutions, we chose to solve a similar inference problem using the different methods. The task was to obtain the posterior distribution of the five parameters of an absorbed dual-component model (tbabs*(powerlaw+blackbodyrad)) fitted to an observation of NGC 7793 ULX-4. Ultra-luminous X-ray sources (ULXs, e.g., Kaaret et al. 2017) are highly accreting stellar-mass binary systems, in which the precise physical processes at play are still largely debated. In particular, some ULXs display a two-component spectral emission in X-rays (e.g., Sutton et al. 2013), the first component (thermal) generally being interpreted as an accretion disk and the second (power-law-like) as either a hot accretion column or a Compton-scattering outflow (e.g., Gúrpide et al. 2021). The relative temporal evolution of one component with respect to the other is generally different in ULXs compared to standard X-ray binaries (e.g., Koliopanos et al. 2017). As such, precisely and carefully constraining the parameters from both components can shed some light on the physics of these objects. We used the XMM-Newton observations of NGC 7793 ULX-4 as reduced in Quintin et al. (2021), and focused on the spectrum produced by the EPIC-PN instrument, with no background. All the calculations described in this section are performed on a single core in order to obtain comparable results between the different methods used, but it is worth noting that they all benefit from being performed on multiple cores.
For this benchmark, we ran MCMC chains using AIES and NUTS and measured how quickly the chain converged to a stationary distribution using the 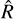 statistic (Vehtari et al. 2021) computed for an increasing number of samples. The
statistic (Vehtari et al. 2021) computed for an increasing number of samples. The 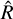 statistic compares the intra- and inter-chain variance to assess their individual convergence. AIES was run with 25 = 32 walkers, as suggested by the number of parameters in our model, while NUTS was run with four chains. We ran 103 burn-in steps and 105 sampling steps, and computed the
statistic compares the intra- and inter-chain variance to assess their individual convergence. AIES was run with 25 = 32 walkers, as suggested by the number of parameters in our model, while NUTS was run with four chains. We ran 103 burn-in steps and 105 sampling steps, and computed the 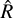 statistic for an increasing number of samples, with a step of 1000. The
statistic for an increasing number of samples, with a step of 1000. The 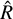 statistic was computed using only the best four chains of each sampler, defined in terms of the best likelihood on average. We show in the left panel of Fig. 1 that the
statistic was computed using only the best four chains of each sampler, defined in terms of the best likelihood on average. We show in the left panel of Fig. 1 that the 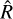 decreases as the number of steps increases, as the chains begin to converge. The usual convergence threshold of
decreases as the number of steps increases, as the chains begin to converge. The usual convergence threshold of 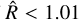 is reached well within the first 1000 steps with NUTS, ~5000 steps with AIES in jaxspec, and 25 000 steps with AIES in xspec. The right panel of Fig. 1 shows the individual samples of a single chain using the normBB parameter. As expected, NUTS is much better at providing uncorrelated samples, while AIES and especially the xspec implementation provide samples with visible correlations, meaning that it takes a large number of steps and additional thinning to get a meaningful sample of parameters from the posterior distribution.
is reached well within the first 1000 steps with NUTS, ~5000 steps with AIES in jaxspec, and 25 000 steps with AIES in xspec. The right panel of Fig. 1 shows the individual samples of a single chain using the normBB parameter. As expected, NUTS is much better at providing uncorrelated samples, while AIES and especially the xspec implementation provide samples with visible correlations, meaning that it takes a large number of steps and additional thinning to get a meaningful sample of parameters from the posterior distribution.
 |
Fig. 1 Comparison of the sampling quality using jaxspec and xspec. Left: |
3.2 Comparison of inference times for various methods
Another common approach to solving Bayesian inference problems is to use NS (see e.g. Büchner 2023), which is a powerful alternative to MCMC sampling. NS relies on a population of points in the parameter space that evolves according to their likelihood at each step. As the number of steps increases, the points with the lowest likelihood are excluded and new points are drawn according to the distribution of the remaining points. Such evolutionary approaches shrink the volume occupied by the samples until there is no further improvement in likelihood. Unlike MCMC approaches, NS provides a stopping criterion and can explore a much larger part of the parameter space, providing robust estimates for the posterior distribution, especially in multi-mode cases. A popular implementation of NS used in X-ray spectral fitting is BXA (Buchner et al. 2014), which interfaces the NS algorithm of ultranest (Büchner 2021) with xspec or sherpa.
We used different inference algorithms and compared their results and total inference time. We used the previously introduced NUTS and AIES samplers implemented in j axspec and xpsec. We also compared the existing BXA sampler (with xspec interface) to the implementation of phantom-powered nested sampling (PPNS, Albert 2023) provided in jaxns. We used the same observational setup as described in the previous subsection and fitted the same five-parameter model. We ran all algorithms with default hyperparameters for sampling and termination, and used the previously determined number of steps to convergence for the MCMC sampler.
The time for 100 runs of each inference approach is plotted in Fig. 2. For this particular case, NUTS is an order of magnitude faster than the other approaches, AIES in jaxspec is slightly faster than other approaches, and PPNS in jaxspec is the equivalent to NS in BXA in terms of speed. For a well-behaved inference problem, NUTS can generate stable posterior distributions in less than a minute. In Fig. 3, we show the results of a single run of each algorithm. The posterior distributions are in good agreement. We note that the AIES implementation in numpyro, which is used in jaxspec, produces marginal distributions that are tighter than the other algorithms, due to differences in the underlying implementations. In a nutshell, the xspec implementation uses the ‘stretch’ move from Goodman & Weare (2010) while j axspec uses the ‘differential evolution’ move from Nelson et al. (2014). The second converges faster but struggles to explore the tail of the distribution, slightly underestimating the spread of the parameters. Increasing the number of walkers should solve this. In either case, the user can choose to use the stretch move or a combination of the two moves in numpyro to achieve the desired behaviour. A composite model like the one presented in this benchmark is a standard use case in the community, meaning this benchmark is representative of a typical inference case for accreting objects. As it is easy to choose a specific sampler in jaxspec, the user can try different approaches to solving a single problem, leading to robust results in the end.
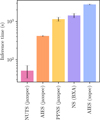 |
Fig. 2 Time per run and standard deviation for NUTS, AIES and NS in both jaxspec, BXA and xspec, estimated for 100 runs of each algorithm on a five-parameter, three-component inference problem. |
4 High-resolution spectroscopy with jaxspec
For the sake of demonstrating the capabilities of jaxspec, we considered the high-resolution X-ray spectrum from the Hitomi/SXS observations of the Perseus core, obtained with the exquisite spectral resolution of ~5eV, which enabled the first high-precision direct measurement of the motions of the intracluster gas (Hitomi Collaboration 2016, 2018). By studying the Fe xxv Heα, Heβ and Heγ complexes, the bulk and velocity dispersions have been constrained to ~50 km/s and ~200 km/s, respectively, in the central regions of the cluster. The high spectral resolution results in extremely dense spectra with large response matrices, which makes direct minimisation more difficult and the general inference more computationally expensive within existing frameworks. Here we demonstrate the use of jaxspec for accurately modelling the observations of the Perseus core with Hitomi. To achieve this, we used the publicly available data, bearing in mind that these data are subject to calibration problems that limit the scientific scope of the results. We used the pipeline products from ObsIds 40, 50 and 60. The spectra weree optimally binned using the algorithm from Kaastra & Bleeker (2016). As in Hitomi Collaboration (2016), we focused on modelling the Fe XXV Hea complex with Gaussian emission lines of known energies in the [6.49, 6.61] keV band. The measurement of the centroid shift and the broadening of these lines provide information about the dynamics of the intra-cluster medium along the line of sight, and is a direct measure of the turbulent motions. In Appendix B, we define a spectral model consisting of nine Gaussian emission lines with known energies to assess the centroid shift and broadening resulting from the gas motion. We used the cluster redshift determination from Hitomi Collaboration (2018) and assumed a Gaussian prior such as z ~ 𝒩(0.017284,0.00005). All the model parameters were constrained using the three observations simultaneously.
As a novelty, we solved this Bayesian inference problem using a VI approach. This family of methods takes a different approach from the MCMC family. Instead of sampling directly from the posterior distribution, it analytically computes an approximation to the posterior density. It requires the specification of a family of distributions, q(θ), called the variational distribution, which is fitted to the true posterior distribution. In practice, this is equivalent to saying that the posterior distribution would be well approximated by, for example a Gaussian distribution for each variable, a multivariate Gaussian for all parameters with a mean and a correlation matrix to be determined, or any analytically computable and parameterised probability density. Selecting a surrogate posterior distribution from a set of known densities transforms the inference problem into an optimisation problem in which we try to recover the best parameters of the surrogate distribution. This in turn requires defining a distance between the variational distribution and the true posterior, minimised by adjusting the variational distribution parameters. One commonly used measure between two distributions in machine learning studies is the Kullback-Leibler divergence (KL divergence; Kullback & Leibler 1951). It shows how much information is lost when a model distribution is used to approximate the true underlying distribution. For the optimisation process in VI, the commonly used metric is the Evidence Lower Bound, which is directly derived from the KL divergence between the variational distribution and the posterior distribution. For further insight, we direct the interested reader to the review by Blei et al. (2017). The ELBO is defined as the difference between the expectation (with respect to the variational distribution, q(θ)) of the logarithm of the joint distribution, p (θ, X), and the logarithm of the variational distribution,
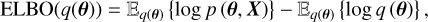 (2)
(2)
while the best surrogate posterior distribution, q*(θ), is the one that maximises the ELBO,
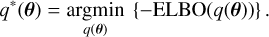 (3)
(3)
We aim to demonstrate the feasibility and effectiveness of VI for X-ray spectral fitting. To our knowledge, this is the first time that such methods have been used for X-ray spectroscopy in astrophysics, with only a handful of works on VI in astrophysics in general (e.g. Gunapati et al. 2022). It has to be noted that classical approaches can also work here. We assumed a multivariate Gaussian distribution as the variational distribution for these observations. This optimisation problem takes particular advantage of the differentiability of its metric, provided here by the auto-differentiation in JAX. This makes it possible to mobilise first-order optimisers (e.g. adam, Kingma & Ba 2017) using gradient information to find a satisfactory minimum for the problem. These algorithms require the user to set hyperparameters, such as the learning rate, which defines the length of each step in the parameter space, or the total number of iterations. For this particular problem, we used the adamw optimiser (Loshchilov & Hutter 2019) with default parameters and a learning rate of 5−4 for 105 iterations. The gradient descent can be run on a GPU and takes ~7 minutes on a Nvidia A2. In Fig. 4 we show the ELBO evolution for the 105 adamw steps, the resulting redshift, bulk motion and velocity dispersion in the observer frame, and the distribution of the posterior folded spectra. The stationarity of ELBO, coupled with the small residuals on the observed spectra, indicates a qualitative fit. The line-of-sight bulk motion of 51 ± 15 km/s and the velocity dispersion of 196 ± 4 km/s are compatible with those measured by Hitomi Collaboration (2016) in the central region of Perseus. However, we stress that our results are not directly comparable, as our analysis is averaged over all Perseus observations and all SXS pixels, and a more exhaustive treatment that includes systematic uncertainties and calibration issues is beyond the scope of this paper. We also show that the posterior has the expected behaviour, as no insight into the cluster redshift is gained due to a degeneracy with the bulk motion captured by our variational distribution. This confirms the efficiency of VI methods for X-ray spectral fitting.
 |
Fig. 3 Posterior distribution of tbabs*(powerlaw+blackbodyrad) parameters from this benchmark, drawn with the 104 last steps of a run of NUTS and AIES using the jaxpsec and xspec implementations, and as provided by the NS algorithms implemented in BXA and jaxspec. |
5 Enabling a community-driven package
As the X-ray spectral fitting ecosystem is already relatively crowded, we feel it is important to justify our efforts to add a new library to it. Beyond the efficiency of JAX and the complexity of scientific use cases enabled by the implementation of state-of-the-art sampling algorithms, the key strengths of jaxspec are its ease of installation and use. It is worth noting that our long-term goal is to exploit the scientific data produced by high-resolution spectrometers such as XR/SM/Resolve and the future newAthena/X-ray Integral Field Unit (XIFU; Barret et al. 2023), which would greatly benefit from modern and fast spectral fitting software.
 |
Fig. 4 Variational inference results for the core of Perseus as seen by Hitomi. (a) ELBO metric during variational distribution optimisation. (b) Redshift, bulk motion (vbulk), and velocity dispersion (σv) posterior distributions obtained for the central regions of the Perseus cluster as seen by Hitomi/SXS, superimposed on the prior distribution for the redshift and the previous results from (Hitomi Collaboration 2016) in the central region. (c) Count spectra of the observations used in this spectral fit, superimposed on the folded model for each observation, and the corresponding residuals in σ. |
5.1 From the casual user’s point of view
Our objective is to provide users with a straightforward software solution for spectral inference that is both readily deployable and intuitive to use. As jaxspec is not dependent on xspec or any equivalent, the installation process is as straightforward as that of any Python package, requiring only the pip command. The software is fully documented and provides examples of inference. As detailed in Appendix A, the syntax for building models and fitting them to observations is kept as simple as possible. For scientists using other tools, the interface we propose should be familiar. The default setups for inference are fast and efficient at providing reliable scientific results. Nevertheless, as jaxspec exposes its likelihoods, the user can extend its use beyond what is provided in the package.
5.2 From the contributor’s point of view
The jaxspec codebaserepresents a fresh start from the existing frameworks. It greatly reduces the code complexity when compared to existing alternatives. Relying on the Python ecosystem for data science reduces the need for maintaining heavy boilerplates. The continuous integration framework, with automated tests, code linters, and automated documentation, allows updates and patches to be deployed easily. The package is open source and hosted on GitHub, and individual contributions are encouraged. This facilitates a collaborative environment in which users can raise issues and directly contribute to the codebase by correcting and extending source code. In particular, it is possible to extend the spectral models, as was previously possible with xspec and other similar software. Analytical models and models interpolated on regular grids can be readily implemented.
6 Conclusions
In this paper, we have presented jaxspec, a pure Python and JAX software for X-ray spectral fitting. Since JAX is differentiable and compilable, powerful samplers such as NUTS can be used to solve the inference problems quickly and reliably, running seamlessly on CPUs or GPUs. We show that it outperforms existing software by an order of magnitude in execution time on a five-parameter, three-component model, while providing robust posterior distributions. The compilable and auto-differentiable likelihood provided by jaxspec allows the use of VI, which can provide accurate results for high-dimensional models, as demonstrated on high-energy-resolution Hitomi/SXS spectra. The likelihood functions built into jaxspec are exposed so that it can be interfaced with external packages such as ultranest, giving users many options.
The current limitation of jaxspec is the library of spectral models that can be fitted, as models must be translated in pure JAX. Regularly tabulated models are already easy to port. We also plan to integrate existing features from other software, such as direct minimisation, multi-instrument gain and shift, convolutional spectral components, and a restriction prior as implemented in SIXSA, and to systematically implement xspec models, which could be used with non-differentiable methods. We also plan to explore the possibility of using neural networks to create surrogate models to port existing models to our codebase. If successful, this approach would have the advantage of providing naturally differentiable codes that are fast to run on CPUs and GPUs, at the cost of controlled error in model evaluation (see e.g. Varma et al. 2019a,b for gravitational waves or Euclid Collaboration 2021 for cosmology applications). As we have taken great care in building this software using good software engineering practices, with a contribution policy, automated testing, and code quality linters, we hope that it will evolve according to the needs of the community. We encourage individual contributions to the codebase and hope to provide astrophysicists with a simple yet reliable tool for X-ray spectral fitting.
Acknowledgements
S.D. and D.B. would like to thank Florent Castellani, and Alexeï Molin for their early contributions to this project, and Fabio Acero and Johannes Buchner for the fruitful discussions about spectral fitting. S.D. and D.B. thank the Centre National d’Etudes Spatiales for financial support. All the calculations involving GPUs were carried out on the SSPCloud (Comte et al. 2022), a platform freely provided to French academics. This work made use of various open-source packages such as numpy (Harris et al. 2020) matplotlib (Hunter 2007), astropy (Astropy Collaboration 2013, 2018, 2022), ChainConsumer (Hinton 2016), cmasher (Velden 2020), haiku (Hennigan et al. 2020).
Appendix A Basic cookbook
The user can install jaxspec with a simple call to pip.
pip install jaxspec
We recommend the user start from a fresh Python 3.10 or 3.11 environment. To build a spectral model, additive and multiplicative components can be tied together as follows :
from jaxspec .model.addi tiveimport Powerlawfrom jaxspec .model.addi tiveimport Blackbodyradfrom jaxspec .model.multiplicativeimport Tbabs model = Tbabs() * (Powerlaw() + Blackbodyrad())
If the data used are compliant with the OGIP standard, they can be loaded as follows :
from jaxspec .dataimport ObsConfiguration obs = ObsConfiguration.from_pha_file(‘path/to/data.pha’ , low_energy=0.5, high_energy=10# RMF and ARF can be explicitly stated #rmf_path=‘path/to/data.rmf’, #arf_path=‘path/to/data.arf’, )
Then, the data can be fitted by providing prior distributions.
from jaxspec .fit import MCMCFitter
from numpyro.distributions import Uniform,
LogUniform
prior = {
“blackbodyrad_l_kT” : Uniform (0, 3),
“blackbodyrad_l_norm” : LogUniform(1e-3, 1),
“ powerlaw_1_alpha” : Uni form(0, 3) ,
“powerlaw_1_norm” : LogUniform(1e-5, 1e-1),
“tbabs_1_N_H” : Uniform(0, 1)
}
result = MCMCFitter(model, prior, obs).fit()
From this result, one can plot the posterior distributions, and perform posterior predictive checks.
result.plot_corner() result.plot_ppc()
We refer the interested user to the documentation of jaxspec, which will evolve, unlike what is presented in this article. It can be found at http://jaxspec.rtfd.io/.
Appendix B Perseus model
The unfolded spectrum is modelled by nine Gaussian emission lines with a common broadening 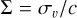 and energy shift δ = vbulk/c. For each of these lines, we fitted a free normalisation and an additional intrinsic energy perturbation, which should be much smaller than the total shift.
and energy shift δ = vbulk/c. For each of these lines, we fitted a free normalisation and an additional intrinsic energy perturbation, which should be much smaller than the total shift.
where Etab,i is the expected energy of line i which can be found in the appendix of Hitomi Collaboration (2016). This spectrum is then folded into Hitomi responses for the three observations; for two of them we added a gain and shift parameter. An additional count-rate baseline was added for each instrument to model the continuum. The prior used for each parameter and the posterior values are displayed in Table B.1. We also used the automatic re-parametrisation provided by numpyro to rescale and de-center the Gaussian prior distributions, and represent the loguniform prior in a flat space, which regularises the likelihood and facilitates the gradient descent.
Prior distribution and posterior quantiles for the parameters of the Perseus core region model.
References
- Abadi, M., Agarwal, A., Barham, P., et al. 2015a, https://www.tensorflow.org/ [Google Scholar]
- Abadi, M., Barham, P., Chen, J., et al. 2015b, https://www.tensorflow.org/about/bib [Google Scholar]
- Albert, J. G. 2023, arXiv e-prints [arXiv: 2312.11330] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Balkenhol, L., Trendafilova, C., Benabed, K., & Galli, S. 2024, A&A, 686, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barret, D., & Cappi, M. 2019, A&A, 628, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barret, D., & Dupourqué, S. 2024, A&A, 686, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barret, D., Albouys, V., Herder, J.-W. D., et al. 2023, Exp. Astron., 55, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Betancourt, M. J., & Girolami, M. 2013, Hamiltonian Monte Carlo for Hierarchical Models [arXiv:1312.0906] [Google Scholar]
- Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. 2017, J. Am. Stat. Assoc., 112, 859 [CrossRef] [Google Scholar]
- Bonson, K., & Gallo, L. C. 2016, MNRAS, 458, 1927 [NASA ADS] [CrossRef] [Google Scholar]
- Bradbury, J., Frostig, R., Hawkins, P., et al. 2018, JAX: composable transformations of Python+NumPy programs [Google Scholar]
- Buchner, J. 2021, J. Open Source Software, 6, 3001 [CrossRef] [Google Scholar]
- Buchner, J. 2023, Stat. Surveys, 17, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., & Boorman, P. 2023, arXiv e-prints [arXiv:2309.05705] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campagne, J.-E., Lanusse, F., Zuntz, J., et al. 2023, Open J. Astrophys., 6, https://doi.org/18.21185/astro.2382.85163 [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Choudhury, K., Garcia, J. A., Steiner, J. F., & Bambi, C. 2017, ApJ, 851, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Comte, F., Degorre, A., & Lesur, R. 2022, Courrier des Statistiques, 7, 68 [Google Scholar]
- Doe, S., Nguyen, D., Stawarz, C., et al. 2007, ASP Conf. Ser, 376, 543 [NASA ADS] [Google Scholar]
- Euclid Collaboration (Knabenhans, M., et al.) 2021, MNRAS, 505, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Freeman, P., Doe, S., & Siemiginowska, A. 2001, SPIE, 4477, 76 [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Gunapati, G., Jain, A., Srijith, P. K., & Desai, S. 2022, PASA, 39, e001 [NASA ADS] [CrossRef] [Google Scholar]
- Gúrpide, A., Godet, O., Koliopanos, F., Webb, N., & Olive, J. F. 2021, A&A, 649, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Heinke, C. O., Rybicki, G. B., Narayan, R., & Grindlay, J. E. 2006, ApJ, 644, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Hennigan, T., Cai, T., Norman, T., & Babuschkin, I. 2020, Haiku: Sonnet for JAX [Google Scholar]
- Hinton, S. 2016, J. Open Source Softw., 1, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Hitomi Collaboration 2016, Nature, 535, 117 [CrossRef] [Google Scholar]
- Hitomi Collaboration 2018, PASJ, 70, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, M. D., & Gelman, A. 2014, J. Mach. Learn. Res., 15, 1593 [Google Scholar]
- Houck, J. C., & Denicola, L. A. 2000, ASP Conf. Ser., 216, 591 [Google Scholar]
- Humphrey, P. J., Liu, W., & Buote, D. A. 2009, ApJ, 693, 822 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Kaastra, J. S. 2017, A&A, 605, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, 11th Colloquium on UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, 411 [Google Scholar]
- Kingma, D. P., & Ba, J. 2017, Adam: A Method for Stochastic Optimization [arXiv:1412.6980] [Google Scholar]
- Koliopanos, F., Vasilopoulos, G., Godet, O., et al. 2017, A&A, 608, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kullback, S., & Leibler, R. A. 1951, Annal. Math. Stat., 22, 79 [CrossRef] [Google Scholar]
- Loshchilov, I., & Hutter, F. 2019, Decoupled Weight Decay Regularization, [arXiv:1711.05101] [Google Scholar]
- Nelson, B., Ford, E. B., & Payne, M. J. 2014, ApJS, 210, 11 [Google Scholar]
- Paszke, A., Gross, S., Massa, F., et al. 2019, PyTorch: An Imperative Style, High-Performance Deep Learning Library [arXiv:1912.01703] [Google Scholar]
- Phan, D., Pradhan, N., & Jankowiak, M. 2019, Composable Effects for Flexible and Accelerated Probabilistic Programming in NumPyro [arXiv:1912.11554] [Google Scholar]
- Piras, D., & Mancini, A. S. 2023, Open J. Astrophys., 6, https://doi.org/18.21185/astro.2385.86347 [CrossRef] [Google Scholar]
- Quintin, E., Webb, N. A., Gúrpide, A., Bachetti, M., & Fürst, F. 2021, MNRAS, 503, 5485 [NASA ADS] [CrossRef] [Google Scholar]
- Rumelhart, D. E., Hinton, G. E., & Williams, R. J. 1986, Nature, 323, 533 [Google Scholar]
- Sutton, A. D., Roberts, T. P., & Middleton, M. J. 2013, MNRAS, 435, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Varma, V., Field, S. E., Scheel, M. A., et al. 2019a, Phys. Rev. Res., 1, 033015 [NASA ADS] [CrossRef] [Google Scholar]
- Varma, V., Field, S. E., Scheel, M. A., et al. 2019b, Phys. Rev. D, 99, 064045 [NASA ADS] [CrossRef] [Google Scholar]
- Vehtari, A., Gelman, A., Simpson, D., Carpenter, B., & Bürkner, P.-C. 2021, Bayesian Anal., 16, 667 [CrossRef] [Google Scholar]
- Velden, E. V. D., 2020, J. Open Source Softw., 5, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
Implemented models are available at https://jaxspec.rtfd.io/en/stable/references/model/
Note that in Eq. (1) we write Γ(ci + 1) instead of ci!. The numerical evaluation of Euler Γ can be much faster and easier to differentiate. However, since this term does not vary for a given inference problem, its value is cached during the sampling.
All Tables
Prior distribution and posterior quantiles for the parameters of the Perseus core region model.
All Figures
 |
Fig. 1 Comparison of the sampling quality using jaxspec and xspec. Left: |
| In the text | |
 |
Fig. 2 Time per run and standard deviation for NUTS, AIES and NS in both jaxspec, BXA and xspec, estimated for 100 runs of each algorithm on a five-parameter, three-component inference problem. |
| In the text | |
 |
Fig. 3 Posterior distribution of tbabs*(powerlaw+blackbodyrad) parameters from this benchmark, drawn with the 104 last steps of a run of NUTS and AIES using the jaxpsec and xspec implementations, and as provided by the NS algorithms implemented in BXA and jaxspec. |
| In the text | |
 |
Fig. 4 Variational inference results for the core of Perseus as seen by Hitomi. (a) ELBO metric during variational distribution optimisation. (b) Redshift, bulk motion (vbulk), and velocity dispersion (σv) posterior distributions obtained for the central regions of the Perseus cluster as seen by Hitomi/SXS, superimposed on the prior distribution for the redshift and the previous results from (Hitomi Collaboration 2016) in the central region. (c) Count spectra of the observations used in this spectral fit, superimposed on the folded model for each observation, and the corresponding residuals in σ. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.