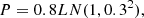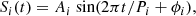| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202451684 | |
| Published online | 09 October 2024 | |
Letter to the Editor
Undersampling effects on observed periods of coronal oscillations
1
Centre for mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
2
Solar-Terrestrial Centre of Excellence – SIDC, Royal Observatory of Belgium, Ringlaan -3- Av. Circulaire, 1180 Brussels, Belgium
3
Centre for Fusion, Space and Astrophysics, Physics Department, University of Warwick, Coventry CV4 7AL, UK
4
Engineering Research Institute “Ventspils International Radio Astronomy Centre (VIRAC)”, Ventspils University of Applied Sciences, Ventspils LV-3601, Latvia
5
School of Earth and Space Sciences, Peking University, Beijing 100871, People’s Republic of China
Received:
28
July
2024
Accepted:
18
September
2024
Context. Recent observations of decayless transverse oscillations have revealed two branches in the relationship between period and loop length. One is a linear relationship, interpreted as a standing mode, while the other shows almost no correlation and has not yet been interpreted conclusively.
Aims. We investigated the undersampling effect on observed periods of decayless oscillations.
Methods. We considered oscillating coronal loops that closely follow the observed loop length distribution. Assuming that all oscillations are standing waves, we modelled a signal that represents decayless oscillations where the period is proportional to the loop length and the amplitude and phase are randomly drawn. We generated a downsampled signal from the original signal by considering different sample rates that mimic temporal cadences of telescopes, and analysed the periods for sampled signals using the fast Fourier transform.
Results. When the sampling cadence approaches the actual oscillation period, there is a greater tendency to overestimate the periods in short loops. We find the same two branches in the relationship between loop length and period of the sampled signals as those seen in the observations.
Conclusions. We find that long periods of decayless oscillations occurring in short loops could be the result of undersampling.
Key words: waves / Sun: corona / Sun: oscillations
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the last decade, the Solar Dynamics Observatory/Atmospheric Imaging Assembly (SDO/AIA; Lemen et al. 2012) and Solar Orbiter/Extreme Ultraviolet Imager (EUI; Rochus et al. 2020), with their high spatial resolution and unprecedented high temporal cadence, have provided many observations of decayless transverse oscillations of solar coronal loops. These oscillations have relatively small displacement amplitudes, that are comparable to or smaller than the minor radius of the oscillating loop, without significant damping, and are well described with a harmonic function (Wang et al. 2012; Tian et al. 2012; Nakariakov et al. 2021; Zhong et al. 2022a, 2022b, 2023a; Zhong et al. 2023b; Mandal et al. 2022; Petrova et al. 2023; Li & Long 2023; Shrivastav et al. 2024). The decayless oscillations are considered a common feature in the solar corona and can be excited without intermittent solar energetic events (Anfinogentov et al. 2015; Gao et al. 2022; Lim et al. 2024).
In the case of decayless oscillations occurring in longer loops with an average length of about 200 Mm, statistical analyses showed that the observed periods which range from around 1.5 min to 10 min have a clear linear relationship with loop length (Anfinogentov et al. 2013; Nisticò et al. 2013; Anfinogentov et al. 2015; Mandal et al. 2022; Zhong et al. 2022a; Li & Long 2023). This is in agreement with a characteristic of a standing mode. The interpretation as a standing mode was established as additional observations, e.g., consistent oscillation phase (Anfinogentov et al. 2015) and multiple harmonics (Duckenfield et al. 2018), were discovered.
The decayless oscillations were also observed in shorter loops with an average length of about 20 Mm, and the lengths of the oscillating loops showed no correlation with periods ranging between about 10 s and 5 min (Gao et al. 2022; Shrivastav et al. 2024). Attempts were made to find phase relations in the oscillations along the loop axis in order to interpret them (Petrova et al. 2023; Shrivastav et al. 2024), however, the short lengths prevented the authors from concluding that they were either standing or propagating from an observational perspective. Theoretical and numerical studies have begun to pay attention to why these oscillations have periods that are much longer than expected given their loop lengths. Gao et al. (2023) found that decayless oscillations with a long period of about 5 min in a short coronal loop with a length of 30 Mm could be directly driven by the photospheric p-mode driver. Lopin & Nagorny (2024) suggested that decayless oscillations that have longer periods in shorter loops could be the manifestation of slow mode oscillations driven by the p-modes.
In addition to the possible physical models that can explain long-period decayless oscillations in short loops, in this Letter, we show that they can also be caused by undersampling. In signal processing, undersampling occurs when a sampling rate to receive signal data is insufficient to reconstruct a real signal. This causes a false spectral peak at a frequency lower than the actual frequency. Even though we now image the Sun almost continuously at a faster cadence (e.g. from 12 s by AIA down to 2 s by EUI) than ever before, this could still be insufficient to detect the short-period oscillations that occur in small-scale loops.
2. Results
In order to model oscillating coronal loops and their oscillations, we consider the observed parameters of decayless transverse oscillations in the literature (Wang et al. 2012; Nisticò et al. 2013; Anfinogentov et al. 2013, 2015; Duckenfield et al. 2018; Anfinogentov & Nakariakov 2019; Gao et al. 2022; Zhong et al. 2022a, 2022b, 2023b; Mandal et al. 2022; Li & Long 2023; Petrova et al. 2023; Shrivastav et al. 2024). These oscillations were observed by AIA with a cadence of 12 s and EUI with a cadence of 2, 3, and 5 s. As already mentioned above, the relationships between lengths and periods showed two branches (Figure 1). One follows a linear function with a slope of approximately 0.8 s Mm−1, and the other is distributed almost vertically between loop lengths of 0 and 50 Mm.
 |
Fig. 1. Scatter plot of the periods and loop lengths of decayless transverse oscillations of coronal loops observed by SDO/AIA (blue) and Solar Orbiter/EUI (red). |
Using a Monte Carlo approach, we considered 1000 lengths (L) randomly drawn from a log-normal distribution lnN(5, 0.52) which gives an arithmetic mean loop length of about 170 Mm, and a standard deviation of around 90 Mm (see the left panel of Figure 2). Our choices of the mean, standard deviation, and distribution type are driven by the observed loop lengths shown in Figure 1. We assume that all decayless oscillations occurring in the loops are in standing mode. Hence, the period should increase linearly with the loop length. To simulate the linear branch in the observed relationship between length and period, we consider the period (P) as follows:
 |
Fig. 2. Loop length distribution (left panel) and the scatter plot between the loop lengths and periods derived from it (right panel). |
where N(1, 0.32) is a normal distribution with the mean of 1 s Mm−1 and the standard deviation of 0.3 s Mm−1, and all the parameters are justified by observations. The right panel of Figure 2 shows that the relationship between the simulated period and loop length closely mimics the linear relationship between the observed period and loop length. Using these periods, we modelled 1000 signals (S) for decayless oscillations described by a sine function,
where i is an index for each signal, x and t are a position and time, A is the displacement amplitude randomly drawn from the range of 10 and 400 km according to observed parameters, and ϕ is a randomly drawn temporal phase. Each signal has 3600 data points, and we assume that the time difference between two data points is equally 1 s to help us understand by converting it into a period we are familiar with.
In order to investigate the effect of undersampling on detected periods, we sampled each signal at different rates, that is, we selected signal data with cadences of 3, 6, and 12 s. These different sampling rates mimic different temporal cadences of imaging observations. Figure 3 presents examples of original signals and sampled signals. We can see that the signals show different apparent periodicities depending on the sampling cadence. We investigated the periodicity of the sampled signals using a fast Fourier transform (FFT) with a 95% significance level. The relationship between the detected period for each sampled case and loop length is shown in Figure 4. For short loop lengths between about 0 and 50 Mm, longer periods are found depending on the sampling cadence compared to the original relationship (Figure 2), and this effect is further enhanced as the sampling cadence increases, that is, when the cadence time approaches the oscillation period. The relationship between the loop length and period of the signals sampled at 12 s correctly reconstructs the two branches that appear in the observed relationship shown in Figure 1. It is worth mentioning here that the detected periods are not affected by the time difference between two data points (i.e. the number of data points for one period) or the total duration of signals.
 |
Fig. 3. Examples of original signals (top), and sampled signals at 3 s (second row), 6 s (third row), and 12 s (fourth row). Left panels: True periods and detected periods from sampled signals from top to bottom are 1, 16, 16, and 45 s. Middle panels: 12, 12, 12, and 1455 s. Right panels: 200, 200, 200, and 200 s. |
 |
Fig. 4. Scatter plots between loop length and detected period from sampled signals at 3 data points (left panel), 6 data points (middle panel), and 12 data points (right panel). |
3. Implications of the proposed interpretation
Our results indicate that when interpreting long-period decayless oscillations in short loops, there is a possibility that, due to undersampling, they are falsely detected as long-periods, when in fact they are standing modes with short periods. This effect should be taken into consideration. Considering Nyquist’s theorem which states that a periodic signal must be sampled at more than twice the highest frequency of the signal, the shortest period that we can detect without undersampling is 24 s for AIA (with a 12 s cadence) and 6 s for EUI (with a 3 s cadence). In other words, periods shorter than 24 s (6 s) may be incorrectly detected as longer periods in AIA (EUI) observations.
Both AIA (Gao et al. 2022) and EUI (Li & Long 2023; Shrivastav et al. 2024) have detected oscillations with a period of longer than about 150 s in loop length of between 0 and 50 Mm (belonging to the branch that deviates from the linear relationship). The average length of the loops that show oscillations corresponding to this branch observed by EUI is approximately 10 Mm. If a standing mode following the linear relationship shown in Figure 1 occurs in this loop, its period will be about 8 s, which is detectable with the 3 s cadence of EUI according to the Nyquist theory. However, the possibility of an undersampling effect in EUI cannot be ruled out. For example, Shrivastav et al. (2024) detected an oscillation with a period of approximately 220 s in a loop about 3 Mm in length. This oscillation was observed with a 3 s cadence in HRIEUV. It is possible that the actual period could be closer to 5 s (suggesting a phase speed of 1200 km s−1 under the assumption of a standing mode), which would be undetectable by HRIEUV according to Nyquist’s theorem. Therefore, the long-period oscillations in short loops detected with EUI could be driven by physical mechanisms and may also be influenced by the undersampling effect. In the case of AIA, the oscillations following the branch that is not the linear relationship occurred in loops with an average length of around 20 Mm. A possible period of a standing mode in this loop would be approximately 16 s, which is not possible to detect with the 12 s cadence of AIA given the Nyquist frequency. Therefore, the long-period oscillations in short loops observed by AIA could be the effect of undersampling and their periods could be actually shorter than the period that can be detected according to Nyquist’s theorem, that is, shorter than 24 s.
This interpretation has implications for the seismological estimations discussed in Gao et al. (2022). They reported 30 decayless oscillations with a period of longer than 100 s in small-scale coronal loops observed with AIA. When interpreting these oscillations as the fundamental kink mode, the derived phase speed has an average value of about 200 km s−1, and the average magnetic field strength measured by seismological inference was about 3 G; both of these values are lower than typical coronal values. Considering that the period that can be detected by AIA without undersampling effects is 24 s or longer, it is possible that these oscillations were incorrectly detected because their periods were shorter than 24 s. If we assume that their true periods are approximately 12 s, the inferred average magnetic field strength is about 50 G, which is closer to the coronal magnetic field in active regions.
Moreover, decayless oscillations have received significant attention in terms of the energy content that they can contribute to coronal heating (Gao et al. 2022; Petrova et al. 2023; Li & Long 2023; Shrivastav et al. 2024). The energy flux (F) of standing transverse oscillation is proportional to
An overestimated period leads to an underestimated energy flux. Lim et al. (2023) performed a meta-analysis and estimated the average energy flux of the oscillations detected by Gao et al. (2022), finding a value of about 0.2 W m−2. However, assuming that they are all a standing mode with a short period of about 12 s as assumed above, the average energy flux is estimated to be about 800 W m−2. It is important to note that this value represents an upper limit, and the actual dissipated energy is likely to be lower. Using the analytical model of dissipation rates presented by Hillier et al. (2020), we calculated the dissipation rates for 31 oscillations from Gao et al. (2022), using the corrected periods. The dissipation rates ranged from approximately 1% to 60%, with an average dissipated energy flux of around 2 W m−2.
We do not rule out the possibility that long periods occurring in short loops could be driven by physical mechanisms. However, we would like to emphasise that observed oscillation parameters, such as periods, are used in seismological tools and energy content estimations, requiring a precise understanding of the observed oscillations, including the physical mechanisms behind them and the uncertainties arising from the limitations of the instrument specifications. Solar Orbiter/EUI allows us to investigate coronal structures at smaller and smaller scales, which requires the highest cadence possible to avoid the effects of undersampling. We could also expect this from future missions targeting high resolution and high temporal cadence, such as the Multi-slit Solar Explorer (down to 0.5 s; De Pontieu et al. 2022) and the Solar-C EUV High-Throughput Spectroscopic Telescope (maximum at 1 s; Shimizu et al. 2019). Observational support for the arguments presented in this paper could be achieved by comparing the detected periods of oscillations observed simultaneously with high-cadence EUI and AIA. We will pursue this approach in the future when more suitable datasets become available.
Acknowledgments
Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The EUI instrument was built by CSL, IAS, MPS, MSSL/UCL, PMOD/WRC, ROB, LCF/IO with funding from the Belgian Federal Science Policy Office (BELSPO/PRODEX PEA C4000134088); the Centre National d’Etudes Spatiales (CNES); the UK Space Agency (UKSA); the Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft- und Raumfahrt (DLR); and the Swiss Space Office (SSO). DL was supported by a Senior Research Project (G088021N) of the FWO Vlaanderen. TVD was supported by the C1 grant TRACEspace of Internal Funds KU Leuven and a Senior Research Project (G088021N) of the FWO Vlaanderen. Furthermore, TVD received financial support from the Flemish Government under the long-term structural Methusalem funding program, project SOUL: Stellar evolution in full glory, grant METH/24/012 at KU Leuven. The research that led to these results was subsidised by the Belgian Federal Science Policy Office through the contract B2/223/P1/CLOSE-UP. The paper is also part of the DynaSun project and has thus received funding under the Horizon Europe programme of the European Union under grant agreement (no. 101131534). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union and therefore the European Union cannot be held responsible for them. We also acknowledge funding from the STFC consolidated grant ST/X000915/1 (DYK) and Latvian Council of Science Project No. lzp2022/1-0017 (DYK and VMN). Y.G. was supported by China Scholarship Council under file No. 202206010018.
References
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anfinogentov, S. A., & Nakariakov, V. M. 2019, ApJ, 884, L40 [CrossRef] [Google Scholar]
- Anfinogentov, S. A., Nakariakov, V. M., & Nisticò, G. 2015, A&A, 583, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Testa, P., Martínez-Sykora, J., et al. 2022, ApJ, 926, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Duckenfield, T., Anfinogentov, S. A., Pascoe, D. J., & Nakariakov, V. M. 2018, ApJ, 854, L5 [Google Scholar]
- Gao, Y., Tian, H., Van Doorsselaere, T., & Chen, Y. 2022, ApJ, 930, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., Guo, M., Van Doorsselaere, T., Tian, H., & Skirvin, S. J. 2023, ApJ, 955, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, A., Van Doorsselaere, T., & Karampelas, K. 2020, ApJ, 897, L13 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Li, D., & Long, D. M. 2023, ApJ, 944, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, D., Van Doorsselaere, T., Berghmans, D., et al. 2023, ApJ, 952, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, D., Van Doorsselaere, T., Berghmans, D., & Petrova, E. 2024, A&A, 689, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopin, I., & Nagorny, I. 2024, MNRAS, 527, 5741 [Google Scholar]
- Mandal, S., Chitta, L. P., Antolin, P., et al. 2022, A&A, 666, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Anfinogentov, S. A., Antolin, P., et al. 2021, Space Sci. Rev., 217, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrova, E., Magyar, N., Van Doorsselaere, T., & Berghmans, D. 2023, ApJ, 946, 36 [CrossRef] [Google Scholar]
- Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimizu, T., Imada, S., Kawate, T., et al. 2019, SPIE Conf. Ser., 11118, 1111807 [NASA ADS] [Google Scholar]
- Shrivastav, A. K., Pant, V., Berghmans, D., et al. 2024, A&A, 685, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tian, H., McIntosh, S. W., Wang, T., et al. 2012, ApJ, 759, 144 [Google Scholar]
- Wang, T., Ofman, L., Davila, J. M., & Su, Y. 2012, ApJ, 751, L27 [Google Scholar]
- Zhong, S., Nakariakov, V. M., Kolotkov, D. Y., & Anfinogentov, S. A. 2022a, MNRAS, 513, 1834 [NASA ADS] [CrossRef] [Google Scholar]
- Zhong, S., Nakariakov, V. M., Kolotkov, D. Y., Verbeeck, C., & Berghmans, D. 2022b, MNRAS, 516, 5989 [NASA ADS] [CrossRef] [Google Scholar]
- Zhong, S., Nakariakov, V. M., Kolotkov, D. Y., et al. 2023a, Nat. Commun., 14, 5298 [NASA ADS] [CrossRef] [Google Scholar]
- Zhong, S., Nakariakov, V. M., Miao, Y., Fu, L., & Yuan, D. 2023b, Sci. Rep., 13, 12963 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Scatter plot of the periods and loop lengths of decayless transverse oscillations of coronal loops observed by SDO/AIA (blue) and Solar Orbiter/EUI (red). |
| In the text | |
 |
Fig. 2. Loop length distribution (left panel) and the scatter plot between the loop lengths and periods derived from it (right panel). |
| In the text | |
 |
Fig. 3. Examples of original signals (top), and sampled signals at 3 s (second row), 6 s (third row), and 12 s (fourth row). Left panels: True periods and detected periods from sampled signals from top to bottom are 1, 16, 16, and 45 s. Middle panels: 12, 12, 12, and 1455 s. Right panels: 200, 200, 200, and 200 s. |
| In the text | |
 |
Fig. 4. Scatter plots between loop length and detected period from sampled signals at 3 data points (left panel), 6 data points (middle panel), and 12 data points (right panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.