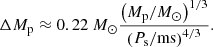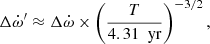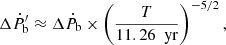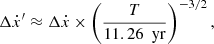| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A253 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202450724 | |
| Published online | 15 October 2024 | |
PSR J1227−6208 and its massive white dwarf companion: Pulsar emission analysis, timing update, and mass measurements
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, D-53121, Bonn, Germany
2
Dept. of Materials and Production, Aalborg University, DK-9220 Aalborg Øst, Denmark
3
INAF – Osservatorio Astronomico di Cagliari, via della Scienza 5, 09047 Selargius (CA), Italy
4
Centre for Astrophysics and Supercomputing, Swinburne University of Technology, P.O. Box 218 Hawthorn, Vic 3122, Australia
5
SKA Observatory, Jodrell Bank, Lower Withington, Macclesfield SK11 9FT, United Kingdom
6
Australia Telescope National Facility, CSIRO, Space and Astronomy, PO Box 76 Epping, NSW 1710, Australia
7
Department of Physics and Astronomy, University of the Western Cape, Bellville, Cape Town 7535, South Africa
Received:
14
May
2024
Accepted:
16
July
2024
PSR J1227−6208 is a 34.53-ms recycled pulsar with a massive companion. This system has long been suspected to belong to the emerging class of massive recycled pulsar−ONeMg white dwarf systems such as PSR J2222−0137, PSR J1528−3146, and J1439−5501. Here, we present an updated emission and timing analysis with more than 11 years of combined Parkes and MeerKAT data, including 19 hours of high-frequency data from the newly installed MeerKAT S-band receivers. We measure a scattering timescale of 1.22 ms at 1 GHz with a flat scattering index of 3.33 < β < 3.62, and a mean flux density of 0.53 − 0.62 mJy at 1 GHz with a steep spectral index of 2.06 < α < 2.35. Around 15% of the emission is linearly and circularly polarised, but the polarisation angle does not follow the rotating vector model. Thanks to the sensitivity of MeerKAT, we successfully measure a rate of periastron advance of ω7 = 0.0171(11) deg yr−1, and a Shapiro delay with an orthometric amplitude of h3 = 3.6 ± 0.5 μs and an orthometric ratio of ς = 0.85 ± 0.05. The main source of uncertainty in our timing analysis is chromatic correlated dispersion measure noise, which we model as a power law in the Fourier space thanks to the large frequency coverage provided by the Parkes UWL receiver. Assuming general relativity and accounting for the measurements across all the implemented timing noise models, the total mass, companion mass, pulsar mass, and inclination angle are constrained at 2.3 < Mt/M⊙ < 3.2, 1.21 < Mc/M⊙ < 1.47, 1.16 < Mp/M⊙ < 1.69, and 77.5 < i/deg < 80.3. We also constrain the longitude of ascending node to either Ωa = 266 ± 78 deg or Ωa = 86 ± 78 deg. We argue against a neutron star nature of the companion based on the very low orbital eccentric of the system (e = 1.15 × 10−3), and instead classify the companion of PSR J1227−6208 as a rare, massive ONeMg white dwarf close to the Chandrasekhar limit.
Key words: binaries: general / stars: evolution / stars: fundamental parameters / stars: neutron / stars: individual: PSR J1227-6208 / white dwarfs
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1. Introduction
The Chandrasekhar limit of white dwarf (WD) masses (MWD) is a topic of ongoing research in astrophysics and theoretical physics. Studies show that maximally rotating rigid WDs could sustain up to MWD ≈ 1.48 M⊙ (Yoon & Langer 2005), but several effects have been speculated to allow them to exist beyond this limit, such as differential rotation (Yoon & Langer 2005) or high magnetisation (Kundu & Mukhopadhyay 2012), and super-Chandrasekhar masses have been inferred indirectly from some Type Ia supernovae (Tomaschitz 2018). Additionally, extensions or modifications of general relativity (GR) must incorporate a prediction for the upper mass limit of WDs (e.g. Gregoris & Ong 2023; Mathew & Nandy 2021). To test these postulations, the empirical measurement of MWD values close to the Chandrasekhar limit is required. However, WDs with MWD ≳ 1.3 M⊙ are a rarity in the Galactic field. One of their windows of study is optical photometry, which has enabled the characterisation of their masses based on emission models (e.g. Caiazzo et al. 2021; Hollands et al. 2020; Külebi et al. 2010; Miller et al. 2023; Pshirkov et al. 2020). The other window of study is mass measurements of binary radio pulsars with massive WD companions obtained via pulsar timing. This technique allows for the measurement of relativistic effects in the orbital motion and in the light propagation time; these are quantified by the post-Keplerian (PK) parameters. Under the assumption of GR, such measurements can result in the precise measurement of the WD and pulsar masses (Lorimer & Kramer 2005).
Timing measurements of pulsars with massive WD companions are relevant not only for probing the Chandrasekhar limit, but also for testing binary evolution and fundamental physics. In recycled pulsar binaries, we can test how binary interaction affects the resulting WD and neutron star (NS) mass distribution (for general insigts into binary evolution and pulsar recycling, see Tauris & van den Heuvel 2023). For instance, there is a bi-modality in the MWD distribution, with MWD ≲ 0.5 M⊙ WDs being found with fully recycled pulsars and MWD ≳ 0.7 M⊙ WDs with mildly recycled pulsars (McKee et al. 2020; Shamohammadi et al. 2023). This divide is well understood thanks to models of binary evolution (Lazarus et al. 2014; Tauris et al. 2012; Tauris & van den Heuvel 2023), but the upper end of the MWD distribution (MWD ≳ 1.1 M⊙) remains relatively unsampled. The birth NS mass distribution can also be directly sampled in these kinds of systems given the small amount of mass accretion occurring during recycling (e.g. Lazarus et al. 2014; Cognard et al. 2017). For instance, the measurement of a pulsar mass of Mp = 1.831(10) M⊙ in PSR J2222−0137 (Guo et al. 2021) is evidence that NSs can be born massive (heavier than 1.4 M⊙) instead of acquiring large amounts of extra mass via accretion (Cognard et al. 2017). Furthermore, the NS mass distribution is a probe of the physics of matter under conditions of extreme density (e.g. Özel & Freire 2016; Fonseca et al. 2021; Hu et al. 2020). Finally, in the most compact systems, the timing of pulsars with WD companions also provides extremely precise tests of gravity theories (e.g. Voisin et al. 2020), as is shown by the strict constraints on dipolar gravitational wave emission from PSR J2222−0137 (Guo et al. 2021), which have ruled out the phenomenon of spontaneous scalarisation predicted by some alternative gravity theories (Zhao et al. 2022).
As of today, only four pulsars with WD companions at the upper end of the mass distribution have been characterised. The most studied one is PSR J2222−0137, a 32.8-ms recycled pulsar in a circular 2.45-day orbit with a MWD = 1.319(4) M⊙ companion (Boyles et al. 2013; Cognard et al. 2017; Guo et al. 2021). The system distance of 268 pc, measured via very-long-baseline interferometry observations (Deller et al. 2013; Guo et al. 2021), and the lack of an optical detection imply a cold WD (T < 3000 K) with a cooling age of at least several Gyr (Kaplan et al. 2014). A similar case is PSR J1528−3146, a 60.8-ms recycled pulsar in a circular 3.18-day orbit with a 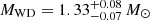 companion (Jacoby et al. 2006, 2007; Berthereau et al. 2023). In this case, the optical detection implies a cooling age between 1.5 and 3.2 Gyr (Jacoby et al. 2006), consistent with the pulsar characteristic age of 3.9 Gyr estimated by Berthereau et al. (2023). A third system is PSR J1439−5501, with a 28.6-ms pulsar in a 2.12-day orbit with a
companion (Jacoby et al. 2006, 2007; Berthereau et al. 2023). In this case, the optical detection implies a cooling age between 1.5 and 3.2 Gyr (Jacoby et al. 2006), consistent with the pulsar characteristic age of 3.9 Gyr estimated by Berthereau et al. (2023). A third system is PSR J1439−5501, with a 28.6-ms pulsar in a 2.12-day orbit with a 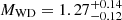 M⊙ optically detected companion with a cooling age of 0.1−0.5 Gyr (Jang et al., in prep. Faulkner et al. 2004; Lorimer et al. 2006; Pallanca et al. 2013). The final system is PSR B2303+46, with a young 0.937-s pulsar in a highly eccentric 12.34-day orbit with a
M⊙ optically detected companion with a cooling age of 0.1−0.5 Gyr (Jang et al., in prep. Faulkner et al. 2004; Lorimer et al. 2006; Pallanca et al. 2013). The final system is PSR B2303+46, with a young 0.937-s pulsar in a highly eccentric 12.34-day orbit with a 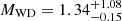 M⊙ companion (Thorsett et al. 1993; Thorsett & Chakrabarty 1999). The WD companion is hot and young, implying a system age of 30 Myrs (van Kerkwijk & Kulkarni 1999).
M⊙ companion (Thorsett et al. 1993; Thorsett & Chakrabarty 1999). The WD companion is hot and young, implying a system age of 30 Myrs (van Kerkwijk & Kulkarni 1999).
In this work, we present a detailed study of PSR J1227−6208 (J1227−6208 from now on). Discovered independently by three different studies in data from the Murriyang Parkes telescope1 (Bates et al. 2015; Knispel et al. 2013; Mickaliger et al. 2012), it is a 34.5-ms mildly recycled pulsar in orbit with a massive companion. With an orbital period of Pb = 6.72 days and a projected semimajor axis of x = 23.2 light seconds (ls), it has a high mass function of fM = 0.297 M⊙. Assuming a pulsar mass Mp = 1.35 M⊙, this leads to a minimum companion mass of Mc > 1.27 M⊙. Its low orbital eccentricity (e = 1.15 × 10−3) makes the possibility of a NS companion unlikely, giving more weight to a massive WD hypothesis instead. However, owing to the low orbital eccentricity, and large timing uncertaintes, precise measurements of PK parameters in this system have been impossible until now.
It is for these reasons that the system was included in the Relativistic Binary program (RelBin, Kramer et al. 2021) of MeerTIME (Bailes et al. 2020), a large science project that takes advantage of the high sensitivity of the MeerKAT telescope2 (Jonas & MeerKAT Team 2016) to improve the timing precision of southern pulsars. The RelBin project is designed to measure masses and test theories of gravity in 25 selected binary pulsar systems (Kramer et al. 2021), including J1227−6028. The updated timing analysis of J1227−6028 presented here includes a decade-long timing baseline of Parkes/Murriyang observations and two years of dedicated MeerKAT observations. This is the first timing experiment to include data from the newly commissioned S-band MeerKAT receivers (Barr 2018).
This paper is structured as follows. Section 2 details the observations used in this study and the data reduction for timing. Section 3 reports the emission study, including the modelling of the profile, scattering, and spectral properties, and the detection of polarised light. Section 4 reports the timing analysis, including the modelling of several timing noises, constraints on PK parameters, mass measurements, and an exploration of the orbital orientation. Section 5 discusses the astrophysical implications of our measurements. In Section 6 we outline future prospects and lines of action for the study of this system. Finally, Section 7 concludes the paper and summarises the key aspects of our measurements and discussions.
2. Data acquisition and reduction
2.1. Parkes/Murriyang
Table 1 shows the four data sets used in this work. Observations were performed first with the central beam of the 21-cm multibeam receiver (Staveley-Smith et al. 1996) and later with the ultra-wide bandwidth low-frequency receiver (UWL, Hobbs et al. 2020). The multibeam data set provides the longest baseline for the measurement of secular variations in the Keplerian parameters, while the UWL observations are particularly useful for constraining the dispersion measure (DM) evolution due to their overlap with the MeerKAT observations and their very large bandwidth. UWL observations also include three dense orbital campaigns on the dates of 4–10 October 2020, 20–26 July 2022, and 3–9 May 2023, with seven observations each, accumulating 5.74, 10.41, and 17.63 hours each. These campaigns have two aims: aiding in the measurement of the time delay of the pulses as they propagate through the gravitational field of the companion (Shapiro delay, Shapiro 1964) and constraining DM evolution within a single orbit. In line with this objective, the first of the orbital campaign was coordinated with the MeerKAT orbital campaign with the L-band receivers (Section 2.2) so that observations alternate each other.
Summary of the data sets used in this analysis.
The multibeam receiver data were recorded by the Center for Astronomy Signal Processing and Electronics Research (CASPER) Parkes Swinburne Recorder (CASPSR, Sarkissian et al. 2011) backend. The data were folded with 512 frequency channels, four polarisation channels, 1024 phase bins, and with coherent de-dispersion at DM ≈ 363 cm−3 pc. Each observation was accompanied by a noise-diode observation for polarisation calibration. Calibration was performed on each file with the pac command from the PSRCHIVE3 software package (Hotan et al. 2004). The archives were manually excised of radio-frequency-interference (RFI) with the PSRCHIVE/pazi interface, and the 80 bottom channels and 32 top channels were zero-weighted with the PSRCHIVE/paz command to remove Gaussian noise caused by the loss of sensitivity at the edge of the bandpass. The bands were then scrunched to four frequency sub-bands, a single intensity channel, and a single subintegration per observation with the PSRCHIVE/pam command for the production of frequency-resolved times of arrival (ToAs). To derive timing templates for each band, we obtained a frequency-resolved standard profile resulting from the time integration of all multibeam CAPSR observations (with the exclusion of three heavily RFI-affected observations) into a single rotational phase cycle. The analytic timing templates were then produced for each sub-band by fitting a combination of von Mises functions with PSRCHIVE/paas program. The ToAs were produced with the PSRCHIVE/pat command using the FDM algorithm with the two-dimensional, frequency-resolved timing template, where each subintegration resulted a ToA from each of the four sub-bands.
The UWL receiver data were recorded by the Medusa cluster (Hobbs et al. 2020) with 3 328 frequency channels, four polarisation channels, 1024 phase bins, and with coherent de-dispersion at DM ≈ 363 cm−3 pc. In addition, the data were also recorded with real-time folding based on an early pulsar ephemeris. The data were processed using the psrpype processing pipeline4. This pipeline carries out flux and polarisation calibration, and also automatically removes RFI using clfd5. It results in data that is cleansed of RFI, calibrated, and broken down into various time, frequency, and polarisation resolutions. The RFI excision step also excises a standard set of frequencies, on top of whichever part of the data that the algorithm considers to be contaminated. These frequency sets were decided based on the knowledge of the known transmitter frequencies that routinely affect the data. To boost the quality of ToAs, the data was scrunched into total intensity, eight frequency channels, and subintegrations of two hours in length with the PSRCHIVE/pam command. The ToAs were produced with the PSRCHIVE/pat command using the FDM algorithm. Analogously to the multibeam CASPSR data set, the timing template was modelled with PSRCHIVE/paas from the integration of all of the files into a two-dimensional frequency-resolved standard profile, with the exclusion of three severely RFI-affected observations.
2.2. MeerKAT
The MeerKAT data sets provide the most precise ToAs owing to the large sensitivity of the telescope. Most of the data were recorded with the L-band receivers (26 hours, 856–1712 MHz), but 19 hours were recorded with the new S-band receivers in the S1 configuration (1968–2843 MHz, Barr 2018) on 12–28 May 2023 to ensure a measurement of the Shapiro delay with a significant reduction of DM noise (see Table 1). The data were recorded with the pulsar timing user-supplied equipment (PTUSE, Bailes et al. 2020) machines as part of the MeerTIME science program (Bailes et al. 2020), and included an orbital campaign on the dates of 4–11 October 2020 that accumulated 13 hours over nine L-band observations, with a dedicated five-hour-long observation at superior conjunction on 11 October 2020, aimed at constraining the Shapiro delay.
Both data sets were recorded with 1024 frequency channels, four polarisation channels, and coherent dedisperion at DM ≈ 363 cm−3 pc. The L-band data were processed, cleaned of RFI, and calibrated with the meerpipe pipeline6, which resulted in the trimming of the outer edges, leaving only 926 channels of useful data with a bandwidth of 775.5 MHz. Any remaining RFI was manually removed with the PSRCHIVE/paz command. Observations were then fully summed in polarisation, and scrunched into eight frequency channels and 20-min-long subintegrations to extract frequency-resolved ToAs with the PSRCHIVE/pat command. Analogous to the Parkes data sets (Section 2.1), the frequency-resolved timing template was derived using the PSRCHIVE/paas on frequency-resolved standard profiles resulting from the time integration of the observations in the October 4−11 October 2020 orbital campaign. Unfortunately, calibration files were not available for the S-band data set, as it was taken jointly with commissioning data, and therefore it could not be calibrated nor band-pass corrected. This, however, is unlikely to affect our timing precision. S-band data were cleaned of RFI with the clfd software, and it was sub-banded to four frequency channels for frequency-resolved timing, with the profile being created from the integration of all of the observations, following the same steps as the L-band data.
3. Emission analysis
3.1. Profile evolution
J1227−6208 suffers from significant scattering and has a steep flux density spectrum. Fig. 1 shows time-integrated, frequency-resolved standard profiles from the four different receivers listed in Table 1. The most obvious feature is scattering at the MeerKAT L-band and the bottom of the Parkes UWL band, resulting in an exponential, frequency-dependent tail of the pulse profile. In addition, the pulse brightness fades quickly at the top of the Parkes UWL band. It should be noted that the dark bands in the Parkes UWL profile are a result of the RFI excision processes, and are not intrinsic to the pulsar emission. To measure the scattering timescale, τs, we modelled the pulse at each frequency, f, as a single Gaussian function convolved with a scattering exponential tail,
where b is the spin phase in bins, and b0 and Δb stand for the Gaussian centre and the standard deviation, respectivelly. We measured the scattering index, α, by fitting the evolution of τs as a power law function of f,
where τGHz is the reference value at f = 1 GHz. For the flux density spectral index, β, we measured the mean flux density, Fm, across the pulse phase at each sub-band, deriving the uncertainty from the off-pulse baseline noise, and fitted another power law,
where FGHz is the reference value at f = 1 GHz.
 |
Fig. 1. Time-integrated pulse profiles of J1227−6208 as recorded with the different receivers (from left to right: Parkes multibeam, MeerKAT L-band, Parkes UWL, and MeerKAT S-band). The top plots show the intensity of the integrated emission, while the bottom plots are frequency-resolved. Only the MeerKAT L-band and Parkes UWL data sets are flux calibrated. The plots were made with PSRCHIVE/psrplot. |
We performed least-χ2 fits of equations (1), (2), and (3) on the frequency-resolved, time-integrated MeerKAT L-band and Parkes UWL profiles (second and third plots in Fig. 1) with the python module scipy (Virtanen et al. 2020). As is shown in the upper part of Fig. 2, the scattered Gaussian modelling of the profile adjusts well to the data, with only some minor residual structure after subtraction of the model. The intrinsic pulse width stays consistent at 150 < Δb < 170 μs across the whole band, and the parameter τs becomes redundant in the modelling of the pulse at f > 2 GHz in the Parkes UWL dataset, where a simple Gaussian function provides an adequate description. Thus, we restricted the measurement of τGHz and α at f < 2 GHz. To ensure a proper uncertainty estimation on the scattering and spectral parameters, we multiplied the individual measurement uncertainties of τs and Fm by the error factors στ and σF (δ′=σ × δ, where δ is the set of measurement uncertainties). Subsequently, we tuned the values of στ and σF to achieve a reduced χ2 = 1 in the fit of equations (2) and (3).
 |
Fig. 2. Frequency evolution of the scattering and mean flux density, and their modelling. Top: pulse profiles of J1227−6208 at f = 902 MHz and f = 1397 MHz as is seen by the MeerKAT L-band receiver (left and middle plots), and at f = 2388 MHz as is seen by the Parkes UWL receiver (right plot). The data (cyan lines) is shown against the best model (red dashes, fitted with equation 1) and the fit residuals (blue lines). The fit parameters τs and Δb from equation (1), and the mean flux density Fm are quoted on each profile. Bottom: measurements of Δτ and Fm at each frequency on the MeerKAT L-band and Parkes UWL profiles (dots with uncertainties), and the best fits of the power laws (2) and (3) (red lines). The data points are displayed accounting for the error factors στ and σF, and the relevant τGHz, α, FGHz, and β values are quoted in the legend. |
Our fits confirmed the steep spectrum of J1227−6208 and measure a scattering index of α < 4. The lower part of Fig. 2 shows the fit parameters for τGHz, α, Fm, and β from equations (2) and (3) on the measurements of τs and Fm in the MeerKAT L-band and Parkes UWL datasets. The power law describes τs accurately for the MeerKAT L-band data set, with τGHz = 1244 ± 4 μs and α = 3.601(15). However, this is different from the measurement performed in the Parkes UWL profile, which resulted in τGHz = 1190 ± 10 μs and α = 3.37(15). The difference likely comes from the different frequency coverage and the low quality of measurements at f < 900 MHz. Nonetheless, both fits agree on α < 4, far from the α = 4.4 predicted from a Kolmogorov medium and the α = 4 from Gaussian inhomogeneities (Rickett 1977; Romani et al. 1986), as already seen in some pulsars behind complex ISM environments (e.g. Löhmer et al. 2004; Krishnakumar et al. 2019; Oswald et al. 2021). On the other hand, our Fm measurements are not as precise, as indicated by the σF > 3 values. The most likely explanation is the lower S/N of the Parkes standard profiles due to its lower gain and the large degree of zapping of frequency channels during RFI excision. Nonetheless, both the MeerKAT L-band and Parkes UWL agree on a very steep spectrum, with β = 2.10(4) and β = 2.28(7), respectively, on the steeper side the typically observed values of β = 1.4 ± 1.0 (Bates et al. 2013). The derived reference flux densities are FGHz = 535 ± 5 μJy and FGHz = 605 ± 15 μJy. Regarding the peak flux density, the combined effect of scattering and spectral behaviour results in the brightest observed peak flux density of 13–14 mJy -and highest S/N at f ≈ 1200 − 1300 MHz.
3.2. Polarised emission
We performed a rotation measure (RM) fit on the MeerKAT L-band and Parkes UWL profiles with PSRCHIVE/rmfit, finding the maximum of integrated linearly polarised flux density at RM = 47.7 and 46.2 rad cm−1, with full widths at half maximums of 50 and 30 rad cm−1, respectively. These two values are consistent with each other, and they imply an average magnetic field parallel to the line of sight (LOS) of 0.16 μG. Fig. 3 shows the polarised emission of J1227−6208 at f = 1574 − 1670 MHz from the MeerKAT L-band profile, and at f = 2368 − 4029 MHz from the Parkes UWL profile. Approximately 15% of the total intensity is linearly polarised, and a similar fraction of circular polarisation is detected. Linear polarisation is more prominent in the first half of the pulse, peaking before the total intensity, while circular polarisation peaks along with the total intensity. The position angle (PA) of the linear polarisation shows an increase before the linearly polarised emission peaks, and a decrease afterwards, instead of following the rotating vector model from Radhakrishnan & Cooke (1969). In the MeerKAT L-band, scattering drags some of the polarised emission into the scattering tail, resulting in some spurious PA angle measurements towards the end of the pulse. In the Parkes data set, an extra feature of the profile was revealed at the beginning of the pulse, making it slightly asymmetric. This feature is coincident with the off-centre linearly polarised emission.
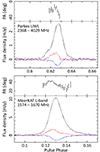 |
Fig. 3. Parkes UWL (top) and MeerKAT L-band (bottom) polarisation profiles of J1227−6208, RM-corrected at 47.3 rad cm−1. Total flux density (black lines), linearly polarised intensity (red lines), circularly polarised intensity (blue lines), and the PA angle (black error bars) are plotted as a function of the pulse phase. |
4. Timing analysis
4.1. Noise modelling
We fitted the entire ToA time series with the DDH model, a modified version of the Damour-Deurelle timing model (DD, Damour & Deruelle 1986) that includes the orthometric parametrisation of the Shapiro delay (Freire & Wex 2010). The fit itself was performed with the pulsar timing software TEMPO27(Edwards et al. 2006; Hobbs et al. 2006) and its plug-in TEMPO2/TempoNEST8, which implements multi-nested Bayesian sampling of the highly multidimensional space of the timing model, including the pulsar spin and astrometric parameters, the DM evolution, the five Keplerian parameters, and five independent PK parameters. In addition, TEMPO2/TempoNEST also fits for Gaussian white noise and correlated red noise.
The ToA time series is affected by Gaussian instrumental noise, red spin nosie, and DM noise, which can significantly contaminate the measurement of other parameters in the timing model. In particular, there is a significant DM variability as measured in different observations, an effect that becomes very prominent in the MeerKAT L-band and Parkes UWL data sets. Following the method first described in van Haasteren et al. (2009), we modelled the presence of red noise as a power spectral density in the Fourier domain described with a power law,
where A = {Aspin, ADM} is the dimensionless amplitude of the correlation matrix, ν is the spectral frequency, and γ = {γspin, γDM} is the power law index. We accounted for two possible sources of red noise: spin noise caused by the rotational variations originating within the pulsar, and DM noise originated by variations within the interstellar medium (ISM) along the LOS. The spin noise is frequency-independent (achromatic), while the DM noise is defined by its frequency dependence (chromatic), with
where ADM corresponds to the amplitude of red DM noise at f = 1400 MHz. To account for uncorrelated Gaussian (white) instrumental and pulsar noise for each telescope backend k (Section 2), we add the EQUADk and EFACk parameters that re-scale the ToA uncertainties, σk, into
where k is specific to each telescope backend. As a starting point, TEMPO2/TempoNEST only requires the extra assumption of a cut-off frequency for the correlated noises as a user-given input. We performed six different TEMPO2/TempoNEST runs: half of them include white noise and red DM noise, while the other half also include red spin noise. Each of these runs has different noise cut-offs, chosen from νcut−1 = 30, 50, 100, and 500 days. The resulting noise models, listed in Table 2, were named according to the cut-offs and inclusion or exclusion of red spin noise: loose (L), loose with spin (Ls), constrained (C), constrained with spin (Cs), very constrained (VC), and very constrained with spin (VCs).
Resulting noise models as derived by TEMPO2/TempoNEST.
All of the noise models provide an adequate description of the data, including those that do not include red spin noise, and red DM noise is always dominant over red spin noise when both are included. As is shown in Table 2, models that include both noises are favoured by the nested importance sampling global log-evidence (log E), and ADM is two orders of magnitude larger than Aspin. That is not surprising, as J1227−6028 is a recycled pulsar with an expected high rotational stability, and it shows that the main source of timing noise is indeed the ISM. Furthermore, Table 2 also shows that models with shorter νcut−1 values are favoured by the log E. Nonetheless, the resulting χ2 < 0.95 values for the VC and VCs models hint towards the possibility of over-fitting when accounting for large frequencies in the red noises.
4.2. Post-Keplerian parameter constraints
We fitted five PK parameters to constrain the component masses and the effects of proper motion. These are the rate of periastron advance, 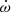 , the orthometric amplitude and ratio parameters of the Shapiro delay, h3 and ς, as defined in Freire & Wex (2010), the orbital period derivative, Ṗb, and the projected semi-major axis derivative, ẋ. From the preliminary timing solution, we expect
, the orthometric amplitude and ratio parameters of the Shapiro delay, h3 and ς, as defined in Freire & Wex (2010), the orbital period derivative, Ṗb, and the projected semi-major axis derivative, ẋ. From the preliminary timing solution, we expect 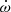 to be dominated by the relativistic precession of the Keplerian orbit as predicted by GR,
to be dominated by the relativistic precession of the Keplerian orbit as predicted by GR,
where the total system mass, Mt, is expressed in units of M⊙, and T⊙ = G M⊙/c3 = 4.92549094764 μs as defined in Prša et al. (2016). The Shapiro delay describes the periodic time delay of the pulses as they propagate through the gravitational field of the companion (Shapiro 1964). However, as its periodicity is equal to Pb, part of its signal is degenerate with the Rømer delay for systems with low inclination angles. Therefore, we used h3 and ς to model the residual unabsorbed component of the Shapiro delay instead (Freire & Wex 2010). The orthometric amplitude,
describes the amplitude of the unabsorbed component, which depends on the companion mass, Mc, and the inclination angle, i, while the orthometric ratio,
describes the shape of the delay in the orbital phase, depending only on i.
The remaining PK parameters, Ṗb and ẋ, have the estimated GR contributions of 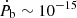 s s−1 and
s s−1 and 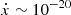 ls s−1, but much more dominant contributions are those of the Galactic acceleration field and the proper motion. For Ṗb, we expected the Shklovskii effect and the Galactic acceleration field to be the dominant contributors (Shklovskii 1970; Damour & Taylor 1991), which introduce a derivative based on the Doppler factor (D) derivatives:
ls s−1, but much more dominant contributions are those of the Galactic acceleration field and the proper motion. For Ṗb, we expected the Shklovskii effect and the Galactic acceleration field to be the dominant contributors (Shklovskii 1970; Damour & Taylor 1991), which introduce a derivative based on the Doppler factor (D) derivatives:
where μ = (μRA, μDEC) is the sky proper motion of the pulsar, K0 is the Solar System barycentre (SSB) to pulsar system unit vector, and aPSR and aSSB are the Galactic acceleration field measured at the pulsar system and the SSB, respectively. On the other hand, the contribution to ẋ was expected to be dominated by the geometric effect introduced by the proper motion of the system on the sky (Kopeikin 1996):
where Ωa is the longitude of ascending node. Finally, we did not include the amplitude of the Einstein delay γE, as for circular systems like J1227−6208 it is expected to be highly degenerate with ẋ, and its inclusion would lead to the non-detection of ẋ instead (see Ridolfi et al. 2019 for a detailed discussion of this phenomenon).
To measure the PK parameters, we assumed the noise models found by TEMPO2/TempoNEST and performed a global re-fit of all model parameters with TEMPO2. We quote the fit values and 1σ uncertainties as reported by the least-χ2 TEMPO2 fit, which are consistent with the ones reported by TEMPO2/TempoNEST but with slightly larger uncertainties. We chose this because the TEMPO2 fits are more consistent across noise models, because it provides a more conservative uncertainty estimate, and because it is consistent with the use of TEMPO2 in the mass measurements presented in the following sections.
The measured PK parameters are consistent across all noise models. Table 3 presents the measured value of each PK parameter for each assumed noise model in the global fit. The rate of periastron advance presents a very consistent value of 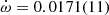 deg yr−1 if we consider extended uncertainties from all of the measurements listed in Table 3, which results in a ∼15σ detection and indicates a total system mass of Mt = 2.9 ± 0.3 M⊙. The Shapiro delay parameters h3 = 3.6 ± 0.5 μs and ς = 0.85 ± 0.05 were measured with high significance for the first time, presenting ∼7σ and ∼17σ detections if we consider extended uncertainties from across all the noise models.
deg yr−1 if we consider extended uncertainties from all of the measurements listed in Table 3, which results in a ∼15σ detection and indicates a total system mass of Mt = 2.9 ± 0.3 M⊙. The Shapiro delay parameters h3 = 3.6 ± 0.5 μs and ς = 0.85 ± 0.05 were measured with high significance for the first time, presenting ∼7σ and ∼17σ detections if we consider extended uncertainties from across all the noise models.
Constraints on the PK parameters and the component masses from the global fits.
The red DM noise is a major source of uncertainty in our measurements. The parameters most affected by the choice of the noise model is h3, ranging from 3.8(3) μs in the L model to 3.4(2) μs in the VCs. In general, we measured lower values in models with high-frequency cut-offs, and with both spin and DM noise. A possible explanation is that unmodelled red noise can bias the Shapiro delay measurement to higher amplitude values, especially achromatic spin noise. A similar phenomenon can occur in the opposite direction, with noise models removing power from the Shapiro delay signal when the orbital period is close to νcut. That may be a potential explanation for the χ2 < 0.95 value in the VC and VCs models (Table 2). Nonetheless, the measured PK values of all parameters are consistent across all noise models within the 1σ uncertainty ranges.
The MeerKAT data set dominates the measurement of the orthometric Shapiro delay parameters. Fig. 4 shows the timing residuals as a function of the orbital phase under the assumption of the Cs noise model. Despite some small gaps in orbital coverage, only the MeerKAT-derived ToAs have enough precision to detect the Shapiro delay with high significance, and therefore to constrain the component masses in this system. To corroborate this, we have attempted to fit the h3 and ς parameters on each ToA dataset. The MeerKAT L-band ToAs reproduced the measurement from the global fit, while the S-band ToAs yielded only a slight loss of precision owing to the sparser orbital coverage. On the other hand, the Parkes multibeam data set provided only very loose constraints, as is discussed in Section 4.4, and the Parkes UWL dataset was unable to converge on significant values.
 |
Fig. 4. Timing residuals under the assumption of the Cs noise model. Top: ToA residuals as a function of MJD, showing flat, Gaussian residuals. Middle: ToA residuals as a function of the orbital phase (orbital position from the ascending node, true anomaly + periastron) excluding the h3 and ς parameters from the timing model, showing the full amplitude of the Shapiro delay signal. The continuous blue line depicts the predicted Shapiro delay described by h3 = 3.45 μs and ς = 0.858. Bottom: same as the middle plot, but the orthometric Shapiro delay parameters are now included in the model, resulting in flat, Gaussian residuals. |
The two remaining PK parameters, Ṗb and ẋ, did not yield a significant detection with the current timing baseline but still offer useful constraints. Table 5 presents the values for all the timing parameters of the global fit using the Cs noise model, as well as thee expected contributions to Ṗb and ẋ. The DM-derived distance from the NE2001 (Cordes 2004) and YMW16 (Yao et al. 2017) electron density models are d = 8.3 kpc and d = 8.5 kpc, respectively. With the detected proper motion vector of μ = ( − 6.1 ± 0.3, 0.41 ± 0.36) mas yr−1 and the Galactic gravitational potential from McMillan (2017) in eq. (10), we predict an order of magnitude of 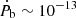 s s−1. Likewise, assuming i ≈ 79 deg (Section 4.3) in equation (11), we predict a maximum value of
s s−1. Likewise, assuming i ≈ 79 deg (Section 4.3) in equation (11), we predict a maximum value of 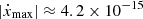 ls s−1 in case of a favourable Ωa value. These estimates are of the same order of magnitude as the constraints on Ṗb and ẋ presented in Table 3, which also present a consistent sign across all noise models, suggesting that the constraints can provide some physical information. Taking this into account, in Section 4.5 we translate the constraint on ẋ into constraints on the orbital geometry of the system, and in Section 4.6 we discuss the possible implications of the Ṗb constraints for the measurement of the spin period derivative Ṗs.
ls s−1 in case of a favourable Ωa value. These estimates are of the same order of magnitude as the constraints on Ṗb and ẋ presented in Table 3, which also present a consistent sign across all noise models, suggesting that the constraints can provide some physical information. Taking this into account, in Section 4.5 we translate the constraint on ẋ into constraints on the orbital geometry of the system, and in Section 4.6 we discuss the possible implications of the Ṗb constraints for the measurement of the spin period derivative Ṗs.
Data reduction, model fit, spin, DM, and astrometric parameters from the DDH TEMPO2/TempoNEST fits.
4.3. Mass constraints
In a common Bayesian approach (e.g. Splaver et al. 2002), we enforced the consistency of the PK parameters with GR and derived constraints on Mp, Mc, and i. We use the DDGR model, a modified version of the DD model that implements the PK effects directly from Mt and Mc as predicted by GR (Taylor & Weisberg 1989). This allows us to explore a two-dimensional space of parameters to constrain the mass components and orbital inclination. For each noise model derived by TEMPO2/TempoNEST, we performed TEMPO2 fits with the DDGR model in a uniform grid in the Mt − cos i space, where the uniform spacing on cos i was chosen to achieve a uniform sampling of the possible orbital geometries of the system. At each point in the grid, we registered the resulting χ2 and transformed it into a probability value, deriving a likelihood distribution. Subsequently, the distribution was integrated into marginal one-dimensional probability distributions for Mp, Mc, and i. Given that Ṗb and ẋ are influenced by the proper motion of J1227−6208 and the Galactic acceleration field, we included them as independent excess parameters that do not need to be consistent with GR.
The resulting values of Mp, Mc, and i are listed in Table 3. They are consistent across all noise models, but there is some tension between the DDGR constraints and the ς parameter. Fig. 5 depicts the constraints on the Mc − cos i and Mc − Mp spaces as derived both with the DDGR χ2 mapping method and the constraints imposed by the independently measured 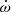 , h3, and ς parameters, in both cases under the assumption of the Cs noise model. The resulting DDGR constraints are 1σ consistent with the measurement of
, h3, and ς parameters, in both cases under the assumption of the Cs noise model. The resulting DDGR constraints are 1σ consistent with the measurement of 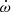 and h3, and 2σ consistent with ς. This is also observed with the noise models Ls, C, VC, and VCs. Only the assumption of the L noise model results in self-consistent constraints. The median values and the 68.2% percentiles of the marginal one-dimensional distributions for Mp, Mc, and i are quoted as the measurements and their 1σ uncertainties in Table 3, where it is seen that all noise models present 1σ consistent constraints. We note that models with high-frequency cut-offs resulted in slightly lower mass ranges, going from Mp = 1.59(10) M⊙ and Mc = 1.42(5) M⊙ in Ls (Fig. A.1) to Mp = 1.51(11) M⊙ and Mc = 1.38(5) M⊙ in VCs (Fig. A.2). That is consistent with the variation in the h3 values across noise models as exposed in Section 4.2, and it shows how the DM noise is the main limiting factor in the precision of our mass measurements. On the other hand, the constraints on i are more sensitive to the inclusion or exclusion of red spin noise, with i = 79.2(7) deg for the L, C, and VC models and ranging from i = 78.6(7) deg to i = 78.2(7) deg from Ls to VCs models. Using extended uncertainty ranges from all the values listed in Table 3, we quote Mt = 2.9 ± 0.3 M⊙, Mp = 1.54(15) M⊙, Mc = 1.40(7) M⊙, and i = 78.7 ± 1.2 deg, which constitute 10σ, 10σ, 20σ, and 65σ constraints.
and h3, and 2σ consistent with ς. This is also observed with the noise models Ls, C, VC, and VCs. Only the assumption of the L noise model results in self-consistent constraints. The median values and the 68.2% percentiles of the marginal one-dimensional distributions for Mp, Mc, and i are quoted as the measurements and their 1σ uncertainties in Table 3, where it is seen that all noise models present 1σ consistent constraints. We note that models with high-frequency cut-offs resulted in slightly lower mass ranges, going from Mp = 1.59(10) M⊙ and Mc = 1.42(5) M⊙ in Ls (Fig. A.1) to Mp = 1.51(11) M⊙ and Mc = 1.38(5) M⊙ in VCs (Fig. A.2). That is consistent with the variation in the h3 values across noise models as exposed in Section 4.2, and it shows how the DM noise is the main limiting factor in the precision of our mass measurements. On the other hand, the constraints on i are more sensitive to the inclusion or exclusion of red spin noise, with i = 79.2(7) deg for the L, C, and VC models and ranging from i = 78.6(7) deg to i = 78.2(7) deg from Ls to VCs models. Using extended uncertainty ranges from all the values listed in Table 3, we quote Mt = 2.9 ± 0.3 M⊙, Mp = 1.54(15) M⊙, Mc = 1.40(7) M⊙, and i = 78.7 ± 1.2 deg, which constitute 10σ, 10σ, 20σ, and 65σ constraints.
 |
Fig. 5. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model. The constraints have been derived in the global fit and under the assumption of the Cs noise model (Table 2). Central plots: two-dimensional constraints on the Mc − cos i and Mc − Mp spaces. The solid coloured lines represent the nominal values of the PK parameters, the dashed coloured lines their 1σ limits, and the solid black lines the 1σ and 3σ limits from DDGR. The shaded grey area in the right plot is the region excluded by the mass function (i > 90 deg). Corner plots: marginalised one-dimensional probability densities for Mp, Mc, and cos i from DDGR χ2 mapping, showcasing the median value (solid black line) and the 31.4%, 47.4%, and 49.9% percentiles on both sides (shaded areas under the curve). |
4.4. Discrepancies between post-Keplerian parameters and General Relativity
As is shown in Fig. 5, ς is only 2σ consistent with the DDGR constraints, and the h3 and 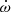 parameters. To explore the cause of this slight discrepancy, we analysed the individual contributions to the PK parameters from segregated data sets. Keeping the noise models derived by TEMPO2/TempoNEST, we created two new isolated ToA time series: one with the ToAs derived from Parkes multibeam observations (multibeam), and another one with the ToAs derived from MeerKAT and the Parkes UWL observations (MeerKAT+UWL). These two sets differ significantly both in timing baseline and in ToA quality, with the Parkes multibeam-derived ToAs providing the longest baseline, but with the MeerKAT+UWL ToAs being much more precise and providing observing frequency information (Figs. 1 and 4). Subsequently, we repeated the TEMPO2 fits on each side.
parameters. To explore the cause of this slight discrepancy, we analysed the individual contributions to the PK parameters from segregated data sets. Keeping the noise models derived by TEMPO2/TempoNEST, we created two new isolated ToA time series: one with the ToAs derived from Parkes multibeam observations (multibeam), and another one with the ToAs derived from MeerKAT and the Parkes UWL observations (MeerKAT+UWL). These two sets differ significantly both in timing baseline and in ToA quality, with the Parkes multibeam-derived ToAs providing the longest baseline, but with the MeerKAT+UWL ToAs being much more precise and providing observing frequency information (Figs. 1 and 4). Subsequently, we repeated the TEMPO2 fits on each side.
The Shapiro delay measurement is not significantly affected by the split. In the multibeam fits, the orthometric Shapiro delay parameters were measured with larger uncertainties across all noise models (h3 = 4.1 − 4.7 ± 2.1 μs, ς = 0.69 − 0.76 ± 0.29), but they are still consistent with the measurements from the global fit. On the other hand, the MeerKAT+UWL h3 and ς values listed in Table 6 are almost identical to the ones from the global fit quoted in Table 3. That is consistent with the Shapiro delay being primarily constrained by the MeerKAT ToAs owing to their higher precision (see Section 4.2).
Orbital Keplerian and PK parameters from the DDH TEMPO2/TempoNEST fits, and mass constraints from the DDGR χ2 mapping fits.
Constraints on the PK parameters and the component masses from the MeerKAT+UWL fits.
The tension between the PK parameters was reduced in the MeerKAT+UWL fits. In the multibeam fits, the periastron advance 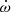 increased to
increased to 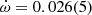 deg yr−1, which is more than 1σ away from the global fit. Not only is this an unrealistic value, as it implies total system mass of Mt = 5.5 ± 1.7 M⊙, but it also suggests that the multibeam data set is somehow biased towards a larger
deg yr−1, which is more than 1σ away from the global fit. Not only is this an unrealistic value, as it implies total system mass of Mt = 5.5 ± 1.7 M⊙, but it also suggests that the multibeam data set is somehow biased towards a larger 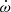 value. However, the MeerKAT+UWL fits give values much more consistent with the global fits, with
value. However, the MeerKAT+UWL fits give values much more consistent with the global fits, with 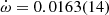 deg yr−1 from the extended uncertainties. The median value of
deg yr−1 from the extended uncertainties. The median value of 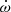 was slightly reduced within the 1σ uncertainties consistently across all noise models (Table 6) with only a small increase in uncertainty compared to the global fit (
was slightly reduced within the 1σ uncertainties consistently across all noise models (Table 6) with only a small increase in uncertainty compared to the global fit (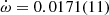 deg yr−1, Table 3). With this subtle change,
deg yr−1, Table 3). With this subtle change, 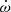 , h3, and ς became 1σ consistent with each other across all noise models.
, h3, and ς became 1σ consistent with each other across all noise models.
In an attempt to understand the origin of the apparent biases introduced by the multibeam data set, we performed two extra TEMPO2/TempoNEST runs with νspin−1 = 100 days and νDM−1 = 50 days on the multibeam and MeerKAT+UWL data sets, and compared the resulting noise and timing parameters with those of the Cs model derived in the global fit (Table 2). Tables 4 and 5 show the global fit, the multibeam fit and the MeerKAT+UWL fit results side to side. In Table 4, it becomes readily evident that TEMPO2/TempoNEST converged on similar timing noise models for the global and MeerKAT+UWL data sets. Table 5 also shows that the MeerKAT+UWL PK parameter measurements are also virtually identical to those derived with the assumption of the Cs model, presented in Table 6. However, the noise model diverges in the isolated multibeam data set, and it was unable to converge on realistic values, showing that the Parkes multibeam data does not have enough timing precision and bandwidth to constrain the spin and DM timing noise. This could explain why the multibeam gives a discrepant 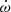 measurement, and why it could be biasing the global fit measurements as well.
measurement, and why it could be biasing the global fit measurements as well.
In light of this, we repeated the χ2 mapping of DDGR solutions with the MeerKAT+UWL data set only and with the assumption of the noise models derived in the global TEMPO2/TempoNEST fits (Table 2), deriving the Mp, Mc, and i constraints quoted in Table 6. Similar to the global fits, 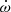 and h3 dominate the constraints, but this time, the DDGR limits were 1σ consistent with all of the PK parameters. Like in the global fits, the more constraining noise models resulted in lower mass ranges, going from Mp = 1.31(31) M⊙ and Mc = 1.28(7) M⊙ with the VCs noise model (Fig. A.3) to Mp = 1.43(14) M⊙ and Mc = 1.34(7) M⊙ with the Ls noise model (Fig. A.4). For reference, Fig. A.5 in the Appendix (A) shows the counterpart for Fig. 5, with the assumption of the Cs noise model on the MeerKAT+UWL data set. Nonetheless, the uncertainty ranges are still 1σ consistent with the global fits presented in Table 3. Accounting for extended uncertainties from all measurements in Table 6, we quote Mt = 2.7 ± 0.4 M⊙, Mp = 1.36(21) M⊙, Mc = 1.30(9) M⊙, and i = 79.3 ± 1.1 deg from the MeerKAT+UWL global fits, which are 7σ, 6σ, 14σ, and 77σ measurements, and are in 1σ consistency with the ones quoted in Section 4.3.
and h3 dominate the constraints, but this time, the DDGR limits were 1σ consistent with all of the PK parameters. Like in the global fits, the more constraining noise models resulted in lower mass ranges, going from Mp = 1.31(31) M⊙ and Mc = 1.28(7) M⊙ with the VCs noise model (Fig. A.3) to Mp = 1.43(14) M⊙ and Mc = 1.34(7) M⊙ with the Ls noise model (Fig. A.4). For reference, Fig. A.5 in the Appendix (A) shows the counterpart for Fig. 5, with the assumption of the Cs noise model on the MeerKAT+UWL data set. Nonetheless, the uncertainty ranges are still 1σ consistent with the global fits presented in Table 3. Accounting for extended uncertainties from all measurements in Table 6, we quote Mt = 2.7 ± 0.4 M⊙, Mp = 1.36(21) M⊙, Mc = 1.30(9) M⊙, and i = 79.3 ± 1.1 deg from the MeerKAT+UWL global fits, which are 7σ, 6σ, 14σ, and 77σ measurements, and are in 1σ consistency with the ones quoted in Section 4.3.
Finally, we attested that Ṗb and ẋ can only be constrained in the global fit. Both the multibeam and the MeerKAT+UWL fits were unable to constrain to Ṗb and ẋ. As is shown in Table 5, the uncertainties on both parameters increase by an order of magnitude. Therefore, it is evident that only the accumulated baseline of the global fit can constrain them.
4.5. Orbital geometry constraints
In Section 4.2, it is noted that the uncertainty in the constraints of ẋ across have a similar size as the 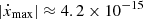 expected from the proper motion, as quoted in Table 5. Therefore, we investigated how the DDGR solutions are affected upon enforcement of consistency between ẋ, μ, and the orbital geometry of the system. Assuming the noise models derived with TEMPO2/TempoNEST, we implemented the same likelihood approach from Section 4.3 with two major modifications. First, the mapping was done in a uniform three-dimensional grid on the Mt − cos i − Ωa space. Second, equation (11) was implemented by forcing the excess ẋ value to be consistent with the i, Ωa, and μ = (μRA, μDec) values. To compensate for the extra dimensionality, the grid resolution was reduced to avoid a manifold increase of the computational running time of this experiment, with only 64 points along the Mt axis across 10σ, 60 points along the cos i across 12σ, and 180 points across the 0 ≤ Ωa < 360 range. In addition, equation (11) is symmetric with respect to the transformation i → 180 deg − i and Ωa → Ωa + 180 deg. Therefore, the cos i < 0 side of the explored space was derived by implementing this transformation. This last point is true only because the distance to J1227−6208 is large enough so that the orbital motion of Earth does not introduce year-long periodic contributions to ẋ. Finally, we integrated the likelihood distribution along the Mt axis to derive two-dimensional likelihood distribution on the Ωa − cos i space, from which the marginal probability distributions for Ωa and cos i were derived.
expected from the proper motion, as quoted in Table 5. Therefore, we investigated how the DDGR solutions are affected upon enforcement of consistency between ẋ, μ, and the orbital geometry of the system. Assuming the noise models derived with TEMPO2/TempoNEST, we implemented the same likelihood approach from Section 4.3 with two major modifications. First, the mapping was done in a uniform three-dimensional grid on the Mt − cos i − Ωa space. Second, equation (11) was implemented by forcing the excess ẋ value to be consistent with the i, Ωa, and μ = (μRA, μDec) values. To compensate for the extra dimensionality, the grid resolution was reduced to avoid a manifold increase of the computational running time of this experiment, with only 64 points along the Mt axis across 10σ, 60 points along the cos i across 12σ, and 180 points across the 0 ≤ Ωa < 360 range. In addition, equation (11) is symmetric with respect to the transformation i → 180 deg − i and Ωa → Ωa + 180 deg. Therefore, the cos i < 0 side of the explored space was derived by implementing this transformation. This last point is true only because the distance to J1227−6208 is large enough so that the orbital motion of Earth does not introduce year-long periodic contributions to ẋ. Finally, we integrated the likelihood distribution along the Mt axis to derive two-dimensional likelihood distribution on the Ωa − cos i space, from which the marginal probability distributions for Ωa and cos i were derived.
The constraints on cos i and Ωa are drawn on Fig. 6. As expected, the constraints on i are consistent with those derived in Section 4.3. The value of Ωa is not constrained owing to the large overlap of the cos i > 0 and cos i < 0 probability distributions, but the probability density contours show that two regions in the cos i − Ωa are preferred. For cos i > 0, the longitude of ascending node is constrained at Ωa = 266 ± 78 deg, while for cos i < 0 it is constrained at Ωa = 86 ± 78 deg. From equation 11, using the values of x, i, μRA, and μDec presented in Table 4 and Ωa = 266 deg, we predict a value of 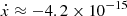 ls s−1, in full consistency with the values presented in Table 3. Therefore, it is clear that the measured excess ẋ originates from the proper motion of the system in the sky.
ls s−1, in full consistency with the values presented in Table 3. Therefore, it is clear that the measured excess ẋ originates from the proper motion of the system in the sky.
 |
Fig. 6. Constraints on the orbital orientation from the χ2 mapping of DDGR solutions consistent with Eq. (11). The constraints have been derived in the global fit and assuming the Cs noise model (Table 2) Central plots: two-dimensional constraints in the Ωa − cos i space. The solid contours represent the explored space (cos i > 0), while the dashed contours are derived from symmetries in eq. (11) (cos i < 0). Corner plots, top: marginalised one-dimensional probability densities for cos i, showcasing the median value (solid black lines) and the 31.4%, 47.4%, and 49.9% percentiles (shaded areas under the curve, blue for cos i > 0 and purple for cos i < 0). Corner plot, right: marginalised one-dimensional probability densities for Ωa from cos i > 0 and cos i < 0 (solid and dashed lines, respectively) and the addition of both (shaded cyan area). |
4.6. Spin and orbital period evolution constraints
As is shown in Table 4, in the global fit we measured the spin evolution parameters Ps and Ṗs with high significance, showing that J1227−6208 is indeed a mildly recycled pulsar. However, the Shklovskii effect and Galactic potential field affect Ṗs in the same way as they affect Ṗb, following equation (10). The estimated values of these contributions are listed at the end of Table 4, making it evident that albeit they are smaller than the measurement (∼10−20 s s−1 against 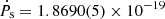 s s−1), they can nonetheless be significant. Thus, we should be cautious of pulsar parameters derived from Ps and Ṗs. Since a parallax distance measurement is out of the question, the best prospect for constraining the true combined contributions of the Shklovskii effect and the Galactic potential field is to improve the Ṗb measurement, on which these effects are orders of magnitude larger than the GR prediction. Therefore, a measurement of Ṗb will be direct measurement of the Doppler factor derivative. Nonetheless, with the current observations, the consistently positive sign of Ṗb across all noise models (Table 3) already suggests a dominance of the Shklovskii effect over the Galactic potential contribution.
s s−1), they can nonetheless be significant. Thus, we should be cautious of pulsar parameters derived from Ps and Ṗs. Since a parallax distance measurement is out of the question, the best prospect for constraining the true combined contributions of the Shklovskii effect and the Galactic potential field is to improve the Ṗb measurement, on which these effects are orders of magnitude larger than the GR prediction. Therefore, a measurement of Ṗb will be direct measurement of the Doppler factor derivative. Nonetheless, with the current observations, the consistently positive sign of Ṗb across all noise models (Table 3) already suggests a dominance of the Shklovskii effect over the Galactic potential contribution.
5. Astrophysical Implications
5.1. J1227−6208 as a DNS system
The mass ranges derived in Sections 4.3 and 4.4 and presented in Tables 3 and 6 are consistent with the mass distribution of the double-NS (DNS) population, with Mc being significantly above the current lower mass limit of a NS (1.17 M⊙, Martinez et al. 2015), making a NS nature a hypothesis in need of consideration.
Recycled pulsars with massive WD and NS companions follow a similar evolutionary path. With original companions more massive than 5 M⊙ (Lazarus et al. 2014), these systems go through a intermediate-mass or high-mass X-ray binary (IMXB or HMXB) stage, resulting in a dynamically unstable mass transfer and the formation of a common envelope (CE, e.g. van den Heuvel 2019). After the hydrogen-rich CE is expelled, the system becomes a circular PSR−He naked star. Stable mass accretion on to the NS occurs when the companion leaves the He main sequence and the system enters a short-lasted (less than 100 kyr) Case BB RLO stage, leading to the partial recycling of the pulsar (Lazarus et al. 2014). Afterwards, and if the stripped He star has retained enough mass (≳1.45 M⊙), the companion will undergo an electron-capture supernova, forming a second NS (Tauris et al. 2015, 2017). This process entails the loss 0.2 − 0.4 M⊙ and a supernova kick of < 50 km s−1 that either disrupts the system or introduces a significant orbital eccentricity (e ≳ 0.1, Tauris et al. 2017). On the other hand, if the stripped companion is unable to trigger a supernova, it becomes a massive WD instead (Lazarus et al. 2014; Tauris et al. 2012).
We argue that J1227−6208 is very unlikely to be a DNS system based on its orbital eccentricity. The left plot of Fig. 7 depicts the orbital eccentricity e of recycled pulsars against Mc and it shows that, while the Mp in J1227−6208 is consistent with the DNS population, its e value is two orders of magnitude below those of known DNS systems. Instead, it lays among other massive recycled PSR−CO/ONeMg WD systems. While Tauris et al. (2017) show that very low eccentricities (e < 0.01) in DNS are technically possible, they also argue that this scenario is extremely unlikely, requiring an extraordinary fine-tuning of the supernova kick magnitude and direction. That is strong evidence against the companion of J1227−5936 having undergone a supernova, making it a massive WD instead.
 |
Fig. 7. Comparison of orbital and mass constraints between Galactic pulsar−WD systems, Galactic DNS systems, and J1227−6208. For J1227−6208, the extended uncertainties from the global (red star, Table 3) and the MeerKAT+UWL fits (magenta cross, Table 6) are quoted. Left: orbital eccentricity against companion mass from recycled binary pulsars in the Galactic field, distinguished by the nature of their companions. For systems without timing mass measurements (“Undetermined” in the legend), the lower constraints on the minimum and median Mc values derived from the mass function (assuming i = 90, 60 deg) are plotted. Right: WD mass against pulsar mass of PSR−WD systems in the Galactic field. References: constraints on systems besides J1227−6208 are taken from https://www3.mpifr-bonn.mpg.de/staff/pfreire/NS_masses.html and references therein, and from Camilo et al. (2001) (PSR J1435−6100), Cruces et al. (2021) (PSR J2338+4818), Edwards & Bailes (2001) (PSR J1157−5112), Gautam et al. (2022) (PSR J1952+2630), Jang et al., in prep. (PSR J1439−5501), Martinez et al. (2019) (PSR J0709+0458), Parent et al. (2019) (PSR J1932+1756), and Tan et al. (2020) (PSR J1658+3630). |
5.2. J1227−6208 as a massive PSR−WD system
J1227−6208 thus belongs to an emerging class of massive recycled PSR−ONeMg WD systems. The right side of Fig. 7 maps measured PSR−WD component masses in a Mc − Mp diagram, showing that J1227−6208 lies among the well-studied massive systems PSR J2222−0137, PSR J1528−3146, and J1439−5501, represented by the green triangles. J1227−6208 also shares with these three systems similar spin properties (P0 = 34.52 ms against 32.82, 60.82, and 28.64 ms), binary period (Pb = 6.72 days against 2.45, 3.18, and 2.12 days), and orbital eccentricity (e = 1.15 × 10−3 against 4.65×10−4, 2.13×10−4, and 4.99×10−5), suggesting a similar nature. Therefore, it is very plausible that J1227−6208 has followed the evolutionary path of recycled PSR−ONeMg WD systems (MWD ≳ 1.1 M⊙). It should be noted that the young system PSR B2303+46, shown as a black square in Fig. 7, is the result of an exotic evolution where the WD formed before the pulsar and thus no recycling has occurred in it (van Kerkwijk & Kulkarni 1999; Tauris & Sennels 2000).
As we argue in favour of a WD nature for the companion, the possibility of Mc laying beyond the Chandrasekhar limit (Section 4.3) is brought into question. Theoretical models predict that fast-rotating WDs may exist in the 1.38 < MWD/M⊙ < 1.48 mass range without collapsing in a supernova (e.g. Yoon & Langer 2005). However, these conditions can only be the result of accretion and the spin-up in the WD, or be the product of a WD merger. Both of these scenarios are difficult to reconcile with the evolutionary model proposed above and the low orbital eccentricity, and therefore the mass of the companion of J1227−6208 is likely lower than 1.38 M⊙. Continued timing in the future will be essential to increase the precision of the mass constraints so that a more definitive statement can be made on this aspect.
J1227−6208 and its companion are the fourth partially recycled pulsar with a MWD > 1.2 M⊙ ONeMg WD companion with mass measurements from timing. As is seen on the right plot of Fig. 7, an apparent gap in MWD values is arising at MWD ≈ 1.1 M⊙, in addition to the already-known separation between massive CO WD systems (0.7 ≲ MWD ≲ 1.0 M⊙) and the fully recycled millisecond pulsars with light He and CO WD companions (MWD ≲ 0.5 M⊙) McKee et al. (2020), Shamohammadi et al. (2023), implying a trimodality in the MWD distribution. However, such gap is not predicted by theory and the left plot of Fig. 7 shows that a handful of known massive systems without mass measurements can potentially fill this gap: PSR J1435−6100 (Camilo et al. 2001), PSR J2338+4818 (Cruces et al. 2021), PSR J1157−5112 (Edwards & Bailes 2001), PSR J1952+2630 (Jang et al., in prep.), PSR J0709+0458 (Martinez et al. 2019), PSR J1932+1756 (Parent et al. 2019), and PSR J1658+3630 (Tan et al. 2020). Thus, this gap could be spurious, arising from the reduced size of the sample of mass measurements in massive systems. New mass measurements and the discovery and follow-up of further massive partially recycled PSR−ONeMg WD systems will be key in confirming whether the MWD distribution is trimodal or if this notion is just a statistical fluke.
5.3. The pulsar mass of J1227−6208
Theoretical models for recycled pulsars with the most massive WD companions suggest that these systems went through a short phase of accretion during post-CE Case BB RLO from their naked He-star companion, resulting in observed spin-up periods of Ps ≳ 20 ms. According to Tauris et al. (2012), the amount of mass accreted by a recycled pulsar given a Ps can be estimated with the following equation:
Assuming its current spin period of Ps ≈ 34.5 ms results in the accretion of 0.0022 M⊙ from its companion during recycling. On the other hand, assuming a possible initial spin-up period of Ps ≈ 20 ms results in the accretion of at most 0.0045 M⊙ from its companion. In both cases, the implication is that the current Mp measurement is close its birth mass. Therefore a more precise measurement of Mp will contribute to the statistics of NS birth masses, like in the similar systems PSR J2222−0137, PSR J1534−3146, and PSR J1439−5501. In fact, the measurement of Mp = 1.76(6) M⊙ in PSR J2222−0137 by Cognard et al. (2017) (Mp = 1.831(10) M⊙ in Guo et al. 2021) has already expanded such distribution on its upper end.
If the amount of accreted matter estimated from theory is correct, the mass-transfer rate was likely Eddington or super-Eddington. For a NS of 1.5 M⊙, the Eddington luminosity limit is L ≈ 1.5 × 1038 erg s−1, and the accretion-to-luminosity efficiency is 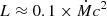 (Shakura & Sunyaev 1973; Poutanen et al. 2007), resulting in a maximum accretion rate of
(Shakura & Sunyaev 1973; Poutanen et al. 2007), resulting in a maximum accretion rate of 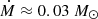 Myr−1. Simulations find that the duration of the accretion stage during the Case BB RLO is ≲100 000 yr for massive PSR−WD systems (Lazarus et al. 2014; Tauris et al. 2015, e.g.), and Cognard et al. (2017) even found that the accretion time was ≲20 000 yr for the massive PSR−ONeMg WD system in PSR J2222−0137. The Eddington limit would allow for the accretion of at most 0.003 M⊙ in the span of 100 000 yr, and 5 × 10−4 M⊙ in 20 000 yr, implying that if the recycling process occurred on a similar time span for J1227−6208, then it has accreted either close to the Eddington limit or significantly above it like in PSR J2222−0137. This is a plausible scenario, as super-Eddington accretion onto NSs has been directly observed in extra-galactic ultra-luminous X-ray sources such as NGC 5907 X-1 (Israel et al. 2017), NGC 300 ULX1 (Carpano et al. 2018), and M82 X-2 (Bachetti et al. 2014). However, an alternative explanation is that the spin-up efficiency is larger than what is predicted by Tauris et al. (2012), requiring less mass accretion to reach a similar Ps.
Myr−1. Simulations find that the duration of the accretion stage during the Case BB RLO is ≲100 000 yr for massive PSR−WD systems (Lazarus et al. 2014; Tauris et al. 2015, e.g.), and Cognard et al. (2017) even found that the accretion time was ≲20 000 yr for the massive PSR−ONeMg WD system in PSR J2222−0137. The Eddington limit would allow for the accretion of at most 0.003 M⊙ in the span of 100 000 yr, and 5 × 10−4 M⊙ in 20 000 yr, implying that if the recycling process occurred on a similar time span for J1227−6208, then it has accreted either close to the Eddington limit or significantly above it like in PSR J2222−0137. This is a plausible scenario, as super-Eddington accretion onto NSs has been directly observed in extra-galactic ultra-luminous X-ray sources such as NGC 5907 X-1 (Israel et al. 2017), NGC 300 ULX1 (Carpano et al. 2018), and M82 X-2 (Bachetti et al. 2014). However, an alternative explanation is that the spin-up efficiency is larger than what is predicted by Tauris et al. (2012), requiring less mass accretion to reach a similar Ps.
6. Future prospects
6.1. Prospects for timing
Future timing observations of J1227−6208 should seek to strike a balance between its steep spectrum and the ISM-induced effects. Fig. 8 portrays how ToA uncertainty evolves with f across different receivers, and it shows that scattering affects the ToA quality negatively at f < 1300 MHz, leading to an increase of timing uncertainty. The best ToA quality is found at the f = 1.3 − 2.2 GHz range, while at f > 2200 MHz the steep spectrum starts hampering the S/N, leading to another increase in timing uncertainty. Another factor to take into account is that, as reported in Section 4.1, red DM noise is very prominent, making it preferable to observe at high frequencies where its amplitude is lower. However, doing so comes at the price of achieving a sub-optimal S/N and ToA quality due to the steep spectral index reported in Section 3. Therefore, MeerKAT observations with the S-band receivers at the S0 configuration (1750–2625 MHz) will offer the best compromise between a high ToA precision and a reduced ISM influence, with ADM,1700 = 0.68 × ADM and ADM,2600 = 0.28 × ADM, thus enabling a precision increase on the measurement of PK parameters. In complement to this, UWL observations will be essential to track the DM evolution to properly model the still-present DN noise in the MeerKAT S-band ToAs.
 |
Fig. 8. ToA uncertainty against observing frequency for each telescope receiver. The highest and lowest frequencies of the Parkes multibeam and MeerKAT S-band data sets are biased upwards because the signal drops off at the edge of the bands (see Fig. 1). |
The significance of the PK parameters will improve with an increasing baseline. The most significant improvement in the mass constraints will come from an improved measurement of 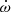 . Assuming that the uncertainty on
. Assuming that the uncertainty on 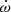 scales with the timing baseline according to the power law (Damour & Taylor 1992)
scales with the timing baseline according to the power law (Damour & Taylor 1992)
where 4.31 yr is the timing baseline of the MeerKAT+UWL data set, we expect 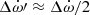 with just two extra years of timing. This improvement will reduce the total mass measurement uncertainty by 65% if we assume the current MeerKAT ToA uncertainty, aiding a more robust settlement or confirmation of any discrepancies between the PK parameters in the global fit.
with just two extra years of timing. This improvement will reduce the total mass measurement uncertainty by 65% if we assume the current MeerKAT ToA uncertainty, aiding a more robust settlement or confirmation of any discrepancies between the PK parameters in the global fit.
Tighter constraints on Ṗb and ẋ will also lead to an independent estimate of the distance of J1227−6208 and a better constraint on its orbital geometry. However, since these measurements are dependent on the global 11.26 year baseline, reducing uncertainty will require more time. Assuming once again a power law evolution of the uncertainties Ṗb (Damour & Taylor 1992)
then another decade of timing will be required to achieve a 3σ detection of Ṗb. Constraints on the orbital geometry will also require an improvement of the measurement of the proper motion. Following the power law evolution of the uncertainty on ẋ (Damour & Taylor 1992)
two more decades of timing will be necessary to achieve a 3σ detection on ẋ. However, as is seen in Section 4.5, constraints on the Ωa − cos i can already be achieved even with a low-significance detection. Furthermore, the proper motion vector measurement will continue to improve alongside it, leading to more significant constraints in the Ωa − cos i space before that time.
6.2. Prospects for an optical detection
There would be obvious benefits to having an optical detection of the companion of J1227−6208. Besides the confirmation of its WD nature, a measurement of its colour index and magnitude could be used to constrain its age with the help of WD evolutionary models. This would provide an independent measurement of the mass and age of the companion of J1227−6208 like other massive PSR−WD systems, such as PSR J1528−3146 (Jacoby et al. 2006) and PSR J1439−5501 (Pallanca et al. 2013). That would allow, for example, for a true estimate the initial spin-up period.
As of now, we are unable to report an optical detection. Gaia DR3 is sensitive to sources with magnitude G ≈ 20.7 (Gaia Collaboration 2016, 2023). Assuming the YMW16-derived DM distance of d = 8.5 kpc, detection would require an absolute magnitude of at most MG ≈ 6 to be detected, too bright for any WD. The closest reported Gaia DR3 source9 is 0.29 arcsec away from the timing position, with a colour index of B − R = 1.59 and a magnitude of G = 17.4. Its parallax distance is d = 5.3 ± 2.0, giving it an absolute magnitude of MG = 3 − 5, and putting it either on the main sequence or the giant branch. Therefore, this source is most likely not associated with J1227−6208.
A potential detection will be possible only with the most powerful optical and infrared telescopes available. Assuming d = 8.5 kp, we use the cooling tracks provided by Bergeron et al. (2011)10 for a MWD = 1.3 M⊙ with a He atmosphere to predict visible and infrared magnitudes given an age. If the age of the system is consistent with the characteristic age of τc = 2.93 Gyr, then the companion will have a optical, red, and infrared magnitudes of V, R, I > 30 and it will be undetectable. But if, like in PSR J1439−5501, the true age is significantly younger than τc for instance only 100 Myr old (Pallanca et al. 2013), the magnitudes could reach V, R, I < 27, making is potentially detectable in long exposure by sensitive optical and infrared telescopes such as the Very Large Telescope, the Hubble Space Telescope or the James Webb Space Telescope.
7. Conclusions
This study adds J1227−6208 to the rare class of confirmed mildly recycled pulsars with massive ONeMg WD companions (MWD > 1.1 M⊙), along with PSR J2222−0137, PSR J1528−3146, and PSR J1439−5501. In addition, we have provided a detailed study of the pulsar’s emission and the origin of the PK parameters measured in pulsar timing. The study includes 33 hours of Parkes multibeam data since 2012, 72 hours of Parkes ULW data since 2020, 25 hours of MeerKAT data since 2019 and 19 hours of MeerKAT S-band data from 2023, producing a timing baseline of more than 11 years.
Taking advantage of the large frequency coverage offered by these receivers to study the profile evolution of J1227−6208, we measure a steep flux density spectral index of 2.06 < α < 2.35 and a flat scattering index 3.33 < β < 3.62, with a scattering timescale of τs ≈ 1.2 ms and a mean flux density of Fm = 530 − 620 μJy at the reference frequency of 1 GHz. Due to the combined effect of scattering and spectral properties, the largest peak flux density is observed at the frequency of 1.2 − 1.3 GHz, with Fmax = 13 − 14 mJy. Around 15% of the emission of J1227−6208 is linearly polarised, with a behaviour that does not resemble the rotating vector model, and a further ∼15% of the emission is circularly polarised.
The timing of J1227−6208 suffers from red spin noise and, more prominently, red DM noise. We have implemented a Bayesian nested sampling algorithm to measure the parameters of the DDH timing model, including the spectral modelling of red DM noise, red spin noise, and white noise, and the timing model parameters. We derived six different noise models: three with correlated spin noise and three without it, using different frequency cut-offs in all cases. We find that the red DM noise amplitude at 1400 MHz is almost two orders of magnitude larger than the red spin noise amplitude, and that models with both correlated spin and correlated DM noise with high-frequency cut-offs are favoured by the sampling evidence. Nonetheless, all of the resulting PK parameters are consistent across models within 1σ uncertainty. The Shapiro delay orthometric parameters, h3 and ς, and the periastron advance 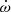 are dominated by the MeerKAT-derived ToAs, while the constraints of the orbital period derivative Ṗb and the projected semi-major axis derivative ẋ are possible only with the accumulated timing baseline.
are dominated by the MeerKAT-derived ToAs, while the constraints of the orbital period derivative Ṗb and the projected semi-major axis derivative ẋ are possible only with the accumulated timing baseline.
We argue that the constraints on Ṗb and ẋ are physical despite their low significance. Ṗb presents a consistent sign across all noise models and is about the same order of magnitude as the combined prediction of the Shklovskii effect given by the DM distance and the proper motion vector and the Galactic acceleration fields (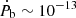 s s−1), therefore implying that a more significant detection will occur in the following years. This detection will also clarify the magnitude of the Shklovskii effect and the Galactic acceleration on the spin period derivative Ṗs. The situation is similar for ẋ, as we predict
s s−1), therefore implying that a more significant detection will occur in the following years. This detection will also clarify the magnitude of the Shklovskii effect and the Galactic acceleration on the spin period derivative Ṗs. The situation is similar for ẋ, as we predict 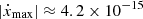 ls s−1 for from the proper motion vector, i = 79 deg and a favourable longitude of ascending node angle Ωa, which is of the same order of magnitude as the timing constraints. The mapping of solutions that implement consistency with the excess ẋ, the proper motion, i and Ωa indicate that the resulting χ2 is indeed sensitive to the location in the Ωa − cos i grid, with a preference for either Ωa = 266 ± 78 deg and i = 79 deg, or Ωa = 86 ± 78 deg and i = 101 deg. This parameter is also likely to get a more significant detection in the following years.
ls s−1 for from the proper motion vector, i = 79 deg and a favourable longitude of ascending node angle Ωa, which is of the same order of magnitude as the timing constraints. The mapping of solutions that implement consistency with the excess ẋ, the proper motion, i and Ωa indicate that the resulting χ2 is indeed sensitive to the location in the Ωa − cos i grid, with a preference for either Ωa = 266 ± 78 deg and i = 79 deg, or Ωa = 86 ± 78 deg and i = 101 deg. This parameter is also likely to get a more significant detection in the following years.
With the noise models from the DDH fits, we measure Mp, Mc, and i by performing a mapping of solutions under the assumption of GR across all noise models, and attest that they are consistent with the PK parameters. In the global fit, the h3 = 3.6 ± 0.5 μs and 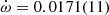 deg yr−1 measurements are 1σ consistent with the assumption of GR, while ς = 0.85 ± 0.05 is 2σ consistent with GR, resulting in Mp = 1.54(15) M⊙, Mc = 1.40(7) M⊙, and i = 78.7 ± 1.2 deg in a conservative uncertainty range that includes all noise models. However, if we exclude the Parkes multibeam observations from the analysis, the median of the periastron advance is reduced to
deg yr−1 measurements are 1σ consistent with the assumption of GR, while ς = 0.85 ± 0.05 is 2σ consistent with GR, resulting in Mp = 1.54(15) M⊙, Mc = 1.40(7) M⊙, and i = 78.7 ± 1.2 deg in a conservative uncertainty range that includes all noise models. However, if we exclude the Parkes multibeam observations from the analysis, the median of the periastron advance is reduced to 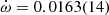 deg yr−1, resulting in 1σ consistency between the three PK parameters and GR, and the mass constraints of Mp = 1.36(20) M⊙, Mc = 1.31(10) M⊙, and i = 79.2 ± 1.1 deg. All of these measurements are within 1σ uncertainty overlap, and they result in the total ranges of possible values of 2.3 < Mt/M⊙ < 3.2, 1.16 < Mp/M⊙ < 1.69, 1.21 < Mc/M⊙ < 1.47 M⊙, and 75.5 < i/deg < 80.3. This wide range of possible values demonstrates that DM variability and its modelling as red DM noise is the main limiting factor of the precision of our timing analysis.
deg yr−1, resulting in 1σ consistency between the three PK parameters and GR, and the mass constraints of Mp = 1.36(20) M⊙, Mc = 1.31(10) M⊙, and i = 79.2 ± 1.1 deg. All of these measurements are within 1σ uncertainty overlap, and they result in the total ranges of possible values of 2.3 < Mt/M⊙ < 3.2, 1.16 < Mp/M⊙ < 1.69, 1.21 < Mc/M⊙ < 1.47 M⊙, and 75.5 < i/deg < 80.3. This wide range of possible values demonstrates that DM variability and its modelling as red DM noise is the main limiting factor of the precision of our timing analysis.
Despite the companion mass uncertainty range extending into the regime of known NS masses, the probability of it being a NS is extremely low due to the very small orbital eccentricity (e = 1.15 × 10−3), which is much more consistent with the massive recycled PSR−CO/ONeMg WD population. The MWD measured in this work is significant as it overlaps with the companion masses measured for three other similar systems. This measurement explores the potential multi-modality of the MWD distribution noted in previous works, which suggests that the MWD distribution is not continuous, but characterised by discrete clumps. Whether WDs with MWD ≳ 1.2 M⊙ are segregated from their 0.7 ≲ M/M⊙ ≲ 1.0 counterparts or not will be decided by further measurements of systems in these mass ranges. Regarding the pulsar mass, given the relatively large spin period of 34 ms, J1227−6208 has likely accreted no more than 0.0045 M⊙ during the recycling process, that a precise measurement of Mp will contribute to the NS birth amass distribution. However, if accretion occurred in a time period significantly shorter than 100,000 years like in the case of PSR J2222−0137 (Cognard et al. 2017), this would imply either super-Eddington accretion or a larger spin-up efficiency than predicted in Tauris et al. (2012).
Future timing of this system will be key for constraining the PK parameters and the mass constraints even further. The most precise ToAs are produced in the 1.3 − 2.2 GHz frequency range due to the balance between the steep spectral index and scattering. However, the presence of red DM noise requires that future observations are taken at higher frequencies, making the 1.7 − 2.6 GHz MeerKAT S-band receiver on the S0 configuration the best observing band in the future. Optical detection of the WD companion may be possible in long exposures with the most powerful optical/infrared telescopes if the system is younger than a few hundred million years, leading to an independent confirmation of the nature of the system, or otherwise to a lower limit of its true age.
Tables available here: https://www.astro.umontreal.ca/~bergeron/CoolingModels/
Acknowledgments
The MeerKAT telescope is operated by the South African Radio Astronomy Observatory (SARAO), which is a facility of the National Research Foundation, an agency of the Department of Science and Innovation. SARAO acknowledges the ongoing advice and calibration of GPS systems by the National Metrology Institute of South Africa (NMISA) and the time space reference systems department of the Paris Observatory. The Parkes radio telescope is part of the Australia Telescope National Facility (ATNF), which is funded by the Australian Government for operation as a National Facility managed by the Commonwealth Scientific and Industrial Research Organisation (CSIRO). We acknowledge the Wiradjuri people as the Traditional Owners of the Observatory site. This work used the OzSTAR national facility at Swinburne University of Technology. OzSTAR is funded by Swinburne University of Technology and the National Collaborative Research Infrastructure Strategy (NCRIS). All authors affiliated with the Max Planck Institute for radioastronomy (MPIfR) acknowledge the continuing valuable support from the Max-Planck Society (MPG). Vivek Venkatraman Krishnan acknowledges financial support from the European Research Council (ERC) starting grant ‘COMPACT’ (grant agreement number: 101078094). Alessandro Ridolfi is supported by the Italian National Institute for Astrophysics (INAF) through an “IAF - Astrophysics Fellowship in Italy” fellowship (Codice Unico di Progetto: C59J21034720001; Project “MINERS”). We acknowledge the team of P789 and P1032 Parkes observers and the SARAO operators for the data acquisition. We give our sincere thanks to the anonymous referee and Dr. Huanchen Hu for their comments on this article.
References
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Bailes, M., Jameson, A., Abbate, F., et al. 2020, PASA, 37, e028 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, E. D. 2018, IAU Symp., 337, 175 [NASA ADS] [Google Scholar]
- Bates, S. D., Lorimer, D. R., & Verbiest, J. P. W. 2013, MNRAS, 431, 1352 [Google Scholar]
- Bates, S. D., Thornton, D., Bailes, M., et al. 2015, MNRAS, 446, 4019 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [Google Scholar]
- Berthereau, A., Guillemot, L., Freire, P. C. C., et al. 2023, A&A, 674, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyles, J., Lynch, R. S., Ransom, S. M., et al. 2013, ApJ, 763, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Caiazzo, I., Burdge, K. B., Fuller, J., et al. 2021, Nature, 595, 39 [CrossRef] [Google Scholar]
- Camilo, F., Lyne, A. G., Manchester, R. N., et al. 2001, ApJ, 548, L187 [NASA ADS] [CrossRef] [Google Scholar]
- Carpano, S., Haberl, F., Maitra, C., & Vasilopoulos, G. 2018, MNRAS, 476, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Cognard, I., Freire, P. C. C., Guillemot, L., et al. 2017, ApJ, 844, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M. 2004, ASP Conf. Ser., 317, 211 [NASA ADS] [Google Scholar]
- Cruces, M., Champion, D. J., Li, D., et al. 2021, MNRAS, 508, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Damour, T., & Deruelle, N. 1986, Ann. Inst. Henri Poincaré Phys. Théor, 44, 263 [Google Scholar]
- Damour, T., & Taylor, J. H. 1991, ApJ, 366, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Damour, T., & Taylor, J. H. 1992, Phys. Rev. D, 45, 1840 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Boyles, J., Lorimer, D. R., et al. 2013, ApJ, 770, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, R. T., & Bailes, M. 2001, ApJ, 553, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, R. T., Hobbs, G. B., & Manchester, R. N. 2006, MNRAS, 372, 1549 [Google Scholar]
- Faulkner, A. J., Stairs, I. H., Kramer, M., et al. 2004, MNRAS, 355, 147 [Google Scholar]
- Fonseca, E., Cromartie, H. T., Pennucci, T. T., et al. 2021, ApJ, 915, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., & Wex, N. 2010, MNRAS, 409, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gautam, T., Freire, P. C. C., Batrakov, A., et al. 2022, A&A, 668, A187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregoris, D., & Ong, Y. C. 2023, Ann. Phys., 452, 169287 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y. J., Freire, P. C. C., Guillemot, L., et al. 2021, A&A, 654, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655 [Google Scholar]
- Hobbs, G., Manchester, R. N., Dunning, A., et al. 2020, PASA, 37, e012 [NASA ADS] [CrossRef] [Google Scholar]
- Hollands, M. A., Tremblay, P. E., Gänsicke, B. T., et al. 2020, Nat. Astron., 4, 663 [CrossRef] [Google Scholar]
- Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [Google Scholar]
- Hu, H., Kramer, M., Wex, N., Champion, D. J., & Kehl, M. S. 2020, MNRAS, 497, 3118 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belfiore, A., Stella, L., et al. 2017, Science, 355, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A., Chakrabarty, D., van Kerkwijk, M. H., Kulkarni, S. R., & Kaplan, D. L. 2006, ApJ, 640, L183 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A., Bailes, M., Ord, S. M., Knight, H. S., & Hotan, A. W. 2007, ApJ, 656, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Jonas, J., & MeerKAT Team 2016, MeerKAT Science: On the Pathway to the SKA, 1 [Google Scholar]
- Kaplan, D. L., Boyles, J., Dunlap, B. H., et al. 2014, ApJ, 789, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Knispel, B., Eatough, R. P., Kim, H., et al. 2013, ApJ, 774, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Kopeikin, S. M. 1996, ApJ, 467, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Stairs, I. H., Venkatraman Krishnan, V., et al. 2021, MNRAS, 504, 2094 [CrossRef] [Google Scholar]
- Krishnakumar, M. A., Maan, Y., Joshi, B. C., & Manoharan, P. K. 2019, ApJ, 878, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Külebi, B., Jordan, S., Nelan, E., Bastian, U., & Altmann, M. 2010, A&A, 524, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kundu, A., & Mukhopadhyay, B. 2012, Mod. Phys. Lett. A, 27, 1250084 [CrossRef] [Google Scholar]
- Lazarus, P., Tauris, T. M., Knispel, B., et al. 2014, MNRAS, 437, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Löhmer, O., Mitra, D., Gupta, Y., Kramer, M., & Ahuja, A. 2004, A&A, 425, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy (Cambridge University Press) [Google Scholar]
- Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, J. G., Stovall, K., Freire, P. C. C., et al. 2015, ApJ, 812, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, J. G., Gentile, P., Freire, P. C. C., et al. 2019, ApJ, 881, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, A., & Nandy, M. K. 2021, R. Soc. Open Sci., 8, 210301 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, J. W., Freire, P. C. C., Berezina, M., et al. 2020, MNRAS, 499, 4082 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Mickaliger, M. B., Lorimer, D. R., Boyles, J., et al. 2012, ApJ, 759, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, D. R., Caiazzo, I., Heyl, J., et al. 2023, ApJ, 956, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Oswald, L. S., Karastergiou, A., Posselt, B., et al. 2021, MNRAS, 504, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., & Freire, P. 2016, ARA&A, 54, 401 [Google Scholar]
- Pallanca, C., Lanzoni, B., Dalessandro, E., et al. 2013, ApJ, 773, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Parent, E., Kaspi, V. M., Ransom, S. M., et al. 2019, ApJ, 886, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [Google Scholar]
- Pshirkov, M. S., Dodin, A. V., Belinski, A. A., et al. 2020, MNRAS, 499, L21 [Google Scholar]
- Radhakrishnan, V., & Cooke, D. J. 1969, Astrophys. Lett., 3, 225 [NASA ADS] [Google Scholar]
- Rickett, B. J. 1977, ARA&A, 15, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Ridolfi, A., Freire, P. C. C., Gupta, Y., & Ransom, S. M. 2019, MNRAS, 490, 3860 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., Narayan, R., & Blandford, R. 1986, MNRAS, 220, 19 [NASA ADS] [Google Scholar]
- Sarkissian, J. M., Carretti, E., & van Straten, W. 2011, in Am. Inst. Phys. Conf. Ser., 1357, 351 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shamohammadi, M., Bailes, M., Freire, P. C. C., et al. 2023, MNRAS, 520, 1789 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, I. I. 1964, Phys. Rev. Lett., 13, 789 [Google Scholar]
- Shklovskii, I. S. 1970, Sov. Astron., 13, 562 [NASA ADS] [Google Scholar]
- Splaver, E. M., Nice, D. J., Arzoumanian, Z., et al. 2002, ApJ, 581, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Staveley-Smith, L., Wilson, W. E., Bird, T. S., et al. 1996, PASA, 13, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, C. M., Bassa, C. G., Cooper, S., et al. 2020, MNRAS, 492, 5878 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & Sennels, T. 2000, A&A, 355, 236 [NASA ADS] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2023, Physics of Binary Star Evolution. From Stars to X-ray Binaries and Gravitational Wave Sources (Princeton University Press) [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2012, MNRAS, 425, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Langer, N., & Podsiadlowski, P. 2015, MNRAS, 451, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Kramer, M., Freire, P. C. C., et al. 2017, ApJ, 846, 170 [Google Scholar]
- Taylor, J. H., & Weisberg, J. M. 1989, ApJ, 345, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Thorsett, S. E., & Chakrabarty, D. 1999, ApJ, 512, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Thorsett, S. E., Arzoumanian, Z., McKinnon, M. M., & Taylor, J. H. 1993, ApJ, 405, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Tomaschitz, R. 2018, Phys. Stat. Mech. Appl., 489, 128 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 2019, IAU Symp., 346, 1 [NASA ADS] [Google Scholar]
- van Haasteren, R., Levin, Y., McDonald, P., & Lu, T. 2009, MNRAS, 395, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- van Kerkwijk, M. H., & Kulkarni, S. R. 1999, ApJ, 516, L25 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Voisin, G., Cognard, I., Freire, P. C. C., et al. 2020, A&A, 638, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S. C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J., Freire, P. C. C., Kramer, M., Shao, L., & Wex, N. 2022, CQG, 39, 11LT01 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional mass constraints plots
 |
Fig. A.1. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the global fit and under the assumption of the Ls noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
 |
Fig. A.2. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the global fit and under the assumption of the VCs noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
 |
Fig. A.3. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the MeerKAT+UWL fit and under the assumption of the VCs noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
 |
Fig. A.4. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the MeerKAT+UWL fit and under the assumption of the Ls noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
 |
Fig. A.5. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the MeerKAT+UWL fit and under the assumption of the Cs noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
All Tables
Data reduction, model fit, spin, DM, and astrometric parameters from the DDH TEMPO2/TempoNEST fits.
Orbital Keplerian and PK parameters from the DDH TEMPO2/TempoNEST fits, and mass constraints from the DDGR χ2 mapping fits.
Constraints on the PK parameters and the component masses from the MeerKAT+UWL fits.
All Figures
 |
Fig. 1. Time-integrated pulse profiles of J1227−6208 as recorded with the different receivers (from left to right: Parkes multibeam, MeerKAT L-band, Parkes UWL, and MeerKAT S-band). The top plots show the intensity of the integrated emission, while the bottom plots are frequency-resolved. Only the MeerKAT L-band and Parkes UWL data sets are flux calibrated. The plots were made with PSRCHIVE/psrplot. |
| In the text | |
 |
Fig. 2. Frequency evolution of the scattering and mean flux density, and their modelling. Top: pulse profiles of J1227−6208 at f = 902 MHz and f = 1397 MHz as is seen by the MeerKAT L-band receiver (left and middle plots), and at f = 2388 MHz as is seen by the Parkes UWL receiver (right plot). The data (cyan lines) is shown against the best model (red dashes, fitted with equation 1) and the fit residuals (blue lines). The fit parameters τs and Δb from equation (1), and the mean flux density Fm are quoted on each profile. Bottom: measurements of Δτ and Fm at each frequency on the MeerKAT L-band and Parkes UWL profiles (dots with uncertainties), and the best fits of the power laws (2) and (3) (red lines). The data points are displayed accounting for the error factors στ and σF, and the relevant τGHz, α, FGHz, and β values are quoted in the legend. |
| In the text | |
 |
Fig. 3. Parkes UWL (top) and MeerKAT L-band (bottom) polarisation profiles of J1227−6208, RM-corrected at 47.3 rad cm−1. Total flux density (black lines), linearly polarised intensity (red lines), circularly polarised intensity (blue lines), and the PA angle (black error bars) are plotted as a function of the pulse phase. |
| In the text | |
 |
Fig. 4. Timing residuals under the assumption of the Cs noise model. Top: ToA residuals as a function of MJD, showing flat, Gaussian residuals. Middle: ToA residuals as a function of the orbital phase (orbital position from the ascending node, true anomaly + periastron) excluding the h3 and ς parameters from the timing model, showing the full amplitude of the Shapiro delay signal. The continuous blue line depicts the predicted Shapiro delay described by h3 = 3.45 μs and ς = 0.858. Bottom: same as the middle plot, but the orthometric Shapiro delay parameters are now included in the model, resulting in flat, Gaussian residuals. |
| In the text | |
 |
Fig. 5. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model. The constraints have been derived in the global fit and under the assumption of the Cs noise model (Table 2). Central plots: two-dimensional constraints on the Mc − cos i and Mc − Mp spaces. The solid coloured lines represent the nominal values of the PK parameters, the dashed coloured lines their 1σ limits, and the solid black lines the 1σ and 3σ limits from DDGR. The shaded grey area in the right plot is the region excluded by the mass function (i > 90 deg). Corner plots: marginalised one-dimensional probability densities for Mp, Mc, and cos i from DDGR χ2 mapping, showcasing the median value (solid black line) and the 31.4%, 47.4%, and 49.9% percentiles on both sides (shaded areas under the curve). |
| In the text | |
 |
Fig. 6. Constraints on the orbital orientation from the χ2 mapping of DDGR solutions consistent with Eq. (11). The constraints have been derived in the global fit and assuming the Cs noise model (Table 2) Central plots: two-dimensional constraints in the Ωa − cos i space. The solid contours represent the explored space (cos i > 0), while the dashed contours are derived from symmetries in eq. (11) (cos i < 0). Corner plots, top: marginalised one-dimensional probability densities for cos i, showcasing the median value (solid black lines) and the 31.4%, 47.4%, and 49.9% percentiles (shaded areas under the curve, blue for cos i > 0 and purple for cos i < 0). Corner plot, right: marginalised one-dimensional probability densities for Ωa from cos i > 0 and cos i < 0 (solid and dashed lines, respectively) and the addition of both (shaded cyan area). |
| In the text | |
 |
Fig. 7. Comparison of orbital and mass constraints between Galactic pulsar−WD systems, Galactic DNS systems, and J1227−6208. For J1227−6208, the extended uncertainties from the global (red star, Table 3) and the MeerKAT+UWL fits (magenta cross, Table 6) are quoted. Left: orbital eccentricity against companion mass from recycled binary pulsars in the Galactic field, distinguished by the nature of their companions. For systems without timing mass measurements (“Undetermined” in the legend), the lower constraints on the minimum and median Mc values derived from the mass function (assuming i = 90, 60 deg) are plotted. Right: WD mass against pulsar mass of PSR−WD systems in the Galactic field. References: constraints on systems besides J1227−6208 are taken from https://www3.mpifr-bonn.mpg.de/staff/pfreire/NS_masses.html and references therein, and from Camilo et al. (2001) (PSR J1435−6100), Cruces et al. (2021) (PSR J2338+4818), Edwards & Bailes (2001) (PSR J1157−5112), Gautam et al. (2022) (PSR J1952+2630), Jang et al., in prep. (PSR J1439−5501), Martinez et al. (2019) (PSR J0709+0458), Parent et al. (2019) (PSR J1932+1756), and Tan et al. (2020) (PSR J1658+3630). |
| In the text | |
 |
Fig. 8. ToA uncertainty against observing frequency for each telescope receiver. The highest and lowest frequencies of the Parkes multibeam and MeerKAT S-band data sets are biased upwards because the signal drops off at the edge of the bands (see Fig. 1). |
| In the text | |
 |
Fig. A.1. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the global fit and under the assumption of the Ls noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
| In the text | |
 |
Fig. A.2. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the global fit and under the assumption of the VCs noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
| In the text | |
 |
Fig. A.3. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the MeerKAT+UWL fit and under the assumption of the VCs noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
| In the text | |
 |
Fig. A.4. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the MeerKAT+UWL fit and under the assumption of the Ls noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
| In the text | |
 |
Fig. A.5. Mass and inclination angle constraints from the DDH PK measurements and the χ2 mapping with the DDGR model, both from the MeerKAT+UWL fit and under the assumption of the Cs noise model (Table 2). Contours have been drawn following the same principles as in Fig. 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



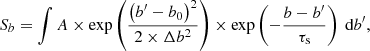
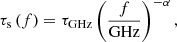
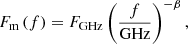
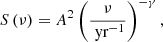
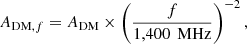
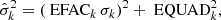
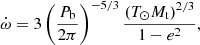
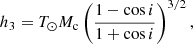
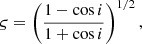
![$$ \begin{aligned} \frac{\dot{P}_\text{b}}{P_\text{b}}=-\left( \frac{\dot{D}}{D}\right)_\text{Shkl}-\left(\frac{\dot{D}}{D}\right)_\text{Gal}=\frac{1}{c} \left[ |\,\boldsymbol{\mu }\,|^{2} d+\boldsymbol{K_0}(\boldsymbol{a}_\text{PSR}-\boldsymbol{a}_\text{SSB}) \right] \text{,}\end{aligned} $$](/articles/aa/full_html/2024/10/aa50724-24/aa50724-24-eq18.gif)