| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A213 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202449722 | |
| Published online | 09 October 2024 | |
Full non-LTE spectral line formation
III. The case of a two-level atom with broadened upper level
1
Indian Institute of Astrophysics,
Koramangala,
Bengaluru
560034,
India
2
Université de Toulouse, UPS-Observatoire Midi-Pyrénées, Cnrs, Cnes, Irap,
Toulouse,
France
3
Cnrs, Institut de Recherche en Astrophysique et Planétologie,
14 av. E. Belin,
31400
Toulouse,
France
4
LESIA, Observatoire de Paris, Université PSL, Sorbonne Université, Université Paris Cité, CNRS,
Meudon,
France
★ Corresponding author; sampoorna@iiap.res.in
Received:
24
February
2024
Accepted:
10
August
2024
In the present paper we consider the full nonlocal thermodynamic equilibrium (non-LTE) radiation transfer problem. This formalism allows us to account for deviation from equilibrium distribution of both the radiation field and the massive particles. In the present study, two-level atoms with broadened upper level represent the massive particles. In the absence of velocity-changing collisions, we demonstrate the analytic equivalence of the full non-LTE source function with the corresponding standard non-LTE partial frequency redistribution (PFR) model. We present an iterative method based on operator splitting techniques that can be used to numerically solve the problem at hand. We benchmark it against the standard non-LTE transfer problem for a two-level atom with PFR. We illustrate the deviation of the velocity distribution function of excited atoms from the equilibrium distribution. We also discuss the dependence of the emission profile and the velocity distribution function on elastic collisions and velocity-changing collisions.
Key words: line: formation / line: profiles / radiation mechanisms: general / radiative transfer / methods: numerical / stars: atmospheres
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In a series of two papers (Paletou & Peymirat 2021; Paletou et al. 2023), we revisited the problem of so-called “full” nonlocal thermodynamic equilibrium (non-LTE) radiation transfer originally formulated by Oxenius (1986). This formalism accounts not only for deviation of the radiation field from the Planckian equilibrium distribution, but also for the deviation of the velocity distribution of massive particles from the Maxwellian equilibrium distribution. While Paletou & Peymirat (2021) focused on re-formulating the basic elements of full non-LTE formalism using standard notations, Paletou et al. (2023) considered its numerical solution for the case of coherent scattering (CS) in the frame of the atom, which corresponds to scattering on a two- level atom with (putative) infinitely sharp energy levels. In the present paper, we further extend these works to scattering on a two-level atom with an infinitely sharp lower level and a more realistic broadened upper level (which may already be suitable for the modeling of strong resonance lines).
The full non-LTE radiation transfer formalism is based on the kinetic theory of particles and photons (Oxenius 1986). In particular, it is founded on a semi-classical description of light scattering in spectral lines. As described in Hubeny & Mihalas (2014), the semi-classical picture combines concepts from classical theory and the more exact quantum mechanical description of the problem at hand, thereby providing a very intuitive and compelling approach to the problem. Clearly, the semi-classical picture is not a self-consistent theory and therefore contains a number of not so well defined concepts. However, it has been very successful in describing several of the line-scattering mechanisms in astrophysical conditions (see the above-cited books for details). For the problem considered in this paper, the poorly defined concepts from the physical point of view are those related to the rate of velocity-changing collisions and a clear distinction between these and elastic collisions. However, despite this, we introduce separate rates for the elastic and velocitychanging collisions. Although it is not completely clear how they would be evaluated for actual cases, and indeed a proper quantum-mechanical definition of these quantities is uncertain, their introduction and usage in the present paper is fully in line with the semi-classical picture that we adopt here. Indeed this semi-classical theory provides a way to treat the problem, namely including a self-consistent determination of the velocity distribution of atoms in the upper level of the transition. For a more detailed outline of the semi-classical picture, we refer the reader to Hubeny & Mihalas (2014, see their Chapter 10, specifically pp. 291–294).
In the full non-LTE formalism, the kinetic equation for the velocity distribution of the massive particles (namely the atoms or ions and free electrons) and that for the photons (namely the radiative transfer equation for the intensity of the radiation field) have to be formulated and solved simultaneously and self-consistently. As the velocity distribution functions (VDFs) of the atomic levels are not known a priori, the absorption and emission profiles that enter the radiative transfer equation need to be obtained by convolving the corresponding atomic quantities with the VDFs, wherein the velocity of the massive particle is measured in the observer’s frame. An evaluation of the need to use this formalism has so far remained unexplored because of the numerical complexity involved in its implementation. The aim of the present series of papers is to clarify this question through detailed numerical calculations. For this purpose, we have embarked upon developing suitable numerical techniques to implement this formalism. As a first step, Paletou et al. (2023) considered the two-distribution problem, namely the intensity of the radiation field and the VDF of the excited atoms are the only two distributions that need to be determined simultaneously and self-consistently. In other words, two-level atoms represent the massive particles, with their lower (ground) level exhibiting the equilibrium Maxwellian distribution (Oxenius 1986; Paletou & Peymirat 2021). Furthermore, stimulated emission was neglected, and the free electrons that are responsible for inelastic collisions between the two levels of the atom were also assumed to obey the equilibrium Maxwellian distribution. In the present paper, we continue to consider this two-distribution problem, with an important difference being that the lower level of the atom continues to be infinitely sharp, while the upper level is broadened. In this case, the atomic absorption profile is a Lorentzian and the atomic emission profile already depends on the radiation field. This introduces some difficulties in the numerical solution of the corresponding full non-LTE problem, namely we need to accurately compute Voigt-like function, which involves a Lorentzian function in its integrand (Paletou et al. 2020). Following a method developed previously by Bommier (1997a,b), in the present paper we present a simple and efficient technique to compute such an integral involving Lorentzian function.
The basic equations of the two-distribution problem are detailed in Paletou et al. (2023, see also Paletou & Peymirat 2021). Hence, we do not repeat them here, and only the equations relevant to the two-level atom with broadened upper level are discussed. The outline of the present paper is as follows. In Section 2, we discuss the explicit forms of the absorption and emission profiles for a two-level atom with a broadened upper level. The full non-LTE source function is presented in Section 3, wherein we also demonstrate the analytic equivalence with the corresponding standard non-LTE source function in the absence of velocity-changing collisions. In Section 4, we describe and clarify the three different types of collisions (namely the inelastic, elastic, and velocity-changing collisions) considered in this paper. In Section 5, we present the numerical method to solve the full non-LTE problem considered here. Our numerical results are illustrated and discussed in Section 6. Conclusions are presented in Section 7.
2 The absorption and emission profiles
As in the standard non-LTE formalism (see e.g., Hubeny & Mihalas 2014, who also adopt the semi-classical picture), the absorption and emission profiles (and also the frequency redistribution functions) are first determined in the atomic rest frame, and then transformed to the observer’s frame to account for the Doppler motion of the atoms in a stellar atmosphere. In the standard non-LTE formalism with complete frequency redistribution (CFR), the VDF of all the atomic levels is assumed to be the equilibrium Maxwellian distribution, while when partial frequency redistribution (PFR) is included, this assumption is limited to only the lower level. However, the standard non-LTE formalism with PFR does not provide access to the VDF of the upper level. This is provided by the full non-LTE formalism. Therefore, in this section we discuss the absorption and emission profiles first in the atomic frame and then in the observer’s frame.
For the case of a two-level atom with a broadened upper level, the atomic absorption profile is given by (see Appendix B.2 of Oxenius 1986, see also Paletou & Peymirat 2021)
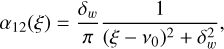 (1)
(1)
where ξ is the photon frequency in the atomic frame, ν0 is the line-center frequency, and the damping width δw = (A21 + Q1 + QE)/(4π), with A21 being the Einstein coefficient for spontaneous emission or radiative de-excitation rate, QI the inelastic collisional de-excitation rate (denoted as C21 in Paletou & Peymirat 2021), and QE the total elastic collision rate.
The absorption profile in the observer’s frame is given by
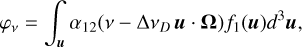 (2)
(2)
where u is the atomic velocity1 normalized to the thermal velocity (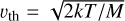 , with k being the Boltzmann constant, T the temperature, and M the mass of the atom), Ω is the propagation direction of the ray, and ΔνD is the Doppler width. In this paper, we do not account for bulk velocities resulting from mass motion of the massive particles. In other words only the Doppler motion of atoms is taken into account, consequently the corresponding velocities are in the nonrelativistic regime, wherein only the photon frequency is subject to Lorentz transformation between the atomic rest frame and the observer’s frame, while the photon direction remains unchanged (i.e., aberration is neglected; see also Eqs. (2.4.3a)–(2.4.3e) in page 54 of Oxenius 1986). Therefore, in the above equation, we used the Fizeau–Doppler relationship (see Eq. (9) of Paletou & Peymirat 2021), which relates the frequencies in the atomic frame (ξ) and the observer’s frame (ν). Furthermore, f1 represents the VDF of the lower level of the atom. In the weak radiation field regime, f1 can be assumed to be the equilibrium distribution, namely a Maxwellian fM (Oxenius 1986; Paletou & Peymirat 2021). With this assumption, it is straightforward to show that the resulting absorption profile in the observer’s frame is a normalized Voigt function φ(x) = H(a, x), where a = δw/ΔνD and x = (ν − ν0)/ΔνD, with ν0 being the line-center frequency. In the following subsections, we discuss the emission profile first in the atomic frame (see Section 2.1) and then in the observer’s frame (see Section 2.2).
, with k being the Boltzmann constant, T the temperature, and M the mass of the atom), Ω is the propagation direction of the ray, and ΔνD is the Doppler width. In this paper, we do not account for bulk velocities resulting from mass motion of the massive particles. In other words only the Doppler motion of atoms is taken into account, consequently the corresponding velocities are in the nonrelativistic regime, wherein only the photon frequency is subject to Lorentz transformation between the atomic rest frame and the observer’s frame, while the photon direction remains unchanged (i.e., aberration is neglected; see also Eqs. (2.4.3a)–(2.4.3e) in page 54 of Oxenius 1986). Therefore, in the above equation, we used the Fizeau–Doppler relationship (see Eq. (9) of Paletou & Peymirat 2021), which relates the frequencies in the atomic frame (ξ) and the observer’s frame (ν). Furthermore, f1 represents the VDF of the lower level of the atom. In the weak radiation field regime, f1 can be assumed to be the equilibrium distribution, namely a Maxwellian fM (Oxenius 1986; Paletou & Peymirat 2021). With this assumption, it is straightforward to show that the resulting absorption profile in the observer’s frame is a normalized Voigt function φ(x) = H(a, x), where a = δw/ΔνD and x = (ν − ν0)/ΔνD, with ν0 being the line-center frequency. In the following subsections, we discuss the emission profile first in the atomic frame (see Section 2.1) and then in the observer’s frame (see Section 2.2).
2.1 The atomic emission profile
The explicit form of the atomic emission profile in the absence of velocity-changing collisions is given in Eq. (B.2.26) of Oxenius (1986) and in Eq. (4.32) of Hubeny et al. (1983a). Although the notations used in these publications are somewhat different, it can be readily shown that both the mentioned expressions are identical. In the presence of velocity-changing collisions, the atomic emission profile is given in Hubeny et al. (1983b, see their Section 4.1). In their notation, this atomic emission profile is given by
![${\eta _{21}}(\xi ,\tau ) = {{{B_{12}}I_{12}^*{j_{121}}(\xi ,\tau ) + \left[ {{S_{12}} + {\gamma _2}\left( {{n_2}/{n_1}} \right)} \right]{r_{12}}(\xi )} \over {{B_{12}}I_{12}^* + {S_{12}} + {\gamma _2}\left( {{n_2}/{n_1}} \right)}},$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq4.png) (3)
(3)
where B12 is the Einstein coefficient for radiative absorption, S12 is the collisional excitation rate, γ2 is the velocity-changing collision rate, n1 and n2 are the number density of the atoms in lower and upper levels, respectively, and τ is the line center optical depth. In Eq. (3), the generalized redistribution function r12(ξ) = α12(ξ) (see Eq. (6.3.55) of Oxenius 1986), the quantity 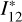 is given by
is given by
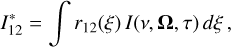 (4)
(4)
with 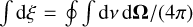 . In the above equations, I(ν, Ω, τ) is the specific intensity, and r121(ξ′,ξ) is the generalized atomic redistribution function (Hubeny et al. 1983a), which describes the joint probability of absorbing a photon of frequency ξ′ and spontaneously re-emitting a photon of frequency ξ.
. In the above equations, I(ν, Ω, τ) is the specific intensity, and r121(ξ′,ξ) is the generalized atomic redistribution function (Hubeny et al. 1983a), which describes the joint probability of absorbing a photon of frequency ξ′ and spontaneously re-emitting a photon of frequency ξ.
We note that the quantity 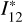 introduced by Hubeny et al. (1983a,b) is the same as I12 introduced in Eq. (B.2.20) of Oxenius (1986). In the notations of Paletou & Peymirat (2021, see also Paletou et al. 2023), we readily identify
introduced by Hubeny et al. (1983a,b) is the same as I12 introduced in Eq. (B.2.20) of Oxenius (1986). In the notations of Paletou & Peymirat (2021, see also Paletou et al. 2023), we readily identify 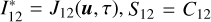 , and γ2 = QV2. Therefore, we rewrite Eq. (3) in the present notations as follows:
, and γ2 = QV2. Therefore, we rewrite Eq. (3) in the present notations as follows:
![${\eta _{21}}(\xi ,\tau ) = {{{B_{12}}{J_{12}}({\bf{u}},\tau ){j_{121}}(\xi ,\tau ) + \left[ {{C_{12}} + {Q_V}\left( {{n_2}/{n_1}} \right)} \right]{\alpha _{12}}(\xi )} \over {{B_{12}}{J_{12}}({\bf{u}},\tau ) + {C_{12}} + {Q_V}\left( {{n_2}/{n_1}} \right)}},$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq11.png) (6)
(6)
where J12(u, τ) is defined as (see e.g., Eq. (8) of Paletou & Peymirat 2021)
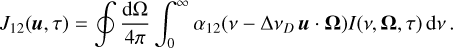 (7)
(7)
Also, in our notations, the quantity j121(ξ, τ) takes the form
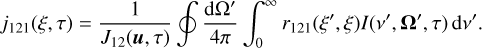 (8)
(8)
The atomic frequencies appearing in the above equation are related to their counterparts in the observer’s frame through the Fizeau-Doppler relationship, namely, ξ′ = ν′ − ΔνD u • Ω′ and ξ = ν − ΔvD u • Ω.
2.2 The emission profile in the observer’s frame
The emission profile in the observer’s frame is given by
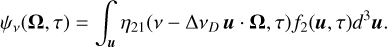 (9)
(9)
The VDF of the upper level, including the velocity-changing collisions, is given in Eq. (3) of Paletou et al. (2023). However, for the purpose of deriving the emission profile in the observer’s frame, we use the VDF as given in Eq. (19) of Paletou & Peymirat (2021), namely
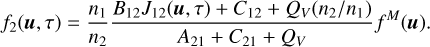 (10)
(10)
Substituting Eqs. (6) and (10) into Eq. (9), the latter takes the form
![$\eqalign{ & {\psi _v}({\bf{\Omega }},\tau ) = \int_u {\left\{ {{{{n_1}} \over {{n_2}}}\left[ {{{{B_{12}}{J_{12}}(u,\tau ){j_{121}}(\xi ,\tau ) + {C_{12}}{\alpha _{12}}(\xi )} \over {{A_{21}} + {C_{21}} + {Q_V}}}} \right]} \right.} \cr & & \left. { + {{{Q_V}{\alpha _{12}}(\xi )} \over {{A_{21}} + {C_{21}} + {Q_V}}}} \right\}{f^M}({\bf{u}}){d^3}{\bf{u}}. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq16.png) (11)
(11)
Following Section 5 of Paletou & Peymirat (2021), we assume LTE values for n1 (namely, 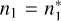 ), and introduce the normalized populations
), and introduce the normalized populations 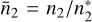 . Substituting for j121 (cf. Eq. (8)), the first term in the curly brackets of the above equation can be rewritten as
. Substituting for j121 (cf. Eq. (8)), the first term in the curly brackets of the above equation can be rewritten as
![${1 \over {{{\bar n}_2}}}{1 \over {1 + \zeta }}\left[ {\varepsilon {\alpha _{12}}(\xi ) + (1 - \varepsilon )\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_0^\infty {{r_{121}}} \left( {{\xi ^\prime },\xi } \right)I\left( {{v^\prime },{{\bf{\Omega }}^\prime },\tau } \right){\rm{d}}{v^\prime }} \right],$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq19.png)
where we make use of Eqs. (23)–(27) of Paletou & Peymirat (2021), and I(ν′, Ω′, τ) is now normalized to the Planck function in the Wien limit. In the above expression,
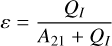 (12)
(12)
is the usual collisional destruction probability and the quantity
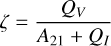 (13)
(13)
represents the amount of velocity-changing collisions. Similarly, the last term in the curly brackets of Eq. (11) reduces to ζα12(ξ)/(1 + ζ). Using Eq. (29) of Paletou & Peymirat (2021), the emission profile can be rewritten as
![$\eqalign{ & {\psi _v}({\bf{\Omega }},\tau ) = \int_{\bf{u}} {{f^M}} ({\bf{u}}){d^3}{\bf{u}}\left\{ {{\zeta \over {1 + \zeta }}{\alpha _{12}}(\xi ) + {1 \over {1 + \zeta }}{1 \over {\varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau )}}} \right. \cr & & \left. { \times \left[ {\varepsilon {\alpha _{12}}(\xi ) + (1 - \varepsilon )\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_0^\infty {{r_{121}}} \left( {{\xi ^\prime },\xi } \right)I\left( {{v^\prime },{{\bf{\Omega }}^\prime },\tau } \right){\rm{d}}{v^\prime }} \right]} \right\}, \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq22.png) (14)
(14)
In the above equation, 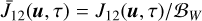 , with 𝓑W denoting the Planck function in the Wien limit. Substituting for J12(u,τ) from Eq. (7) and using Eq. (2), it can be easily shown that
, with 𝓑W denoting the Planck function in the Wien limit. Substituting for J12(u,τ) from Eq. (7) and using Eq. (2), it can be easily shown that
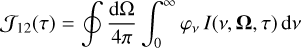 (16)
(16)
is simply the frequency integrated mean intensity (also referred to as the “CFR scattering integral”) appearing in the standard non-LTE problem. Furthermore, we may readily identify that ʃ r121(ξ′,ξ) fM (u)d3 u = R121(ν′, Ω′,ν, Ω), namely the angledependent generalized redistribution function in the observer’s frame. Furthermore, using Eq. (2), we obtain the emission profile in the observer’s frame as
![$\eqalign{ & {\psi _v}({\bf{\Omega }},\tau ) = {\zeta \over {1 + \zeta }}{\varphi _v} + {1 \over {1 + \zeta }}{1 \over {\varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau )}} \cr & \,\,\,\,\,\,\,\,\, \times \left[ {\varepsilon {\varphi _v} + (1 - \varepsilon )\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_0^\infty {{R_{121}}} \left( {{v^\prime },{{\bf{\Omega }}^\prime },v,{\bf{\Omega }}} \right)I\left( {{v^\prime },{{\bf{\Omega }}^\prime },\tau } \right){\rm{d}}{v^\prime }} \right]. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq26.png) (17)
(17)
We note that the emission profile given above is the same as that originally derived in Hubeny et al. (1983b, see their Eq. (4.15)), although we present it here in a slightly different form and also use the notations adopted in this paper. Furthermore, Hubeny & Cooper (1986) demonstrated that the emission profile derived from the semi-classical picture of Hubeny et al. (1983b) fully agrees with that derived from the quantum mechanical approach of Cooper et al. (1982).
In the present paper, we consider the angle-averaged emission profile, namely
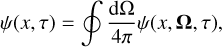 (18)
(18)
wherein we have transformed the real frequency ν into the nondi- mensional frequency x. The resulting angle-averaged emission profile is given by
![$\eqalign{ & \psi (x,\tau ) = {\zeta \over {1 + \zeta }}\varphi (x) + {1 \over {1 + \zeta }}{1 \over {\varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau )}} \cr & \,\,\,\,\, \times \left[ {\varepsilon \varphi (x) + (1 - \varepsilon )\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_{ - \infty }^{ + \infty } {{R_{121}}} \left( {{x^\prime },x} \right)I\left( {{x^\prime },{\Omega ^\prime },\tau } \right){\rm{d}}{x^\prime }} \right]. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq28.png) (19)
(19)
For a two-level atom with a broadened upper level and in the absence of velocity-changing collisions, the generalized redistribution function R121 is given by the observer’s frame counterpart of the usual atomic frame PFR function derived by Omont et al. (1972, see Milkey & Mihalas 1973 and Mihalas 1978 for the corresponding observer’s frame expression). In the presence of velocity-changing collisions, the explicit form of the PFR function R121 has been derived in Hubeny & Cooper (1986, see their Eqs. (3.15) and (3.16)) starting from the quantum mechanical approach of Cooper et al. (1982). In the present paper, we adopt this PFR function, which in our notation takes the following form:
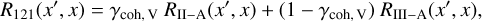 (20)
(20)
where RII–A and RIII–A are the type-II and type-III angle-averaged PFR functions of Hummer (1962), respectively, and the coherence fraction is given by
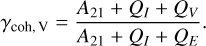 (21)
(21)
Clearly, in the absence of velocity-changing collisions, the coherence fraction as well as the PFR function become identical to those derived by Omont et al. (1972).
To clearly bring out the departure of the emission profile from CFR, we may rewrite Eq. (19) as
![$\eqalign{ & \psi (x,\tau ) = \varphi (x) + {1 \over {1 + \zeta }}{{(1 - \varepsilon )} \over {\varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau )}} \cr & \quad \times \left[ {\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_{ - \infty }^{ + \infty } {{R_{121}}} \left( {{x^\prime },x} \right)I\left( {{x^\prime },{{\bf{\Omega }}^\prime },\tau } \right){\rm{d}}{x^\prime } - {{\cal J}_{12}}(\tau )\varphi (x)} \right]. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq31.png) (22)
(22)
The above equation can easily be deduced from Eq. (19) by simply adding unity to and subtracting unity from ζ as it appears in the numerator of the first term of that equation3.
3 The source function
In the full non-LTE formalism, the source function for a two- level atom with a broadened upper level is of the form (see Eq. (7) of Paletou et al. 2023)
![$S(x,\tau ) = \left[ {\varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau )} \right]\left[ {{{\psi (x,\tau )} \over {\varphi (x)}}} \right],$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq32.png) (23)
(23)
where ψ(x, τ) is given by Eq. (19) or Eq. (22) and φ(x) is the normalized Voigt function.
In the absence of velocity-changing collisions (namely, ζ = 0), the source function (23) reduces to the corresponding expression for the standard non-LTE PFR model for a two-level atom with a broadened upper level. To demonstrate this, we first note that the emission profile for ζ = 0 (cf. Eq. (19)) takes the following form:
![$\eqalign{ & \psi (x,\tau ) = {1 \over {\varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau )}} \cr & \quad \times \left[ {\varepsilon \varphi (x) + (1 - \varepsilon )\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_{ - \infty }^{ + \infty } {{R_{121}}} \left( {{x^\prime },x} \right)I\left( {{x^\prime },{\Omega ^\prime },\tau } \right){\rm{d}}{x^\prime }} \right]. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq33.png) (24)
(24)
Substituting Eq. (24) into Eq. (23), we readily obtain
![$S(x,\tau ) = \varepsilon + (1 - \varepsilon )\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_{ - \infty }^{ + \infty } {\left[ {{{{R_{121}}\left( {{x^\prime },x} \right)} \over {\varphi (x)}}} \right]} I\left( {{x^\prime },{{\bf{\Omega }}^\prime },\tau } \right){\rm{d}}{x^\prime },$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq34.png) (25)
(25)
thereby establishing the equivalence of the source function derived from the full and standard non-LTE models. This is an important result that justifies the use of numerically relatively simple standard non-LTE formalism in the absence of velocity-changing collisions.
In the presence of velocity-changing collisions, the source function is obtained by substituting Eq. (22) into Eq. (23), namely
![$\eqalign{ & S(x,\tau ) = \varepsilon + (1 - \varepsilon ){{\cal J}_{12}}(\tau ) + {{(1 - \varepsilon )} \over {1 + \zeta }} \cr & \quad \times \left\{ {\oint {{{{\rm{d}}{\Omega ^\prime }} \over {4\pi }}} \int_{ - \infty }^{ + \infty } {\left[ {{{{R_{121}}\left( {{x^\prime },x} \right)} \over {\varphi (x)}}} \right]} I\left( {{x^\prime },{{\bf{\Omega }}^\prime },\tau } \right){\rm{d}}{x^\prime } - {{\cal J}_{12}}(\tau )} \right\}. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq35.png) (26)
(26)
We recall that, as in Paletou & Peymirat (2021) and Paletou et al. (2023), the source function and intensity are normalized to the Planck function in the Wien limit. When velocity-changing collisions are significant (namely, ζ >> 1), the third term in Eq. (26) is negligible and the source function tends to the CFR source function.
4 A clarification regarding collisions
In the present paper, we consider three types of collisions:
inelastic collisions,
elastic collisions, and
velocity-changing collisions.
For the massive particles (two-level atoms in the present paper), we distinguish between
the “internal variables” (the energy and quantum numbers of the levels), and
the “external variables” (the position and velocity).
The inelastic collisions are those responsible for collisional transitions between the lower and upper levels; they enter the kinetic (or statistical equilibrium) equation for atoms as inducing transitions, which further lead to the ε factor in the radiative transfer equation. In an inelastic collision, the internal variables change, whereas the external variables may or may not change.
The elastic collisions do not modify the level populations. They are responsible for line broadening. In a strictly elastic collision, both the internal and external variables remain unchanged before and after the collision. In a weakly elastic collision, the internal variables, namely the energy value of the level and the quantum numbers, may change (e.g., collisions between fine structure levels, between hyperfine structure levels, or between Zeeman sublevels in the presence of a weak magnetic field), while the external variables remain unchanged. It is also important to note that elastic collisions between degenerate Zeeman sublevels also lead to changes in the internal variables (as they change the magnetic quantum number before and after collisions, although not the atomic energy). Indeed, in the present paper, we consider isolated spectral lines and do not consider magnetic fields. Thus, the Zeeman sublevels are degenerate. If an elastic collision changes the Zeeman sublevel (namely the magnetic quantum number M is changed to M′ , with M ≠ M′), then it will have a polarizing or, more frequently, depolarizing effect (we note that polarization results from unequal populations between the Zeeman sublevels). On the contrary, if an elastic collision does not change the Zeeman sublevel (namely, M → M), then it only broadens the line, namely it is only a linebroadening collision. As clarified in Sahal-Bréchot & Bommier (2019), line broadening and depolarizing collisions are different, and both contribute to the line broadening and hence to the elastic collision rate QE .
In addition to contributing to line broadening, the elastic collisions take part in the frequency redistribution of the scattered radiation in the line as shown by, for example, Omont et al. (1972, see also Bommier 1997a,b; Sahal-Bréchot & Bommier 2019). In particular, they are responsible for CFR in the atomic frame. In the full non-LTE formalism, both these effects of elastic collisions are included following the works of Omont et al. (1972, see also Appendix B.2 of Oxenius 1986) and Hubeny & Cooper (1986) in the absence and presence of velocity-changing collisions, respectively. This is done by including QE in the total damping width of the absorption profile (see Eq. (1)) and using the appropriate PFR function of Omont et al. (1972) and Hubeny & Cooper (1986) for the generalized redistribution function (see Eq. (20)).
On the other hand, collisions where the internal variables remain unchanged while the external variables – such as atomic velocity (in particular its modulus) – are changed are called velocity-changing collisions. We believe that, as the internal variable is unchanged, Oxenius (1986) refers to velocitychanging collisions as elastic. However, as the atomic velocity is changed during the collision, we feel that it may not be appropriate to refer to this type of collision as elastic. Indeed Landi Degl’Innocenti & Landolfi (2004) do not refer to them as elastic. Also, most likely, the velocity-changing collisions represented by QV include both elastic and inelastic contributions. Furthermore, these types of collisions are close collisions or strong collisions with a small impact parameter. For the two-distribution problem considered in this paper, the velocity-changing collisions enter the kinetic equation for excited atoms as a relaxation term, as they are responsible for relaxing the VDF of the upper level to its equilibrium distribution function. This relaxation term is of the form given in Eq. (7) of Paletou & Peymirat (2021, see also Eq. (6.3.12) in page 167 of Oxenius 1986).
In general, a given collision can modify both the internal and external variables. Those collisions that modify only the internal variables are most likely long-range collisions (although short-range collisions can also modify the internal variables), and those collisions that modify the external variable (namely velocity) are most likely strong short-range collisions. In this respect, QV is a part of QE (see Sections 4.1.1 and 4.1.2 of Bommier 2016a, see also Section II(a) of Hubeny & Cooper 1986). Even if velocity-changing collisions are part of the linebroadening collisions, the method of calculation of QV is not the same as the method of calculation of QE, because QE addresses the atomic internal variables, while QV addresses the atomic external variables, although the colliding particles are the same. The velocity-changing collisions are atom–atom collisions, while the elastic and inelastic collisions may also be caused by electron–atom collisions (in addition to atom–atom collisions).
Hubeny & Cooper (1986) show that when lower state interaction is negligibly small (namely when the collisional scattering amplitude of the lower level is much smaller than that of the upper level), the total elastic collision rate QE associated with the upper level can be decomposed into two parts, one corresponding to only phase changes without change in velocity (denoted qE) and the other corresponding to both phase and velocity changes (denoted ν by Hubeny & Cooper 1986). Such a decomposition is well suited for the resonance lines to which our present full non-LTE approach is applicable. Therefore, following Hubeny & Cooper (1986), we write QE = qE + QV after identifying their ν as our QV. Furthermore, Hubeny & Cooper (1986) show that qE = αQE and QV = (1 − α) QE with α in the range of 0 to 1. These authors also give an estimate of (1 − α). When m << M (with m denoting the mass of the perturber and M denoting the mass of the radiator), they show that (1 − α) = (m/M)2, and when m ~ M, they estimate (1 − α) = 0.1.
It is known that the phase-changing elastic collision rate qE can be obtained from Van der Waals approximation or using the more precise semi-classical theory developed in the 1990s by Anstee, Barklem, and O’Mara (the so-called ABO theory; see e.g., Barklem & O’Mara 1998; Barklem et al. 1998, and references cited therein). Regarding the velocity-changing collision rate QV, a precise calculation of the corresponding collision cross-section will depend on the atomic species under consideration. Landi Degl’Innocenti & Landolfi (2004) give only a rough order of magnitude for this cross-section (on the order of 10 to 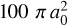 , with a0 being the Bohr radius). Specific calculations would be necessary to achieve greater precision. A laboratory study was carried out by Brechignac et al. (1978), who measured the effects of the velocity-changing collisions between the excited Kr atoms and the He and/or Ar perturbers. Here the authors show that a “hard-sphere” collision model is suitable for interpreting their experimental measurements. According to this model, the collisional cross-section is given by π(rA + rB)2, where rA and rB are the radii of the atoms participating in the collision. The atomic radii for any atomic species (including also the ions) are listed by Allen (1973, see page 45); the authors used these to compute the collisional cross-section for Kr*–He and Kr*–Ar collisions. In the present paper, all three collisional rates are assumed to be input parameters, and hence we do not compute them using the collisional dynamics. Consequently, we do not determine the velocity distribution of the colliders.
, with a0 being the Bohr radius). Specific calculations would be necessary to achieve greater precision. A laboratory study was carried out by Brechignac et al. (1978), who measured the effects of the velocity-changing collisions between the excited Kr atoms and the He and/or Ar perturbers. Here the authors show that a “hard-sphere” collision model is suitable for interpreting their experimental measurements. According to this model, the collisional cross-section is given by π(rA + rB)2, where rA and rB are the radii of the atoms participating in the collision. The atomic radii for any atomic species (including also the ions) are listed by Allen (1973, see page 45); the authors used these to compute the collisional cross-section for Kr*–He and Kr*–Ar collisions. In the present paper, all three collisional rates are assumed to be input parameters, and hence we do not compute them using the collisional dynamics. Consequently, we do not determine the velocity distribution of the colliders.
In order to evaluate the importance of velocity-changing collisions in a stellar atmosphere, Landi Degl’Innocenti & Landolfi (2004) provide a way to estimate the critical density of the perturbers or colliders (see their Eq. (13.6) in page 694). This is done by comparing an order-of-magnitude rate for velocitychanging collisions (given by nqv, where n is the number density of the perturbers, q is the cross section for velocity-changing collisions, and v is the average velocity of perturbers relative to the atom) with the rate for spontaneous emission (namely, A21). The density for which these two rates are nearly the same gives the critical density: 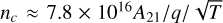 (in units of cm−3). Here, A21 is in units of 107 s−1, temperature T is in units of 104 K, and q is in units of
(in units of cm−3). Here, A21 is in units of 107 s−1, temperature T is in units of 104 K, and q is in units of 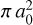 . For densities greater than this critical density, velocity-changing collisions are significant. Landi Degl’Innocenti & Landolfi (2004) estimate q to be in a range4 that is rarely larger than 10 to 100. Using this, Bommier (2016a) provided an estimate of the critical density of colliders, which is in the order of 1020 cm−3. We recalculated this estimate for the identical set of parameters used by this latter author (namely, A21 = 1). However, in Section 4.1.1 of Bommier (2016a), she does not mention the temperature value that she uses. Hence, we have chosen T = 0.5 here. We find the critical density nc to be in the range of 1.103 × 1016 to 1.103 × 1015 cm−3. This is about 4 to 5 orders of magnitude smaller than the density mentioned in Bommier (2016a). As the collisions with neutral hydrogen are expected to be the dominant source of both elastic and velocitychanging collisions in a stellar atmosphere, we compare nc with the hydrogen density in the solar photosphere, which is on the order of 1017 cm−3 . Clearly, the velocity-changing collisions are important in the lower solar atmosphere, and hence have to be accounted for. Furthermore, the collisional destruction probability ε (which depends on the inelastic collision rate C21 or QI; see Eq. (12)) also becomes non-negligible in the lower solar atmosphere (see e.g., Fig. 2c of Anusha et al. 2010). Finally, as discussed in Section 4.1.1 of Bommier (2016a), the elastic collision rate QE is also significant in the lower solar atmosphere. Thus, the present full non-LTE formalism is applicable in the lower solar atmosphere when velocity-changing collisions are important. In the upper solar atmosphere, where velocitychanging collisions are negligible, one may use the numerically relatively simple standard non-LTE PFR formalism.
. For densities greater than this critical density, velocity-changing collisions are significant. Landi Degl’Innocenti & Landolfi (2004) estimate q to be in a range4 that is rarely larger than 10 to 100. Using this, Bommier (2016a) provided an estimate of the critical density of colliders, which is in the order of 1020 cm−3. We recalculated this estimate for the identical set of parameters used by this latter author (namely, A21 = 1). However, in Section 4.1.1 of Bommier (2016a), she does not mention the temperature value that she uses. Hence, we have chosen T = 0.5 here. We find the critical density nc to be in the range of 1.103 × 1016 to 1.103 × 1015 cm−3. This is about 4 to 5 orders of magnitude smaller than the density mentioned in Bommier (2016a). As the collisions with neutral hydrogen are expected to be the dominant source of both elastic and velocitychanging collisions in a stellar atmosphere, we compare nc with the hydrogen density in the solar photosphere, which is on the order of 1017 cm−3 . Clearly, the velocity-changing collisions are important in the lower solar atmosphere, and hence have to be accounted for. Furthermore, the collisional destruction probability ε (which depends on the inelastic collision rate C21 or QI; see Eq. (12)) also becomes non-negligible in the lower solar atmosphere (see e.g., Fig. 2c of Anusha et al. 2010). Finally, as discussed in Section 4.1.1 of Bommier (2016a), the elastic collision rate QE is also significant in the lower solar atmosphere. Thus, the present full non-LTE formalism is applicable in the lower solar atmosphere when velocity-changing collisions are important. In the upper solar atmosphere, where velocitychanging collisions are negligible, one may use the numerically relatively simple standard non-LTE PFR formalism.
5 The numerical method of solution
We solve the full non-LTE transfer problem for the case of a two-level atom with broadened upper level using a modified version of the accelerated lambda iteration (ALI) method developed by Paletou & Auer (1995) for the corresponding standard PFR model. Here we present this ALI method in some detail, focusing on the changes brought about by the full non-LTE nature of the problem at hand. As in the standard PFR model, the source function given by Eq. (26) is iterated until convergence using the approximate lambda operator (ALO), which is chosen to be the diagonal of the full lambda operator (Olson et al. 1986).
In the one-dimensional planar atmosphere considered here, the radiation field is axisymmetric. Thus, the specific intensity depends only on the inclination θr of the ray about the atmospheric normal. In other words I(x, Ω, τ) = I(x,µ,τ), where µ = cos θr. Thus, the formal solution of the radiative transfer equation can be stated as
![${I_{x\mu }} = {\Lambda _{x\mu }}\left[ {{S_x}} \right],$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq39.png) (27)
(27)
where for notational convenience we have suppressed the dependence on optical depth, and the dependence on frequency and angular variables appear as subscript. Moreover, Λxµ denotes the frequency and angle-dependent integral operator. Given an estimate of the source function at the nth iteration, the iterative scheme will be given by
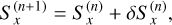 (28)
(28)
where 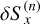 is the iterative correction on the source function. Using the operator splitting technique (Cannon 1973), namely
is the iterative correction on the source function. Using the operator splitting technique (Cannon 1973), namely 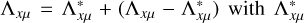 being the ALO - chosen here to be the diagonal of the full lambda operator after Olson et al. (1986) –, and following a rather standard procedure (Paletou & Auer 1995, see also Sampoorna & Trujillo Bueno 2010), we arrive at the following expression for the iterative correction:
being the ALO - chosen here to be the diagonal of the full lambda operator after Olson et al. (1986) –, and following a rather standard procedure (Paletou & Auer 1995, see also Sampoorna & Trujillo Bueno 2010), we arrive at the following expression for the iterative correction:
![$\eqalign{ & \delta S_x^{(n)} - (1 - \varepsilon )\int_0^\infty {{\varphi _x}} \Lambda _x^*\left[ {\delta S_x^{(n)}} \right]{\rm{d}}x - {{(1 - \varepsilon )} \over {(1 + \zeta )}} \cr & \,\,\,\,\,\, \times \left\{ {\int_0^\infty {\left[ {{{{R_{121}}\left( {{x^\prime },x} \right)} \over {{\varphi _x}}}} \right]} \Lambda _{{x^\prime }}^*\left[ {\delta S_{{x^\prime }}^{(n)}} \right]{\rm{d}}{x^\prime } - \int_0^\infty {{\varphi _x}} \Lambda _x^*\left[ {\delta S_x^{(n)}} \right]{\rm{d}}x} \right\} \cr & \,\,\,\,\, = r_x^{(n)}. \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq43.png) (29)
(29)
In order to deduce the above equation, we used Eq. (16) and also the fact that, for a static atmosphere, the radiation field is symmetric about the line-center, meaning that only half the profile can be considered. In the above equation, the frequency-dependent ALO is given by
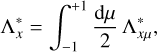 (30)
(30)
and the residual 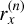 has the form
has the form
![$\eqalign{ & r_x^{(n)} = \varepsilon + (1 - \varepsilon ){\cal J}_{12}^{(n)}(\tau ) + {{(1 - \varepsilon )} \over {1 + \zeta }} \cr & \,\,\,\, \times \left\{ {\int_0^\infty {\left[ {{{{R_{121}}\left( {{x^\prime },x} \right)} \over {{\varphi _x}}}} \right]} {\Lambda _{{x^\prime }}}\left[ {S_{{x^\prime }}^{(n)}} \right]{\rm{d}}{x^\prime } - {\cal J}_{12}^{(n)}(\tau )} \right\} - S_x^{(n)}, \cr} $](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq46.png) (31)
(31)
where 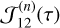 and the integral involving the angle-averaged PFR function are obtained from the formal solver using the nth iteration of the source function. To this end, we used the short-characteristic method of Olson & Kunasz (1987, see also Lambert et al. 2016). At each iteration, the system of linear equations (29) can be resolved using either a frequency-by- frequency (FBF) method or a core-wing method (Paletou & Auer 1995). In the following subsections, we briefly describe both these methods for the full non-LTE case considered here.
and the integral involving the angle-averaged PFR function are obtained from the formal solver using the nth iteration of the source function. To this end, we used the short-characteristic method of Olson & Kunasz (1987, see also Lambert et al. 2016). At each iteration, the system of linear equations (29) can be resolved using either a frequency-by- frequency (FBF) method or a core-wing method (Paletou & Auer 1995). In the following subsections, we briefly describe both these methods for the full non-LTE case considered here.
5.1 Frequency-by-frequency method
For a given depth point, the system of Equation (29) consists of Nx number of linear equations, with Nx representing the number of frequency points. In matrix form, this system of linear equations can be written as
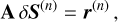 (32)
(32)
where at each depth point, δS(n) and r(n) are vectors of length Nx and A is a matrix of dimension Nx × Nx. Following Paletou & Auer (1995), we solve Eq. (32) using the LU decomposition scheme (see e.g., Press et al. 1986). As the FBF method involves matrix manipulations, such as inversion and multiplication, it is somewhat computationally expensive when compared to the core-wing method presented in the following subsection.
5.2 Core-wing method
Based on the behavior of the type-II PFR function of Hummer (1962), a core-wing method was proposed by Paletou & Auer (1995) that allowed the computation of a system of linear equation (29) through simple algebraic manipulations, thereby considerably reducing the computational costs involved. In this method, the type-II PFR function is approximated by CFR in the line core and CS in the wings for the computation of the source function corrections. An extension of this method for the type-III PFR function was given by Fluri et al. (2003), wherein this function is approximated by CFR in the line core and set to zero in the wings. We apply both the above-mentioned core-wing approximations to the R121 function appearing in Eq. (29). Furthermore, in Eq. (29) we make the approximation of computing the frequency integral involving the absorption profile φx only in the line core and set it to zero in the wings. This approximation is similar to the core-wing approximation made for the type-III PFR function. With these approximations, we can easily deduce the following core-wing approximation for Eq. (29):
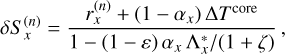 (33)
(33)
where αx is the core-wing separation coefficient given by
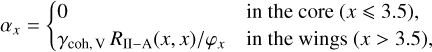 (34)
(34)
which can be easily evaluated as described in Paletou & Auer (1995, see their Section 5.1). As in Sampoorna & Trujillo Bueno (2010), we find that when the elastic collision rate QE and/or velocity-changing collision rate QV are large, the approximation of setting the type-III PFR function and the 𝒥12(τ) integral to zero in the wings leads to convergence problems. In such cases, we use the CFR approximation throughout the line profile. This typically occurs for QE /A21 > 1 and/or QV /A21 > 1, when the medium is optically thick or semi-infinite. We verified that both the core-wing and FBF methods give identical results. Therefore, all the solutions presented in this paper are computed with the core-wing method.
5.3 Numerical computation of 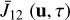
The full non-LTE formalism gives us access to the VDF f2 of the upper level, which depends on 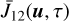 (see Eq. (3) of Paletou et al. 2023). In the case of a two-level atom with broadened upper level, the computation of
(see Eq. (3) of Paletou et al. 2023). In the case of a two-level atom with broadened upper level, the computation of 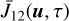 is numerically more complex than the CS case considered in Paletou et al. (2023). This is because, in the case of CS, the integrand in
is numerically more complex than the CS case considered in Paletou et al. (2023). This is because, in the case of CS, the integrand in 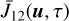 contained a delta function (see their Eq. (1)), while the integrand in the present case involves a Lorentzian function (see Eq. (7)). Integrals involving Lorentzian are known to be notoriously difficult to evaluate due to the sharp peaked nature of the Lorentzian function. Therefore, we need to devise a suitable method to evaluate such integrals accurately. Here we describe such a numerical method following Bommier (1997a,b).
contained a delta function (see their Eq. (1)), while the integrand in the present case involves a Lorentzian function (see Eq. (7)). Integrals involving Lorentzian are known to be notoriously difficult to evaluate due to the sharp peaked nature of the Lorentzian function. Therefore, we need to devise a suitable method to evaluate such integrals accurately. Here we describe such a numerical method following Bommier (1997a,b).
In terms of the adimensional frequency x, the quantity 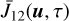 is given by (cf. Eq. (7))
is given by (cf. Eq. (7))
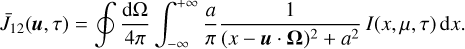 (36)
(36)
The dot product of the velocity vector u with the ray direction Ω is evaluated using Eq. (9) of Paletou et al. (2023), which requires us to construct the corresponding quadratures for polar angles θu and θr . As the radiation field is axisymmetric, it is sufficient to construct the quadrature directly for the azimuth difference (φr − φu). The dot product u • Ω can take both positive and negative values. Thus, the frequency integral in Eq. (36) has to include the entire range from −∞ to +∞. The intensity for the negative x values can be easily obtained from the corresponding positive values using the symmetry relation. We used 13 Gauss- Legendre nodes for the direction cosines corresponding to both the ray and velocity vector in the [0,1] domain, and a quadrature made up of 20 equally spaced points for their azimuth difference (φr − φu) in the [0,2π] domain. For each pair of θr, θu, and (φr −φu), we first perform the frequency integral and then the angular integration.
Evaluating integrals involving Lorentzian function poses accuracy issues (see e.g., Fig. 1 of Paletou et al. 2020). In the present paper, we apply a method originally developed by Bommier (1997a,b) to compute the angle-dependent type-III PFR function of Hummer (1962), which is known to involve an integration over the Lorentzian function (see e.g., Eq. (61) of Bommier 1997b). Following the method used by this latter author, we computed the frequency integral in Eq. (36) using the trapezoidal method with varying integration steps. The integration begins from the center of the Lorentzian (namely, at x = u • Ω), and proceeds symmetrically thereafter. The integration step is originally set as one-tenth of the damping width a and is multiplied by 1.05 at each step of the integration (a geometric progression). As discussed above, the quantity u • Ω is evaluated as described in Paletou et al. (2023, see their Eq. (9)). Thus, the integration needs to be performed for each value of u and γ (which is the cosine of the angle between the velocity vector and the ray direction). As the frequency integration step size is varied as described above, the intensity computed on a standard frequency grid used for radiative transfer needs to be interpolated at every step of the frequency integration. We use the spline interpolation for this purpose.
However, the method described above to compute 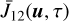 is somewhat slow. For a typical case of a semi-infinite atmosphere with 10 points per decade, 65 frequency points, and the angular quadrature mentioned above, it requires about 67 minutes of computing time on a Intel(R) Xeon(R) Gold 5122 processor with 3.6GHz, 10.4 GT/s clock speed. Clearly, computing this quantity and subsequently the VDF f2 of the upper level at every iteration would be computationally very expensive. However, as the ALI method described above does not require us to compute
is somewhat slow. For a typical case of a semi-infinite atmosphere with 10 points per decade, 65 frequency points, and the angular quadrature mentioned above, it requires about 67 minutes of computing time on a Intel(R) Xeon(R) Gold 5122 processor with 3.6GHz, 10.4 GT/s clock speed. Clearly, computing this quantity and subsequently the VDF f2 of the upper level at every iteration would be computationally very expensive. However, as the ALI method described above does not require us to compute 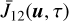 and f2 at every iteration (see Eq. (29)), we compute these quantities once the ALI solution has converged, which typically takes 15 seconds of computing time.
and f2 at every iteration (see Eq. (29)), we compute these quantities once the ALI solution has converged, which typically takes 15 seconds of computing time.
 |
Fig. 1 Validation of our iterative method for the full non-LTE transfer problem (compare with Fig. 3c of Hummer 1969). The normalized source function is displayed as a function of frequency at different line center optical depths within the atmosphere: namely at τ = 0, 1, 10, 100, 103, and 104. For comparison, we also show the corresponding CFR source function (constant with frequency) as dashed lines. |
6 The numerical results
In this section, we first validate our iterative method by reproducing the benchmark result of Hummer (1969), and then illustrate the new quantities, namely the VDF of the upper level and the emission profiles together with source function with and without elastic and/ or velocity-changing collisions. We also illustrate a comparison of the normally emergent intensity profiles for the cases of a two-level atom with infinitely sharp upper and lower levels considered in Paletou et al. (2023), and a two- level atom with broadened upper level considered in this paper, along with the corresponding CFR standard non-LTE models. For the numerical studies presented here, we consider a onedimensional, isothermal, semi-infinite, planar atmosphere with a total optical thickness at line center of T = 106 and є = 10−4. The radiative width of the upper level parameterized as aR = A21 /(4πΔνD) is chosen to be 10−3; it is related to the total damping parameter via a = aR[1 + (QI + QE)/A21]. Unless otherwise mentioned, both the rates qE/A21 and QV/A21 are set to zero.
6.1 Validation
For the atmospheric model described above, the standard non- LTE source function for the RII–A PFR model is illustrated in Fig. 3c of Hummer (1969). In order to validate our numerical method, we reproduced this benchmark result in our Figure 1, which displays the source function S (x, τ) for different optical depths as a function of frequency. These solutions are computed with the ALI method presented in Section 5 together with the core-wing method (cf. Section 5.2) for calculating the source function corrections. A comparison of our Fig. 1 with Fig. 3c of Hummer (1969), clearly shows that our numerical method satisfactorily reproduces the benchmark solutions, thereby validating our iterative method. This is expected, as the source function derived from full non-LTE formalism is equivalent to the corresponding standard non-LTE PFR model when velocitychanging collisions are neglected (cf. Section 3).
Unlike the standard non-LTE PFR model considered by Hummer (1969), the full non-LTE model considered here gives access to the VDF of the upper level. The emission profile on the other hand can be obtained from both the above-mentioned formalisms; however, it is rarely shown in the literature. Therefore, in this paper, we illustrate both the emission profile and the VDF of the upper level. Figures 2 and 3 exhibit respectively the ratios ψ(x,τ)/φ(x) and f2(u, τ)/fM(u) for different line center optical depths within the atmosphere. Figure 3 in the present paper is equivalent to Fig. 3 in Paletou et al. (2023), but for the case of scattering on a two-level atom with naturally broadened upper level. For ease of comparison, in Figs. 2 and 3, we also show as dashed lines the corresponding quantities at τ = 1 for CS in the atomic frame (namely the case of a two-level atom with infinitely sharp lower and upper levels) considered in Paletou et al. (2023).
For the standard non-LTE CFR model, the emission and the absorption profiles are identical (Hubeny & Mihalas 2014). Thus, to demonstrate the departure of the emission profile from CFR, we plot in Fig. 2 the ratio ψ(x,τ)/φ(x) at different line center optical depths within the atmosphere. Clearly, the emission profile departs from CFR for x > 1. As the optical depth increases, this departure from CFR decreases. Furthermore, the differences in ψ(x,τ)/φ(x) between the present and CS cases are significant (compare green solid and gray dashed lines in Fig. 2).
Because we consider an angle-averaged emission profile here, the VDF of the excited atom depending only on the modulus of velocity u is illustrated. As in the CS case, deviation from the Maxwellian distribution is significant for u > 2 and for optical depths close to the surface, which then decreases with increasing optical depth (compare the Fig. 3 here with Fig. 3 of Paletou et al. 2023). However, unlike the CS case, the overpopulation of the excited level for u > 2 is relatively small in the present case of a two-level atom with a naturally broadened upper level (compare green solid and gray dashed lines in Fig. 3). We note here that a departure of the VDF of the upper level from the Maxwellian distribution was also obtained by Bommier (2016b, see her Section 5.3) through a self-consistent solution of the statistical equilibrium equations for each velocity class of the velocity-dependent atomic density matrix elements and the radiative transfer equation for the polarized radiation in the case of Na I D1 and D2 lines. This departure can be attributed to the radiative processes between the interacting atom and the incident radiation field, which is spectrally structured (i.e., nonflat) within the radiative width of the upper level.
Figure 4 displays a comparison of the normally emergent intensity for the CS and the present case of a two-level atom with a radiatively broadened upper level. We also plot the corresponding CFR cases, namely for the damping parameter a = 0 and a = 10−3 . While the CS and the corresponding CFR (a = 0) cases nearly coincide (compare orange and green lines in Fig. 4), significant differences are seen in the wings for x > 3 between the CS and PFR cases (compare green and blue lines). Moreover, the PFR intensity differs significantly from the corresponding CFR intensity for x > 2 (compare blue and red lines in Fig. 4). In particular, we recover the lowering/dip of emergent intensity in the wings before finally reaching the continuum level, a well-known effect of PFR (RII–A ).
 |
Fig. 2 Departure of emission profile ψ(x, τ) from CFR for the case of scattering on a two-level atom with radiatively broadened upper level. Different lines correspond to ψ(x,τ)/φ(x) at different line-center optical depths within the atmosphere (indicated in the figure legend). For comparison ψ(x, τ = 1)/φ(x), corresponding to scattering on a two-level atom with infinitely sharp upper and lower levels (namely CS in the atomic frame), is shown as a dashed line. |
 |
Fig. 3 Departure of the VDF of the naturally broadened upper level (f2(u, τ)) of a two-level atom from the Maxwellian equilibrium distribution f M(u) at different line center optical depths within the atmosphere (indicated in the figure legend). For comparison, the corresponding quantity at τ = 1 for the CS case is shown as a dashed line. There is clearly a greater overpopulation of f2 at large u in the CS case than in the present case of a two-level atom with a naturally broadened upper level. |
6.2 Impact of velocity-changing collisions (QV/A21)
Unlike the standard non-LTE PFR formalism, the full non-LTE formalism of Oxenius (1986) takes into account the influence of velocity-changing collisions characterized here by QV/A21. To highlight the impact of velocity-changing collisions, here we consider the extreme limit of a = 0, corresponding to the case of strong collisions (in the kinetic sense; see Hubeny & Cooper 1986). When a = 0, the total elastic collision rate QE is entirely provided by QV, which leads to simultaneous phase and velocity changes. In this respect, QV here actually represents the effective velocity-changing collision rate. Figures 5–7 display the influence of QV/A21 on the source function, emission profile, and the VDF of the upper level at optical depth τ = 1, respectively. The model parameters used are the same as those for Figures 1–3, but we now vary QV/A21 from 0 to 50 in much the same way as ζ is varied in Section 7 of Paletou et al. (2023) for the CS case. As we have chosen є = 10−4, the ratio QI/A21 is relatively small, such that ζ (see Eq. (13)) is nearly the same as QV/A21. Thus, our Fig. 5 is equivalent to Fig. 4 of Paletou et al. (2023), but for the case of the broadened upper level. However, unlike the CS case, the frequency grid is much more extended in the present case. This is to take into account the fact that the absorption profile is now a Voigt function with rather broad damping wings. As in the CS case, the source function at τ = 1 approaches the CFR limit with increasing values of QV/A21 or ζ (see Fig. 5). This is also in general the trend exhibited by the emission profile (see Fig. 6) and the VDF of the upper level (see Fig. 7). As discussed in Section 4, the velocity-changing collisions are non-negligible in the lower solar atmosphere, wherein QV/A21 or ζ may take moderate values when full non-LTE formalism has to be adopted for an accurate determination of the source function (cf. Fig. 5) and the radiation field.
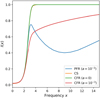 |
Fig. 4 Comparison of normally emergent intensity computed using the full non-LTE model for a two-level atom with infinitely sharp levels (CS) and radiatively broadened upper level (PFR) and standard non-LTE model with CFR. We note that the intensity for CS and the corresponding CFR (a = 0) case nearly coincide. |
6.3 Impact of phase-changing elastic collisions (qE/A21)
The phase-changing elastic collisions that are normally accounted for in spectral line formation theory through their effect on broadening the spectral line and leading to CFR in the atomic frame are characterized by qE /A21. By considering a = 1, here we present its impact on the source function, emission profile, and the VDF of the upper level at τ = 1. When a = 1, the total elastic collision rate QE is entirely contributed by the phase-changing collisions, which are weak collisions (Hubeny & Cooper 1986). The dependence of the source function on qE /A21 is known from the standard non-LTE PFR formalism. With an increase in qE /A21, the source function approaches the CFR limit, which is indeed the case as seen from Fig. 8. This is also true for the emission profile, namely ψ(x, τ) → φ(x) with increasing values of the phase-changing elastic collision rate (see Fig. 9). Regarding the VDF of the upper level, its departure from the Maxwellian distribution initially increases until qE/A21 = 0.5 and then decreases with further increase in qE/A21 (see Fig. 10).
 |
Fig. 5 Influence of velocity-changing collisions on the normalized source function at τ = 1. As expected, with increasing values of QV/A21, the source function approaches the CFR limit, which is shown as a horizontal dashed line. |
 |
Fig. 6 Dependence of the ratio of emission to absorption profile at τ = 1 (namely, ψ(x,τ = 1)/φ(x)) on velocity-changing collisions. As expected, the emission profile approaches the CFR limit, namely ψ(x, τ) → φ(x) with increasing values of QV /A21. |
7 Conclusions
Full non-LTE radiative transfer, although formulated in the 1980s (Oxenius 1986), has remained largely unexplored because of the complexity involved in its numerical implementation (see however Borsenberger et al. 1986, 1987; Atanackovič et al. 1987, who considered the limiting case of a pure Doppler profile). More recently, Paletou & Peymirat (2021) reconsidered this problem, and expressed its basic elements in terms of the prevailing standard notations in this field of research. Paletou et al. (2023) then made a numerical implementation of this formalism for the case of CS in the atomic frame using the usual numerical iterative methods that are in use for the standard non-LTE transfer problem. In the present paper, we solve, for the first time, a full non-LTE radiative transfer problem considering the case of a two-level atom with infinitely sharp lower level and broadened upper level. For this purpose, we applied, after suitable modifications, the well-known operator perturbation methods developed for standard PFR models (Paletou & Auer 1995, see also Sampoorna & Trujillo Bueno 2010; Lambert et al. 2016). We validate our iterative method against the standard non-LTE transfer problem with an angle-averaged RII–A PFR function (Hummer 1962, 1969). We illustrate the new quantities, namely the emission profile and the VDF of the upper level, and also make a comparison with the case of a two-level atom with infinitely sharp lower and upper levels (namely the CS case considered in Paletou et al. 2023). We clearly demonstrate the influence of phase-changing elastic collisions (qE , which lead to spectral line broadening and CFR in the atomic frame) and the velocity-changing collisions (QV) on the source function, emission profile, and the VDF of the upper level. In particular, we show that for moderate values of QV/A21 (or equivalently ζ; see Eq. (13)), one has to adopt the full non-LTE formalism presented here to accurately determine the source function (see Fig. 5) and the radiation field. Results presented in this paper may serve as benchmarks for future works on this topic (and will be made available upon request to the corresponding author).
In the present paper, we show that in the absence of velocitychanging collisions, the full non-LTE formalism is equivalent to the standard non-LTE PFR formalism, thereby validating the use of the numerically relatively simple standard non-LTE PFR formalism. However, unlike this latter, the full non-LTE formalism can also account for the velocity-changing collisions, which may become significant in the lower solar atmosphere (see Section 4). Given this, the accurate determination of velocity-changing collision rates for astrophysical applications becomes crucial. Until such calculations become available, the hard-sphere collision model provides an excellent way to determine the cross-section for velocity-changing collisions.
For computational simplicity, in the present paper we consider the angle-averaged emission profile (cf. Eq. (18)), and thereby the angle-averaged redistribution functions (cf. Eq. (20)). A near-future goal would be to relax this assumption, which would allow us to explore the angular dependence of the VDF of the excited level.
The next crucial step will be to consider the full non-LTE transfer problem for multilevel atoms. In particular we intend to take this work forward by considering a three-level atom, which would involve dealing with three distributions, one for the photon and two more for the excited atoms. Further, another important step would be to relax the usual assumption of Maxwellian velocity distribution for the free electrons.
 |
Fig. 7 Dependence of the ratio of the VDF of the upper level to the Maxwellian distribution at τ = 1 (namely, f2(u,τ = 1)/fM(u)) on velocity-changing collisions. With increasing values of QV/A21, the departure of the f2 from Maxwellian initially increases for QV /A21 = 0.25 in the regime of intermediate velocities and then decreases. |
 |
Fig. 8 Influence of phase-changing elastic collision rate qE/A21 on the normalized source function at τ = 1. As expected, the source function approaches the CFR limit (shown as horizontal dashed line) with increasing values of qE /A21. |
 |
Fig. 9 Dependence of the ratio of the emission to absorption profile at τ = 1 (namely, ψ(x, τ = 1)/φ(x)) on the phase-changing elastic collision rate qE/A21 (indicated in the figure legend). As expected, the emission profile approaches the CFR limit (namely, ψ(x, τ) → φ(x)) with increasing phase-changing elastic collision rate. |
 |
Fig. 10 Dependence of the ratio of the VDF of the upper-level to the Maxwellian distribution at τ = 1 (namely, f2(u,τ = 1)/fM(u)) on the phase-changing elastic collision rate qE/A21 (indicated in the figure legend). With increasing values of qE/A21, the departure of the f2 from Maxwellian initially increases (until qE/A21 = 0.5) and then decreases. |
Acknowledgements
M.S. acknowledges the support from the Science and Engineering Research Board (SERB), Department of Science and Technology, Government of India via a SERB-Women Excellence Award research grant WEA/2020/000012. We acknowledge the use of the high-performance computing facility (https://www.iiap.res.in/?q=facilities/computing/nova) at the Indian Institute of Astrophysics. M.S. would like to thank Prof. Helene Frisch of OCA, Nice, France for useful discussions. Authors thank an anonymous referee for constructive comments. Authors are also thankful to the referee Prof. Ivan Hubeny for carefully reviewing the work presented in this paper and for his valuable comments.
References
- Allen, C. W. 1973, Astrophysical Quantities (London: The Athlone Press) [Google Scholar]
- Anusha, L. S., Nagendra, K. N., Stenflo, J. O., et al. 2010, ApJ, 718, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Atanackovic, O., Borsenberger, J., Oxenius, J., & Simonneau, E. 1987, J. Quant. Spectr. Rad. Transf., 38, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1998, MNRAS, 300, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Anstee, S. D., & O’Mara, B. J. 1998, PASA, 15, 336 [Google Scholar]
- Bommier, V. 1997a, A&A, 328, 706 [NASA ADS] [Google Scholar]
- Bommier, V. 1997b, A&A, 328, 726 [NASA ADS] [Google Scholar]
- Bommier, V. 2016a, A&A, 591, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bommier, V. 2016b, A&A, 591, A60 [EDP Sciences] [Google Scholar]
- Borsenberger, J., Oxenius, J., & Simonneau, E. 1986, J. Quant. Spectr. Rad. Transf., 35, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Borsenberger, J., Oxenius, J., & Simonneau, E. 1987, J. Quant. Spectr. Rad. Transf., 37, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Brechignac, C., Vetter, R., & Berman, P. R. 1978, Phys. Rev. A, 17, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, C. J. 1973, ApJ, 185, 621 [Google Scholar]
- Cooper, J., Ballagh, R. J., Burnett, K., & Hummer, D. G. 1982, ApJ, 260, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Fluri, D. M., Nagendra, K. N., & Frisch, H. 2003, A&A, 400, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I., & Cooper, J. 1986, ApJ, 305, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres. An Introduction to Astrophysical Non-equilibrium Quantitative Spectroscopic Analysis (Princeton, NJ: Princeton University Press) [Google Scholar]
- Hubeny, I., Oxenius, J., & Simonneau, E. 1983a, J. Quant. Spectr. Rad. Transf., 29, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Oxenius, J., & Simonneau, E. 1983b, J. Quant. Spectr. Rad. Transf., 29, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G. 1962, MNRAS, 125, 21 [Google Scholar]
- Hummer, D. G. 1969, MNRAS, 145, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, J., Paletou, F., Josselin, E., & Glorian, J.-M. 2016, Eur. J. Phys., 37, 015603 [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres (San Francisco: W.H. Freeman) [Google Scholar]
- Milkey, R. W., & Mihalas, D. 1973, ApJ, 185, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, G. L., & Kunasz, P. B. 1987, J. Quant. Spectr. Rad. Transf., 38, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, G. L., Auer, L. H., & Buchler, J. R. 1986, J. Quant. Spectr. Rad. Transf., 35, 431 [Google Scholar]
- Omont, A., Smith, E. W., & Cooper, J. 1972, ApJ, 175, 185 [Google Scholar]
- Oxenius, J. 1986, Kinetic Theory of Particles and Photons. Theoretical Foundations of Non-LTE Plasma Spectroscopy (Berlin: Springer) [Google Scholar]
- Paletou, F., & Auer, L. H. 1995, A&A, 297, 771 [NASA ADS] [Google Scholar]
- Paletou, F., & Peymirat, C. 2021, A&A, 649, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paletou, F., Peymirat, C., Anterrieu, E., & Böhm, T. 2020, A&A, 633, A111 [EDP Sciences] [Google Scholar]
- Paletou, F., Sampoorna, M., & Peymirat, C. 2023, A&A, 671, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical Recipes. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Sahal-Bréchot, S., & Bommier, V. 2019, ASP Conf. Ser., 526, 35 [Google Scholar]
- Sampoorna, M., & Trujillo Bueno, J. 2010, ApJ, 712, 1331 [NASA ADS] [CrossRef] [Google Scholar]
In Paletou & Peymirat (2021) and Paletou et al. (2023), the velocitychanging collision rate QV is denoted Q2. We adopt the QV notation here in order to avoid the possible confusion with the notation Q2 used in Hubeny & Mihalas (2014, see e.g., their Eq. (10.151) in page 327) for the elastic collision rate.
We remark that Eq. (22) can be more easily related to Eq. (4.15) of Hubeny et al. (1983b).
We verified that the range of q values suggested by Landi Degl’Innocenti & Landolfi (2004) approximately agrees with those determined from the hard-sphere collision model. For example, using the atomic radii listed in Allen (1973, see page 45), we find q for H– H collisions to be 7, He–H collisions to be 12.9, and that for Cs–Cs collisions to be 137 (note that Cs has the largest atomic radius).
All Figures
 |
Fig. 1 Validation of our iterative method for the full non-LTE transfer problem (compare with Fig. 3c of Hummer 1969). The normalized source function is displayed as a function of frequency at different line center optical depths within the atmosphere: namely at τ = 0, 1, 10, 100, 103, and 104. For comparison, we also show the corresponding CFR source function (constant with frequency) as dashed lines. |
| In the text | |
 |
Fig. 2 Departure of emission profile ψ(x, τ) from CFR for the case of scattering on a two-level atom with radiatively broadened upper level. Different lines correspond to ψ(x,τ)/φ(x) at different line-center optical depths within the atmosphere (indicated in the figure legend). For comparison ψ(x, τ = 1)/φ(x), corresponding to scattering on a two-level atom with infinitely sharp upper and lower levels (namely CS in the atomic frame), is shown as a dashed line. |
| In the text | |
 |
Fig. 3 Departure of the VDF of the naturally broadened upper level (f2(u, τ)) of a two-level atom from the Maxwellian equilibrium distribution f M(u) at different line center optical depths within the atmosphere (indicated in the figure legend). For comparison, the corresponding quantity at τ = 1 for the CS case is shown as a dashed line. There is clearly a greater overpopulation of f2 at large u in the CS case than in the present case of a two-level atom with a naturally broadened upper level. |
| In the text | |
 |
Fig. 4 Comparison of normally emergent intensity computed using the full non-LTE model for a two-level atom with infinitely sharp levels (CS) and radiatively broadened upper level (PFR) and standard non-LTE model with CFR. We note that the intensity for CS and the corresponding CFR (a = 0) case nearly coincide. |
| In the text | |
 |
Fig. 5 Influence of velocity-changing collisions on the normalized source function at τ = 1. As expected, with increasing values of QV/A21, the source function approaches the CFR limit, which is shown as a horizontal dashed line. |
| In the text | |
 |
Fig. 6 Dependence of the ratio of emission to absorption profile at τ = 1 (namely, ψ(x,τ = 1)/φ(x)) on velocity-changing collisions. As expected, the emission profile approaches the CFR limit, namely ψ(x, τ) → φ(x) with increasing values of QV /A21. |
| In the text | |
 |
Fig. 7 Dependence of the ratio of the VDF of the upper level to the Maxwellian distribution at τ = 1 (namely, f2(u,τ = 1)/fM(u)) on velocity-changing collisions. With increasing values of QV/A21, the departure of the f2 from Maxwellian initially increases for QV /A21 = 0.25 in the regime of intermediate velocities and then decreases. |
| In the text | |
 |
Fig. 8 Influence of phase-changing elastic collision rate qE/A21 on the normalized source function at τ = 1. As expected, the source function approaches the CFR limit (shown as horizontal dashed line) with increasing values of qE /A21. |
| In the text | |
 |
Fig. 9 Dependence of the ratio of the emission to absorption profile at τ = 1 (namely, ψ(x, τ = 1)/φ(x)) on the phase-changing elastic collision rate qE/A21 (indicated in the figure legend). As expected, the emission profile approaches the CFR limit (namely, ψ(x, τ) → φ(x)) with increasing phase-changing elastic collision rate. |
| In the text | |
 |
Fig. 10 Dependence of the ratio of the VDF of the upper-level to the Maxwellian distribution at τ = 1 (namely, f2(u,τ = 1)/fM(u)) on the phase-changing elastic collision rate qE/A21 (indicated in the figure legend). With increasing values of qE/A21, the departure of the f2 from Maxwellian initially increases (until qE/A21 = 0.5) and then decreases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



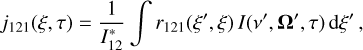
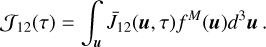
![$\Delta {T^{{\rm{core }}}} = (1 - \varepsilon )\int_{{\rm{core }}} {{\varphi _x}} \Lambda _x^*\left[ {\delta S_x^{(n)}} \right]{\rm{d}}x,$](/articles/aa/full_html/2024/10/aa49722-24/aa49722-24-eq51.png)