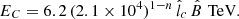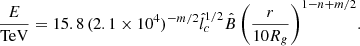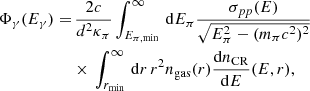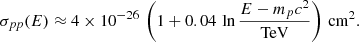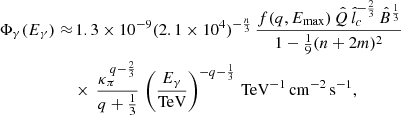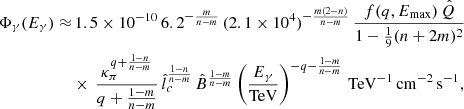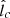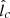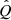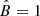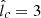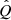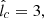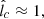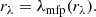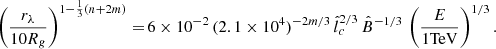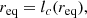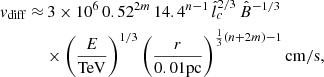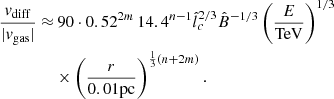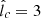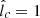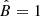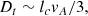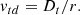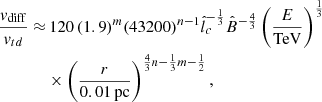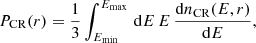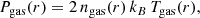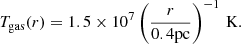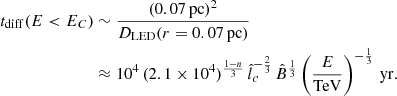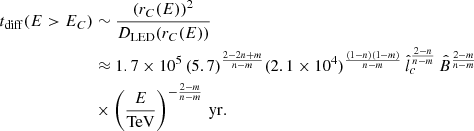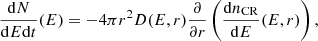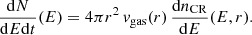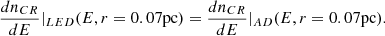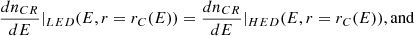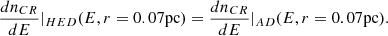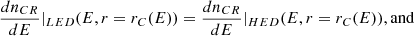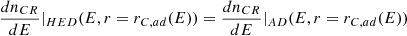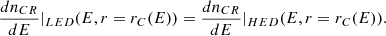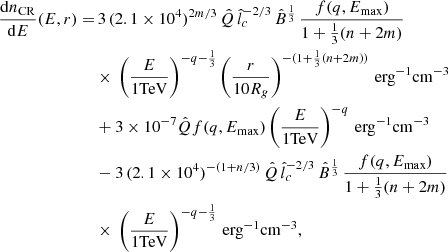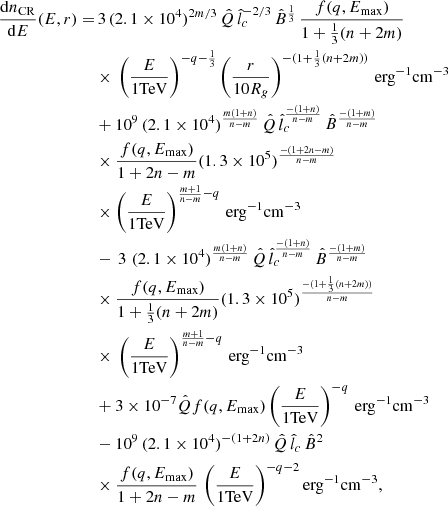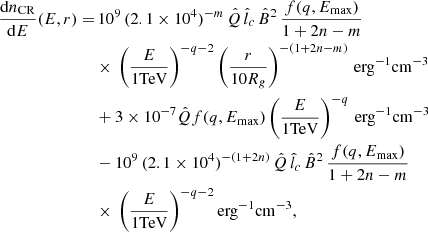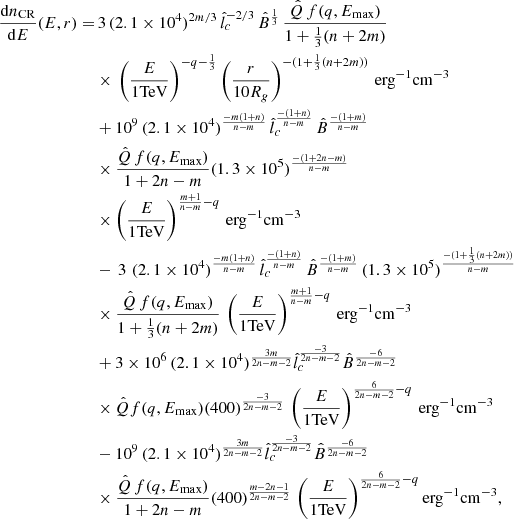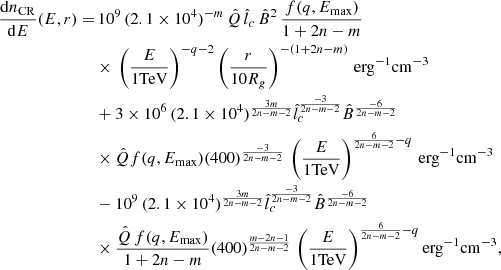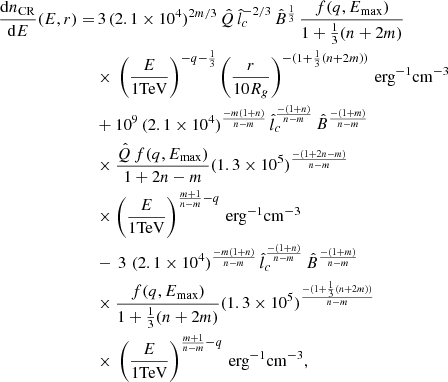| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A216 | |
| Number of page(s) | 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202449851 | |
| Published online | 13 September 2024 | |
HESS J1745−290 spectrum explained by a transition in the diffusion regime of PeV cosmic rays in the Sgr A* accretion flow
1
Departamento de Física, Facultad de Ciencias Físicas y Matemáticas (FCFM), Universidad de Chile, Beauchef 850, Santiago, Chile
2
Departamento de Física, Facultad de Ciencias Básicas, Universidad Metropolitana de Ciencias de la Educación, Av. José Pedro Alessandri 774, Ñuñoa, Chile
Received:
4
March
2024
Accepted:
12
June
2024
Context. The diffuse TeV gamma-ray emission detected in the inner ∼100 pc of the Galactic center suggests the existence of a central cosmic-ray accelerator reaching ∼PeV energies. It is interesting to associate this so-called “PeVatron” with the point source HESS J1745−290, whose position is consistent with that of the central supermassive black hole Sgr A*. However, the point source shows a spectral break at a few TeV that is not shown by the diffuse emission, challenging this association.
Aims. We seek to build an emission model for the point source that is consistent with both emissions being produced by the same population of relativistic protons continuously injected with a power-law spectrum up to ∼PeV energies near Sgr A*.
Methods. In our model, we assume that the point source is produced by hadronic collisions between the cosmic rays and the gas in the accretion flow of Sgr A*. The cosmic-ray density is calculated taking into consideration cosmic-ray transport due to diffusion and advection, while the properties of the gas are obtained from previous numerical simulations of the accretion flow.
Results. Our model succeeds in explaining both the point source and the diffuse emission with the same cosmic rays injected in the vicinity of Sgr A*, as long as the coherence length of the magnetic turbulence in the accretion flow is lc ∼ (1 − 3)×1014 cm. The spectral break of the point source appears naturally due to an energy-dependent transition in the way the cosmic rays diffuse within the inner ∼0.1 pc of the accretion flow (where most of the emission is produced).
Conclusions. Our model supports the idea that Sgr A* can be a PeVatron, whose accelerated cosmic rays give rise to both the point source and the diffuse emission. Future TeV telescopes such as CTAO will be able to test this model.
Key words: cosmic rays / ISM: magnetic fields / Galaxy: center / gamma rays: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The very-high energy (VHE) gamma-ray source HESS J1745−290, located at the Galactic center, has been observed by several imaging atmospheric Cherenkov telescopes (IACTs), such as CANGAROO, VERITAS, H.E.S.S., and MAGIC (Tsuchiya et al. 2004; Kosack et al. 2004; Aharonian et al. 2004; Albert et al. 2006; HESS Collaboration 2016, 2018; MAGIC Collaboration 2020; Adams et al. 2021). This source is usually characterized by a hard power-law spectrum with a photon index of ∼2.1 and an exponential cutoff at ∼10 TeV. However, its spectral shape is also compatible with a broken power law with the break energy at a few TeV (Aharonian et al. 2009; Adams et al. 2021)1.
Although several models have been proposed to explain this source, HESS J1745−290 has not yet been associated with a particular astrophysical object. This is mainly because of the limited ∼3′ angular resolution of current IACTs, which translates to ∼10 pc in projected distance from the Galactic center (Funk & Hinton 2008). However, some processes have been proposed: (1) dark matter annihilation in a density cusp at the Galactic center (Hooper et al. 2004; Profumo 2005; Aharonian et al. 2006; Cembranos et al. 2012), (2) inverse Compton emission by relativistic electrons in the pulsar wind nebula G359.95-0.04 (Hinton & Aharonian 2007; Wang et al. 2006), and (3) the decay of neutral pions produced by hadronic collisions of cosmic rays (CRs) accelerated by the central supermassive black hole Sagittarius A* (Sgr A*) with background protons in the interstellar gas (Aharonian & Neronov 2005; Chernyakova et al. 2011; Rodríguez-Ramírez et al. 2019).
In the present work we focus on the last scenario. Although Sgr A* is today a relatively quiescent black hole, it has most likely gone through significantly more active phases in the past. This is suggested by the presence of the Fermi bubbles, which are plausibly caused by intense accretion activity some ∼106 − 107 years ago (Su et al. 2010). Also, the observations of X-ray echoes coming from dense gas in the Galactic center region suggest an intense flaring activity in the past few hundred years (Clavel et al. 2013; Marin et al. 2023). Thus, assuming some efficient accretion-driven CR acceleration mechanism, Sgr A* may be powering HESS J1745−290 as its accelerated CRs propagate away from the Galactic center and interact hadronically with the surrounding gas.
The potentially important role of Sgr A* in producing the TeV emission of HESS J1745−290 is also supported by the diffuse VHE gamma-ray emission from the central molecular zone (CMZ) located in the inner few hundred parsecs of the Galaxy (HESS Collaboration 2016). This emission is correlated with the density of molecular gas, suggesting hadronic emission due to CR collisions with background protons. The CR density profile inferred from this assumption is consistent with a 1/r dependence (where r is the distance to the Galactic center), supporting the radial diffusion of CRs continuously injected from the inner tens of parsecs around the Galactic center2. The gamma-ray spectrum of this emission is characterized by a single power law with an index of ∼2.3 up to tens of TeV, without a statistically significant spectral cutoff, as shown by H.E.S.S. and VERITAS (HESS Collaboration 2016; Adams et al. 2021), although some controversy remains due to indications of a spectral turnover around 20 TeV reported by MAGIC (MAGIC Collaboration 2020). The possible lack of a cutoff in the diffuse CMZ emission is interesting, because it allows the possibility of the existence of a PeV proton accelerator, or “PeVatron”, to be present within the inner tens of parsecs of the Galaxy. These observations have thus been considered as strong indications that Sgr A* is operating as a PeVatron (HESS Collaboration 2016), although contributions from other possible CR acceleration systems have also been considered. One possible contribution includes CRs accelerated in the shock fronts of the supernova remnants Sgr A East (HESS Collaboration 2016; Scherer et al. 2022, 2023) and G0.9+01 (Dörner et al. 2024). Another possibility is related to the multiple shocks formed by stellar winds in the Nuclear, Arches, and Quintuplet clusters of young massive stars (Aharonian et al. 2019; Scherer et al. 2022, 2023), with the Arches and Quintuplet clusters being located at a projected distance of ∼25 pc from Sgr A*, while the dynamic center of the Nuclear cluster coincides with it (Hosek et al. 2022).
Even though the scenario in which Sgr A* drives the emissions of both HESS J1745−290 and the CMZ is appealing, one of its main challenges is the clear presence of a spectral turnover (either an exponential cutoff or a spectral break) at a few to ∼10 TeV in HESS J1745−290, which appears to be absent from the CMZ emission. One possible way to alleviate this discrepancy is by invoking the absorption of ≳10 TeV gamma rays from HESS J1745−290 by e+e− pair production due to their interaction with the interstellar radiation field (ISRF). Although this absorption is not expected to be important given the known ISRF in the Galactic center (Zhang et al. 2006; Aharonian et al. 2009), its effect may become significant due to clumpiness of the interstellar medium (Guo et al. 2017). Another possibility is simply a relatively recent decrease in the power of CR injection (Liu et al. 2016), which would mean that the diffuse emission is powered by CRs with up to ∼ PeV energies accelerated by Sgr A* ≳104 years ago, and that HESS J1745−290 is associated with a less efficient acceleration period over the last ∼10 − 100 years.
In this paper, we present an alternative scenario, in which the spectral turnover of HESS J1745−290 is caused by an energy-dependent transition in the diffusion regime of CRs injected by Sgr A*. In our model, HESS J1745−290 is caused by CRs experiencing hadronic collisions as they diffuse out through the accretion flow of Sgr A* (r ≲ 0.1 pc). Although the injected CRs in our proposed scenario have an energy distribution given by a single power law up to ∼ PeV energies, the transition in their diffusion regime significantly reduces their number density within the accretion flow for energies of ≳20 TeV. This density reduction in turn imprints a break in the gamma-ray emission spectrum at a few TeV.
Our proposed model requires three basic ingredients:
The first ingredient corresponds to the radial profiles for the density, velocity, and magnetic field strength in the gas at r ≲ 1 pc. The gas has been proposed to mainly come from the wind of ∼ 30 Wolf-Rayet (WR) stars, which belong to the Nuclear cluster and orbit around Sgr A* at a distance of ∼0.1 − 1 pc (Cuadra et al. 2006, 2007). These profiles are obtained from previously reported hydrodynamic (Ressler et al. 2018) and magnetohydrodynamic (MHD; Ressler et al. 2020a) simulations of the Sgr A* accretion flow. Interestingly, despite the relatively large magnetic fields used for the stellar winds in the MHD studies, their obtained angle-averaged gas density, temperature, and velocity are largely insensitive to the assumed magnetic field strength and are essentially the same as those found in the hydrodynamic simulations (Ressler et al. 2020a). Because of this, below we refer to both hydrodynamic and MHD results when describing the assumed gas behavior in our model.
A second ingredient is given by the diffusion and advection properties of the CRs within the MHD turbulence in the r ≲ 1 pc region. While the properties of the gas flow are obtained from previous hydrodynamic and MHD simulations, the CR diffusion properties are inferred from previous studies of test-particle CRs propagating in synthetic turbulence, which we assume to be strong (i.e., the mean large-scale magnetic field is much weaker than the fluctuating field), isotropic, and with a Kolmogorov spectrum (Subedi et al. 2017; Mertsch 2020; Dundovic et al. 2020). One of the main assumptions made in this work is that the mean field is much weaker than the turbulent field, which allows us to neglect a possible anisotropy in the CR diffusion, as has been found in test-particle simulations (see, e.g., Reichherzer et al. 2022a,b, 2023).
Finally, we assume a flux of centrally injected CRs whose spectral distribution corresponds to a single power law whose index, normalization, and maximum energy (reaching ∼PeV energies) are consistent with estimates obtained from the diffusive CMZ emission (HESS Collaboration 2016).
Most parameters in our model are thus relatively well constrained by previously reported hydrodynamic and MHD simulations of the Sgr A* accretion flow, as well as by the spectral properties of the CMZ emission. The only exception is the coherence length lc of the MHD turbulence in the accretion flow, which, despite playing a critical role in the diffusion properties of the CRs, is a poorly known parameter of our model. Interestingly, we find that by choosing lc ∼ (1 − 3) × 1014 cm, our model is capable of matching the main spectral features of HESS J1745−290 fairly well, including its spectral turnover, while being consistent with the injected CR spectrum required to reproduce the CMZ emission.
We note that, in our model, the CR injection occurs within a radius of r ≲ 10Rg, where Rg is the gravitational radius of the black hole (or Schwarzschild radius, which in the case of Sgr A* is Rg ≈ 1012 cm). This is justified by the fact that electron acceleration events in Sgr A* are routinely inferred in association with near-infrared and X-ray flares (likely powered by reconnection events; Ponti et al. 2017; Subroweit et al. 2020; Scepi et al. 2022), whose emission regions have been located at a few Rg from the central black hole (GRAVITY Collaboration 2018). Although this injection region may itself be the source of significant gamma-ray emission (Rodríguez-Ramírez et al. 2019), our work specifically focuses on the emission produced at r ≳ 10Rg (which, as we show, is dominated by r ≫ 10Rg).
Our paper is organized as follows. In Sect. 2, we calculate the CR density as a function of radius and energy within the accretion flow of Sgr A*, considering the diffusion properties of CRs in that region, as well as the velocity profile of the background gas. In Sect. 3, we calculate the gamma-ray emission resulting from the hadronic interaction of the CRs with the background gas. In Sect. 4, we verify the consistency of the assumptions made in our calculations. In Sect. 5, we provide a discussion regarding CR diffusion timescales and how they could be used to observationally test our model. Finally, our conclusions are presented in Sect. 6.
2. Cosmic ray density model
In this work, we assume that CRs are ultrarelativistic protons being steadily injected near the event horizon of Sgr A* and propagate to larger radii r through its accretion flow. This accretion flow originates mainly from the gas being injected by a cluster of WR stars orbiting at ∼0.1 − 1 pc from Sgr A* (Cuadra et al. 2006, 2007). The CR transport equation can be written as (e.g., Strong et al. 2007)
where dnCR/dE(E, r, t) is the CR density per unit energy E as a function of position r and time t. The term S(E, r, t) is the source term that quantifies CR injection, D(E, r) is the CR diffusion coefficient and v(r, t) is the gas velocity, which allows advection to contribute to CR propagation. In Eq. 1 we neglect possible CR energy gains (e.g., due to stochastic acceleration) and energy losses (we verified that energy losses are indeed small by comparing the CR diffusion times found in Sect. 5 with the cooling times due to hadronic CR interactions). For simplicity, and as a first approach to this problem, in this work we solve Eq. 1 assuming a stationary and spherically symmetric CR density model. In what follows, we describe the parameters and assumptions regarding CR injection and transport.
2.1. Cosmic-ray injection
In our model, we assume that the CR injection occurs only within a radius of r < 10Rg, and solve for dnCR/dE(E, r) at r > 10Rg. Thus, our calculations do not require the exact form of the source term S(E, r) in Eq. 1, but only the total number of injected CRs per unit energy E and per unit time t within the injection region, which is given by
For this, we assume a power-law dependence of
for E smaller than a maximum energy Emax, and dN/(dEdt) = 0 otherwise. Here, q is the spectral index of the injected CR spectrum, 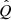 is a parameter that quantifies the injection power, and
is a parameter that quantifies the injection power, and
while, if q = 2,
and so the CR injection power for E ≥ 10 TeV is
2.2. Cosmic-ray transport
As our model is stationary and assumes spherical symmetry, integrating Eq. 1 over a spherical volume of radius r, and considering the definition of dN/dEdt(E) provided by Eq. 3, we obtain
where vgas(r) is the angle-averaged gas velocity in the radial direction at a radius r. We see that both diffusion and advection are expected to contribute to CR propagation. However, below we show that, in our model, diffusion is the dominant process at r ≲ 0.07 pc for all energies of interest, while for r ≳ 0.07 pc advection dominates for CRs with sufficiently low energies. Thus, as an approximation, in our calculations of dnCR/dE(E, r) from Eq. (8) we impose that, at a given radius r and energy E, CRs are transported entirely by one process, either diffusion or advection (i.e., keeping only one of the two terms on the right-hand side of Eq. (8)), depending on which one is more efficient. This is done by comparing the radial gas velocity vgas to the diffusion velocity,
and neglecting the diffusion (advection) term on the right-hand side of Eq. (8) if vgas (vdiff) is larger3. We note that CRs can also be advected by the turbulent motions of the gas, giving rise to turbulent diffusion. We show below that this effect can be neglected for the cases of interest (see Sect. 4), and so CR transport in our model is determined by the properties of D(E, r) and vgas(r).
2.2.1. Diffusion model
In order to model D(E, r), we use results from previous test particle simulations of CRs propagating in synthetic MHD turbulence (i.e., magnetostatic turbulence with a prespecified spectrum), which we assume to be strong in the sense that the rms magnetic field magnitude is much larger than any large-scale mean field, is isotropic, and has a Kolmogorov spectrum (Subedi et al. 2017; Mertsch 2020; Dundovic et al. 2020). This turbulence is characterized by a coherence length lc, which is the spatial scale within which most of the turbulent magnetic energy is contained (Fleishman & Toptygin 2013). These simulations identify two main diffusion regimes, which are also consistent with theoretical diffusion models (Aloisio & Berezinsky 2004; Subedi et al. 2017). The “high-energy diffusion”(HED) regime occurs when the energy of the CRs is such that their Larmor radii RL satisfy RL ≫ lc (RL = E/eB, where e is the proton electric charge and B is the magnitude of the magnetic field), while the “low-energy diffusion”(LED) regime occurs when RL ≪ lc. We obtain expressions for the effective mean free path λmfp of CRs in these two diffusion regimes from Subedi et al. (2017) (where a broken power-law shape is assumed for the turbulence spectrum). Figure 1 of Subedi et al. (2017) shows that, for RL ≪ lc (LED), λmfp is given by
while for RL ≫ lc (HED),
with a smooth transition for RL ∼ lc. (In Appendix B we give heuristic derivations for the dependence on lc and RL in these two limiting regimes.) We note that, as Eqs. 10 and 11 are approximate expressions obtained from Fig. 1 of Subedi et al. (2017), their normalizations should only be considered to have an accuracy at the ∼10% level. Another approximation is that, in our calculations, the transition in the λmfp behavior at RL ∼ lc is satisfied by assuming
Thus, in order to obtain D(E, r) = λmfp(E, r)c/3 (where c is the speed of light), we need an expression for the rms magnitude of the magnetic field B as a function of r. Based on the MHD simulations of the Sgr A* accretion flow of Ressler et al. (2020a), we assume it to have a power-law profile,
where n ≈ 1, while 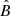 is a factor of order unity, and is relatively independent of the conditions assumed for the wind of the WR stars. From this, we obtain a space- and energy-dependent Larmor radius of
is a factor of order unity, and is relatively independent of the conditions assumed for the wind of the WR stars. From this, we obtain a space- and energy-dependent Larmor radius of
In contrast, the value of the coherence length lc in the accretion flow is highly uncertain. In order to model the possible radial dependence of this parameter, we also assume a power-law shape for it, with
where 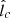 and m are free parameters of our model.
and m are free parameters of our model.
Thus, the diffusion coefficient in the LED regime, RL ≪ lc, is
while in the HED regime, RL ≫ lc,
2.2.2. Advection model
In order to model vgas(r), we need to characterize the gas dynamics within the Sgr A* accretion flow. For this, we use the hydrodynamic simulations presented by Ressler et al. (2018), which assume that the gas is mainly provided by the wind of a cluster of WR stars orbiting at 0.1 − 1 pc from Sgr A*. Interestingly, these simulations show no significant differences with the MHD simulations of (Ressler et al. 2020a) when angle-averaged quantities are considered. For simplicity, we assume that this gas is a plasma composed of electrons and protons of equal number density ne(r) = np(r) = ngas(r). The profile of the gas density ngas is obtained from Fig. 11 of Ressler et al. (2018), which provides quantities averaged over angle and time (over the 100 years previous to the present day). This density profile can be approximated by4
We note that, according to Fig. 11 of Ressler et al. 2018, the ngas(r) profile at 0.07 pc ≲ r ≲ 0.4 pc is steeper than ngas(r)∝r−1. However, we show in Sect. 3.1 that the gamma-ray emission from this region is expected to be ≲20 − 30% of the total emission at all energies. Therefore, as a reasonable approximation, we use Eq. 18 to describe ngas(r) at all radii smaller than 0.4 pc.
Regarding the gas velocity, Ressler et al. (2018) identify four regions within the accretion flow:
Region I: This is the outflow-dominated region defined by r > 0.4 pc. Here, the gas moves away from the Galactic center and vgas(r) is essentially given by the speed of the WR star winds.
Region II: Located at 0.07 pc < r < 0.4 pc, this region corresponds to the “feeding” region, where most of the gas injection from the WR star winds occurs, and in which the gas motion predominantly points away from the Galactic center.
Region III: Corresponds to a “stagnation” region at 0.01pc < r < 0.07 pc, which is characterized by inflows and outflows of gas, with the net mass-accretion rate nearly vanishing.
Region IV: Corresponds to an inflow-dominated region at r < 0.01 pc, where the mass-accretion rate Ṁ is roughly constant.
In region IV, we consider a constant mass-accretion rate Ṁ ≈ 10−8 M⊙/yr (Ressler et al. 2020b; Dexter et al. 2020), with which we find that
where mp is the proton mass.
In region III, the average radial velocity of the gas tends to cancel out, and therefore CR transport should not be significantly affected by advection. In what follows, we neglect the effect of vgas(r) for regions III and IV, for which we assume that CR transport is dominated by diffusion. The validity of this assumption is verified in Sect. 4.
In regions I and II (r > 0.07 pc), we can estimate vgas from Fig. 18 in Ressler et al. (2018), which can be approximated by
In this case, vgas dominates CR transport for sufficiently low energies, while diffusion dominates for higher-energy particles. Thus, for 0.07 pc < r < 0.4 pc, we consider diffusive transport at energies for which vdiff > vgas, and advective transport in the opposite case. For simplicity, at r > 0.4 pc, we assume the same transport mechanism that dominates at r = 0.4 pc, which, depending on E, could either be HED or advection. As discussed in Sect. 4.2, this should not affect our main results.
2.3. Previous constraints on parameters
As our purpose is to build a model for the point source HESS J1745−290 that is compatible with the diffuse emission from the CMZ, the injection parameters q, 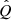 , and Emax have to obey restrictions related to the CMZ emission. This emission has been found to be consistent with a CR proton spectral index of Γp ≈ 2.3 (HESS Collaboration 2016). This, however, does not correspond to the index q of the injected CRs, as the CR spectrum in the CMZ is also affected by the energy-dependent residence time of the CRs in this region, which is inversely proportional to the CR diffusion coefficient in the CMZ, which itself is assumed to have a power-law shape of DCMZ(E)∝Eδ. This implies that Γp = q + δ, with the value of δ likely between δ ≈ 1/3 and 1/2, as expected for Kolmogorov and Kraichnan types of magnetic turbulence, respectively (Aharonian 2004). Thus, a reasonable expectation for q is ≈2. Also, making different assumptions regarding the magnitude of DCMZ(E), HESS Collaboration (2016) and Scherer et al. (2022) found the CR injection power for E > 10 TeV to be Q(E > 10 TeV)≈8 × 1037erg s−1 and 3 × 1036erg s−1, implying
, and Emax have to obey restrictions related to the CMZ emission. This emission has been found to be consistent with a CR proton spectral index of Γp ≈ 2.3 (HESS Collaboration 2016). This, however, does not correspond to the index q of the injected CRs, as the CR spectrum in the CMZ is also affected by the energy-dependent residence time of the CRs in this region, which is inversely proportional to the CR diffusion coefficient in the CMZ, which itself is assumed to have a power-law shape of DCMZ(E)∝Eδ. This implies that Γp = q + δ, with the value of δ likely between δ ≈ 1/3 and 1/2, as expected for Kolmogorov and Kraichnan types of magnetic turbulence, respectively (Aharonian 2004). Thus, a reasonable expectation for q is ≈2. Also, making different assumptions regarding the magnitude of DCMZ(E), HESS Collaboration (2016) and Scherer et al. (2022) found the CR injection power for E > 10 TeV to be Q(E > 10 TeV)≈8 × 1037erg s−1 and 3 × 1036erg s−1, implying 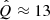 and 0.5, respectively. Additionally, the spectrum of the diffuse emission restricts the maximum CR energy to Emax ≳ 1 PeV (HESS Collaboration 2016; Adams et al. 2021).
and 0.5, respectively. Additionally, the spectrum of the diffuse emission restricts the maximum CR energy to Emax ≳ 1 PeV (HESS Collaboration 2016; Adams et al. 2021).
Further parameter restrictions can be obtained from previous MHD simulations of the Sgr A* accretion flow. For instance, Ressler et al. (2018) show that assuming a beta parameter in the winds of the WR stars βW = 104, the magnetic field near Sgr A* reaches the value B(r = 10Rg)≈10 G (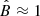 ), and the parameter n (defined in Eq. (13)) is approximately n ≈ 1. In the case of βW = 102, these latter authors obtain almost the same
), and the parameter n (defined in Eq. (13)) is approximately n ≈ 1. In the case of βW = 102, these latter authors obtain almost the same 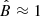 , while B(r = 0.1 pc) is approximately a factor 4 larger than in the βW = 104 case. For our assumed power-law dependence B ∝ r−n (Eq. (13)), the latter implies n ≈ 0.9.
, while B(r = 0.1 pc) is approximately a factor 4 larger than in the βW = 104 case. For our assumed power-law dependence B ∝ r−n (Eq. (13)), the latter implies n ≈ 0.9.
Given these considerations, below we restrict our analysis to cases with 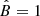 and q = 2, and consider two possible values for n, namely n = 1 and 0.9. We show below that, with these choices, our model can reproduce the main features of the emission from HESS J1745−290 relatively well if
and q = 2, and consider two possible values for n, namely n = 1 and 0.9. We show below that, with these choices, our model can reproduce the main features of the emission from HESS J1745−290 relatively well if 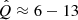 and Emax ≳ 1 PeV, which respects the restrictions related to the diffuse CMZ emission provided by HESS Collaboration (2016). Regarding the more uncertain parameters
and Emax ≳ 1 PeV, which respects the restrictions related to the diffuse CMZ emission provided by HESS Collaboration (2016). Regarding the more uncertain parameters 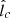 and m, we show that fitting the data of HESS J1745−290 is strongly dependent on
and m, we show that fitting the data of HESS J1745−290 is strongly dependent on 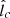 being in the range of
being in the range of 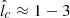 (for n = 1 and 0.9, respectively), while m must be small (m ≲ 0.3). In other words, the coherence length lc must depend only weakly on r.
(for n = 1 and 0.9, respectively), while m must be small (m ≲ 0.3). In other words, the coherence length lc must depend only weakly on r.
2.4. Cosmic-ray density profiles
Considering our assumptions regarding CR injection and transport described in Sect. 2.1 and Sect. 2.2, we solve Eq. (8) assuming continuity in dnCR/dE at the transition between regions dominated by diffusion and by advection5. Figure 1 shows examples of the CR density profile for two combinations of parameters (Cases 2 and 4b in Table 1), where we can identify the three main transport regimes mentioned above:
 |
Fig. 1. Cosmic-ray density per unit energy dnCR/dE as a function of the radial coordinate r (horizontal axis) and the CR energy E (vertical axis) for cases 2 (panel a) and 4b (panel b) specified in Table 1. The color scale gives log10(E7/3rξdnCR/dE) in cgs units (with ξ = 4/3 in panel a and ξ = 1.3 in panel b), and the dashed lines mark the boundaries between the three CR transport regimes discussed in the text, namely the low-energy diffusion (LED), high-energy diffusion (HED), and advection-dominated (AD) regimes. |
Different model parameter combinations considered in this work. In all cases,  and q = 2.
and q = 2.
(i) Low-energy diffusive (LED) regime: In this region, CR transport is dominated by diffusion, with λmfp in the RL < 0.38 lc regime of Eq. (12). Solving Eq. (8) in that regime, we obtain:
For simplicity, Eq. (21) does not include the terms that ensure continuity of dnCR/dE at the boundaries between regions dominated by different transport regimes, which are subdominant. These continuity terms are, however, included in the calculation shown in Fig. 1 as well as in the gamma-ray emission calculations shown in Sect. 3. In Appendix C, we provide the full expression for dnCR/dE in the LED regime, including the boundary terms.
(ii) High-energy diffusive (HED) regime: In this case, CR transport is also dominated by diffusion, but with λmfp in the RL > 0.38 lc regime of Eq. (12). In this case, the CR density is given by
dropping off much faster with increasing r (or increasing E), as seen in the upper right corner of Fig. 1. (Here, we are also excluding subdominant terms that ensure continuity of dnCR/dE, but we provide the full expression in Appendix C.)
(iii) Advection-dominated (AD) regime: In this regime, CR propagation is dominated by advection, and their density is given by
for 0.07 pc ≤r≤ 0.4 pc, and
for r > 0.4 pc, where again in both cases the CR density drops off much faster with increasing r than in the LED regime, as seen in the lower right corner of Fig. 1. (No boundary terms are neglected in Eqs. (23) and (24).)
As seen in Figure 1, high-energy CRs diffusing out from the central source undergo a transition from the LED regime to the HED regime at an energy-dependent critical radius rC determined by the condition RL = 0.38 lc, yielding
which is marked by the diagonal dashed lines in the high-energy part of Figs. 1a and 1b. At lower energies, instead, CRs transit from the LED regime to the advective regime at a fixed radius r = 0.07 pc. The energy separating these two types of transition, EC, is determined by rC(EC) = 0.07 pc (corresponding to the inner boundary of the feeding region), which yields
Figures 1a and 1b also show that, at energies of E > EC, advection continues to be dominant over HED for r > 0.07 pc until an energy E* ∼ (2 − 3)Ec, after which HED dominates at r > 0.07 pc. We note that the maximum energy at which advection dominates for r > 0.07 pc is constant in Case 2 (Fig. 1a), but has a weak dependence on r in Case 4b (Fig. 1b). This is because, in the range 0.07pc < r < 0.4pc, making vgas(r) equal to vdiff(E, r) in the HED regime, we obtain
This implies that in Case 2 (n = 1, m = 0), the limit between the AD and HED regimes is simply given by E = E*, while in Case 4b (n = 0.9, m = 0), this energy becomes E ∝ r0.1. For r > 0.4 pc, we assume, for simplicity, that CR transport is dominated by the same process that dominates at r = 0.4 pc (which explains why in Figure 1b the energy that divides the HED and AD regimes becomes constant at r > 0.4 pc). We show in Sect. 4.2 that this approximation does not affect our results, given that emission at r > 0.4 pc is negligible in our model.
3. Gamma-ray emission
Using the CR density determined in Sect. 2, in this section we calculate the gamma-ray spectrum due to the decay of neutral pions (π0) produced in collisions between the CRs and the background gas, both assumed to be composed of protons. Following Aharonian (2004), the gamma-ray flux per unit gamma-ray energy Eγ received at Earth is given by
where 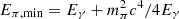 ,
, 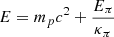 , Eπ is the energy of the neutral pion produced in the collisions, mp and mπ are the proton and pion masses, κπ ≈ 0.17 is the mean fraction of the CR kinetic energy transferred to neutral pions in the collisions (Aharonian 2004), d ≈ 8 kpc is the distance between Sgr A* and the Earth, and rmin is the minimum radius considered for the emissivity calculation. Unless stated otherwise, we take rmin = 1013 cm ≈10 Rg in all our calculations. The cross-section for π0 production through proton-proton collisions in a proton reference frame is given by (Aharonian 2004)
, Eπ is the energy of the neutral pion produced in the collisions, mp and mπ are the proton and pion masses, κπ ≈ 0.17 is the mean fraction of the CR kinetic energy transferred to neutral pions in the collisions (Aharonian 2004), d ≈ 8 kpc is the distance between Sgr A* and the Earth, and rmin is the minimum radius considered for the emissivity calculation. Unless stated otherwise, we take rmin = 1013 cm ≈10 Rg in all our calculations. The cross-section for π0 production through proton-proton collisions in a proton reference frame is given by (Aharonian 2004)
As we are interested in very-high-energy protons, with E ≳ 1 TeV, we neglect the proton and pion masses in all calculations.
3.1. Behavior of the gamma-ray spectrum
Figure 2 shows the differential gamma-ray flux as a function of r and Eγ for Case 2 of Table 1. This flux is clearly in correspondence with the CR density shown in Fig. 1, considering the approximate energy rescaling Eγ ≈ κπE. The fact that dnCR/dE drops off more quickly as a function of r in the HED and AD regimes than in the LED regime show that the gamma-ray flux is dominated by the CRs in the LED regime for any value of Eγ, with a maximum around the transition from the LED to the HED or AD regimes. This means that, in our model, the emission is dominated by r ∼ 0.07 pc for Eγ ≲ 3 TeV, and by 3 × 10−4 pc ≲r ≲ 0.07 pc (equivalent to 103Rg ≲ r ≲ 2 × 105Rg) for 3 TeV ≲Eγ ≲ 200 TeV. In other words, the gamma-ray emission should only be significant in the range 103Rg < r < 0.07 pc. This can be seen from Fig. 3, which shows the total emission spectrum for Case 2 (blue line) and compares it with the contributions from r > 0.4 pc (solid purple line) and from 0.07 pc < r < 0.4 pc (dashed purple line). We see that the emissions from these two ranges of radii only account for at most ∼20 − 30% of the total emission at all the energies considered. Furthermore, one can also see from Fig. 4 that the resulting spectrum (up to ∼100 TeV) for Case 2 is quite insensitive to the choice of rmin as long as this parameter is in the range ∼(10 − 103) Rg, confirming that most of the emission comes from r ≳ 103Rg.
 |
Fig. 2. Differential gamma-ray flux per logarithmic interval of r, dΦγ/dlog10(r), as a function of Eγ and r for Case 2 in Table 1. |
 |
Fig. 3. Full and approximate models for the gamma-ray spectrum of HESS J1745−290 with the parameters of Case 2 of Table 1. The solid blue line represents the total gamma-ray emission calculated from the full model. The dashed blue line is the “LED model”, considering only the emission from CRs in the LED regime. The dashed green line shows our simplified model, given by Eqs. (30) and (31). The solid and dashed purple lines represent the contributions from CRs at r > 0.4 pc and 0.07 pc < r < 0.4 pc, respectively. The red dots correspond to the H.E.S.S. measurements (HESS Collaboration 2016). |
 |
Fig. 4. Gamma-ray spectra for Case 2 of Table 1 for different minimum radii rmin from which the gamma-ray emission is integrated (see Eq. (28)). The red dots correspond to the H.E.S.S. measurements of the source HESS J1745−290 (HESS Collaboration 2016). |
From Fig. 2 we also see that, for CR energies E > EC, the LED region is constrained to progressively smaller radii rC(E) as E increases, thus progressively decreasing the effective emitting volume. This causes a break in the gamma-ray spectrum (obtained by integrating the flux over the whole volume out to r → ∞ and shown as the solid blue line in Fig. 3) at Eγ, b ∼ κπEC, beyond which it decreases more steeply, as in the observed spectrum of HESS J1745−290.
The hypothesis that the gamma-ray spectrum is essentially determined by the shape of the LED region in Fig. 1 is confirmed by recalculating Φ(Eγ) considering only the gamma-ray emission from CRs in this regime (i.e., setting dnCR/dE = 0 in the HED and AD regimes). This calculation is shown by the dashed blue line in Fig. 3, which shows a similar broken power-law behavior as in the full calculation represented by the solid blue line. Thus, the predicted emission in our model is indeed determined by the CRs in the LED regime, and its broken power-law behavior is a consequence of the energy-dependent transition in the CR diffusion regime at rC(E) for E > EC.
3.2. Simplified model
In order to understand how the main features of the HESS J1745−290 spectrum restrict our model parameters, it is useful to provide approximate analytical expressions for our calculated gamma-ray emission. As this emission is dominated by CRs in the LED regime, it can be approximated by considering only the contribution from that regime. For further simplicity, we approximate the CR density in the LED regime by Eq. (21) (neglecting subdominant terms that ensure continuity with the other regimes), ignore the (weak) energy-dependence of σpp by fixing E = 1 TeV in Eq. (29), and integrate Eq. (28) from Eπ = Eπ, min = Eγ to Eπ, max = +∞ and from r = 0 to r = 0.07 pc for Eγ < Eγ, b and to r = rC(E) for Eγ > Eγ, b. (We note that the integral is dominated by the largest radii and the smallest energies over which it integrates.) This way, we obtain relatively simple expressions for Φγ(Eγ), which preserve the main features of our model, while showing the effect of the model parameters on the emitted spectrum. For Eγ ≲ Eγ, b,
while, for Eγ ≳ Eγ, b,
both of which are represented by the dashed green line in Fig. 3.
In order to reproduce the observations of HESS J1745−290, the broken power law predicted by our model needs to reproduce the values for its low- and high-energy indices, αLE and αHE (defined as α ≡ −dlogΦγ/dlog Eγ in the respective regimes), as well as the energy of the spectral break, Eγ, b.
Assuming q ≈ 2, as suggested by the spectrum in the CMZ (see Sect. 2.3), our model yields αLE = q + 1/3 ≈ 2.3, in good agreement with the observations (HESS Collaboration 2016), as can be seen from Fig. 3. At high energies, assuming also n ≈ 1, as suggested by the previous MHD simulations, our model yields αHE = q + (1 − m)/(n − m)≈3, which is relatively independent of the value of m. This result also appears to be consistent with the H.E.S.S. data (as seen in Fig. 3), although this part of the spectrum is less well constrained by the observations.
If Eγ, b ≈ 3 TeV, as suggested by the observed spectrum, the critical energy EC = Eγ, b/κπ ≈ 20 TeV. Comparing to Eq. (26) with 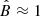 and n ≈ 0.9 − 1, as inferred from the MHD simulations of the Sgr A* accretion flow, this strongly constrains
and n ≈ 0.9 − 1, as inferred from the MHD simulations of the Sgr A* accretion flow, this strongly constrains 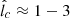 .
.
3.3. Constraints from our full model
In this section, we use our full model to show how our parameters are further constrained by the main features of the HESS J1745−290 spectrum.
The restrictions on 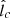 can be seen in Figure 5, which confirms that, for n = 1 and n = 0.9, the data favor the values
can be seen in Figure 5, which confirms that, for n = 1 and n = 0.9, the data favor the values 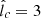 and
and 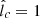 , respectively. As expected, the effect of increasing
, respectively. As expected, the effect of increasing 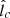 is to proportionally increase EC and therefore the energy of the spectral break, Eγ, b, as seen from Equation (26). This equation implies that cases with different
is to proportionally increase EC and therefore the energy of the spectral break, Eγ, b, as seen from Equation (26). This equation implies that cases with different 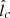 can produce the same Eγ, b ≈ 3 TeV, as long as
can produce the same Eγ, b ≈ 3 TeV, as long as 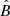 and n are adjusted accordingly. However, as argued above, the fact that the MHD simulations favor
and n are adjusted accordingly. However, as argued above, the fact that the MHD simulations favor 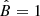 and n = 0.9 − 1 strongly constrains
and n = 0.9 − 1 strongly constrains  to the rather small range of
to the rather small range of 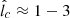 .
.
 |
Fig. 5. Gamma-ray spectrum for different choices of the parameters n and |
The effect of the cutoff energy of the CR injection spectrum, Emax, is shown in Fig. 6. As expected, it causes the gamma-ray spectrum to cut off around Eγ ∼ κπEmax.
 |
Fig. 6. Gamma-ray spectrum for different maximum energies Emax = 1, 3, and 10 PeV (Cases 11, 2, and 12, respectively), all with the same parameter values n = 1, m = 0, q = 2, |
In Sect. 3.2, we use approximate expressions for Φγ(Eγ) (Eqs. 30 and 31) to argue that the exponent m of the radial profile of the coherence length lc should not significantly affect the spectral index of the gamma-ray spectrum at low or high energies (αLE and αHE, respectively) or the gamma-ray energy that separates these two power-law regimes (Eγ ∼ 3 TeV). This is largely confirmed by Fig. 7a, which compares spectra for different values of m in the case n = 1. However, Eq. (31) implies that, in the case where n = 0.9, increasing the parameter m can weakly increase the index αHE of the high-energy emission, making this part of the spectrum steeper. This is indeed what is seen in Fig. 7b, where only the case where m = 0.4 shows a noticeably steeper spectrum. However, we show in Sect. 4 that the self-consistency of our model requires m to be small (≲0.3), and so we do not expect any significant effect of the parameter m as long as this restriction is met.
 |
Fig. 7. Dependence of the gamma-ray spectrum on the exponent m of the coherence length profile. Panel a: n = 1, |
Our findings therefore shows that models with 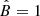 , q = 2, and Emax ≳ 1 PeV can accurately reproduce the main features of the spectrum of HESS J1745−290, including its break at Eγ, b ≈ 3 TeV. This happens for a narrow range of parameters spanned by the cases with n ≈ 1,
, q = 2, and Emax ≳ 1 PeV can accurately reproduce the main features of the spectrum of HESS J1745−290, including its break at Eγ, b ≈ 3 TeV. This happens for a narrow range of parameters spanned by the cases with n ≈ 1, 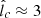 , and
, and 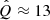 on the one hand, and n ≈ 0.9,
on the one hand, and n ≈ 0.9, 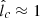 , and
, and 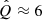 on the other. Remarkably, these values of q,
on the other. Remarkably, these values of q, 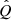 , and Emax are in good agreement with the estimates from the diffuse CMZ emission, in particular those obtained by HESS Collaboration (2016). Regarding m, its effect on the spectrum is relatively weak, and it only appears at Eγ ≳ Eγ, b. These results, however, establish a strong restriction on the largely unknown parameter
, and Emax are in good agreement with the estimates from the diffuse CMZ emission, in particular those obtained by HESS Collaboration (2016). Regarding m, its effect on the spectrum is relatively weak, and it only appears at Eγ ≳ Eγ, b. These results, however, establish a strong restriction on the largely unknown parameter 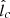 , which needs to be in the range
, which needs to be in the range 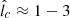 (equivalent to a coherence length of lc ≈ (1 − 3)×1014 cm).
(equivalent to a coherence length of lc ≈ (1 − 3)×1014 cm).
4. Consistency
In this section we check the consistency of several simplifying assumptions made in the calculation of the gamma-ray emission.
4.1. Gas-density profile ngas(r) for 0.07 pc < r< 0.4 pc.
According to Fig. 11 of Ressler et al. 2018, the ngas(r) profile at 0.07pc ≲ r ≲ 0.4pc is steeper than the ngas(r)∝r−1 profile assumed in our calculations (Eq. 18). This means that our calculated gamma-ray emission is somewhat larger than what we would obtain if a more accurate profile were assumed.
Here we show that using Eq. 18 to model ngas(r) in the range 0.07pc < r < 0.4pc only leads to a ∼20 − 30% overestimate in the emission and therefore does not affect significantly our results. This is shown in Fig. 3, where the purple dashed line represents the emission from 0.07pc < r < 0.4pc in our Case 2. We see that this emission is ≲20 − 30% of the total emission at all the energies of interest. Thus, assuming ngas(r)∝r−1 at all radii r < 0.4 pc should not significantly affect our main results.
4.2. Cosmic-ray transport for radii r > 0.4 pc
Even though CR transport at radii r > 0.4 pc is expected to be a combination of advection and diffusion, in our calculations we simply assume that transport at r > 0.4 pc is the same as at r = 0.4 pc. This should lead to an overestimate of the CR density in this region (as the assumed transport process may not be the most efficient one) and therefore provides an upper limit to its corresponding emission from r > 0.4 pc. In Fig. 3, the purple line represents this upper limit to the gamma-ray emission from r > 0.4 pc. We see that this emission is ≲3% of the total emission for all the energies of interest, and so this overestimate should not affect the accuracy of our results.
4.3. Validity of diffusion at r < 0.07 pc
In our calculations, we assume that diffusion is the dominant process for CR transport between r = rmin ∼ 10 Rg (where we expect the CRs to be injected) and r = 0.07 pc. In particular, at r ∼ 10 Rg, diffusion in the LED regime is assumed for CRs of all energies (as seen in the two cases (Case 2 and Case 4b) shown in Fig. 1). However, diffusive transport is a valid approximation for CR propagation only when r ≫ rλ, where rλ is defined as the radius where the CRs’ mean free path is equal to the radius itself, that is,
From Eq. (16), we can obtain the expression for the mean free path of the CRs in the LED regime and show that rλ satisfies
As the right hand side of Eq. (33) is a growing function of E, its upper limit is obtained by evaluating it at the maximum CR energy considered in this work, E = 10 PeV. This way we see that rλ/(10 Rg) is always ≲2.7, implying that assuming diffusion in the LED regime is a valid approximation for r larger than ∼30Rg, which is just outside the region where CRs are injected in our model.
We note, however, that applying Eq. (33) to values of rλ of as small as r ∼ 10 Rg may not be entirely consistent with the fact that Eq. (15) predicts the existence of a radius req defined by
such that, at r ≲ req, Eq. (15) is no longer a valid description of lc(r) (because lc(r) cannot be larger than r). Also, at r < req, the diffusion process should behave more as a 1D process, in the sense that the propagation occurs along a nearly homogeneous background magnetic field. Therefore, in obtaining Eq. (33), we are implicitly making the simplifying assumption that the dependence of the CR mean free path on r at r < req is the same as for r > req. Given that this simplification only applies to r between ∼10Rg (∼1013 cm) and req (≲1014 cm for 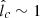 ), whereas most of the emission comes from large radii, we believe that it should not significantly affect the accuracy of our results.
), whereas most of the emission comes from large radii, we believe that it should not significantly affect the accuracy of our results.
4.4. Neglecting advection for r < 0.07 pc
In addition to influencing diffusion, advection can also contribute to CR transport because of the average radial gas velocity vgas at r < 0.07 pc. Ressler et al. (2018) show that for 0.01 pc ≲ r ≲ 0.07 pc, there is a stagnation region where the mass-accretion rate averaged over the whole solid angle approaches Ṁ ≈ 0, indicating that vgas should have a small effect on the CR transport in that region. In addition, for r ≲ 0.01 pc there is an inflow-dominated region where Ṁ is nearly constant. Taking Ṁ ≈ 10−8 M⊙/year near the black hole (Dexter et al. 2020), we obtain the expression for vgas given by Eq. (19). In order to neglect the effect of vgas on the transport of the CRs, its magnitude has to be smaller than vdiff for the lowest-energy CRs, which diffuse in the LED regime for all radii r < 0.07 pc (as seen in Fig. 1). Considering the definition of vdiff from Eq. (9), we obtain:
from which we obtain that the ratio vdiff/|vgas| is
As we are focusing on emission with Eγ ≳ 0.2 TeV, the lowest CR energy that we consider is E ∼ 0.2/κπ TeV ≈1 TeV. Therefore, since the ratio vdiff/|vgas| is an increasing function of r, neglecting advection requires vdiff/|vgas|≳1 for E = 1 TeV and r = 10Rg.
Figure 8a shows vdiff/|vgas| as a function of m for E = 1 TeV and r = 10Rg, for the two favored cases in this work: n = 1, 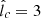 , and n = 0.9,
, and n = 0.9, 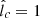 , shown in blue and red, respectively. We see that for n = 1,
, shown in blue and red, respectively. We see that for n = 1, 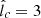 , neglecting advection requires m ≲ 0.4, while for n = 0.9,
, neglecting advection requires m ≲ 0.4, while for n = 0.9, 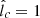 , it requires m ≲ 0.3. This result shows that the consistency of our calculations demands a weak dependence of lc on r, as assumed throughout this work.
, it requires m ≲ 0.3. This result shows that the consistency of our calculations demands a weak dependence of lc on r, as assumed throughout this work.
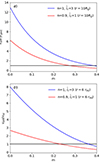 |
Fig. 8. Panel a shows vdiff/|vgas| (Eq. (36)) as a function of m for E = 1 TeV and r = 10Rg. Panel b shows vdiff/vtd (Eq. (39)) as a function of m for E = 1 TeV and r = 6req. In both panels, the blue line represents the case n = 1, |
Interestingly, the dependence of vdiff/|vgas| on E also implies that, in our model, CRs of energies E≪ 1 TeV are significantly affected by advection towards the black hole, in principle not being able to propagate beyond r ∼ 10Rg. This implies that a significant fraction of these particles should simply be accreted onto the black hole, with their gamma-ray emission for Eγ ≪ κπ × 1TeV ∼ 0.2 TeV not being captured by our model.
Cosmic rays could also be advected by the random motions of the MHD turbulence in the accretion flow, which we neglect in our model. If we estimate this turbulent velocity from the Alfvén velocity of the gas, 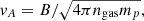 and its length scale from lc, the motion of the turbulence eddies should induce a CR diffusion characterized by a turbulent diffusion coefficient Dt given by
and its length scale from lc, the motion of the turbulence eddies should induce a CR diffusion characterized by a turbulent diffusion coefficient Dt given by
which allows us to estimate a turbulent diffusion velocity, vtd, as
Combining Eqs. (13), (15), (18), (35), (37), and (38), one can show that
which, for the values of n and m of interest (n ≈ 1 and m ≪ 1) is a growing function of r. Figure 8b shows vdiff/vtd as a function of m in the case where r = 6 req, where req is defined by Eq. (34), and for the smallest relevant energy E = 1 TeV. We can see that, in the cases of interest shown in the figure, vdiff/vtd ≳ 1 as long as m ≲ 0.3, which also satisfies the conditions for neglecting the effect of vgas. Thus, as vdiff/vtd is a growing function of r, vtd can be safely neglected for r ≳ 6 req. On the other hand, the effect of turbulent diffusion should be valid only for r ≳ req. This means that there is a range of radii, req ≲ r ≲ 6 req, in which turbulent diffusion can contribute significantly to CR transport, implying that the CR density dnCR/dE in that region should be somewhat smaller than what is obtained in our model. In order to find an upper limit to this effect, Figure 9 compares gamma-ray spectra calculated with rmin = 10 Rg and with rmin = 6 req, otherwise with the same parameters. We see that there are only small differences (at Eγ ≳ 100 TeV) between the calculations with rmin = Rg and rmin = 6 req, implying that neglecting turbulent diffusion should not significantly affect the accuracy of our results.
 |
Fig. 9. Effect of using different minimum radii rmin on the gamma-ray spectra. The solid and dashed lines represent analogous cases using rmin = 10 Rg and rmin = 6 req, respectively. Panels a and b show the cases where n = 1, |
This finding also reinforces the idea that gamma-ray emission is mainly produced at large radii, either close to 0.07 pc for Eγ ≲ 3 TeV or close to rC(Eγ/κπ) for Eγ ≳ 3 TeV, as shown in Fig 2.
4.5. Cosmic-ray, gas, and magnetic pressures
Our calculations assume that the gas properties in the accretion flow are determined by the hydrodynamic evolution of the wind of ∼30 WR stars that feed Sgr A*, as in the simulations of Ressler et al. (2018, 2020a) on which our results are based. However, the presence of CRs diffusing out from the central black hole can be dynamically important in this evolution if the CR pressure becomes comparable to the gas pressure. Figure 10 shows these two pressures as functions of r for the Cases 2 and 4b in Table 1 (corresponding to our fiducial cases with n = 1 and n = 0.9 shown in Fig. 1). The CR pressure is calculated as
 |
Fig. 10. Cosmic-ray, gas and magnetic pressure comparison (PCR, Pgas and PB, respectively). The values of the parameters considered correspond to cases 2 (solid lines) and 4b (dashed lines) in Table 1. |
where Emin = 1 TeV (as the CR density should be significantly suppressed for E ≪ 1 TeV, as shown in Sect. 4.4), and Emax = 3 PeV, while the gas pressure is calculated as
where kB is the Boltzmann constant, ngas(r) is the gas density specified in Eq. (18), and Tgas(r) is the angle- and time-averaged temperature of the gas obtained from Fig. 11 of Ressler et al. (2018),6 as
For completeness, we have also added the magnetic pressure profile for Cases 2 and 4b. We see that the gas pressure is dominant at almost all radii, with the CR pressure becoming relevant at r ∼ 0.07 pc, around the inner boundary of the region where the WR star winds feed the accretion flow (∼0.1 − 1 pc). The fact that PCR and Pgas are comparable at r ∼ 0.07 pc may somewhat modify the evolution of the accreting gas near the feeding region. However, regarding the hydrodynamic properties of the gas, we use the fact that PCR should only change the gas pressure by a factor ∼2 near r ∼ 0.07 pc, and thus assume that the gas dynamics at those radii is fairly well described by hydrodynamic considerations.
5. Diffusion timescales
The timescale for diffusion from the central black hole to a certain radius r can be estimated as tdiff ∼ r2/D(r) (valid as long as D(r) grows more slowly than r2). Above, we show that for CR energies E < EC ∼ 20 TeV, most of the emission occurs close to the radius r ≈ 0.07 pc where the transition from the LED to the advection regime occurs. Therefore, the time for CRs to diffuse out and produce the gamma-ray emission below the break energy is
On the other hand, for E > EC, most of the emission occurs near the transition radius rC(E) from the LED to the HED regime, for which the diffusion time is found to be
For any given gamma-ray energy Eγ, the emission currently observed roughly averages over the injection rate of CRs of energy E ∼ Eγ/κπ over the last tdiff(E). As expected, for all relevant energies, these diffusion times are much shorter than those corresponding to the CMZ, and therefore the gamma-ray emission of the point source is sensitive to much more recent activity (or inactivity) of the central black hole than the diffuse emission. Thus, the injection rate inferred from the point-source emission must not necessarily be the same as that explaining the CMZ; although we find them to be consistent with each other (with sizeable error bars on both).
It can also be seen from Eq. 44 that, for E > EC, tdiff is a quickly decreasing function of E, mostly because of the decreasing critical radius rC(E) (Eq. 25), which in turn is due to the rapidly increasing diffusion coefficient in the HED regime. For parameter choices favored by our model (n = 1, m = 0, 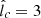 ,
, 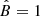 ), we obtain tdiff ∼ 0.5 yr(E/PeV)−2. Therefore, if the CR injection rate at PeV energies varies significantly on a comparable timescale (i.e., of the order of a few months), as suggested by the enhanced activity of Sgr A* in the radio, near-infrared, and X-ray bands during 2019 (Weldon et al. 2023 and references therein), this should be reflected in a significant variation of the gamma-ray emission at Eγ ≳ 100 TeV. This variable gamma-ray emission might be detectable in the near future by the Cherenkov Telescope Array Observatory (CTAO; Cherenkov Telescope Array Consortium 2019; Viana et al. 2019).
), we obtain tdiff ∼ 0.5 yr(E/PeV)−2. Therefore, if the CR injection rate at PeV energies varies significantly on a comparable timescale (i.e., of the order of a few months), as suggested by the enhanced activity of Sgr A* in the radio, near-infrared, and X-ray bands during 2019 (Weldon et al. 2023 and references therein), this should be reflected in a significant variation of the gamma-ray emission at Eγ ≳ 100 TeV. This variable gamma-ray emission might be detectable in the near future by the Cherenkov Telescope Array Observatory (CTAO; Cherenkov Telescope Array Consortium 2019; Viana et al. 2019).
6. Conclusions
The spatial distribution of the diffuse gamma-ray emission detected in the CMZ (corresponding to the inner ∼100 pc of the Milky Way), along with its extended spectrum reaching ∼100 TeV energies, suggests the presence in the Galactic center of a “PeVatron”, that is, a CR accelerator capable of reaching PeV energies, which has been associated to the supermassive black hole Sgr A* (HESS Collaboration 2016). In addition, due to the apparently coincident position of the point-like gamma-ray source HESS J1745−290 with Sgr A*, a PeVatron could potentially allow an explanation of both the diffuse CMZ emission and the point source as being due to the same CRs accelerated in the immediate vicinity of Sgr A* and diffusing outwards from it. This scenario, however, is challenged by the fact that the spectrum of the point source shows a power-law behavior with a spectral turnover at a few TeV, which is not shown by the diffuse emission in the CMZ. Although this turnover is usually characterized as an exponential cutoff, the spectrum of the point source is also compatible with a broken power law (Aharonian et al. 2009; Adams et al. 2021), as we also show in Appendix A using observations from HESS Collaboration (2016).
In order to reconcile the CMZ and point source spectra, we propose a model for the point source in which the CRs are continuously injected near Sgr A* (within a radius r ∼ 10Rg) and subsequently diffuse through its accretion flow (r ≲ 0.1 pc). This way, very high-energy gamma rays are emitted in the accretion flow via inelastic hadronic collisions between the CR protons and the background protons. A key feature of this model is the existence of two CR diffusion regimes within the accretion flow of Sgr A*. These regimes, according to theoretical arguments and test-particle simulations of CR propagation in synthetic MHD turbulence (which we assume is strong and has a Kolmogorov spectrum), depend on the ratio between the Larmor radius, RL, of the CRs and the coherence length, lc, of the turbulence. This way, the transition between these two regimes gives rise to a significant depletion of the highest-energy CRs (RL/lc ≫ 1) within the emission region, which explains the existence of a break in the point-source spectrum.
The free parameters of our model characterize the spectrum of the injected CRs, their propagation efficiency through the accretion flow, and the properties of the background gas. Interestingly, the values of these parameters, which are required to fit HESS J1745-290, are all consistent with expectations from the observations of the diffuse emission from the CMZ and with previous hydrodynamical and MHD simulations of the Sgr A* accretion flow. The only exception is given by the (very uncertain) coherence length of the magnetic turbulence, which needs to have an approximately homogeneous value, lc ∼ (1 − 3)×1014 cm ≈ (3 × 10−5 − 10−4) pc. Although disentangling the possible origin of this rather small coherence length is beyond the scope of this work, we speculate that its value might be affected by various processes, such as hydrodynamic instabilities in the colliding winds of the WR stars (Calderón et al. 2020) or even MHD instabilities driven by the CRs themselves. Indeed, in Sect. 4.5 we show that the CR pressure can be dynamically important within the feeding region (0.07 pc ≲ r ≲ 0.4 pc), where gas injection from the WR stars occurs. This region thus appears as an ideal environment for the action of, for example, the nonresonant instability, which is driven by the electric current of the CRs and has the potential to produce highly nonlinear MHD turbulence (Bell 2004, 2005; Riquelme & Spitkovsky 2009, 2010). We defer the study of these possible sources of turbulence to future research.
Our results therefore support the hypothesis that Sgr A* is capable of accelerating CRs up to a few PeV, contributing to explaining the origin of Galactic CRs up to the “knee”. It is worth emphasizing, however, that although we define our CR acceleration region very close to Sgr A* (at r ∼ 10Rg), the obtained emission spectra from our model are highly insensitive to the precise location of the injection region, as long as this region is anywhere in the range r ∼ (10 − 103) Rg (see discussion in Sect. 3.1).
Our model has the potential to be tested by future TeV telescopes, such as CTAO (Cherenkov Telescope Array Consortium 2019). Given the small size of the emitting region (r ≲ 0.1 pc, equivalent to ≲3 arcsec in angular size), our model predicts a gamma-ray source that cannot be resolved by any foreseeable TeV observatory. However, an interesting prediction of our model is that the spectrum of the point source should be a broken power law, with specific spectral indices αLE ≈ 2.3 for Eγ ≲ 3 TeV and αHE ≈ 3 for Eγ ≳ 3 TeV (see discussion in Sect. 3.2). This is in contrast to a single power law with an exponential cutoff, as has been suggested by other models (e.g., Guo et al. 2017). This means that, at gamma-ray energies of ≳ 10 TeV, the gamma-ray spectrum obtained from our model becomes notably different from other competing models. This is particularly interesting given that CTAO will be approximatelly ten times more sensitive than H.E.S.S., thus allowing us, in principle, to discriminate between the different models. Further model discrimination might be done using the possible time variability of HESS J1745−290 at the highest energies. This is interesting given the significant variability exhibited by Sgr A* at various wavelengths. Although our model assumes a steady injection of CRs, in Sect. 5 we estimate that, if CR injection were variable, our model would predict potentially significant variability at Eγ ∼ 100 TeV on timescales of as short as months. To date, however, observations have failed to detect variability of the HESS J1745−290 gamma-ray point source, possibly because current observatories do not possess the required sensitivity to detect such variability. In this respect, the upcoming observations with CTAO may, in principle, have sufficiently sensitivity to detect the point-source variability. We defer the study of this possibility to future research.
We confirm this point in Appendix A, using up-to-date H.E.S.S. data from HESS Collaboration (2016).
HESS Collaboration (2016) assumed isotropic diffusion. Alternative models with anisotropic diffusion have recently been explored by Dörner et al. (2024).
The first of these relations is nearly identical to that inferred by Eatough et al. (2013) from the X-ray observations reported by Muno et al. (2004).
The time averages presented in Fig. 11 of Ressler et al. (2018) are performed over the 100 years previous to the present day.
Acknowledgments
The authors gratefully acknowledge support from ANID-FONDECYT grants 1191673 and 1201582, as well as the Center for Astrophysics and Associated Technologies (CATA; ANID Basal grant FB210003).
References
- Adams, C. B., Benbow, W., Brill, A., et al. 2021, ApJ, 913, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. 2004, Very High Energy Cosmic Gamma Radiation: a Crucial Window on the Extreme Universe (World Scientific) [CrossRef] [Google Scholar]
- Aharonian, F., & Neronov, A. 2005, Astrophys. Space Sci., 300, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K. M., et al. 2004, A&A, 425, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Phys. Rev. Lett., 97, 221102 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al. 2009, A&A, 503, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Yang, R., & de Oña Wilhelmi, E. 2019, Nat. Astron., 3, 561 [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006, ApJ, 638, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Aloisio, R., & Berezinsky, V. 2004, ApJ, 612, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Bell, A. R. 2005, MNRAS, 358, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Calderón, D., Cuadra, J., Schartmann, M., et al. 2020, MNRAS, 493, 447 [Google Scholar]
- Cembranos, J. A. R., Gammaldi, V., & Maroto, A. L. 2012, Phys. Rev. D, 86, 103506 [NASA ADS] [CrossRef] [Google Scholar]
- Cherenkov Telescope Array Consortium (Acharya, B. S., et al.) 2019, Science with the Cherenkov Telescope Array [Google Scholar]
- Chernyakova, M., Malyshev, D., Aharonian, F. A., Crocker, R. M., & Jones, D. I. 2011, ApJ, 726, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Clavel, M., Terrier, R., Goldwurm, A., et al. 2013, A&A, 558, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuadra, J., Nayakshin, S., Springel, V., & Di Matteo, T. 2006, MNRAS, 366, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Cuadra, J., Nayakshin, S., & Martins, F. 2007, MNRAS, 383, 458 [Google Scholar]
- Dexter, J., Jiménez-Rosales, A., Ressler, S. M., et al. 2020, MNRAS, 494, 4168 [NASA ADS] [CrossRef] [Google Scholar]
- Dörner, J., Becker Tjus, J., Blomenkamp, P. S., et al. 2024, ApJ, 965, 180 [CrossRef] [Google Scholar]
- Dundovic, A., Pezzi, O., Blasi, P., Evoli, C., & Matthaeus, W. H. 2020, Phys. Rev. D, 102, 103016 [NASA ADS] [CrossRef] [Google Scholar]
- Eatough, R. P., Falcke, H., Karuppusamy, R., et al. 2013, Nature, 501, 391 [Google Scholar]
- Fleishman, G. D., & Toptygin, I. N. 2013, Cosmic Electrodynamics: Electrodynamics and Magnetic Hydrodynamics of Cosmic Plasmas (Springer), 388 [CrossRef] [Google Scholar]
- Funk, S., & Hinton, J. A. 2008, Am. Inst. Phys. Conf. Ser., 1085, 882 [NASA ADS] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Y.-Q., Tian, Z., Wang, Z., Li, H.-J., & Chen, T.-L. 2017, ApJ, 836, 233 [NASA ADS] [CrossRef] [Google Scholar]
- HESS Collaboration (Abramowski, A., et al.) 2016, Nature, 531, 476 [Google Scholar]
- HESS Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinton, J. A., & Aharonian, F. A. 2007, ApJ, 657, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, D., de la Calle Perez, I., Silk, J., Ferrer, F., & Sarkar, S. 2004, JCAP, 2004, 002 [CrossRef] [Google Scholar]
- Hosek, M. W., Do, T., Lu, J. R., et al. 2022, ApJ, 939, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kosack, K., Badran, H. M., Bond, I. H., et al. 2004, ApJ, 608, L97 [CrossRef] [Google Scholar]
- Liu, R.-Y., Wang, X.-Y., Prosekin, A., & Chang, X.-C. 2016, ApJ, 833, 200 [NASA ADS] [CrossRef] [Google Scholar]
- MAGIC Collaboration (Acciari, V. A., et al.) 2020, A&A, 642, A190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marin, F., Churazov, E., Khabibullin, I., et al. 2023, Nature, 619, 41 [Google Scholar]
- Mertsch, P. 2020, Ap&SS, 365, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Baganoff, F. K., Bautz, M. W., et al. 2004, ApJ, 613, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., George, E., Scaringi, S., et al. 2017, MNRAS, 468, 2447 [NASA ADS] [CrossRef] [Google Scholar]
- Profumo, S. 2005, Phys. Rev. D, 72, 103521 [NASA ADS] [CrossRef] [Google Scholar]
- Reichherzer, P., Becker Tjus, J., Zweibel, E. G., Merten, L., & Pueschel, M. J. 2022a, MNRAS, 514, 2658 [NASA ADS] [CrossRef] [Google Scholar]
- Reichherzer, P., Merten, L., Dörner, J., et al. 2022b, SN Appl. Sci., 4, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Reichherzer, P., Bott, A. F. A., Ewart, R. J., et al. 2023, ArXiv e-prints [arXiv:2311.01497] [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2018, MNRAS, 478, 3544 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2020a, MNRAS, 492, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., White, C. J., Quataert, E., & Stone, J. M. 2020b, ApJ, 896, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Riquelme, M. A., & Spitkovsky, A. 2009, ApJ, 694, 626 [Google Scholar]
- Riquelme, M. A., & Spitkovsky, A. 2010, ApJ, 717, 1054 [CrossRef] [Google Scholar]
- Rodríguez-Ramírez, J. C., de Gouveia Dal Pino, E. M., & Alves Batista, R. 2019, ApJ, 879, 6 [Google Scholar]
- Scepi, N., Dexter, J., & Begelman, M. C. 2022, MNRAS, 511, 3536 [NASA ADS] [CrossRef] [Google Scholar]
- Scherer, A., Cuadra, J., & Bauer, F. E. 2022, A&A, 659, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherer, A., Cuadra, J., & Bauer, F. E. 2023, A&A, 679, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [Google Scholar]
- Subedi, P., Sonsrettee, W., Blasi, P., et al. 2017, ApJ, 837, 140 [Google Scholar]
- Subroweit, M., Mossoux, E., & Eckart, A. 2020, ApJ, 898, 138 [CrossRef] [Google Scholar]
- Tsuchiya, K., Enomoto, R., Ksenofontov, L. T., et al. 2004, ApJ, 606, L115 [CrossRef] [Google Scholar]
- Viana, A., Ventura, S., Gaggero, D., et al. 2019, Int. Cosmic Ray Conf., 36, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Q. D., Lu, F. J., & Gotthelf, E. V. 2006, MNRAS, 367, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Weldon, G. C., Do, T., Witzel, G., et al. 2023, ApJ, 954, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J. L., Bi, X. J., & Hu, H. B. 2006, A&A, 449, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Fitting HESS J1745-290 spectrum with a broken power law
The central point source HESS J1745-290 is usually characterized by a hard power law spectrum with a photon index ∼2.1 and an exponential cutoff at ∼10 TeV. When compared with a pure power law, the power law with an exponential cutoff (ECPL) is clearly preferred by the data (HESS Collaboration 2016).
Besides a power law with an exponential cutoff, the spectral shape of HESS J1745-290 has also been shown to be compatible with a broken power law with the break energy at a few TeV (Aharonian et al. 2009; Adams et al. 2021). Here we use more up-to-date H.E.S.S. observations of this source obtained from HESS Collaboration (2016) to confirm this point.
Fig. A.1 shows two least-squares fits of the point source (for which we used the Levenberg-Marquardt algorithm). The blue line corresponds to a broken power-law (BPL) model for the photon flux, Φγ(Eγ), given by
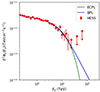 |
Fig. A.1. Least squares fits of the point source spectrum. The blue and green lines correspond to a BPL model and a single ECPL model for photon fluxes given by Eqs. A.1 and A.2, respectively. The red circles correspond to H.E.S.S. data from HESS Collaboration (2016). |
for which we obtain Φ0 = (2.44 ± 1.2)×10−14 TeV−1 cm−2 s−1, Ec = 8.22 ± 1.4 TeV, Γ1 = 2.18 ± 0.04, Γ2 = 3.89 ± 0.52, a p-value of p = 0.63, and χ2/DOF = 0.87.
The green line corresponds to a ECPL model given by
for which we find Φ0 = (1.83 ± 0.88)×10−14 TeV−1 cm−2 s−1, Ec = 10.13 ± 1.89 TeV, Γ1 = 2.13 ± 0.03, a p-value of p = 0.62, and χ2/DOF = 0.88. The similar values of p and χ2/DOF obtained from these two fits imply that the BPL and ECPL models are both compatible with the current H.E.S.S. data from HESS Collaboration (2016).
Appendix B: Heuristic derivation of the diffusion coefficients
Here, we give simple, rough, physical derivations of the effective mean free paths, λmfp, and therefore of the diffusion coefficients, D = λmfpc/3, of relativistic, charged particles in a medium with isotropic, magnetic Kolmogorov turbulence with coherence length lc and Larmor radius RL. For the HED regime, RL ≫ lc, a similar derivation has been given by Subedi et al. (2017), and we give it here for completeness. For the LED regime, RL ≪ lc, we are not aware of a similar derivation in the literature. For simplicity and given the rough approximations involved, we generally ignore numerical factors ∼2π and smaller.
B.1. High-energy diffusion (HED) regime
If RL ≫ lc, as a particle crosses a coherence length lc, it deviates only by a small angle, θ1 ∼ lc/RL. These deviations are random, in different directions for successive steps of size lc. Therefore, the direction of motion undergoes a random walk, accumulating a typical deviation 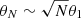 after N such steps. The direction of motion will have changed significantly once θN ∼ 1, implying N ∼ (RL/lc)2, which defines the mean free path
after N such steps. The direction of motion will have changed significantly once θN ∼ 1, implying N ∼ (RL/lc)2, which defines the mean free path 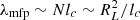 .
.
B.2. Low-energy diffusion (LED) regime
On scales ≪lc, the magnetic field can be approximated by B = B0 + δBr), where B0 = constant and |δB(r)| ≪ B0. If RL ≡ γmc2/(qB0)≪lc, where γ, m, and q are the Lorentz factor, the mass, and the charge of the particles, respectively, the latter will follow a roughly helical motion, typically with velocity components of similar magnitude (not much smaller than c) along B0, v‖, and perpendicular to it, v⊥. Thus, the particles will move a distance ∼RL along B0 while completing an orbit of radius ∼RL in the perpendicular plane.
The equation of motion for the parallel velocity component is
Since the direction of v⊥ completes a loop while the particle travels a distance ∼RL, v‖ will be mostly affected by field perturbations on roughly the same scale, which we will call δB*. Its typical change while traveling this scale will be small, Δv∥, 1 ∼ cδB*/B0, but these random changes can accumulate, yielding a substantial change 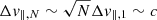 after N ∼ (c/Δv∥, 1)2 steps, corresponding to a one-dimensional mean free path (along B0) given by λmfp ∼ RL(B0/δB*)2. For Kolmogorov turbulence, B0/δB* ∼ (lc/RL)1/3, therefore the one-dimensional mean free path is
after N ∼ (c/Δv∥, 1)2 steps, corresponding to a one-dimensional mean free path (along B0) given by λmfp ∼ RL(B0/δB*)2. For Kolmogorov turbulence, B0/δB* ∼ (lc/RL)1/3, therefore the one-dimensional mean free path is
with a corresponding diffusion coefficient D1D = λmfpc/3.
The time required to diffuse a distance lc along B0 is 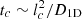 . On each patch of size lc, the magnetic field has a random orientation. Thus, on larger scales, the diffusion process becomes three-dimensional, with steps of size lc traversed at a typical speed vc ∼ lc/tc, so the large-scale, three-dimensional diffusion coefficient is
. On each patch of size lc, the magnetic field has a random orientation. Thus, on larger scales, the diffusion process becomes three-dimensional, with steps of size lc traversed at a typical speed vc ∼ lc/tc, so the large-scale, three-dimensional diffusion coefficient is 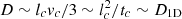 , as in the one-dimensional analysis above.
, as in the one-dimensional analysis above.
Appendix C: Full expressions for dnCR/dE
In this appendix we describe the analytical treatment for the CR density distribution per unit energy dnCR/dE of our full model described in Sect. 2.
C.1. Continuity and boundary conditions
As explained in 2.1, in order to determine the CR density distribution on the Sgr A* accretion flow, we solve Eq. 8 neglecting one of the two terms on the right hand side, depending on whether diffusion of advection dominates. In the case dominated by diffusion, we have
while is advection is the dominant transport mechanism of CRs,
The above equations for dnCR/dE are constrained by continuity restrictions, which we characterize in Fig. C.1, noting that: rC(E) represent the critical radius at which a CR of energy E will transit from the LED regime to HED regime (see Eq. 25), rC, ad(E) represent the radius at which a CR of energy E transit from the HED regime to the AD regime (see Eq. 27), given that the gas velocity is determined by Eq. 20.
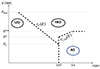 |
Fig. C.1. Schematic representation of the different CR transport regimes used to calculate dnCR/dE, as a function of radius r and CR energy E. These regimes correspond to low-energy diffusion (LED), high-energy diffusion (HED) and advection-dominated (AD). |
Fig C.1, shows a schematic representation of the different CR transport regimes used to calculate dnCR/dE, as a function of radius r and CR energy E. We see that, besides EC (defined by rC(E) = 0.07 pc), the limits between these regions are characterized by the energies E* and E**, corresponding to the energies where rC, ad(E) becomes equal to 0.07 pc and 0.4 pc, respectively. Thus, the continuity conditions for the CR density can be described within the four energy ranges shown in Fig C.1:
-
Energy range E ϵ [1TeV − EC]:
-
Energy range E ϵ [EC − E*]:
-
Energy range E ϵ [E* − E**]:
-
Energy range E ϵ [E** − Emax]:
In all cases, we impose dnCR/dE(E, r → ∞)→0.
C.2. Full model for the CR density distribution
Here we show the full expression for dnCR/dE obtained from solving Eqs. C.1 and C.2 under the aforementioned restrictions, for the four different energy ranges depicted in Fig. C.1 and for the different radial ranges within them.
-
Energy range E ϵ [1TeV − EC]: In the case of r ≤ 0.07 pc,
where the first term on the right hand is the same as the right hand side of Eq. 21, in which boundary condition terms were neglected. In the cases 0.07 pc ≤r ≤ 0.4 pc and r ≥ 0.4 pc, the expressions for dnCR/dE are the same as Eqs. 23 and 24, respectively, since no boundary terms were neclected in those cases.
-
Energy range E ϵ [EC − E*]: If r ≤ rC(E),
where, the first term on the right hand side is again equal to the right hand side of the simpler Eq. 21. If rC(E)≤r ≤ 0.07 pc,
where the first term on the right hand side is the same as the right hand side of Eq. 22, which does not include boundary terms. In the cases 0.07 pc ≤r ≤ 0.4 pc and r ≥ 0.4 pc, the expressions for dnCR/dE are the same as those provided by Eqs. 23 and 24, since in those cases no boundary terms were neglected.
-
Energy range E ϵ [E* − E**]: If r ≤ rC(E)
where the first term on the right hand side coincides with the right hand side of Eq. 21. If rC(E)≤r ≤ rC, ad(E),
where the first term on the right hand side coincides with the right hand side of Eq. 22. If rC, ad(E)≤r ≤ 0.4 pc and r ≥ 0.4 pc, once again, the expressions for dnCR/dE are the same as those provided in the main text for the ADV regime (Eqs. 23 and 24, respectively).
-
Finally, the energy range E ϵ [E**, Emax]: If r ≤ rC(E),
where the first term on the right hand side is the same as the right hand side of Eq. 21. In the radial range r ≥ rC(E), the expression for dnCR/dE is the same as Eq. 22, since in the energy range E ϵ [E**, Emax], the CR density in the HED regime simply needs to satisfy the boundary condition dnCR/dE(E, r → ∞)→0, which is already satisfied by Eq. 22.
All Tables
Different model parameter combinations considered in this work. In all cases, 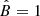 and q = 2.
and q = 2.
All Figures
 |
Fig. 1. Cosmic-ray density per unit energy dnCR/dE as a function of the radial coordinate r (horizontal axis) and the CR energy E (vertical axis) for cases 2 (panel a) and 4b (panel b) specified in Table 1. The color scale gives log10(E7/3rξdnCR/dE) in cgs units (with ξ = 4/3 in panel a and ξ = 1.3 in panel b), and the dashed lines mark the boundaries between the three CR transport regimes discussed in the text, namely the low-energy diffusion (LED), high-energy diffusion (HED), and advection-dominated (AD) regimes. |
| In the text | |
 |
Fig. 2. Differential gamma-ray flux per logarithmic interval of r, dΦγ/dlog10(r), as a function of Eγ and r for Case 2 in Table 1. |
| In the text | |
 |
Fig. 3. Full and approximate models for the gamma-ray spectrum of HESS J1745−290 with the parameters of Case 2 of Table 1. The solid blue line represents the total gamma-ray emission calculated from the full model. The dashed blue line is the “LED model”, considering only the emission from CRs in the LED regime. The dashed green line shows our simplified model, given by Eqs. (30) and (31). The solid and dashed purple lines represent the contributions from CRs at r > 0.4 pc and 0.07 pc < r < 0.4 pc, respectively. The red dots correspond to the H.E.S.S. measurements (HESS Collaboration 2016). |
| In the text | |
 |
Fig. 4. Gamma-ray spectra for Case 2 of Table 1 for different minimum radii rmin from which the gamma-ray emission is integrated (see Eq. (28)). The red dots correspond to the H.E.S.S. measurements of the source HESS J1745−290 (HESS Collaboration 2016). |
| In the text | |
 |
Fig. 5. Gamma-ray spectrum for different choices of the parameters n and |
| In the text | |
 |
Fig. 6. Gamma-ray spectrum for different maximum energies Emax = 1, 3, and 10 PeV (Cases 11, 2, and 12, respectively), all with the same parameter values n = 1, m = 0, q = 2, |
| In the text | |
 |
Fig. 7. Dependence of the gamma-ray spectrum on the exponent m of the coherence length profile. Panel a: n = 1, |
| In the text | |
 |
Fig. 8. Panel a shows vdiff/|vgas| (Eq. (36)) as a function of m for E = 1 TeV and r = 10Rg. Panel b shows vdiff/vtd (Eq. (39)) as a function of m for E = 1 TeV and r = 6req. In both panels, the blue line represents the case n = 1, |
| In the text | |
 |
Fig. 9. Effect of using different minimum radii rmin on the gamma-ray spectra. The solid and dashed lines represent analogous cases using rmin = 10 Rg and rmin = 6 req, respectively. Panels a and b show the cases where n = 1, |
| In the text | |
 |
Fig. 10. Cosmic-ray, gas and magnetic pressure comparison (PCR, Pgas and PB, respectively). The values of the parameters considered correspond to cases 2 (solid lines) and 4b (dashed lines) in Table 1. |
| In the text | |
 |
Fig. A.1. Least squares fits of the point source spectrum. The blue and green lines correspond to a BPL model and a single ECPL model for photon fluxes given by Eqs. A.1 and A.2, respectively. The red circles correspond to H.E.S.S. data from HESS Collaboration (2016). |
| In the text | |
 |
Fig. C.1. Schematic representation of the different CR transport regimes used to calculate dnCR/dE, as a function of radius r and CR energy E. These regimes correspond to low-energy diffusion (LED), high-energy diffusion (HED) and advection-dominated (AD). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



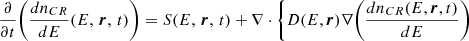
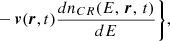
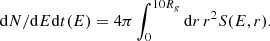
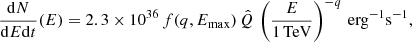
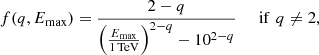
![$$ \begin{aligned} f(q=2,E_{\mathrm{max}})=\left[\ln \left(\frac{E_{\mathrm{max}}}{1 \,\mathrm{TeV}}\right)-\ln (10)\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2024/09/aa49851-24/aa49851-24-eq7.gif)
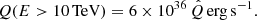
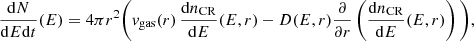
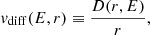
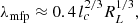
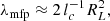
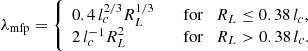
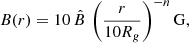
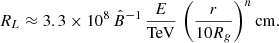
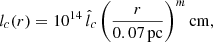
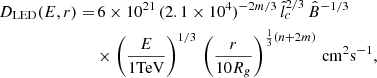
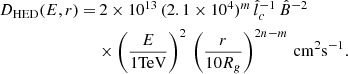
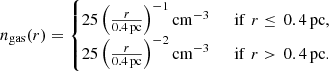
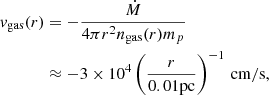
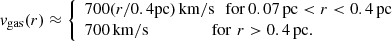
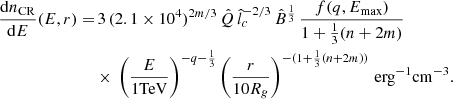
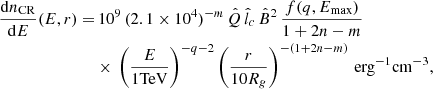
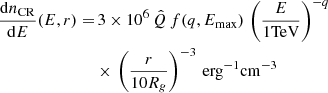
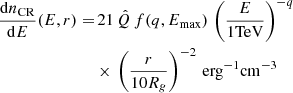
![$$ \begin{aligned} r_C(E)=0.07 \left[\frac{1.3\times 10^5 \, \hat{l}_c \, \hat{B}}{(2.1\times 10^4)^n}\right]^{\frac{1}{n-m}} \left(\frac{E}{\mathrm{TeV}}\right)^{-\frac{1}{n-m}} \, \mathrm{pc}, \end{aligned} $$](/articles/aa/full_html/2024/09/aa49851-24/aa49851-24-eq40.gif)