| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A278 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202450053 | |
| Published online | 22 July 2024 | |
Asteroid-NeRF: A deep-learning method for 3D surface reconstruction of asteroids
Research Centre for Deep Space Explorations | Department of Land Surveying & Geo-Informatics, The Hong Kong Polytechnic University,
Hung Hom,
Kowloon,
Hong Kong
e-mail: bo.wu@polyu.edu.hk
Received:
21
March
2024
Accepted:
15
May
2024
Context. Asteroids preserve important information about the origin and evolution of the Solar System. Three-dimensional (3D) surface models of asteroids are essential for exploration missions and scientific research. Regular methods for 3D surface reconstruction of asteroids, such as stereo-photogrammetry (SPG), usually struggle to reconstruct textureless areas and can only generate sparse surface models. Stereo-photoclinometry (SPC) can reconstruct pixel-wise topographic details but its performance depends on the availability of images obtained under different illumination conditions and suffers from uncertainties related to surface reflectance and albedo.
Aims. This paper presents Asteroid-NeRF, a novel deep-learning method for 3D surface reconstruction of asteroids that is based on the state-of-the-art neural radiance field (NeRF) method.
Methods. Asteroid-NeRF uses a signed distance field (SDF) to reconstruct a 3D surface model from multi-view posed images of an asteroid. In addition, Asteroid-NeRF incorporates appearance embedding to adapt to different illumination conditions and to maintain the geometric consistency of a reconstructed surface, allowing it to deal with the different solar angles and exposure conditions commonly seen in asteroid images. Moreover, Asteroid-NeRF incorporates multi-view photometric consistency to constrain the SDF, enabling optimised reconstruction.
Results. Experimental evaluations using actual images of asteroids Itokawa and Bennu demonstrate the promising performance of Asteroid-NeRF, complementing traditional methods such as SPG and SPC. Furthermore, due to the global consistency and pixel-wise training of Asteroid-NeRF, it produces highly detailed surface reconstructions. Asteroid-NeRF offers a new and effective solution for high-resolution 3D surface reconstruction of asteroids that will aid future exploratory missions and scientific research on asteroids.
Key words: techniques: image processing / minor planets, asteroids: general / planets and satellites: surfaces
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Asteroids are remnants of planetary bodies and may preserve materials from the early stages of the Solar System that contain critical information about its origin and evolution (Festou et al. 2004; Lauretta et al. 2022). Therefore, space exploration missions have frequently targeted asteroids (Giese et al. 2006; Preusker et al. 2015; Hirata et al. 2020) due to the significant scientific interest they garner. Three-dimensional (3D) surface models of asteroids are essential for scientific exploration, operational planning, and spacecraft navigation, and also provide clues about asteroid formation and their geological and surfi-cial evolution (Yeomans et al. 1999; Abe et al. 2006; Scheeres et al. 2016; Wu et al. 2018). Remote sensing images collected by a spacecraft during flyby or at orbit are typically used to reconstruct an asteroid’s surface (Gaskell et al. 2008). At present, stereo-photogrammetry (SPG) (Wu 2017; Scholten et al. 2019; Edmundson et al. 2020) and stereo-photoclinometry (SPC) (Barnouin et al. 2019; Gaskell et al. 2008; Liu et al. 2018) are the two image-based algorithms most often used to reconstruct surface models of asteroids.
Stereo-photogrammetry uses stereo images to calculate disparity and depth by observing an area with a degree of overlap (Do & Nguyen 2019). Structure from motion (SfM) is a typical method employed to obtain a scene’s depth and involves using a single moving camera to capture multi-view images (Ullman 1979; Schonberger & Frahm 2016). SPG has been used to reconstruct asteroid surface models in many exploratory missions to asteroids, such as Phoebe (Giese et al. 2006), 67P/Churyumov-Gerasimenko (Preusker et al. 2015), and Ryugu (Hirata et al. 2020). SPG of asteroids often involves stereo-image selection followed by feature matching to derive stereo pairs and image coordinates of tie points among them. Subsequently, the exterior orientation parameters and tie-point coordinates are calculated using bundle adjustment (Wu 2017). Finally, subsets are fused into a global surface model (Preusker et al. 2019). SPG can obtain an accurate asteroid surface model from images with similar spatial resolutions and illumination and sufficient overlap from different views (Preusker et al. 2015). However, SPG can struggle to deal with shadow changes in images captured at different times, viewing angle limitations caused by spacecraft orbit constraints, and textureless areas on asteroids, resulting in reconstructions with reduced accuracy and levels of completion (Kim et al. 2023; Long & Wu 2019). Moreover, SPG can only generate sparse surface models with spatial resolutions 4–20 times those of images, depending on an image’s textural conditions (Wu 2017; Liu & Wu 2021).
Stereo-photoclinometry is a combination of SPG and photo-clinometry. First, SPC uses SPG to calculate the 3D positions of maplets (Gaskell et al. 2008), which are small local surface patches containing geometric and albedo information, and then uses photoclinometry to reconstruct high-resolution topography of maplets through pixel-to-pixel slope estimation. Finally, SPC merges maplets and performs optimisation to generate a complete 3D surface model (Gaskell et al. 2008, 2023; Palmer et al. 2016, 2022). SPC has demonstrated favourable performance in reconstructing surface models of many asteroids, such as Itokawa (Gaskell et al. 2008), Vesta (Gaskell 2012), Ryugu (Watanabe et al. 2019), and Bennu (Barnouin et al. 2019). However, SPC usually uses a coarse-to-fine strategy to itera-tively refine and update a shape model and thus requires manual assistance and a large number of images, leading to long preparation and processing times (Al Asad et al. 2021; Palmer et al. 2022; Weirich et al. 2022). Moreover, for good performance, SPC should be conducted under various illumination conditions and viewing directions, but these may be limited by orbital and mission design (Liu & Wu 2021). Furthermore, SPC generates surface reflectance models and determines albedo based on assumptions or simplifications of a real situation, which may lead to uncertainties or errors in surface reconstruction (Liu et al. 2018; Liu & Wu 2020).
There have been rapid advancements in deep learning technologies in recent years. For example, novel neural network methods have been developed for 3D scene representation, such as neural implicit representation and neural radiance field (NeRF), which exhibit state-of-the-art performance (Chen & Zhang 2019; Mescheder et al. 2019; Park et al. 2019). NeRF and related methods are of particular interest due to their ability to reconstruct 3D scenes from multi-view images and render photorealistic images (Mildenhall et al. 2021; Wang et al. 2021a,b; Barron et al. 2021; Li et al. 2023). NeRF uses 2D images to perform volume rendering – a differentiable rendering method – for optimisation. Volume rendering has shown excellent performance in synthesising images of complex scenes but has difficulty in extracting accurate geometric information due to its unclear surface definition (Mildenhall et al. 2021; Tewari et al. 2022). In contrast, NeRF, combined with a signed distance field (SDF) – which is a form of surface representation – performs 3D reconstruction based on images named neural implicit surfaces (NeuS) (Wang et al. 2021a). Similarly, Neuralangelo, which is based on NeuS, combines a progressive learning strategy and hash grid representation to ensure efficiency while achieving high-accuracy reconstruction of complex targets and large-scale scenes (Li et al. 2023).
This paper presents Asteroid-NeRF, a novel deep-learning method for 3D surface reconstruction of asteroids based on neural implicit representation. Unlike SPG and SPC, which estimate the locations of subsurfaces locally and fuse them into a complete model, Asteroid-NeRF utilises a continuous and global SDF to reconstruct the shape and radiance of a target. Moreover, Asteroid-NeRF incorporates novel appearance-embedding strategies to deal with asteroid images captured under varying lighting environments and employs multi-view photometric consistency to optimise a surface.
The remainder of this paper is organised as follows. Section 2 provides a brief review of related work. Section 3 details Asteroid-NeRF. Section 4 presents experimental results using real images of the asteroids Itokawa and Bennu and compares these with the results obtained using other methods. Section 5 contains a discussion and our conclusions.
2 Related work
In the past few decades, there have been substantial improvements in SPG and SPC methods and both have been applied in multiple asteroid exploration missions to aid spacecraft navigation (Giese et al. 2006; Gaskell et al. 2008), maximise the number of samples returned, and support subsequent scientific research (Palmer et al. 2016; Preusker et al. 2019; Barnouin et al. 2020; Gaskell et al. 2023). In this section, we introduce the development of neural implicit representation, with a focus on its use in 3D geometry reconstruction.
Results generated by traditional methods, such as SPG and SPC, are explicit representations, such as point clouds, voxel grids, and meshes, which have insufficient visual quality, such as discontinuous or overly smoothed surfaces, topological noise, and irregularities (Chen & Zhang 2019; Remondino et al. 2014). Neural implicit representations are globally consistent and continuous, which means that they can represent a scene’s appearance and geometry from the 3D position and 2D viewing direction as input with a high degree of detail. These representations have been employed in a variety of applications, such as novel view rendering (Mildenhall et al. 2021; Barron et al. 2021, 2022), camera pose estimation (Yen-Chen et al. 2021; Yan et al. 2024), shape generation and completion (Liu et al. 2023), and surface reconstruction (Wang et al. 2021a; Li et al. 2023). Moreover, given that geometrically accurate 3D reconstruction is crucial in photogrammetry and remote sensing, neural implicit representation has been used to reconstruct 3D scenes and extract geometric information, as described below.
Due to the high degree of consistency of neural implicit representations, some researchers have fused NeRF with an SDF to narrow the gap between volumes and surfaces to implicitly reconstruct geometry. Implicit Differentiable Renderer (IDR) is a neural network architecture that applies differentiable rendering to an SDF and then allocates a mask to the reconstructed object to directly fit the object’s surface (Yariv et al. 2020). Unifying Neural Implicit Surfaces and Radiance Fields (UNISURF) is a technology that integrates SDF differentiable rendering and NeRF volume rendering technology, allowing it to directly reconstruct 3D models without additional input (Oechsle et al. 2021). NeuS modifies the volume-rendering process to make it unbiased to a surface and meet occlusion-aware needs, thereby enabling reconstruction of a 3D surface that is more accurate than the initial surface (Wang et al. 2021a). The Manhattan-world hypothesis posits that the floors and walls of indoor and outdoor city scenes predominantly align with three principal orientations (Coughlan & Yuille 1999). Building on this premise, Guo et al. (2022) applied planar constraints to the areas associated with floors and walls for neural implicit surface reconstruction in indoor environment. High-frequency NeuS (HF-NeuS) utilises a base function for overall geometric structure and a displacement function for high-frequency details to perform gradual reconstruction of a surface (Wang et al. 2022). However, although NeuS is one of the most well-known frameworks for neural implicit global reconstruction, it requires excessively long training times. Instant neural graphics primitives (Instant-NGP) proposes a multi-resolution hash grid to integrate and encode a position, leading to a significant acceleration in training and rendering (Müller et al. 2022). NeuS2 incorporates a multi-resolution hash grid into NeuS and alleviates the computational complexity of the second derivative in order to reduce training time (Wang et al. 2023). Neuralangelo reconstructs thin structures of the real world by replacing analytical gradients with numerical gradients in a smoothing function and uses a coarse-to-fine strategy on a hash grid to gradually increase the level of detail in a reconstruction (Li et al. 2023). However, all of the above-described methods are designed for processing images captured on Earth, such as in daily life with a commercially available camera; this is significantly different from processing images captured during space exploration. Consequently, we improve Neuralangelo for images captured by narrow-angle cameras in different illumination environments and use multi-view photometric consistency to smooth surfaces in textureless areas.
Compared with existing methods based on neural implicit representation, Asteroid-NeRF has three key novel features. First, it utilises a sparse point cloud to constrain the sampling range of ray matching to that of images. The constraint on sampling range is specifically designed for images captured by narrow-angle cameras employed on spacecraft. Second, it uses appearance embedding – which decouples geometric and appearance information – to deal with differences between the lighting in images obtained at different times. Third, it employs multi-view photometric consistency to regulate surface optimisation, making it suitable for the weakly textured areas often found on asteroid surfaces.
3 Asteroid-NeRF for asteroid surface reconstruction
Figure 1 presents an overview of Asteroid-NeRF that demonstrates its use of appearance embedding and a multi-view photometric consistency constraint for asteroid surface reconstruction. To obtain the exterior orientation (EO) parameters and sparse point cloud, the images are initially processed by SfM, and the bounding box of the target asteroid is calculated. Subsequently, the algorithm samples along the ray in each pixel of an image, as shown in Fig. 1a, based on the EO parameters in the bounding box. The sampled locations are then embedded by hash encoding and input to a multi-layer perceptron (MLP) together with the view direction and appearance embedding, as illustrated in Fig. 1b. Next, a rendered image is generated by volume rendering and is then compared with the captured image to calculate the colour and multi-view photometric difference. Subsequently, the MLP is optimised together with hash encoding and appearance embedding. Finally, after training, a detailed asteroid mesh is extracted through a marching cube (Wang et al. 2021a), as depicted in Fig. 1c.
3.1 Principles of NeRF
3.1.1 Neural volume rendering
NeRF (Mildenhall et al. 2021) uses colour fields and volume density to represent 3D scenes. Specifically, it uses an MLP to map the position xi of a point and the view direction di to the colour ci and volume density σi, as formulated in Eq. (1). Each pixel on the image can be viewed as the projection of a virtual ray. Given a set of posed images, the pose and location of each virtual ray are determined, followed by the calculation of the positions of sample points along the ray. Subsequently, an MLP is inquired to obtain the colour radiance and volume density of each sample point.
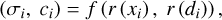 (1)
(1)
where f represents the neural radiance field, and r is the ray. Next, the colour of each pixel is approximated by integrating samples queried along rays, as shown in Eq. (2).
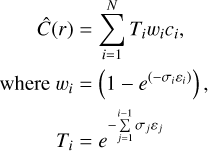 (2)
(2)
where Ti is the accumulated transmittance, wi is the opacity of point i, and εi is the distance between adjacent samples i and i + 1. Thus, to optimise the MLP, the loss between the rendered image and the captured image is calculated.
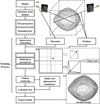 |
Fig. 1 Workflow of the Asteroid-NeRF method with appearance embedding and multi-view photometric consistency for asteroid surface reconstruction. |
3.1.2 Neural volume for an SDF
NeRF was devised by Yariv et al. (2021) and is a 3D representation without a clear surface definition, leading to noisy or unrealistic geometries being extracted from volume density. In contrast, an SDF is a representation of the surface, which maps the position in the 3D scene to the distance from the surface with a negative value inside the object and a positive one outside. The target surface is the zero-level set of an SDF, that is, S = {x ∈ ℝ3|g(x) = θ} is the SDF value. NeuS (Wang et al. 2021a) uses a logistic function to convert a predicted SDF into a volume density to allow optimisation with volume rendering. The corresponding opacity wi and accumulated transmittance Ti of a 3D point xi in Eq. (2) can be calculated using Eq. (3):
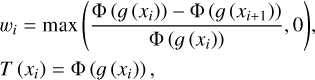 (3)
(3)
where Φ is the sigmoid function.
3.1.3 Multi-resolution hash encoding and numerical gradient computation
Recently, multi-resolution hash encoding was demonstrated to significantly improve the training efficiency of NeRF and preserve high-fidelity details (Müller et al. 2022), and thus we adopt multi-resolution hash encoding in our approach. Figure 1b shows a multi-resolution hash grid in two dimensions, where each grid cell has hash codes at its corners to represent the scene. We use {G1,…, GL} to denote the multi-resolution hash grid. First, we identify grid Gl at different resolutions; this grid contains the point xi in the 3D scene, and then trilinearly interpolates the hash features at the grid vertices to obtain the hash code h(xi,j) of point xi. Subsequently, we concatenate the hash features from different resolutions of the hash grid, as described in Eq. (4)
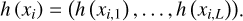 (4)
(4)
The hash code is the input of a shallow MLP, as in the original NeRF, and is also optimised in training. To ensure that a reconstructed surface is smoothed without losing details, a variant of NeuS named Neuralangelo (Li et al. 2023) uses a multi-resolution hash grid as a neural SDF representation - with numerical gradients instead of analytical gradients - to calculate high-order derivatives, such as the surface normal. Additionally, a coarse-to-fine strategy is essential for restoring a structure and then its details. Accordingly, this strategy is also incorporated into our approach for asteroid surface reconstruction.
3.2 Asteroid-NeRF
NeRF-based methods have shown promising performances in novel view rendering and surface reconstruction from regular images. However, these methods cannot be used directly for asteroid surface reconstruction, as images of asteroids are usually collected at great distances by narrow-angle cameras on board spacecraft and therefore usually have large illumination differences and substantial shadows. Therefore, the following new strategies are employed in Asteroid-NeRF for asteroid surface reconstruction.
3.2.1 Volume rendering sampling of asteroid images
It is crucial to sample along a camera’s view in 3D space to obtain colour and SDFs for SDF-based volume rendering. Moreover, to allow a network to learn scene information, the sampling range must be within the area of interest (Zhang et al. 2020). That is, a sampling range that is too close to or far from the area of interest results in ambiguities and distortions in the implicit field. Moreover, if a convergence result is geometrically incorrect, NeRF identifies a family of radiance fields that perfectly explain the training images but have poor generalisability to different points of view.
We use sparse point clouds from SfM as constraints to solve this problem. Specifically, sampling is performed within only the outer bounding box of a sparse point cloud to ensure that information is obtained within a suitable range. The outer bounding box’s far and near intersection points are calculated for each ray as a constraint on the sampling range, as shown in Fig. 2.
3.2.2 Appearance embedding
During the image-acquisition process, the relative positions of an asteroid and the Sun are not constant, resulting in inconsistent brightness in observations, which creates challenges for reconstruction. Therefore, our approach uses appearance embedding to produce a vector ln,j of length n for each image j to represent different conditions, such as different lighting conditions and exposure. In addition, the image-independent colour ci in the scene is replaced by image-dependent colour ci,j, as defined in Eq. (5).
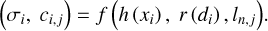 (5)
(5)
The embedding ln,j is also optimised in training. The use of appearance encoding and direction encoding as the input of the radiation network ensures that the emission radiation in the scene can be freely changed, while the scene geometric information remains unchanged. Setting the appearance embedding to a small dimension allows Asteroid-NeRF to fit different lighting environments, thereby rendering novel views under the same lighting conditions (as demonstrated in Fig. 3) and eliminating geometric ambiguities.
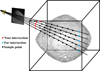 |
Fig. 2 Illustration of the sampling range with the outer bounding box used as a constraint. |
 |
Fig. 3 Example of use of appearance embedding to eliminate colour differences in Bennu data. The left part illustrates the original image, and the right part illustrates the rendered image with colour differences eliminated. |
3.2.3 Multi-view photometric consistency
The above-described method can reconstruct a model of an asteroid’s surface via a coarse-to-fine strategy. Nevertheless, many weak and repeated textured areas remain on a model that lacks supervision. Additionally, due to differences in lighting environments, images captured at different times may exhibit variations in radiance. In comparison, the underlying texture of an asteroid remains consistent from different views. Therefore, Asteroid-NeRF utilises multi-view photometric consistency in multi-view stereo (MVS) as a supervisory approach to guarantee geometric consistency.
Multi-view photometric consistency is based on the assumption that there should be minimal photometric differences between images projected by the same surface position. To impose this constraint on an SDF, we need to identify the first point of intersection between a ray and an asteroid’s surface. Along a ray, we sample I points with corresponding coordinates [x1,…, xI} and SDF value g(xi). There are two adjacent points in the light passing through the surface: one is inside the object and has an SDF value of less than 0, and the other is outside the object and has an SDF value of greater than 0, as shown in Eq. (6).
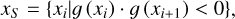 (6)
(6)
where xS is the set of sample points that satisfy the condition, and · means multiplication. Equation (6) describes the process of identifying two adjacent sampling points along the rays such that the product of their SDF value is negative, thereby confirming that the points are in close proximity to the surface. Based on a linear interpolation, the intersection point xs can be calculated using Eq. (7).
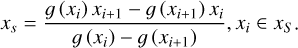 (7)
(7)
Given that a ray passing through a surface has at least two intersection points, we must select the point closest to the camera. The normal vector Ns of a surface point xs can be calculated using Ns = ∇g (xs), and the small patch around the intersection can be represented by Eq. (8).
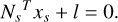 (8)
(8)
In traditional MVS (Hartley & Zisserman 2003; Schönberger et al. 2016), the relationship between image point x in pixel patch pr of reference image Ir and image point x′ in pixel patch ps of source image Is can be described via plane-induced homography, as shown in Eq. (9).
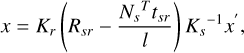 (9)
(9)
where Kr and Ks are the intrinsic parameters of Ir and Is, respectively; and Rsr and tsr denote the pose of Ir relative to Is. To facilitate a focus on the geomatic information, colour images are converted to greyscale, and a normalised cross-correlation operator is used to measure the similarity between a reference pixel patch and a source pixel patch calculated using Eq. (10).
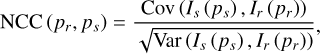 (10)
(10)
where Cov and Var are the covariance and variance functions, respectively. The patch size is set to 33. To improve the robustness and handle occlusions, our approach selects the top four by calculating the normalised cross correlation of the ten reference images and using this as the photometric consistency loss.
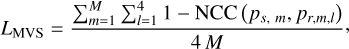 (11)
(11)
where M is the number of sampled rays on the source image, which is also the batch size. The rendering loss of volume rendering often results in geometric inconsistencies, that is, it results in the radiance field being fitted to the fixed training images with the wrong geometry. However, photometric consistency loss can act directly on the surface of an SDF, thereby avoiding volume rendering.
3.2.4 Loss functions
In addition to the loss function LMVS, which is used for constraining multi-view photometric consistency, three other loss functions are used in our method: LRGB, Leik, and Lcurv. Here, LRGB represents the mean squared error between the rendered and true images. Leik represents the eikonal loss of the sample points and is imposed to regularise the SDF by preventing a sudden change; it does this by ensuring that the gradient of SDF almost everywhere satisfies ||∇g (x)||2 = 1 (Gropp et al. 2020). Lcurv represents the mean curvature loss and is introduced to further smooth the asteroid surface by minimising the mean curvature. The above-mentioned loss functions and the total loss are shown in Eq. (12).
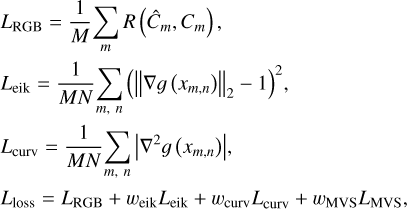 (12)
(12)
where M is the total batch size of pixels used for training, and N is the total number of sample points along a ray. We set weik to 0.1 and wMVS to 0.5. The weight of the curvature regularisation item wcurv linearly increases and then decreases as in Neuralangelo (Li et al. 2023).
4 Experimental results
4.1 Datasets and implementation
We evaluate the performance of Asteroid-NeRF using data for two asteroids: Itokawa (25143) and Bennu (101955). Itokawa is a near-Earth peanut-shaped/sea-otter-shaped asteroid that was explored by the Hayabusa spacecraft, which was launched by the fifth Mu V launch vehicle on 9 May 2003 (Fujiwara et al. 2006). The Asteroid Multi-band Imaging Camera (AMICA) was a narrow-angle camera on board Hayabusa that was designed to capture high spatial-resolution images of Itokawa (Gaskell et al. 2006). At the beginning of the rendezvous phase, an AMICA sensor was used to scan Itokawa and obtain lateral and polar images with a resolution of 0.3–0.7 m (Demura et al. 2006). The experiments in the present study are based on 172 images captured from 28 September to 2 October 2005 during the rendezvous phase. The coordinate system is based on the Itokawa body-fixed frame, as used by Gaskell et al. (2008). The second column of Table 1 lists the basic information of the dataset used, and Fig. 4a shows example images with a resolution of 1024 × 1024 pixels.
NASA’s Origins, Spectral Interpretation, Resource Identification, and Security–Regolith Explorer (OSIRIS-REx) mission was designed to return a sample from Bennu, which is a rubble-pile asteroid shaped like a spinning top (Lauretta et al. 2017). PolyCam, a narrow-angle, panchromatic, and high-resolution sensor on board OSIRIS-REx, was used to capture images of Bennu from a range of millions of kilometers to approximately 200 m (Edmundson et al. 2020). When OSIRIS-REx passed over the surface of Bennu, images were acquired by PolyCam as it slewed alternately north and south. Our experiment utilises 2231 images with different illumination conditions from the OSIRIS-REx mission. The basic information of these images is shown in the third column of Table 1, and Fig. 4b shows example images with a resolution of 1024 × 1024 pixels. The coordinate system corresponds to the surface model of Daly et al. (2020). All images are orientated through SfM, and the same IO and EO parameters are used by Asteroid-NeRF and the SPG method.
As shown in Fig. 4, some parts of the images are entirely dark, namely the backgrounds and areas not directly illuminated by the Sun, and thus contain little valid information. Therefore, we created a mask to label these pixels and added a greater proportion of illuminated areas than shadows into the training set for the Itokawa dataset. This approach was adopted because the asteroid – corresponding to the bright areas – occupies only a minor portion of the images. Illuminated areas comprise 75% of the area, meaning that in a training batch, 75% of pixels are bright, and 25% are less bright, and appear to be background or shadow. In the Bennu dataset, we set all the pixels as equally selected because dark areas do not comprise a large proportion of each image.
In the experiments, 5% of the images are randomly removed from training to evaluate the reconstruction quality. The experiments are performed on an RTX3090 GPU with a batch size of 512. The maximum batch number for Itokawa is set to 100 000, which requires a training time of 7.7 h. In comparison, the Bennu dataset contains more images and thus needs more training batches, and thus the batch number is set to 300 000, which requires a training time of 17.1 h.
Contrary to initiating the optimisation process with a sparse 3D model derived from SfM, Asteroid-NeRF begins with a 3D sphere that is randomly initialised. Consequently, the role of the sparse point cloud is to delineate the shape or extent of the asteroid, thereby constraining the sampling range for volume rendering of Asteroid-NeRF. In our experiments, the point cloud comprises merely 6004 points for Itokawa and 102 505 points for Bennu following the application of SfM.
We compare the geometric accuracy and level of detail of our models with those of the SPG, SPC, and laser scanning models. The SPG models are produced by photogrammetry software with the same input as Asteroid-NeRF. The SPC model of Itokawa is that produced by Gaskell et al. (2008), and the SPC and laser scanning models are those generated by Daly et al. (2020) and Lauretta et al. (2022), respectively. All the SPC and laser scanning models are downloaded from the Small Body Mapping Tool (Barnouin et al. 2018).
Basic information of the Itokawa and Bennu datasets.
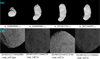 |
Fig. 4 Examples of images used for evaluating the Asteroid-NeRF of (a) Itokawa and (b) Bennu. |
 |
Fig. 5 Overview of a 3D surface model of Itokawa reconstructed by Asteroid-NeRF (plus and minus symbols indicate different viewing directions). |
4.2 Itokawa
This section reports the Asteroid-NeRF results for Itokawa and compares their geometric accuracy and details with those of the SPG and SPC results for Itokawa. Figure 5 shows the surface model reconstructed by Asteroid-NeRF, revealing that it has numerous high-frequency features without any holes, despite being based on only 172 images. This demonstrates that Asteroid-NeRF successfully reconstructs Itokawa’s overall structure and various topographic features. Itokawa is regarded by some as being shaped like a sea otter, with a ‘body’ and ‘head’ connected by a ‘neck’ (Fujiwara et al. 2006). Its surface has complex features, including boulders, craters, and smooth terrains. Based on 172 images, these features are not effectively captured by SPG but are well captured by Asteroid-NeRF.
Figure 6 compares the geometric surface models generated by Asteroid-NeRF with the corresponding images and SPG and SPC models (Gaskell et al. 2008) in detail, illustrating that the Asteroid-NeRF models have a higher level of detail and accuracy than the SPG and SPC models. The model reconstructed by SPG lacks many details and its surface is not smooth, as it contains many edges and corners. The surfaces around large boulders are distorted, and smaller boulders are smoothed out, as shown in the blue boxes in Figs. 6a,b. The model reconstructed by SPC contains most of Itokawa’s details but differs from the actual images. For example, by comparing the SPC model with the outline of Itokawa in the image, it can be seen that the SPC model lacks some small stones (Fig. 6d) and the narrowing of the lower part of Yoshinodai, which is the largest boulder on the surface (Saito et al. 2006) (Fig. 6c). Overall, Asteroid-NeRF models have features that are consistent with those of the SPG and SPC models, but have more high-frequency features. The features on the images correspond one-to-one – and with high fidelity – to those of the surface model; examples are shown in the blue boxes in Figs. 6a,b. Moreover, the edges of the model match the outlines of Itokawa in images, as shown in the blue boxes in Figs. 6c,d. To evaluate the level of detail across various models, we calculated the average edge length for each mesh of Itokawa. The mesh generated by our method has an average edge length of 0.311 m, which is significantly finer than the 12.579 m for the SPG method and 0.595 m for the SPC method, indicating a superior level of detail.
The difference maps between the Asteroid-NeRF model and the SPC model, and between the SPG model and the SPC model are shown in Fig. 7 with the same colour bar. With SPC as the source, a quantitative comparison of SPG and Asteroid-NeRF with SPC is displayed in Table 2. The Asteroid-NeRF model, with a mean distance of 0.058 m and a standard deviation (std) of 0.858 m, outperforms the SPG models, which have a mean distance of approximately 1.776 m and a std of approximately 1.389 m. In addition, the Asteroid-NeRF model is consistent with the SPC model, although some deviations can be observed near irregular boulders with little texture. One of the most significant differences between the Asteroid-NeRF and SPC models is the omission of a boulder by the latter model. As can be seen in Fig. 6A, the Asteroid-NeRF model successfully captures this boulder. The difference map between the two models is shown in Fig. 7A. The differences at (B) and (C) in Fig. 7 are mainly due to a lack of textural constraints, as shown in Fig. 7c, and occlusion by boulders or undulating topography from other views. Overall, compared with the difference map between the Asteroid-NeRF model and the SPC model, the difference map between the SPG model and the SPC model is more yellowish (Fig. 7b), indicating that it contains larger distances, which are consistent with the results in Table 2. In addition, the areas in the blue boxes in Fig 7b reveal that the SPG model contains more noise than the Asteroid-NeRF model.
In addition to NeRF-based methods exhibiting good performance in surface model reconstruction, they exhibit outstanding performance in novel image synthesis. To evaluate rendering quality, 5% of the images are not used in training but are rendered with the same EO and IO to compare with the ground truth (original images). We use three widely used metrics for image similarity assessment: the peak signal-to-noise ratio (PSNR), the structural similarity index (SSIM), and the learned perceptual image patch similarity (LPIPS) (Barron et al. 2021; Mildenhall et al. 2021; Wang et al. 2021a). PSNR is a measure of the ratio between the maximum signal of an image and the background noise. Similarly, SSIM is a metric modelled on the human visual system that quantifies the structural similarity between two images. For these two metrics, higher values indicate better results. Generally, a PSNR of greater than 40 indicates that the quality of a generated image is almost as good as that of the original image. LPIPS is also known as ‘perceptual loss’ and is a measure of the difference between two images, where a lower value indicates a better result (Zhang et al. 2018). Figure 8 shows a qualitative comparison between the ground truth and the rendered images obtained from Asteroid-NeRF. The PSNR is 46.215, the SSIM is 0.984, and the LPIPS is 0.004, which means that the rendered images are almost the same as the ground truth. In addition, due to appearance embedding, instantaneous features such as shadows in the image are well restored.
 |
Fig. 6 Comparison of the 3D surface models of Itokawa generated by SPG, SPC, and Asteroid-NeRF. The left column shows the original images, for reference. |
Mean differences and standard deviations of the 3D surface models of Itokawa.
4.3 Bennu
We also tested Asteroid-NeRF on Bennu and compared the resulting model with the SPG, SPC (Lauretta et al. 2022), and laser scanning models (Daly et al. 2020). A model overview of Bennu is shown in Fig. 9, revealing its spinning-top-like shape with a muted equatorial ridge and diamond-shaped poles, the same as generated by Barnouin et al. (2019). Overall, Asteroid-NeRF realistically reconstructs the densely bouldered rough surface of Bennu from 2231 images. Compared with training with a lower number of images, training with a higher number of images tends to be more challenging because neural networks may forget previously learned information when learning new data (Jung et al. 2018). It is more difficult to accurately reconstruct Bennu based on images with more details under different environmental lighting fields in original NeRF, which demonstrates the robustness of Asteroid-NeRF.
Figure 10 depicts a detailed comparison of SPG, SPC, laser scanning, and Asteroid-NeRF surface models of Bennu from the same viewpoint. The SPG and laser scanning models invariably lack or have distorted surface features, such as boulders and craters, and the SPC model tends to over-smooth the surface and fails to reproduce fine structures. In contrast, the Asteroid-NeRF model successfully reconstructs small boulders and maintains high accuracy. In the boxed areas marked ‘(A)’ in Fig. 10, two and four boulders can be seen in the laser scanning and SPG models, respectively, while the boulders are not visible in the SPC model. However, Asteroid-NeRF reconstructs not only these prominent boulders but also the tiny features in the top part of the area. Furthermore, in the boxed areas marked ‘(B)’ in Fig. 10, a shield-shaped feature is visible in the original image. This feature is successfully reconstructed only by Asteroid-NeRF; in contrast, it is reconstructed containing various levels of distortion by SPG and laser scanning, and is not reconstructed at all by SPC. The mesh of Bennu, generated by our method, has an average edge length of 0.303 m. This measurement indicates the highest level of detail among the compared methods, and significantly surpasses the average edge lengths of 2.871 m for the SPG method and 0.802 m for the SPC method.
In a few viewed areas, such as polar areas, as shown in Fig. 11, SPG retrieves the rough terrain but struggles to capture the fine-grained surface features, indicating that a large amount of manual editing would be required to obtain a refined model. In comparison, SPC restores more thin structures but the result is unnatural and lacks detail. Asteroid-NeRF recovers most of the details based on the same camera coverage as SPG, and achieves the best performance out of all the image-based methods, but is still outperformed by the laser scanning model. The global high-density coverage of the laser scanning method enables it to directly measure the shape and topography of Bennu, meaning that it achieves the highest accuracy.
A comparison between the Asteroid-NeRF model and the laser scanning model (Fig. 12a) shows that the differences are distributed around zero, as the mean distance is 0.014 m and the std is 0.239 m; these results are superior to those of the SPG and SPC models (as shown in Table 3). Thus, the Asteroid-NeRF model exhibits a high degree of consistency with the laser scanning model, and the most significant disparity between these models is in the boxed area marked ‘(A)’ in Fig. 12, which is to the north of the boulder and is obscured (Fig. 12d). Due to the lack of valid information, this part can only be interpolated and smoothed by the neural network of Asteroid-NeRF, leading to a low-quality reconstruction. Panels b and c of Fig. 12 show the difference maps between the SPC and laser scanning models, and between the SPG and laser scanning models, respectively, with the same colour scale as in Fig. 12a. The difference map of the SPC and laser scanning models is mostly greater than zero, while the opposite is true for the difference map of the SPG and laser scanning models, which is consistent with the statistical values shown in Table 3. Compared to difference map between Asteroid-NeRF and Laser scanning models, the areas in the blue boxes contain greater distances on the 3D surface near the boulders and craters.
The rendered images presented in Fig. 13 exhibit high fidelity, as evidenced by the PSNR of 44.039, the SSIM of 0.961, and the LPIPS of 0.009. The use of appearance embedding allows Asteroid-NeRF to learn background light field information from images with different levels of lighting and thereby render novel views under a given environmental light. Figure 14 reveals that the images used for training have different brightnesses, but given that static appearance embedding is used for synthesising images, the outputs have the same brightness. Appearance embedding can decouple geometric information and appearance information, where appearance information includes the Sun’s altitude angle, shadow, brightness, camera exposure, and aperture, and these elements can be controlled using specific encodings during image synthesis.
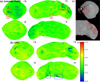 |
Fig. 7 Difference maps of (a) the Asteroid-NeRF model and the SPC model, and (b) the SPG model and the SPC model of Itokawa’s surface. (c) Corresponding images of Itokawa, for reference. Plus and minus symbols indicate different viewing directions. |
 |
Fig. 8 Comparison of rendered images (upper row) and original images (lower row) of Itokawa. |
 |
Fig. 9 Overview of the 3D surface model of Bennu reconstructed using Asteroid-NeRF (plus and minus symbols indicate different viewing directions). |
 |
Fig. 10 Comparison of the 3D surface models of Bennu generated using SPG, SPC, laser scanning, and Asteroid-NeRF, respectively. The top row shows the original images, for reference. |
 |
Fig. 11 Geometry comparison of SPG, SPC, Asteroid-NeRF, and laser scanning models of a few captured areas of Bennu. The top row displays the north pole, and the bottom row displays the south pole. |
5 Discussion and conclusion
This paper presents Asteroid-NeRF, a deep-learning-based method with appearance embedding and multi-view photometric consistency that can reconstruct very fine shape models of asteroids under various environmental illumination conditions. The algorithm of Asteroid-NeRF determines the boundaries of a target using sparse point clouds as priors, reconstructs an asteroid via a coarse-to-fine strategy, and then uses the marching cubes algorithm to extract a surface from an SDF. Asteroid-NeRF represents a scene as a multi-resolution hash table with 3D coordinates, 2D observation direction, and appearance encoding of each image as input, and produces a signed distance from the target surface and red-green-blue colour as output. In addition, to constrain the geometry of an SDF directly, Asteroid-NeRF selects stereo images, projects the pixel patches of the reference image onto the source image according to geometric relationships, and refines the geometry through photometric differences. Therefore, Asteroid-NeRF correctly represents the geometric surface of a scene and gradually recovers all features visible in the image as a fine reconstruction process proceeds.
We conducted experiments based on two asteroids, Itokawa and Bennu, and compared the performance of Asteroid-NeRF with that of the existing highest-precision methods, namely the SPC for Itokawa and the laser scanning for Bennu. For the Itokawa dataset, an end-to-end Asteroid-NeRF method uses only 172 images to restore the surface model in 7.7 h. In contrast, the SPC involves iterative updates to refine a surface, meaning that it uses over 600 images captured from long to short distances from an asteroid, and thereby consumes a large amount of computational time, typically weeks to months (Gaskell et al. 2008; Palmer et al. 2022). To cover the entire surface of Bennu, we select 2231 images collected in a detailed survey period for training Asteroid-NeRF, which takes 17.1 h, whereas SPC uses all of the images available (Barnouin et al. 2020). Training with a greater number of images is more challenging for Asteroid-NeRF because deep learning methods tend to forget what was learnt earlier (Jung et al. 2018). However, Asteroid-NeRF has a large model capacity, indicating its robustness. The mean distances of our models are 0.058 and 0.014 m, respectively, and the stds are 0.858 and 0.239 m, respectively, which indicates that the Asteroid-NeRF performs better than traditional image-based methods, which is due to its continuous nature and global consistency. Moreover, Asteroid-NeRF accurately restores most details without distortion, deformation, or discontinuity, even in observation areas with only a few views. In summary, after image orientation, Asteroid-NeRF efficiently reconstructs the surface of an asteroid with high precision, capturing subtle details, complementing traditional methods such as SPG and SPC.
Nevertheless, Asteroid-NeRF has some limitations. First, although it can replace the surface reconstruction part of the traditional pipeline, it cannot perform image orientation, unlike SPG or SfM. Thus, EO and IO parameters remain the essential inputs of Asteroid-NeRF. Therefore, as the surface of an asteroid usually contains many weak and repeated textural areas, a large number of manually selected tie points must be used during the image orientation process. Therefore, in future work, we will explore image pose estimation to improve Asteroid-NeRF. Second, although Asteroid-NeRF is considerably more efficient than SPC, it is far less efficient than SPG, and even more inefficient compared with commercial photogrammetry software. Thus, we will endeavour to improve the efficiency of the algorithm of Asteroid-NeRF, such that it is akin to commercial software and can generate results within one or two hours. Third, existing studies indicate that NeRF-based methods necessitate a high degree of image overlap, typically involving more than ten views for effective application (Mildenhall et al. 2021; Wang et al. 2021a; Li et al. 2023). Based on our experience, approximately 10 to 14 views are sufficient to accurately reconstruct the surface of a target area, though there remains room for enhancement in this process1.
 |
Fig. 12 Difference maps of Bennu’s surface between (a) the Asteroid-NeRF model and the laser scanning model, (b) the SPC model and the laser scanning model, and (c) the SPG model and the laser scanning model. (d) Corresponding images of Bennu, for reference, where the plus and minus symbols indicate different viewing directions. |
Mean differences and standard deviations of the 3D surface models of Bennu.
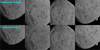 |
Fig. 13 Comparison of rendered images (upper row) and real images (lower row) of Bennu. |
 |
Fig. 14 Example of the use of Asteroid-NeRF to eliminate colour or light differences. The top row shows the original image, and the bottom row shows the image with colour differences eliminated. |
Acknowledgements
This work was supported by grants from the Research Grants Council of Hong Kong (RIF Project No: R5043-19; Project No: PolyU 15210520; Project No: 15219821). The authors appreciate the efforts of individuals who helped to make archives of the images of the asteroids Itokawa and Bennu, and related datasets, publicly available.
References
- Abe, S., Mukai, T., Hirata, N., et al. 2006, Science, 312, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Al Asad, M., Philpott, L., Johnson, C., et al. 2021, Planet. Sci. J., 2, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Barnouin, O., Ernst, C., & Daly, R. 2018 in Planetary Science Informatics and Data Analytics Conference, 2082, 6043 [NASA ADS] [Google Scholar]
- Barnouin, O., Daly, M., Palmer, E., et al. 2019, Nat. Geosci., 12, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Barnouin, O., Daly, M., Palmer, E., et al. 2020, Planet. Space Sci., 180, 104764 [NASA ADS] [CrossRef] [Google Scholar]
- Barron, J. T., Mildenhall, B., Tancik, M., et al. 2021, in Proceedings of the IEEE/CVF International Conference on Computer Vision, 5855 [Google Scholar]
- Barron, J. T., Mildenhall, B., Verbin, D., Srinivasan, P. P., & Hedman, P. 2022, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 5470 [Google Scholar]
- Chen, Z., & Zhang, H. 2019, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 5939 [Google Scholar]
- Coughlan, J. M., & Yuille, A. L. 1999, Proceedings of the seventh IEEE international conference on computer vision, 2, 941 [CrossRef] [Google Scholar]
- Daly, M., Barnouin, O., Seabrook, J., et al. 2020, Sci. Adv., 6, eabd3649 [NASA ADS] [CrossRef] [Google Scholar]
- Demura, H., Kobayashi, S., Nemoto, E., et al. 2006, Science, 312, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Do, P. N. B., & Nguyen, Q. C. 2019, in 19th International Symposium on Communications and Information Technologies (ISCIT), 138 [Google Scholar]
- Edmundson, K., Becker, K., Becker, T., et al. 2020, Remote Sens. Spatial Inform. Sci., 3, 587 [Google Scholar]
- Festou, M., Keller, H. U., & Weaver, H. A. 2004, Comets II (Tucson: University of Arizona Press) [Google Scholar]
- Fujiwara, A., Kawaguchi, J., Yeomans, D., et al. 2006, Science, 312, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, R. W. 2012, AAS/Div. Planet. Sci. Meeting Abstracts, 44, 209 [Google Scholar]
- Gaskell, R., Barnouin-Jha, O., Scheeres, D., et al. 2006, in AIAA/AAS Astrody-namics Specialist Conference and Exhibit, 6660 [Google Scholar]
- Gaskell, R., Barnouin-Jha, O., Scheeres, D. J., et al. 2008, Meteor. Planet. Sci., 43, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, R., Barnouin, O., Daly, M., et al. 2023, Planet. Sci. J., 4, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Giese, B., Neukum, G., Roatsch, T., Denk, T., & Porco, C. C. 2006, Planet. Space Sci., 54, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Gropp, A., Yariv, L., Haim, N., Atzmon, M., & Lipman, Y. 2020, in Proceedings of Machine Learning and Systems 2020, 3569 [Google Scholar]
- Guo, H., Peng, S., Lin, H., et al. 2022, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 5511 [Google Scholar]
- Hartley, R., & Zisserman, A. 2003, Multiple View Geometry in Computer Vision (Cambridge: Cambridge University press) [Google Scholar]
- Hirata, N., Sugiyama, T., Hirata, N., et al. 2020, Annual Lunar Planet. Sci. Conf., 2326, 2015 [Google Scholar]
- Jung, H., Ju, J., Jung, M., et al. 2018 in Proceedings of the AAAI Conference on Artificial Intelligence, 32 [Google Scholar]
- Kim, J., Lin, S.-Y., & Xiao, H. 2023, Remote Sens., 15, 2954 [NASA ADS] [CrossRef] [Google Scholar]
- Lauretta, D., Balram-Knutson, S., Beshore, E., et al. 2017, Space Sci. Rev., 212, 925 [CrossRef] [Google Scholar]
- Lauretta, D., Adam, C., Allen, A., et al. 2022, Science, 377, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Müller, T., Evans, A., et al. 2023, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8456 [Google Scholar]
- Liu, W. C., & Wu, B. 2020, ISPRS J. Photogramm. Remote Sens., 159, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W. C., & Wu, B. 2021, ISPRS J. Photogramm. Remote Sens., 182, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W. C., Wu, B., & Wöhler, C. 2018, ISPRS J. Photogramm. Remote Sens., 136, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z., Feng, Y., Black, M. J., et al. 2023, in International Conference on Learning Representations, [arXiv:2303.08133] [Google Scholar]
- Long, J., & Wu, F. 2019, J. Guidance Control Dyn., 42, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S., & Geiger, A. 2019, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 4460 [Google Scholar]
- Mildenhall, B., Srinivasan, P. P., Tancik, M., et al. 2021, Commun. ACM, 65, 99 [Google Scholar]
- Müller, T., Evans, A., Schied, C., & Keller, A. 2022, ACM Transactions on Graphics, 41, 1 [CrossRef] [Google Scholar]
- Oechsle, M., Peng, S., & Geiger, A. 2021, in Proceedings of the IEEE/CVF International Conference on Computer Vision, 5589 [Google Scholar]
- Palmer, E. E., Head, J. N., Gaskell, R. W., Sykes, M. V., & McComas, B. 2016, Earth Space Sci., 3, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, E. E., Gaskell, R., Daly, M. G., et al. 2022, Planet. Sci. J., 3, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J. J., Florence, P., Straub, J., Newcombe, R., & Lovegrove, S. 2019, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 165 [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2015, A&A, 583, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preusker, F., Scholten, F., Elgner, S., et al. 2019, A&A, 632, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remondino, F., Spera, M. G., Nocerino, E., Menna, F., & Nex, F. 2014, Photogramm. Record, 29, 144 [CrossRef] [Google Scholar]
- Saito, J., Miyamoto, H., Nakamura, R., et al. 2006, Science, 312, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J., Hesar, S. G., Tardivel, S., et al. 2016, Icarus, 276, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Scholten, F., Preusker, F., Elgner, S., et al. 2019, A&A, 632, L5 [Google Scholar]
- Schonberger, J. L., & Frahm, J.-M. 2016, in Proceedings of the IEEE conference on computer vision and pattern recognition, 4104 [Google Scholar]
- Schönberger, J. L., Zheng, E., Frahm, J.-M., & Pollefeys, M. 2016, in Computer Vision-ECCV 2016, Proceedings, Springer, Part III, 501 [CrossRef] [Google Scholar]
- Tewari, A., Thies, J., Mildenhall, B., et al. 2022 in Computer Graphics Forum, Wiley Online Library, 703 [CrossRef] [Google Scholar]
- Ullman, S. 1979, Proc. R. Soc. London Ser. B Biol. Sci., 203, 405 [NASA ADS] [Google Scholar]
- Wang, P., Liu, L., Liu, Y., et al. 2021a, arXiv e-prints [arXiv:2106.10689] [Google Scholar]
- Wang, Z., Wu, S., Xie, W., Chen, M., & Prisacariu, V. A. 2021b, arXiv e-prints [arXiv:2102.07064] [Google Scholar]
- Wang, Y., Skorokhodov, I., & Wonka, P. 2022, Adv. Neural Inform. Process. Syst., 35, 1966 [Google Scholar]
- Wang, Y., Han, Q., Habermann, M., et al. 2023, in Proceedings of the IEEE/CVF International Conference on Computer Vision, 3295 [Google Scholar]
- Watanabe, S., Hirabayashi, M., Hirata, N., et al. 2019, Science, 364, 268 [NASA ADS] [Google Scholar]
- Weirich, J., Palmer, E. E., Daly, M. G., et al. 2022, Planet. Sci. J., 3, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, B. 2017, International Encyclopedia of Geography; American Cancer Society: Atlanta, GA, USA, 1 [Google Scholar]
- Wu, B., Liu, W. C., Grumpe, A., & Wöhler, C. 2018, ISPRS J. Photogramm. Remote Sens., 140, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, Q., Wang, Q., Zhao, K., et al. 2024 in Proceedings of the AAAI Conference on Artificial Intelligence, 38, 6440 [CrossRef] [Google Scholar]
- Yariv, L., Kasten, Y., Moran, D., et al. 2020, Adv. Neural Inform. Process. Syst., 33, 2492 [Google Scholar]
- Yariv, L., Gu, J., Kasten, Y., & Lipman, Y. 2021, Adv. Neural Inform. Process. Syst., 34, 4805 [Google Scholar]
- Yen-Chen, L., Florence, P., Barron, J. T., et al. 2021, in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), IEEE, 1323 [Google Scholar]
- Yeomans, D., Antreasian, P., Cheng, A., et al. 1999, Science, 285, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, R., Isola, P., Efros, A. A., Shechtman, E., & Wang, O. 2018, in Proceedings of the IEEE conference on computer vision and pattern recognition, 586 [Google Scholar]
- Zhang, K., Riegler, G., Snavely, N., & Koltun, V. 2020, arXiv e-prints [arXiv:2010.07492] [Google Scholar]
The neural networks and surface models reconstructed by our method are available at https://zenodo.org/records/11174638
All Tables
All Figures
 |
Fig. 1 Workflow of the Asteroid-NeRF method with appearance embedding and multi-view photometric consistency for asteroid surface reconstruction. |
| In the text | |
 |
Fig. 2 Illustration of the sampling range with the outer bounding box used as a constraint. |
| In the text | |
 |
Fig. 3 Example of use of appearance embedding to eliminate colour differences in Bennu data. The left part illustrates the original image, and the right part illustrates the rendered image with colour differences eliminated. |
| In the text | |
 |
Fig. 4 Examples of images used for evaluating the Asteroid-NeRF of (a) Itokawa and (b) Bennu. |
| In the text | |
 |
Fig. 5 Overview of a 3D surface model of Itokawa reconstructed by Asteroid-NeRF (plus and minus symbols indicate different viewing directions). |
| In the text | |
 |
Fig. 6 Comparison of the 3D surface models of Itokawa generated by SPG, SPC, and Asteroid-NeRF. The left column shows the original images, for reference. |
| In the text | |
 |
Fig. 7 Difference maps of (a) the Asteroid-NeRF model and the SPC model, and (b) the SPG model and the SPC model of Itokawa’s surface. (c) Corresponding images of Itokawa, for reference. Plus and minus symbols indicate different viewing directions. |
| In the text | |
 |
Fig. 8 Comparison of rendered images (upper row) and original images (lower row) of Itokawa. |
| In the text | |
 |
Fig. 9 Overview of the 3D surface model of Bennu reconstructed using Asteroid-NeRF (plus and minus symbols indicate different viewing directions). |
| In the text | |
 |
Fig. 10 Comparison of the 3D surface models of Bennu generated using SPG, SPC, laser scanning, and Asteroid-NeRF, respectively. The top row shows the original images, for reference. |
| In the text | |
 |
Fig. 11 Geometry comparison of SPG, SPC, Asteroid-NeRF, and laser scanning models of a few captured areas of Bennu. The top row displays the north pole, and the bottom row displays the south pole. |
| In the text | |
 |
Fig. 12 Difference maps of Bennu’s surface between (a) the Asteroid-NeRF model and the laser scanning model, (b) the SPC model and the laser scanning model, and (c) the SPG model and the laser scanning model. (d) Corresponding images of Bennu, for reference, where the plus and minus symbols indicate different viewing directions. |
| In the text | |
 |
Fig. 13 Comparison of rendered images (upper row) and real images (lower row) of Bennu. |
| In the text | |
 |
Fig. 14 Example of the use of Asteroid-NeRF to eliminate colour or light differences. The top row shows the original image, and the bottom row shows the image with colour differences eliminated. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


