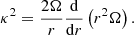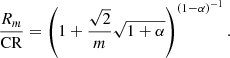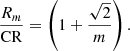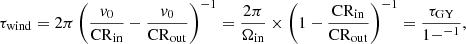| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | L14 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202450602 | |
| Published online | 14 June 2024 | |
Letter to the Editor
Resonance coupling in spiral arms
Patterns for flat rotation curve
1
Central (Pulkovo) Astronomical Observatory, Russian Academy of Sciences, Pulkovskoye chaussee 65/1, St. Petersburg 196140, Russia
2
Saint Petersburg State University, Universitetskijpr. 28, St. Petersburg 198504, Russia
e-mail: a.a.marchuk+astro@gmail.com
Received:
3
May
2024
Accepted:
23
May
2024
Context. To address questions about the physical nature and origin of spiral arms in galaxies, it is necessary to measure their dynamical properties, such as the angular speed, Ωp, or the corotation radius. Observations suggest that galaxies may contain several independent spiral patterns simultaneously. It was shown that so-called non-linear resonance coupling plays an important role in such systems.
Aims. We aim to identify cases of independent spiral patterns for galaxies with a flat rotation curve and to investigate what relative pattern velocities, Ωpout/Ωpin, they might have for all possible cases of coupling between the main resonances.
Methods. We solved equations for the main resonance positions (1:1, 2:1, 4:1) and estimated the ratio ϖ of the corotation radii for two subsequent patterns. For six close galaxies with flat rotation curves, we collected the measurements of the corotation radii in the literature, using at least three different methods in each case for credibility. We found at least two independent spiral patterns for each galaxy and measured the ϖ ratios.
Results. We found ϖ ratios for all possible cases for the main resonances. For three cases, we obtained ϖ > 3, indicating that it would be difficult to fit two or even more spiral patterns in the disc. These ratios have been used to derive the wind-up time for spirals, estimated to be several galactic rotations. We find that three pairs of coupling cases, including those that have been vastly acknowledged in galaxies, namely, OLRin = CRout & CRin = IUHRout, have very close ϖ ratios; hence, they ought to be found simultaneously, as observed. We find a strongly confirmed apparent resonance coupling for six galaxies and we show that the observed ϖ is in agreement with theory. In two of them, we identified a previously unreported form of simultaneous coupling, namely, OLRin = OUHRout & OUHRin = CRout. This result was also predicted from the proximity of ϖ.
Key words: galaxies: fundamental parameters / galaxies: spiral / galaxies: structure
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Spiral arms are present in most galaxies (Conselice 2006; Willett et al. 2013) and as large-scale prominent structures across the disc, they play an essential role in their evolution (Dobbs & Baba 2014; Shu 2016; Sellwood & Masters 2022). Such processes as angular momentum transfer or disc heating are crucial for understanding galaxies, thus highlighting the importance of researching spiral arms. However, the key question of their nature – namely, whether they rotate at an angular speed, Ωp, that is similar to that of the disc Ω(r) – has not yet been resolved for observations of real objects en masse. Although, in some papers, spiral arms have been linked to the presence of bars or companion satellites (Kormendy & Norman 1979; Struck et al. 2011), in most cases (especially in numerical models), spirals are expected to be long-lived density waves with Ωp ≈ const (Lin & Shu 1964; Bertin et al. 1989) or rapidly evolving transient features with Ωp ≈ Ω, often called dynamic arms (Sellwood & Carlberg 1984, 2019).
Among many other reasons, this question remains unanswered because spiral arms are probably not that simple in structure, as originally formulated in the aforementioned theories. It has been shown for both observed galaxies (Buta & Zhang 2009; Font et al. 2014; Meidt et al. 2009) and N-body numerical models (Rautiainen & Salo 1999; Quillen et al. 2011) that they can contain multiple patterns, rotated with individual Ωp. It was also shown theoretically that in such cases individual patterns do not have arbitrary angular speeds; rather, they form a so-called “resonance coupling”. Using well-established mathematics for the description of density waves, Tagger et al. (1987) and Sygnet et al. (1988) suggested that global modes in stellar discs could be coupled through non-linear interactions, namely, the first wave excites the second one through second-order coupling terms, which are large when resonances coincidence by radii. In their scenario, the corotation radius of an inner pattern overlaps with the inner Lindblad resonance of an outer one. This overlap makes the interaction between the two patterns much more efficient, enabling the transfer of energy and angular momentum between the bar, spiral density wave, and so-called beat waves, which result from the conservation law. This behaviour is in fact a general property of non-linear wave coupling and has also been observed in other fields, such as plasma physics (Tagger & Pellat 1982). Masset & Tagger (1997) theoretically and numerically justified such couplings, not only between bar and spiral, but also between spiral modes. This result has been firmly confirmed via the N-body simulations of Rautiainen & Salo (1999), which report remarkable coincidences for other resonances, along with more recent simulations of galactic discs (Minchev et al. 2012).
Despite the fact that resonance coupling has been predicted in theory, demonstrated in models, and formally found in observations of real galaxies, it remains poorly understood. In particular, we do not know which resonances can be coupled, in principle, and which limitations coupling imposes on the velocities of the inner 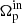 and outer
and outer 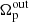 patterns. In this Letter we clarify these issues for the simple case of a flat rotation curve and for all possible cases of main resonances, regardless of whether they have been previously demonstrated to be the case in real galaxies or not.
patterns. In this Letter we clarify these issues for the simple case of a flat rotation curve and for all possible cases of main resonances, regardless of whether they have been previously demonstrated to be the case in real galaxies or not.
2. Resonance coupling
2.1. Which resonances can be coupled
We use the standard notations Ω for angular velocity, Ωp for spiral pattern speed, κ for epicyclic frequency. For each pattern, a resonance of order m is described by a curve Ω + κ/m. A 1:1 resonance (hereafter CR) is defined by Ωp = Ω, i.e. material component (stars and gas) co-rotate with density wave. A 2:1 resonance is called a Lindblad resonance, and we discern the inner one (ILR, m = −2) and the outer one (OLR, m = 2). These are the main resonances, encircle the limits where the density wave can propagate (Lynden-Bell & Kalnajs 1972). Besides CR, ILR and OLR, we mention the inner and outer 4:1 resonances, also referred to as ‘ultraharmonic’ resonances. We use the abbreviations IUHR and OUHR for them, where m is equal −4 and 4, respectively. Resonances of higher order values of m are rarely used in studies of the dynamics of real galaxies and, thus, they are not considered in this analysis. We note that all resonance notations used here represent a radial position of that particular resonance.
To date, at least five different cases are known where two resonances of inner (in) and outer (out) patterns overlap, possibly forming a non-linear coupling. All have been shown to occur in real galaxies, and often in numerical N-body simulations, and are listed below. First is CRin = ILRout, predicted by Masset & Tagger (1997) and found, for example, for IC342 in Fig. 8 in Meidt et al. (2009). The second is CRin = IUHRout, demonstrated by Meidt et al. (2008) for M51 and supported by Muñoz-Mateos et al. (2013) findings. The third is OLRin = ILRout, demonstrated for NGC 4736 (Moellenhoff et al. 1995). The fourth is OLRin = IUHRout, as found to be the case in M 101 (Meidt et al. 2009) and in NGC 3433 (Beckman et al. 2018). The fifth is OLRin = CRout, which was found in NGC 3433 by Beckman et al. (2018). Curiously, the latter should also be the case for Sellwood & Lin (1989), Sellwood & Carlberg (2019) groove instability cycle, where each next mode is generated exactly as it’s OLR is congruent with the previous CR.
The seminal work of Rautiainen & Salo (1999) demonstrates the possibility of all of these cases except the forth, both for bar and spiral, and for spiral-spiral coupling. In Font et al. (2014) authors study change of radial velocity sign in the kinematics of 104 galaxies using Hα data. They find the same repeating pattern in over 70% of their sample, which is CRin = IUHRout and OLRin = CRout simultaneously. The coincidence has been found up to four times in one galaxy, and is repeated at least twice in many objects. Theoretically, their method is able to detect all the main resonances, but it is difficult to discriminate between them, and often there are several possible interpretations.
In principle, other forms of coupling are possible, at least formally. The following analysis will be constrained not only to the cases listed, which have already been shown to hold in real galaxies, but to all combinations of main resonances, presented in Table 1. We naturally assume that when CRin < CRout, then every resonance from the sequence ILR-IUHR-CR-OUHR-OLR of the inner pattern can be formally coupled with all those resonances of the outer pattern, which are placed to the left of it in this sequence. It is also important to note that coupling with bar is better studied, but we focus on the spiral-spiral case, and most or all of the above examples have been shown to be possible for spirals as well.
All possible combinations and ratio ϖ for main resonances.
2.2. Relative corotation radii positions
In this subsection, we will investigate the possible relative CR positions for consequent patterns, assuming resonance coupling. Let the rotation curve (RC) have the form v(r)∝rα and the equation for the epicyclic frequency, κ, to be:
Then, it is trivial to find the position of any resonance Rm, where m values are listed for particular resonances in Sect. 2.1, relative to CR of the same pattern:
The Eq. (1) can be found in Elmegreen et al. (1992) and Elmegreen & Elmegreen (1995)1, but for the inverse sign of m. We apply this equation to all observed coupling cases, assuming the case of flat RC: v(r) = v0 = const, α = 0. Such a choice is motivated firstly by the simplicity of Eq. (1) in this case and, secondly, by the findings of Rautiainen & Salo (1999), who estimated that mode coupling seems to be the strongest when the halo contribution to the RC is large. Of course, real RCs are often flat in parts where spiral arms are hosted, but not in the central region.
Under the selected assumption, we get a simple expression:
For each of the observed coupling cases, we solve a trivial set of equations. By defining ϖ = CRout/CRin as a ratio of the inner CR to the outer CR (ϖ > 1) we get ten different values, which are presented in Table 1. For example, OLRin = ILRout congruence, shown to be the case in NGC 4736, gives 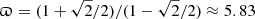 , and other cases are calculated in a similar way. We note that for flat RC ϖ−1 is equal to the ratio of pattern speeds
, and other cases are calculated in a similar way. We note that for flat RC ϖ−1 is equal to the ratio of pattern speeds 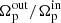 . Such simple considerations produce nevertheless several findings.
. Such simple considerations produce nevertheless several findings.
First, we demonstrate that in case of flat RC, regardless of whether it is bar or spirals, we only get a limited set of possibilities where the next pattern could be found. Secondly, Font et al. (2014) findings of simultaneous couplings coexisting naturally appear in the presented case, because ϖ is close for them. Since Ω is subject to RC errors, and given that the radial extent of resonant orbits can be quite large, for all ϖ = 1.62 ± 0.08 or even for a larger range, we will find OLRin = CRout & CRin = IUHRout within the errors. Third, it is easy to see that a similar situation holds for two other pairs of coupling: for ϖ = 1.31 ± 0.04 we simultaneously observe OUHRin = CRout & OLRin = OUHRout, and for ϖ = 2.15 ± 0.06 we will find OUHRin = IUHRout & IUHRin = ILRout. In both cases, the uncertainty is smaller than in the case of Font et al. (2014), namely, the apparent overlaps are spatially less extensive and, to the best of our knowledge, this result has not been noticed before.
Finally, we see that for all the remaining cases there is almost no room for a second pattern in the disc for flat RC and spiral-spiral coupling. In these cases, if the CRin is further than 0.3r25 from the center, which is observed in a significant fraction of galaxies (Elmegreen & Elmegreen 1995), then CRout is far beyond the optical radius. Theoretically, this could be possible if the outer spiral extends significantly beyond the disc (e.g. Mosenkov et al. 2024) or if it lies entirely inside the CR, meaning that it rotates faster than the disc. Both of these possibilities are hard to imagine being frequently occurred, making the discussed coupling unlikely.
2.3. Winding time
The problem of winding of spiral arms have been recognised for some time. Formulated by Oort et al. (1962) as the ‘winding dilemma’, it states that if spiral arms were material features, they would wind more and more and tightly, until they finally disappear, on timescales of ∼100 Myr. Advances in density wave theory, as detailed in Lin & Shu (1966) and other works (e.g. see Shu 2016 and Marochnik 2005) allow this puzzle to be solved. However, in the presence of two or more separate spiral patterns, as in the resonance coupling cases considered, the same dilemma reappears: the inner part inevitably rotates faster than the outer, and the tips of the spirals should diverge from each other, forming bifurcations or gaps in the arms.
Following Merrifield et al. (2006), we define the winding time τwind as the time needed for the patterns to diverge by one full rotation, namely, τwind = 2π/(Ωmax − Ωmin). Under the given assumptions, it should then be transformed into:
where τGY is a time of one disc rotation (or ‘galactic year’) in a place of the inner pattern CR. Therefore, for ϖ values from Table 1 we get values of τwind between 1.2τGY and 4.8τGY. The obtained results show that for most of the presented cases of resonance coupling, the global spiral pattern should wind up in less than three rotations of the disc, if all individual patterns are stationary, and often even twice faster. In Masset & Tagger (1997) authors had already noticed this for bars, that for different pattern speeds the tips of the bar and beginnings of the spirals should be found at random relative azimuthal positions. At the same time, simulations of Minchev et al. (2012) and others demonstrate a preserved and consistent pattern regardless of the coupling in the system. It was explained in Minchev et al. (2012) that each time the bar encounters the spiral, the inner wave is regenerated, accelerating to catch up with the spiral. It is likely that a similar behavior may work for the spiral-spiral case or perhaps spirals are transient in nature rather than long-lived, as Merrifield et al. (2006) concluded, and follow some form of recurrence (Sellwood & Lin 1989).
3. Comparison with observations
We go on to demonstrate the feasibility of obtained results using observations for six nearby galaxies, listed in Table A.1. These are well-known and well-studied objects of late Hubble types and intermediate inclinations. We note that the conducted analysis is not dependent on the exact inclination and PA adopted. All galaxies demonstrate a multi-arm morphology, often with two main arms of greater contrast, as seen in images from the DESI Legacy Imaging Surveys (Dey et al. 2019) in Fig. A.2. According to the literature, only NGC 3344 and NGC 5371 contain a noticeable bar.
Due to the importance of CR estimations for processes related to bars and spirals in galaxies, there are dozens of various methods for estimating it. These include a direct Tremaine-Weinberg method (Tremaine & Weinberg 1984; Fathi et al. 2009; Williams et al. 2021), with modifications (generalisation to multiple pattern speeds in Meidt et al. 2009), a measurement of the shift between potential and density (Buta & Zhang 2009), various angular offset-based methods (Cepa & Beckman 1990; Tamburro et al. 2008; Abdeen et al. 2020; Sakhibov et al. 2021), detections of morphological peculiarities (Roberts et al. 1975; Elmegreen et al. 1992; Elmegreen & Elmegreen 1995), N-body modelling (Kranz et al. 2003), abundance gradients (Vila-Costas & Edmunds 1992; Scarano & Lépine 2013), and radial velocity sign changes (Font et al. 2011, 2014). These are not all approaches to CR detection available, with new ones reported regularly (Marchuk et al. 2024b), but the absolute majority of works use a selection of them.
The values of CR, estimated in different works, tend to be inconsistent with each other (Kostiuk et al. 2024). We present reliable CR estimates for the galaxies under consideration in Fig. 1 and in Table A.2. For each galaxy we have at least three different CR measurements, obtained by at least three different methods, using all the aforementioned works. For NGC 2403, NGC 3893, and NGC 5676 we found data to be consistent with three different CRs, and for three other galaxies we find two. We note that each CR, except the first one for NGC 2403, has been confirmed by at least two different measurements. This fact, together with the visible agreement of individual values obtained using both ISM and stellar data sources with different photometric bands, significantly increases the certainty and reliability of the CR estimate.
 |
Fig. 1. Positions of CR from Table A.2 (points). Colored vertical areas show boundaries of assumed CR for each pattern, dashed red line shows average value for points within each CR. Vertical axis is shown for illustrative purposes only. |
Individual RCs and their approximations are shown in Fig. A.1. For each galaxy, we find HI observations in order to track cold circular velocity, in some cases backed with additional observations. Indeed, it is easy to see from Fig. A.1 that all RCs are flat over the range of radii considered to be important in this work, but with two sidenotes. Firstly, we note that the first CR in NGC 3893 is located before v(r) reaches the plateau velocity, v0. Secondly, in NGC 5371, data points do not agree perfectly with each other resulting in what is probably a larger v0 value than in the fit, but all this does not greatly affect the colored areas shown in Fig. A.1. We note that all CRs are located within the canonical optical radius r25, found in Makarov et al. (2014).
We present the frequency curves Ω(r) and their associated resonances in Fig. 2. It is easy to see that all 6 galaxies demonstrate the apparent pattern coupling, visible in this figure. In all cases (except NGC 2403, where it is also presented, but not for subsequent patterns), we see the same repetitive situation: OLR of the inner pattern coincides with CR of the next, and CR of inner lies within the radius of the outer IUHR. For one galaxy, NGC 5675, we even see it repeated twice for three separate spiral patterns. We note that the ratio ϖ between corotation radii, shown in Fig. 2, is in all cases in a good agreement within uncertainties with predictions listed in Table 1 and the predictions from Sect. 2.2, along with the same occurrence of according couplings.
 |
Fig. 2. Angular velocity and resonances curves: solid lines show Ω, ILR, and OLR; dotted lines show IUHR and OUHR. Areas filled with gray colour represent error associated with RC. Red points show the average position of each CR. Horizontal lines demonstrate extension of each spiral pattern from it’s inner resonance (ILR or IUHR) to the outer one (OLR). Numbers show ϖ for consecutive patterns. Blue hatched areas mark bar size from Herrera-Endoqui et al. (2015). |
Several insights come from Fig. 2. First, the case of special interest is the galaxy NGC 2403 and the first resonance coupling in NGC 3893. Here, we see the case where OLRin = OUHRout and OUHRin = CRout, neither of which has been previously reported as far as we aware. Their synchronous appearance is not accidental and also shows agreement with Sect. 2.2, which gives exactly the predicted ϖ for NGC 2403, where it is repeated twice. This is not the case for NGC 3893, because the first CR is not located within the RC plateau. Secondly, we notice that for galaxies with more than two patterns, the central CR is coupled with both of them. This is very similar to the case of NGC 3433 presented in Beckman et al. (2018), where the central pattern is also supported from both sides. Finally, if we also mark the bar size, which is 25.5 arcsec for NGC 3344 and 19.3 arcsec for NGC 5371 (Herrera-Endoqui et al. 2015), and taking into account that the bar ends near its CR, we find that the bar is coupled with ILR of spiral pattern for both galaxies.
4. Discussion, additional notes, and conclusion
For several of the galaxies included in this study, we are not the first to report resonance coupling. As already mentioned, Font et al. (2011, 2014) studied changes of radial velocity sign and found them in many cases, including the presented NGC 3344, NGC 3893, and NGC 5676 (UGC5840, UGC6778 and UGC9366 in their works). Along with other sources, we also used their CRs measurements in these galaxies too, as indicated in Table A.2. Therefore, the results for these galaxies may seem trivial at first sight. However, firstly, we used other sources and methods to confirm the measurements and, secondly, interpretation plays a crucial role here. For example, Font et al. (2014) for NGC 3344 interpret last CR as OLR of the second pattern, without mentioning the coupling. For NGC 3893, they did not notice the coupling at 63 ± 3 arcsec and interpreted the last point as a separate pattern, when it should be OUHR. Finally, in Font et al. (2014) authors did not detect the important last CR we found in NGC 5676 and their 47.2 ± 2.6 arcsec point is likely not another CR; instead it is an OUHR, as Fig. 2 clearly shows. In summary, we show that even in these galaxies, the reported coupling has not been fully recognised.
Foyle et al. (2011) studied angular offsets between different indicators using the cross-correlation method to find that they are not consistent with a stable density wave, including NGC 628 and NGC 2403, which we analyse here. However, Font et al. (2014) found that measured offsets are actually broadly consistent with density wave, assuming the existence of multiple patterns. Indeed, we see the expected zero angular offsets in radii close to CRs obtained in NGC 628 and for the first CR in NGC 2403, where the Foyle et al. (2011) analysis is not sufficiently extended. In any case, the application of the cross-correlation method to azimuthal profiles is difficult for galaxies with complex morphologies.
We also want to mention some supporting evidence that indicates the estimated CRs are correct. For example, we can see that the angular offsets measured by Tamburro et al. (2008) for NGC 2403 could easily be fitted by two curves, or that the metallicity values in Berg et al. (2013) for the same galaxy show a break at the location of the first CR. For NGC 5371, we find that the residuals of the velocity field for the HI data in Begeman (1987) are consistent with Fig. 1, when we apply the Font et al. (2011) method.
Coupling could also leave an imprint on the galactic morphology. For all galaxies, we see a complex morphology, that there are several long extended arms and many that diverge from them, which look shorter and weaker (Fig. A.2). Font et al. (2014) called this “organised pseudo-flocculence.” Similarly to our case, we are able to see clear bifurcations for NGC 3433 in Beckman et al. (2018) in their Fig. 1. The reason is probably the winding, as demonstrated in Sect. 2.3, or it is due to the existence of beat waves (Masset & Tagger 1997; Elmegreen et al. 1992). The simulations from Quillen et al. (2011) and Minchev et al. (2012) clearly show gaps and discontinuities in the main spiral arms, arguing that they indicate changes in the dominant pattern, namely, the transition between the inner and outer structures. Finally, the Landau damping mechanism could also be the reason, as Mattor & Mitchell (1996) suggested.
Another feature of a galaxy’s appearance that is relevant to his discussion consists of the breaks in their discs. Minchev et al. (2012) and Roškar et al. (2012) used numerical models to demonstrate that resonance overlap leads to the eventual formation of a break at the position of CR. This is exactly what could be found, for example, for NGC 3893. In the case, we see a remarkable coincidence between the estimated CRs (see Fig. 1) of individual patterns and the change on the exponential scale, presented on the azimuthally averaged profile from Salo et al. (2015). Another interesting piece of evidence that may support this theory comes from Muñoz-Mateos et al. (2013), who found that many galaxies have disc breaks at about 3.5Rbar, where Rbar is a half-size of a bar major axis. These authors have made similar arguments about the flat RC and interpretation that the break occurs at the spiral’s OLR due to coupling. However, we want to note that it can alternatively be explained by the fact that Rbar ≈ RCR and, according to Table 1, we can observe that breaks form exactly at the spiral’s CR, which is in better agreement with Minchev et al. (2012) and Roškar et al. (2012) predictions. Certainly, the question under consideration is more difficult than that, because we can find CRs exactly where spirals form “bump” on top of the disc (Kendall et al. 2011; Marchuk et al. 2024a) or the breaks themselves could be the reason for several patterns and apparent coupling (Fiteni et al. 2024). This topic needs a separate and careful investigation.
The reliable estimations of CR or equivalent Ωp presented in this work are important in and of themselves for a number of reasons, including the crucial role of CR in the swing amplification mechanism (Toomre 1981), its connection with orbital (Contopoulos & Harsoula 2013) and gravitational (Inoue et al. 2021) stability, chemical evolution (Vila-Costas & Edmunds 1992) in the disc, and other issues, such as local star formation (Williams et al. 2022). In addition, we would like to emphasise that resonance coupling may be of great importance not only for angular momentum transfer (Sellwood & Binney 2002; Masset & Tagger 1997; Minchev et al. 2012), but also for disc heating (Minchev & Quillen 2006) and for magnetic field generation on the galactic scale, as suggested by Chamandy et al. (2014). Another important application of the results obtained relates to our own Galaxy. Shaviv (2003) summarised the Ωp measurements for MW in their Table 3, where the measurements are clearly concentrated in two sets with average about 22–26 km s−1 kpc−1 and 14 km s−1 kpc−1 (see also Bobylev & Bajkova 2022; Vallée 2021; Naoz & Shaviv 2007). Given that RC of Galaxy to a first approximation is flat here (Russeil et al. 2017), we obtained ϖ ≈ 1.7, namely, MW show signs of the ongoing coupling between patterns as found in Font et al. (2014).
The nature of spiral arms remains elusive en masse. In this preliminary study, our conclusions are as follows.
(i) Assuming a flat rotation (RC) curve and spiral-spiral resonance coupling, we find the ratio ϖ = CRout/CRin of corotation radii (CRs) of two consequent patterns for all main resonances overlapping, presented in Table 1. In three cases, we get ϖ values greater than 3, so there is barely enough space for two or more spiral patterns in the disc. We thus predict that examples of such galaxies are expected to be rare, if they even exist.
(ii) We demonstrate that simultaneous coupling OLRin = CRout & CRin = IUHRout, observed in many galaxies by Font et al. (2014), appears very naturally in our formulation due to the very close ϖ ratio in both cases. This is also true for two other pairs, mentioned in Sect. 2.2.
(iii) For six galaxies with flat RC, we estimate several corotation radii, using measurements from other works (Table A.2). For each galaxy, we used at least three different independent methods to increase the level of confidence. We predict that new accurate measurements will fit with the presented CRs and found supporting evidence.
(iv) For these galaxies, we demonstrate that the estimated observational resonances are visually coupled (Fig. 2) and agree with expectations, as well as the ϖ ratio. This is not the first time, when coupling has been demonstrated in real galaxies, but it is now well motivated. The substantial arguments found for resonance coupling provide strong observational evidence for the existence of several individual spiral patterns simultaneously in one galaxy.
(v) We demonstrate that resonance coupling inevitably means that spirals are expected to ‘wind up’ in several rotations. We estimate the wind-up time τwind for each case in terms of rotations.
(vi) We find a new resonance coupling variant in NGC 2403 (twice) and NGC3893, specifically OLRin = OUHRout & OUHRin = CRout. We believe that both separate and simultaneous cases have not been noticed before and, similarly to the case of Font et al. (2014), this coincidence ought to be expected from the proximity of ϖ.
In a future work, we will continue to explore the dynamics and nature of spiral arms by extending this analysis to new objects. Thus, we plan to focus on the galaxy M109 (NGC 3992), which has a flat RC and obvious coupling, but with only one measurement for each CR. Another is M101 (NGC 5457), where we see the same case of coupling repeated three times according to the measured ϖ, but where the HI RC is limited and contains only the first CR. In total, we have at least ten less reliable candidate galaxies with probable observed resonance coupling. We will also generalise the obtained result for non-flat RC and take a closer examination of the interplay between morphological features (number of arms, disc breaks) and properties of individual spiral patterns.
References
- Abdeen, S., Kennefick, D., Kennefick, J., et al. 2020, MNRAS, 496, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Beckman, J. E., Font, J., Borlaff, A., et al. 2018, ApJ, 854, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Begeman, K. K. G. 1987, Ph.D. Thesis, Kapteyn Astronomical Institute, University of Groningen, The Netherlands [Google Scholar]
- Berg, D. A., Skillman, E. D., Garnett, D. R., et al. 2013, ApJ, 775, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, G., Lin, C. C., Lowe, S. A., et al. 1989, ApJ, 338, 78 [CrossRef] [Google Scholar]
- Bobylev, V. V., & Bajkova, A. T. 2022, Astron. Lett., 48, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., & Zhang, X. 2009, ApJS, 182, 559 [Google Scholar]
- Cepa, J., & Beckman, J. E. 1990, ApJ, 349, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Subramanian, K., & Quillen, A. 2014, MNRAS, 437, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, MNRAS, 373, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G., & Harsoula, M. 2013, MNRAS, 436, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
- Dobbs, C., & Baba, J. 2014, PASA, 31, e035 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., & Montenegro, L. 1992, ApJS, 79, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., & Elmegreen, B. G. 1995, ApJ, 445, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Fathi, K., Beckman, J. E., Piñol-Ferrer, N., et al. 2009, ApJ, 704, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Fiteni, K., De Rijcke, S., Debattista, V. P., et al. 2024, MNRAS, 529, 4879 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J., Beckman, J. E., Epinat, B., et al. 2011, ApJ, 741, L14 [Google Scholar]
- Font, J., Beckman, J. E., Querejeta, M., et al. 2014, ApJS, 210, 2 [Google Scholar]
- Foyle, K., Rix, H.-W., Dobbs, C. L., et al. 2011, ApJ, 735, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Fridman, A. M., Afanasiev, V. L., Dodonov, S. N., et al. 2005, A&A, 430, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrido, O., Marcelin, M., Amram, P., et al. 2005, MNRAS, 362, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Endoqui, M., Díaz-García, S., Laurikainen, E., et al. 2015, A&A, 582, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, S., Takagi, T., Miyazaki, A., et al. 2021, MNRAS, 506, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, S., Kennicutt, R. C., & Clarke, C. 2011, MNRAS, 414, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Norman, C. A. 1979, ApJ, 233, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Kostiuk, V., Marchuk, A., & Gusev, A. 2024, RAA, 475, 1 [Google Scholar]
- Kranz, T., Slyz, A., & Rix, H.-W. 2003, ApJ, 586, 143 [Google Scholar]
- Li, A., Fraternali, F., Marasco, A., et al. 2023, MNRAS, 520, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. C., & Shu, F. H. 1964, ApJ, 140, 646 [Google Scholar]
- Lin, C. C., & Shu, F. H. 1966, Proc. Nat. Acad. Sci., 55, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Kalnajs, A. J. 1972, MNRAS, 157, 1 [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., et al. 2014, A&A, 570, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchuk, A. A. 2018, MNRAS, 476, 3591 [NASA ADS] [CrossRef] [Google Scholar]
- Marchuk, A. A., Chugunov, I. V., Gontcharov, G. A., et al. 2024a, MNRAS, 528, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Marchuk, A. A., Mosenkov, A. V., Chugunov, I. V., et al. 2024b, MNRAS, 527, L66 [Google Scholar]
- Marochnik, L. S. 2005, A&AS, 207, 3101 [Google Scholar]
- Martínez-García, E. E., González-Lópezlira, R. A., & Bruzual-A, G. 2009, ApJ, 694, 512 [CrossRef] [Google Scholar]
- Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
- Mattor, N., & Mitchell, T. B. 1996, ApJ, 472, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Rand, R. J., Merrifield, M. R., et al. 2008, ApJ, 688, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Rand, R. J., & Merrifield, M. R. 2009, ApJ, 702, 277 [Google Scholar]
- Merrifield, M. R., Rand, R. J., & Meidt, S. E. 2006, MNRAS, 366, L17 [NASA ADS] [Google Scholar]
- Minchev, I., & Quillen, A. C. 2006, MNRAS, 368, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moellenhoff, C., Matthias, M., & Gerhard, O. E. 1995, A&A, 301, 359 [Google Scholar]
- Mosenkov, A. V., Panasyuk, A. D., Turner, S., et al. 2024, MNRAS, 527, 10615 [Google Scholar]
- Muñoz-Mateos, J. C., Sheth, K., Gil de Paz, A., et al. 2013, ApJ, 771, 59 [Google Scholar]
- Naoz, S., & Shaviv, N. J. 2007, New A, 12, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Oort, J. H. 1962, in Interstellar Matter in Galaxies, ed. L. Woltjer (New York: Benjamin), 234 [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., et al. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Rautiainen, P., & Salo, H. 1999, A&A, 348, 737 [NASA ADS] [Google Scholar]
- Roberts, W. W., Roberts, M. S., & Shu, F. H. 1975, ApJ, 196, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Rosado, M., Gabbasov, R., & Fuentes-Carrera, I. 2011, Tracing the Ancestry of Galaxies, 277, 259 [NASA ADS] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., et al. 2012, MNRAS, 426, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Zavagno, A., Mège, P., et al. 2017, A&A, 601, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakhibov, F., Gusev, A. S., & Hemmerich, C. 2021, MNRAS, 508, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H., Laurikainen, E., Laine, J., et al. 2015, ApJS, 219, 4 [Google Scholar]
- Sanders, R. H. 1996, ApJ, 473, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & Verheijen, M. A. W. 1998, ApJ, 503, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Scarano, S., & Lépine, J. R. D. 2013, MNRAS, 428, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [Google Scholar]
- Sellwood, J. A., & Carlberg, R. G. 1984, ApJ, 282, 61 [Google Scholar]
- Sellwood, J. A., & Carlberg, R. G. 2019, MNRAS, 489, 116 [CrossRef] [Google Scholar]
- Sellwood, J. A., & Lin, D. N. C. 1989, MNRAS, 240, 991 [NASA ADS] [Google Scholar]
- Sellwood, J. A., & Masters, K. L. 2022, ARA&A, 60, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Shaviv, N. J. 2003, New A, 8, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 2016, ARA&A, 54, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Struck, C., Dobbs, C. L., & Hwang, J.-S. 2011, MNRAS, 414, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Sygnet, J. F., Tagger, M., Athanassoula, E., et al. 1988, MNRAS, 232, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Tagger, M., & Pellat, R. 1982, Plasma Phys., 24, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Tagger, M., Sygnet, J. F., Athanassoula, E., et al. 1987, ApJ, 318, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Tamburro, D., Rix, H.-W., Walter, F., et al. 2008, AJ, 136, 2872 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1981, Structure and Evolution of Normal Galaxies, 111 [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, ApJ, 282, L5 [Google Scholar]
- Vallée, J. P. 2021, MNRAS, 506, 523 [CrossRef] [Google Scholar]
- van der Hulst, J. M., van Albada, T. S., & Sancisi, R. 2001, ASP COnf. Ser., 240, 451 [NASA ADS] [Google Scholar]
- Verdes-Montenegro, L., Bosma, A., & Athanassoula, E. 2000, A&A, 356, 827 [NASA ADS] [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Willett, K. W., Lintott, C. J., Bamford, S. P., et al. 2013, MNRAS, 435, 2835 [Google Scholar]
- Williams, T. G., Schinnerer, E., Emsellem, E., et al. 2021, AJ, 161, 185 [Google Scholar]
- Williams, T. G., Sun, J., Barnes, A. T., et al. 2022, ApJ, 941, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., & Buta, R. J. 2007, AJ, 133, 2584 [Google Scholar]
Appendix A: Observational data
Here in Table A.2 we list corotation measurements compiled from the literature for six galaxies and references for them, and in Table A.1 present main properties of used galaxies. In Figure A.1 we show rotation curves, compiled from the literature sources.
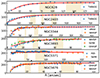 |
Fig. A.1. Rotation curves (markers) and their fits (solid line) with 7% relative error. Triangle symbol marks r25/2 position. References: F05 (Hα): Fridman et al. (2005); THINGS (HI): de Blok et al. (2008); GHASP (Hα): Garrido et al. (2005); SV98 (HI): Sanders & Verheijen (1998); VM00 (optical): Verdes-Montenegro et al. (2000); WHISP (HI): van der Hulst et al. (2001); and Sa96 (HI): Sanders (1996). |
 |
Fig. A.2. Thumbnail images of galaxies from DESI Legacy Imaging Surveys (Dey et al. 2019) in the g band. Images are in logarithmic scale in arbitrary units, circles show the average positions of each CR accordingly, and the scalebar length in each frame is equal to 2 arcmin. |
Parameters of galaxies. References are: (i) Marchuk (2018); (ii) Li et al. (2023); (iii) Meidt et al. (2009); (iv) Font et al. (2014); (v) Fathi et al. (2009).
CR measurements and reference works: [1] Elmegreen & Elmegreen (1995); [2] Meidt et al. (2009); [3] Font et al. (2011, 2014); [4] Tamburro et al. (2008); [5] Scarano & Lépine (2013); [6] Fathi et al. (2009); [7] Martínez-García et al. (2009); [8] Roberts et al. (1975); [9] Kranz et al. (2003); [10] Williams et al. (2021); [11] Abdeen et al. (2020); [12] Buta & Zhang (2009); [13] Vila-Costas & Edmunds (1992); [14] Cepa & Beckman (1990); [15] Sakhibov et al. (2021); [16] Elmegreen et al. (1992); [17] Marchuk et al. (2024b).
All Tables
Parameters of galaxies. References are: (i) Marchuk (2018); (ii) Li et al. (2023); (iii) Meidt et al. (2009); (iv) Font et al. (2014); (v) Fathi et al. (2009).
CR measurements and reference works: [1] Elmegreen & Elmegreen (1995); [2] Meidt et al. (2009); [3] Font et al. (2011, 2014); [4] Tamburro et al. (2008); [5] Scarano & Lépine (2013); [6] Fathi et al. (2009); [7] Martínez-García et al. (2009); [8] Roberts et al. (1975); [9] Kranz et al. (2003); [10] Williams et al. (2021); [11] Abdeen et al. (2020); [12] Buta & Zhang (2009); [13] Vila-Costas & Edmunds (1992); [14] Cepa & Beckman (1990); [15] Sakhibov et al. (2021); [16] Elmegreen et al. (1992); [17] Marchuk et al. (2024b).
All Figures
 |
Fig. 1. Positions of CR from Table A.2 (points). Colored vertical areas show boundaries of assumed CR for each pattern, dashed red line shows average value for points within each CR. Vertical axis is shown for illustrative purposes only. |
| In the text | |
 |
Fig. 2. Angular velocity and resonances curves: solid lines show Ω, ILR, and OLR; dotted lines show IUHR and OUHR. Areas filled with gray colour represent error associated with RC. Red points show the average position of each CR. Horizontal lines demonstrate extension of each spiral pattern from it’s inner resonance (ILR or IUHR) to the outer one (OLR). Numbers show ϖ for consecutive patterns. Blue hatched areas mark bar size from Herrera-Endoqui et al. (2015). |
| In the text | |
 |
Fig. A.1. Rotation curves (markers) and their fits (solid line) with 7% relative error. Triangle symbol marks r25/2 position. References: F05 (Hα): Fridman et al. (2005); THINGS (HI): de Blok et al. (2008); GHASP (Hα): Garrido et al. (2005); SV98 (HI): Sanders & Verheijen (1998); VM00 (optical): Verdes-Montenegro et al. (2000); WHISP (HI): van der Hulst et al. (2001); and Sa96 (HI): Sanders (1996). |
| In the text | |
 |
Fig. A.2. Thumbnail images of galaxies from DESI Legacy Imaging Surveys (Dey et al. 2019) in the g band. Images are in logarithmic scale in arbitrary units, circles show the average positions of each CR accordingly, and the scalebar length in each frame is equal to 2 arcmin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.