| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202449169 | |
| Published online | 03 June 2024 | |
Examining the detectability of ringing on highly eccentric exoplanets
1
Institute for Astronomy (IvS), KU Leuven,
Celestijnenlaan 200D,
3001
Leuven,
Belgium
e-mail: mathijs.vanrespaille@kuleuven.be
2
Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Science Park 904,
1098 XH
Amsterdam,
The Netherlands
3
Centre for ExoLife Sciences, Niels Bohr Institute,
Øster Voldgade 5,
1350
Copenhagen,
Denmark
4
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz,
Austria
Received:
5
January
2024
Accepted:
4
March
2024
Context. Eccentric exoplanets offer an opportunity to study the response of an atmosphere to changing thermal forcing and the robustness of the super-rotating equatorial jet seen on tidally locked hot Jupiters. However, the atmospheric dynamics on eccentric planets strongly depend on the planetary rotation period, which is difficult to constrain observationally. The ringing phenomenon, whereby the observed emission increases and decreases after the periastron passage as the flash-heated hemisphere rotates into and out of view, can provide a tight constraint on rotation.
Aims. We studied five highly eccentric transiting exoplanets HAT-P-2 b, HD 80606 b, TOI-3362 b, TOI-4127 b and HD 17156 b to find which displays strong ringing signals that are sufficiently strong for the James Webb Space Telescope (JWST) to detect.
Methods. We implemented the treatment of eccentricity and non-synchronous rotation in the non-grey climate model expeRT/MITgcm and generated synthetic light curves.
Results. We find four detectable ringing peaks on HD 80606 b and some undetectable ringing on TOI-4127 b and HD 17156 b. The lack of clouds, photo-chemistry and obliquity in our models may have led us to overestimate the amplitude of the ringing however. The strength of the ringing signal is mostly determined by the eccentricity, planetary rotation period, planet-to-star radius ratio and apparent magnitude of the system. We searched for more exoplanets that could show ringing but found no candidates as promising as HD 80606 b.
Conclusions. We recommend prioritising HD 80606 b as a target for ringing with JWST. A baseline of five days after the periastron passage would capture three ringing peaks, which is sufficient to tightly constrain the planetary rotation period. An extension to seven days would add a fourth peak, which would allow us to verify the rotation period.
Key words: planets and satellites: atmospheres / planets and satellites: individual:: HAT-P-2 b / planets and satellites: individual: HD 80606 b / planets and satellites: individual: TOI-3362 b / planets and satellites: individual: TOI-4127 b / planets and satellites: individual: HD 17156 b
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In the past few decades there have been great advances in the study of exoplanetary atmospheres. The observations of the recently launched James Webb Space Telescope (JWST) have already contributed greatly to these efforts (e.g. JWST Transiting Exoplanet Community Early Release Science Team et al. 2023; Feinstein et al. 2023; Tsai et al. 2023a; Dyrek et al. 2024). Because of the complicated nature of exoplanetary atmospheres, observations should be compared to global circulation models (GCMs) to be interpreted properly. These GCMs require well-constrained orbital and planetary parameters, such as the planet’s radius, rotation period, and orbital eccentricity, as input (Showman et al. 2020). If the planet transits its parent star, most of these quantities can be reliably measured, with the notable exception of the rotation period (Sing 2018).
Most studies so far have focussed on hot Jupiters because their size and brightness makes it relatively easy to achieve a high observational signal-to-noise (Showman et al. 2020). As a result of their close-in orbits, hot Jupiters are often on a tidally circularised orbit. Based on timescale arguments, it can then safely be assumed that the planet’s rotation period is equal to the orbital period (Hut 1981; Socrates et al. 2012; Rauscher 2017) and that its obliquity is zero (Rauscher 2017; Rauscher et al. 2023). Consequently, the irradiation these planets receive is constant in intensity and always illuminates the same hemisphere. On the dayside hemisphere, the illumination creates a pattern of geostrophic winds that transport angular momentum towards the equator (Showman & Polvani 2010, 2011). Consequently, these winds form a remarkable circulation pattern that is dominated by an eastward flow of gas centred on the equator and extending around the planet, which typically reaches speeds of several km s−1. This flow is called the equatorial super-rotating jet. The existence of such jets is well established both theoretically (e.g. Showman & Guillot 2002; Showman et al. 2009, 2020; Tsai et al. 2014; Amundsen et al. 2016; Carone et al. 2020) and observationally (e.g. Knutson et al. 2007; Snellen et al. 2010; Zellem et al. 2014; Louden & Wheatley 2015; May et al. 2022). Because of the major role of the Coriolis force in atmospheric dynamics, the planet’s rotation period is a decisive parameter in the shaping of these circulation patterns (e.g. Showman et al. 2009, 2015; Showman & Polvani 2010; Rauscher & Kempton 2014; Baeyens et al. 2021; May et al. 2022).
Planets on eccentric orbits can no longer be assumed to rotate synchronously (Hut 1981). Despite the increased difficulty, studying eccentric and non-synchronously rotating exoplanets is worthwhile as it allows one to examine the response of the atmosphere’s dynamics, chemistry, and cloudiness to changing thermal forcing (Kataria et al. 2013; Lewis et al. 2017; Tsai et al. 2023b). Moreover, transit spectroscopy of cool planets on far-out, circular orbits is rarely available as the distance to the star reduces the likelihood that a transit would take place. For an eccentric planet, on the other hand, a transit is more likely to take place around periastron, when the atmosphere still contains traces of the cooler regime around apastron that is otherwise difficult to observe. Finally, about half of the known Jupiter-like planets are eccentric, especially those with a longer orbital period due to the distance dependence of tidal circularisation (Malmberg & Davies 2009; Dawson & Murray-Clay 2013; Bitsch et al. 2020).
A number of previous studies have examined the role of eccentricity and non-synchronous rotation in the atmospheric circulation of hot and warm Jupiters. Showman et al. (2009, 2015) and Rauscher & Kempton (2014) used 3D GCMs to study the effect of non-synchronous rotation, concluding that a shorter rotation period weakens the equatorial jet. They disagree on the effect of an increased rotation period, though, with Rauscher & Kempton (2014) claiming that a westward flow develops and Showman et al. (2009, 2015) finding that it leads to significantly broader and faster eastward jets. Nonetheless, these studies all show that the rotation period plays a major role in atmospheric circulation. In a similar vein, Kataria et al. (2013) examined the impact of eccentricity in a theoretical scenario, pointing out that while jets are still ubiquitous, they tend to be faster the greater the eccentricity is and change quite notably in the upper atmosphere throughout the orbit. This is in agreement with the results of Lewis et al. (2014), who simulated the eccentric planet HAT-P-2 b, and Lewis et al. (2017) and Tsai et al. (2023b), who examined the extremely eccentric HD 80606 b. The latter two studies show that the jet speed on HD 80606 b decreases between periastron passages. Lewis et al. (2017) also highlight the impact of the rotation period on the circulation, composition, and lofting of clouds and, consequently, the photometric observations of highly eccentric planets.
During the periastron passage, when an eccentric planet is briefly but intensely heated, most of the flash-heating occurs on the side facing the star. As the planet moves farther from the star and cools, that heated hemisphere rotates into and out of view of an observer on Earth. Consequently, the total brightness of the star and planet combined may display a number of local maxima, which is known as ringing. Thus, by studying the system’s light curve after the periastron passage, one can constrain the planet’s rotation period as well as how efficiently the temperature is homogenised by circulation. Using a simple thermal model without consistent dynamics or radiative transfer, Cowan & Agol (2011) predicted the presence of such ringing on the exoplanets HAT-P-2 b, HD 80606 b, and HD 17156 b, among others. This stands in contrast to the work of Iro & Deming (2010), who, with another simple radiative model, found little ringing in their synthetic light curves of these three planets. Kataria et al. (2013) examined the phenomenon in a theoretical case with a 3D GCM coupled to radiative transfer, highlighting the importance of the viewing geometry. Ringing has not yet been observed on any exoplanet, though. de Wit et al. (2016) and Lewis et al. (2017) used the lack of ringing in Spitɀer observations of HD 80606 b to constrain its rotation period and infer the likely presence of clouds, demonstrating that even the non-detection of ringing holds valuable information in some systems. As these Spitɀer observations had a short baseline – a maximum of two days after the periastron passage and shorter still at the longer wavelengths more suitable to observe ringing – this does not exclude the possibility that a future JWST observation with a longer baseline may detect ringing.
No recent work employing a 3D GCM with full coupling to a non-grey radiative transfer implementation has simulated multiple known eccentric exoplanets to predict their photometric signals. Therefore, it is as of yet unclear how many and which planets are likely to display ringing. In this study we generated synthetic light curves of five highly eccentric transiting exoplanets to examine whether JWST would be able to detect any ringing. Our ultimate goal is to inform the planning of JWST observing time by identifying viable targets and determining the baseline required for a ringing observation.
2 Eccentric exoplanet GCM
2.1 expeRT/MITgcm
We employed the atmospheric model expeRT/MITgcm (Carone et al. 2020; Schneider et al. 2022b), which features 3D hydrodynamics coupled to a full non-grey radiative transfer solution. It is built upon the MITgcm dynamical core of Adcroft et al. (2004), which solves the primitive equations of hydrodynamics assuming an ideal gas. The model also assumes the planet to be a rigidly rotating sphere. We used a C32 cubed-sphere grid with 47 vertical layers, the upper 41 of which are logarithmically spaced in pressure between 10−5 and 100 bar and the lower six linearly spaced in steps of 100 bar down to 700 bar. A dynamical time-step of 25 s reliably obeys the Courant-Friedrichs-Lewy stability criterion (Courant et al. 1928). To smoothen small-scale noise, a fourth-order Shapiro filter with a 1 day timescale is applied (Shapiro 1971). At the top boundary, unphysical gravity waves are dampened by a soft sponge layer, as described by Schneider et al. (2022b). Meanwhile, we applied Rayleigh friction below 200 bar to emulate magnetic drag, which Carone et al. (2020) find improves the stability of the model. We also employed the heating term due to this parameterised drag introduced by Schneider et al. (2022a).
expeRT/MITgcm features a radiative transfer treatment including scattering using the Feautrier method with accelerated lambda iteration. Following Schneider et al. (2022b), we used a radiative time-step of 100 s, meaning the radiation field is only updated after every fourth dynamical time-step. Moreover, the radiative flux is only computed for every second column and then interpolated in between. We used six correlated-k bins (Goody et al. 1989) with sixteen Gaussian quadrature points each to discretise our 0.26-300 µm wavelength range (Schneider et al. 2022b). We employed the pre-computed opacity table of the chemical equilibrium model of Mollière et al. (2019), which minimises the Gibbs free energy on a grid of 1000 temperatures at our 47 pressures. It includes: the molecules H2O, CO2, CH4, NH3, CO, H2S, HCN, PH3, and FeH and the atoms Na and K as line opacity sources; Rayleigh scattering by H2 and He; and absorption collisionally induced by interactions between H2-H2, H2-He, and H−. TiO and VO were not added in our models as they often produce temperature inversions in the models (e.g. Showman et al. 2009; Lewis et al. 2014; Kataria et al. 2015; Schneider et al. 2022b) and such inversions are only observed on the hottest exoplanets (Heng & Marley 2018; Arcangeli et al. 2018; Parmentier et al. 2018; Lothringer et al. 2018). The effects of clouds and hazes were not included in our model. Since measurements of the obliquity are available for few exoplanets and typically have a large uncertainty (Rauscher 2017; Ohno & Zhang 2019b; Adams et al. 2019; Bryan et al. 2020, 2021), we neglected obliquity in our model. Finally, we assumed each atmosphere has a solar chemical composition, as is commonly done (e.g. Showman et al. 2009; Kataria et al. 2013; Amundsen et al. 2016; Lewis et al. 2017).
Relevant orbital, planetary, and stellar parameters of the five planetary systems in our sample.
2.2 Implementation of eccentricity and non-synchronous rotation
We extended expeRT/MITgcm to allow for non-synchronous rotation and eccentric orbits as it was limited to tidally locked planets before. On tidally locked planets, the incoming irradiation is constant in intensity and always centred on the same point. On an eccentric and non-synchronously rotating planet on the other hand, the irradiation varies in two ways. Firstly, the intensity changes as r−2, with distance r, which depends on the true anomaly v as r = a(1 − e2)(1 + e cos ν)−1. Herein, a is the semi-major axis and e the eccentricity. Secondly, the position of the substellar point in the planet’s co-rotating reference frame as 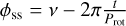 with t the time and Prot the rotation period.
with t the time and Prot the rotation period.
Since there is no analytical formula to calculate v for any given t, we applied an iterative Newton-Raphson method to the Kepler equation (Gregory 2006) until the error in time was smaller than 10−6 of the orbital period at each radiative time-step. This method needs no more than ten iterations, making it both precise and computationally cheap. However, the radiative transfer requires more iterations when the temperature structure changes due to the changing irradiation, which can increase the total computation time of the model by a factor of up to two.
2.3 Setup of the simulations
In this study we examined five exoplanets with a high eccentricity covering a range of orbital periods, including a number of targets that have been studied before and are to be revisited by JWST. The chosen planets are HAT-P-2 b (Bakos et al. 2007), HD 80606 b (Naef et al. 2001), TOI-3362 b (Dong et al. 2021), TOI-4127 b (Gupta et al. 2023), and HD 17156 b (Fischer et al. 2007). The relevant planetary, orbital and stellar parameters are listed in Table 1. The argument of periastron ω defines the viewing geometry, as visualised in Fig. 1. The rotation periods of the planets were computed using the commonly used pseudo-synchronous period Pps of Hut (1981; e.g. Kataria et al. 2013; Lewis et al. 2014, 2017; Tsai et al. 2023b) given in Eq. (1), where the rotation period is synchronised with the orbital motion around the periastron passage since that is where the tidal effects are strongest. As a result, the substellar point moves little during the periastron passage:
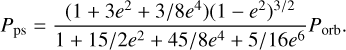 (1)
(1)
Upon initialisation, the wind speed was zero everywhere. The temperature was horizontally homogeneous with a vertical profile comprised of three parts. The upper atmosphere at pressures smaller than 1 bar was given a constant temperature based on the analytical model of Parmentier et al. (2015). That model requires an estimate of the intrinsic temperature, which is computed using the relation developed in Thorngren et al. (2019). The layers deeper than 10 bar followed an adiabatic profile with a temperature of 1400 K at 1 bar, which Sainsbury-Martinez et al. (2019) find to be appropriate for the tidally locked hot Jupiter HD 209458 b. For the exoplanets modelled in this study, which have lower mean equilibrium temperatures than HD 209458 b, this deep temperature profile is likely too hot. However, Sainsbury-Martinez et al. (2019) advise using too hot a profile as atmospheric models converge more rapidly when cooling down than when heating up. Between 1 and 10 bar, the temperature profile is linearly interpolated in pressure.
To reduce the total computation time, each planet was first treated as if it were tidally locked at a distance of the semi-major axis for 1000 d to let the temperature structure partly converge. Next, it was simulated for another 1000 d as an eccentric and non-synchronously rotating planet. On HD 80606 b, TOI-3362 b, and TOI-4127 b, the temperature structure or jet speed at the apastron still changed considerably between consecutive orbits, so the run continued for another 1000 d, after which the jet speed or the upper atmosphere’s temperature did not monotonically change between orbits. However, the deep atmosphere’s temperature was still not fully converged in any model. Schneider et al. (2022a) simulated the ultra hot Jupiter WASP-76 b for 86 000 d and even after such a long run, the deep atmosphere’s temperature had not fully converged. As such, achieving complete convergence is unfeasible. Mayne et al. (2017) and Carone et al. (2020) show that the dynamics of the deep atmosphere can considerably affect the upper atmosphere. However, Tsai et al. (2023b) indicate that additional internal heat from the overly hot deep atmosphere is unlikely to strongly affect the temperature and wind of the upper atmosphere of HD 80606 b, resulting in only a minor increase in planetary emission. Since the jet speed of the deep atmosphere has converged, we do not expect the incomplete temperature convergence of the deep atmosphere to notably affect our synthetic light curves. Therefore, our models are sufficiently converged for our purposes.
 |
Fig. 1 Drawings showing the orientation of the observer relative to the planet at its periastron passage for each of the five exoplanets (not to scale). The parent star is represented by a red star symbol and the planet by a disk, with the dayside coloured yellow and the nightside black. The blue arrow indicates the direction towards Earth. A solid black line shows the scale of the orbit. The orbital trajectory along which the planet moves in an anticlockwise direction is shown as a dashed grey line. The planet rotates anticlockwise as well. |
2.4 Computing synthetic light curves
Synthetic light curves were calculated during the postprocessing of our GCMs using prt_phasecurve1 (Schneider et al. 2022b), based on the petitRADTRANS code (Mollière et al. 2019, 2020). We first computed a detailed radiation field throughout the atmosphere, which was then interpolated to a grid of 100 points on the side of the planet facing a hypothetical observer. We then integrated the outgoing flux over those 100 points and the chosen wavelength regime, making sure to take the viewing angle into account assuming an inclination of 90°. Finally, we divided by the stellar flux in the same wavelength range. For this work, we reduced the original forty streams used in the initial radiation field computation to six streams and the wavelength resolution from 1000 to 100. This drastically reduces the computation time of the light curve while affecting the precision of a test case based on the tidally locked exoplanet HD 209458 b by less than 1%.
We generated light curves in a wavelength range of 5–12 µm to represent the wavelength range of the Mid-InfraRed Instrument (MIRI) low resolution spectroscopy (LRS) mode aboard JWST. This instrument is commonly used to study exoplanets (Rieke et al. 2015; Kendrew et al. 2015), including some planets in our sample2. To gain some understanding of how sensitive the light curve is to the wavelength regime, we also separated the wavelength range into four sub-ranges, which approximately represent the F560W, F770W, F1000W, and F1130W imaging filters of MIRI (Rieke et al. 2015).
3 Results
3.1 Pseudo-synchronously rotating models
Each of the five eccentric exoplanets in our sample features a prominent equatorial super-rotating jet throughout the entire orbit. Kataria et al. (2013), Lewis et al. (2014, 2017), and Tsai et al. (2023b) find a jet on highly eccentric planets as well, demonstrating that the dynamical regime is quite robust. As in these previous works, the jet in the upper atmosphere is briefly replaced by fast day-to-night wind during the periastron passage, only to be quickly restored as the planet-star distance increases again. Lewis et al. (2017) and Tsai et al. (2023b) also note that the jet speed on HD 80606 b decreases over the orbit. Examining Fig. 2, which shows the maximal jet speed of each planet over time, we see that the jet slows down from about 1400 to 1000 m s−1 on HD 80606 b, in reasonable agreement with Lewis et al. (2017) and Tsai et al. (2023b). TOI-4127 b’s jet similarly slows down from 1700 to 1400 m s−1. The other three planets do not undergo such a consistent deceleration because their jets are continuously driven by the fairly strong irradiation they receive, as indicated by the equilibrium temperature shown in Fig. 3. The equilibrium temperature Teq is the black body temperature a planet needs to radiate away the irradiation. Neglecting the albedo effect, it is
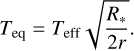 (2)
(2)
Herein, Teff and R* are the effective temperature and radius of the host star and r is the distance to the planet. As they are not as strongly irradiated, the thermal forcing on HD 80606 b and TOI-4127 b is insufficient to continuously feed the super-rotation. Instead, their jets are only driven around the periastron passage when the irradiation is intense and the substellar point does not move as much because of the assumed pseudosynchronous rotation period, resulting in a thermal forcing regime that strongly resembles that of a tidally locked hot Jupiter. Outside the periastron passage, the jet continues under its inertia, but is slowly decelerated by friction processes.
Figure 4 displays the contribution of the planet to the total brightness of each system in different wavelength ranges. The solid black line shows the integral of the full 5–12 µm range. The planet’s relative contribution is greater at longer wavelengths because of its cooler temperature, which is especially notable on HD 80606 b, TOI-4127 b, and HD 17156 b. Each planet’s global maximum in emission occurs shortly after the periastron passage, except for HD 80606 b’s due to its illuminated side being in the observer’s view before the periastron passage, as shown in Fig. 1. After this initial periastron peak, the brightness of HAT-P-2 b and TOI-3362 b decreases mostly monotonically until the next periastron passage. TOI-4127 b, on the other hand, shows one local maximum after the first peak while HD 80606 b has four. These ringing peaks are especially high at longer wavelengths. HD 17156 b has local maxima with small amplitudes only at longer wavelengths.
 |
Fig. 2 Speed of the equatorial jet throughout an orbit for each planet. The speed is computed as the maximum of the zonal wind speed between 100 and 0.01 bar after averaging over 1/50th of the orbital period, taking the zonal mean across the whole planet and the meridional mean between ±20°. We calculated the equatorial jet speed at 50 times and used cubic interpolation between these 50 times. Note that each panel has a different scaling on the two axes. The equatorial jet speed is quite consistent on HAT-P-2 b, TOI-3362 b, and HD 17156 b, apart from some erratic behaviour around the periastron passage. On HD 80606 b and TOI-4127 b, however, it slows down considerably over the orbit after a period of acceleration after the periastron passage. |
3.2 Breaking pseudo-synchronicity on HD 80606 b
To demonstrate the influence of the planet’s rotation period, we repeated the HD 80606 b model with a rotation period equal to half and double the pseudo-synchronous period. Figure 5 shows how the speed of the equatorial jet differs from the pseudo-synchronous case. We note that a longer rotation period leads to a significantly faster equatorial jet. This is explained by the substellar point moving eastwards during the periastron passage if the rotation period is longer than pseudo-synchronous. This leads to more irradiation getting deposited into the already hot part of the atmosphere, thereby increasing the temperature gradient and thus the geostrophic wind speed, resulting in stronger angular momentum transport to the equator and hence a faster jet (Showman et al. 2009, 2015). Moreover, the jet is broader with a longer rotation period as explained by the equatorial Rossby deformation length LD, a measure of the typical jet width given by
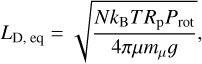 (3)
(3)
with N the Brunt-Väisälä frequency, kB Boltzmann’s constant, T the temperature, µ the mean molecular weight, mµ the atomic mass, and g the surface gravity (Showman & Guillot 2002). Consequently, the redistribution of heat becomes far more efficient with a longer rotation period. When decreasing the rotation period, the opposite occurs. The substellar point rapidly moves west at all times, even during the periastron passage, so the irradiation is spread thin and the resulting weak temperature gradient fails to pump sufficient angular momentum to the equator.
Figure 6 demonstrates the importance of the planetary rotation period to the ringing phenomenon, as the case with a longer rotation period displays only one strong peak for two reasons. Firstly, heat is distributed more effectively by the circulation, which reduces the temperature contrast between the flash-heated and unheated hemispheres and hence the ringing amplitude. Secondly, as the rotation period is longer, it takes longer for the heated side to come into view, allowing it more time to cool and for the heat to be distributed. For the opposite reasons, the case with a short rotation period shows ten local maxima, the first of which are taller than in the pseudo-synchronously rotating case. Interestingly, the rapidly rotating case still shows small peaks over 8 d after the periastron passage, whereas the pseudo-synchronous case’s last local maximum occurs about 6 d after the periastron passage, demonstrating that the lowered efficiency of heat redistribution by circulation plays an important role.
4 Discussion
4.1 Timing of the ringing peaks
Due to the strong increase in heating, the emission of the planet peaks sharply around the periastron passage on highly eccentric exoplanets. The timing of this peak relative to the periastron passage is affected by a number of parameters, including the planet’s rotation period, thereby offering a rare opportunity for an observational constraint on planetary rotation, a route taken by de Wit et al. (2016) and Lewis et al. (2017). Consider as an example the emission of HAT-P-2 b, where about half of the dayside is in the viewing disk of an observer on Earth, as visualised in Fig. 1. In that case, one might expect the dayside to come entirely into view after 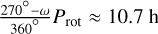 . However, our synthetic light curve shown in Fig. 4 predicts that the maximum in observed emission would occur 4.7 h after the periastron passage. Here we ought to include the effect of the super-rotating equatorial jet, which pushes the gas heated during the heating flash eastwards, hence bringing it into view earlier. We can roughly estimate the jet-enhanced timing of the periastron peak to be
. However, our synthetic light curve shown in Fig. 4 predicts that the maximum in observed emission would occur 4.7 h after the periastron passage. Here we ought to include the effect of the super-rotating equatorial jet, which pushes the gas heated during the heating flash eastwards, hence bringing it into view earlier. We can roughly estimate the jet-enhanced timing of the periastron peak to be
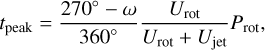 (4)
(4)
where 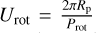 is the eastward speed at the equator due to rotation and Ujet the jet speed after periastron. For HAT-P-2 b, we estimate Ujet = 4400 m s−1 from Fig. 2 and Urot = 2500 m s−1, resulting in tpeak = 4.0 h. This matches the predicted peak timing of 4.7 h given the temporal resolution of about 2 h.
is the eastward speed at the equator due to rotation and Ujet the jet speed after periastron. For HAT-P-2 b, we estimate Ujet = 4400 m s−1 from Fig. 2 and Urot = 2500 m s−1, resulting in tpeak = 4.0 h. This matches the predicted peak timing of 4.7 h given the temporal resolution of about 2 h.
The maximum in emission is also expedited by the cooling of the gas after the periastron passage as cooling leads to a decrease in emission over time. This is especially important shortly after the periastron passage, when the planet is still hot and the emission decreases more rapidly, as demonstrated by the ∝ T−3 dependence of the radiative cooling timescale τth given by
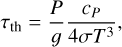 (5)
(5)
with cP the heat capacity at constant pressure and σ the Stefan-Boltzmann constant (Showman & Guillot 2002). On TOI-4127 b for instance, we estimate the maximum to occur 21 h after the periastron passage using Eq. (4), while the synthetic light curve predicts 13 h after the periastron passage. As such, the cooling after periastron passage and the degeneracy between rotation and the super-rotating jet seriously complicate the extraction of the rotation period from the periastron peak, leading to large uncertainties in studies such as de Wit et al. (2016).
Under the right circumstances, ringing can isolate the rotation period from the timing of the ringing peaks. In the HD 80606 b simulation, the spacings between the peaks are 1.52 d, 1.46 d, 1.67 d, and 1.72 d with a resolution of about 0.05 d, and the rotation period is 1.73 d. The spacing between the periastron peak and first and second ringing peaks is shorter than the rotation period. To account for the super-rotating jet, we used
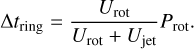 (6)
(6)
Using Urot = 3000 m s−1 and Ujet = 1400 m s−1 for HD 80606 b, we estimate ∆tring = 1.18 d. This underestimates the modelled peak spacings in part because of the thinness of the jet due to HD 80606 b’s short rotation period and low temperature reducing the equatorial Rossby deformation radius (see Eq. (3)). Figure 7 shows the temperature evolution on HD 80606 b after periastron passage at 1 bar as seen by an observer on Earth. Initially, the flash heated gas is concentrated in one hemisphere. As the thin equatorial jet drags the hot gas at the equator eastwards, the spacing between ringing peaks is smaller than the rotation period. However, as the jet is quite thin, some flash-heated gas remains to the north-east and south-east of the substellar point at the periastron, indicated by the green dot. After an advection timescale given by
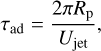 (7)
(7)
the temperature on the equator is mostly homogenised by the jet. On HD 80606 b we estimate τad = 3.0 d, matching the fourth panel of Fig. 7. Yet the parcels of flash-heated gas outside the jet still maintain their higher temperature. As that gas continues to rotate in and out of view the last two ringing peaks follow with a spacing consistent with the rotation period. Consequently, the degeneracy between the rotation period and wind speed is broken, so the rotation period can be directly measured from the spacing between the last peaks.
 |
Fig. 3 Equilibrium temperature assuming zero albedo over the orbit of the five exoplanets in our sample. A red star symbol indicates the position of the parent star. A solid black line shows the scale of the orbit. The effective temperature averaged over an orbital period is reported for each planet. |
 |
Fig. 4 Synthetic light curves of all five planets relative to the brightness of the parent star in different wavelength ranges. We show the eight days after the periastron passage, except for HAT-P-2 b because of its short orbital period. A vertical grey line in the top right indicates the typical MIRI LRS precision when using the full 5–12 µm range for a star of that visual magnitude. Ringing is seen as the local maxima in the light curves of HD 80606 b and TOI-4127 b, which is especially pronounced at longer wavelengths. HD 17156 b also displays a local maximum after the periastron peak in the long wavelength regimes. |
 |
Fig. 5 Speed of the equatorial jet on HD 80606 b with different rotation periods, computed using the method described in Fig. 2. Each panel shares the same horizontal axis but has a unique vertical axis. The speed increases as the rotation period increases, although the jet is still only driven around periastron. When halving the rotation period, a consistent jet fails to form around the whole equator, so the zonally averaged zonal wind speed is decreased. |
 |
Fig. 6 Synthetic light curves of HD 80606 b relative to the brightness of the home star for different rotation periods. The halved rotation period leads to more and stronger peaks forming, while the doubled period results in only one notable peak. |
4.2 Detecting ringing on these five exoplanets
Figure 4 predicts that HD 80606 b and TOI-4127 b show some ringing in the MIRI LRS wavelength regime, while HD 17156 b would have some small local maxima at long wavelengths. For a solar-like star with an apparent magnitude of 9 such as HD 80606, MIRI is expected to reach a precision of approximately 25 ppm (Greene et al. 2016; Batalha et al. 2019). As such, we might expect at the four ringing peaks on HD 80606 b to be detectable. The first local maximum on TOI-4127 b may seem detectable as well, although its second, smaller bump would not be. However, considering its V-band magnitude is 11.44, the precision lies around 75 ppm instead, which the first ringing peak does not attain. Finally, the small local maximum at long wavelengths for HD 17156 b would not be detected, especially as one would have to limit oneself to the longer wavelengths of the instrument. As such, of the five exoplanets examined in this study, only HD 80606 b would exhibit any detectable ringing.
Lewis et al. (2017) demonstrate that clouds may seriously diminish ringing on HD 80606 b. Since our model does not include the effects of clouds, we likely overestimate the amplitude of the ringing peaks. Similarly, Tsai et al. (2023b) show that including photo-chemistry in the post-processing of their HD 80606 b models slightly reduces the emission magnitude after the periastron passage. However, unlike clouds this is unlikely to qualitatively alter the light curve as the composition at photospheric altitudes returns close to pre-periastron levels by the time the first ringing peak occurs. On top of the lack of clouds, our model also assumes an obliquity of 0°. HD 80606 b, TOI-4127 b, and HD 17156 b have an orbital period greater than the 20 d limit beyond which one cannot safely assume tides to have aligned the rotational and orbital axes (Rauscher et al. 2023). Using a simple 2D shallow-water model, Ohno & Zhang (2019a,b) show how the obliquity and corresponding viewing geometry can strongly affect the light curve, which is confirmed by Rauscher et al. (2023). If, for instance, one of the poles receives most of the flash-heating at the periastron, that heat would not be brought in and out of view by rotation, and hence no ringing. This too points towards our synthetic light curves overestimating the amplitude of the ringing. If little or no ringing is detected on HD 80606 b, this could be explained by a rotation period longer than pseudo-synchronous, clouds or obliquity. If clouds were responsible, one might expect to detect them using transit spectroscopy. If the non-detection of ringing were due to a long rotation period or an oblique orbit, the planet would prove itself useful to the research of tidal evolution and possibly to the detection of obliquity using secondary eclipse mapping (Rauscher 2017; Rauscher et al. 2023).
In our synthetic light curve of HD 80606 b, the final ringing peak takes place 6.5 d after the periastron passage. To include the decline after that local maximum, one would need a baseline stretching until approximately 7 d after the periastron passage. As the global maximum occurs shortly before the periastron passage, the baseline should be approximately 8 d long to cover all peaks. This baseline is considerably longer than those of currently accepted proposals for JWST observations of HD 80606 b, which were allotted a prime time of approximately one day3. As the amplitude of the ringing in our synthetic light curves is likely overestimated, it is uncertain whether the fourth ringing peak is indeed detectable. Therefore, it may be reasonable to shorten the baseline to omit the fourth ringing peak, in which case the baseline would stretch until approximately 5 d after the periastron passage. Alternatively, a weaker constraint can be placed on the rotation period through a comparison of observations to GCMs with different rotation periods as in Fig. 6. To clearly distinguish the Prot = Pps case from the Prot = 2Pps case of HD 80606 b, a run ought to last for about 3 d after the periastron when the observed emission on the Prot = Pps case increases while the Prot = 2Pps emission continues to decrease.
 |
Fig. 7 Horizontal slices of the temperature at 1 bar on HD 80606 b at different times after the periastron passage. The right panels correspond to observed emission maxima, and the left panels correspond to minima. Each panel is centred on the point below an observer on Earth, and grey triangles enclose the hemisphere in view, pointing towards the sub-observer point. Black arrows show the horizontal wind velocity. A cyan cross indicates the current substellar point and a green dot the substellar point at the periastron passage. |
4.3 Why only HD 80606 b displays ringing
In our sample of five highly eccentric exoplanets, no planet displays any detectable ringing peaks except HD 80606 b, which has four. This remarkable difference in the level of ringing may be explained by a number of factors. Firstly, the extremely eccentric orbit of HD 80606 b results in a great difference in irradiation at the periastron compared to throughout most of the orbit, resulting in a large temperature contrast. As ringing is the consequence of a difference in emission between two hemispheres, a high eccentricity increases the amplitude of ringing peaks. Furthermore, under the assumption that the planet rotates pseudo-synchronously, a high eccentricity leads to a short rotation period, meaning little of the heat is distributed by circulation or irradiated away between rotations. Indeed, HD 80606 b has the second shortest pseudo-synchronous rotation period in our sample (see Table 1). However, Kataria et al. (2013) find an increase in the speed of the equatorial jet with eccentricity, which can raise the effectiveness of the circulation. Nevertheless, their work still suggests that a high eccentricity is beneficial for ringing, as they found no ringing on a hypothetical planet with e = 0.5 and strong ringing on a similar case with e = 0.75.
Secondly, ringing in our sample is anti-correlated with the mean equilibrium temperature shown in Fig. 3. HD 80606 b has the lowest mean equilibrium temperature, while the two most irradiated cases, HAT-P-2 b and TOI-3362 b do not display any ringing. This is in part due to the long radiative cooling timescale of cool gas, which helps maintain the temperature contrast between the two hemispheres. Furthermore, weaker irradiation is known to lead to a slower equatorial jet and hence less efficient heat redistribution (Kataria et al. 2013; Showman et al. 2015). However, Kataria et al. (2013) note that a shorter orbital period and hence a greater equilibrium temperature leads to more and higher ringing peaks in their model with e = 0.75. They indicate that the strengthened ringing is aided by the shortened pseudo-synchronous rotation period. As such, the net effect of the orbital period and mean equilibrium temperature is still unclear.
Thirdly, HD 80606 b has the largest ratio of planetary radius to stellar radius of our five cases. This large ratio increases the planet’s contribution to the total brightness of the system, hence increasing the ringing signal. Moreover, a large radius also means that circulation needs to travel longer to distribute heat across the entire planet, as demonstrated by the advection timescale in Eq. (7). Finally, the fairly low apparent visual magnitude of HD 80606 b means MIRI can achieve a high precision, making ringing easier to detect.
 |
Fig. 8 Orbital period and eccentricity of each confirmed Jupiter-like planet in the Encyclopaedia of Exoplanetary Systems (Schneider et al. 2011) as of 23 November 2023. Only planets with a mass of at least 0.1 MJ and a radius of at least 0.4 RJ are included. The black squares indicate the planets modelled in this work, and the purple stars mark three other potential candidates for the observation of ringing. |
4.4 More potential ringing targets
We conducted a search through the Encyclopaedia of Exoplanetary Systems4 (Schneider et al. 2011) for more ringing candidates with a high eccentricity, short pseudo-synchronous rotation period, large planet-to-star radius fraction and low visual magnitude. Figure 8 shows the observed eccentricity and orbital period of each confirmed exoplanet in the encyclopaedia with an entry for these two quantities. Some exoplanets are not included in the graph because their eccentricity or orbital period is not given in the catalogue, even if they are available elsewhere in the literature as is the case for TOI-4127 b for example. In order to prioritise planets with well-constrained observed parameters, we limited ourselves to transiting systems.
Some planets worth considering in future theoretical or observational studies of ringing are Kepler-1656 b (Brady et al. 2018), TOI-4562 b (Heitzmann et al. 2023), and Kepler-419 b (Dawson et al. 2012), highlighted by the purple stars in Fig. 8.
Unfortunately, none of these planets seem as promising a target as HD 80606 b. Kepler-1656 b has a small radius of 0.45 Rj and long pseudo-synchronous period while Kepler-419 b and TOI-4562 b orbit quite large and hot stars. Moreover, all three systems are rather dim with visual magnitudes of 11.67 for Kepler-1656 (Høg et al. 2000), 12.09 for TOI-4562 (Zacharias et al. 2013), and 13.04 for Kepler-419 (Zacharias et al. 2013). Therefore, we recommend prioritising searches for ringing on HD 80606 b.
5 Conclusions
We examined which eccentric transiting exoplanets are likely to display detectable ringing, which is a series of detectable local maxima in the light curves due to the side of the planet that received the heating flash at periastron rotating into and out of view. To do so, we used the 3D GCM with full radiative transfer coupling expeRT/MITgcm and adapted it to include non-synchronous rotation and eccentric orbits. We simulated five highly eccentric transiting exoplanets, namely HAT-P-2 b, HD 80606 b, TOI-3362 b, TOI-4127 b, and HD 17156 b, using the pseudo-synchronous rotation period from Hut (1981). From these atmospheric models, we generated synthetic light curves in the wavelength range of the LRS mode of the MIRI aboard JWST.
All five planets in our sample feature an equatorial jet throughout their entire orbit, showing that this dynamical regime is quite robust to changing irradiation due to eccentricity. However, the jets of HD 80606 b and TOI-4127 b, the planets with the longest orbital period in our sample, are only driven during the periastron passage and continue under their inertia while slowly decelerating. The planetary rotation period plays a critical role in the dynamical regime, which is exemplified well by the lack of a consistent equatorial jet when HD 80606 b’s rotation period is decreased to half pseudo-synchronous. The rotation period is also crucial to the ringing phenomenon, as it strongly affects both the amplitude and, especially, the number of ringing peaks. As a result, an observation of ringing or a lack thereof can provide a strong constraint on the rotation period, which is otherwise difficult to get. This would allow one to test the assumption of pseudo-synchronous rotation on highly eccentric planets.
Our synthetic light curves predict local maxima on HD 80606 b and TOI-4127 b, while the other three planets only show some small humps in the 5–12 µm wavelength range. TOI-4127 b’s one ringing maximum is not detectable because of its rather dim parent star. For a 9 mag star such as HD 80606, JWST’s detection threshold is roughly 25 ppm; this is attained by four ringing peaks on HD 80606 b, making it a promising observation target. However, our models neglect the effects of clouds and obliquity, both of which can obstruct ringing. Therefore, our synthetic light curves likely overestimate the amplitude of the ringing peaks. As a result, it is uncertain how many of the four predicted peaks on HD 80606 b are truly detectable. The timing of these peaks is affected by a complicated interplay between the planetary rotation period, equatorial jet speed, viewing geometry, and cooling after the periastron passage. If the ringing lasts longer than an advection timescale, however, the spacing between peaks approaches the rotation period, allowing one to extract the rotation period more reliably. An observation run with a baseline stretching seven days after the periastron passage would include all predicted peaks. A five-day-long observation would still cover three likely detectable peaks, enough to get the spacing between peaks after an advection timescale.
From the study of these five exoplanets, we have tentatively deduced what factors facilitate observational ringing. They are a high eccentricity, a low apparent magnitude of the home star, a large planet-to-star radius ratio, and a short pseudo-synchronous rotation period. In our sample of five exoplanets, the ringing is more prominent on planets with a lower equilibrium temperature and a long orbital period; this contradicts the results of previous works, so the role of the orbital period is still unclear. Based on these conditions, we searched for other transiting exoplanets in the Encyclopaedia of Exoplanetary Systems that may display observable ringing but did not find a candidate as promising as HD 80606 b. Therefore, we conclude that HD 80606 b is currently the best known transiting exoplanet candidate for ringing.
Acknowledgements
The research presented in this paper was part of MV’s master thesis, supervised by LD and co-supervised by RB, ADS and LC. A.D.S., L.D. and L.C .acknowledge funding from the European Union H2020-MSCA-ITN-2019 under Grant no. 860470 (CHAMELEON). L.D. further acknowledges support from the KU Leuven IDN/19/028 grant ESCHER. R.B. acknowledges support from the ‘Origins’ investment incentive. The authors would like to thank the unknown referee for their helpful comments. The data presented in this work were collected using the ‘pleiads’ computer cluster of the Institute of Astronomy, KU Leuven, maintained by Maarten Dirickx. In this work, we have made use of the GCM post-processing library gcm_toolkit Schneider et al. (2022b).
References
- Adams, A. D., Millholland, S., & Laughlin, G. P. 2019, AJ, 158, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Adcroft, A., Campin, J.-M., Hill, C., & Marshall, J. 2004, Monthly Weather Rev., 132, 2845 [NASA ADS] [CrossRef] [Google Scholar]
- Amundsen, D. S., Mayne, N. J., Baraffe, I., et al. 2016, A&A, 595, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcangeli, J., Désert, J.-M., Line, M. R., et al. 2018, ApJ, 855, L30 [Google Scholar]
- Baeyens, R., Decin, L., Carone, L., et al. 2021, MNRAS, 505, 5603 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Kovács, G., Torres, G., et al. 2007, ApJ, 670, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. E., Lewis, T., Fortney, J. J., et al. 2019, ApJ, 885, L25 [Google Scholar]
- Bitsch, B., Trifonov, T., & Izidoro, A. 2020, A&A, 643, A66 [EDP Sciences] [Google Scholar]
- Brady, M. T., Petigura, E. A., Knutson, H. A., et al. 2018, AJ, 156, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, M. L., Chiang, E., Bowler, B. P., et al. 2020, AJ, 159, 181 [Google Scholar]
- Bryan, M. L., Chiang, E., Morley, C. V., Mace, G. N., & Bowler, B. P. 2021, AJ, 162, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Carone, L., Baeyens, R., Mollière, P., et al. 2020, MNRAS, 496, 3582 [NASA ADS] [CrossRef] [Google Scholar]
- Courant, R., Friedrichs, K., & Lewy, H. 1928, Mathematische Annalen, 100, 32 [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 726, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., Johnson, J. A., Morton, T. D., et al. 2012, ApJ, 761, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [Google Scholar]
- de Wit, J., Lewis, N. K., Langton, J., et al. 2016, ApJ, 820, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, J., Huang, C. X., Zhou, G., et al. 2021, ApJ, 920, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Dyrek, A., Min, M., Decin, L., et al. 2024, Nature, 625, 51 [Google Scholar]
- Feinstein, A. D., Radica, M., Welbanks, L., et al. 2023, Nature, 614, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., Vogt, S. S., Marcy, G. W., et al. 2007, ApJ, 669, 1336 [NASA ADS] [CrossRef] [Google Scholar]
- Goody, R., West, R., Chen, L., & Crisp, D. 1989, J. Quant. Spec. Radiat. Transf., 42, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, T. P., Line, M. R., Montero, C., et al. 2016, ApJ, 817, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, R. D. 2006, Classical Mechanics (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Gupta, A. F., Jackson, J. M., Hebrard, G., et al. 2023, AJ, 165, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Heitzmann, A., Zhou, G., Quinn, S. N., et al. 2023, AJ, 165, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., & Marley, M. S. 2018, in Handbook of Exoplanets, eds. H. J. Deeg & J. A. Belmonte (Berlin: Springer), 102 [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Iro, N., & Deming, L. D. 2010, ApJ, 712, 218 [NASA ADS] [CrossRef] [Google Scholar]
- JWST Transiting Exoplanet Community Early Release Science Team (Ahrer, E.-M., et al.) 2023, Nature, 614, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Kataria, T., Showman, A. P., Lewis, N. K., et al. 2013, ApJ, 767, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Kataria, T., Showman, A. P., Fortney, J. J., et al. 2015, ApJ, 801, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kendrew, S., Scheithauer, S., Bouchet, P., et al. 2015, PASP, 127, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, N. K., Parmentier, V., Kataria, T., et al. 2017, arXiv e-prints [arXiv:1706.00466] [Google Scholar]
- Lewis, N. K., Showman, A. P., Fortney, J. J., Knutson, H. A., & Marley, M. S. 2014, ApJ, 795, 150 [Google Scholar]
- Lothringer, J. D., Barman, T., & Koskinen, T. 2018, ApJ, 866, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Louden, T., & Wheatley, P. J. 2015, ApJ, 814, L24 [CrossRef] [Google Scholar]
- Malmberg, D., & Davies, M. B. 2009, MNRAS, 394, L26 [NASA ADS] [CrossRef] [Google Scholar]
- May, E. M., Stevenson, K. B., Bean, J. L., et al. 2022, AJ, 163, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., Debras, F., Baraffe, I., et al. 2017, A&A, 604, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A&A, 627, A67 [Google Scholar]
- Mollière, P., Stolker, T., Lacour, S., et al. 2020, A&A, 640, A131 [Google Scholar]
- Moutou, C., Hébrard, G., Bouchy, F., et al. 2009, A&A, 498, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Latham, D. W., Mayor, M., et al. 2001, A&A, 375, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nutzman, P., Gilliland, R. L., McCullough, P. R., et al. 2011, ApJ, 726, 3 [CrossRef] [Google Scholar]
- Ohno, K., & Zhang, X. 2019a, ApJ, 874, 1 [CrossRef] [Google Scholar]
- Ohno, K., & Zhang, X. 2019b, ApJ, 874, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Bakos, G. Á., Torres, G., et al. 2010, MNRAS, 401, 2665 [CrossRef] [Google Scholar]
- Parmentier, V., Guillot, T., Fortney, J. J., & Marley, M. S. 2015, A&A, 574, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, K. A., Beichman, C., Fulton, B. J., et al. 2022, AJ, 164, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E. 2017, ApJ, 846, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., & Kempton, E. M. R. 2014, ApJ, 790, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., Cowan, N. B., & Luger, R. 2023, AJ, 165, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Wright, G. S., Böker, T., et al. 2015, PASP, 127, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Sainsbury-Martinez, F., Wang, P., Fromang, S., et al. 2019, A&A, 632, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, A. D., Carone, L., Decin, L., Jørgensen, U. G., & Helling, C. 2022a, A&A, 666, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, A. D., Carone, L., Decin, L., et al. 2022b, A&A, 664, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, R. 1971, J. Atmos. Sci., 28, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., & Polvani, L. M. 2010, Geophys. Res. Lett., 37, L18811 [Google Scholar]
- Showman, A. P., & Polvani, L. M. 2011, ApJ, 738, 71 [Google Scholar]
- Showman, A. P., Fortney, J. J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Lewis, N. K., & Fortney, J. J. 2015, ApJ, 801, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Tan, X., & Parmentier, V. 2020, Space Sci. Rev., 216, 139 [Google Scholar]
- Sing, D. K. 2018, arXiv e-prints [arXiv:1804.07357] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [Google Scholar]
- Socrates, A., Katz, B., & Dong, S. 2012, ArXiv e-prints [arXiv:1209.5724] [Google Scholar]
- Southworth, J. 2010, MNRAS, 408, 1689 [Google Scholar]
- Thorngren, D., Gao, P., & Fortney, J. J. 2019, ApJ, 884, L6 [Google Scholar]
- Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsai, S.-M., Dobbs-Dixon, I., & Gu, P.-G. 2014, ApJ, 793, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, S.-M., Lee, E. K. H., Powell, D., et al. 2023a, Nature, 617, 483 [CrossRef] [Google Scholar]
- Tsai, S.-M., Steinrueck, M., Parmentier, V., Lewis, N., & Pierrehumbert, R. 2023b, MNRAS, 520, 3867 [NASA ADS] [CrossRef] [Google Scholar]
- Tsantaki, M., Sousa, S. G., Santos, N. C., et al. 2014, A&A, 570, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2009, ApJ, 693, 794 [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [Google Scholar]
- Zellem, R. T., Lewis, N. K., Knutson, H. A., et al. 2014, ApJ, 790, 53 [Google Scholar]
Approved cycle 1 programme #2008 A Blast From the Past: A Spectroscopic look at the Flash Heating of HD 80606b. https://www.stsci.edu/jwst/science-execution/program-information?id=2008
Approved cycle 1 programme #2008, A Blast From the Past: A Spectroscopic look at the Flash Heating of HD 80606b. https://www.stsci.edu/jwst/science-execution/program-information?id=2008 and Approved cycle 1 program #2488, Real Time Exoplanet Meteorology: Direct Measurement of Cloud Dynamics on the High-Eccentricity Hot Jupiter HD 80606 b. https://www.stsci.edu/jwst/science-execution/program-information?id=2488
All Tables
Relevant orbital, planetary, and stellar parameters of the five planetary systems in our sample.
All Figures
 |
Fig. 1 Drawings showing the orientation of the observer relative to the planet at its periastron passage for each of the five exoplanets (not to scale). The parent star is represented by a red star symbol and the planet by a disk, with the dayside coloured yellow and the nightside black. The blue arrow indicates the direction towards Earth. A solid black line shows the scale of the orbit. The orbital trajectory along which the planet moves in an anticlockwise direction is shown as a dashed grey line. The planet rotates anticlockwise as well. |
| In the text | |
 |
Fig. 2 Speed of the equatorial jet throughout an orbit for each planet. The speed is computed as the maximum of the zonal wind speed between 100 and 0.01 bar after averaging over 1/50th of the orbital period, taking the zonal mean across the whole planet and the meridional mean between ±20°. We calculated the equatorial jet speed at 50 times and used cubic interpolation between these 50 times. Note that each panel has a different scaling on the two axes. The equatorial jet speed is quite consistent on HAT-P-2 b, TOI-3362 b, and HD 17156 b, apart from some erratic behaviour around the periastron passage. On HD 80606 b and TOI-4127 b, however, it slows down considerably over the orbit after a period of acceleration after the periastron passage. |
| In the text | |
 |
Fig. 3 Equilibrium temperature assuming zero albedo over the orbit of the five exoplanets in our sample. A red star symbol indicates the position of the parent star. A solid black line shows the scale of the orbit. The effective temperature averaged over an orbital period is reported for each planet. |
| In the text | |
 |
Fig. 4 Synthetic light curves of all five planets relative to the brightness of the parent star in different wavelength ranges. We show the eight days after the periastron passage, except for HAT-P-2 b because of its short orbital period. A vertical grey line in the top right indicates the typical MIRI LRS precision when using the full 5–12 µm range for a star of that visual magnitude. Ringing is seen as the local maxima in the light curves of HD 80606 b and TOI-4127 b, which is especially pronounced at longer wavelengths. HD 17156 b also displays a local maximum after the periastron peak in the long wavelength regimes. |
| In the text | |
 |
Fig. 5 Speed of the equatorial jet on HD 80606 b with different rotation periods, computed using the method described in Fig. 2. Each panel shares the same horizontal axis but has a unique vertical axis. The speed increases as the rotation period increases, although the jet is still only driven around periastron. When halving the rotation period, a consistent jet fails to form around the whole equator, so the zonally averaged zonal wind speed is decreased. |
| In the text | |
 |
Fig. 6 Synthetic light curves of HD 80606 b relative to the brightness of the home star for different rotation periods. The halved rotation period leads to more and stronger peaks forming, while the doubled period results in only one notable peak. |
| In the text | |
 |
Fig. 7 Horizontal slices of the temperature at 1 bar on HD 80606 b at different times after the periastron passage. The right panels correspond to observed emission maxima, and the left panels correspond to minima. Each panel is centred on the point below an observer on Earth, and grey triangles enclose the hemisphere in view, pointing towards the sub-observer point. Black arrows show the horizontal wind velocity. A cyan cross indicates the current substellar point and a green dot the substellar point at the periastron passage. |
| In the text | |
 |
Fig. 8 Orbital period and eccentricity of each confirmed Jupiter-like planet in the Encyclopaedia of Exoplanetary Systems (Schneider et al. 2011) as of 23 November 2023. Only planets with a mass of at least 0.1 MJ and a radius of at least 0.4 RJ are included. The black squares indicate the planets modelled in this work, and the purple stars mark three other potential candidates for the observation of ringing. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


