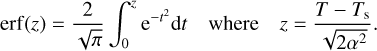| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202348154 | |
| Published online | 28 May 2024 | |
Laboratory simulations of ice growth in space: An expected nonuniform ice mantle composition
1
INAF – Osservatorio Astronomico di Palermo,
P.za Parlamento 1,
90134
Palermo, Italy
e-mail: antonio.jimenez@inaf.it
2
Department of Physics, National Central University,
Zhongli Dist.,
Taoyuan City
320317, Taiwan
e-mail: asperchen@phy.ncu.edu.tw
3
Institute of Low Temperature Science, Hokkaido University,
Sapporo,
Hokkaido
060-0819, Japan
4
Centro de Astrobiología (INTA-CSIC),
Ctra. de Ajalvir, km 4,
28850
Torrejón de Ardoz, Madrid, Spain
Received:
4
October
2023
Accepted:
6
March
2024
Context. In dense, cold molecular regions, gas-phase chemical species freeze out onto grain surfaces. These icy condensates become an important reservoir of volatile elements and feedstock for molecular diversity.
Aims. While there is a fairly general agreement on the chemical composition of icy mantles, there are differences in how the various molecular components are perceived to be present. Should the materials composing the ice be mixed or are they segregated into distinct chemical zones?
Methods. To answer such a question, we performed a few exploratory experiments that allowed the adsorbing surface (mimic dust grains) to slowly relax to very low temperatures while gas-phase mixtures of H2O, NH3, and CO embed onto it.
Results. We find that mantles are far from being uniform, and they could evolve into completely mixed ices only if the ambient temperature undergoes a catastrophic collapse.
Conclusions. Under the typical conditions of an interstellar dense cloud, ices present a high degree of molecular segregation, with possible consequences on the ice chemistry and the desorption mechanisms.
Key words: astrochemistry / methods: laboratory: solid state / protoplanetary disks
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Icy grain mantles are thought to form by accretion and reaction of gas-phase species onto grain surfaces. Hydrogenation of O, C, and N atoms on such surfaces produces a mixture of water, H2O, methane, CH4, ammonia, NH3, and other reduced species. On top of this coating, molecular species that are synthesized in the gas phase and require lower temperatures to stick onto the dust (e.g., carbon monoxide) form an additional layer. This more realistic description of ices covering dust grains (e.g., Tielens et al. 1991; Pontoppidan et al. 2008) has been constrained by comparing ice inventories toward different types of protostars and background stars (Öberg et al. 2011) following the evolution of ices during the star formation process.
In the past years, experiments on layered ice analogs have focused on a number of components that are present in interstellar ices (Fraser et al. 2004; Collings et al. 2014; Dawes et al. 2016), although more than two components have never been analyzed in a layered distribution. These experiments were performed within temperature ranges that are too high for comparison with, for example, dense molecular clouds. Only recently, more comprehensive laboratory simulations have been carried out (Ciaravella et al. 2020; Jiménez-Escobar et al. 2022; Müller et al. 2021) in an attempt to discriminate between mixed and layered ices and constrain their basic composition while providing evidence of variations in both composition and structure with environment.
It has been well known for many years that in cold, low excitation regions, ice is dominated by H2O, CO, and CO2, with water typically being the most abundant (~60–70%). Water molecules formed by gas-phase reactions are not abundant enough to account for the ice mantles by adsorption onto grains, so they must form directly in a solid phase (through hydrogenation of O and OH). The condensable species CO is sufficiently abundant to contribute significantly to the ices by adsorption. Once stuck to a grain, CO may be efficiently oxidized to CO2 or hydrogenated first to HCO and subsequently to formaldehyde and methanol (Watanabe & Kouchi 2002; Chuang et al. 2016). In high-density regions of molecular clouds, most of the oxygen is locked in CO and, virtually all the available hydrogen is converted efficiently to H2, which is relatively unreactive and remains in the gas at interstellar temperatures. Thus, hydrogenation reactions are restrained, and ice mantle growth is dominated by direct freeze-out of gas-phase CO molecules, giving rise to a stratified molecular composition.
A detailed spectroscopic characterization of the features of the main ice components embedded in different mixtures may potentially identify the ice’s composition, structure, and evolutionary history and thus put tight constraints on current theories of solid-phase chemistry (e.g., Müller et al. 2021).
While the multilayered nature of dust is consistent with our current picture of molecular clouds, there is less of a consensus on the presence of stratified ices in protoplanetary disks.
Cometary ices resemble the composition of interstellar ice mantles, suggesting that such ice mantles could be preserved in some regions of disks (e.g., Bergner & Ciesla 2021). Conversely, if ices are formed from scratch on top of bare grains, the condensation would occur while dust particles experience temperature gradients during their motion within the disk. It is therefore of interest to perform laboratory simulations of the ice-growth formation reflecting “realistic” environmental conditions. Such an investigation is all the more timely in light of the wealth of data expected by the advent of the James Webb Space Telescope, whose instruments (e.g., NIRSpec) are able to observe the spectral changes in position and shape for the bands of interest.
In the present exploratory work, we focus on molecular cloud interiors in regions dense enough to provide shielding of harmful (for molecules) radiation. We study the structure of an ice obtained by condensation of a ternary gas mixture of H2O:NH3:CO onto a surface as it slowly cools from 200 K down to 10 K. We describe the experiments and the results in Sects. 2 and 3, respectively. Discussion of the results is presented in Sect. 4 and the extrapolation to astrophysical environments in Sect. 5. The last section contains our conclusions.
2 Experiments
The ice experiments described in this paper were performed with the Interstellar Energetic-Process System (IEPS) facility, an ultrahigh vacuum chamber of base pressure 5 × 10−10 Torr equipped with a closed-cycle helium cryostat (CTI M350) mounted on a rotating platform. An infrared transparent window was mounted on the sample holder of the cryostat, whose temperature ranges from 11 to 340 K. Infrared diagnostics were performed with a mid-infrared spectrometer (Bruker VERTEX 70) operating between 900 and 4000 cm−1 that was equipped with an MCT detector kept in vacuum. Gas-phase diagnostics were carried out with a quadrupole mass spectrometer (QMS; Hiden analysis/3F RC PIC) monitoring masses in the 1–200 amu range. We refer to Huang et al. (2020) for details.
After cooling the cryostat to 200 K, we waited about 30 min for the thermalization of the CaF2 window. Subsequently, we began to introduce a gas mixture of H2O:NH3:CO (2:1:6) prepared in a premixing chamber until we reached a specific initial deposition pressure Pd (at 200 K). Then, while maintaining the injection of gas into the chamber, we cooled the substrate down to 11 K at a rate of 2 K min−1. We used H2O from Merck, GC-mass grade, freeze-pump-thaw degassing more than three times and CO and NH3 from Matheson (99.99% purity). We performed three experiments using three constant values of the inlet flux corresponding to the initial deposition pressures (at 200 K) Pd = 6 × 10−7, 1 × 10−7 and 1 × 10−8 Torr in order to assess a possible dependence of the results on the deposition pressure. With this procedure, we expected the formation of layered ices as different gases freeze out at different temperatures (and then times). Such an approach is closer to what is occurring in space, as compared to building ices by directly depositing layers of different composition at 10 K.
We note that the abundance ratios in the gas mixture were not representative of those in the final ices. We tuned our initial choice to mimic the actual ice concentration at very low temperatures. The initial greater amount of CO with respect to water did not affect the construction of the ice, as CO molecules did not deposit until the temperature was well below 40 K. We discuss this point further later in the paper.
We adopted the band strengths ACO = 1.1 × 10−17 cm molecule−1 at 2136 cm−1 (Jiang et al. 1975); 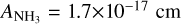 molecule−1 at 1070 cm−2 (D’Hendecourt et al. 1986); and
molecule−1 at 1070 cm−2 (D’Hendecourt et al. 1986); and 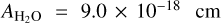 molecule−1 at 1659 cm−1 (Bouilloud et al. 2015). Since the H2O band at ~1660 cm−1 is blended with the NH3 band at ~1625 cm−1 (A = 9 × 10−18 cm molecule−1, Bouilloud et al. 2015), we obtained the integrated absorbance by subtracting the NH3 contribution. This was done by scaling the integrated absorbance of the band at 1070 cm−1.
molecule−1 at 1659 cm−1 (Bouilloud et al. 2015). Since the H2O band at ~1660 cm−1 is blended with the NH3 band at ~1625 cm−1 (A = 9 × 10−18 cm molecule−1, Bouilloud et al. 2015), we obtained the integrated absorbance by subtracting the NH3 contribution. This was done by scaling the integrated absorbance of the band at 1070 cm−1.
3 Results
The infrared spectra of the ice during the simultaneous cooling and deposition for the three experiments are shown in Fig. 1 (top panels). During the cooling, H2O was the first species to deposit onto the window. This occurred around 140 K. The second species was NH3, whose deposition started around 110 K, and CO was unambiguously detected at 30 K, although traces were seen at 40 K.
The column densities of the three species as functions of temperature are plotted in the middle panels of Fig. 1. Between 140 and 110 K, a pure H2O ice layer formed whose thickness increased with the deposition pressure. A second layer composed of a mixture of H2O and NH3 appeared in the temperature range 110−40 K. Finally, a third layer with CO, the main component of the ternary ice mixture, formed below 40 K. At these temperatures, the ice composition in the newly deposited layers reflects the original gas composition in the premixing chamber. However, the column density abundance ratios in the ice approach H2O:NH3:CO ~ (2:1:1) (see middle panel of Fig. 1).
Mass spectra of the gas in the chamber during the three experiments are shown in the bottom panels of Fig. 1. Here, the m/z = 19, 15, and 29 amu represent H2O, NH3, and CO, respectively. These masses correspond to the less intense fragments DHO+, 15NH+, and 13CO+ selected to protect the mass spectrometer during the two experiments at higher deposition pressure. We observed a decrease of the mass signal at ~140, 110, and 30 K, when the three species started to deposit onto the window. These temperatures agree with those derived from the infrared spectra. The plateau in the count profiles indicates a constant deposition rate. Since m/z = 19, 15, and 29 amu are not the major components in the gas phase, their measurements are rather noisy. This is particularly true for m/z = 19, corresponding to DHO that is ~1.5 × 10−4 less abundant than H2O. Consequently, this feature shows a much less evident decrease. We note that the mass m/z = 19 is not a good tracer of water when it is not abundantly present. Consequently, when decreasing the deposition pressure, the water contribution falls rather quickly and ends up submerged within the intrinsic noise of this feature.
4 Discussion
The pressure in the chamber is linked to the fraction of molecules deposited on the sample surface. If the surface temperature is kept above the deposition temperature of a specific molecule, the pressure reaches a maximum value (i.e., the net deposition rate is zero). On the other hand, if the surface temperature is below the deposition temperature, molecules stick onto the surface, and the pressure reaches a minimum value that depends on the pressure in the chamber, the molecular beam divergence, and the pumping capacity of the sample surface.
The sticking coefficient is generally estimated using the King-Wells technique (e.g., He et al. 2016b). This requires a fixed temperature in the chamber. In our case, we continually decrease the temperature from 200 to 10 K while keeping the flow rate constant. As a consequence, rather than the standard sticking coefficient, we derive the net deposition rate, namely, the balance between deposition and desorption (see, e.g., Acharyya et al. 2007). To define Q as the normalized QMS signal, we identified the net deposition rate with D(T) = 1 – Q(T), and we represented it through the sigmoid function
![$D\left( T \right) = {1 \over 2}\left[ {1 - {\rm{erf}}\left( {{{T - {T_{\rm{s}}}} \over {\sqrt {2{\alpha ^2}} }}} \right)} \right]$](/articles/aa/full_html/2024/06/aa48154-23/aa48154-23-eq3.png) (1)
(1)
In these equations, T is the temperature and Ts and α are two fitting parameters associated with the deposition temperature (and approximately the desorption temperature) and its variance in the inherently stochastic process of the condensation of a gas onto a surface.
Figure 2 shows the normalized QMS spectra for the three components of the ice mixture for the experiment with initial pressure Pd = 6 × 10−7 Torr. The red dots are the derivative of the column density with respect to the temperature. The blue line is the QMS fitting using the relation Q = 1 – D. These plots evidence the good agreement between infrared and QMS data.
Fit results are reported in Table 1, where we also show the ratio γ between the deposition temperature Ts and the binding energy Eb. Values for this quantity have been taken from different studies. In particular, He et al. (2016a,b) derived this quantity for CO and a few other species deposited onto nonporous, amorphous water surfaces in low coverage and monolayer regimes.
The deposition temperature Ts ~ 30 K inferred in the present work for CO is significantly lower than that derived by He et al. (2016b). However, one must consider the fact that the values obtained in our experiments are not real sticking coefficients, as instead they are net deposition rates. We show our derived net deposition rates D for water, ammonia, and carbon monoxide in Fig. 3. These values are much more similar to those reported in Acharyya et al. (2007), which used a temperature programmed desorption technique for CO sticking over a CO surface. They obtained values around 0.86 and 0.9 for T = 25 and 14 K respectively, against 0.84 and ~1 obtained in our experiment.
We analytically described the evolutionary profile of the ice structure using the calculated net deposition rate D given in Eq. (1)
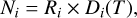 (3)
(3)
where the index i refers to a molecular component of the mixture and R, the final deposition rate (see e.g., Fig. 2), takes the values R = 7.5, 4.5, and 26.4 ML K−1 for H2O, NH3, and CO, respectively. The ice composition is shown in Fig. 4. At each temperature step Tk, we defined the total column density of the ice as
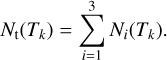 (4)
(4)
For each species, single points represent the increase in the fractional abundance (in percent) at a given temperature
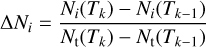 (5)
(5)
versus the total thickness of the ice reached at Tk. The representation (3) of the ice evolution matches the experimental data reasonably well considering the uncertainty in the H2O column density determination. The errors bars in Fig. 4 for CO and NH3 are 10% and mostly due to uncertainties in the band strengths. For H2O, whose band is blended with that at 1625 cm−1 of ammonia, the error is larger, namely ~20%.
 |
Fig. 1 Evolution of the ice during simultaneous cooling and deposition at three different pressures. Top panels: infrared spectra of the experiments. Middle panels: column densities of H2O, NH3, CO (in ML) as functions of the temperature. Bottom panels: mass spectra of H2O; m/z = 19, NH3; m/z = 15; and CO, m/z = 29 as functions of the temperature. The pressures reported in the panels indicate their initial values. |
 |
Fig. 2 Normalized QMS ion counts for m/z = 19 (DHO), 15 (NH), and 29 (13CO) as functions of the temperature at the deposition pressure of Pd = 6 × 10−7 Torr. The three species are representative of H2O, NH3, and CO, respectively. The blue line represents the best fit using the relation Q = 1 - D. Red dots are the derivative of the column density expressed in monolayers (right vertical axes). |
Fit parameters.
 |
Fig. 3 Net deposition rates D for H2O, NH3, and CO as functions of the temperature. |
 |
Fig. 4 Fractional ice composition AN as a function of the ice thickness (symbols). Solid lines are the simulated evolutionary profiles of the ice components following the temperature decrease. Black circles represent H2O, orange triangles indicate NH3, and blue diamonds symbolize CO. |
5 The interstellar case
Exploiting the results described above, we simulate the ice growth on dust following a molecular cloud evolving from diffuse to dense regime (~5000 to 10 K). We trace the structure and thickness of the theoretical ice during the contraction (and cooling) of the molecular cloud material. Initially, dust cores are assumed to be bare. Then, materials condense from the gas phase at a rate depending on the gas density, temperature and their net deposition rates. In this model we do not consider any energetic processing of the ice, so that we are excluding e.g., photochemistry and photodesorption.
We modeled the accretion rate following the procedure described by Cecchi-Pestellini et al. (2014), and it is summarized as follows:
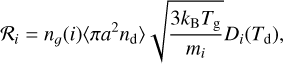 (6)
(6)
where kB is the Boltzmann constant, a and nd are the size and number density of dust grains, Td is the dust temperature, Tg is the gas temperature, and ng(i) and mi are the gas-phase number density and mass of the ith species. The average geometrical cross section of dust grains is given by Whittet (2022)
![$\left\langle {\pi {a^2}{n_{\rm{d}}}} \right\rangle \~{{{R_V}n\left( {\rm{H}} \right)} \over {5.9 \times {{10}^{21}}}}{{{\rm{c}}{{\rm{m}}^{ - 1}}} \over {\left[ {\rm{H}} \right]}},$](/articles/aa/full_html/2024/06/aa48154-23/aa48154-23-eq9.png) (7)
(7)
where RV is the ratio of the total to selective extinction and n(H) is the number density of hydrogen in all forms. Gas and dust are thermally coupled in very dense regions, n(H) > 105 cm−3 (Kruegel & Walmsley 1984). However, the gas may be warmer than dust in more diffuse environments. Thus, we also discriminated between gas and dust temperatures. In that case, we set Tg – Td = 50 K, which is a difference large enough to embed most of the thermal conditions in cold clouds.
Since in molecular clouds water and ammonia are formed on dust grains by hydrogenation, the application of the results of the present experiment in the astrophysical context implicitly assumes instantaneous hydrogenation of the precursors once they are adsorbed onto dust surfaces, with their sudden transformation into water and ammonia molecules. Such an assumption is very reasonable because it requires only the diffusion of atomic hydrogen, which is very mobile on the grain surfaces even at very low temperatures (T ~ 10 K). This process occurs with high efficiency for the formation of water, but ammonia and methane (not present in the mixture) are produced in smaller quantities because the sticking of atomic N and C is in competition with their fast reactivity in the gas phase to form CO and N2 (Daranlot et al. 2012). However, models suggest that large amounts of H2O, NH3, CH4, and CH3OH are formed on the grains before the catastrophic freeze-out of CO. Furthermore their abundances keep increasing afterward (e.g., Clément et al. 2023).
Since we were only exploring gas condensation, we considered a putative environment for which the ices along the line of sight have not been modified by energetic processes in order to predict the thickness and structure of an interstellar ice in a molecular cloud during its lifetime. Elias 16, a K1 III giant located behind the Taurus molecular cloud showing a visual extinction of 23.5 mag (Teixeira & Emerson 1999), may be considered an appropriate template. We assumed that all the components of our ternary ice mixture are initially in the gas phase and equal to the observed abundances in this region (Gibb et al. 2004). These molecules may or may not stick onto grains, depending on the ambient dust temperature (at least in the conditions of the present experiment). Since some of the CO molecules were observed to reside in the gas-phase, we needed to consider both gas and solid-state column densities when estimating the initial abundances. The abundance of carbon monoxide in the gas phase was derived from that of 18CO (Boogert et al. 2002). Finally, the column density of molecular hydrogen was 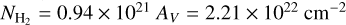 (Frerking et al. 1982). With these values of the relevant quantities, we assumed that the fractional abundances with respect to H2 of water and carbon monoxide are
(Frerking et al. 1982). With these values of the relevant quantities, we assumed that the fractional abundances with respect to H2 of water and carbon monoxide are 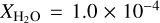 and XCO = 1.3 × 10−4, respectively. Following Gibb et al. (2004), we set the ammonia fractional abundance to 10% of H2O,
and XCO = 1.3 × 10−4, respectively. Following Gibb et al. (2004), we set the ammonia fractional abundance to 10% of H2O, 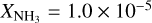 .
.
The temperature decay profile was calculated in Clark et al. (2012), which explored both rapid and slow star formation. These authors adopted initial conditions characteristic of the warm neutral medium and two different flow velocities, 13.6 and 6.8 km s−1. In the rapid case, the temperature decay time is a factor of two slower than the free fall time (~1.5 My) for a gas density n(H) = 5 × 103 cm−3, and it is the value kept by the density for most of the collapse time (Clark et al. 2012). During the collapse, we followed the growth of icy mantles through Eq. (6) for Td ≤ 200 K. Simulations are shown in Fig. 5, where we present the accretion rate for each species and the molecule fractional concentrations in the ice. The difference between dust and gas temperatures while shifting the evolutionary profiles does not produce qualitative variations.
The maximum accretion rates in the case of the fast flow velocity result are R = 6.9 × 10−14, 0.7 × 10−14, and 3.5 × 10−14 cm−3 s−1 at 1.04, 1.07, and 1.41 Myr for H2O, NH3, and CO, respectively. In the slow mode, these values are R = 6.2 × 10−14, 0.6 × 10−14, and 1.6 × 10−14 cm−3 s−1 at 2.94, 3.01, and 4.86 Myr, respectively. With this parameter set, most of the molecules are deposited on dust grains after 3 Myr since the beginning of the cloud contraction in the fast case and 8 Myr in the slow case. Looking at the ice thickness evolution as a function of the ice composition, we distinguished three different regions with two interfaces where the ice components start to merge. In the fast star formation mode, we have an inner pure H2O ice layer placed in contact with the dust surface of thickness ~3 ML; an intermediate region composed of an H2O:NH3 binary ice mixture, ~10 ML; and a very thick external layer, ~34 ML, composed of ~85% CO. The first interface from pure H2O to H2O:NH3 (0.78:0.22) has a thickness of ~4 ML. The second interface that separates the H2O:NH3 and H2O:NH3:CO layers has a thickness of ~7 ML. A faster deposition rate following the increase in the gas temperature (with respect to dust) provides a slightly thicker layer of hydrogenated species and a smaller concentration of these species in the upper CO-rich ice. The slow velocity flow case produces inner, intermediate, and top layers of ~4, 20, and 33 ML in size, respectively. The interfaces between these regions are very thin, and no significant variations arise increasing the gas temperature with respect to dust temperature. If the temperature decay timescale is very rapid, the above configuration of chemical segregation may vary significantly and can even be disrupted in the presence of very fast cooling.
6 Conclusions
In this laboratory study, we followed the formation of grain mantles with time while the adsorbing surface in our experiment slowly cooled from 200 down to 10 K. This approach enabled us to follow the chemical differentiation within the grain mantle, showing that mantles are far from having a uniform composition. Using a mixture containing water, ammonia, and carbon monoxide, we found evidence of segregation of these species when the mantle accretes, with the innermost layers being rich in H2O, the intermediate layers having an abundance of H2O and NH3, and the outermost layers being rich in CO, reflecting the different desorption temperatures of each species in the mantle.
We considered a gas-phase mixture that contains CO three times more abundant than water. This particular choice was motivated by the need to obtain a final ice composition similar to those observed in dense molecular clouds and to reproduce the conditions in very dense cores, where most of the gas-phase oxygen and carbon are locked in CO molecules. From Fig. 1, we derived a final abundance ratio H2O:NH3:CO = 2:1:1. Even if CO is too abundant with respect to water in the chamber at very early times, its presence is immaterial, as this species does not stick onto the window covered with water ice at temperatures higher than ~40 K. At that temperature in a cloud, carbon monoxide is actually the most abundant species (with the exception of molecular hydrogen), and it is removed quickly by freeze-out, at least in the densest regions of a cloud (e.g., Punanova et al. 2022). We note that residual nitrogen-bearing species such as N2H+, which are otherwise destroyed by CO molecules, can accumulate in the gas phase and trace the denser cloud regions (Lippok et al. 2013), and at very late times, they condense onto the outer CO-rich ice layer.
The most important factors shaping the evolution of the ice we studied - which to some extent are conceivable a priori - are the gas density, determined by the initial deposition pressure, and the rate of temperature decay. The extrapolation to interstellar conditions suggests that hardly realistic icy mantles can evolve to have a uniform composition throughout unless the ambient temperature undergoes a catastrophic breakdown.
It is sufficiently clear that other factors, not considered in this exploratory work, might affect the texture of the ice. When disordered or amorphous surfaces of mixed composition are concerned, which is the case for ices in the interstellar medium, we expect variations of the deposition temperature with coverage. Moreover, radiative effects such as photochemistry, photodes-orption, or the impact of ionizing energetic photons (see, e.g., Jiménez-Escobar et al. 2022 in isothermal conditions) may critically contribute to the chemical structure of the ice. Since molecular segregation gives rise to distinct chemical environments, there is a real need for accurate empirical molecular data pertaining to these processes. Based on our experimental results, it appears that the composition of the accreted ice mantles is inhomogeneous.
 |
Fig. 5 Morphological structure of an interstellar ice. Top panels: accretion rate during the molecular cloud collapse. Bottom panels: fractional ice composition AN as a function of the ice thickness (in ML). Left-hand side column: fast flow. Right-hand side column: slow flow. Black indicates H2O, orange represents NH3, and blue symbolizes CO. Red lines are for the cloud thermal profile. Dashed lines in the bottom panels represent the case in which gas and dust temperatures differ (Tg – Td = 50 K). |
Acknowledgements
We are grateful for the financial contribution from INAF Bando Astrofisica Fondamentale 2022: Laboratori Spaziali C73C22000340005, Mini-Grants C73C23000130005 and C73C23000150005. This work was also financially supported by the National Science and Technology Council, Taiwan, under grant no. NSTC 110-2628-M-008-004-MY4 (Y-JC).
References
- Acharyya, K., Fuchs, G. W., Fraser, H. J., van Dishoeck, E. F., & Linnartz, H. 2007, A&A, 466, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergner, J. B., & Ciesla, F. 2021, ApJ, 919, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Hogerheijde, M. R., Ceccarelli, C., et al. 2002, ApJ, 570, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Bouilloud, M., Fray, N., Bénilan, Y., et al. 2015, MNRAS, 451, 2145 [Google Scholar]
- Cecchi-Pestellini, C., Casu, S., Mulas, G., & Zonca, A. 2014, ApJ, 785, 41 [CrossRef] [Google Scholar]
- Chuang, K. J., Fedoseev, G., Ioppolo, S., van Dishoeck, E. F., & Linnartz, H. 2016, MNRAS, 455, 1702 [Google Scholar]
- Ciaravella, A., Muñoz Caro, G. M., Jiménez-Escobar, A., et al. 2020, PNAS, 117, 16149 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bonnell, I. A. 2012, MNRAS, 424, 2599 [CrossRef] [Google Scholar]
- Clément, A., Taillard, A., Wakelam, V., et al. 2023, A&A, 675, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collings, M. P., Dever, J. W., & McCoustra, M. R. S. 2014, Phys. Chem. Chem. Phys. (Incorp. Faraday Trans.), 16, 3479 [Google Scholar]
- Daranlot, J., Hincelin, U., Bergeat, A., et al. 2012, PNAS, 109, 10233 [NASA ADS] [CrossRef] [Google Scholar]
- Dawes, A., Mason, N. J., & Fraser, H. J. 2016, Phys. Chem. Chem. Phys. (Incorp. Faraday Trans.), 18, 1245 [Google Scholar]
- D’Hendecourt, L. B., Allamandola, L. J., Grim, R. J. A., & Greenberg, J. M. 1986, A&A, 158, 119 [Google Scholar]
- Fayolle, E. C., Öberg, K. I., Cuppen, H. M., Visser, R., & Linnartz, H. 2011, A&A, 529, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraser, H. J., Collings, M. P., Dever, J. W., & McCoustra, M. R. S. 2004, MNRAS, 353, 59 [CrossRef] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Acharyya, K., & Vidali, G. 2016a, ApJ, 825, 89 [Google Scholar]
- He, J., Acharyya, K., & Vidali, G. 2016b, ApJ, 823, 56 [Google Scholar]
- Huang, C. H., Ciaravella, A., Cecchi-Pestellini, C., et al. 2020, ApJ, 889, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G. J., Person, W. B., & Brown, K. G. 1975, J. Chem. Phys., 62, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Escobar, A., Ciaravella, A., Cecchi-Pestellini, C., et al. 2022, ApJ, 926, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Kruegel, E., & Walmsley, C. M. 1984, A&A, 130, 5 [NASA ADS] [Google Scholar]
- Lippok, N., Launhardt, R., Semenov, D., et al. 2013, A&A, 560, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Doménech, R., Mufloz Caro, G. M., Bueno, J., & Goesmann, F. 2014, A&A, 564, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, B., Giuliano, B. M., Goto, M., & Caselli, P. 2021, A&A, 652, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [Google Scholar]
- Pontoppidan, K. M., Boogert, A. C. A., Fraser, H. J., et al. 2008, ApJ, 678, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Punanova, A., Vasyunin, A., Caselli, P., et al. 2022, ApJ, 927, 213 [CrossRef] [Google Scholar]
- Teixeira, T. C., & Emerson, J. P. 1999, A&A, 351, 292 [NASA ADS] [Google Scholar]
- Tielens, A. G. G. M., Tokunaga, A. T., Geballe, T. R., & Baas, F. 1991, ApJ, 381, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [Google Scholar]
- Whittet, D. C. B. 2022, Dust in the Galactic Environment, 3rd edn. (IOP Publishing) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the ice during simultaneous cooling and deposition at three different pressures. Top panels: infrared spectra of the experiments. Middle panels: column densities of H2O, NH3, CO (in ML) as functions of the temperature. Bottom panels: mass spectra of H2O; m/z = 19, NH3; m/z = 15; and CO, m/z = 29 as functions of the temperature. The pressures reported in the panels indicate their initial values. |
| In the text | |
 |
Fig. 2 Normalized QMS ion counts for m/z = 19 (DHO), 15 (NH), and 29 (13CO) as functions of the temperature at the deposition pressure of Pd = 6 × 10−7 Torr. The three species are representative of H2O, NH3, and CO, respectively. The blue line represents the best fit using the relation Q = 1 - D. Red dots are the derivative of the column density expressed in monolayers (right vertical axes). |
| In the text | |
 |
Fig. 3 Net deposition rates D for H2O, NH3, and CO as functions of the temperature. |
| In the text | |
 |
Fig. 4 Fractional ice composition AN as a function of the ice thickness (symbols). Solid lines are the simulated evolutionary profiles of the ice components following the temperature decrease. Black circles represent H2O, orange triangles indicate NH3, and blue diamonds symbolize CO. |
| In the text | |
 |
Fig. 5 Morphological structure of an interstellar ice. Top panels: accretion rate during the molecular cloud collapse. Bottom panels: fractional ice composition AN as a function of the ice thickness (in ML). Left-hand side column: fast flow. Right-hand side column: slow flow. Black indicates H2O, orange represents NH3, and blue symbolizes CO. Red lines are for the cloud thermal profile. Dashed lines in the bottom panels represent the case in which gas and dust temperatures differ (Tg – Td = 50 K). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.