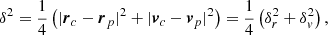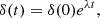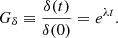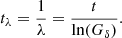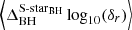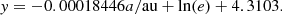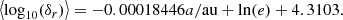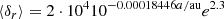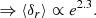| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 3 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348361 | |
| Published online | 30 April 2024 | |
Individual chaotic behaviour of the S-stars in the Galactic centre
1
Leiden Observatory, Leiden University, 2300 RA Leiden, The Netherlands
e-mail: beckers@strw.leidenuniv.nl; cpoppelaars@strw.leidenuniv.nl
2
NASA Ames Research Center, Moffett Field, CA 94035, USA
Received:
23
October
2023
Accepted:
15
February
2024
Located at the core of the Galactic centre, the S-star cluster serves as a remarkable illustration of chaos in dynamical systems. The long-term chaotic behaviour of this system can be studied with gravitational N-body simulations. By applying a small perturbation to the initial position of star S5, we can compare the evolution of this system to its unperturbed evolution. This results in two solutions that diverge exponentially, defined by the separation in position space δr, with an average Lyapunov timescale of ∼420 yr, corresponding to the largest positive Lyapunov exponent. Even though the general trend of the chaotic evolution is governed in part by the supermassive black hole Sagittarius A∗ (Sgr A∗), individual differences between the stars can be noted in the behaviour of their phase-space curves. We present an analysis of the individual behaviour of the stars in this Newtonian chaotic dynamical system. The individuality of their behaviour is evident from offsets in the position space separation curves of the S-stars and the black hole. We propose that the offsets originate from the initial orbital elements of the S-stars, where Sgr A∗ is considered in one of the focal points of the Keplerian orbits. Methods were considered to find a relation between these elements and the separation in position space. Symbolic regression provides the clearest diagnostics for finding an interpretable expression for the problem. Our symbolic regression model indicates that ⟨δr⟩ ∝ e2.3, implying that the time-averaged individual separation in position space increases rapidly with the initial eccentricity of the S-stars.
Key words: chaos / methods: numerical / celestial mechanics / stars: black holes / stars: fundamental parameters / Galaxy: center
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the pursuit of understanding the nature of chaos and its manifestation in the Universe, the S-star cluster is used as a laboratory for experimenting with the underlying astrophysics that give rise to chaos. The orbital data of 27 S-stars orbiting the supermassive black hole Sagittarius A∗ from (Gillessen et al. 2009) are employed as initial conditions for a Newtonian gravitational N-body simulation of the S-star cluster. The orbital evolution of the system was tracked over 104 yr by (Portegies Zwart et al. 2023; Boekholt et al. 2023). When perturbing the initial conditions of star S5 by displacing its initial x coordinate by dx = 15 m, the evolution of the perturbed solution diverges exponentially from the canonical solution, implying that the system is chaotic.
In this paper, we present the methods we used to quantify chaos in the simulation of the S-star cluster and delve into the individual differences in the chaotic behaviour of the S-stars and Sgr A*. For more details of the simulation, we refer to (Portegies Zwart et al. 2023).
2. Measuring chaos
In the gravitational N-body problem, chaos can be measured with the Lyapunov timescale. The Lyapunov timescale represents the timescale on which the system becomes unpredictable. We describe the chaotic S-star orbital evolution with phase-space distance. Phase-space distance as a function of time is defined as
where r and v are the position and velocity vectors of an S-star, and c and p denote the canonical and perturbed solutions, respectively. We define an (initial) perturbation at t = 0, δ(0). The evolution of δ(t) is then approximately described by an exponential function with a time dependence
where λ is the maximum positive Lyapunov exponent. The growth factor, Gδ(t), is the value of δ at some time t as a fraction of the initial perturbation, δ(0), that is,
From this equation, we can find λ = ln(Gδ)/t, which is the reciprocal of the Lyapunov timescale,
3. Separation in position space
We calculated the time evolution of the separation in position space between the canonical and perturbed solution, δr, for each S-star and Sgr A*. We show this time evolution in the left panel of Fig. 1.
 |
Fig. 1. Position-space separations as a function of time before and after reducing the spread in the curves. Left: Time evolution of separation in position space for each S-star and the central black hole. Right: y = −0.00018446 ⋅ a/au + log(e)+4.3103 subtracted from the time evolution of log10(δr) for each S-star. The grey shading shows the region between the non-reduced maxima and minima of δr over the whole system at each time step, indicating the magnitude of reduction in the spread of the curves, although its lower section is obscured by the coloured curves. |
The separation in position space grows approximately exponentially, as expected from Eq. (2). From a least-squares fit to the curve of each star and the black hole, we infer an ensemble mean Lyapunov timescale of tλ ≃ 420 yr. The black hole is less sensitive to the perturbation than most stars, as seen from its δr values, which are generally lower in magnitude than those of the S-stars. We attribute this to the mass difference of about 105 M⊙ between the central body and the stars, leading to much higher inertia. This stabilizes the black hole position, even in the presence of perturbations. Perturbations caused by close encounters between stars are propagated through the entire system, driven by feedback from the black hole (Portegies Zwart et al. 2023). Hence, large events with multiple close encounters, such as the event at t = 2876 yr, influence the general trend of all curves. However, it is not immediately evident why there are vertical offsets in the S-star curves, as the S-stars have been given identical masses in this simulation. Furthermore, while differences in the shapes of the individual curves could account for an offset, the curves as a whole exhibit a noticeable shift relative to each other.
4. Position-space separation offsets
The systematic offsets found in the position-space separation curves must be an effect of some underlying astrophysics. The (initial) S-star orbits can introduce variations in the evolution of δr of each star, and therefore, it is worthwhile to investigate the Keplerian elements.
To map the separations of S-star curves and Sgr A*, we subtracted the black hole curve from each S-star curve and took the temporal mean for each S-star; we define this as 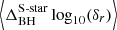 . To find a relation between this and the Keplerian elements of the stars, we used the initial orbital parameters from Gillessen et al. (2009). We expect to see that a low semi-major axis (a) corresponds to a higher magnitude in δr, as stars that are close to the black hole should be more sensitive to the changes inside the system. Moreover, eccentricity (e) and δr should be directly correlated because a highly elliptical orbit has a closer pericenter to the black hole. In Fig. 2, we show the relation between a, e, and
. To find a relation between this and the Keplerian elements of the stars, we used the initial orbital parameters from Gillessen et al. (2009). We expect to see that a low semi-major axis (a) corresponds to a higher magnitude in δr, as stars that are close to the black hole should be more sensitive to the changes inside the system. Moreover, eccentricity (e) and δr should be directly correlated because a highly elliptical orbit has a closer pericenter to the black hole. In Fig. 2, we show the relation between a, e, and 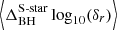 .
.
 |
Fig. 2. Initial semi-major axis and eccentricity of each S-star. |
The pattern that emerges in the colour gradient in Fig. 2 indicates that eccentricity and semi-major axis play a major role in the curve separations. The influence of eccentricity and semi-major axis on the mean separation are both important. The other orbital parameters can be compared with each other in a similar fashion, but no apparent pattern is found. This observation suggests that their influence on 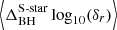 is negligible compared to that of the eccentricity and semi-major axis. Furthermore, the stars with the highest colour values in Fig. 2 are S21 and S29. Portegies Zwart et al. (2023) demonstrated that S21 is one of the stars that were part of the large event at 2876 yr. Moreover, S29 was shown to have six close encounters during the simulation. In addition, S67 has ten close encounters, which is more than for any other star. Therefore, despite its relatively low eccentricity and large semi-major axis, it is not green in Fig. 2, in contrast to its nearest neighbour, S87.
is negligible compared to that of the eccentricity and semi-major axis. Furthermore, the stars with the highest colour values in Fig. 2 are S21 and S29. Portegies Zwart et al. (2023) demonstrated that S21 is one of the stars that were part of the large event at 2876 yr. Moreover, S29 was shown to have six close encounters during the simulation. In addition, S67 has ten close encounters, which is more than for any other star. Therefore, despite its relatively low eccentricity and large semi-major axis, it is not green in Fig. 2, in contrast to its nearest neighbour, S87.
5. Symbolic regression
We adopted PySR (Cranmer 2023), a symbolic regression Python package for discovering interpretable analytical equations that describe an underlying pattern in a dataset. Only the semi-major axis and the eccentricity are used in the model because symbolic regression may not provide accurate results when the dimensionality of the data is high (Matchev et al. 2022). Moreover, PySR does not correctly interpret the evolution of δr, a, and e for each star, suggesting that it does not support time-series data1. Therefore, we provide the model with 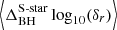 and the initial semi-major axis and eccentricity. The results can be found in Table 1.
and the initial semi-major axis and eccentricity. The results can be found in Table 1.
Symbolic regression results on the initial semi-major axis [au] and eccentricity and mean offsets between the S-star and the black hole.
From the optimal equation, which balances accuracy and simplicity, we can derive the following:
y is a measure of log10(δr),
We used this to estimate δr approximately as
Subtracting Eq. (5) from log10(δr) reduces the offsets significantly, as shown in the right panel of Fig. 1.
6. Conclusions
We aimed to characterize the individual behaviour of stars during the evolution of a Newtonian chaotic dynamical system. Using a gravitational N-body simulation of the S-star cluster, we derived the Lyapunov timescale of the system over 104 yr to be ∼420 yr.
In the position space of the S-stars, we find a vertical offset between their curves. A relation with the Keplerian orbits of the S-star was proposed to explain this offset in δr. We adopted symbolic regression to find the relation ⟨δr⟩ = 2 ⋅ 10410−0.00018446a/aue2.3, where a and e were taken from the initial orbit. We conclude that ⟨δr⟩ ∝ e2.3; the time-averaged individual phase-space distance with respect to the black hole increases rapidly with the orbital eccentricity of the star.
Eureqa (not open-source) claims to be able to handle time-series data (see https://www.creativemachineslab.com/eureqa.html).
Acknowledgments
This publication is funded by the Dutch Research Council (NWO) with project number OCENW.GROOT.2019.044 of the research programme NWO XL. It is part of the project “Unravelling Neural Networks with Structure-Preserving Computing”. In addition, part of this publication is funded by the Nederlandse Onderzoekschool Voor Astronomie (NOVA). T.B.’s research was supported by an appointment to the NASA Postdoctoral Program at the NASA Ames Research Center, administered by Oak Ridge Associated Universities under contract with NASA. We greatly thank the referee for taking the time to read this manuscript carefully and providing us with well-considered comments.
References
- Boekholt, T. C. N., Portegies Zwart, S. F., & Heggie, D. C. 2023, Int. J. Mod. Phys. D, 2342003 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, M. 2023, arXiv e-prints [arXiv:2305.01582] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Matchev, K. T., Matcheva, K., & Roman, A. 2022, ApJ, 930, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., Boekholt, T. C. N., & Heggie, D. C. 2023, MNRAS, 526, 5791 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Symbolic regression results on the initial semi-major axis [au] and eccentricity and mean offsets between the S-star and the black hole.
All Figures
 |
Fig. 1. Position-space separations as a function of time before and after reducing the spread in the curves. Left: Time evolution of separation in position space for each S-star and the central black hole. Right: y = −0.00018446 ⋅ a/au + log(e)+4.3103 subtracted from the time evolution of log10(δr) for each S-star. The grey shading shows the region between the non-reduced maxima and minima of δr over the whole system at each time step, indicating the magnitude of reduction in the spread of the curves, although its lower section is obscured by the coloured curves. |
| In the text | |
 |
Fig. 2. Initial semi-major axis and eccentricity of each S-star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.