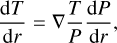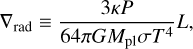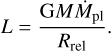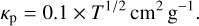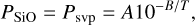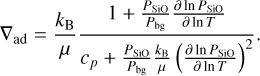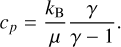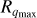EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A217 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A217
Number of page(s) 9
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202349052
Published online 22 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Around one half of all Sun-like stars are thought to be orbited by planets with radii between 0.5 and 1.5 R⊕ (Dressing & Charbonneau 2013; Silburt et al. 2015; Bryson et al. 2021). The mass-radius relationship for this type of planet is consistent with a rocky composition similar to Earth (Rogers 2015; Wolfgang & Lopez 2015; Zeng et al. 2019). Rocky planets are traditionally thought to form by giant impacts between planetary embryos after the dissipation of the protoplanetary disks (Raymond et al. 2009, 2020; Batygin & Morbidelli 2023). However, rocky planets may also form already in the protoplanetary disk phase by pebble accretion (Levison et al. 2015; Johansen et al. 2015, 2021; Lambrechts et al. 2019). In this scenario, the planets grow during the lifetime of the protoplanetary disk by accreting small solids, referred to as pebbles. These pebbles feel the drag of the surrounding gas, which increases their accretion cross section compared to the pure gravitational cross section (Johansen & Lacerda 2010; Ormel & Klahr 2010; Lambrechts & Johansen 2012). Once a protoplanet reaches lunar mass, it starts to acquire a hydrostatic spherical envelope (Ikoma & Hori 2012; Lee et al. 2014). This envelope is characterized by an increase in density compared to the local gas density in the disk. The composition of the envelope is dominated by H2 and He (Ikoma & Hori 2012).

The release of gravitational potential during the pebble accretion process heats the envelope from the bottom. Due to their small size, the pebbles are in thermal equilibrium with the envelope. Recent works have shown that the temperature in the envelope is high enough for the sublimation of pebbles to play an important role in the growth process (Alibert 2017; Brouwers et al. 2018; Steinmeyer et al. 2023). Already Alibert (2017) proposed that the sublimation of pebbles in the envelope leads to an end of direct growth of planets by pebble accretion as the released vapor is recycled back into the disk. However, hydro-dynamical simulations have found silicate vapor recycling to be inefficient (Wang et al. 2023). Furthermore, Alibert (2017) did not take the change of composition of the envelope due to pebble sublimation into account.

In contrast, Ormel et al. (2021), building on Brouwers et al. (2018) and Brouwers & Ormel (2020), modeled the evolution of a planet including the enrichment of the envelope and the time-dependent heat transport. In their model, an outer region saturated in SiO2 resides on top of a possibly undersaturated region. However, this model does not take into account that rapidly formed rocky planets undergo a magma ocean phase during their formation by pebble accretion (Olson et al. 2022; Johansen et al. 2023). Furthermore, chemical equilibrium models show that the dominant gas species of Si in equilibrium with molten silicates (MgSiO3 or Mg2SiO4) is SiO and not SiO2 (Schaefer et al. 2012; Herbort et al. 2020). Similarly, Melosh (2007) found that the dominant gas species after vaporization of SiO2 is SiO. We ignore the contribution of O2 and O in this work.

In this paper, we therefore analyze a vapor equilibrium model to represent the envelopes of accreting rocky planets close to the ice line in the mass range of 0.1 M⊕ to 3 M⊕. At this location, water ice sublimates and is recycled back into the protoplanetary disk even at low planet masses (Johansen et al. 2021). Therefore, this paper focuses on the accretion and sublimation of silicate pebbles. We want to point out three key differences to Ormel et al. (2021). Firstly, we focus on equilibrium states and do not evolve our model in time. Secondly, we represent the sublimated silicates by SiO instead of SiO2. Thirdly, the underlying magma ocean acts as the major source of SiO in our model. Therefore, the envelope is assumed to always be saturated in SiO. This extension is based on recent models of the envelopes of super-Earths and sub-Neptunes (Markham et al. 2022; Misener & Schlichting 2022).

Since SiO is heavier than the surrounding H2/He gas, condensation of SiO has a stabilizing effect on the envelope, leading to the buildup of an inner radiative region where the SiO contents rise to provide a significant fraction of the pressure (Guillot 1995; Leconte et al. 2017; Misener & Schlichting 2022). We find that this inner radiative region first appears for Mpl ≈ 0.3 M⊕. The partial pressure of SiO increases steeply with temperature. Below the inner radiative region, the increasing temperature thus leads to complete dominance of SiO in supporting the hydrostatic equilibrium. In the innermost region, the stabilizing effect of SiO condensation is gone, and the envelope becomes con-vective again. The main product of this paper is our calculation of the mass needed to keep the envelope saturated in SiO. We find that it is lower than the difference between two consecutive planet masses for planets with Mpl < 2.0 M⊕. This implies that direct core growth by pebble accretion is possible up to masses well above one Earth mass.

The paper is organized as follows: we first describe the model for the envelope structure and the treatment of SiO vapor in Sect. 2. In Sect. 3, we discuss the effect of the envelope enrichment on the envelope structure. We also test if the treatment of the opacity and the pebble accretion rate influence the envelope structure significantly. We discuss the implication of SiO enrichment on the growth of the rocky planets in Sect. 4. Section 5 discusses the main limitations of the model. We conclude with a summary of the paper in Sect. 6.

2 Envelope model

2.1 Structure equations

We calculate the envelope structure in 1D of a planet with mass Mpl under the assumption that the envelope is in hydrostatic balance and spherically symmetric. The radial structure of the envelope thus follows the standard structure equations of hydrostatic balance and thermal gradient (e.g Kippenhahn et al. 2013),

dPdr=−Gmr2ρ ${{{\rm{d}}P} \over {{\rm{d}}r}} = - {{Gm} \over {{r^2}}}\rho $(1a) dTdr=∇TPdPdr,${{{\rm{d}}T} \over {{\rm{d}}r}} = \nabla {T \over P}{{{\rm{d}}P} \over {{\rm{d}}r}},$(1b)

where ρ, P, and T are the density, gas pressure, and temperature respectively, and ∇ = ∂ ln T/∂ ln P is the logarithmic temperature gradient. The mass enclosed at distance r from the surface of the planet is given by m and G is the gravitational constant.

In the case where envelope pollution is not taken into account, the gradient in Eq. (1b) is given by the minimum of the radiative and convective gradient (Schwarzschild criterion). The radiative temperature gradient is given by

∇rad≡3κP64πGMplσT4L,${\nabla _{{\rm{rad}}}} \equiv {{3\kappa P} \over {64\pi G{M_{{\rm{pl}}}}\sigma {T^4}}}L,$(2)

where κ is the opacity in the envelope and σ the Stefan–Boltzmann constant. The luminosity of the planet comes from the accretion process through the expression

L=GMM˙plRrel.$L = {{{\rm{G}}M{{\dot M}_{{\rm{pl}}}}} \over {{R_{{\rm{rel}}}}}}$(3)

Here, Ṁpl is the pebble accretion rate. The accretion energy is released at the surface of the planet and Rrel = Rpl = (3Mpl/(4πρp))1/3. We assume that the density of the planet corresponds to the density of the uncompressed Earth, ρp = 4050 kg m−3 (Hughes 2006).

The opacity plays an important role in setting the envelope structure and depends on the temperature, pressure, and composition of the envelope. The main opacity sources in the envelope are the gas molecules, pebbles, and dust grains. However, the contribution of each source remains poorly constrained. We describe the molecular gas opacity κg by the analytic fit from Freedman et al. (2014) with a solar gas metallicity and the opacity coming from the dust with the power law from Bell & Lin (1994). The latter is given by

κp=0.1×T1/2 cm2 g−1. ${\kappa _{\rm{p}}} = 0.1 \times {T^{1/2}}\,{\rm{c}}{{\rm{m}}^2}\,{{\rm{g}}^{ - 1}}{\rm{.}}$(4)

The total opacity in the nominal case is then

κ=κg+κp.$\kappa = {\kappa _{\rm{g}}} + {\kappa _{\rm{p}}}.$(5)

We discuss the effect the treatment of the opacity has on the structure of the envelope in Sect. 3.2.

2.2 Treatment of silicate vapor

Initially, the envelope has the same composition as the surrounding protoplanetary disk and consists of a mixture of hydrogen and helium (H2/He). As the planet grows, it will melt and differentiate into an iron-rich core and a magma ocean (Olson et al. 2022; Johansen et al. 2023). The envelope is assumed to be in vapor equilibrium with this magma ocean at all times. Therefore, silicate vapor evaporated from the magma ocean will become stable in the envelope. For simplicity, we assume that the representative gas-phase molecule in equilibrium with the magma ocean is SiO. The partial pressure of SiO then follows the saturated vapor pressure of SiO. We take the expression from Fegley & Schaefer (2012) and Visscher & Fegley (2013),

PSiO=Psvp=A10−B/T,${P_{{\rm{SiO}}}} = {P_{{\rm{svp}}}} = A{10^{ - B/T}},$(6)

where Psvp is given in bar, A = 108.203 bar and B = 25 898.9 K.

The adiabatic temperature gradient of an atmosphere with a condensable species, in this case SiO, is described by the moist adiabatic gradient (Leconte et al. 2017; Misener & Schlichting 2022),

∇ad=kBμ1+PSiOPbg∂ lnPSiO∂ lnTcp+PSiOPbgkBμ (∂ lnPSiO∂ lnT)2.${\nabla _{{\rm{ad}}}} = {{{k_{\rm{B}}}} \over \mu }{{1 + {{{P_{{\rm{SiO}}}}} \over {{P_{{\rm{bg}}}}}}{{\partial \ln {P_{{\rm{SiO}}}}} \over {\partial \ln T}}} \over {{c_p} + {{{P_{{\rm{SiO}}}}} \over {{P_{{\rm{bg}}}}}}{{{k_{\rm{B}}}} \over \mu }\,{{\left( {{{\partial \ln {P_{{\rm{SiO}}}}} \over {\partial \ln T}}} \right)}^2}}}.$(7)

Here kB is the Boltzmann constant and Pbg = P – PSiO is the partial pressure of H2 and He. The heat capacity of a gas with mean molecular weight µ and an adiabatic index of γ is

cp=kBμγγ−1.${c_p} = {{{k_{\rm{B}}}} \over \mu }{\gamma \over {\gamma - 1}}.$(8)

The dominant gas species are the diatomic molecules SiO and H2, which both display γ = 1.4 under the assumption of ideal gas behavior. If PSiO ≪ Pbg, Eq. (7) follows the dry adibat ∇ad=γ−1γ.${\nabla _{{\rm{ad}}}} = {{\gamma - 1} \over \gamma }.$(9)

The local mean molecular weight of the enriched envelope is given by 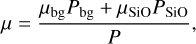μ=μbgPbg+μSiOPSiOP,$\mu = {{{\mu _{{\rm{bg}}}}{P_{{\rm{bg}}}} + {\mu _{{\rm{SiO}}}}{P_{{\rm{SiO}}}}} \over P},$(10)

with µbg = 2.34 and µSiO = 44 given in atomic mass units.

According to Eq. (6) the hotter the envelope is, the more SiO will be contained in the envelope. This increase in µ with temperature has a stabilizing effect on the envelope (Guillot 1995; Leconte et al. 2017). If the mass mixing ratio 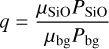q=μSiOPSiOμbgPbg$q = {{{\mu _{{\rm{SiO}}}}{P_{{\rm{SiO}}}}} \over {{\mu _{{\rm{bg}}}}{P_{{\rm{bg}}}}}}$(11)

reaches a threshold value qth, convection is inhibited. The threshold mixing ratio is given by Guillot (1995) and Leconte et al. (2017) as 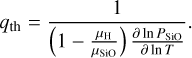qth=1(1−μHμSiO)∂ lnPSiO∂ lnT.${q_{{\rm{th}}}} = {1 \over {\left( {1 - {{{\mu _{\rm{H}}}} \over {{\mu _{{\rm{SiO}}}}}}} \right){{\partial \ln {P_{{\rm{SiO}}}}} \over {\partial \ln T}}}}.$(12)

This criterion is different from the Ledoux (1947) criterion for stability in a medium with a mean molecular weight gradient. In the case of the Ledoux criterion, the composition of a moving gas element is fixed while the local background mean molecular weight changes, whereas Eq. (12) takes the change of mean molecular weight of a moving gas element due to condensation into account. In regions where q > qth, the temperature gradient follows Eq. (2). However, if the local mass mixing ratio reaches a value q = qmax ≫ 1, the local envelope mainly consists of SiO and the stabilizing effect no longer holds. Thus, for q > qmax convection sets in again. In this region the saturated vapor pressure of SiO dominates, PSiO ≫ Pbg, and the moist adiabatic gradient follows the coexistence curve of SiO 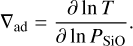∇ad=∂ lnT∂ lnPSiO.${\nabla _{{\rm{ad}}}} = {{\partial \ln T} \over {\partial \ln {P_{{\rm{SiO}}}}}}.$(13)

The temperature and pressure close to the surface will eventually become hot enough to reach the critical point of SiO at temperature Tcrit ≈ 6600 K and pressure Pc ≈ 1400 bar (Xiao & Stixrude 2018). We therefore treat the region with T > Tc as the outer mantle or supercritical magma ocean (Bodenheimer et al. 2018; Markham et al. 2022). The radius of the supercritical magma ocean, Rcrit, is defined as the radius where T > Tcrit for the first time. In this case, the accretion heating is no longer released at the surface of the planet but on top of the supercritical magma ocean, which translates to Rrel = Rcrit in Eq. (3). We treat the region below Rcrit as part of the mantle of the planet and not the envelope, similar to Bodenheimer et al. (2018). A consequence of this is that the temperature at the bottom of the envelope never exceeds Tc.

The different phases of the planet and envelope in our model are shown in Fig. 1. In Phase 1, the undifferentiated planet is surrounded by a H2/He rich envelope. The temperature gradient in the envelope is set by ∇ = min(∇ad, ∇rad). The temperature in the inner envelope increases and the planet differentiates into a metal core and a magma ocean mantle. SiO will start to evaporate from the magma ocean in order to keep the equilibrium between the magma ocean and the surrounding envelope. Once q reaches the critical value, an inner radiative region appears (Phase 2). As the magma ocean temperature increases, more SiO enters the envelope and a SiO-dominated convective region forms beneath the inner radiative zone (Phase 3). In Phase 4, the temperature close to the surface of the planet has become hot enough to transition the magma ocean into a supercritical magma ocean state.

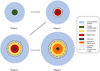thumbnail Fig. 1

Illustration of the different phases of the planet and envelope during the growth process. In the beginning, the undifferentiated planet is surrounded by a H2/He rich envelope (Phase 1). In Phase 2, the planet has differentiated into a metallic core and a magma ocean. Enough silicates sublimate in the atmosphere to inhibit convection in this phase. In Phase 3, the region close to the surface of the planet is dominated by SiO and becomes convective again. The planet becomes hot enough to form a supercritical magma ocean in Phase 4.

2.3 Numerical method

We solve Eq. (1) together with Eq. (10) by integrating from the outer boundary down to the surface of the planet, using a 4th order Runge–Kutta method. We set the outer boundary to the Hill radius of the planet, RH=a (Mpl3M⋆)1/3, ${R_{\rm{H}}} = a\,{\left( {{{{M_{{\rm{pl}}}}} \over {3{M_ \star }}}} \right)^{1/3}}{\rm{,}}$(14)

where a is the distance of the planet from the star. We take the stellar mass M* to be equal to 1 M⊙. The density and temperature at the Hill radius are set to match the surrounding protoplanetary disk, ρ = ρd and T = Td. We determine the step size dr via 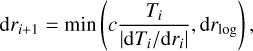dri+1=min (cTi| dTi/dri |,drlog),${\rm{d}}{r_{i + 1}} = \min \,\left( {c{{{T_i}} \over {\left| {{\rm{d}}{T_i}/{\rm{d}}{r_i}} \right|}},{\rm{d}}{r_{\log }}} \right),$(15)

with c ≤ 10−3 and drlog from a logarithmically spaced grid. We chose this set up to account for the steep temperature gradients that appear in the enriched inner envelope.

Initially, we set the mean molecular weight in the envelope to be that of a mixture of H2 and He, µ0 = 2.34 mu. After solving for the envelope structure, we calculate the new mean molecular weight profile of the envelope via Eqs. (7) and (10). The mean molecular weight gradient determines the adiabatic gradient and consequently the temperature and pressure profile in the envelope. We then solve Eq. (1) again using the new mean molecular weight profile. For each iteration, we calculate the total mass in SiO as a function of the resulting temperature and pressure profile according to 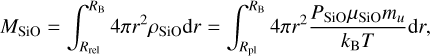MSiO=∫RrelRB4πr2ρSiOdr=∫RrelRB4πr2PSiOμSiOmukBTdr,${M_{{\rm{SiO}}}} = \int_{{R_{{\rm{rel}}}}}^{{R_{\rm{B}}}} {4\pi {r^2}} {\rho _{{\rm{SiO}}}}{\rm{d}}r = \int_{{R_{{\rm{rel}}}}}^{{R_{\rm{B}}}} {4\pi {r^2}} {{{P_{{\rm{SiO}}}}{\mu _{{\rm{SiO}}}}{m_u}} \over {{k_{\rm{B}}}T}}{\rm{d}}r,$(16)

as well as the new mean molecular weight profile. The outer radius in Eq. (16) is set to RB since material outside this radius is likely replenished by H2-rich gas from the disk (Lambrechts & Lega 2017; Kurokawa & Tanigawa 2018). Additionally, the temperatures in the outer envelope are too low to contain a significant amount of SiO. We repeat this process until the SiO mass of the envelope converges. On average, it took 10 iterations for each planet mass to converge.

3 Effect of SiO vapor on the envelope structure

3.1 Nominal case

We calculate the envelope profile of planets between 0.1 M⊕ and 3 M⊕ with a mass step of ΔMpl = 0.01 M⊕. The location of the planet is kept constant at 1 au with Td = 150 K and ρd = 1.7 × 10−8 kg m−3. This corresponds to a gas surface density of Σg ≈ 310 kg m−2, which is two orders of magnitude lower than the gas surface density at 1 au given by the Minimum Mass Solar Nebulae, Σg(MMSN) ≈ 1.7 × 104 kg m−2 (Hayashi 1981). However, the pressure and temperature in the inner region of the envelope are relatively independent of the outer boundary condition. The nominal pebble accretion rate is set to Ṁp = 10−6 M⊕ yr−1. Figure 2 compares the enriched envelope profiles of selected masses to the structure of pure H2/He envelopes. The outer envelope is too cold for silicate sublimation to play an important role. As a consequence, the envelope profiles in the outer envelope of all planet masses are equal to the pure H2/He envelopes.

Phase 1 in which the whole envelope contains mainly H2/He ends after approximately Mpl ≥ 0.29 M⊕. At this point the surface temperature is 2000 K and the planet has therefore melted and differentiated into a metal core and a molten silicate magma ocean. Since the saturated vapor pressure is a strong function of the temperature, the envelope around low mass planets is easily saturated in SiO from the magma ocean at this stage. Therefore, the incoming pebbles continue to move through the envelope without sublimation. The temperature and saturated vapor pressure in the inner region of the envelope are high enough so that the mass mixing ratio reaches the critical value to suppress convection by SiO cloud condensation. The envelope thus develops an inner radiative region. The radiative temperature gradient in this inner region is much steeper than the adiabatic gradient, which leads to an increase in temperature compared to the H2/He envelopes; this is clear from the top left plot in Fig. 2. Increasing the planetary mass further, the envelope temperature increases and the SiO mixing ratio increases accordingly, as is seen in the bottom right plot in Fig. 2. This is denoted Phase 2 in Fig. 1. Once Mpl > 0.34 M⊕, the mass mixing ratio becomes larger than qmax and an inner convective region develops (Phase 3). The total pressure in this region is completely dominated by the partial pressure of SiO, which leads to a significant increase in pressure compared to the pure H2/He envelopes. The critical point of SiO is first reached for a planet with Mpl = 0.75 M⊕. The temperature at the bottom of the envelope is constant, because the region below Rcrit is part of mantle of the planet.

Figure 3 shows the outer (q = qth) and inner edge (q = qmax) of the inner radiative region as well as the surface of the supercritical magma ocean as a function of the planet mass. The width of the inner radiative region increases from 0.08 R⊕ at Mpl = 0.34 M⊕ to 0.61 R⊕ at Mpl = 3.0 M⊕. The extent of the SiO-dominated region below the inner radiative exceeds 1 R⊕ for Mpl > 1.19 M⊕.

3.2 Influence of opacity

Bell & Lin (1994) assume a solid-to-gas ratio of Z = 0.01 in micron-sized particles to calculate the dust opacity. However, the actual solid-to-gas ratio in a planetary envelope is likely higher (Ali-Dib & Thompson 2020; Johansen & Nordlund 2020). We therefore compare three different opacity cases in Fig. 4. The standard model “g+1xd” is given by Eq. (5) while in the model “g+10xd” we increase the dust contribution and use κ = κg + 10 × κp. Lastly, in model “g” we calculate the envelope using only the gas opacities following Freedman et al. (2014). For all three opacity models in Fig. 4, the mass of the planet is Mpl = 0.8 M⊕ and the pebble accretion rate is Ṁp = 10−6 M⊕ yr−1. Increasing the contribution of the dust to the opacity leads to a small increase in temperature. Therefore, qth and qmax are reached further out in the envelope for model “g+10xd”. The profile of the envelope changes significantly if we consider only the gas opacity. Due to the low gas opacity in the outer envelope, the envelope cools effectively and the outer isothermal region reaches further into the envelope. As a consequence, the temperatures in the envelope are lower than if the dust opacity is included. Due to the strong increase in pressure in the isothermal region, the overall pressure structure is higher in model “g”. The critical mass mixing ratio is only reached at 0.006 RH compared to 0.009 RH for “g+1xd” and 0.01 RH for “g+10xd”. The temperature gradient in the inner radiative region in model “g” is very steep. Therefore, the envelope almost immediately becomes dominated by SiO with ΔRrad = 0.0004 R⊕.

3.3 Influence of pebble accretion rate

For completeness, we also calculate the envelope profiles for a lower pebble accretion rate of Ṁp = 10−7 M⊕ yr−1. As is shown in Fig. 5, the temperatures in the envelope of a given planet mass are lower compared to the case where Ṁp = 10−6 M⊕ yr−1. This is because the accretion heating scales with the pebble accretion rate, see Eq. (3). Otherwise, there is no significant difference between a high and a low pebble accretion rate.

thumbnail Fig. 2

Envelope profiles of a selected set of planet masses accreting at Ṁp = 10−6 M⊕ yr−1. The distance to the core is given in units of the Hill radius. The color corresponds to the mass of the planet. The top row shows the temperature (left) and pressure (right). Solid lines include the enrichment with SiO while dashed lines correspond to a pure H2/He envelope. The bottom row shows the moist adiabatic gradient including the latent heat from SiO condensation (left) and the mass mixing radio (right). The critical mass ratio is shown by dashed lines. In all four plots, the squares indicate the start of the inner radiative region and the filled circles the end. Planets larger than 0.75 M⊕ possess a supercritical magma ocean. The surface of this ocean is marked by the triangles.
thumbnail Fig. 3

Key radii as a function of the planet mass. The dashed orange line indicates the location where q > qth for the first time, while the purple dash-dotted line shows the location where q > qmax for the first time. The solid green line indicates the surface of the supercritical magma ocean, and the dotted pink line the radius of the planet without the supercritical magma ocean. For planets with Mpl ≥ 0.75 M⊕, the accretion heating from the incoming pebbles is released at the surface of this supercritical magma ocean. The feature between 2.1 M⊕ and 2.5 M⊕ in Rcrit and Rqmax${R_{{q_{\max }}}}$ is due to slight discontinuities in the solution, caused by the finite numerical grid.

4 Implication for planetary growth

4.1 Total atmosphere mass

The total mass in SiO and H2/He as a function of planet mass is shown in Fig. 6. As expected, the total mass in the envelope is dominated by H2/He for Mpl < 0.4 M⊕. The envelope mass increases steeply until the critical point of SiO is reached at Mpl = 0.75 M⊕. The temperature at the bottom of the envelope is set constant at Tc for higher masses. The envelope thus only grows by heating the outer parts of the envelope. Therefore, the mass in the envelope increases weakly with planetary mass. The total mass of SiO is almost two orders of magnitude larger than the total mass in H2/He for Mpl > 0.73 M⊕.

In Steinmeyer et al. (2023), we proposed that the sublimation of silicates and other refractory mineral species will create a layer rich in heavy gas species, such as SiO, close to the surface of the planet. We further proposed that this layer is protected from recycling flows by an inner radiative zone. This is in line with hydrodynamic simulation of atmospheric recycling (Wang et al. 2023). We now test this hypothesis by plotting the cumulative mass distribution of the SiO in the envelope for different planet masses in Fig. 7. Almost all SiO is indeed concentrated below the inner radiative region. As discussed before, this is because the saturated vapor pressure is low in the outer envelope. Therefore, pebbles plunge into the magma ocean without experiencing sublimation in the envelope. The magma ocean in turn acts as a reservoir of SiO to saturate the envelope at the temperature conditions given by the planetary mass and accretion rate.

thumbnail Fig. 4

Comparison of the temperature, pressure, and SiO mass mixing ratio profiles of a planet with Mpl = 0.8 M⊕ for three different treatments of the opacity. The model “g+1xd” corresponds to the nominal case. In model “g+10xd”, the dust contribution is increased by a factor 10. In model “g”, the gas is the only opacity source considered. Due to the larger outer isothermal region in model “g”, the temperature in the envelope is lower than in the other models while the pressure is higher.
thumbnail Fig. 5

Temperature profiles of a selected set of planet masses and Ṁpeb = 10−7 M⊕ yr−1. Colors and line styles have the same meaning as in Fig. 2. At a given mass, the envelopes are slightly colder than in the nominal case Ṁpeb = 10−6 M⊕ yr−1. As a result, the enriched envelopes start to differ from the pure H2/He envelopes only after Mpl > 0.4 M⊕.

4.2 End of direct core growth

It has been proposed by other authors that direct growth stops after the planet reaches a mass as low as 0.5 M⊕, because all incoming pebbles are destroyed before they reach the core (Alibert 2017; Brouwers et al. 2018; Brouwers & Ormel 2020; Ormel et al. 2021). We therefore calculate the amount of SiO that is needed to keep the envelope saturated by calculating the change in SiO in the envelope, ΔMSiO, between two consecutive masses and compare it to the accreted mass ΔMpl. The total envelope mass shows some noise for planets with masses between 2.1 M⊕ to 2.5 M⊕. The most likely cause for this is that the surface of the magma ocean lies at the border of two grid cells. We therefore used a boxcar average to smooth the total SiO mass in the envelope in order to avoid negative values in ΔMSiO. The results are shown in Fig. 8. Similarly to the total envelope mass, the ratio ΔMSiO/ΔMpl increases steeply until the supercritical magma ocean forms. However, for Mpl < 0.6 M⊕, ΔMSiO/ΔMpl is very small with a value of less than 0.01. Once Mpl > 2.0 M⊕, ΔMSiO/ΔMpl becomes larger than unity. We propose that in this case the pebbles actually sublimate in the envelope and the region where the accretion heat is released moves outward. The envelope cools to restore vapor equilibrium at the modified accretion luminosity profile. At the same time, the underlying supercritical magma ocean continues to act as a source of SiO.

This way, the envelope will maintain saturation in SiO as the accretion heat is released well above the magma ocean surface.

Ormel et al. (2021) modeled the evolution of a planet including the time evolution of the heat transport and the moist adiabat. Although this is a different approach than the vapor equilibrium model presented in this paper, we can still compare the general conclusions. Ormel et al. (2021) found that the envelope is divided in an outer region which is saturated in SiO2 and an inner under-saturated region. However, the key difference in assumptions between Ormel et al. (2021) and the model presented in this paper is the existence of a magma ocean and later a supercritical magma ocean. Figure 8 shows that if the critical point of SiO is ignored, the amount needed to keep the envelope saturated in SiO becomes larger than ΔMpl already for Mpl ≥ 0.8 M⊕. More importantly, in the case without considering the transition to a supercritical fluid, ΔMSiO/ΔMpl > 102 for Mpl ≳ 1.0 M⊕. In this case the envelope becomes undersaturated in SiO as predicted by Ormel et al. (2021).

The main heat source of the envelope is the transformation of gravitational potential to thermal energy during the accretion process. The pebble flux could cease either due to depletion radial drift or if an outer planet opens a gap that interrupts the pebble flux (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014; Gurrutxaga et al. 2024). In any case, the envelope will begin to cool down and the supercritical magma ocean will transition into a normal magma ocean. As the temperatures in the envelope become lower, the saturated vapor pressure of silicate decreases. As a consequence, the silicate vapor will condense and rain out on the surface of the planet (Brouwers & Ormel 2020; Vazan & Ormel 2023).

thumbnail Fig. 6

Total envelope mass in Earth masses as a function of the planet mass. The solid lines show the SiO mass while the dotted lines show the mass of H2/He in the envelope. The SiO mass dominates the total mass budget for planets with Mpl > 0.6 M⊕. The kink shows the start of the supercritical magma ocean after which the amount of SiO and H2/He in the envelope increases only by heating the outer parts of the envelope.
thumbnail Fig. 7

Cumulative mass distribution of SiO for different planet masses. The distance to the surface of the planet is given in units of the Hill radius of the respective planet. The filled circles mark the end of the inner radiative zone. Most of the SiO vapor mass is concentrated inside the radiative region.
thumbnail Fig. 8

Ratio of the amount of SiO needed to keep the envelope saturated to the total mass added to the planet as a function of the planet mass. The green line shows the nominal model where the critical point of SiO is considered. The orange line shows the case where the critical point is not taken into account. In the nominal case, ΔMSiO/ΔMpl becomes larger than unity for Mpl > 2.0 M⊕. However, ΔMSiO/ΔMpl never becomes larger than 2 and the envelope is always saturated in SiO. In the model without Tcrit, ΔMSiO/ΔMpl reaches unity already at Mpl = 0.8 M⊕. The key different between the two models, however, is that the amount of SiO needed to keep the envelope saturated in the model without Tc becomes larger than the total mass of the planet for Mpl ≳ 1.0 M⊕. In this case, the envelope is most likely undersaturated. The feature between 2.1 M⊕ and 2.5 M⊕ is likely caused by the inner boundary of the envelope switching between two grid cells.

4.3 Long-term evolution of composition gradients

According to structure models of Jupiter that are based on measurements by the Juno and Galileo missions, the planet contains an extended region in its deep interior that is rich in heavy elements (Wahl et al. 2017; Debras & Chabrier 2019; Militzer & Hubbard 2024). This region is referred to as the “dilute” or “fuzzy core” of Jupiter. An outward decreasing interior composition gradient is furthermore consistent with the available measurements of Uranus and Neptune (Marley et al. 1995; Podolak et al. 2000; Helled et al. 2011). These composition gradients can be seen as a remnant of compositional gradients coming from formation (Venturini & Helled 2020; Ormel et al. 2021). However, all these planets have accreted a significant amount of H2/He-gas. We find that low mass planets, Mpl < 2.5 M⊕, that only accreted modest amounts of H2/He-gas have steep compositional gradients, see Fig. 2. Furthermore, the envelope is always saturated in SiO. Hence, our results are not directly applicable to ice and gas giants. The presence of extended vapor regions in our model may nevertheless be important for understanding the dilute cores of giant planets. Adding gas accretion and mixing between vapor and accreted gas will nevertheless be needed to understand the connection between the vapor-rich cores found here and the dilute cores observed in the giant planets of the Solar System.

5 Limitations of the model

5.1 Evaporation timescale

In this work, we assumed that the evaporation of SiO from the magma ocean is a very efficient process. The mass loss rate due to evaporation is (Ros et al. 2019) 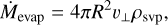M˙evap =4πR2v⊥ρsvp , ${{\dot M}_{{\rm{evap}}}} = 4\pi {R^2}{v_ \bot }{\rho _{{\rm{svp}}}}{\rm{,}}$(17)

where R is the radius of the planet, 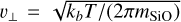v⊥=kbT/(2πmSiO)${v_ \bot } = \sqrt {{k_b}T/\left( {2\pi {m_{{\rm{SiO}}}}} \right)}$ the average speed of vapor, and ρsvp = µSiOPsvp/(kBT). Based on Fig. 2, typical values for Psvp at the surface of the planets are on the order of 103 bar, which translates to ρsat ~ 100 kg m−3. The average speed of the vapor is υ⊥ ~ 100 m s−1. For 1 M⊕, this corresponds to a mass loss rate of Ṁevap ~ 10−7 M⊕ s−1. Therefore, the evaporation rate of the planet will be extremely fast compared to the accretion timescale even at low ρsat/ρp. For this reason, the envelope is in equilibrium with the magma ocean at any time.

5.2 Composition of pebbles

The main assumption in this paper is that the pebbles are purely made out of silicates and that these silicates turn into SiO vapor after sublimation. Pebbles that formed in an environment with solar composition have a water ice-to-rock ratio of roughly 1:1 (Lodders 2003). Therefore, planets forming outside the water ice line should accrete water ice as well as silicates. However, Johansen et al. (2021) found that in the vicinity of the water ice line, water ice will start to sublimate in the envelope once the planet reaches a mass of 0.02 M⊕. The resulting water vapor can easily be recycled back into the protoplanetary disk (Johansen et al. 2021; Wang et al. 2023).

While pebbles can contain a variety of mineral species with different sublimation behavior, the fraction of both more refractory (e.g., Al2O3) and less refractory (e.g., FeS) species is low compared to water ice and silicates (Pollack et al. 1994). For that reason, we can assume that the incoming pebbles only contain silicates. The most likely silicates to form if the pebbles condensed out of solar composition material is enstatite (MgSiO3; Gail 1998). Experiments have shown that the sublimation of silicates is a fast process (Tsuchiyama et al. 1999; Tachibana et al. 2002). Enstatite sublimates by forming a layer of forsterite (Mg2SiO4; Tachibana et al. 2002). The final sublimation products of enstatite and forsterite are atomic Mg, SiO, and O2 (Tachibana et al. 2002; Schaefer & Fegley 2009). In the inner envelope the temperature and pressure are high enough for Si and O to be stable (Melosh 2007). Since atomic Mg, Si, and O as well as O2 have a lower molecular weight than SiO, our assumption of purely SiO gas overestimates the mean molecular weight of the heavy gas species. Furthermore, we neglected the possibility of reactions between SiO and H2, which can lead to the production of species such as SiH4 or H2O (Misener et al. 2023). Nevertheless, using SiO as the key gas species is a good first approximation for the sublimation of refractory rocky material in the envelope of an accreting planet.

The molecular gas opacity scales with the metallicity of the gas (Freedman et al. 2014). The release of SiO due to pebble sublimation in the innermost region increases the metallicity of the gas, which therefore leads to an increase of the gas opacity. However, regions where the change in metallicity is significant are anyway convective, and hence the opacity plays no role for heat transport in these regions. Therefore, we used a constant solar metallicity in order to calculate the molecular gas opacity.

5.3 Critical point of SiO

We set the critical point of SiO to Tc = 6600 K and Pc = 140 MPa (Xiao & Stixrude 2018). Literature values for the critical temperature are in the range of 5000 to 15 000 K (Melosh 2007; Kraus et al. 2012; Iosilevskiy et al. 2014; Connolly 2016). The critical point determines the onset of the supercritical magma ocean. If the critical temperature is lower than 6600 K, the supercritical magma ocean will appear already at lower masses. Therefore, the amount of gaseous SiO in the envelope is lower. If, on the other hand, the critical temperature is higher, the total amount of SiO in the envelope becomes higher. In that case, the direct core growth stops at lower planet masses.

5.4 Adiabatic index and EOS

The adiabatic index of SiO based on the data from the NIST-JANAF Themochemical Tables is in the range of γ = 1.25–1.4 (Chase 1998). Therefore, a realistic adiabatic index of a gas mixture of H2, He, and SiO is likely γ < 1.4, which is the value used in this paper. We compared the envelope profile calculated using a realistic adiabatic index to the case of γ = 1.4 and found no significant difference. This is because the latent heat term dominates the moist adiabatic gradient in Eq. (7). Ormel et al. (2021) compared envelopes with nonideal, tabulated EOS values to the case of ideal EOS. They found no significant difference between the two models while the planet is still accreting pebbles. However, they found that the nonideal EOS plays an important role for the post disk evolution of the planet.

5.5 Energy transport

We employed the classic approach to assume that, in areas where the envelope is stable against convection, energy is instead transported via radiation. However, the temperatures and pressures in the inner envelope might be high enough for conduction to become an effective way of energy transport (Vazan & Helled 2020; Misener & Schlichting 2022; Misener et al. 2023). We followed Misener et al. (2023) and compared the conductivity λeond to the equivalent term of radiative energy transport 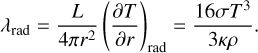λrad=L4πr2 (∂T∂r)rad=16σT33κρ.${\lambda _{{\rm{rad}}}} = {L \over {4\pi {r^2}}}\,{\left( {{{\partial T} \over {\partial r}}} \right)_{{\rm{rad}}}} = {{16\sigma {T^3}} \over {3\kappa \rho }}.$(18)

Conduction becomes important when λeond/λrad > 1, where λeond ≈ 4 W m−1 K−1 (Stevenson et al. 1983). For our parameters, this only happens deep in the envelope, where q > qmax and energy is transported efficiently by convection anyway.

In addition, the diffusion of heat and vapor have different efficiency, which can lead to double-diffusive convection (Stern 1960; Rosenblum et al. 2011). However, Leconte et al. (2017) found that condensation in a saturated medium also stabilizes the medium against double-diffusive convection. Therefore, we can assume that in regions that are stable against convection, energy is transported via radiation.

6 Summary and conclusion

In this paper, we present a vapor equilibrium model for the envelope of an accreting rocky planet close to the water ice line. The model takes the enrichment of the envelope due to the evaporation of SiO from the magma ocean. The key assumption of this model is that the envelope is always in equilibrium with the underlying magma ocean. We then calculated the envelope structure of planets in the mass range Mpl = 0.1 M⊕ to Mpl = 3 M⊕. Compared to pure H2/He envelopes, the temperatures in the inner envelope of planets with Mpl > 0.29 M⊕ are higher if magma ocean evaporation is taken into account. This is due to the buildup of a mean molecular weight gradient, which stabilizes the transition from H2-dominated to SiO-dominated gas against convection. Therefore, an inner radiative region with a steep temperature gradient forms. The region interior of the radiative zone of the planet is dominated in mass by gaseous SiO for Mpl > 0.4 M⊕.

Almost all the SiO vapor is concentrated inside the inner radiative region and therefore protected from recycling flows that penetrate from the protoplanetary disk. As the planet grows, the saturated vapor pressure increases and more SiO vapor evaporates from the magma ocean. For planets with Mpl ≥ 2.0 M⊕, the amount of SiO needed to keep the envelope saturated is larger than the incoming pebble flux. At this point, the accreted pebbles sublimate their SiO directly in the envelope and the luminosity profile of the envelope changes to reach vapor equilibrium at a lowered accretion luminosity.

Overall, we showed that our results are relatively independent of the pebble accretion rate and the detailed treatment of opacity in the envelope. However, envelopes where only gas opacity is considered tend to be slightly colder than envelopes where both dust and gas are considered as opacity sources. Similarly, for the same planet mass, a lower pebble accretion rate leads to lower temperatures in the envelope.

The sublimation of pebbles in the envelope is an important aspect of the formation of planets by pebble accretion. In combination with other envelope processes such as recycling, the sublimation of volatile to moderately volatile elements can shape the composition of the planet (Johansen et al. 2021; Steinmeyer et al. 2023; Wang et al. 2023). At the same time, the enrichment of the envelope in H2O and SiO can also lead to increased gas accretion rates, which facilitates the formation of gas giants (Venturini et al. 2015; Valletta & Helled 2020; Ormel et al. 2021). One of the most important consequences of pebble sublimation, however, is the buildup of a composition gradient in the envelope even at low planet masses. Future work is needed to study the long-term evolution of these envelopes for a wide range of parameters. In this work we focused on the accretion of silicates for planets located at 1 au. A logical next step different is therefore to study the envelope structure of planets at larger orbital distances. At these distance, the accretion of water ice will play an important role. Therefore water vapor should be added to the model in the future.

Additionally, more work is needed to study the dynamics of these envelopes in 2-D or 3-D simulations. It is also important that the effects of SiO saturation are included in population synthesis models to better connect our understanding of planet formation to the observed exoplanet population.

Acknowledgements

We thank the anonymous reviewer for their useful comments. We thank Jérémy Leconte for helpful discussions on the topic of convective processes. A.J. acknowledges funding from the European Research Foundation (ERC Consolidator Grant 724687-PLANETESYS), the Knut and Alice Wallenberg Foundation (Wallenberg Scholar Grant 2019.0442), the Swedish Research Council (Project Grant 2018-04867), the Danish National Research Foundation (DNRF Chair Grant DNRF159), the Göran Gustafsson Foundation and the Carlsberg Foundation (Semper Ardens: Advance grant FIRSTATMO). This paper makes use of the following Python3 packages: numpy (Harris et al. 2020) and matplotlib (Hunter 2007).

References

  1. Ali-Dib, M., & Thompson, C. 2020, ApJ, 900, 96 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alibert, Y. 2017, A & A, 606, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Batygin, K., & Morbidelli, A. 2023, Nat. Astron., 7, 330 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bodenheimer, P., Stevenson, D. J., Lissauer, J. J., & D'Angelo, G. 2018, ApJ, 868, 138 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brouwers, M., & Ormel, C. 2020, A & A, 634, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Brouwers, M. G., Vazan, A., & Ormel, C. W. 2018, A & A, 611, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bryson, S., Kunimoto, M., Kopparapu, R. K., et al. 2021, AJ, 161, 36 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chase, M. W. 1998, NIST-JANAF Thermochemical Tables, 4th edn. (Washington, DC: American Chemical Society; New York: American Institute of Physics for the National Institute of Standards and Technology) [Google Scholar]
  10. Connolly, J. A. D. 2016, J. Geophys. Res. Planets, 121, 1641 [NASA ADS] [CrossRef] [Google Scholar]
  11. Debras, F., & Chabrier, G. 2019, ApJ, 872, 100 [Google Scholar]
  12. Dressing, C. D., & Charbonneau, D. 2013, ApJ, 767, 95 [Google Scholar]
  13. Fegley, B. Jr, & Schaefer, L. 2012, ArXiv e-prints [arXiv: 1210.0270] [Google Scholar]
  14. Freedman, R. S., Lustig-Yaeger, J., Fortney, J. J., et al. 2014, ApJS, 214, 25 [CrossRef] [Google Scholar]
  15. Gail, H. P. 1998, A & A, 332, 1099 [NASA ADS] [Google Scholar]
  16. Guillot, T. 1995, Science, 269, 1697 [CrossRef] [Google Scholar]
  17. Gurrutxaga, N., Johansen, A., Lambrechts, M., & Appelgren, J. 2024, A & A, 682, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]
  19. Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
  20. Helled, R., Anderson, J. D., Podolak, M., & Schubert, G. 2011, ApJ, 726, 15 [Google Scholar]
  21. Herbort, O., Woitke, P., Helling, C., & Zerkle, A. 2020, A & A, 636, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hughes, D. 2006, J. Br. Astron. Assoc., 116, 21 [NASA ADS] [Google Scholar]
  23. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  24. Ikoma, M., & Hori, Y. 2012, ApJ, 753, 66 [NASA ADS] [CrossRef] [Google Scholar]
  25. Iosilevskiy, I., Gryaznov, V., & Solovev, A. 2014, High Temp. High Press., 43, 227 [Google Scholar]
  26. Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
  27. Johansen, A., & Nordlund, Å. 2020, ApJ, 903, 102 [NASA ADS] [CrossRef] [Google Scholar]
  28. Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 1500109 [CrossRef] [Google Scholar]
  29. Johansen, A., Ronnet, T., Bizzarro, M., et al. 2021, Sci. Adv., 7, eabc0444 [NASA ADS] [CrossRef] [Google Scholar]
  30. Johansen, A., Ronnet, T., Schiller, M., Deng, Z., & Bizzarro, M. 2023, A & A, 671, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Heidelberg: Springer Berlin) [Google Scholar]
  32. Kraus, R. G., Stewart, S. T., Swift, D. C., et al. 2012, J. Geophys. Res. Planets, 117, E09009 [Google Scholar]
  33. Kurokawa, H., & Tanigawa, T. 2018, MNRAS, 479, 635 [Google Scholar]
  34. Lambrechts, M., & Johansen, A. 2012, A & A, 544, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Lambrechts, M., & Lega, E. 2017, A & A, 606, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A & A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A & A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Leconte, J., Selsis, F., Hersant, F., & Guillot, T. 2017, A & A, 598, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lee, E. J., Chiang, E., & Ormel, C. W. 2014, ApJ, 797, 95 [Google Scholar]
  41. Levison, H. F., Kretke, K. A., Walsh, K. J., & Bottke, W. F. 2015, PNAS, 112, 14180 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
  43. Markham, S., Guillot, T., & Stevenson, D. 2022, A & A, 665, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Marley, M. S., Gómez, P., & Podolak, M. 1995, J. Geophys. Res., 100, 23349 [NASA ADS] [CrossRef] [Google Scholar]
  45. Melosh, H. J. 2007, Meteor. Planet. Sci., 42, 2079 [NASA ADS] [CrossRef] [Google Scholar]
  46. Militzer, B., & Hubbard, W. B. 2024, Icarus, 411, 115955 [NASA ADS] [CrossRef] [Google Scholar]
  47. Misener, W., & Schlichting, H. E. 2022, MNRAS, 514, 6025 [CrossRef] [Google Scholar]
  48. Misener, W., Schlichting, H. E., & Young, E. D. 2023, MNRAS, 524, 981 [NASA ADS] [CrossRef] [Google Scholar]
  49. Morbidelli, A., & Nesvorny, D. 2012, A & A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Olson, P., Sharp, Z., & Garai, S. 2022, Earth Planet. Sci. Lett., 587, 117537 [CrossRef] [Google Scholar]
  51. Ormel, C. W., & Klahr, H. H. 2010, A & A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Ormel, C. W., Vazan, A., & Brouwers, M. G. 2021, A & A, 647, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Podolak, M., Podolak, J. I., & Marley, M. S. 2000, Planet. Space Sci., 48, 143 [NASA ADS] [CrossRef] [Google Scholar]
  54. Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [Google Scholar]
  55. Raymond, S. N., O’Brien, D. P., Morbidelli, A., & Kaib, N. A. 2009, Icarus, 203, 644 [NASA ADS] [CrossRef] [Google Scholar]
  56. Raymond, S. N., Izidoro, A., & Morbidelli, A. 2020, in Planetary Astrobiology, eds. V. S. Meadows, G. N. Arney, B. E. Schmidt, & D. J. Des Marais, 287 [Google Scholar]
  57. Rogers, L. A. 2015, ApJ, 801, 41 [Google Scholar]
  58. Ros, K., Johansen, A., Riipinen, I., & Schlesinger, D. 2019, A & A, 629, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Rosenblum, E., Garaud, P., Traxler, A., & Stellmach, S. 2011, ApJ, 731, 66 [NASA ADS] [CrossRef] [Google Scholar]
  60. Schaefer, L., & Fegley, B. 2009, ApJ, 703, L113 [CrossRef] [Google Scholar]
  61. Schaefer, L., Lodders, K., & Fegley, B. 2012, ApJ, 755, 41 [NASA ADS] [CrossRef] [Google Scholar]
  62. Silburt, A., Gaidos, E., & Wu, Y. 2015, ApJ, 799, 180 [Google Scholar]
  63. Steinmeyer, M.-L., Woitke, P., & Johansen, A. 2023, A & A, 677, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Stern, M. E. 1960, Tellus, 12, 172 [Google Scholar]
  65. Stevenson, D. J., Spohn, T., & Schubert, G. 1983, Icarus, 54, 466 [NASA ADS] [CrossRef] [Google Scholar]
  66. Tachibana, S., Tsuchiyama, A., & Nagahara, H. 2002, Geochim. Cosmochim. Acta, 66, 713 [NASA ADS] [CrossRef] [Google Scholar]
  67. Tsuchiyama, A., Tachibana, S., & Takahashi, T. 1999, Geochim. Cosmochim. Acta, 63, 2451 [NASA ADS] [CrossRef] [Google Scholar]
  68. Valletta, C., & Helled, R. 2020, ApJ, 900, 133 [NASA ADS] [CrossRef] [Google Scholar]
  69. Vazan, A., & Helled, R. 2020, A & A, 633, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Vazan, A., & Ormel, C. W. 2023, A & A, 676, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Venturini, J., & Helled, R. 2020, A & A, 634, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Venturini, J., Alibert, Y., Benz, W., & Ikoma, M. 2015, A & A, 576, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Visscher, C., & Fegley, B. Jr, 2013, ApJ, 767, L12 [NASA ADS] [CrossRef] [Google Scholar]
  74. Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
  75. Wang, Y., Ormel, C. W., Huang, P., & Kuiper, R. 2023, MNRAS, 523, 6186 [NASA ADS] [CrossRef] [Google Scholar]
  76. Wolfgang, A., & Lopez, E. 2015, ApJ, 806, 183 [NASA ADS] [CrossRef] [Google Scholar]
  77. Xiao, B., & Stixrude, L. 2018, PNAS, 115, 5371 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, PNAS, 116, 9723 [Google Scholar]

All Figures

thumbnail Fig. 1

Illustration of the different phases of the planet and envelope during the growth process. In the beginning, the undifferentiated planet is surrounded by a H2/He rich envelope (Phase 1). In Phase 2, the planet has differentiated into a metallic core and a magma ocean. Enough silicates sublimate in the atmosphere to inhibit convection in this phase. In Phase 3, the region close to the surface of the planet is dominated by SiO and becomes convective again. The planet becomes hot enough to form a supercritical magma ocean in Phase 4.
In the text
thumbnail Fig. 2

Envelope profiles of a selected set of planet masses accreting at Ṁp = 10−6 M⊕ yr−1. The distance to the core is given in units of the Hill radius. The color corresponds to the mass of the planet. The top row shows the temperature (left) and pressure (right). Solid lines include the enrichment with SiO while dashed lines correspond to a pure H2/He envelope. The bottom row shows the moist adiabatic gradient including the latent heat from SiO condensation (left) and the mass mixing radio (right). The critical mass ratio is shown by dashed lines. In all four plots, the squares indicate the start of the inner radiative region and the filled circles the end. Planets larger than 0.75 M⊕ possess a supercritical magma ocean. The surface of this ocean is marked by the triangles.
In the text
thumbnail Fig. 3

Key radii as a function of the planet mass. The dashed orange line indicates the location where q > qth for the first time, while the purple dash-dotted line shows the location where q > qmax for the first time. The solid green line indicates the surface of the supercritical magma ocean, and the dotted pink line the radius of the planet without the supercritical magma ocean. For planets with Mpl ≥ 0.75 M⊕, the accretion heating from the incoming pebbles is released at the surface of this supercritical magma ocean. The feature between 2.1 M⊕ and 2.5 M⊕ in Rcrit and Rqmax${R_{{q_{\max }}}}$ is due to slight discontinuities in the solution, caused by the finite numerical grid.
In the text
thumbnail Fig. 4

Comparison of the temperature, pressure, and SiO mass mixing ratio profiles of a planet with Mpl = 0.8 M⊕ for three different treatments of the opacity. The model “g+1xd” corresponds to the nominal case. In model “g+10xd”, the dust contribution is increased by a factor 10. In model “g”, the gas is the only opacity source considered. Due to the larger outer isothermal region in model “g”, the temperature in the envelope is lower than in the other models while the pressure is higher.
In the text
thumbnail Fig. 5

Temperature profiles of a selected set of planet masses and Ṁpeb = 10−7 M⊕ yr−1. Colors and line styles have the same meaning as in Fig. 2. At a given mass, the envelopes are slightly colder than in the nominal case Ṁpeb = 10−6 M⊕ yr−1. As a result, the enriched envelopes start to differ from the pure H2/He envelopes only after Mpl > 0.4 M⊕.
In the text
thumbnail Fig. 6

Total envelope mass in Earth masses as a function of the planet mass. The solid lines show the SiO mass while the dotted lines show the mass of H2/He in the envelope. The SiO mass dominates the total mass budget for planets with Mpl > 0.6 M⊕. The kink shows the start of the supercritical magma ocean after which the amount of SiO and H2/He in the envelope increases only by heating the outer parts of the envelope.
In the text
thumbnail Fig. 7

Cumulative mass distribution of SiO for different planet masses. The distance to the surface of the planet is given in units of the Hill radius of the respective planet. The filled circles mark the end of the inner radiative zone. Most of the SiO vapor mass is concentrated inside the radiative region.
In the text
thumbnail Fig. 8

Ratio of the amount of SiO needed to keep the envelope saturated to the total mass added to the planet as a function of the planet mass. The green line shows the nominal model where the critical point of SiO is considered. The orange line shows the case where the critical point is not taken into account. In the nominal case, ΔMSiO/ΔMpl becomes larger than unity for Mpl > 2.0 M⊕. However, ΔMSiO/ΔMpl never becomes larger than 2 and the envelope is always saturated in SiO. In the model without Tcrit, ΔMSiO/ΔMpl reaches unity already at Mpl = 0.8 M⊕. The key different between the two models, however, is that the amount of SiO needed to keep the envelope saturated in the model without Tc becomes larger than the total mass of the planet for Mpl ≳ 1.0 M⊕. In this case, the envelope is most likely undersaturated. The feature between 2.1 M⊕ and 2.5 M⊕ is likely caused by the inner boundary of the envelope switching between two grid cells.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.