| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202347769 | |
| Published online | 04 March 2024 | |
Faint calcium-rich transient from a double detonation of a 0.6 M⊙ carbon-oxygen white dwarf star
1
Heidelberger Institut für Theoretische Studien (HITS), Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
e-mail: javier.moranfraile@h-its.org
2
Zentrum für Astronomie der Universität Heidelberg, Institut für Theoretische Astrophysik, Philosophenweg 12, 69120 Heidelberg, Germany
3
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
4
Zentrum für Astronomie der Universität Heidelberg, Astronomisches Rechen-Institut, Mönchhofstr. 12-14, 69120 Heidelberg, Germany
Received:
21
August
2023
Accepted:
7
December
2023
We have computed a 3D hydrodynamic simulation of the merger between a massive (0.4 M⊙) helium white dwarf (He WD) and a low-mass (0.6 M⊙) carbon-oxygen white dwarf (CO WD). Despite the low mass of the primary, the merger triggers a thermonuclear explosion as a result of a double detonation, producing a faint transient and leaving no remnant behind. This type of event could also take place during common-envelope mergers whenever the companion is a CO WD and the core of the giant star has a sufficiently large He mass. The spectra show strong Ca lines during the first few weeks after the explosion. The explosion only yields < 0.01 M⊙ of 56Ni, resulting in a low-luminosity Type Ia supernova-like light curve that resembles the Ca-rich transients within this broad class of objects, with a peak magnitude of Mbol ≈ −15.7 mag and a rather slow decline rate of Δm15bol ≈ 1.5 mag. Both its light curve shape and spectral appearance resemble the appearance of Ca-rich transients, suggesting such mergers as a possible progenitor scenario for this class of events.
Key words: hydrodynamics / nuclear reactions / nucleosynthesis / abundances / radiative transfer / supernovae: general / white dwarfs
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Binary white dwarf (WD) systems are the most common type of double compact objects in our Galaxy (Nelemans et al. 2001). Consequently, their mergers are a common occurrence. They can take place because gravitational wave emission, common-envelope (CE) events, three-body interactions, and other processes can shrink the orbit of the binaries down to the point of Roche-lobe overflow (RLOF), giving rise to a variety of astronomical transients depending on the mass and composition of the involved WDs. These mergers have been primarily studied with the goal of finding the progenitors of Type Ia supernovae (SNe Ia, Liu et al. 2023), which are thought to be produced by thermonuclear explosions in carbon-oxygen (CO) WDs. To increase the chance of igniting a thermonuclear explosion and to ensure the production of the ∼0.5 M⊙ of 56Ni required to power the light curve of a normal SN Ia, most of the previous research has focused on mergers involving CO WDs with masses above 0.9 M⊙ (Sim et al. 2010; Shen et al. 2021). The exact mechanism that initiates the explosion is debated, but most of the proposed scenarios involve a so-called double detonation. In this scenario, a helium (He) shell surrounding the CO WD is ignited initially. The detonation of the He shell converges near the core of the CO WD. At the convergence point, the density and temperature rise significantly and a detonation wave is launched that propagates outward, incinerating the CO WD material. But higher-mass CO WDs are less abundant in nature than their lower-mass counterparts, both among single stars (Kepler et al. 2007) and in binaries (Nelemans et al. 2001; Toonen et al. 2012). If low-mass CO WDs were to produce some type of detectable transient, they could potentially be much more frequent than SNe Ia due to their ubiquity. At masses ∼0.6 M⊙, the central density of CO WDs is one order of magnitude below that of their 0.9 M⊙ counterparts, making the conditions for carbon ignition (Seitenzahl et al. 2009) difficult to attain, even under the double-detonation scenario. For these low-mass CO WDs to explode, a new mechanism for their detonation must be found or they must be enveloped in a very massive He shell that generates a more potent compression than in the classic double-detonation scenario, compressing the CO WD core enough to reach the conditions of carbon ignition.
Only material burned at densities over ρ > 107 g cm−3 is able to produce 56Ni (see, e.g., Sim et al. 2010), and therefore any potential explosion of a low-mass CO WD would result in a very low 56Ni yield. As a direct consequence of the low 56Ni yield, these explosions would produce transients much fainter than SNe Ia.
Here we present a 3D magnetohydrodynamic (MHD) simulation of a merger between a 0.4 M⊙ He WD and a 0.6 M⊙ CO WD that leads to an explosion in a double-detonation scenario with no bound remnant. The outcome is a faint transient that shares features with Ca-rich transients (Perets et al. 2010; Waldman et al. 2011; Kasliwal et al. 2012; Taubenberger 2017; Shen et al. 2019). Throughout this paper we use the term “Ca-rich”, but we note that it is debated whether a substantial amount of calcium is required to excite the Ca line in the late spectra (Shen et al. 2019; Jacobson-Galán et al. 2020).
The thermonuclear explosion takes place minutes after the disruption of the He WD, as the disrupted material is accreted by the CO WD.
2. Methods
2.1. Hydrodynamic explosion simulation
The hydrodynamic simulation was carried out with the AREPO code (Springel 2010; Pakmor et al. 2011, 2016; Weinberger et al. 2020), which is a 3D MHD code that uses a second-order finite volume approach on an unstructured moving Voronoi mesh. In our simulation, we employed methods similar to those in Pakmor et al. (2021). We used explicit refinement and de-refinement for cells that are more than a factor of 2 away from the target mass of the cells (mtarget = 5 × 10−7 M⊙), which results in ∼2 × 106AREPO cells. Self-gravity is treated as Newtonian and computed using an oct-tree-based algorithm. We used the Helmholtz equation of state (Timmes & Swesty 2000), including Coulomb corrections. We also included a 55 isotope nuclear reaction network coupled to hydrodynamics (Pakmor et al. 2012a, 2021; Gronow et al. 2021) that includes the following isotopes: n, p, 4He, 11B, 12 − 13C, 13 − 15N, 15 − 17O, 18F, 19 − 22Ne, 22 − 23Na, 23 − 26Mg, 25 − 27Al, 28 − 30Si, 29 − 31P, 31 − 33S, 33 − 35Cl, 36 − 39Ar, 39K, 40Ca, 43Sc, 44Ti, 47V, 48Cr, 51Mn, 52, 56Fe, 55Co, and 56, 58 − 59Ni. We used the JINA reaction rates (Cyburt et al. 2010). Nuclear reactions were computed for all cells with T > 2 × 107 K, but we limited burning at the shock front, as described by Pakmor et al. (2021).
2.2. Setup
Our initial binary system consists of a 0.6 M⊙ WD with an equal-by-mass mixture of carbon and oxygen and an initial radius of 0.0121 R⊙1, and a 0.4 M⊙ WD composed entirely of He with a radius of 0.0156 R⊙. Our simulation setup is similar to that of Pakmor et al. (2021). The stellar models are constructed in hydrostatic equilibrium assuming a uniform temperature of T = 106 K. We mapped the density profiles to a 3D mesh in AREPO and assigned the cells the appropriate internal energy for the given temperature using the Helmholtz equation of state. The stars were first relaxed separately to ensure hydrostatic equilibrium and remove noise introduced by the mapping process. The relaxation procedure was the same for both stars: they were placed in a cubic box of 2 × 1010 cm sides, with a uniform background grid density of ρ = 10−5 g cm−3 and a thermal energy of 1014 erg g−1 (T ∼ 5 × 105 K). The duration of the relaxation was chosen to be ten times the dynamical timescale of each star, namely 20 s for the 0.6 M⊙ CO WD and 37 s for the 0.4 M⊙ He WD. During the first half of the relaxation, we damped the spurious velocities introduced by discretization errors. During the second half of the relaxation, the stars were left to evolve freely without the damping force, and we verified that the density profiles remain unchanged.
After the relaxation, we placed both stars in a box with a size of 7.1 × 1011 cm and a uniform background density of ρ = 10−5 g cm−3. To avoid large tidal forces when putting the WDs together in the box, we chose the initial distance between the WDs to be 9.4 × 109 cm, which is equal to three times the separation at the point of RLOF. We then artificially shrank the orbit on a timescale larger than the dynamical timescales of the WDs so that potential tidal effects can still take place. This orbital shrinking followed the scheme described in Pakmor et al. (2021), and it was stopped at the point of RLOF, when a steady mass transfer sets in. This happens at an orbital separation of 3.14 × 109 cm, with a total angular momentum of L = 3.2 × 1050 g cm2 s−1. From this point on, we let the system evolve freely. We ran the simulation with the nuclear network disabled during the artificial inspiral to reduce the computational cost, as no significant fraction of mass is expected to undergo any nuclear reaction during this stage. We enabled the nuclear network once the artificial orbital shrinking was terminated.
2.3. Prediction of observables
For a precise computation of the optical spectrum emitted by the event, we post-processed the simplified nucleosynthesis of our AREPO run by following the thermodynamic trajectories of 106 tracer particles during the explosion and using them as an input for a 384 isotope nuclear reaction network (Seitenzahl et al. 2010; Pakmor et al. 2012b; Seitenzahl & Townsley 2017) to obtain more accurate nucleosynthetic yields in the ejecta and assuming solar metallicity (Asplund et al. 2009). The explosion was simulated in AREPO until the ejecta reach homologous expansion. At this point, the ejecta structure as determined in the nucleosynthetic postprocessing step was mapped to the 3D Monte Carlo radiative transfer code ARTIS (Sim 2007; Kromer & Sim 2009; Bulla et al. 2015; Shingles et al. 2022) following the methods described by Gronow et al. (2020) to derive synthetic observables. The post-processed yields of the ejecta structure were mapped to a 503 Cartesian grid on which the Monte Carlo radiation transfer is computed. We tracked 108 energy packets as they propagated through the ejecta for 100 logarithmically spaced timesteps between 2 and 60 days after the explosion.
3. Results
3.1. Merger and double detonation
The evolution of the system is visualized in Fig. 1 and in the complementary movies2. Both stars were initialized with a dipolar magnetic field with a value of 10 G at the equator; nevertheless, magnetic fields play a minor role in this simulation. When reaching the point of RLOF, He is transferred from the larger, less massive He WD onto the surface of the CO WD. Being composed of fully degenerate matter, the He WD expands as it loses mass, increasing the mass-transfer rate. This shrinks the orbit in a runaway process that ends when the He WD is tidally disrupted by the CO WD after 550 s. The disrupted stellar material initially forms a spiral arm, efficiently transferring angular momentum outward (Figs. 1d–g). This allows a large fraction of the disrupted gas to spiral inward, closer to the CO WD, where it begins to form a nonhomogeneous He “shell” that completely engulfs the CO WD. This process is complex and we refer the reader to the complementary movies for a better visualization. Due to a tidal interaction, part of the infalling material intersects itself and gets “trapped”, forming an overdense and cold fluid parcel. While the rest of the accreting material circularizes and heats up due to shear and turbulent motions, this overdense structure remains colder with respect to the surrounding gas that forms the He “shell”. As the fluid parcel draws closer to the surface of the CO WD, it gets compressed and increases its density up to 3 × 105 g cm−3.
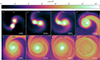 |
Fig. 1. Hydrodynamic evolution of the WD–WD merger. The panels show slices of the orbital plane color coded by density from the beginning of the interaction until the moment that the double detonation takes place. |
When this overdense material reaches the surface of the CO WD, it shears against it (the overdense material is best identified in Fig. 2a as the colder region), heating up and compressing the contact region. The shear dredges up a small fraction of C and O from the primary that is mixed with He in the “shell”. In this shearing layer, the density reaches values of up to 3 × 105 g cm−3 and temperatures of 7 × 108 K.
 |
Fig. 2. Snapshots of immediately before the first detonation (t = 0 s) and immediately after He ignition (t = 0.1 s), and the propagation of the shock produced by this detonation through the CO WD (t = 1.51 s), converging at 2.7 × 108 cm from the center of the CO WD (t = 2.7 s). Top: temperature in K. Bottom: kinetic pressure in erg cm−3. |
A He detonation takes place 381.5 s after the disruption of the He WD. The detonation is shown in Fig. 2. The explosion originates from the region between the cold and overdense He structure and the CO WD (Figs. 2b and f). The shock propagates through the CO WD heating and compressing the material while the detonation wave propagates around the CO WD (Figs. 2c and g) releasing 3 × 1050 erg of nuclear energy (Table 1). The shocked CO does not reach temperatures or densities high enough to trigger burning inside the CO WD as the shock passes through it. The shock wave converges at a distance of 2.7 × 108 cm from the center of the CO WD (Figs. 2d and h) 2.7 s after the first detonation, compressing the material to densities of ρ = 1.2 × 107 g cm3 and temperatures up to T = 4.5 × 109 K, igniting a carbon detonation that propagates outward, incinerating the CO material, and releasing 6.8 × 1050 erg (Table 1). The CO WD is completely disrupted, with the ejecta having a partial axial symmetry due to the interaction with the disrupted stellar material located mainly on the orbital plane.
Final abundances and energy released by the He and CO detonations, and in the entire event.
3.2. Ejecta and radiative transfer
The final yields and explosion energies of the merger are listed in Table 1. Out of the total ejecta mass of about 1 M⊙, a substantial amount (about 33%) is composed of He that remains unburnt. O contributes around 20% to the total ejecta mass, whereas the iron-group elements constitute less than 5%. The remainder consists of intermediate-mass elements, with Ca making up around 2.5% of the final composition. The ∼0.08 M⊙ of He that is ignited burns mainly into 40Ca and 32S, and this burning is the origin of all the 44Ti and 48Cr produced in the simulation. A small fraction of the burnt He produces 12C and around 40% of the total 56Ni yield of the event. After the CO detonation, ∼30% of the initial 12C remains unburned; the rest was burnt to produce 16O, the majority of the produced intermediate-mass elements, and 60% of the total 56Ni yield (Table 1).
What stands out in the ejecta composition as listed in Table 1 is the rather low 56Ni abundance compared with a substantial amount of 40Ca. This composition, combined with the low luminosity implied by the low 56Ni yield, suggests that our model may resemble a Ca-rich transient (see, e.g., Taubenberger 2017). Furthermore, the 56Ni yield also suggests that this event is less luminous than a normal SN Ia.
This is confirmed in our radiative transfer simulations, which predict low-luminosity light curves powered by the radioactive decay of 56Ni (Fig. 3) that resemble the Ca-rich transients within the broader class of SN Ia-like objects. The angle-averaged light curves show a bolometric peak magnitude of Mbol ≈ −15.7 mag and a rather slow decline rate of 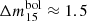 mag. Furthermore, we observe a substantial viewing angle dispersion in peak magnitudes with values ranging from Mbol ≈ −15.4 mag to Mbol ≈ −16.0 mag and decline rates ranging from
mag. Furthermore, we observe a substantial viewing angle dispersion in peak magnitudes with values ranging from Mbol ≈ −15.4 mag to Mbol ≈ −16.0 mag and decline rates ranging from 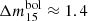 mag to
mag to 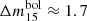 mag. This large scatter can be attributed to the pronounced asymmetry in the ejecta structure as a result of the double-detonation explosion mechanism. A detailed analysis of the viewing angle dependence, however, is beyond the scope of this study and will be discussed in future work.
mag. This large scatter can be attributed to the pronounced asymmetry in the ejecta structure as a result of the double-detonation explosion mechanism. A detailed analysis of the viewing angle dependence, however, is beyond the scope of this study and will be discussed in future work.
 |
Fig. 3. Bolometric and broadband light curves of the merger model. Several Ca-rich transient candidates are plotted as well for comparison: SN 2005E Perets et al. (2010), SN 2007ke, SN 2010et Kasliwal et al. (2012), and SN 2012hn Valenti et al. (2014). All data are taken from the Open Supernova Catalog (Guillochon et al. 2017). |
We compare the resulting broadband and bolometric light curves to several typical Ca-rich transient candidates in Fig. 3, where find a rather good qualitative agreement, particularly in the V- and R-band peak magnitudes and decline rates. However, the spectra obtained from our radiative transfer simulation only somewhat resemble the observed spectra of Ca-rich transients, as is illustrated in Fig. 4. While we reasonably reproduce the calcium feature, we consistently lack the feature visible at around 5900 Å, marked in red in Fig. 4, interpreted as either a He-I or Na-I line.
 |
Fig. 4. Spectral comparison between our merger model and various Ca-rich transient candidates (Perets et al. 2010; Kasliwal et al. 2012; Valenti et al. 2014; Shivvers et al. 2019). The prominent calcium feature (green marking) and the poorly reproduced Na-I/He-I feature (red marking) can be seen. It should be noted that these markings do not indicate the precise location of the respective features, but rather serve as a guide for the eye. All data are from WISeREP (Yaron & Gal-Yam 2012). Left: spectra around peak magnitude. Right: spectra ∼20 days after peak magnitude. |
4. Discussion and conclusions
The cells in the region of He ignition have temperatures of T ∼ 7 × 108 K, densities of ρ ∼ 3 × 105 g cm−3, and typical sizes of ∼90 km. We also find a small fraction of C (about 15%) mixed into the composition of the detonating material, which is known to facilitate He ignition. These conditions are consistent with simulations of resolved He detonations (Shen & Moore 2014) where the ignition points have length scales of hundreds of kilometers. We see the ignition of He in several cells and consider it marginally resolved in our simulation. This is not the case for the triggering of the CO detonation, which takes place on centimeter scales (Seitenzahl et al. 2009), that is to say, far below the typical resolution of ∼15 km in the CO detonation ignition region in our simulation. Still, at the point of shock convergence, we measure densities of ρ = 1.2 × 107 g cm3 and temperatures of up to T = 4.5 × 109 K, which are consistent with those found in simulations of resolved CO detonations (Seitenzahl et al. 2009). Therefore, we argue that the detonations we observe in our simulation are physically plausible. One caveat is the simplistic initial composition used for the explosion simulation. More realistic WD models should include 22Ne in the CO material and 14N in the He to represent the metallicity of the original star. It has been shown that these pollutants facilitate He ignition (Shen & Moore 2014) and alter the composition of the burning products.
The mass distribution of CO WDs is skewed toward lower masses, and, due to their low central densities, low-mass WDs were previously believed to be very unlikely to produce a thermonuclear explosion. We find that the double-detonation mechanism resulting from mergers with massive He WDs can lead to an explosion of such low-mass CO WDs. The He WD companions in the merger result from the cores of red giant (RG) stars whose envelope is removed during the binary interaction. Stars born with masses of up to ∼2.3 M⊙ (Kippenhahn et al. 2012) form cores consisting of up to 0.48 M⊙ of degenerate He. However, we expect the mechanism to work only in a very restricted parameter range. The formation and survival of a cold, overdense structure (part of it originating from the core of the He WD) during the circularization of the accreting material seems to be key in the He ignition mechanism. The survival of this overdense region is expected to depend sensitively on the masses of the components: increasing the CO WD mass leads to higher central densities, which favors the CO ignition, but the increased tidal forces imply that the disruption of the He WD will take place farther away from the CO WD and that the disrupted material will be more thoroughly homogenized by the time it is accreted, and therefore He ignition may be avoided in the first place. Decreasing the mass of the CO will lower the densities even further and, although the survival chances of the overdense He region could increase, the conditions for the CO detonation will be more difficult to meet. Even if the core is able to detonate, less material will be burned and less 56Ni will be produced, making the event even fainter. Furthermore, as a lower-mass CO WD is less compact, the accreted He at its surface is more unlikely to trigger a detonation.
In our setup, the He WD had a mass of 0.4 M⊙. In principle, a more massive He shell will increase the chances of triggering both the He and the CO detonations, but as the core of a RG star, its mass cannot exceed 0.48 M⊙ (Kippenhahn et al. 2012). In contrast, if the mass of the He WD is reduced, its compactness and central density are also reduced; therefore, tidal disruption will take place at greater distances and the material will have lower densities, diminishing its chances of forming the overdense structure required for He ignition.
The conditions for He ignition seem rather restrictive in the mass ranges of both WDs. Therefore, we do not expect all similar systems to undergo thermonuclear explosions, and our scenario leaves room for the formation of R CrB stars from WD mergers.
If the conditions for triggering a detonation are met, the large amount of He mass accumulated on top of the CO WD helps quickly spread the He detonation around the CO WD. Therefore, the convergence of the shockwave is more symmetric than in other scenarios (Fink et al. 2010), and therefore the convergence happens closer to the center of the CO WD. This is important because the density and temperature of this low-mass object are low, and a more central convergence helps ignite the second detonation.
The progenitor of our considered system has to evolve through a CE phase. Whether this CE interaction leads to a successful ejection of the RG envelope is a topic of ongoing research. Successful envelope ejection has been observed in CE simulations of systems such as that considered here only under the assumption of local thermalization of recombination energy, which is challenged by the possibility of energy transport due to radiation or convection (see Röpke & De Marco 2023, and references therein). If the envelope is successfully ejected, the resulting binary system will consist of a He WD and a CO WD in a tight orbit. The merger and subsequent explosion would then take place after sufficient orbital shrinkage due to the release of gravitational waves. This gives rise to the scenario we have discussed. However, if the envelope is not successfully ejected, the CE event results in the merger between the core of the RG and the companion WD, sometimes called a “failed CE event” or a “CE merger” (see, e.g., Röpke & De Marco 2023). To test whether our proposed explosion mechanism still triggers an explosion when the secondary star is not a He WD but a RG core, we carried out a second simulation with the same parameters but with the initially uniform temperature of the He WD increased to 2 × 107 K. This structure is somewhat less compact than the cold He WD in our original simulation. With this altered setup, we still observe the same explosion mechanism, which releases roughly the same nuclear energy and produces equivalent nucleosynthetic yields. This scenario is reminiscent of the core-degenerate scenario (Kashi & Soker 2011; Ilkov & Soker 2012) for SNe Ia, where the merger between the core of an asymptotic giant branch star and a CO WD after a failed CE ejection results in a super-Chandrasekhar-mass WD that explodes as a SN Ia inside the CE. Our setup differs from the original core-degenerate scenario because our explosion results from a double detonation of a sub-Chandrasekhar-mass CO WD due to a merger with the core of a RG star. With the chosen typical mass of a CO WD, this results in an event much fainter than a SN Ia.
This simulation shows that it is possible to produce thermonuclear transients in a realistic scenario that synthesize even less 56Ni and substantially more 40Ca than what is usually obtained in simulations of the double-detonation scenario that aim to model SNe Ia (Boos et al. 2021). We reach good agreement with several light curves of observed Ca-rich transients, both in terms of shape and peak magnitude. The spectra produced by our model, however, do not reproduce the feature at around 5900 Å, which is a major discrepancy with the observed spectra.
While Zenati et al. (2023) reproduce this feature rather well, it is entirely missing from our spectra. The authors argue that their simulation does not have enough remaining He to produce strong He features, suggesting that this feature results from sodium. We find, however, that even increasing the sodium content by a factor of 100, the spectral appearance remains virtually unchanged. This suggests that the feature is a He-I line, which ARTIS cannot model in the utilized setup, and the majority of the sodium has been ionized to higher states. It should be pointed out that although Zenati et al. (2023) reproduce this feature, their simulation differs from ours. The key difference is that in their model, the core of the He-CO WD companion is assumed to survive the event. This has significant implications for the ejecta structure and composition, in particular regarding the distribution of He in the ejecta and the subsequent potential imprint of He on the spectra. It remains to be seen if the feature around 5900 Å is indeed a He-I line or rather a Na-I line. A strong He-I feature, for example, would suggest that substantial amounts of He are required in the ejecta, making the disruption of the He-carrying companion the more likely scenario, and vice versa. Our results so far indicate that this is a He-I line, which is simply beyond the capabilities of our utilized ARTIS setup.
In the nebular phase, Ca-rich transients typically show a high ratio of Ca/O. Our model predicts substantial amounts of oxygen in the ejecta resulting from unburnt material and from C-burning at low densities in the outer regions of the WD. Whether this oxygen produces a strong feature in the nebular spectra that leads to a conflict with observed nebular spectra of Ca-rich transients has to be tested in detailed radiative transfer simulations that are beyond the scope of this paper. Ca-rich transients are known to also occur far from the centers of their host galaxies (Shen et al. 2019). Whether the progenitor system for our mergers is also located far from the center of galaxies must be tested with population synthesis studies. Investigating these questions and the nature of the He-I and/or Na-I region is needed before we can fully assign our model as a Ca-rich transient progenitor and will be the focus of future work.
In contrast, if the detonation were to take place inside a CE, the spectra and light curve would change significantly due to the interaction of the ejecta with the envelope material, showing hydrogen features in the spectra and likely resembling an interacting SN. This interaction has to be modeled in the framework of radiation hydrodynamics and will be further discussed in Kozyreva et al. (2024).
The transients resulting from these mergers could be faint but very frequent, depending on the sensitivity of the explosion mechanism to the masses of the components. These explosions could be interesting targets for the Zwicky Transient Facility (Bellm et al. 2019; Graham et al. 2019) or the future Vera Rubin Observatory (Ivezić et al. 2019). Detecting these explosions from both bare core mergers and inside an envelope might also provide information about the CE mechanism.
Available on Zenodo (https://doi.org/10.5281/zenodo.8268166, showing the temperature, magnetic fields, temperature and kinetic pressure).
Acknowledgments
J.M.-F. and A.H. are fellows of the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg (IMPRS-HD) and acknowledge financial support from IMPRS-HD. This work acknowledges support by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 759253 and 945806, the Klaus Tschira Foundation, and the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 37/935-1 FUGG. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC).
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
- Boos, S. J., Townsley, D. M., Shen, K. J., Caldwell, S., & Miles, B. J. 2021, ApJ, 919, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Bulla, M., Sim, S. A., & Kromer, M. 2015, MNRAS, 450, 967 [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, M., Röpke, F. K., Hillebrandt, W., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graham, M. J., Kulkarni, S. R., Bellm, E. C., et al. 2019, PASP, 131, 078001 [Google Scholar]
- Gronow, S., Collins, C., Ohlmann, S. T., et al. 2020, A&A, 635, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gronow, S., Collins, C. E., Sim, S. A., & Röpke, F. K. 2021, A&A, 649, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillochon, J., Parrent, J., Kelley, L. Z., & Margutti, R. 2017, ApJ, 835, 64 [Google Scholar]
- Ilkov, M., & Soker, N. 2012, MNRAS, 419, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
- Jacobson-Galán, W. V., Margutti, R., Kilpatrick, C. D., et al. 2020, ApJ, 898, 166 [CrossRef] [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kasliwal, M. M., Kulkarni, S. R., Gal-Yam, A., et al. 2012, ApJ, 755, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O., Kleinman, S. J., Nitta, A., et al. 2007, MNRAS, 375, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Kozyreva, A., Moran-Fraile, J., Holas, A., et al. 2024, A&A, submitted https://doi.org/10.1051/0004-6361/202348281 [Google Scholar]
- Kromer, M., & Sim, S. A. 2009, MNRAS, 398, 1809 [Google Scholar]
- Liu, Z.-W., Röpke, F. K., & Han, Z. 2023, Res. Astron. Astrophys., 23, 082001 [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pakmor, R., Bauer, A., & Springel, V. 2011, MNRAS, 418, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Edelmann, P., Röpke, F. K., & Hillebrandt, W. 2012a, MNRAS, 424, 2222 [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012b, ApJ, 747, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Springel, V., Bauer, A., et al. 2016, MNRAS, 455, 1134 [Google Scholar]
- Pakmor, R., Zenati, Y., Perets, H. B., & Toonen, S. 2021, MNRAS, 503, 4734 [Google Scholar]
- Perets, H. B., Gal-Yam, A., Mazzali, P. A., et al. 2010, Nature, 465, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., & De Marco, O. 2023, Liv. Rev. Comput. Astrophys., 9, 2 [CrossRef] [Google Scholar]
- Seitenzahl, I. R., & Townsley, D. M. 2017, Handbook of Supernovae (Springer International Publishing AG), 1955 [CrossRef] [Google Scholar]
- Seitenzahl, I. R., Meakin, C. A., Townsley, D. M., Lamb, D. Q., & Truran, J. W. 2009, ApJ, 696, 515 [Google Scholar]
- Seitenzahl, I. R., Röpke, F. K., Fink, M., & Pakmor, R. 2010, MNRAS, 407, 2297 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Moore, K. 2014, ApJ, 797, 46 [Google Scholar]
- Shen, K. J., Quataert, E., & Pakmor, R. 2019, ApJ, 887, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Boos, S. J., Townsley, D. M., & Kasen, D. 2021, ApJ, 922, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Shingles, L. J., Flörs, A., Sim, S. A., et al. 2022, MNRAS, 512, 6150 [NASA ADS] [CrossRef] [Google Scholar]
- Shivvers, I., Filippenko, A. V., Silverman, J. M., et al. 2019, MNRAS, 482, 1545 [Google Scholar]
- Sim, S. A. 2007, MNRAS, 375, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A., Röpke, F. K., Hillebrandt, W., et al. 2010, ApJ, 714, L52 [Google Scholar]
- Springel, V. 2010, MNRAS, 401, 791 [Google Scholar]
- Taubenberger, S. 2017, in Handbook of Supernovae, eds. A. Alsabti, & P. Murdin (Springer), 317 [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., Nelemans, G., & Portegies Zwart, S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, S., Yuan, F., Taubenberger, S., et al. 2014, MNRAS, 437, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Waldman, R., Sauer, D., Livne, E., et al. 2011, ApJ, 738, 21 [Google Scholar]
- Weinberger, R., Springel, V., & Pakmor, R. 2020, ApJS, 248, 32 [Google Scholar]
- Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [Google Scholar]
- Zenati, Y., Perets, H. B., Dessart, L., et al. 2023, ApJ, 944, 22 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Final abundances and energy released by the He and CO detonations, and in the entire event.
All Figures
 |
Fig. 1. Hydrodynamic evolution of the WD–WD merger. The panels show slices of the orbital plane color coded by density from the beginning of the interaction until the moment that the double detonation takes place. |
| In the text | |
 |
Fig. 2. Snapshots of immediately before the first detonation (t = 0 s) and immediately after He ignition (t = 0.1 s), and the propagation of the shock produced by this detonation through the CO WD (t = 1.51 s), converging at 2.7 × 108 cm from the center of the CO WD (t = 2.7 s). Top: temperature in K. Bottom: kinetic pressure in erg cm−3. |
| In the text | |
 |
Fig. 3. Bolometric and broadband light curves of the merger model. Several Ca-rich transient candidates are plotted as well for comparison: SN 2005E Perets et al. (2010), SN 2007ke, SN 2010et Kasliwal et al. (2012), and SN 2012hn Valenti et al. (2014). All data are taken from the Open Supernova Catalog (Guillochon et al. 2017). |
| In the text | |
 |
Fig. 4. Spectral comparison between our merger model and various Ca-rich transient candidates (Perets et al. 2010; Kasliwal et al. 2012; Valenti et al. 2014; Shivvers et al. 2019). The prominent calcium feature (green marking) and the poorly reproduced Na-I/He-I feature (red marking) can be seen. It should be noted that these markings do not indicate the precise location of the respective features, but rather serve as a guide for the eye. All data are from WISeREP (Yaron & Gal-Yam 2012). Left: spectra around peak magnitude. Right: spectra ∼20 days after peak magnitude. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


