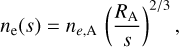| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A179 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202348076 | |
| Published online | 23 February 2024 | |
Fluorescent Fe K line emission of γ Cas stars
I. Do γ Cas stars host propelling neutron stars?
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6 Août, 19c, Bât B5c,
4000
Liège,
Belgium
e-mail: g.rauw@uliege.be
Received:
26
September
2023
Accepted:
15
December
2023
Context. γ Cas stars are early-type Be stars that exhibit an unusually hard and bright thermal X-ray emission. One of the proposed scenarios to explain these properties postulates the existence of a neutron star companion in the propeller stage, during which the magnetosphere of a rapidly rotating neutron star repels infalling material.
Aims. To test this model, we examined the fluorescent Fe Kα emission line at ~6.4keV in the X-ray spectra of γ Cas stars, which offers a powerful diagnostic of both the primary source of hard X-rays and the reprocessing material.
Methods. We computed synthetic line profiles of the fluorescent Fe Kα emission line in the framework of the propelling neutron star scenario. Two reservoirs of material contribute to the fluorescence in this case: the Be circumstellar decretion disk and a shell of cool material that surrounds the shell of X-ray-emitting plasma around the putative propelling neutron star.
Results. We analysed the synthetic line profiles and expected equivalent widths of the lines for three well-studied γ Cas stars. The predicted line strengths fall short of the observed values by at least an order of magnitude. Pushing the model parameters to reproduce the observed line strengths led to column densities towards the primary X-ray source that exceed the observationally determined values by typically a factor of 20, and would further imply a higher X-ray luminosity than observed.
Conclusions. The strengths of the observed Fe Kα fluorescent emission lines in γ Cas stars are inconsistent with the expected properties of a propeller scenario as proposed in the literature.
Key words: line: formation / binaries: close / stars: emission-line / Be – X-rays: stars
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The unusually hard and bright X-ray emission of the B0.5 IVe star γ Cassiopeiae has been a puzzle ever since its discovery (see Smith et al. 2016 for a review and Rauw et al. 2022 for a recent observational study). Over the last two decades, a number of similar objects have been identified (e.g. Lopes de Oliveira et al. 2006; Nazé & Motch 2018; Nazé et al. 2020, 2022b; Nazé & Robrade 2023), and γ Cas is now the prototype of a steadily growing class of over 30 (currently) known objects (Nazé & Robrade 2023). All of them are early Be or late Oe stars. They display log LX values (in the 0.5–10 keV band) ranging from ~31.6 to 33.2, log(LX/Lbol) between ~−6.2 and −4, and their X-ray emission is due to a thermal plasma with a temperature kT ≥ 5 keV.
Several scenarios have been formulated to explain this X-ray emission. Historically, the first explanation that was proposed was accretion onto a neutron star (NS) companion (White et al. 1982). However, the absence of pulsations and X-ray bursts as well as the thermal nature and luminosity of the X-ray emission are arguments against this scenario. Postnov et al. (2017) nevertheless revived the idea of a NS companion. They suggested that the properties of γ Cas could be explained provided the companion were a rapidly spinning magnetic NS. This object would then be in the propeller regime, where the rapid rotation of the magnetosphere prohibits accretion. Accretion onto a white dwarf companion was proposed by several authors as an alternative to the NS scenario (e.g. Murakami et al. 1986; Tsujimoto et al. 2023; Gies et al. 2023, and references therein). To power the observed level of X-ray emission, this white dwarf scenario would require a rather large mass-transfer rate from the Be star. In view of these difficulties and to account for the observed correlation between X-ray and UV variability, Smith et al. (1998) and Smith & Robinson (1999) elaborated another scenario in which small-scale magnetic fields at the Be star surface interact with a magnetic field generated in the Be disk. Finally, Langer et al. (2020) proposed that the hard X-ray emission might come from the collision between the wind of a stripped helium subdwarf (sdO) companion and the circumstellar disk of the Be star. In addition to a number of conceptual problems, this scenario was refuted by observing the X-ray properties of a sample of established and suspected Be + sdO systems (Nazé et al. 2022b).
Much like other Be stars, γ Cas and a number of its siblings have been found to be binary systems with orbital periods in the range of several weeks to several months (Nazé et al. 2022a, and references therein). The nature of the companions remains uncertain, but the most likely values of the companion masses allow for stripped helium subdwarfs, white dwarfs, or, in some cases, NSs.
To discriminate between the various scenarios, a different road must be followed. In the present work, we focus on the fluorescent Fe Kα emission line near 6.4 keV seen in the X-ray spectra of γ Cas stars (e.g. Giménez-García et al. 2015, and references therein). The strength of these lines offers a diagnostic of the properties of the illuminating hard X-ray source and of the illuminated material. Moreover, in the future, X-ray microcalorimeters on board the X-ray and Imaging Spectroscopy Mission (XRISM, Ishisaki et al. 2022) and Athena (Barret et al. 2023) will provide high spectral resolution over the 6–7 keV energy band. This will then allow the detailed morphologies of the Fe Kα line to be observed, thereby offering an even more powerful diagnostic. As a first application, the present paper concentrates on the Postnov et al. (2017) scenario, in which the hard X-rays are thought to arise from a shell of hot material around a NS in the propeller regime. Section 2 describes the ingredients of our calculations of synthetic fluorescent Fe Kα line profiles in the propelling NS scenario. The results of the model applied to the specific case of γ Cas are presented in Sect. 3, whilst Sect. 4 outlines the cases of two other γ Cas stars. The implications of our results are discussed in Sect. 5.
2 The Fe Kα fluorescent line
The illumination of a cloud of relatively cool gas by a bright source of hard X-rays leads to inner-shell photoionization of the atoms and ions in the cool material. In this process, a photon with an energy above the K-shell ionization edge of the corresponding ion is absorbed, thereby creating a vacancy on the K shell. This vacancy is filled by an electron from the L or M shell decaying to the K shell. The excess energy of this electron is shed either via Auger auto-ionization or by the emission of a fluorescent line photon (e.g. Palmeri et al. 2003). When the de-excitation involves an electron from the L shell or the M shell, the fluorescent photons are named respectively Kα or Kβ. Fluorescent emission of Fe Kα photons is of particular interest, because the corresponding line occurs in a relatively clean spectral domain around 6.4 keV and because Fe ions have relatively high fluorescent yields1 near 0.3 (Kallman et al. 2004). In X-ray astrophysics, the Fe Kα line bears a considerable diagnostic potential for both the properties of the primary source of hard X-rays and the properties of the illuminated gas. Observationally, fluorescent Fe Kα lines have been found in various astrophysical environments, including accretion disks around supermassive black holes in active galactic nuclei (e.g. Tanaka et al. 1995; Brenneman & Reynolds 2006), accretion disks around NSs in low-mass X-ray binaries (e.g. Cackett et al. 2008), accretion flows onto white dwarfs (e.g. Ezuka & Ishida 1999; Xu et al. 2016), flaring or outbursting pre-main-sequence stars (e.g. Skinner et al. 2016; Hamaguchi et al. 2010), and highly active late-type stars (e.g. Drake et al. 2008; Czesla & Schmitt 2010). However, with the clear exception of γ Cas stars (Giménez-García et al. 2015) and possibly some Wolf-Rayet stars (Oskinova et al. 2012), fluorescent Fe Kα emission is not seen in the X-ray spectra of massive stars (e.g. Rauw 2022, for a review on X-ray emission of massive stars).
2.1 Modelling fluorescent emission
In γ Cas stars, several media provide reservoirs of material that can potentially contribute to the fluorescent line emission. These include cool plasma in the vicinity of the primary source of hard X-rays, the Be circumstellar disk and the Be photosphere. If the fluorescence arises from hard X-rays illuminating an optically thin slab of cold material, then the ensuing line emission strength is essentially proportional to the column density of the slab. For re-processor column densities higher than 1024 cm−2, this simple relation breaks down, and absorption and scattering effects become important (Kallman 1995). For a given column density of the fluorescent material, the Fe Kα line luminosity scales mostly with the flux of the illuminating source at the position of the fluorescent material. The equivalent width (EW) of the fluorescent Fe Kα line is mostly set by the solid angle occupied by the fluorescent material as seen from the illuminating hard X-ray source. In the present work, where we focus on the propeller scenario, we can safely neglect the contribution from the Be photosphere as the source of hard X-rays is typically located at a distance of several tens of Be stellar radii (a ~ 35 R* for γ Cas), therefore leading to a very small contribution to the EW.
We provide here an overview of our model calculations for the fluorescent line profile. We started by considering a cell of material at location d from the primary X-ray source and at location r from the centre of the Be star. The cell has a hydrogen particle density nH(r) and its volume is dV. To compute the iron K-shell ionization in the cell, we integrated the hard X-ray photon flux per unit energy f(E, d) attenuated by the optical depth (τ(E, d)) along the path of the incoming ionizing photon times the K-shell ionization cross-section σ(E). The hard X-ray spectrum is represented by an APEC optically thin thermal plasma model (Smith et al. 2001) of solar abundance (Asplund et al. 2009) extended at energies above 100 keV by a bremsstrahlung continuum. τ(E, d) is obtained by multiplying σ(E) by the column density of iron atoms along the line joining the cell to the source of hard X-rays. The K-shell photo-ionization cross-sections are modelled using the parametrizations of Verner & Yakovlev (1995) for the Fe ion under consideration. The Fe Kα emissivity of a cell of material that is exposed to the hard X-ray source (i.e. the primary source as seen from the cell is not occulted by the Be star) is given by
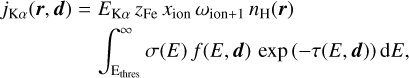 (1)
(1)
where Ethres is the threshold energy for K-shell ionization (Verner & Yakovlev 1995), EKα is the energy of the Kα line (Yamaguchi et al. 2014), zFe is the abundance of iron with respect to hydrogen (Asplund et al. 2009), xion is the relative abundance of a specific Fe ion, and ωion+1 the associated Kα fluorescent yield (Kallman et al. 2004).
The contribution of the cell to the total line luminosity is then evaluated as
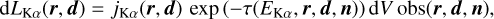 (2)
(2)
where jKα given by Eq. (1) is expressed in units erg s−1 cm−3, and the obs(r, d, n) parameter is equal to 1 or 0 depending on whether or not the cell can be seen by the observer located in the direction n. The quantity τ(EKα, r, d, n) yields the optical depth at the energy of the Kα line from the position (r, d) along the direction n.
To compute synthetic line profiles as they would be seen by an external observer, we distinguished between the individual line profiles and the morphology of the full Fe Kα complex. Indeed, we must keep in mind that what we call the Kα line is actually an unresolved array of transitions that arise from the various combinations of L and K shell electronic configurations (Palmeri et al. 2003). Each of these transitions has its own energy and intrinsic strength. The resulting morphology of the Fe Kα line is thus obtained by convolving the energy distribution of the transitions with the individual line profile weighted by the intrinsic strength of the transitions. For the computation of the individual line profile, we accounted for the Doppler shift of each cell of fluorescent material and built a histogram of the line emission in radial velocity bins of 50 km s−1. Doppler shifts arise for instance from the Keplerian rotation of the material in the cir-cumstellar Be disk. As the illuminating source (in the present scenario associated with the NS) orbits around the Be star, the Doppler shift of those parts of the Be disk that are closest to the source, and thus produce the strongest contribution to the fluorescent line, varies. Therefore, the contribution of the Be disk to the individual line profile is expected to change its morphology as a function of orbital phase.
2.2 Fluorescence from the circumstellar Be disk
The decretion disk of the Be star provides an important reservoir of relatively cool material that can contribute to the formation of the Fe Kα line. In the scenario that we test here, the disk is illuminated by a roughly point-like source associated with the hot shell around the NS’s magnetosphere. To model the fluorescence from the disk, a number of input parameters are needed. These include the properties of the hard X-ray emission, estimates of the mass and radius of the Be star, the density profile of the circumstellar disk, the disk’s inclination to our line of sight, as well as orbital parameters of the binary system.
The X-ray spectrum of γ Cas is described well by a combination of up to four optically thin thermal plasma components, with the hottest plasma providing the dominant contribution. For this hot component, Rauw et al. (2022) determined a mean plasma temperature of kT = 12.5 keV and a mean flux, corrected for absorption by the interstellar medium, of 1.5 × 10−10 erg cm−2 s−1 in the 2.0–10.0 keV energy band. To convert the fluxes into luminosities, we adopted a distance of 190 pc (Nazé & Motch 2018). The fluorescent Fe Kα line observed in the XMM-Newton and Chandra spectra of γ Cas has an EW in the range between 34 and 59 eV (Rauw et al. 2022).
The mass of the B0.5 IVe star is usually estimated between 15 and 17 M⊙ (Stee et al. 1998; Sigut & Jones 2007). We thus adopted a value of 16 M⊙. Estimates of the stellar radius range between 8.2 and 10 R⊙ (Quirrenbach et al. 1997; Stee et al. 1998, 2012; Sigut & Jones 2007; Klement et al. 2017), with a majority of values at 10 R⊙.
There is considerably more dispersion among the literature values of the disk parameters. This could result from either a genuine epoch-dependence of the disk properties or degeneracies of the model parameters. For the disk inclination, the literature values, based either on interferometric observations or fitting of the Hα line profile, range between 42° (Stee et al. 2012) and 59° (Sigut et al. 2020). The majority of the values gather around 45° (Quirrenbach et al. 1997; Stee et al. 1998; Silaj et al. 2010) and we thus adopted this value. With the stellar mass and radius considered here, the Keplerian rotation speed at the inner edge of the disk amounts to vrot(R*) = 550 km s−1, in agreement with the (550 ± 50) km s−1 obtained by Stee et al. (2012) using interferometry. For the hydrogen number density distribution of the decretion disk, we adopted the commonly used power-law relation (e.g. Hummel & Vrancken 2000)
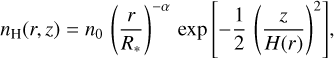 (3)
(3)
where r and z are the radial and vertical coordinates of the axisymmetric disk, n0 is the hydrogen number density at the inner edge of the disk, and H(r) is the disk scale height, which varies with r as
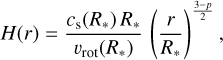 (4)
(4)
with cs(R*) the speed of sound at the inner disk edge and p is the power-law exponent of the radial temperature profile of the disk as introduced by Kurfürst et al. (2014). According to these authors, p should be in the range 0–0.5. Here we adopt p = 0. 25. Assuming solar chemical composition, the density determinations in the literature correspond to n0 in the range 3.6 × 1012 cm−3 and 3.6 × 1014 cm−3 (Stee et al. 1998; Sigut & Jones 2007; Silaj et al. 2010; Grzenia et al. 2013; Klement et al. 2017; Sigut et al. 2020). This rather wide range probably reflects a mix of genuine variability, model degeneracy, and model limitations. Discarding the two most extreme values yields a mean of 2.2 × 1013 cm−3, which we adopted as our default value. For α, one can find values ranging from 1.5 to 3.95 (Silaj et al. 2010; Grzenia et al. 2013; Klement et al. 2017; Sigut et al. 2020). We adopted α = 2.5 as our default value. In low-eccentricity Be binary systems, the circumstellar disk is expected to be truncated by gravitational interaction with the companion at the 3:1 resonance radius (Okazaki & Negueruela 2001). In the case of γ Cas, this resonance radius corresponds to about 176 R⊙ (Rauw et al. 2022), which we adopted as the outer radius of the Keplerian disk.
The binary orbit of γ Cas has a period of 203.523 days and is nearly circular (Nemravová et al. 2012; Smith et al. 2012). The semi-amplitude of the radial velocity curve of the Be star amounts to 4.1 km s−1 and leads to a mass function of 0.00146 M⊙ (Rauw et al. 2022). Adopting a mass of 16 M⊙ for the Be star and an orbital inclination of 45° yields a mass estimate of 1.1 M⊙ for the companion and an orbital separation of a = 375 R⊙ (Rauw et al. 2022). This corresponds to a mass ratio 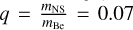 . Using the formalism of Eggleton (1983), we estimated the radii of the Roche lobe of the binary components to be 0.61 a for the Be star and 0.18 a for the NS. Our default model parameters for γ Cas are summarized in Table 1. Throughout this paper, we assume that the companion’s orbital plane coincides with the Be star’s equatorial plane, which itself contains the circumstellar Be disk.
. Using the formalism of Eggleton (1983), we estimated the radii of the Roche lobe of the binary components to be 0.61 a for the Be star and 0.18 a for the NS. Our default model parameters for γ Cas are summarized in Table 1. Throughout this paper, we assume that the companion’s orbital plane coincides with the Be star’s equatorial plane, which itself contains the circumstellar Be disk.
The presence of a hard X-ray source near the disk could in principle alter the ionization of the disk material. This is expressed via the ξ parameter defined as
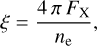 (5)
(5)
where ne is the electron density and FX is the X-ray flux over the 1–1000 Ry energy domain (e.g. Kallman et al. 2004). Figure 1 illustrates the distribution of this ionization parameter over the Be decretion disk. The value of ξ inside the disk is the result of two competing effects. On the one hand, the r−α dependence of ne with distance from the centre of the Be star implies higher ξ values as r increases for a given FX. On the other hand, the dependence of FX on d−2 where d is the distance from the source of hard X-rays (located here at x = 375 R⊙, y = 0), leads to a reduction of ξ as we move away from the NS’s position. The largest values of ξ are thus logically expected in the outer areas of the Be disk facing directly the source of hard X-rays. Our calculations show that the highest values of log ξ is expected to be about −4.0. Given this low value of ξ, the ionization state of the Be disk is not strongly impacted by the presence of the hard X-ray source (Kallman et al. 2004).
The vertical column density of the Be disk, measured from the disk plane where most of the fluorescence takes place, is given by
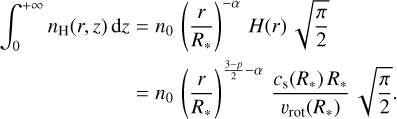 (6)
(6)
Because 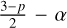 is negative for all values of α that have been proposed for γ Cas, the maximum value of the column density occurs at the inner edge of the disk and amounts to
is negative for all values of α that have been proposed for γ Cas, the maximum value of the column density occurs at the inner edge of the disk and amounts to 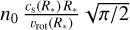 . With the default model parameters of Table 1, this quantity amounts to 6.3 × 1023 cm−2, making the inner disk mildly optically thick. In the present case, most of the fluorescence occurs however in the outer disk regions where the column density is significantly lower and the relevant parts of the disk are thus optically thin.
. With the default model parameters of Table 1, this quantity amounts to 6.3 × 1023 cm−2, making the inner disk mildly optically thick. In the present case, most of the fluorescence occurs however in the outer disk regions where the column density is significantly lower and the relevant parts of the disk are thus optically thin.
Model parameters for three γ Cas binary systems.
 |
Fig. 1 Distribution of the ionization parameter, ξ, over the Be decretion disk for our γ Cas default model (Table 1). The hard X-ray source is located to the right at x = 375 R⊙, y = 0. The labels on the different contours correspond to the value of log ξ (from –4.0 for the blue-violet contour to –6.5 for the red contour). The hatched area lies in the shadow of the Be star and is thus not illuminated by the hard X-ray source. |
2.3 Fluorescence from the cool propeller shell
Postnov et al. (2017) proposed that the γ Cas phenomenon could be explained if the companion of the Be star is a rapidly rotating magnetic NS in the so-called propeller stage. In this situation, direct accretion of material onto the NS is inhibited by the centrifugal barrier of the NS’s rigidly rotating magnetosphere, which at its outer boundary rotates faster than the Keplerian velocity. As a result, the gravitationally captured material from the Be star outflow would accumulate in a shell around the magnetosphere. Postnov et al. (2017) infer a gravitational luminosity of the shell equal to 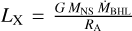 where MNS is the mass of the NS,
where MNS is the mass of the NS, 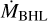 is the rate at which mass is accumulated via the Bondi-Hoyle-Lyttleton mechanism, and RA is the NS’s Alfvén radius. At RA, for which Postnov et al. (2017) propose a value of 104 km, the shell material would reach temperatures of order TA ≃ 100 MK as the infalling material bounces against the rigidly rotating magnetosphere.
is the rate at which mass is accumulated via the Bondi-Hoyle-Lyttleton mechanism, and RA is the NS’s Alfvén radius. At RA, for which Postnov et al. (2017) propose a value of 104 km, the shell material would reach temperatures of order TA ≃ 100 MK as the infalling material bounces against the rigidly rotating magnetosphere.
This shell of gravitationally captured material should extend between RA and the Bondi-Hoyle-Lyttleton radius for capture of material from the Be outflow 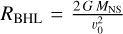 . Here v0 is the relative velocity at which the material from the Be wind or disk outflow encounters the NS. For a NS mass near 1.1 M⊙ and considering v0 ~ 100 km s−1 (Smith et al. 2017), RBHL amounts to about ~2.9 × 107 km or 42 R⊙.
. Here v0 is the relative velocity at which the material from the Be wind or disk outflow encounters the NS. For a NS mass near 1.1 M⊙ and considering v0 ~ 100 km s−1 (Smith et al. 2017), RBHL amounts to about ~2.9 × 107 km or 42 R⊙.
Postnov et al. (2017) consider that the material in the shell behaves as an adiabatic ideal gas. This assumption then leads to a radial profile of the temperature and density that decreases outwards as
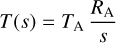 (7)
(7)
where s is the radial distance from the NS.
Postnov et al. (2017) further consider that the gas in the shell moves in turbulent motion at a velocity
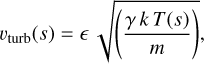 (9)
(9)
with 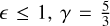 , and m the mean mass of particle. Postnov et al. (2017) adopt vturb = 1000 km s−1 for the hottest gas2. Over the radiative cooling time of ~1000 s, the hot gas would therefore travel out to a distance of order RB ~ 100 RA ~ 106 km. This distance is significantly (29 times) smaller than RBHL. We can thus assume that the hot plasma, which would constitute the primary X-ray source located between RA and RB, should be surrounded by a second shell of cooler gas (T < 1 MK) possibly extending out to RBHL. A schematic view of this situation is provided in Fig. 2. The boundary between these two shells is somewhat arbitrarily set to the radial coordinate s where a temperature of 1 MK is reached according to Eq. (7). In reality, due to the turbulence (see Eq. (9)), several gas temperatures likely coexist over a given range of the radial coordinate s.
, and m the mean mass of particle. Postnov et al. (2017) adopt vturb = 1000 km s−1 for the hottest gas2. Over the radiative cooling time of ~1000 s, the hot gas would therefore travel out to a distance of order RB ~ 100 RA ~ 106 km. This distance is significantly (29 times) smaller than RBHL. We can thus assume that the hot plasma, which would constitute the primary X-ray source located between RA and RB, should be surrounded by a second shell of cooler gas (T < 1 MK) possibly extending out to RBHL. A schematic view of this situation is provided in Fig. 2. The boundary between these two shells is somewhat arbitrarily set to the radial coordinate s where a temperature of 1 MK is reached according to Eq. (7). In reality, due to the turbulence (see Eq. (9)), several gas temperatures likely coexist over a given range of the radial coordinate s.
Adopting the value nHA = 1013 cm−3 advocated by Postnov et al. (2017), the ionization parameter ξ (Eq. (1)) amounts to 0.22 at the inner boundary of the cool shell (RB). This parameter decreases outwards as s−4/3, reaching 0.0024 at RBHL. According to Fig. 5 of Kallman et al. (2004), photoionization of iron would then result in Fe VI and Fe VII being the dominant ionization stages near the inner boundary of the cool shell. Farther out in the cool shell, photoionization would have a significantly lower impact, leaving Fe IV and Fe V as the dominant ionization stages. If we instead adopted nH,A = 5 × 1014 cm−3 (see Sect. 3.2), then log ξ would be reduced by –1.70 and photoionization plays no significant role in setting the ionization stage of iron. Whilst we assume here for simplicity that the fluorescent emission involves ions of a single ionization stage, this assumption has no impact on our main conclusions regarding the overall strength of the fluorescent line.
We thus considered the contribution of this putative cool shell to the fluorescent emission. For this purpose, we discretized the cool shell into 100 sub-shells of linearly increasing radius. Each of these sub-shells is discretized according to polar angle (in steps of 1°) as measured from the direction of the line of sight towards the observer. Whilst the properties of the cool shell solely depend on the radial coordinate s and are independent of polar angle, the column density along the pathway from each sub-shell element to the observer does depend on polar angle. This column density is integrated numerically to compute the optical depth τ at the energy of the Fe Kα photons. The total fluorescent line emission results from the sum of the emission of each sub-shell element attenuated by the associated exp(−τ).
We can estimate the column density towards the primary X-ray source that this shell of cool material would produce
![$\eqalign{ & {N_{\rm{H}}} = \int_{{R_{\rm{B}}}}^{{R_{{\rm{BHL}}.}}} {{n_{\rm{H}}}} {\rm{d}}s = \int_{{R_{\rm{B}}}}^{{R_{{\rm{BHL}}}}} {{n_{{\rm{H}},{\rm{A}}}}} {\left( {{{{R_{\rm{A}}}} \over s}} \right)^{3/2}}{\rm{d}}s \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{n_{{\rm{H}},{\rm{A}}}}{R_{\rm{A}}}{\left( {{{{R_{\rm{A}}}} \over {{R_{\rm{B}}}}}} \right)^{1/2}}\left[ {1 - \sqrt {{{{R_{\rm{B}}}} \over {{R_{{\rm{BHL}}}}}}} } \right]. \cr} $](/articles/aa/full_html/2024/02/aa48076-23/aa48076-23-eq17.png) (10)
(10)
With nH,A ≃ 1013 cm−3 and RA = 104 km (Postnov et al. 2017), we obtain a column density of around 1.6 × 1021 cm−2. This value is comparable to the column densities found empirically in the spectral fitting of the X-ray spectra of γ Cas, although the obser-vationally determined column density varies strongly from one epoch to the other (Rauw et al. 2022). The existence of a shell of cool material around the primary X-ray source is thus not inconsistent with the observations.
As indicated in Eq. (9), the motion of the gas in the Bondi-Hoyle-Lyttleton volume is assumed to be dominated by turbulence with a turbulent velocity that is a fraction of the local speed of sound. As the temperature decreases outwards, the turbulent velocity should thus decrease from about 100 km s−1 at RB to about 20 km s−1 at RBHL. Hence, we expect the contribution of the cool shell to the Fe Kα line profile to have a relatively narrow shape, consisting of the combination of Gaussian line profiles of decreasing widths as we consider the contribution of layers of larger radii. The centre of this profile is expected to be shifted in velocity by the NS’s orbital motion. From the most recent orbital solution of γ Cas, we can estimate an amplitude of the orbital motion of the companion of KNS ≃ 60 km s−1. In our model, we thus assume that the line flux from a layer of radius s in the cool shell is distributed in a Gaussian profile of variance 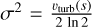 and centred at KNS sin (2 π ϕ). Here ϕ is the orbital phase with φ = 0 at the inferior conjunction of the NS star3. The contribution of the entire cool shell to the individual line profile is then obtained by combining the contributions from each sub-shell of radius s between RB and RBHL.
and centred at KNS sin (2 π ϕ). Here ϕ is the orbital phase with φ = 0 at the inferior conjunction of the NS star3. The contribution of the entire cool shell to the individual line profile is then obtained by combining the contributions from each sub-shell of radius s between RB and RBHL.
 |
Fig. 2 Schematic illustration of the shells of hot and cool material in the propeller NS scenario. The different radii (RA, RB and RBHL) are not to scale. The curved trajectories illustrate the motion of heated particles as they drift outwards over the cooling time. |
3 Results
3.1 Fe Kα emission from the Be disk
We discretized the Be disk into 18 000 cells, each of them spanning 2° in azimuthal angle, and extending over a radial distance dr = (Rout – R*)/100. Our code computes the contribution of each cell according to Eq. (1), accounting for the cell’s visibility and illumination by the primary X-ray source. We ran our code assuming seed Fe ions of Fe I, Fe II, Fe III, or Fe IV. The resulting line luminosities and EWs are very similar for each of these ions. In the following we focus on the line profiles and line characteristics obtained assuming Fe IV seed ions. With our default parameters, we obtain a total line luminosity4 of 9.1 × 1028 erg s−1 and an EW of 1.35 eV. The individual line profiles for three different orbital phases are shown in Fig. 3. As expected, the line emission from the Be disk displays phase-dependent shifts of the line centroid (by about 200 km s−1 peak-to-peak) as well as phase-dependent changes of the full width at half maximum (FWHM). The most important conclusion though is the fact that, with our default parameters, the predicted line EW is much lower than the observed range of EWs (from 34 to 59 eV, Rauw et al. 2022). Whilst we focus mostly on the comparison between the observed and synthetic EWs, exactly the same conclusions are reached by comparing observed and synthetic line fluxes. Indeed, in our calculations the continuum radiation against which the EW is computed is evaluated from the model that best fits the observed spectra, thus making both quantities, line flux and EW, equivalent.
Given our above discussion about the uncertainties affecting the density profile of the Be disk, we can ask ourselves what would be the impact of a different assumption on n0 and α. The highest value of n0 (3.6 × 1014 cm−3) was proposed by Grzenia et al. (2013), along with a value of α = 3.95 (i.e. the steepest density profile proposed for the disk of γ Cas). We thus tested this combination of parameters in our model, keeping all other parameters identical. This results in an EW of 0.83 eV, lower than what we have found with our default parameters. The reason is the high value of α, which leads to low densities in the outer disk regions, which are closest to the hard X-ray source. Hence, instead of looking for higher values of n0, we tried a flatter power law. We thus adopted the density distribution proposed by Silaj et al. (2010) who derived α = 1.5 and n0 = 4.5 × 1013 cm−3. These parameters lead to an EW of 5.90eV, about 4.5 times higher than the value for our default model. The corresponding line profiles are shown in the right panel of Fig. 3. Yet, this value of the EW is still well below the observed values. As a last step, we thus assumed that, instead of being truncated at the 3:1 resonance radius, the disk extended out to the radius of the Be star’s Roche lobe, namely Rout = 229R⊙. For our default density profile, this assumption leads to EW = 2.18 eV, while we obtain 13.6eV when adopting the most extreme density profile (Silaj et al. 2010). The 13.6 eV value likely represents an upper limit to the contribution that we can expect from the Be disk in the case of γ Cas and assuming the NS propeller scenario.
Whilst Postnov et al. (2017) attributed the observed Fe Kα line to fluorescence from the Be disk, our results show that the EWs of the line contributed by the Be disk would be significantly smaller than the observed values. Therefore, we conclude that, additional contributions to the line are needed if the properties of γ Cas are to be explained by a propeller NS scenario.
 |
Fig. 3 Predicted normalized individual Fe Kα line profiles for the Be disk. The line profiles are binned into velocity bins of 50 km s−1 and are normalized by dividing by the total flux over the entire line profile. The blue, black and red profiles correspond to orbital phases 0.75, 0.00 and 0.25 where phase 0.0 corresponds to the inferior conjunction of the NS. The left and right panels respectively illustrate the profiles obtained with our default set of parameters (Table 1) and with the disk density distribution of Silaj et al. (2010). |
3.2 Fe Kα emission from the cool propeller shell
As a next step, we considered the contribution to the Fe Kα line from the cool shell around the NS’s magnetosphere. If we use the parameter nH,A = 1013 cm−3 advocated by Postnov et al. (2017), we obtain an EW of the shell contribution of 0.77 eV. Together with the disk contribution for the default parameters this yields a total EW of 2.12 eV. This is again much lower than the observed line strength. If we rather set nH,A = 5.0 × 1014 cm−3, the shell contributes 33.9 eV and the total EW becomes 35.3 eV. The corresponding individual line profiles are illustrated in Figs. 4 and 5, respectively, for nH,A = 1013 cm−3 and nH,A = 5.0 × 1014 cm−3.
As pointed out above, the Fe Kα feature is not a single line, but instead a complex array of transitions. To illustrate this, the total simulated profiles computed for the set of default parameters are displayed for four orbital phases in Fig. 6. For the purpose of this figure, we have adopted an Fe IV ionization stage for the fluorescent material, though we stress that very similar results are obtained for other ionization stages. In this plot, the blue histograms illustrate the synthetic spectrum with energy bins of 1 eV. The black curves illustrate the result of a convolution of this synthetic spectrum with a Gaussian whose FWHM is equal to 6 eV, which roughly mimics the instrumental response of the Resolve X-ray microcalorimeter aboard the XRISM satellite. Whilst the strength of the line simulated here (EW = 2.12 eV) is well below the actually observed value, it is worth stressing that the expected global shifts of the centroids with orbital phase are very similar if we assume higher values of nH,A or a flatter disk density profile. The amplitude of these shifts are well within the reach of future high-resolution and high-sensitivity instruments such as Resolve on XRISM or the X-ray Integral Field Unit (X-IFU) on Athena, which should have energy resolutions of 5–7 eV and ≤4 eV, respectively.
As we have shown before, the hydrogen column density towards the primary X-ray source scales linearly with nH,A (Eq. (10)). As long as the cool shell remains optically thin, the EW of the fluorescent line also scales linearly with nH,A. At high densities, the relation between EW and NH deviates however from a straight line because of the increasing optical depths. These relations are illustrated in Fig. 7. The horizontal axis of this figure indicates NH in logarithmic scale. The vertical axis yields the EW of the full fluorescent Fe Kα line (i.e. including the contribution from the Be disk) in logarithmic scale. The corresponding curve is shown by the red line for the Be disk with the default parameters. The magenta lines delimit the range of observed values of EW(Fe Kα) from 34 to 59 eV. The cyan hatched area corresponds to the values of NH towards the hot component as determined observationally (Rauw et al. 2022). These values range between 0.035 × 1022cm−2 and 1.38 × 1022 cm−2. Figure 7 shows that the EW model curve does not cross the intersection between the cyan and magenta areas. Reproducing the observed EW range requires nH,A of 4.7 × 1014 cm−3−1015 cm−3, whilst the highest observed absorbing column density restricts nH,A to values below 8 × 1013cm−3. The highest value of the observed column density (1.38 × 1022 cm−2) was measured in an XMM-Newton observation in January 2021 when the X-ray spectrum of γ Cas was extremely absorbed (Rauw et al. 2022). The second highest value (1.16 × 1022 cm−2) was observed in January 2022. However, those high values are thought to be due to transient clouds crossing our line of sight. Most of the time, the column density is at least a factor of 3 lower than in January 2021 (Rauw et al. 2022), which pushes the upper limit on nH,A towards even lower values of about 2.5 × 1013 cm−3. Therefore, in the propeller scenario with the default model parameters we obtain a mismatch by typically a factor of 20 between the values of nH,A required to explain the EW(Fe Kα) and the values allowed by the observed column density5.
A by-product of the above is that, as long as the reprocessing material remains optically thin, one would expect a linear relation between the column density of cool material towards the primary X-ray source and the EW of the fluorescent Fe Kα line. Such a relation is indeed expected theoretically for a spherically symmetric distribution of the reprocessing material (e.g. Kallman et al. 2004), and was empirically established for a sample of X-ray binaries (Torrejón et al. 2010). Yet, no such correlation was found in multi-epoch X-ray data of γ Cas (Rauw et al. 2022).
At this stage, it is important to point out that increasing the value nH,A to match the strength of the observed fluorescent line would also impact the overall X-ray luminosity of the propelling NS. According to Eq. (6) of Postnov et al. (2017), the X-ray luminosity of the hot shell scales with 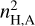 . Therefore, increasing nH,A by a factor of ~20 would not only lead to a mismatch with the observed column density, but would also imply a theoretical X-ray luminosity that exceeds the observed one by a large factor.
. Therefore, increasing nH,A by a factor of ~20 would not only lead to a mismatch with the observed column density, but would also imply a theoretical X-ray luminosity that exceeds the observed one by a large factor.
We tested whether extending the outer radius of the cool shell to the NS’s Roche lobe radius would make a significant change. The answer is no: compared to the situation where the outer radius was set to RBHL, the EW of the line arising from the cool shell increases only by <10%.
As we have shown in Sect. 3.1, the contribution from the disk would be an order of magnitude higher if we adopt a flatter disk density profile (Silaj et al. 2010) and assume the disk to extend out to the Be star’s Roche lobe radius. The dashed blue line in Fig. 7 illustrates this situation. In this case, a range of nH,A values between 2.7 × 1014 and 7.0 × 1014 cm−3 would allow a match between the total theoretical EW and the range of observed values. Even for this extreme disk model, we still find a mismatch by an order of magnitude between the nH,A densities required to explain the EW(Fe Kα) and the values of nH,A allowed from the observed column density.
 |
Fig. 4 Predicted normalized individual Fe Kα line profiles for the propeller NS scenario with nH,A = 1013 cm−3. The line profiles are binned into velocity bins of 50 km s−1 and are normalized by dividing by the total flux over the entire line profile. The blue, black, and red profiles correspond to orbital phases 0.75, 0.00, and 0.25. The left and right panels respectively display the contribution of the cool shell around the propelling NS and the sum of this contribution and of the emission arising from the Be disk. |
 |
Fig. 6 Illustration of the global line profile (i.e. combining the disk and shell contributions and accounting for the full array of transitions), adopting the default parameters of γ Cas at four different orbital phases. The blue histogram shows the spectrum binned in energy bins of 1 eV, whereas the black line provides the result of the convolution with an instrumental response of 6 eV. The magenta lines indicate the position of the centroids of the Kα1 and Kα2 subgroups at phase ϕ = 0.0. |
 |
Fig. 7 Dependence of the total EW(Fe Kα) from both the cool shell around the propelling NS and the Be disk on the hydrogen column density towards the hot X-ray plasma (evaluated according to Eq. (10)). The red and dashed blue curves illustrate the total EW(Fe Kα) computed respectively for the default model parameters and assuming a Be disk with a Silaj et al. (2010) density profile and extending out to the radius of the Roche lobe. The horizontal magenta lines illustrate the range of the observed EW values. The hatched cyan area illustrates the range of observed hydrogen column densities. |
4 Other γ Cas stars
We now turn to the question whether other γ Cas stars display Fe Kα lines that agree with the predictions of the Postnov et al. (2017) model. For this purpose, we consider the cases of π Aqr and ζ Tau. Though there are other γ Cas stars that are brighter in X-rays (e.g. BZ Cru), we focus here on objects with well-established orbital periods and Be disk density profiles. Indeed, a good knowledge of both properties is crucial for our modelling. Among the known γ Cas stars that are established binary systems, π Aqr has the shortest orbital period (84.1 days; Bjorkman et al. 2002), thus illustrating a situation where the companion is closer to the Be disk, which should lead to an enhanced fluorescence by the disk material. On the other hand, ζ Tau illustrates the case of a shell star, where the system is seen in the plane of the Be disk. The parameters of these stars are discussed in Appendix A and are summarized in Table 1.
4.1 π Aqr
Applying our code to the parameters of the π Aqr system (assuming an amplitude of 8.1 km s−1 for the Be star’s RV curve, Nazé et al. 2019a; Tsujimoto et al. 2023), we obtained once again rather low EWs. The contribution from the Be disk would only amount to 0.32 eV. Assuming nH,A = 1013 cm−3, the cool shell would provide 0.75 eV. The combined EW then amounts to 1.07 eV, which is much smaller than the observed value of 68 ± 8 eV (Tsujimoto et al. 2023), and such a weak line would simply remain undetected with current X-ray observatories.
Adopting the same parameters, the value of the column density due to the cool shell would become 1.6 × 1021 cm−2, which is close to the observed value (2.6 × 1021 cm−2). If the cool propeller shell were to account for most of the observed fluorescent line, and taking optical depth effects into account, the nH,A density would have to be at least 120 times higher than our assumed value. This would then lead to a column density near 1.9 × 1023 cm−2 towards the primary X-ray source. This value is 75 times higher than the observational column density, which de facto rules out the existence of such large values of nH,A.
For the π Aqr system, we note that RBHL ≃ 38 R⊙ is essentially identical to the radius of the NS’s Roche lobe (37.4R⊙), provided that the NS has a mass of 1 M⊙ (which is the case for the 8.1 km s−1 amplitude). If instead, we adopt the larger RV amplitude found by Bjorkman et al. (2002) then the NS mass becomes 2.1 M⊙ and the Bondi-Hoyle-Lyttleton radius (80 R⊙) would exceed the NS’s Roche lobe radius (47.3 R⊙) by a significant factor. Hence, if the larger RV amplitude holds, we would have to stop the integration at the NS’s Roche lobe radius, and the EW contributed by the cool shell would thus only increase by 0.03 eV reaching 0.35 eV.
Likewise, if we allow the Be disk to extend out to the Roche lobe radius of the Be star, but keeping the same density profile as before (n0 = 0.45 × 1013 cm−3, α = 2.5), we obtain an EW of 0.45 eV, which will not resolve our issue. Explaining a significant fraction of the observed fluorescent line strength by the effect of the disk, would typically require an increase in n0 by at least an order of magnitude, as well as a flatter density profile.
We thus conclude that, in the case of π Aqr, we are left with the same dilemma as for γ Cas: with the best estimates of the system characteristics it is simply not possible to explain the strength of the observed Fe Kα line within the framework of the propelling NS scenario.
4.2 ζ Tau
Finally, we consider the ζ Tau system. Using our code with the default parameters yields an EW of the truncated Be disk contribution between 1.14 and 1.20 eV depending on orbital phase. If instead the disk extended out to the Be star’s Roche lobe, then it would contribute between 1.67 and 1.73 eV. The mild phase dependence arises from the near edge-on inclination of the Be disk: depending on the orbital phase the Be star occults some parts of the disk illuminated by the primary X-ray source. Accordingly, the highest and lowest emission strengths would be observed respectively at inferior and superior conjunction of the NS. Likewise, adopting nH,A = 1013 cm−3, the cool shell around the propeller would provide 0.70 eV (or 0.73 eV if the shell extends out to the NS’s Roche lobe). This results in a combined EW of 1.84–1.90 eV if we consider the default parameters, which is again much smaller than the observed strength of ~55 ± 8 eV (Nazé et al., in prep.).
The associated column density towards the primary source due to the cool shell would be equal to 1.6 × 1021 cm−2, which is much smaller than the value determined from the Chandra spectrum (1.55 × 1023 cm−2, Nazé et al. 2022b) or from a recent XMM-Newton observation (1.76 × 1023 cm−2, Nazé et al., in prep.). Due to the orientation of the Be disk with respect to our line of sight, such an extremely high value could, to a large extent, reflect the absorption by the Be disk rather than the sole effect of the shell. In the context of our present study, where we wish to test the scenario of a primary X-source arising from the hot shell of a NS in the propeller stage, the observational column density could be reproduced by an increase in nH,A by a factor of ~100 to nH,A = 1.0 × 1015 cm−3. Such a value of the density at the Alfvén radius would render the cool shell mildly optically thick. Accounting for the optical depth, we estimate an EW of 54.5 eV for the corresponding cool shell contribution. Compared to an optically thin shell, the optical depth of the shell leads to a reduction of the EW by 22%. Whilst a value of nH,A = 1.0 × 1015 cm−3 could thus explain both the observed column density and EW of the Fe Kα line, according to Eq. (6) of Postnov et al. (2017), it would imply a drastic increase in the X-ray luminosity of the hot shell well beyond the observed value.
5 Discussion
X-ray spectra of γ Cas stars display a prominent Fe line complex that includes a clear contribution of a fluorescent line due to low-ionization Fe atoms. Our calculations indicate that the model proposed by Postnov et al. (2017) struggles to account for the observed strengths of these fluorescent Fe Kα lines. With the default parameters of the propeller model, the predicted line strength would be way too low for this line to be detectable in all three of the stars investigated in this study.
A way to overcome the problem would be to invoke geometrical effects that either prevent us from seeing the true level of the intrinsic primary X-ray emission or lead to the true column density of the reprocessing material being much higher than what is estimated from the observed photo-absorption column density. Whilst such a scenario could hold for a single system observed at a specific phase (e.g. similar to a high-mass X-ray binary in eclipse), it seems unlikely for three systems that have been observed at a variety of orbital phases and always yielded a similar global picture.
In our model, we consider reprocessing by material in the Be disk and in a cool shell around the propelling NS. One could speculate that the polar wind of the Be star plays some role in the fluorescent process. Using International Ultraviolet Explorer (IUE) spectra, Prinja (1989) detected a wind signature in the CIV λλ 1548, 1550 doublet of γ Cas. From a fit to the line profile, he inferred a terminal wind velocity of 1500 km s−1 and a value of ![$\log \left[ {\dot Mq\left( {{{\rm{C}}^{3 + }}} \right)} \right] = - 10.46\left( {{\rm{in}}{M_ \odot }{\rm{y}}{{\rm{r}}^{ - 1}}} \right)$](/articles/aa/full_html/2024/02/aa48076-23/aa48076-23-eq20.png) . Assuming the same ionization fraction in Be-star winds as in O-star winds, this value would correspond to a mass-loss rate of 3.8 × 10−8 M⊙ yr−1. Smith & Robinson (1999) and Cranmer et al. (2000) measured a higher terminal velocity of 1800 km s−1 from the blue edge of discrete absorption components in the Si IV λλ 1394, 1403 lines observed in Hubble Space Telescope spectra. Adopting a mass-loss rate of 5 × 10−8 M⊙ yr−1 and a wind velocity of 1500 km s−1, a generous upper limit on the electron density at the position of the NS is ~1.7 × 106 cm−3 (see also Cranmer et al. 2000). This is about 50 times lower than the density of the cool shell at its outer boundary, RBHL, assuming nH,A = 1013 cm−3. Hence, this polar wind is extremely unlikely to play any significant role in the formation of the fluorescent line.
. Assuming the same ionization fraction in Be-star winds as in O-star winds, this value would correspond to a mass-loss rate of 3.8 × 10−8 M⊙ yr−1. Smith & Robinson (1999) and Cranmer et al. (2000) measured a higher terminal velocity of 1800 km s−1 from the blue edge of discrete absorption components in the Si IV λλ 1394, 1403 lines observed in Hubble Space Telescope spectra. Adopting a mass-loss rate of 5 × 10−8 M⊙ yr−1 and a wind velocity of 1500 km s−1, a generous upper limit on the electron density at the position of the NS is ~1.7 × 106 cm−3 (see also Cranmer et al. 2000). This is about 50 times lower than the density of the cool shell at its outer boundary, RBHL, assuming nH,A = 1013 cm−3. Hence, this polar wind is extremely unlikely to play any significant role in the formation of the fluorescent line.
The results of our calculations depend on the atomic parameters that were used. Atomic parameters used in astrophysics are subject to uncertainties, and the quantities used in our calculations are no exception to that rule. Comparing Fe K fluorescent transition probabilities computed with different approximations, Palmeri et al. (2003) concluded that the atomic parameters are likely accurate to 10%. To increase the strength of the synthetic lines up to the level of the observed lines, one would need to increase the fluorescence yields and cross-section by much more than this 10%. Moreover, fluorescence yields are by definition lower than 1, but to match the observed line strengths, one would have to increase them by more than a factor of 3, which would make them exceed this upper limit.
Finally, one could ask whether the usage of solar Fe abundance (Asplund et al. 2009) is appropriate. A higher than solar Fe abundance could indeed alleviate the mismatch between calculations and observations. Yet, we need to keep in mind that fluorescent Fe Kα is not the only Fe line in the X-ray spectrum of γ Cas. The primary X-ray spectrum also displays several Fe XVII lines around 0.7–0.8 keV as well as the Fe XXV triplet near 6.7 keV and the Fe XXVI Ly α lines at 6.97 keV. These features help constrain the Fe abundance in global fits of the X-ray spectrum. Such fits do not provide any evidence of higher than solar abundance, and instead yield a sub-solar Fe abundance (Smith et al. 2004; Lopes de Oliveira et al. 2010; Rauw et al. 2022), which would only increase the discrepancy.
Torrejón et al. (2010) analysed Fe K fluorescent lines in Chandra High Energy Transmission Grating high-resolution spectra of a sample of X-ray binaries, including nine high-mass X-ray binaries (HMXBs) and γ Cas. They established that the wavelengths of the fluorescent Fe Kα lines indicate that they arise from Fe ions up to Fe X. Torrejón et al. (2010) further found that the lines are narrow (FWHM < 5 mÅ), which indicates that the reprocessing material is unlikely to rotate at high velocities (as would be the case for the inner regions of an accretion disk close to an accreting NS). The empirical relation between the EW (Fe Kα) and the column density of the absorbing material suggests a roughly spherical distribution of the reprocessing material. Torrejón et al. (2010) also showed that X-ray binaries display a so-called X-ray Baldwin effect, that is to say, an anti-correlation between the X-ray luminosity and EW(Fe Kα). This result was confirmed by Giménez-García et al. (2015) based on an independent sample of the XMM-Newton European Photon Imaging Camera (EPIC-pn) spectra of HMXBs. This effect was interpreted as a decrease in the volume of reprocessing material due to increasing ionization when the X-ray luminosity increases. In the propeller scenario for γ Cas stars, one could expect a very similar behaviour, as the boundary between the hot and cool shell would move farther out in response to an increase in the X-ray luminosity, thereby decreasing the available volume of reprocessing material. Quite interestingly though, this effect is not observed in γ Cas stars as a group (Giménez-García et al. 2015) nor in γ Cas itself when considering observations from different epochs (Rauw et al. 2022). This suggests that the conditions for fluorescence are fundamentally different in supergiant HMXBs and γ Cas stars.
We thus conclude that the observed strength of Fe Kα in γ Cas stars is at odds with the propeller NS scenario. This is actually not the only problem that this scenario encounters. Smith et al. (2017) previously refuted the propeller scenario on other grounds. Indeed, it does not account for the observed correlations between the UV and X-ray emission of γ Cas because the density assumed by Postnov et al. (2017) at the Alfvén radius is too low compared to the density required to explain the very short decay time of the shots seen in the X-ray light curve. Indeed, the X-ray emission of γ Cas stars varies over many different timescales, from a few seconds to months and years. The most rapid variations take the form of shots on timescales as short as 4s (Smith et al. 1998). Such short decay times require densities of >1014 cm−3, which exceed those assumed by Postnov et al. (2017) for the shell of the propeller NS. Finally, based on evolutionary considerations, Smith et al. (2017) show that the short duration of a propeller phase is unlikely to account for the number of γ Cas stars compared to the population of known Be HMXBs. This argument has been reinforced over the last few years as the number of known γ Cas stars has considerably increased since 2017 (Nazé & Motch 2018; Nazé et al. 2020, 2022b; Nazé & Robrade 2023). Therefore, in view of the various results and considerations in this paper as well as the other problems identified by Smith et al. (2017), we can now answer the question raised in the title of this article: it seems very unlikely that the γ Cas phenomenon traces a population of Be stars orbited by a propelling NS.
Acknowledgements
G.R. thanks Dr. Patrick Palmeri for discussion about the details of the fluorescence mechanism, as well as Jahanvi and Drs. Yaël Nazé, Myron Smith and Christian Motch for numerous discussions about various aspects of γ Cas stars. This research is supported by the BELgian federal Science Policy Office (BELSPO) and the European Space Agency through the PRODEX HERMeS grant.
Appendix A Stellar and disk parameters of π Aqr and ζ Tau
In this appendix we provide an overview of the literature on π Aqr and ζ Tau, which is relevant for the input parameters needed for our model (see Table 1).
Pi Aqr (also known as HD 212571) is classified as a B1 III-IVe star. The γ Cas nature of its X-ray emission was discovered by Nazé et al. (2017). The hot plasma component has a temperature of 11.5 keV (Nazé et al. 2017; Nazé & Motch 2018), and the flux (corrected for interstellar absorption) amounts to 1.07 × 10−11 erg cm−2 s−1 in the 0.5–10 keV energy range. The circumstellar hydrogen column density was found to be 0.26 × 1022 cm−2 (Nazé et al. 2017). The EW of the Fe Kα line is reported at a value of (68 ± 8) eV by Tsujimoto et al. (2023). Bjorkman et al. (2002) observed π Aqr when the disk had cleared away and showed that it is a binary with an essentially circular orbit with a period of 84.1 days. These authors obtained an SB2 orbital solution with a semi-amplitude of 16.7 km s−1 for the Be star, and 101.4 km s−1 for the weak Hα emission line that moved in anti-phase with the absorption line of the B1 star. Their results imply dynamical masses of mBe sin3 i = 12.4 M⊙ and mcomp sin3 i = 2.0 M⊙ (Bjorkman et al. 2002). However, more recent studies, performed when the disk had re-developed, led to a significantly lower semi-amplitude of the Be star’s orbital motion of about 8.1 km s−1 (Nazé et al. 2019a,b; Tsujimoto et al. 2023). This situation implies considerable uncertainties on the masses of the components: the Be star’s dynamical mass mBe sin3 i = 12.4 M⊙ obtained by Bjorkman et al. (2002) was converted into a mass of (14 ± 1) M⊙ by Zharikov et al. (2013), whilst Catanzaro (2013) and Nazé et al. (2019b) respectively estimate 13 and (11 ± 1.5) M⊙. Adopting the lower semi-amplitude of the Be star’s RV curve, the dynamical masses become mBe sin3 i = 10.6 M⊙ and mcomp sin3 i = 0.85 M⊙. We adopt here a mass of the Be star of 12.7 M⊙, which is the mean of the above estimates. Kepler’s third law then implies a semi-major axis of 193 R⊙ for the lower RV semiamplitude and 198 R⊙ for the higher RV semi-amplitude. For the stellar radius, Zharikov et al. (2013) estimated 13.0 R⊙ whilst other literature estimates rather fall in the range 5.9 to 7.7 R⊙ (Catanzaro 2013; Arcos et al. 2018; Nazé et al. 2019b). The larger radius proposed by Zharikov et al. (2013) most likely stems from their higher distance estimate of 740 pc, whilst Hipparcos and Gaia parallaxes rather suggest a distance around 240 pc (Nazé & Motch 2018; Arcos et al. 2018). Here, we adopt a value of 6.5 R⊙ for the stellar radius. This then leads to a Keplerian velocity of 610 km s−1 at the inner edge of the Be disk. Effective temperatures between 23.3 and 27.6kK are quoted in the literature (Bjorkman et al. 2002; Frémat et al. 2005; Touhami et al. 2010; Zharikov et al. 2013; Arcos et al. 2018; Nazé & Motch 2018; Nazé et al. 2019b). We take the mean of 25 kK. Orbital and/or disk inclinations are estimated between 50–75° (Bjorkman et al. 2002), 45° (Silaj et al. 2010), 65–85° (Zharikov et al. 2013), 60° (Arcos et al. 2017), 50–75° (Nazé et al. 2019b), and (56 ± 5)° (Sigut & Ghafourian 2023). The lowest values would lead to an unusually large absolute dynamical mass for the Be star. We thus adopt a value of 70° consistent with the estimated dynamical minimum mass and our above mass estimate for the B1 star. The density at the inner edge of the disk was evaluated to be 10−11 gcm−3 (Silaj et al. 2010), 6 × 10−13 gcm−3 (Catanzaro 2013), 7.5 × 10−12−10−11 gcm−3 (Arcos et al. 2017). This rather wide range reflects at least partially the epoch-dependence of the disk strength which has increased significantly over the last decade (Nazé et al. 2019a; Tsujimoto et al. 2023). The values of Arcos et al. (2017) were obtained at epochs close to the XMM-Newton observation. Hence, we adopt here a value of 10−11 gcm−3 which translates into an hydrogen number density of 4.5 × 1012 cm−3. The disk density power-law exponent α of π Aqr ranges between 2.5 and 3.5 (Silaj et al. 2010; Catanzaro 2013; Arcos et al. 2017). We adopted α = 2.5, the value from Arcos et al. (2017). With q = 0.165 (higher RV amplitude) or q = 0.080 (lower RV amplitude), the Roche lobe radius of the Be star is estimated respectively to 106.3 or 115.0 R⊙. Likewise, for the companion we obtain a Roche lobe radius of 47.3 or 37.4 R⊙. Finally, the 3:1 resonance truncation radius of the Be disk amounts to 91 R⊙.
Zeta Tau (= HD 37202) is a B1 IVe shell star. A first estimate of the characteristics of its X-ray spectrum was derived by Nazé et al. (2022b) from a heavily piled-up Chandra spectrum. A plasma temperature of 11.1 ± 4.3 keV was inferred, along with a flux of 1.66 × 10−11 erg cm−2 s−1 evaluated over the 0.5–10 keV band and corrected for ISM absorption. The cir-cumstellar absorption column was found to be rather high with (15.5 ± 2.0) × 1022 cm−2. A recent, pile-up free, XÍMM-Newton observation yielded a plasma temperature of 9.0 ± 0.3 keV, an ISM-corrected flux of 1.76 × 10−11 erg cm−2 s−1 and a circumstellar column density of (17.6 ± 0.2) × 1022 cm−2 (Nazé et al. in prep.). The mass of the Be star is estimated close to 11.2 M⊙ (Gies et al. 2007; Carciofi et al. 2009; Ruždjak et al. 2009; Touhami et al. 2011). For the mean stellar radius, values of 5.5 R⊙ (Gies et al. 2007; Touhami et al. 2011) or 6.1 R⊙ (Cochetti et al. 2019) are given in the literature. Carciofi et al. (2009) accounted for the rotational flattening and rather proposed 5.9 and 7.7 R⊙, respectively, for the polar and equatorial radii. Since we use the stellar radius as the inner radius of the disk, which is assumed to lie in the equatorial plane, we adopt a radius of 7.7 R⊙. These numbers lead to an orbital velocity of 525 km s−1 at the inner edge of the circumstellar disk. Mean effective temperatures were derived in the range from 19.0 to 20.1 kK (Grundstrom & Gies 2006; Gies et al. 2007; Cochetti et al. 2019). Accounting for gravity darkening, Carciofi et al. (2009) inferred 18.0 and 25.0kK, respectively, at the equator and at the pole. We adopt here a value of 20 kK. The inclination of the Be disk is usually given in the range from 75° to 89° (Grundstrom & Gies 2006; Gies et al. 2007; Carciofi et al. 2009; Touhami et al. 2011) with the exception of Cochetti et al. (2019) who rather quote an inclination of 67°. We adopt a value of 85°, consistent with the shell aspect of the Balmer lines. Estimates of the density at the inner edge of the disk range from 5.9 × 10−11 gcm−3 to 1.9 × 10−10 gcm−3 (Gies et al. 2007; Carciofi et al. 2009; Touhami et al. 2011). The mean value 1.3 × 10−10 g cm−3 translates into a hydrogen number density of 5.8 × 1013 cm−3. The α exponent ranges between 2.9 and 3.5 (Gies et al. 2007; Carciofi et al. 2009; Touhami et al. 2011; Klement et al. 2019) and we adopt a value of 3.0. The p exponent was assumed to be 0 by Carciofi et al. (2009). ζ Tau has an orbital period of 132.987 days and a likely companion mass of 0.87–1.02 M⊙ (Ruždjak et al. 2009), which results in a mass ratio q = 0.086. Kepler’s third law then yields an orbital separation of 252 R⊙, and the Roche lobe radii are estimated to 148.7 R⊙ for the Be star and 49.9 R⊙ for its companion. The 3:1 truncation radius of the Be disk amounts to 118 R⊙. The semi-amplitude of the Be star’s orbital motion is 7.4 km s−1 (Ruždjak et al. 2009; Nazé et al. 2022b). For the distance of ζ Tau, we adopt 136pc (Nazé et al. 2022b).
References
- Arcos, C., Jones, C. E., Sigut, T. A. A., Kanaan, S., & Curé, M. 2017, ApJ, 842, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Arcos, C., Kanaan, S., Chavez, J., et al. 2018, MNRAS, 474, 5287 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Albouys, V., den Herder, J.-W., et al. 2023, Exp. Astron., 55, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Bjorkman, K. S., Miroshnichenko, A. S., McDavid, D., & Pogrosheva, T. M. 2002, ApJ, 573, 812 [Google Scholar]
- Brenneman, L. W., & Reynolds, C. S. 2006, ApJ, 652, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Miller, J. M., Bhattacharyya, S., et al. 2008, ApJ, 674, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Carciofi, A. C., Okazaki, A. T., Le Bouquin, J.-B., et al. 2009, A&A, 504, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catanzaro, G. 2013, A&A, 550, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cochetti, Y. R., Arcos, C., Kanaan, S., et al. 2019, A&A, 621, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cranmer, S. R., Smith, M. A., & Robinson, R. D. 2000, ApJ, 537, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Czesla, S., & Schmitt, J. H. M. M. 2010, A&A, 520, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drake, J. J., Ercolano, B., & Swartz, D. A. 2008, ApJ, 678, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Ezuka, H., & Ishida, M. 1999, ApJS, 120, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A.-M., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gies, D. R., Bagnuolo, W. G.Jr., Baines, E. K., et al. 2007, AJ, 654, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Wang, L., & Klement, R. 2023, ApJ, 942, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez-García, A., Torrejón, J. M., Eikmann, W., et al. 2015, A&A, 576, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grundstrom, E. D., & Gies, D. R. 2006, ApJ, 651, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Grzenia, B. J., Tycner, C., Jones, C. E., et al. 2013, AJ, 145, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Hamaguchi, K., Grosso, N., Kastner, J. H., Weintraub, D. A., & Richmond, M. 2010, ApJ, 714, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, W., & Vrancken, M. 2000, A&A, 395, 1075 [NASA ADS] [Google Scholar]
- Ishisaki, Y., Kelley, R. L., Awaki, H., et al. 2022, Proc. SPIE, 12181, 121811S [NASA ADS] [Google Scholar]
- Kallman, T. R. 1995, ApJ, 455, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kallman, T. R., Palmeri, P., Bautista, M. A., Mendoza, C., & Krolik, J. H. 2004, ApJS, 155, 675 [Google Scholar]
- Klement, R., Carciofi, A. C., Rivinius, T., et al. 2017, A&A, 601, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klement, R., Carciofi, A. C., Rivinius, T., et al. 2019, ApJ, 885, 147 [Google Scholar]
- Kurfürst, P., Feldmeier, A., & Krticka, J. 2014, A&A, 569, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, N., Baade, D., Bodensteiner, J., et al. 2020, A&A, 633, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopes de Oliveira, R., Motch, C., Haberl, F., Negueruela, I., & Janot-Pacheco, E. 2006, A&A, 454, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopes de Oliveira, R., Smith, M. A., & Motch, C. 2010, A&A, 512, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murakami, T., Koyama, K., Inoue, H., & Agrawal, P. C. 1986, ApJ, 310, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Nazé, Y., & Motch, C. 2018, A&A, 619, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y., & Robrade, J. 2023, MNRAS, 525, 4186 [CrossRef] [Google Scholar]
- Nazé, Y., Rauw, G., & Cazorla, C. 2017, A&A, 602, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y., Rauw, G., Guarro Fló, J. 2019a, New Astron., 73, 101279 [CrossRef] [Google Scholar]
- Nazé, Y., Rauw, G., & Smith, M. A. 2019b, A&A, 632, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y., Motch, C., Rauw, G., et al. 2020, MNRAS, 493, 2511 [CrossRef] [Google Scholar]
- Nazé, Y., Rauw, G., Czesla, S., Smith, M., & Robrade, J. 2022a, MNRAS, 510, 2286 [CrossRef] [Google Scholar]
- Nazé, Y., Rauw, G., Smith, M. A., & Motch, C. 2022b, MNRAS, 516, 3366 [CrossRef] [Google Scholar]
- Nemravová, J., Harmanec, P., Koubský, P., et al. 2012, A&A, 537, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okazaki, A. T., & Negueruela, I. 2001, A&A, 377, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Gayley, K. G., Hamann, W.-R., et al. 2012, ApJ, 747, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003, A&A, 410, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postnov, K., Oskinova, L., & Torrejón, J. M. 2017, MNRAS, 465, L119 [Google Scholar]
- Prinja, R. K. 1989, MNRAS, 241, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Bjorkman, K. S., Bjorkman, J. E., et al. 1997, ApJ, 479, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Rauw, G. 2022, in Handbook of X-ray and Gamma-ray Astrophysics, eds. C. Bambi, & A. Santangelo, (Springer Living Reference Work), 108 [Google Scholar]
- Rauw, G., Nazé, Y., Motch, C., et al. 2022, A&A, 664, A184 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruždjak, D., Božic, H., Harmanec, P., et al. 2009, A&A, 506, 1319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sigut, T. A. A., & Ghafourian, N. R. 2023, ApJ, 948, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Sigut, T. A. A., & Jones, C. E. 2007, ApJ, 668, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Sigut, T. A. A., Mahjour, A. K., & Tycner, C. 2020, ApJ, 894, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Silaj, J., Jones, C. E., Tycner, C., Sigut, T. A. A., & Smith, A. D. 2010, ApJS, 187, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A., & Robinson, R. D. 1999, ApJ, 517, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A., Robinson, R. D., & Corbet, R. H. D. 1998, ApJ, 503, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [Google Scholar]
- Smith, M. A., Cohen, D. H., Gu, M. F., et al. 2004, ApJ, 600, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. A., Lopes de Oliveira, R., Motch, C., et al. 2012, A&A, 540, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. A., Lopes de Oliveira, R., & Motch, C. 2016, Adv. Space Res., 58, 782 [Google Scholar]
- Smith, M. A., Lopes de Oliveira, R., & Motch, C. 2017, MNRAS, 469, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Skinner, S., Audard, M., & Güdel, M. 2016, ApJ, 826, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Stee, P. Vakili, F., Bonneau, D., & Mourard, D. 1998, A&A, 332, 268 [NASA ADS] [Google Scholar]
- Stee, P., Delaa, O., Monnier, J.D., et al. 2012, A&A, 545, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Torrejón, J. M., Schulz, N. S., Nowak, M. A., & Kallman, T. R. 2010, ApJ, 715, 947 [CrossRef] [Google Scholar]
- Touhami, Y., Richardson, N. D., Gies, D. R., et al. 2010, PASP, 122, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Touhami, Y., Gies, D. R., & Schaefer, G. H. 2011, ApJ, 729, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, M., Hayashi, T., Morihana, K., & Moritani, Y. 2023, PASJ, 75, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109, 125 [NASA ADS] [Google Scholar]
- White, N. E., Swank, J. H., Holt, S. S., & Parmar, A. N. 1982, ApJ, 263, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X.-J., Wang, Q. D., & Li, X.-D. 2016, ApJ, 818, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Yamaguchi, H., Eriksen, K.A., Badenes, C., et al. 2014, ApJ, 780, 136 [Google Scholar]
- Zharikov, S. V., Miroshnichenko, A. S., Pollmann, E., et al. 2013, A&A, 560, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
The fluorescent yield is the probability that inner-shell photoionization is followed by fluorescent line emission (either Kα or Kβ) rather than Auger auto-ionization (e.g. Palmeri et al. 2003).
Smith et al. (2017) pointed out that this value of vturb is a factor of 2–3 higher than the actual line broadening measured in high-resolution X-ray spectra of γ Cas, suggesting that the value of vturb might have to be reduced to below 1000 km s−1.
Nemravová et al. (2012) defined phase 0.0 as the time of minimum radial velocity of the Be star. Hence, our phases are shifted by 0.25 with respect to theirs: ϕ = ϕNemravova + 0.25.
All Tables
All Figures
 |
Fig. 1 Distribution of the ionization parameter, ξ, over the Be decretion disk for our γ Cas default model (Table 1). The hard X-ray source is located to the right at x = 375 R⊙, y = 0. The labels on the different contours correspond to the value of log ξ (from –4.0 for the blue-violet contour to –6.5 for the red contour). The hatched area lies in the shadow of the Be star and is thus not illuminated by the hard X-ray source. |
| In the text | |
 |
Fig. 2 Schematic illustration of the shells of hot and cool material in the propeller NS scenario. The different radii (RA, RB and RBHL) are not to scale. The curved trajectories illustrate the motion of heated particles as they drift outwards over the cooling time. |
| In the text | |
 |
Fig. 3 Predicted normalized individual Fe Kα line profiles for the Be disk. The line profiles are binned into velocity bins of 50 km s−1 and are normalized by dividing by the total flux over the entire line profile. The blue, black and red profiles correspond to orbital phases 0.75, 0.00 and 0.25 where phase 0.0 corresponds to the inferior conjunction of the NS. The left and right panels respectively illustrate the profiles obtained with our default set of parameters (Table 1) and with the disk density distribution of Silaj et al. (2010). |
| In the text | |
 |
Fig. 4 Predicted normalized individual Fe Kα line profiles for the propeller NS scenario with nH,A = 1013 cm−3. The line profiles are binned into velocity bins of 50 km s−1 and are normalized by dividing by the total flux over the entire line profile. The blue, black, and red profiles correspond to orbital phases 0.75, 0.00, and 0.25. The left and right panels respectively display the contribution of the cool shell around the propelling NS and the sum of this contribution and of the emission arising from the Be disk. |
| In the text | |
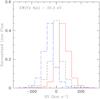 |
Fig. 5 Same as the right panel of Fig. 4, but for nh,a = 5.0 × 1014 cm−3. |
| In the text | |
 |
Fig. 6 Illustration of the global line profile (i.e. combining the disk and shell contributions and accounting for the full array of transitions), adopting the default parameters of γ Cas at four different orbital phases. The blue histogram shows the spectrum binned in energy bins of 1 eV, whereas the black line provides the result of the convolution with an instrumental response of 6 eV. The magenta lines indicate the position of the centroids of the Kα1 and Kα2 subgroups at phase ϕ = 0.0. |
| In the text | |
 |
Fig. 7 Dependence of the total EW(Fe Kα) from both the cool shell around the propelling NS and the Be disk on the hydrogen column density towards the hot X-ray plasma (evaluated according to Eq. (10)). The red and dashed blue curves illustrate the total EW(Fe Kα) computed respectively for the default model parameters and assuming a Be disk with a Silaj et al. (2010) density profile and extending out to the radius of the Roche lobe. The horizontal magenta lines illustrate the range of the observed EW values. The hatched cyan area illustrates the range of observed hydrogen column densities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.