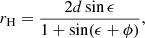EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 682 (February 2024) A&A, 682 (2024) A107 Full HTML
Issue
A&A
Volume 682, February 2024
Solar Orbiter First Results (Nominal Mission Phase)
Article Number A107
Number of page(s) 10
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202347561
Published online 08 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Coronal mass ejections (CMEs) are large-scale transient and energetic expulsion of mass and magnetic flux from the Sun. They have been studied for decades using remote observations and in situ measurements since they were discovered in the early 1970s (Tousey 1973). In white-light coronagraphs, CMEs often appear as a classic three-part structure (bright front, dark cavity, and bright core; see, e.g., Illing & Hundhausen 1985). It has traditionally been supposed that the bright front corresponds to the compressed and pileup material ahead of the eruptive structure, the dark cavity represents the magnetic flux rope (magnetically dominated) structure, and the bright core is related to the filament material. With the SOlar and Heliospheric Observatory (SOHO; Domingo et al. 1995) and the twin Solar Terrestrial Relations Observatory (STEREO; Kaiser et al. 2008) spacecraft, regular monitoring in the white light of CMEs from the low corona to interplanetary space has become available, which extends from 0.15 to ∼1 au with the heliospheric imagers (HIs; Howard et al. 2008) onboard STEREO.

In situ measurements of CMEs (a time series of CME parameters at a single point), provide the local properties of the CME magnetic field and plasma information (see, e.g., Burlaga et al. 1981). CMEs detected in situ typically consist of (a) a magnetic ejecta and (b) a sheath with heated and compressed solar wind plasma ahead of the magnetic ejecta (see the review paper, Kilpua et al. 2017). About 80% of CMEs observed in situ are found to have a sheath region (Salman et al. 2021). Sometimes, the magnetic ejecta region shows magnetic flux rope signatures such as (1) an enhanced magnetic field strength, (2) a smooth rotation of the magnetic field components, and (3) a decrease in the solar wind plasma temperature, and this subset is referred to as a magnetic cloud (Burlaga et al. 1981; Lepping et al. 1990). In this paper, we use the term CME to describe the entire structure consisting of the ejecta and the sheath measured in situ as well as the entire structure imaged remotely. We use the term magnetic ejecta to indicate the CME magnetically dominated structure for both remote and in situ observations.

Remote and in-situ observations have greatly enriched CME studies, among which the radial expansion of CMEs is one of the most outstanding aspects. This radial expansion can be individually studied using (1) extreme-ultraviolet and white-light observations in the corona (e.g., Patsourakos et al. 2010; Balmaceda et al. 2020; Zhuang et al. 2022), (2) heliospheric imagers in interplanetary space (Savani et al. 2009; Möstl et al. 2010; Rouillard 2011; Howard & DeForest 2012), and (3) in situ measurements provided by multiple spacecraft (either for large samples at different distances or for the same CME measured by multiple spacecraft in radial alignment; e.g., Bothmer & Schwenn 1998; Leitner et al. 2007; Gulisano et al. 2010; Winslow et al. 2015, 2021; Lugaz et al. 2020a; Salman et al. 2020; Davies et al. 2021). However, simultaneous remote and in situ observations are rare, especially in the innermost heliosphere where the CME dynamics are relatively strong. Thus, there are few such comprehensive studies on the CME radial expansion (Nieves-Chinchilla et al. 2012; Lugaz et al. 2020b). For example, Nieves-Chinchilla et al. (2012) combined remote images and in situ measurements of multiple spacecraft in radial conjunction from ∼0.4 au to 1 au to investigate the expansion of a CME. For their event, they found that the CME radial sizes estimated in situ at different heliocentric distances are consistent with the estimates obtained based on remote observations. However, consistency of radial expansion during the CME propagation from the corona to interplanetary space is not a common finding.

Based on ∼40 CMEs measured by multiple spacecraft in radial conjunction, Lugaz et al. (2020a) and Davies et al. (2022) found that the CME global expansion estimated by the decrease in the magnetic field strength inside magnetic ejecta with distance does not agree with the local expansion estimated based on the decrease in the magnetic ejecta bulk speed near 1 au. Recently, by combining the remote observations and in situ measurements in radial conjunction of 22 CMEs, Zhuang et al. (2023) further revealed that the CME radial size estimated remotely in the corona is inconsistent with the in situ estimates, especially when the CME propagates farther away from the Sun. They suggested that these inconsistencies may be due to (1) the decrease in the expansion rate during the CME propagation (Lugaz et al. 2020a) and/or (2) the uncertainties in identifying the CME boundaries in both remote and in situ observations (Richardson & Cane 2010; Kilpua et al. 2013). The lack of solar wind plasma measurements for the planetary missions in the innermost heliosphere used in these studies is one key factor for the difficult boundary identification.

Moreover, past studies, focusing on comparing the CME signatures and substructures between remote and in situ observations, had to rely on the spacecraft near 1 au (e.g., Davies et al. 2009; Möstl et al. 2010; Rouillard 2011; Howard & DeForest 2012), where the CME radial expansion may differ significantly from that closer to the Sun. For example, Rouillard (2011) found that two bright ridges associated with a CME observed by STEREO heliospheric imager 2 (HI2) match the density enhancement ahead of and behind the in situ magnetic ejecta at 1 au. Howard & DeForest (2012) focused more on the magnetic ejecta structure and found that the cavity region in HI2 images can be related to the magnetic ejecta structure observed at 1 au. However, no quantification of the evolutions of the CME substructures and the radial size are provided in these studies.

The novel close-to-the-Sun measurements by the Parker Solar Probe (PSP; Fox et al. 2016; Raouafi et al. 2023) and Solar Orbiter (SolO; Müller 2020) enable unprecedented comprehensive studies on the CME structures and radial expansion in the innermost heliosphere, specifically with solar wind plasma measurements. For example, Winslow et al. (2021) investigated the simultaneous in situ measurements of a CME from PSP and the Ahead STEREO (STEREO-A), which were in radial alignment, and revealed the complex evolution of the CME due to interaction with other large-scale transients. In this work, we studied a CME that erupted on 2022 March 10, with emphasis on the evolution of the CME substructures and radial expansion, and we give a comparison between the remote observations and simultaneous in situ measurements from SolO. This CME was continuously tracked by remote observations at STEREO and also observed at SolO between March 11 and 12 in the innermost heliosphere. Laker et al. (2023) also studied this event but focused on validating the ability to use SolO as an upstream monitor to forecast space weather near Earth in real time. In Sect. 2, we introduce the data and methods used and briefly introduce this CME. Section 3 describes the results. Sections 4 and 5 present the discussion and conclusions.

2. Data, method, and event overview

2.1. Instrumentation and methods

To study the CME in remote observations, we use (a) the Large Angle and Spectrometric Coronagraph (LASCO; Brueckner et al. 1995) on board SOHO, (b) the coronagraphs (COR1 and COR2) and the heliospheric imagers (HI1 and HI2; Howard et al. 2008) on board STEREO-A (STA hereafter), and (c) the Extreme Ultraviolet Imager (EUVI; Wuelser et al. 2004) on board STA and the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO). In order to compare the CME substructures and radial expansion properties between remote observations and in situ measurements, we focused on HI1, which has a 20° square field of view (FOV) centered at 14° elongation, and HI2, which has a 70° -by-70° FOV centered at 53.7° elongation. The spatial resolutions for HI1 and HI2 are around 0.02° and 0.07°, and temporal resolutions are 40 min and two hours, respectively. Figure 1 shows the FOVs of HI1 and HI2. It is noted that HI1 and HI2 measure elongation (ϵ) instead of heliocentric distance (rH). The “harmonic mean” method (Lugaz et al. 2009) is used here for the conversion between ϵ and rH according to Eq. (1):

r H = 2 d sin ϵ 1 + sin ( ϵ + ϕ ) , $$ \begin{aligned} r_{\rm H} = \frac{2d \sin \epsilon }{1+\sin (\epsilon +\phi )}, \end{aligned} $$(1)

thumbnail Fig. 1.

Locations of SolO, STA, and Earth relative to Sun in ecliptic plane in heliocentric Earth ecliptic (HEE) coordinate system. The straight lines indicate the FOVs of STA HI1 (red) and HI2 (yellow), and the solid arrow shows the longitude of the CME propagation direction obtained from the GCS model.

where d is the distance from STA to the Sun (0.97 au) and ϕ is the angle between the CME trajectory and Sun-STA line. Taking advantage of multi-viewpoint coronagraphs, we obtain the CME three-dimensional (3D) geometric and propagation parameters using the graduated cylindrical shell (GCS) model, which assumes that the CME is a self-similarly expanding flux rope structure (Thernisien et al. 2006, 2009). In this study, we used the model tool in the Python environment developed by von Forstner (2021).

We also investigated the in situ properties of the CME from SolO at ∼0.44 au and from Wind at 1 au. Those in situ measurements include (a) the Solar Wind Analyzer (SWA; Owen et al. 2020) and the magnetometer (MAG; Horbury et al. 2020) on board SolO and (b) the Solar Wind Experiment (SWE; Ogilvie & Desch 1997), the Magnetic Field Investigation (MFI; Lepping et al. 1995), and the Three-Dimensional Plasma and Energetic Particle Investigation suite (3DP, Lin et al. 1995) on board Wind. The temporal resolution of all in situ data used in this paper is one minute, except for 3DP, which is binned to a two-minute resolution. We note that due to, for example, spacecraft interference, SolO encountering some minor issues during and after commissioning related to instruments and digital processing units in the first few years of the mission, or an instrument turning-off during the period of data downlink, there may be some data gaps. The locations of SolO, STA, and Earth relative to the Sun in the ecliptic plane at 18:00 UT on 2022 March 10 are shown in Fig. 1. At this time, SolO and Wind were in a radial conjunction with a longitudinal separation of 7°. The heliographic latitudes of SolO and Wind were −4° and −7°, respectively. STA was ∼34° to the east of Earth.

In the rest of this work, we estimate the radial size of a specific CME substructure from the in situ measurements as the product of the average speed and duration of that substructure. We also performed an expanding Lundquist flux rope model (Farrugia et al. 1993; Yu et al. 2022) to obtain the in situ parameters for the magnetic ejecta only and found that the radial sizes are similar between these two estimation methods (the fitted results are not used thereafter).

2.2. Event overview

The CME of interest erupted at around 17:10 UT on 2022 March 10, based on STA EUVI observations from active region 12962 (N27W07). No major flare was reported based on the SolarMonitor website1. The CME appeared as a partial halo structure in the SOHO LASCO FOV and was a limb event from the STA viewpoint. Figure 2 shows the CME eruption observed using SDO AIA at a wavelength of304 Å, STA EUVI at a wavelength of 195 Å, STA COR1, SOHO LASCO-C2, and STA COR2 at two time steps: SOHO LASCO-C3, STA HI1 and STA HI2, respectively. These images were processed using the running-difference technique, except for the AIA image. We note that the time intervals of HI1 and HI2 used for the running difference are 40 minutes and two hours, respectively. The SDO AIA image shows post-eruption ribbons associated with the two hooks at the far ends of the two ribbons (marked by the green circles), which indicate the two footpoints of the CME (e.g., Janvier et al. 2014). The remaining eight images display the CME eruption and propagation in chronological sequence.

thumbnail Fig. 2.

2022 March 10 CME observations from SDO, STA, and LASCO. From left to right and from top to bottom: SDO AIA at a wavelength of 304 Å, STA EUVI at a wavelength of 195 Å, STA COR1, SOHO LASCO-C2, STA COR2 at two time-steps: SOHO LASCO-C3, STA HI1 and STA HI2. These images were processed using the running-difference technique, except the first AIA image. The green circles in the top left panel indicate the locations of the CME feet. The orange concentric circles show the elongation angles, and the radial lines show the position angles in the STA HI1 and STA HI2 images.

The most intriguing phenomenon here is that the CME displays two bright fronts observed quite clearly from the STA viewpoint (also discernible in LASCO images). These two fronts are visible during the CME propagation from the low corona in EUVI to interplanetary space in HI2. We also checked the original (without difference-technique processed) images at STA and found that the signatures of the two fronts hold. However, to enhance the visibility of different substructures, we show them here through running-difference images.

Following its propagation in the inner heliosphere, the CME reached SolO and then L1. Figure 3 shows the in situ observations of the CME-driven shock and the magnetic ejecta at SolO (left) and Wind (right), including the magnetic field strength, components in the spacecraft-centered radial tangential normal (RTN) coordinate system, the solar wind proton number density, temperature and speed, and the pitch-angle distribution of suprathermal electrons at ∼265 eV (only at Wind). The CME-driven shock arrived at SolO at 19:52 UT on March 11, and the magnetic ejecta duration was between 22:55 UT on March 11 and 06:40 UT on March 12, at which point magnetic cloud properties were observed. At Wind, the shock and the ejecta front arrived at 10:04 UT and 22:42 UT on March 13, respectively. Even though magnetic cloud properties were also observed at Wind, the identification of the ejecta rear boundary was not conclusive. Thus, we marked two potential boundaries delineated by the third and fourth vertical lines at 17:15 UT on March 14 and 12:10 UT on March 15 (see the discussion in Sect. 4.1).

thumbnail Fig. 3.

In situ measurements at SolO (left) and Wind (right). The magnetic field strength; components in RTN coordinates; the solar wind proton number density, temperature, and speed; and the pitch-angle distribution of suprathermal electrons at ∼265 eV (only at Wind) are shown. At SolO, the three vertical dashed lines indicate the shock boundary and the front and rear boundaries of the magnetic ejecta. At Wind, the first two dashed lines indicate the shock boundary and the ejecta front boundary, while the third and fourth lines correspond to two potential rear boundaries (see text for details).

3. Event analysis

3.1. CME propagation based on the GCS model

Based on the GCS model, the CME propagated in the N24–W08 direction (corresponding to a unit vector [X, Y, Z]=[0.85, 0.12, 0.52] in the HEE coordinate system), with a half angular width of 65°, an aspect ratio of 0.27, a tilt angle of −55°, and a speed of ∼800 km s−1 in the corona based on a linear fit to the height-time data in the GCS model. The solid arrow in Fig. 1 shows the longitude of the CME propagation direction in the HEE coordinate system, which is almost along the Sun-SolO line. The left and middle panels of Fig. 4 present the reconstructed flux rope structure overlaid on the STA COR2 and SOHO LASCO-C3 images at around 21:54 UT on March 10. We note that the large tilt angle indicates the fact that the CME was inclined with its axis quasi-perpendicular to the ecliptic plane. Such an inclined structure in the GCS model is also consistent with the expected layout of a flux rope based on the CME footpoint locations on the solar surface as shown in the top left panel of Fig. 2. Furthermore, considering the latitudes of SolO and Wind, the spacecraft trajectories may cross the flank of the CME instead of the core part.

thumbnail Fig. 4.

3D reconstruction of 2022 March 10 CME. Left and middle panels: Reconstructed flux rope structure from the GCS model (blue) overlaid on the STA COR2 and SOHO LASCO-C3 running-difference images at around 21:54 UT. Right panel: CME structure from GCS model intersected in ecliptic plane. The pink line corresponds to the Sun-SolO line, and the two red dots mark the locations of the intersected points between the CME and the Sun-SolO line.

We also estimated the CME transit times from the Sun to SolO and from SolO to Wind. Considering an average between the speeds of the GCS model intersected in the ecliptic plane and the front of the magnetic ejecta at SolO (680 km s−1), the CME is predicted to arrive at SolO at around 20:02 UT on March 11, which is quite consistent with the real detection (22:55 UT on March 11). From SolO to Wind, we focused on the magnetic ejecta front and used two methods to calculate the CME transit time, which are (a) averaging between the ejecta front speeds measured at SolO and Wind and (b) the drag-based model (DBM), which considers the CME-solar wind interaction (Vršnak et al. 2013). Based on the first method, starting at 22:55 UT on March 11 at SolO with an average speed of 535 km s−1 (620 km s−1 at SolO and 450 km s−1 at Wind), the CME could arrive at Wind at 18:22 UT on March 13, which is ∼4 h earlier than the true detection. Based on the second method, combining an adjusted drag coefficient (0.34) with a constant solar wind speed of 340 km s−1 (an average value before the arrival of the CME at SolO, which is the same as that estimated at Wind), the CME starting at SolO is predicted to arrive at Wind at 20:38 UT (∼2 h earlier than the true detection) on March 13 with an impact speed of 450 km s−1. The predicted arrival time and impact speed based on the DBM model are quite consistent with the in situ measurements at Wind.

3.2. CME substructures in J map

A J map (elongation-time map; Sheeley et al. 1999) is helpful for showing the evolution of the CME substructures and easily tracking the features of interest. The top panel of Fig. 5 shows the J map combining the running-difference images of COR2, HI1, and HI2 along the central horizontal line, while the central line in HIs with the position angle of about −3° is close to the Sun-SolO line in the heliographic latitude of −4°. The CME appears as two bright ridges (called first and second ridges hereafter), which are related to the appearance of the two fronts in Fig. 2. The two bright ridges are not discernible at elongations greater than 40°. The horizontal pink line indicates the elongation of SolO (using Eq. (1) to change the SolO heliocentric distance to elongation with ϕ = 41° and rH = 0.44 au), and the three vertical pink lines correspond to the shock and magnetic ejecta boundaries identified at SolO. We note that the in situ signatures of the CME are quite consistent with the remote signatures: (a) the shock boundary roughly matches the uppermost ridge edge, (b) the ejecta duration at SolO corresponds to the low-brightness region between the R2 (or R3) and R4 ridges (see the definitions of R1 to R4 below), and (c) the plasma density enhancement at the ejecta rear is related to the second bright ridge. Section 4.2 discusses the implication of point (c) in accurately identifying the CME rear edge. These consistencies are based on visual comparisons in the J-map image. In the next two subsections, we present quantitative estimates.

thumbnail Fig. 5.

J-map image combining running-difference images of COR2, HI1, and HI2 along the central horizontal line. The horizontal pink line indicates the elongation of SolO converted using Eq. (1), and the three vertical pink lines correspond to the shock and magnetic ejecta boundaries identified at SolO(see main text for more details). The two bottom panels show the running difference (left) and base difference with the base time at 00:08 UT on March 11 (right) overlaid with the selected data points (the four colors are consistent with the colors of R1 to R4 as shown in the top panel of this figure) at 07:28 UT on March 11 in HI1 FOV.

3.3. Comparison of the CME radial size

We focused on investigating the evolution of the CME radial size from the corona (based on the GCS model) to the interplanetary space (based on HI1 and HI2) and compare it with the radial size estimated by the in situ measurements, especially for the CME at SolO at a distance where the size can also be derived from remote observations.

We first present the in situ estimation. At SolO, the radial sizes of the magnetic ejecta and the whole CME are estimated to be 0.096 au and 0.145 au, respectively. The duration and average speed of the ME are 7.8 h and 513 km s−1, while the duration and average speed of the sheath region are three hours and 606 km s−1. At Wind, the two potential rear boundaries lead to two ejecta parts (a shorter one and a longer one), and thus we estimate four radial sizes of (a) the shorter ejecta (the duration and average speed are 18.6 h and 427 km s−1), (b) the shorter ejecta adding the sheath (the duration and average speed of the sheath are 12.6 h and 470 km s−1), (c) the longer ejecta (the duration and average speed are 37.4 h and 406 km s−1), and (d) the longer ejecta adding the sheath. These four estimated radial sizes are 0.19, 0.32, 0.37, and 0.52 au, respectively. We note that the ejecta size of 0.19 au is comparable to the average radial size of magnetic clouds at 1 au of 0.21 au (see, e.g., Bothmer & Schwenn 1998), while the total size using the first rear boundary is comparable to that of CMEs at 1 au (Richardson & Cane 2010). The larger size using the second rear boundary is significantly larger than typical observations.

In the GCS model, we estimate the size of the flux rope intersected in the ecliptic plane and along the Sun-SolO line, as indicated in the right panel of Fig. 4. Due to the northward propagation of the CME with a large tilt angle, SolO only crossed the CME flank. We calculated the radial size between the two red dots, while the pink line is the Sun-SolO line. We note that the Sun-Wind line does not intersect the CME volume; thus, the in situ detection at Wind indicates that the CME may have experienced deflection, rotation, and/or non-self-similar expansion during its propagation (e.g., Vršnak et al. 2019; Zhuang et al. 2019; Regnault et al. 2023), or that there are uncertainties in the GCS parameters (Thernisien et al. 2009). Compared to SolO, Wind may have more of a grazing incidence encounter of the CME based on the propagation direction and orientation of the CME.

In HI1 and HI2 FOVs, we first calculate the heliocentric distances of different substructures based on the J-map image (Fig. 5) and Eq. (1). In Eq. (1), we have ϕ = 47° by considering the mean longitude of the CME propagation direction obtained from the GCS model and the HELCATS website2. We selected the data points of different parts of the bright ridges, including (1) the front of the first ridge that may correspond to the shock (R1), (2) the sharp ridge inside and the rear of the first ridge (R2 and R3) when the identification of the magnetic ejecta front in HI1 FOV is not clear, and (3) the front of the second ridge indicating the rear of the ejecta (R4). The data groups are indicated using different colors in Fig. 5. In HI2, we considered R3 based on the edge between the extremely bright and faint regions. Uncertainties in pinpointing R1–R4 in running-difference images are discussed in Sect. 4.1.

We then estimate the radial sizes between (a) R1 and R4, (b) R2 and R4, and (3) R3 and R4 based on the assumption that R1 to R4 shared the same propagation direction. The difference between R1 and R4 indicates the radial size of the whole CME. However, the estimation of the magnetic ejecta radial size is not clear: either using R2 to R4 or using R3 to R4 (see discussion in Sect. 4.1). The top panel of Fig. 6 shows the variation of the different estimates of the CME radial size along with the radial distance by combining the GCS model, HI1 and HI2 images, and in situ measurements. The estimated radial distances of R1, R2, and R3 are used for the green, blue, and red data points, respectively. The uncertainties in the GCS model (estimated by combining the errors on the fit height and aspect ratio; see discussion in Thernisien et al. 2009) and HI1 images are too small to be seen. In HI2 (also HI1), the uncertainty in the distance estimation is the product of the half of the temporal resolution and the CME speed of ∼660 km s−1, and the radial size error is based on a measurement error of four pixels in the images.

thumbnail Fig. 6.

Comparison of CME radial size, propagation speed, and expansion speed measured remotely and in situ. Top: Evolution of radial sizes of different CME substructures along with the heliocentric distances of the CME substructure fronts estimated using the GCS model and in STA HIs associated with the in situ estimates at SolO in pink (the whole CME and magnetic ejecta) and Wind in light blue (only the shorter ejecta size is shown). The dashed lines indicate the (two-band) power-law fits of the data points in remote observations. Bottom: Propagation and expansion speeds of different substructures of CME obtained in HI images and at SolO.

We used a power-law equation to fit the data points of radial size versus heliocentric distance. However, the red data points of the R3–R4 region appear to have two slopes, which indicates that different CME radial expansion rates during the CME propagate from the corona to interplanetary space (e.g., Lugaz et al. 2020a; Zhuang et al. 2023). Therefore, we fit them with two power-law bands divided by a specific heliocentric distance (rH0). 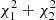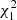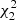rH0 is obtained by minimizing the value of χ 1 2 + χ 2 2 $ \chi_1^2+\chi_2^2 $, where the reduced χ 1 2 $ \chi_1^2 $ and χ 2 2 $ \chi_2^2 $ error statistics correspond to the fits of the two bands. We find that, as for the magnetic ejecta of the region between R3 and R4, the power-law index (α) is estimated to be 1.49 within 0.21 au and 1.09 beyond 0.21 au, where rH0 = 0.21 au and the sum of the reduced chi-squares of the two-band fit is smaller than the reduced chi-square of the one-band power-law fit. α of the whole CME between R1 and R4 (green) is estimated to be 0.89, and α of the R2–R4 region (blue) is estimated to be 1.03. We note that α in the GCS model is one, due to the self-similar expansion assumption. We then discuss these α values together with the radial size estimates.

First, the radial size of the whole CME estimated in HI images is consistent with that estimated in situ at SolO (the top pink square). Second, the ejecta size measured in situ at SolO (bottom pink square) is smaller than that obtained from the remote images between R2 and R4, but larger than that between R3 and R4. However, the differences are relatively small: 12% for the R2–R4 size and 15% for the R3–R4 size compared to the in situ estimate. The α fit from remote images greater than one of the magnetic ejecta part within ∼0.2 au indicate that the CME may overexpand instead of expanding self-similarly (if α = 1). The radial expansion rate of the ejecta is found to decrease as the CME propagates farther away from the Sun, which is indicated by the lower α fit beyond 0.21 au. This is further confirmed by the decrease in the estimated expansion speed (also for the whole CME) in the next subsection.

Third, the radial size of the shorter magnetic ejecta with the first rear edge estimated at Wind is consistent with that as derived from the HI image between R3 and R4 and extrapolated to 1 au. However, the estimated radial sizes of the longer ejecta with the second rear edge and the whole CME (with shorter or longer ejecta) at Wind are significantly larger than the radial sizes estimated by remote observations. We note that these comparisons may be influenced by (a) the lack of direct remote observations at the distance of 1 au (i.e., we used an extrapolation of the fit results) and (b) unclear identification of the rear boundaries of the magnetic ejecta at Wind.

Last, the estimated radial size based on the GCS model for the CME in the corona (gray dashed line) is larger than the magnetic ejecta size estimated in the HI images (blue and red data points) or at SolO (bottom pink square). However, the gray dashed line with the radial distance < 0.4 au is consistent with the green data points of the radial size of the whole CME, which indicates that the reconstruction of the GCS model, which always tracks the CME bright front in use, may consider a part of the sheath region (Fig. 4).

3.4. Comparison of the radial expansion speed

We calculated the propagation speeds of R1, R3, and R4 based on the HI images and compare them with the in situ measurements at SolO in the bottom left panel of Fig. 6. To make the data points more easily visible, the error of the propagation speed is not shown here. Based on the four-pixel-uncertainty assumption (Sect. 3.3), the related error values are around 80 km s−1 and 95 km s−1 in HI1 and HI2 images, respectively. The pink squares from top to bottom indicate the measured plasma speed at the shock, ejecta front, and ejecta rear boundaries. We note that the speeds at the shock and ejecta front measured at SolO are almost the same (Fig. 3). The speeds of the shock and ejecta rear edge estimated remotely and in situ are consistent. However, it is not clear about the ejecta front because (1) there are not enough data points to determine the speed of the R2 front, and (2) the speed of R3 is lower than the front speed at SolO.

We then compared the radial expansion speeds based on the size estimates between R1 and R4 and between R3 and R4 with the in situ estimate in the bottom right panel. We note that the errors on the expansion speed are around 110 km s−1 and 130 km s−1 for the HI1 and HI2 images (error bar is not shown here either). Even though this error is larger than the estimated expansion speeds, we still discuss the comparisons here. It should be noted that this error in speed is directly related to the estimate of the error in the position of four pixels; however, it is unlikely that the position error is random; it is more likely to be a bias, which would result in smaller errors in speed. We find that the expansion speed of R1–R4 at the distance of SolO estimated in the HI2 J-map image is quite consistent with that of the whole CME estimated at SolO, while the expansion speed of R3–R4 is lower than the in situ estimates of the ejecta part. The consistency of the expansion speed when focusing on the whole CME can also be confirmed from the consistency of the propagation speed if we approximate the expansion speed using half the speed difference between the CME front and rear. Additionally, we find that the expansion speeds of both the whole CME and the magnetic ejecta decreased during the CME propagation, which is consistent with expectations. Combining the two bottom panels of Fig. 6, the decrease in the expansion speed of this CME appears to be due primarily to the decrease in the propagation speed of the CME front, as the speed of the rear boundary is approximately constant. The inconsistency of the expansion speed between the R3–R4 region and the ejecta region measured at SolO is likely due to the difficulty in identifying the exact magnetic ejecta front in remote images.

The underestimations of the propagation speed of R3 and expansion speed of the R3–R4 region in HI images further reflect the lower radial size estimate between R3 and R4. We discuss the propagation speed here. In general, the R3–R4 radial size can be estimated using the ejecta duration multiplied by the speed difference between R3 and R4. Since the speeds between R4 and the ejecta rear edge at SolO are consistent, the underestimation of the ejecta radial size is due to the lower R3 speed estimate. In addition, we can provide further findings based on the speed comparison in this event. In the left panel of Fig. 3 of the SolO measurements, the speed inside the sheath region only has a slight decrease, and thus the ejecta front speed is close to the shock speed (see also the bottom left panel of Fig. 6). Therefore, the expansion speed of the whole CME is close to that of the ejecta part, as shown in the bottom right panel of Fig. 6. It indicates that the expansion speed of the whole CME estimated in remote images can be used to indicate the real expansion speed. The fact that the speed inside the sheath region remains constant is quite common for CMEs measured near 1 au with a moderately high speed relative to the local solar wind (Regnault et al. 2020). Furthermore, the speed variation of the sheath may be influenced not only by the speed difference between the solar wind and ejecta, but also by the solar wind plasma density, as well as the ejecta internal magnetic field strength (Salman et al. 2021).

4. Discussion

4.1. Uncertainties

In this section, we discuss the uncertainties in (1) converting from elongation to heliocentric distance, (2) measuring the elongation along the bright-to-dark edge and the selected data points in running-difference images, and (3) a potential CME-CME interaction. First, when converting elongation to heliocentric distance, we assumed that all CME substructures share the same propagation direction and used the “harmonic mean” method. Based on Eq. (1), different propagation directions (longitudes) lead to different radial size conversions. However, fitting the propagation direction of different substructures, for example, using the GCS model, may bring additional uncertainties, because the substructures (except the front one) are quite hard to identify in SOHO LASCO images. Moreover, the deflection of CMEs during their propagation may further bring uncertainties, and such an effect cannot be quantified here.

We calculated the uncertainty in the estimated heliocentric distance by considering errors of ±5° in the estimated longitude of the CME propagation direction and three different methods, which are the “point-p”, “fixed-ϕ”, and “harmonic-mean” methods (Kahler & Webb 2007; Howard et al. 2007; Rouillard et al. 2008; Lugaz et al. 2009; Wood et al. 2009). Based on the STA location at the CME eruption time, the uncertainty in the heliocentric distance estimate increases from 0.0075 to 0.015 au with elongation between 4° and 12° (within HI1 FOV) and then decreases to 0.0025 au with the elongation at 40° (the focused HI2 range in this study). Different methods do not significantly affect the distance estimation for the elongation within 40°, as previously noted. We consider that our approach of considering that all substructures propagate in the same direction and using the “harmonic mean” method is appropriate, at least for R1 and R4, as it yields consistent results between in situ measurements and remote observations for the radial size and propagation speeds (Fig. 6). The assumption for the propagation direction is consistent with the study from Lugaz et al. (2012), where the direction of propagation of different tracks for two CMEs was found to be nearly identical using stereoscopic methods making use of the two STEREO spacecraft.

Second, as mentioned by Lugaz et al. (2012), the bright-to-dark edge with high contrast is easy to track, even though the relationship between the dark edge and the exact physical part of the CME front is unclear. Since the exact identification of the magnetic ejecta front in remote images is difficult, we use both R2 and R3 and compare the related radial size with the in situ estimates. In Fig. 6, the results of (a) the radial size between R3 and R4 being slightly smaller than the ejecta size at SolO and (b) the bulk speed along R3 being lower than the ejecta front speed at SolO indicate that the true ejecta front is located inside the ridge between R1 and R3 (specifically between R2 and R3), which is equivalent to the statement that the bright ridge in running-difference remote images includes not only the sheath region, but also part of the ejecta structure. Remote images from COR2 to HI1 in Fig. 2 show that the width of the CME bright front is larger than or comparable to the dark cavity width, while the sheath size is only half the ejecta size at SolO. However, it is not clear why the ejecta part, which is supposed to be associated with lower density, can appear bright in remote images. The density enhancement near the ejecta front boundary at SolO may be one explanation, but the data gap in solar plasma measurements during the event brings uncertainties.

Using the bright-to-dark edge may lead to underestimations of the radial size and expansion speed, though the dark edge is useful for studying the CME propagation (Lugaz et al. 2012). In addition, as shown in the bottom panels of Fig. 5, we compared the selected data points of R1 to R4 in the running-difference and base-difference images at the same time. We find that these two image-processing techniques do not significantly influence the selection of the data points along R2 and R4 relatively to the CME apparent substructures (R1 is not visible in the base-difference image), while R3 determined from the running-difference image is located even closer to the bright front R2 compared to R2–R3 in the base-difference image. Therefore, if considering the dark cavity as the magnetic ejecta region, the radial size derived from base-difference images is smaller than that derived from running-difference images.

Last, Lavraud et al. (2022) discussed a CME-CME interaction during this event and the fact that the measurements at Wind indicate the existence of two CMEs (e.g., the much longer magnetic ejecta duration). Such an interaction makes the ejecta boundary identification at Wind difficult. They suggested that the density enhancement at the CME rear edge is caused by this interaction when the CME of our interest is the preceding one. We have checked remote observations to find the eruption of the second CME. However, no eruption responsible for the second CME was found that could explain the timing of the interaction. While there was another CME that impacted BepiColombo (0.43 au) at 13:04 UT on March 11 and STEREO-A at 21:13 UT on March 12, (a) the speed difference of ∼500 km s−1, (b) the eruption time of around 19 hours before that of the CME of focus in this work, and (c) the angular separations of 39° in latitude and of 46° in longitude between the propagation directions of the two CMEs make it highly unlikely that these two CMEs are interacting. As such, there may not be CME-CME in the inner heliosphere (if there is any, it will have occurred in the very low corona, which does not affect our conclusions in this paper), at least in the direction of SolO and Wind.

4.2. CME rear edge identification

The accurate identification of the CME boundaries, especially the rear edge and in both remote and in situ observations, is important for better analyzing the CME radial expansion and propagation (Zhuang et al. 2022, 2023), investigating the CME flux balance and CME erosion (Ruffenach et al. 2012; Lavraud et al. 2014), and reconstructing the CME global configuration using CME models and in situ fitting techniques (Riley et al. 2004; Thernisien et al. 2006, 2009). However, the identification of the CME rear edge can be difficult, as discussed in Zhuang et al. (2023; see their Fig. 11). Such difficulty leads to the inconsistency of the radial size between the remote estimation and in situ estimation (Zhuang et al. 2023). In remote images, some observational signatures were seen that could be used to identify the CME rear edge, for example, the higher-density region (Rouillard 2011; Wood et al. 2021), the V-shape structure (Wood et al. 2021), and/or the current sheet (Webb & Vourlidas 2016) behind the CME.

The simultaneous remote and in situ observations for the 2022 March event show that the high-density region at the CME rear observed in the STEREO HI images is consistent with the density enhancement right behind the ejecta rear boundary measured at SolO, and they further support the use of density enhancement to identify the CME rear edge. The density enhancement can be due to the pileup of solar wind materials behind the CME associated with the CME radial expansion (Rouillard 2011), which can facilitate comparison between remote and in situ observations. It was also present for the well-studied 2008 December CME (Howard & DeForest 2012), but this does not occur for all CMEs. In addition, the identification of the CME rear edge based on the trailing density enhancement is helpful for the CME 3D reconstruction. In the GCS model, the aspect ratio is adjusted to make the CME radial size as consistent as possible with the size between R1 and R4 in COR2 images after correcting for the projection effect using the “harmonic mean” method.

5. Conclusions

We studied the CME that erupted on 2022 March 10 by combining remote observations from LASCO and STA and in situ measurements at SolO in the inner heliosphere of 0.44 au between March 11 and 12. The CME can be continuously tracked from the low corona by STA EUVI, COR1, and COR2 to interplanetary space by STA HI1 and HI2, while SolO was in the FOV of HI2.

We focused on the CME radial expansion and compared the CME radial size and radial expansion speed of the CME substructures (i.e., magnetic ejecta only and whole CME consisting of the ejecta and the sheath). We find that the radial size of the whole CME region estimated in remote images is consistent with that estimated in situ at SolO. However, there is no such consistency when comparing the radial size of the magnetic ejecta region in remote and in situ measurements. We estimated the CME propagation speed and radial expansion speed remotely and in situ. The expansion speed is found to decrease during the propagation of the CME, and this appears to be caused primarily by the decrease in the propagation speed of the CME front. Moreover, the remote and in situ speed estimates are consistent for the whole CME but inconsistent for the magnetic ejecta. The inconsistencies of the ejecta region may be due to the fact that the identification of the ejecta front boundary in remote images is difficult.

We also focused on the long-standing question of where the CME rear edge in remote images is. Even though the front edge of the ejecta is difficult to identify for this event, the identification of the rear edge can be done confidently based on the signature of an enhancement of the solar wind plasma density behind the CME. The consistencies of the whole CME radial size and the bulk speeds at the front and rear between the remote and in situ estimations further support the identification of the ejecta rear edge based on the density enhancement at the end of the CME. This event sheds light on the importance of using both remote observations and in situ measurements with solar wind plasma parameters measured in the inner heliosphere to study the evolution of the CME substructures and their radial expansion.

Acknowledgments

We acknowledge NASA/GSFC’s Space Physics Data Facility’s CDAWeb service for the Solar Orbiter and Wind data. We thank the use of the data of SOHO LASCO, SDO AIA, and STEREO SECCHI from Virtual Solar Observatory. Research for this work was made possible by the NASA grant 80NSSC20K0431. B.Z. and N.L. acknowledge the NASA grants 80NSSC17K0009, 80NSSC20K0700, and 80NSSC19K0831 the NSF grant AGS-2301382. C.F. acknowledges the NASA grant 80NSSC19K1293. C.S. acknowledges NASA grants 80NSSC19K0914, 80NSSC20K0197, and 80NSSC20K0700. N.A. acknowledges support from NSF AGS-1954983 and NASA 80NSSC22K0349 and ECIP 80NSSC21K0463. E.D. acknowledges funding by the European Union (ERC, HELIO4CAST, 101042188). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. The measured heights of different CME substructures from the J-map can be found on Zenodo (https://doi.org/10.5281/zenodo.10009808).

References

  1. Balmaceda, L. A., Vourlidas, A., Stenborg, G., & St Cyr, O. C., 2020, Sol. Phys., 295, 107 [Google Scholar]
  2. Bothmer, V., & Schwenn, R. 1998, Ann. Geophys., 16, 1 [Google Scholar]
  3. Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
  4. Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
  5. Davies, E. E., Möstl, C., Owens, M. J., et al. 2021, A&A, 656, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Davies, E. E., Winslow, R. M., Scolini, C., et al. 2022, ApJ, 933, 127 [NASA ADS] [CrossRef] [Google Scholar]
  7. Davies, J. A., Harrison, R. A., Rouillard, A. P., et al. 2009, Geophys. Rev. Lett., 36, L02102 [NASA ADS] [CrossRef] [Google Scholar]
  8. Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [Google Scholar]
  9. Farrugia, C. J., Burlaga, L. F., Osherovich, V. A., et al. 1993, J. Geophys. Res., 98, 7621 [Google Scholar]
  10. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
  11. Gulisano, A. M., Démoulin, P., Dasso, S., Ruiz, M. E., & Marsch, E. 2010, A&A, 509, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Howard, T. A., & DeForest, C. E. 2012, ApJ, 746, 64 [NASA ADS] [CrossRef] [Google Scholar]
  14. Howard, T. A., Fry, C. D., Johnston, J. C., & Webb, D. F. 2007, ApJ, 667, 610 [NASA ADS] [CrossRef] [Google Scholar]
  15. Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
  16. Illing, R. M. E., & Hundhausen, A. J. 1985, J. Geophys. Res., 90, 275 [Google Scholar]
  17. Janvier, M., Aulanier, G., Bommier, V., et al. 2014, ApJ, 788, 60 [Google Scholar]
  18. Kahler, S. W., & Webb, D. F. 2007, J. Geophys. Res. Space Phys., 112, A09103 [Google Scholar]
  19. Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space Sci. Rev., 136, 5 [Google Scholar]
  20. Kilpua, E. K. J., Isavnin, A., Vourlidas, A., Koskinen, H. E. J., & Rodriguez, L. 2013, Ann. Geophys., 31, 1251 [NASA ADS] [CrossRef] [Google Scholar]
  21. Kilpua, E., Koskinen, H. E. J., & Pulkkinen, T. I. 2017, Liv. Rev. Sol. Phys., 14, 5 [Google Scholar]
  22. Laker, R., Horbury, T. S., O’Brien, H., et al. 2023, Space Weather, submitted [arXiv:2307.01083] [Google Scholar]
  23. Lavraud, B., Ruffenach, A., Rouillard, A. P., et al. 2014, J. Geophys. Res. Space Phys., 119, 26 [Google Scholar]
  24. Lavraud, B., Fargette, N., Genot, V. N., et al. 2022, in AGU Fall Meeting Abstracts, SH15A-04 [Google Scholar]
  25. Leitner, M., Farrugia, C. J., Möstl, C., et al. 2007, J. Geophys. Res. Space Phys., 112, A06113 [Google Scholar]
  26. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  27. Lepping, R. P., Jones, J. A., & Burlaga, L. F. 1990, J. Geophys. Res., 95, 11957D [NASA ADS] [CrossRef] [Google Scholar]
  28. Lepping, R. P., Acũna, M. H., Burlaga, L. F., et al. 1995, Space Sci. Rev., 71, 207 [Google Scholar]
  29. Lin, R. P., Anderson, K. A., Ashford, S., et al. 1995, Space Sci. Rev., 71, 125 [CrossRef] [Google Scholar]
  30. Lugaz, N., Vourlidas, A., & Roussev, I. I. 2009, Ann. Geophys., 27, 3479 [Google Scholar]
  31. Lugaz, N., Farrugia, C. J., Davies, J. A., et al. 2012, ApJ, 759, 68 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lugaz, N., Salman, T. M., Winslow, R. M., et al. 2020a, ApJ, 899, 119 [Google Scholar]
  33. Lugaz, N., Winslow, R. M., & Farrugia, C. J. 2020b, J. Geophys. Res. Space Phys., 125, e27213 [NASA ADS] [CrossRef] [Google Scholar]
  34. Möstl, C., Temmer, M., Rollett, T., et al. 2010, Geophys. Rev. Lett., 37, L24103 [Google Scholar]
  35. Müller, D., St Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
  36. Nieves-Chinchilla, T., Colaninno, R., Vourlidas, A., et al. 2012, J. Geophys. Res. Space Phys., 117, A06106 [Google Scholar]
  37. Ogilvie, K. W., & Desch, M. D. 1997, Adv. Space Res., 20, 559 [Google Scholar]
  38. Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
  39. Patsourakos, S., Vourlidas, A., & Stenborg, G. 2010, ApJ, 724, L188 [NASA ADS] [CrossRef] [Google Scholar]
  40. Raouafi, N. E., Matteini, L., Squire, J., et al. 2023, Space Sci. Rev., 219, 8 [NASA ADS] [CrossRef] [Google Scholar]
  41. Regnault, F., Janvier, M., Démoulin, P., et al. 2020, J. Geophys. Res. Space Phys., 125, e28150 [NASA ADS] [CrossRef] [Google Scholar]
  42. Regnault, F., Strugarek, A., Janvier, M., et al. 2023, A&A, 670, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Richardson, I. G., & Cane, H. V. 2010, Sol. Phys., 264, 189 [NASA ADS] [CrossRef] [Google Scholar]
  44. Riley, P., Linker, J. A., Lionello, R., et al. 2004, J. Atmos. Sol. Terr. Phys., 66, 1321 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rouillard, A. P. 2011, J. Atmos. Sol. Terr. Phys., 73, 1201 [CrossRef] [Google Scholar]
  46. Rouillard, A. P., Davies, J. A., Forsyth, R. J., et al. 2008, Geophys. Rev. Lett., 35, L10110 [NASA ADS] [CrossRef] [Google Scholar]
  47. Ruffenach, A., Lavraud, B., Owens, M. J., et al. 2012, J. Geophys. Res. Space Phys., 117, A09101 [Google Scholar]
  48. Salman, T. M., Winslow, R. M., & Lugaz, N. 2020, J. Geophys. Res. Space Phys., 125, e27084 [NASA ADS] [CrossRef] [Google Scholar]
  49. Salman, T. M., Lugaz, N., Winslow, R. M., et al. 2021, ApJ, 921, 57 [NASA ADS] [CrossRef] [Google Scholar]
  50. Savani, N. P., Rouillard, A. P., Davies, J. A., et al. 2009, Ann. Geophys., 27, 4349 [NASA ADS] [CrossRef] [Google Scholar]
  51. Sheeley, N. R., Walters, J. H., Wang, Y. M., & Howard, R. A. 1999, J. Geophys. Res., 104, 24739 [Google Scholar]
  52. Thernisien, A. F. R., Howard, R. A., & Vourlidas, A. 2006, ApJ, 652, 763 [Google Scholar]
  53. Thernisien, A., Vourlidas, A., & Howard, R. A. 2009, Sol. Phys., 256, 111 [Google Scholar]
  54. Tousey, R. 1973, Space Res. Conf., 2, 713 [Google Scholar]
  55. von Forstner, J. L. F. 2021, https://doi.org/10.5281/zenodo.5084818 [Google Scholar]
  56. Vršnak, B., Žic, T., Vrbanec, D., et al. 2013, Sol. Phys., 285, 295 [Google Scholar]
  57. Vršnak, B., Amerstorfer, T., Dumbović, M., et al. 2019, ApJ, 877, 77 [Google Scholar]
  58. Webb, D. F., & Vourlidas, A. 2016, Sol. Phys., 291, 3725 [NASA ADS] [CrossRef] [Google Scholar]
  59. Winslow, R. M., Lugaz, N., Philpott, L. C., et al. 2015, J. Geophys. Res. Space Phys., 120, 6101 [NASA ADS] [CrossRef] [Google Scholar]
  60. Winslow, R. M., Lugaz, N., Scolini, C., & Galvin, A. B. 2021, ApJ, 916, 94 [NASA ADS] [CrossRef] [Google Scholar]
  61. Wood, B. E., Howard, R. A., Plunkett, S. P., & Socker, D. G. 2009, ApJ, 694, 707 [NASA ADS] [CrossRef] [Google Scholar]
  62. Wood, B. E., Braga, C. R., & Vourlidas, A. 2021, ApJ, 922, 234 [NASA ADS] [CrossRef] [Google Scholar]
  63. Wuelser, J. P., Lemen, J. R., & Tarbell, T. D. 2004, SPIE Conf. Ser., 5171, 111 [NASA ADS] [Google Scholar]
  64. Yu, W., Al-Haddad, N., Farrugia, C. J., et al. 2022, ApJ, 937, 86 [NASA ADS] [CrossRef] [Google Scholar]
  65. Zhuang, B., Wang, Y., Hu, Y., et al. 2019, ApJ, 876, 73 [NASA ADS] [CrossRef] [Google Scholar]
  66. Zhuang, B., Lugaz, N., Temmer, M., Gou, T., & Al-Haddad, N. 2022, ApJ, 933, 169 [NASA ADS] [CrossRef] [Google Scholar]
  67. Zhuang, B., Lugaz, N., Al-Haddad, N., et al. 2023, ApJ, 952, 7 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Locations of SolO, STA, and Earth relative to Sun in ecliptic plane in heliocentric Earth ecliptic (HEE) coordinate system. The straight lines indicate the FOVs of STA HI1 (red) and HI2 (yellow), and the solid arrow shows the longitude of the CME propagation direction obtained from the GCS model.
In the text
thumbnail Fig. 2.

2022 March 10 CME observations from SDO, STA, and LASCO. From left to right and from top to bottom: SDO AIA at a wavelength of 304 Å, STA EUVI at a wavelength of 195 Å, STA COR1, SOHO LASCO-C2, STA COR2 at two time-steps: SOHO LASCO-C3, STA HI1 and STA HI2. These images were processed using the running-difference technique, except the first AIA image. The green circles in the top left panel indicate the locations of the CME feet. The orange concentric circles show the elongation angles, and the radial lines show the position angles in the STA HI1 and STA HI2 images.
In the text
thumbnail Fig. 3.

In situ measurements at SolO (left) and Wind (right). The magnetic field strength; components in RTN coordinates; the solar wind proton number density, temperature, and speed; and the pitch-angle distribution of suprathermal electrons at ∼265 eV (only at Wind) are shown. At SolO, the three vertical dashed lines indicate the shock boundary and the front and rear boundaries of the magnetic ejecta. At Wind, the first two dashed lines indicate the shock boundary and the ejecta front boundary, while the third and fourth lines correspond to two potential rear boundaries (see text for details).
In the text
thumbnail Fig. 4.

3D reconstruction of 2022 March 10 CME. Left and middle panels: Reconstructed flux rope structure from the GCS model (blue) overlaid on the STA COR2 and SOHO LASCO-C3 running-difference images at around 21:54 UT. Right panel: CME structure from GCS model intersected in ecliptic plane. The pink line corresponds to the Sun-SolO line, and the two red dots mark the locations of the intersected points between the CME and the Sun-SolO line.
In the text
thumbnail Fig. 5.

J-map image combining running-difference images of COR2, HI1, and HI2 along the central horizontal line. The horizontal pink line indicates the elongation of SolO converted using Eq. (1), and the three vertical pink lines correspond to the shock and magnetic ejecta boundaries identified at SolO(see main text for more details). The two bottom panels show the running difference (left) and base difference with the base time at 00:08 UT on March 11 (right) overlaid with the selected data points (the four colors are consistent with the colors of R1 to R4 as shown in the top panel of this figure) at 07:28 UT on March 11 in HI1 FOV.
In the text
thumbnail Fig. 6.

Comparison of CME radial size, propagation speed, and expansion speed measured remotely and in situ. Top: Evolution of radial sizes of different CME substructures along with the heliocentric distances of the CME substructure fronts estimated using the GCS model and in STA HIs associated with the in situ estimates at SolO in pink (the whole CME and magnetic ejecta) and Wind in light blue (only the shorter ejecta size is shown). The dashed lines indicate the (two-band) power-law fits of the data points in remote observations. Bottom: Propagation and expansion speeds of different substructures of CME obtained in HI images and at SolO.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.