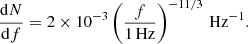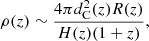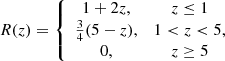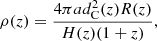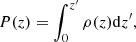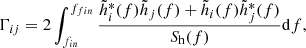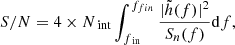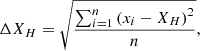| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A177 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202347221 | |
| Published online | 21 February 2024 | |
Deep learning forecasts of cosmic acceleration parameters from DECi-hertz Interferometer Gravitational-wave Observatory
1
College of Physics, Chongqing University, Chongqing 401331, PR China
e-mail: cqujinli1983@cqu.edu.cn
2
Institute for Frontiers in Astronomy and Astrophysics, Beijing Normal University, Beijing 102206, PR China
e-mail: caoshuo@bnu.edu.cn
3
Department of Astronomy, Beijing Normal University, Beijing 100875, PR China
Received:
18
June
2023
Accepted:
17
November
2023
Context. Validating the accelerating expansion of the universe is an important aspect in improving our understanding of the evolution of the universe. By constraining the cosmic acceleration parameter XH, we can discriminate between the cosmological constant plus cold dark matter (ΛCDM) model and the Lemaître–Tolman–Bondi (LTB) model.
Aims. In this paper, we explore the possibility of constraining the cosmic acceleration parameter with the inspiral gravitational waveform of neutron star binaries (NSBs) in the frequency range of 0.1 Hz–10 Hz, which can be detected by the second-generation space-based gravitational wave detector DECIGO.
Methods. We used a convolutional neural network (CNN) and a long short-term memory (LSTM) network combined with a gated recurrent unit (GRU), along with a Fisher information matrix to derive constraints on the cosmic acceleration parameter, XH.
Results. We assumed that our networks estimate the cosmic acceleration parameter without biases (the expected value of the estimation is equal to the true value). Under this assumption, based on the simulated gravitational wave data with a time duration of one month, we conclude that CNN can limit the relative error to 15.71%, while LSTM network combined with GRU can limit the relative error to 14.14%. Additionally, using a Fisher information matrix for gravitational wave data with a five-year observation can limit the relative error to 32.94%.
Conclusions. Under the assumption of an unbiased estimation, the neural networks can offer a high-precision estimation of the cosmic acceleration parameter at different redshifts. Therefore, DECIGO is expected to provide direct measurements of the acceleration of the universe by observing the chirp signals of coalescing binary neutron stars.
Key words: methods: statistical / binaries: close / stars: neutron / cosmological parameters / dark matter / dark energy
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The verification of the acceleration of the cosmic expansion is a crucial subject in current astrophysical research. Cosmic acceleration refers to the phenomenon of the universe expanding at an increasingly fast rate and measuring its acceleration is essential for determining the ultimate fate of the universe. Observing the type-Ia Supernovae has provided evidence to support the accelerating expansion of the universe, focusing on a distinctive correlation between the luminosity and distance of supernovae within a specific distance range (Riess et al. 1998; Aldering et al. 1998). Such a conclusion was further verified by the observations of cosmic microwave background radiation (de Bernardis et al. 2000) based on the results from Wilkinson Microwave Anisotropy Probe (WMAP) program (Spergel et al. 2003) and Planck Collaboration (Planck Collaboration VI 2020). The analysis of various observational data, including baryon acoustic oscillation, Hubble parameters derived from passively evolving galaxies (Cao et al. 2011a, 2015c; Cao & Liang 2013), strong gravitational lensing systems (Cao & Zhu 2012, 2014; Cao et al. 2012a,b, 2015a), and quasars calibrated as standard rulers and standard candles (Cao et al. 2015b, 2017a,b, 2018) has also suggested that the present universe is undergoing an accelerated phase of expansion. We refer to Yang & Gong (2020), Yoo et al. (2008) for the summary of recent observational progress made on such issue. Currently, several theoretical models have been proposed to explain the expansion of the universe. Dark energy and modified gravity theories are widely accepted as explanations for these observational facts. Dark energy’s significant influence on the evolution of the universe has played a pivotal role in its widespread acceptance within the scientific community. However, assuming that we are at the center of the universe and that the universe is no longer isotropic on large scales and becomes non-uniform can explain the current observational results without using a dark energy model or modifying gravity theory (Alnes et al. 2006; Yoo et al. 2010; Garcia-Bellido & Haugboelle 2008a,b, 2009; Bolejko & Wyithe 2009; Caldwell & Stebbins 2008; Clarkson & Regis 2011; Zhang & Stebbins 2011; Zibin et al. 2008; Cao et al. 2011b). Nevertheless, such an assumption clearly violates the Copernican principle. Therefore, directly detecting the acceleration of the universe’s expansion is an important means of verifying the current mainstream theory.
According to the standard cosmological model, the acceleration of the universe’s expansion leads to redshift drift, a crucial phenomenon that provides valuable information for understanding the evolution of the universe. Several methods can be used to observe redshift drift. One method involves using type Ia Supernovae as standard candles (Perlmutter et al. 1997; Riess et al. 1998). Another method involves using observations and calculations of cosmic microwave background radiation (Abazajian et al. 2004; Tegmark et al. 2004). In this study, we analyze the cosmic acceleration parameter by examining the redshift evolution resulting from cosmic accelerating expansion and the corresponding phase shift of gravitational waves. Such a phase shift caused by the cosmic acceleration was demonstrated by Seto et al. (2001), through a decade of observing gravitational wave signals generated by binary neutron stars. In this analysis, we chose the sensitive frequency range of 0.1 Hz–10 Hz for the DECIGO (Deci-hertz Interferometer Gravitational-wave Observatory) detector to capture gravitational waveforms generated during the inspiral phase of binary neutron stars. Yagi et al. (2012) used the covariance matrix derived from the Fisher information matrix to estimate the uncertainty of cosmic acceleration parameter. However, we should note that the phase shift in the low-frequency part of the waveform can be easily overwhelmed by complex noise backgrounds. Therefore, a high-precision parameter estimation method is still required to obtain accurate results. Luckily, the deployment of machine learning algorithms in astronomy has demonstrated its efficacy in accelerating data processing and improving statistical inference. Specially, deep learning in gravitational wave data analysis is becoming crucial to quick and accurate estimation of parameters of interest (McLeod et al. 2022). In this paper we discuss the ability of different deep learning algorithms, a convolutional neural network (CNN), and a long short-term memory (LSTM) network combined with a gated recurrent unit (GRU) to measure the cosmic acceleration parameters, based on the time-series waveform of gravitational wave during the binary neutron star inspiral phase in DECIGO. Our results reveal that deep learning is able to provide measurements of the cosmic acceleration parameter with high-precision.
The paper is structured as follows. Section 2 is dedicated to the framework of the GW simulations produced for our analysis. Section 3 explains how the estimation of the cosmic acceleration parameter is performed, along with the deep learning results with different deep learning methods. Section 4 presents the results with Fisher information matrix for comparison. Finally, our main conclusions and final remarks are presented in Sect. 5.
2. Data simulation
2.1. Simulation of a gravitational wave signal
In this paper, we use natural units with c = G = 1 and select binary neutron stars as our sources of gravitational waves. Our simulation is based on the flat ΛCDM model, with the matter density parameter, ΩM = 0.3, and the Hubble constant, H0 = 70 km s−1 Mpc−1. The relation between redshift drift and the cosmic acceleration parameter is parameterized as (Seto et al. 2001): XH = X(z)/H0, and 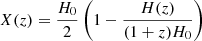 , with the Hubble parameter being
, with the Hubble parameter being 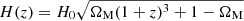 .
.
The gravitational wave waveform in the presence of cosmic acceleration expansion is (Yagi et al. 2012; Seto et al. 2001; Takahashi & Nakamura 2005):
where the acceleration phase Ψacc(f) is derived from:
the waveform of stationary phase approximation without acceleration is given by (Berti et al. 2005; Cutler & Flanagan 1994):
where x = (πℳzf)2/3, 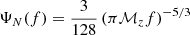 , ℳz = M(1+zc)η3/5 represents the chirp mass with redshift drift, zc represents the redshift taking into account the cosmic acceleration expansion. The chirp mass is defined as ℳ = Mη3/5, with the symmetric mass ratio η = m1m2/M2 and the total mass M = m1 + m2. In the case of a flat universe, the luminosity distance to the source is:
, ℳz = M(1+zc)η3/5 represents the chirp mass with redshift drift, zc represents the redshift taking into account the cosmic acceleration expansion. The chirp mass is defined as ℳ = Mη3/5, with the symmetric mass ratio η = m1m2/M2 and the total mass M = m1 + m2. In the case of a flat universe, the luminosity distance to the source is:
We used the second-order standard post-Newtonian approximation method to construct the gravitational waveforms (Berti et al. 2005):
in the above phase expression, the first term includes the merger time, tc, the second term includes the phase at the merger, ϕc, and the factor in the parentheses is the standard phase for quadrupole radiation in general relativity. The terms in the parentheses are the expansion terms in the post-Newtonian approximation; then, |β|≲9.4 and |σ|≲2.5 represent the contributions from spin-orbit coupling and spin-spin coupling to the phase, respectively (Yagi et al. 2011).
Due to the time-domain signals detected by DECIGO, time-domain signals are more direct and convenient in terms of representation and processing, without the need for additional transformations or processing steps. Furthermore, time-domain signal processing is typically faster than frequency-domain signal processing, which is crucial for handling a large volume of gravitational wave data. In addition, the direct information contained in time-domain signals includes important features and information of gravitational wave signals, such as duration, amplitude, phase, and shape, which are vital for the identification and classification of gravitational wave signals. Moreover, preprocessing and data processing of time-domain signals are relatively simple, allowing the utilization of various filtering techniques, noise reduction methods, and data cleaning techniques to improve the signal-to-noise ratio (S/N) and extract useful features. It is necessary to impose an inverse Fourier transform on the frequency-domain gravitational wave to the time-domain. To simplify the calculations, we employed the average response function RDECIGO of the DECIGO detector (Zhang et al. 2020) as:
where 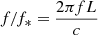 , L = 1000 km is the arm length of the DECIGO detector (Kawamura et al. 2006) and c is the speed of light. Considering that our frequency-domain data are obtained from numerical simulations, we use the 1D discrete inverse Fourier transform,
, L = 1000 km is the arm length of the DECIGO detector (Kawamura et al. 2006) and c is the speed of light. Considering that our frequency-domain data are obtained from numerical simulations, we use the 1D discrete inverse Fourier transform,
where h(t) is the GW strain in the time-domain signal, N is the sample number, and 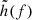 is the GW strain in the frequency-domain, RDECIGO(f) represents the average response function, reflecting the detector’s sensitivity to signals in different frequencies.
is the GW strain in the frequency-domain, RDECIGO(f) represents the average response function, reflecting the detector’s sensitivity to signals in different frequencies.
2.2. Simulation of noise data
The one-sided noise power spectral density for DECIGO is given by (Kawamura et al. 2011; Yagi & Seto 2011):
where fp = 7.36 Hz. The three terms correspond to short noise, radiation pressure noise, and acceleration noise, respectively. Additionally, we need to consider confusion noise from the galactic and extragalactic white dwarfs (Nelemans et al. 2001; Farmer & Phinney 2003):
the noise from the galactic and extragalactic white dwarfs is multiplied by a factor of ℱ = exp{−2(f/0.05 Hz)2}, which corresponds to the high-frequency cutoff. We also considered the superposition of gravitational waves from many binary neutron star systems, which contribute to the background noise as (Yagi & Seto 2011; Cutler & Harms 2006):
Given the overall noise sources, we could obtain the unilateral noise power spectral density (PSD) of DECIGO as (Yagi et al. 2011):
where κ ≃ 4.5, Tobs is the observation time and dN/df is the number density of white dwarfs in the galactic per unit frequency:
The factor of 0.01 in 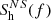 represents the proportion of neutron star noise that cannot be removed. The sensitive frequency range of DECIGO is from fmin = 10−3 Hz to fmax = 100 Hz. In Fig. 1, we show the noise spectral density of different GW detectors, from which one could see that gravitational waves generated by binary neutron stars falls within the observation range of DECIGO instead of LISA.
represents the proportion of neutron star noise that cannot be removed. The sensitive frequency range of DECIGO is from fmin = 10−3 Hz to fmax = 100 Hz. In Fig. 1, we show the noise spectral density of different GW detectors, from which one could see that gravitational waves generated by binary neutron stars falls within the observation range of DECIGO instead of LISA.
 |
Fig. 1. Sensitivity curves for DECIGO (blue line) and LISA (orange line), as well as the gravitational wave amplitude of a binary neutron star (1.4 + 1.4) M⊙ at a luminosity distance of DL = 3Gpc and a frequency range of 10−5 Hz ∼ 100 Hz (green line). The arrows on the graph indicate that when observing at the same high-frequency of 1 Hz, the lowest observational frequency differs depending on the observation time. Specifically, for an observation time of Tobs = 5 years, the lowest observational frequency is fmin = 0.073Hz. For an observation time of Tobs = 1 year, the lowest observational frequency is fmin = 0.133 Hz, and for an observation time of Tobs = 1 month, the lowest observational frequency is fmin = 0.4036 Hz. |
Based on the one-sided noise power spectral density (PSD), we could obtain the time-domain noise signal from the one-sided PSD; in this paper, we utilized the Python function pycbc.noise.gaussian.noise_from_psd (Nitz et al. 2023), which takes a PSD as input and returns colored Gaussian noise, to simulate the time-domain noise received by the DECIGO detector.
2.3. Distribution of BNS and numerical settings
For the probability density function of the distribution of neutron stars, we adopted the following form (Zhao et al. 2011):
where the co-moving distance is 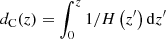 and the evolution of the inflation rate with time is quantified as (Schneider et al. 2001; Cutler & Holz 2009; Cai & Yang 2017):
and the evolution of the inflation rate with time is quantified as (Schneider et al. 2001; Cutler & Holz 2009; Cai & Yang 2017):
the above probability density function is normalized as:
with a normalization factor of 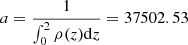 . The distribution function of redshift is given by:
. The distribution function of redshift is given by:
with the probability density function of redshift ρ(z) and the distribution function P(z) are shown in Fig. 2a. We divide the redshift range into 20 intervals according to the distribution function P(z) and randomly select 1000 redshift values that fall into these intervals. The resulting distribution of 1000 GW sources, based on the distribution function P(z) are presented in Fig. 2b.
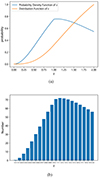 |
Fig. 2. Redshift distribution function and the samples generated according to this distribution. Panel a: probability density function and distribution function of redshift. Panel b: redshift distribution of 1000 sources. The x-axis and y-axis denote the range of each interval and the number of GW sources in each interval. |
In our simulation, we set the masses of neutron stars to m1 = m2 = 1.4 M⊙, the merger time to tc = 0, the coalescence phase ϕc = 0, and the angles to β = σ = 0. Moreover, we do not include the effects of the spins of the merging bodies (S = 0). The high and low frequencies of the gravitational waves and noise are determined as ffin = (fISCO,fend) and fin = max(fobs,fmin). Here fISCO = (63/2πM)−1, and fend = 1 Hz, within the sensitive range of the DECIGO detector. 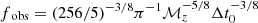 is the lowest frequency that can be observed during the corresponding observation time Δt0 = 1 month (Feng et al. 2019). At the luminosity distance of DL = 3 Gpc, the lowest observational frequency is 0.4036 Hz. Therefore, the frequency range of signal and noise is set as 0.4036 ∼ 1 Hz, as shown in Fig. 3.
is the lowest frequency that can be observed during the corresponding observation time Δt0 = 1 month (Feng et al. 2019). At the luminosity distance of DL = 3 Gpc, the lowest observational frequency is 0.4036 Hz. Therefore, the frequency range of signal and noise is set as 0.4036 ∼ 1 Hz, as shown in Fig. 3.
 |
Fig. 3. Frequency-domain amplitude of gravitational wave signal observed for 1 month (yellow line) and one-sided noise power spectral density of DECIGO (blue line), with a frequency range of 0.4036 ∼ 1 Hz. The binary neutron star with the mass of (1.4 + 1.4) M⊙ is located at a luminosity distance of DL = 3 Gpc. |
3. Estimating the acceleration parameters with deep learning
3.1. Construction of the dataset
We generated 1000 samples of gravitational wave data covering the redshift range of 0 < z < 2. The actual input to the network is the feature amplitude extracted from the time-domain data s(t) = h(t)+n(t), using a single-layer convolutional neural network, where h(t) is the inverse Fourier transform of 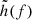 and n(t) is the time-domain noise. The sampling frequency of the data is taken as 2 Hz, the sampling time is one month and the data length is 1 × 5 184 000. However, due to the observation time, resulting in an excessive data length, the total size of our dataset comprising 1000 samples amounts to 38.624 gigabytes (GBs). That leads to significant challenges for training neural networks. Therefore, we employed a 1D convolutional neural network with a single layer for feature extraction from our raw data. Table 1 represents the feature extraction network architecture. Following feature extraction, each sample has a length of 1 × 2000. In Fig. 4b, we illustrate one sample after feature extraction. We divide the 1000 samples into training and testing dataset, and our testing sub-set contains 30% of the original sample size. Then we deploy different machine learning algorithms on the training test. The input data are (x_train, y_train), (x_test, y_test), where x_train and x_test are time-domain data in the training and testing datasets. y_train and y_test are the parameters space here is (ln𝒜, tc, ϕc, lnℳ, lnη, lnℳz, XH) that the neural network needs as labels.
and n(t) is the time-domain noise. The sampling frequency of the data is taken as 2 Hz, the sampling time is one month and the data length is 1 × 5 184 000. However, due to the observation time, resulting in an excessive data length, the total size of our dataset comprising 1000 samples amounts to 38.624 gigabytes (GBs). That leads to significant challenges for training neural networks. Therefore, we employed a 1D convolutional neural network with a single layer for feature extraction from our raw data. Table 1 represents the feature extraction network architecture. Following feature extraction, each sample has a length of 1 × 2000. In Fig. 4b, we illustrate one sample after feature extraction. We divide the 1000 samples into training and testing dataset, and our testing sub-set contains 30% of the original sample size. Then we deploy different machine learning algorithms on the training test. The input data are (x_train, y_train), (x_test, y_test), where x_train and x_test are time-domain data in the training and testing datasets. y_train and y_test are the parameters space here is (ln𝒜, tc, ϕc, lnℳ, lnη, lnℳz, XH) that the neural network needs as labels. 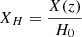 . The S/N values of these 1000 data are shown in Fig. 5.
. The S/N values of these 1000 data are shown in Fig. 5.
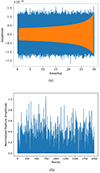 |
Fig. 4. Panel a: a time-domain data sample. Noise represented as the blue curve represents, while the yellow curve shows the gravitational wave (a). The sample’s S/N is 15.739. The observation time for the signal is 1 month, with a frequency range of 0.4036 Hz–1 Hz. The gravitational wave source is a binary neutron star system with a combined mass of (1.4 + 1.4) M⊙ and a luminosity distance of DL = 3 Gpc. Other parameters are set as described in Sect. 2.3. Panel b: corresponding feature of (a), obtained through a single-layer convolutional neural network convoluting with raw data. The horizontal axis of the (b) represents the data length, while the vertical axis represents the normalized feature amplitude. |
 |
Fig. 5. Variation in the S/N with different observation time. The blue line represents a 5-year observation, the green line represents a 1-year observation, and the yellow line represents a 1-month observation. |
Feature extraction network architecture.
Now our analysis will be carried out on all simulated and data-sets with two deep learning algorithms (CNN and LSTM-GRU), as well as the Fisher information matrix estimation.
3.2. Convolutional neural networks
Convolutional neural networks (CNN) offer several advantages for parameter estimation in the analysis of time-domain gravitational wave data. Firstly, a CNN enables automatic feature learning, alleviating the need for manual design of feature extractors (Christensen & Meyer 2022). Secondly, it possesses local perception capabilities, allowing it to extract features at different positions within the input data through convolutional filters (Edwards 2021). This is crucial for capturing local structures and temporal features in time-domain gravitational wave data, facilitating effective discrimination of different gravitational wave signals. Third, CNN employs multiple layers for hierarchical feature representation by stacking convolutional and pooling layers. This progressive learning enables the network to capture abstract features in time-domain gravitational wave data, enhancing the accuracy of parameter estimation. Fourth, CNN exhibits robustness and generalization abilities, acquired through training on large-scale datasets. It demonstrates resilience against noise and non-ideal conditions, which is vital for accurate parameter estimation in the presence of noise and interference in real detectors (George & Huerta 2018). Lastly, CNN excels in handling large-scale datasets, a critical advantage for processing the extensive gravitational wave data (Dreissigacker et al. 2019) expected from the next-generation DECIGO detector. As DECIGO is planned to produce high-temporal-resolution data, efficient data processing methods are essential and CNN is capable of effectively managing large-scale data. Collectively, these advantages establish CNN as a powerful tool for parameter estimation in analysis of DECIGO’s time-domain gravitational wave data. Based on these characteristics, we chose a 1D CNN model for parameter estimation of gravitational wave signals, with our network structure shown in Table 2.
CNN architecture and hyperparameter settings.
3.3. LSTM-GRU hybrid network
The LSTM-GRU hybrid network provides numerous advantages for parameter estimation of time-domain gravitational wave data obtained from the DECIGO detector. Specifically designed to handle sequential data, long short-term memory (LSTM) and gated recurrent unit (GRU) are variants of recurrent neural networks (RNN) that effectively capture the long-term dependencies often observed in DECIGO gravitational wave data. The LSTM-GRU hybrid network demonstrates robustness and generalization capabilities, making it resilient against noise and incomplete training data (Cahuantzi et al. 2021; Elsayed et al. 2019). Given that DECIGO gravitational wave data may contain measurement errors or missing information, the hybrid network leverages its gating mechanisms and memory units to capture crucial features, enabling reliable parameter estimations even in the presence of such challenges. Additionally, the network exhibits strong generalization ability, allowing accurate estimation of parameters for unseen data samples. Moreover, the LSTM-GRU hybrid network excels in capturing both local and global information. While LSTM captures long-term dependencies by utilizing gating mechanisms and memory cells, GRU can swiftly capture short-term local patterns through its update and reset gates. This combination facilitates comprehensive understanding and modeling of DECIGO time-domain gravitational wave data by enabling the network to focus on both local and global features. Furthermore, The LSTM-GRU hybrid network’s nonlinear activation functions and gating mechanisms contribute to its powerful nonlinear modeling capabilities (Lewis & Stevens 1991). Traditional linear models often fail to accurately capture the complex nonlinear relationships present in time-domain gravitational wave data. In contrast, the LSTM-GRU hybrid network, with its flexibility in capturing nonlinear patterns and complex data features, enhances the accuracy of parameter estimation. In conclusion, the LSTM-GRU hybrid network offers a range of advantages, including long-term dependency modeling, long-term memory and forgetting capabilities, robustness and generalization capabilities, the ability to capture both local and global information, and powerful nonlinear modeling capabilities. These attributes make the LSTM-GRU hybrid network a valuable tool for parameter estimation of time-domain gravitational wave data acquired from the DECIGO detector. In this paper, we use LSTM and GRU to construct a hybrid model for parameter estimation and prediction. Our LSTM-GRU hybrid network structure is shown in Table 3.
Hyperparameters of LSTM-GRU hybrid network.
We present the results (under the assumption of unbiased estimation) obtained from the two neural networks in Fig. 6. By comparing the two deep learning methods, we find that the two neural networks perform similarly in terms of parameter estimation in time-domain data. However, due to the fewer trainable parameters in the CNN, the training speed of CNNs is faster. For the task of accelerating parameter estimation with the same dataset, the CNN is more efficient than LSTM-GRU.
 |
Fig. 6. Comparison of XH error estimation using CNNs and LSTM-GRU hybrid networks, for binary neutron stars with one month of observations. |
4. Estimating the acceleration parameter with a Fisher information matrix
In this section, we describe our use of the Fisher information matrix(FIM) for cosmic acceleration parameter estimation. It is based on the methodology of matched filtering to detect gravitational wave signals using fixed templates. The methodology was firstly proposed in Finn (1992), Kucukelbir et al. (2017). Matched filtering convolves the detector output signal with the gravitational wave template in the library to find the template with the maximum correlation. The parameter information of the detection signal is given by the template with the maximum correlation. However, typically the parameter information obtained for the detection signal is not accurate. If the background noise of the signal is Gaussian, the estimated parameters of the signal will have a Gaussian distribution around the actual parameter values.
We assume that λi denotes the actual value of the parameter, λi + Δλi denotes the measured value, and the root-mean-square of Δλi follows a Gaussian distribution: p(Δλi) ∝ exp(−ΓijΔλiΔλj/2). Here Γij is the matrix element of the Fisher information matrix:
where 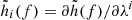 ,
, 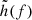 is the frequency-domain form of the gravitational wave signal, and
is the frequency-domain form of the gravitational wave signal, and 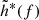 is the complex conjugate of
is the complex conjugate of 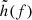 . The root-mean-square error of the ith parameter is
. The root-mean-square error of the ith parameter is 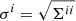 , where Σii = [Γ−1]ii is the covariance matrix element for parameter i. The root-mean-square error of the ith parameter is
, where Σii = [Γ−1]ii is the covariance matrix element for parameter i. The root-mean-square error of the ith parameter is 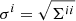 . The off-diagonal elements in the Σ matrix represent the size of the correlation between the ith and jth parameters, denoted as cij and calculated as
. The off-diagonal elements in the Σ matrix represent the size of the correlation between the ith and jth parameters, denoted as cij and calculated as 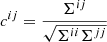 . The parameter space here is (ln𝒜, tc, ϕc, lnℳ, lnη, lnℳz, XH), where
. The parameter space here is (ln𝒜, tc, ϕc, lnℳ, lnη, lnℳz, XH), where 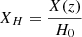 , and all parameter settings are given in Sect. 2. The S/N is calculated as:
, and all parameter settings are given in Sect. 2. The S/N is calculated as:
where Nint = 8 represents the number of effective interferometer arms of DECIGO. The S/N values for observation times of 1 month and 5 years are shown in Fig. 5.
It should be noted that the results obtained by our neural networks are based on the assumption of unbiased estimation. Here, ΔXH represents the standard deviation of XH estimated by our model. For our neural networks model, we performed 1000 predictions, resulting in 1000 samples of XH at each redshift. Subsequently, the standard deviation ΔXH was computed using Eq. (21). In contrast, for our Fisher method, we directly derived the standard deviation by calculating the covariance matrix and taking the square root of its diagonal elements.
where xi represents our samples, n = 1000, which is the size of samples.
Given a one month of observations with DECIGO, the estimated results of ΔXH are shown in Table 4. We further studied the estimated uncertainty ΔXH with 5-year observation of DECIGO. The results in Table 5 are well consistent with those obtained in the previous works (Yagi et al. 2012). Based on five years of observation, we can essentially estimate the acceleration parameter with reasonable uncertainties, allowing for a rough assessment of the cosmic accelerated expansion. Our finding indicate that increasing the observation time can improve the S/N and thus reduce the uncertainties of XH. Such a conclusion is strongly supported by the results shown in Fig. 7, from which we may also find that the estimated error gradually increases with the luminosity distance.
 |
Fig. 7. Comparison of XH estimation from 1-month and 5-year observations of binary neutron stars, based on Fisher information matrix. |
Estimation of ΔXH with 1-month observation of binary neutron stars at different redshifts, based on Fisher information matrix.
Estimation of ΔXH with 5-year observation of binary neutron stars at different redshifts, based on Fisher information matrix.
Finally, Fig. 8 shows the results of both methods. Table 6 provides Estimation of ΔXH using Fisher information matrix with a 5-year observation and deep learning with a 1-month observation. We can also calculate the relative error 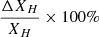 and visualize the results in Fig. 9. Based on the simulated gravitational wave data with a time duration of 1 month, the CNN can limit the relative error to 15.71%, while the LSTM network combined with GRU can limit the relative error to 14.14%. Additionally, using Fisher information matrix for gravitational wave data with a 5-year observation can limit the relative error to 32.94%. Therefore, the neural networks can give a high-precision estimation of the acceleration parameter at different redshifts. In this case, DECIGO is expected to provide direct measurements of the acceleration of the universe, by observing the chirp signals of coalescing binary neutron stars.
and visualize the results in Fig. 9. Based on the simulated gravitational wave data with a time duration of 1 month, the CNN can limit the relative error to 15.71%, while the LSTM network combined with GRU can limit the relative error to 14.14%. Additionally, using Fisher information matrix for gravitational wave data with a 5-year observation can limit the relative error to 32.94%. Therefore, the neural networks can give a high-precision estimation of the acceleration parameter at different redshifts. In this case, DECIGO is expected to provide direct measurements of the acceleration of the universe, by observing the chirp signals of coalescing binary neutron stars.
 |
Fig. 8. XH estimation using deep learning and Fisher information matrix. Panel a: XH estimation using deep learning with 1-month observation and Fisher information matrix with 5-year observation. Panel b: XH estimation using deep learning with 1-month observation and Fisher information matrix with 1-month and 5-year observation. |
 |
Fig. 9. Error estimated by the Fisher matrix for 5-year observation data, shown as a green solid line. The orange solid line represents the error value estimated by the LSTM-GRU networks for one month of observation data, while the blue solid line represents the error value estimated by the CNN networks for one month of observation data. |
Estimation of ΔXH using Fisher information matrix with a 5-year observation and deep learning with a 1-month observation.
5. Summary and discussion
In this paper, we explore the possibility of constraining the cosmic acceleration parameters with the inspiral gravitational waveform of neutron star binaries (NSBs) in the frequency range of 0.1 Hz–10 Hz, which can be detected by the second-generattion space-based gravitational wave detector DECIGO. We use a convolutional neural network (CNN), a long short-term memory (LSTM) network combined with a gated recurrent unit (GRU), and Fisher information matrix to derive constraints on the cosmic acceleration parameter, XH. Under the assumption of unbiased estimation, based on the simulated gravitational wave data with a time duration of 1 month, we conclude that the CNN can limit the relative error to 15.71%, while the LSTM network combined with GRU can limit the relative error to 14.14%. Additionally, using Fisher information matrix for gravitational wave data with a 5-year observation can limit the relative error to 32.94%. Therefore, DECIGO is expected to provide an unprecedented opportunity for high-precision detection of cosmic acceleration, by observing the chirp signals of coalescing binary neutron stars (Seto et al. 2001; Kawamura et al. 2021).
We should stress that the present paper is only an interesting example of extensive applications of deep learning in cosmological studies (Li et al. 2021; He et al. 2019; Lucie-Smith et al. 2020). Still, there are several remarks that remain to be clarified as follows. Firstly, the deep learning models used can be further optimized and enhanced to improve the measurements of cosmic acceleration parameters. We can explore the use of other neural networks or combinations of multiple networks to achieve more stringent cosmological constraints (Wen et al. 2023; Wang et al. 2020; Gómez-Vargas et al. 2023). Combining deep learning methods with other approaches, such as Markov chain Monte Carlo (MCMC) method, could contribute to resolving such an important issue. Secondly, the GW observations provide a powerful and novel method to detect the cosmic acceleration in a cosmological-model-independent way. This strengthens the probative power of such method to inspire new observing programs in the framework of DECIGO, focusing on a large number of neutron-star binaries in inspiraling phases. Finally, in future works, we can apply deep learning methods to constrain the cosmological parameters associated with the selected scientific objectives encompassed by the DECIGO (Cao et al. 2021, 2022b, 2019, 2022a; Piórkowska-Kurpas et al. 2021; Zhang et al. 2022; Geng et al. 2020; Liu et al. 2020; Bian et al. 2021; Hou et al. 2022). This will open up a new window for gravitational-wave cosmology.
Acknowledgments
This work is supported by the National Key Research and Development Program of China (Grant No. 2021YFC2203004); the National Natural Science Foundation of China under Grants Nos. 12021003, 12347101, 11690023, and 11920101003; the Natural Science Foundation of Chongqing (Grant No. CSTB2023NSCQ-MSX0103); the Strategic Priority Research Program of the Chinese Academy of Sciences, Grant No. XDB23000000; and the Interdiscipline Research Funds of Beijing Normal University.
References
- Abazajian, K., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2004, AJ, 128, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Aldering, G., Perlmutter, S., Knop, R., et al. 1998, Am. Astron. Soc. Meet. Abstr., 193, 39 [Google Scholar]
- Alnes, H., Amarzguioui, M., & Grøn, Ø. 2006, Phys. Rev. D, 73, 083519 [NASA ADS] [CrossRef] [Google Scholar]
- Berti, E., Buonanno, A., & Will, C. M. 2005, Phys. Rev. D, 71, 084025 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, L., Cai, R.-G., Cao, S., et al. 2021, Sci. China Phys. Mech. Astron., 64, 120401 [NASA ADS] [CrossRef] [Google Scholar]
- Bolejko, K., & Wyithe, J. S. B. 2009, J. Cosmol. Astropart. Phys., 2009, 020 [CrossRef] [Google Scholar]
- Cahuantzi, R., Chen, X., & Güttel, S. 2021, ArXiv e-prints [arXiv:2107.02248] [Google Scholar]
- Cai, R.-G., & Yang, T. 2017, Phys. Rev. D, 95, 044024 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, R. R., & Stebbins, A. 2008, Phys. Rev. Lett., 100, 191302 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., & Zhu, Z.-H. 2012, A&A, 538, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, S., & Zhu, Z.-H. 2014, Phys. Rev. D, 90, 083006 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., & Liang, N. 2013, Int. J. Mod. Phys. D, 22, 1350082 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Liang, N., & Zhu, Z.-H. 2011a, MNRAS, 416, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Zhu, Z. H., & Liang, N. 2011b, A&A, 529, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, S., Covone, G., & Zhu, Z.-H. 2012a, ApJ, 755, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Pan, Y., Biesiada, M., Godlowski, W., & Zhu, Z.-H. 2012b, J. Cosmol. Astropart. Phys., 2012, 016 [CrossRef] [Google Scholar]
- Cao, S., Biesiada, M., Gavazzi, R., Piórkowska, A., & Zhu, Z.-H. 2015a, ApJ, 806, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Biesiada, M., Zheng, X., & Zhu, Z.-H. 2015b, ApJ, 806, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Chen, Y., Zhang, J., & Ma, Y. 2015c, Int. J. Theoret. Phys., 54, 1492 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Biesiada, M., Jackson, J., et al. 2017a, J. Cosmol. Astropart. Phys., 2017, 012 [CrossRef] [Google Scholar]
- Cao, S., Zheng, X., Biesiada, M., et al. 2017b, A&A, 606, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, S., Biesiada, M., Qi, J., et al. 2018, Eur. Phys. J. C, 78, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Qi, J., Cao, Z., et al. 2019, Sci. Rep., 9, 1 [Google Scholar]
- Cao, S., Qi, J., Biesiada, M., et al. 2021, MNRAS, 502, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Liu, T., Biesiada, M., et al. 2022a, ApJ, 926, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Qi, J., Cao, Z., et al. 2022b, A&A, 659, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen, N., & Meyer, R. 2022, Rev. Mod. Phys., 94, 025001 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, C., & Regis, M. 2011, J. Cosmol. Astropart. Phys., 2011, 013 [CrossRef] [Google Scholar]
- Cutler, C., & Flanagan, E. E. 1994, Phys. Rev. D, 49, 2658 [Google Scholar]
- Cutler, C., & Harms, J. 2006, Phys. Rev. D, 73, 042001 [NASA ADS] [CrossRef] [Google Scholar]
- Cutler, C., & Holz, D. E. 2009, Phys. Rev. D, 80, 104009 [NASA ADS] [CrossRef] [Google Scholar]
- de Bernardis, P., Ade, P. A., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Dreissigacker, C., Sharma, R., Messenger, C., Zhao, R., & Prix, R. 2019, Phys. Rev. D, 100, 044009 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, M. C. 2021, Phys. Rev. D, 103, 024025 [NASA ADS] [CrossRef] [Google Scholar]
- Elsayed, N., Maida, A. S., & Bayoumi, M. 2019, Int. J. Adv. Comput. Sci. Appl., 2019, 10 [Google Scholar]
- Farmer, A. J., & Phinney, E. S. 2003, MNRAS, 346, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, W.-F., Wang, H.-T., Hu, X.-C., Hu, Y.-M., & Wang, Y. 2019, Phys. Rev. D, 99, 123002 [NASA ADS] [CrossRef] [Google Scholar]
- Finn, L. S. 1992, Phys. Rev. D, 46, 5236 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Bellido, J., & Haugboelle, T. 2008a, J. Cosmol. Astropart. Phys., 2008, 016 [CrossRef] [Google Scholar]
- Garcia-Bellido, J., & Haugboelle, T. 2008b, J. Cosmol. Astropart. Phys., 2008, 003 [CrossRef] [Google Scholar]
- Garcia-Bellido, J., & Haugbolle, T. 2009, J. Cosmol. Astropart. Phys., 2009, 028 [CrossRef] [Google Scholar]
- Geng, S., Cao, S., Liu, T., et al. 2020, ApJ, 905, 54 [NASA ADS] [CrossRef] [Google Scholar]
- George, D., & Huerta, E. A. 2018, Phys. Lett. B, 778, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez-Vargas, I., Medel-Esquivel, R., García-Salcedo, R., & Vázquez, J. A. 2023, Eur. Phys. J. C, 83, 304 [CrossRef] [Google Scholar]
- He, S., Li, Y., Feng, Y., et al. 2019, Proc. Natl. Acad. Sci., 116, 13825 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, S., Tian, S., Cao, S., Zhu, Z.-H., et al. 2022, Phys. Rev. D, 105, 064022P [CrossRef] [Google Scholar]
- Kawamura, S., Nakamura, T., Ando, M., et al. 2006, Class. Quant. Grav., 23, S125 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, S., Ando, M., Seto, N., et al. 2011, Class. Quant. Grav., 28, 094011 [CrossRef] [Google Scholar]
- Kawamura, S., Ando, M., Seto, N., et al. 2021, Progr. Theoret. Exp. Phys., 2021, 05A105 [CrossRef] [Google Scholar]
- Kucukelbir, A., Tran, D., Ranganath, R., Gelman, A., & Blei, D. M. 2017, J. Mach. Learn. Res., 18, 1 [Google Scholar]
- Lewis, P. A., & Stevens, J. G. 1991, J. Am. Stat. Assoc., 86, 864 [CrossRef] [Google Scholar]
- Li, Y., Ni, Y., Croft, R. A., et al. 2021, Proc. Natl. Acad. Sci., 118 [Google Scholar]
- Liu, Y., Cao, S., Liu, T., et al. 2020, ApJ, 901, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Lucie-Smith, L., Peiris, H. V., Pontzen, A., Nord, B., & Thiyagalingam, J. 2020, ArXiv e-prints [arXiv:2011.10577] [Google Scholar]
- McLeod, A., Jacobs, D., Chatterjee, C., Wen, L., & Panther, F. 2022, ArXiv e-prints [arXiv:2201.11126] [Google Scholar]
- Nelemans, G., Yungelson, L., & Zwart, S. P. 2001, A&A, 375, 890 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nitz, A., Harry, I., Brown, D., et al. 2023, https://doi.org/10.5281/zenodo.6324278 [Google Scholar]
- Perlmutter, S., Aldering, G., Deustua, S., et al. 1997, Bull. Am. Astron. Soc., 29, 1351 [Google Scholar]
- Piórkowska-Kurpas, A., Hou, S., Biesiada, M., et al. 2021, ApJ, 908, 196 [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [Google Scholar]
- Schneider, R., Ferrari, V., Matarrese, S., & Portegies Zwart, S. F. 2001, MNRAS, 324, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Seto, N., Kawamura, S., & Nakamura, T. 2001, Phys. Rev. Lett., 87, 221103 [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [Google Scholar]
- Takahashi, R., & Nakamura, T. 2005, Progr. Theoret. Phys., 113, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Strauss, M. A., Blanton, M. R., et al. 2004, Phys. Rev. D, 69, 103501 [CrossRef] [Google Scholar]
- Wang, G.-J., Li, S.-Y., & Xia, J.-Q. 2020, ApJS, 249, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Y., Yu, W., Li, D., et al. 2023, New Astron., 99, 101955 [NASA ADS] [CrossRef] [Google Scholar]
- Yagi, K., & Seto, N. 2011, Phys. Rev. D, 83, 044011 [Google Scholar]
- Yagi, K., Tanahashi, N., & Tanaka, T. 2011, Phys. Rev. D, 83, 084036 [NASA ADS] [CrossRef] [Google Scholar]
- Yagi, K., Nishizawa, A., & Yoo, C.-M. 2012, J. Cosmol. Astropart. Phys., 2012, 031 [CrossRef] [Google Scholar]
- Yang, Y., & Gong, Y. 2020, J. Cosmol. Astropart. Physics, 2020, 059 [CrossRef] [Google Scholar]
- Yoo, C.-M., Kai, T., & Nakao, K.-I. 2008, Progr. Theoret. Phys., 120, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Yoo, C.-M., Nakao, K.-I., & Sasaki, M. 2010, J. Cosmol. Astropart. Phys., 2010, 011 [CrossRef] [Google Scholar]
- Zhang, C., Gao, Q., Gong, Y., et al. 2020, Phys. Rev. D, 101, 124027 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., & Stebbins, A. 2011, Phys. Rev. Lett., 107, 041301 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Cao, S., Liu, X., et al. 2022, ApJ, 931, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, W., Van Den Broeck, C., Baskaran, D., & Li, T. 2011, Phys. Rev. D, 83, 023005 [NASA ADS] [CrossRef] [Google Scholar]
- Zibin, J. P., Moss, A., & Scott, D. 2008, Phys. Rev. Lett., 101, 251303 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Estimation of ΔXH with 1-month observation of binary neutron stars at different redshifts, based on Fisher information matrix.
Estimation of ΔXH with 5-year observation of binary neutron stars at different redshifts, based on Fisher information matrix.
Estimation of ΔXH using Fisher information matrix with a 5-year observation and deep learning with a 1-month observation.
All Figures
 |
Fig. 1. Sensitivity curves for DECIGO (blue line) and LISA (orange line), as well as the gravitational wave amplitude of a binary neutron star (1.4 + 1.4) M⊙ at a luminosity distance of DL = 3Gpc and a frequency range of 10−5 Hz ∼ 100 Hz (green line). The arrows on the graph indicate that when observing at the same high-frequency of 1 Hz, the lowest observational frequency differs depending on the observation time. Specifically, for an observation time of Tobs = 5 years, the lowest observational frequency is fmin = 0.073Hz. For an observation time of Tobs = 1 year, the lowest observational frequency is fmin = 0.133 Hz, and for an observation time of Tobs = 1 month, the lowest observational frequency is fmin = 0.4036 Hz. |
| In the text | |
 |
Fig. 2. Redshift distribution function and the samples generated according to this distribution. Panel a: probability density function and distribution function of redshift. Panel b: redshift distribution of 1000 sources. The x-axis and y-axis denote the range of each interval and the number of GW sources in each interval. |
| In the text | |
 |
Fig. 3. Frequency-domain amplitude of gravitational wave signal observed for 1 month (yellow line) and one-sided noise power spectral density of DECIGO (blue line), with a frequency range of 0.4036 ∼ 1 Hz. The binary neutron star with the mass of (1.4 + 1.4) M⊙ is located at a luminosity distance of DL = 3 Gpc. |
| In the text | |
 |
Fig. 4. Panel a: a time-domain data sample. Noise represented as the blue curve represents, while the yellow curve shows the gravitational wave (a). The sample’s S/N is 15.739. The observation time for the signal is 1 month, with a frequency range of 0.4036 Hz–1 Hz. The gravitational wave source is a binary neutron star system with a combined mass of (1.4 + 1.4) M⊙ and a luminosity distance of DL = 3 Gpc. Other parameters are set as described in Sect. 2.3. Panel b: corresponding feature of (a), obtained through a single-layer convolutional neural network convoluting with raw data. The horizontal axis of the (b) represents the data length, while the vertical axis represents the normalized feature amplitude. |
| In the text | |
 |
Fig. 5. Variation in the S/N with different observation time. The blue line represents a 5-year observation, the green line represents a 1-year observation, and the yellow line represents a 1-month observation. |
| In the text | |
 |
Fig. 6. Comparison of XH error estimation using CNNs and LSTM-GRU hybrid networks, for binary neutron stars with one month of observations. |
| In the text | |
 |
Fig. 7. Comparison of XH estimation from 1-month and 5-year observations of binary neutron stars, based on Fisher information matrix. |
| In the text | |
 |
Fig. 8. XH estimation using deep learning and Fisher information matrix. Panel a: XH estimation using deep learning with 1-month observation and Fisher information matrix with 5-year observation. Panel b: XH estimation using deep learning with 1-month observation and Fisher information matrix with 1-month and 5-year observation. |
| In the text | |
 |
Fig. 9. Error estimated by the Fisher matrix for 5-year observation data, shown as a green solid line. The orange solid line represents the error value estimated by the LSTM-GRU networks for one month of observation data, while the blue solid line represents the error value estimated by the CNN networks for one month of observation data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



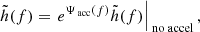
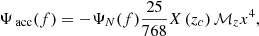
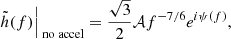
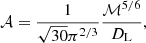
![$$ \begin{aligned} D_{\rm L}=\frac{1+z}{H_{0}} \int _{0}^{z} \frac{\mathrm{d} z^{\prime }}{\left[\Omega _{\rm M}\left(1+z^{\prime }\right)^{3}+\Omega _{\Lambda }\right]^{1 / 2}}. \end{aligned} $$](/articles/aa/full_html/2024/02/aa47221-23/aa47221-23-eq8.gif)
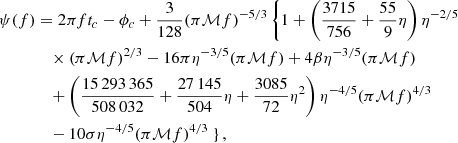
![$$ \begin{aligned} R_{\text{ DECIGO} } \approx \frac{3}{10} \frac{1}{1+\left(f / f_{*}\right)^{2} /\left[1.85{-}0.58 \cos \left(2 f / f_{*}\right)\right]}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa47221-23/aa47221-23-eq10.gif)
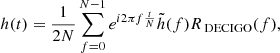
![$$ \begin{aligned} S_{\rm h}^{\text{ DECIGO} }(f)&=7.05 \times 10^{-48}\left[1+\left(\frac{f}{f_{\rm p}}\right)^{2}\right]+4.8 \times 10^{-51}\left(\frac{f}{1\,\mathrm{Hz}}\right)^{-4} \nonumber \\&\quad \times \frac{1}{1+\left(\frac{f}{f_{\rm p}}\right)^{2}}+5.53 \times 10^{-52}\left(\frac{f}{1\,\mathrm{Hz}}\right)^{-4}\,\mathrm{Hz}^{-1}, \end{aligned} $$](/articles/aa/full_html/2024/02/aa47221-23/aa47221-23-eq14.gif)
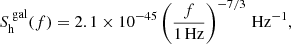
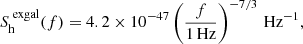
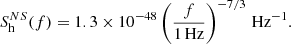
![$$ \begin{aligned} S_{\text{ h,} \text{ DECIGO}}(f)&= \min \left[\frac{S_{\text{ h,} \text{ DECIGO}}^{\text{ inst}}(f)}{\exp \left(-\kappa T_{\text{ obs}}^{-1} \frac{\mathrm{d} N}{\mathrm{d} f}\right)}, S_{\rm h}^{\text{ inst}}(f)+S_{\rm h}^{\text{ gal}}(f) \mathcal{F} (f)\right]\nonumber \\&\quad +S_{\rm h}^{\text{ exgal}}(f) \mathcal{F} (f)+ 0.01 \times S_{\rm h}^{N S}(f), \end{aligned} $$](/articles/aa/full_html/2024/02/aa47221-23/aa47221-23-eq18.gif)