| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202347337 | |
| Published online | 04 December 2023 | |
Design, manufacturing, and testing of phase-induced amplitude apodization and phase-shifting optics for segmented telescopes
1
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
Nice, France
e-mail: patrice.martinez@oca.eu
2
Astrobiology Center, National Institutes of Natural Sciences,
2-21-1 Osawa,
Mitaka, Tokyo, Japan
3
Steward Observatory, University of Arizona,
Tucson,
AZ
85721,
USA
4
National Astronomical Observatory of Japan, Subaru Telescope, National Institutes of Natural Sciences,
Hilo,
HI
96720,
USA
5
Silios Technologies, Rue Gaston Imbert prolonge,
ZI de Peynier-Rousset,
13790
Peynier, France
6
Centre National d’Etudes Spatiales,
18 avenue Edouard Belin,
31401
Toulouse cedex 9, France
Received:
3
July
2023
Accepted:
25
September
2023
Context. The phase-induced amplitude apodization complex mask coronagraph (PIAACMC) is a coronagraph architecture for the direct detection of extrasolar planets. The PIAACMC can achieve close to the theoretical performance limit at small angular sepa-rations. The concept is a high-performance PIAA-based coronagraph that is sufficiently versatile to be designed for next-generation segmented and obscured telescope apertures.
Aims. We present key elements of the design and manufacture of a PIAACMC for the segmented pupil experiment for exoplanet detection (SPEED) testbed. The primary components of a PIAACMC system are the PIAA optics and the complex phase-shifting focal plane mask (FPM). The most challenging part of the system to model is the error on the manufacturing of the two PIAA mirrors.
Methods. In this paper, we describe the design and manufacturing of the FPM and moderate-sag PIAA optics using photolithography and etching. We present the design and fabrication of the PIAACMC, along with metrology, and an initial assessment of the PIAACMC optics efficiency.
Results. Errors in the fabricated component profiles degrade the overall performance. We show that the depth errors involved are of a few tens of nanometers and a few hundred nanometers for the FPM and PIAA optics, respectively. The metrological and individual per¬formance analysis of the FPM and PIAA optics provides us with an in-depth understanding of these optical quality of the components, manufacturing error propagation, and the effects of these on performance. Because the deformable mirror (DM) location is critical in a PIAA system, we show that despite the pupil remapping effect of the PIAA optics, a dual-DM wavefront control and shaping system architecture optimized for short angular separations is operating adequately to compensate for manufacturing errors and for the dark zone generated in the focal plane.
Conclusions. Because the errors involved are comparable to the wavefront error on the optics, wavefront control can compensate for them. Our measurements provide reliable models that, when used in simulations, allow us to refine component specification given the manufacturing errors at the raw coronagraphic performance level as well as after wavefront control and shaping.
Key words: instrumentation: high angular resolution / techniques: high angular resolution / telescopes
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The direct imaging of exoplanets is a science driver for the next generation of ground-based observatories, and has led to the emergence of extremely large telescopes (ELTs; e.g., de Zeeuw et al. 2014; Sanders 2013) and space telescopes in the ultraviolet (UV), optical, and near-infrared (NIR), such as the habitable exoplanet explorer (HABEX, Gaudi et al. 2020) and the large ultra-violet, optical, infrared (LUVOIR, France et al. 2017) surveyor mission concepts under consideration by the NASA decadal survey. These future facilities will use segmented mirrors, where large primary mirrors are required to reduce the impact of zodiacal light on the signal-to-noise ratio (S/N), to observe more distant planets, and to reach the habitable zone of planets on short orbits.
Future high-contrast imaging spectroscopy with a large segmented telescope will ultimately be used to hunt for atmospheric molecules of Earth-like planets around G-, K-, or M-type stars, where the atmosphere spectral characterization will enable investigation of their habitability and of potential bio-signatures on their planetary surface. In this context, increasing the number of target planets requires a coronagraph with a small inner working angle (IWA, Mawet et al. 2012; Stark et al. 2015). Because the baseline coronagraph designs are tailored to the telescope pupil architecture, the phase-induced amplitude apodization complex mask coronagraph (PIAACMC, Guyon et al. 2014) is a leading candidate for segmented telescopes; it gives a desirable balance between several performance characteristics and limitations, including throughput for planet light, a small inner working angle, relatively low sensitivity to tip/tilt errors, other low-order aberrations, and stellar angular size. The PIAACMC theoretically offers complete coronagraphic extinction of a point source, with high throughput and sub-λ/D IWA (where λ is the imaging wavelength and D the telescope diameter), regardless of the aperture shape. Coronagraph efficiency (throughput, IWA, sensitivity, etc.) is critical when seeking to maximize science yield in imaging and spectroscopy for direct imaging telescopes and missions.
PIAA technologies have been developed through modeling and in the laboratory since late 2002 (e.g., Guyon 2003; Guyon et al. 2006) and continue mainly in the most complex and mature form of the original concept: the PIAACMC. In recent years, advances in the PIAA technology readiness level have involved an increased number of laboratory or instrument facilities, and efforts made by a constantly growing part of the high-contrast imaging community. The PIAA coronagraph and its avatars are, for instance, part of the Subaru coronagraphic extreme-adaptive optics (SCExAO, Lozi et al. 2009; Guyon et al. 2012) system, NASA ames coronagraph experiment (ACE, Belikov et al. 2009), the high-contrast imaging testbed (HCIT, Sidick et al. 2009; Kern et al. 2011), and the segmented pupil experiment for exoplanet detection testbed (SPEED, Martinez et al. 2020). The PIAACMC was envisioned for the Nancy Grace Roman space telescope (RST, e.g., Mennesson et al. 2022), where the science yield is expected to be approximately 25 reflected light planets. However, this design was not considered to be sufficiently technologically mature by the time it came to selecting a coronagraph. Nevertheless, the PIAACMC has the potential to fulfill the requirements of a NASA program to realize a space mission to search for bio-signatures from a robust number of about 25 habitable-zone planets (Asto 2020 decadal survey through NASA great observatories mission and technology maturation program, Hartman 2022). Similarly, there are plans to use ground-based ELTs equipped with high-resolution spectroscopy, high-performance adaptive optics, and high-contrast imaging to explore worlds resembling Earth (Kasper et al. 2021). Developing technologies such as the PIAACMC will be of high priority in the coming years. The PIAACMC is based on relatively high-maturity components but requires further design optimization and system-level testing. Identifying high-precision manufacturing solutions for PIAA optics is relevant and timely, where an outstanding issue is the understanding of manufacturing limits and propagation effects with small feature sizes to assess manufacturing error propagation.
The PIAACMC consists of a phase-shift focal plane mask (FPM) combined with an optimized lossless pupil apodization, which are designed to deliver a very small IWA with a high-contrast level for an arbitrary pupil. The phase-shift FPM transmits the light outside a specific radius and induces a phase shift of the light inside the radius so that the stellar Airy disk interferes with itself destructively. The PIAACMC performance is limited by the angular size of the on-axis star (because it has a second-order response to low-order aberrations; Guyon et al. 2006) and the spectral bandwidth is limited because the radius of the phase-changing zones must be proportional to the wavelength. These fundamental limitations are taken into consideration when designing the focal plane mask size by breaking it into zones and defining optimal material thickness for each zone simultaneously for multiple wavelengths, and multiple on-sky directions. In a former study (Martinez et al. 2020, hereafter Paper I), we explored an optimal PIAACMC phase-shift FPM design for the SPEED testbed. We showed high-quality sag manufacturing for a relatively small IWA and reduced sensitivity to spectral bandwidth and investigated the expected manufacturing error impact on the performance based on numerical simulations. In Paper I, the PIAA optics for the apodization were left unexplored (metrology, simulations and testing), as were the overall PIAACMC performance evaluation (combination of our FPM prototype and PIAA mirror prototypes).
In this paper, we present the design, manufacturing, characterization, and testing of all the optical components of our PIAACMC prototype for the SPEED facility. The SPEED testbed is designed for preparatory activities for the planetary camera and spectrograph (PCS) instrument for the ESO/ELT (Kasper et al. 2021) and as a subsystem demonstrator for space missions. The general strategy for the SPEED project, an in-air coronagraphic testbed, is to serve as a pathfinder testbed for high-contrast imaging with segmented telescopes and to explore potentially valuable and perhaps risky new technologies. In this context, we show our recent developments; specifically the design, manufacturing, and testing of the phase-shifting FPM and PIAA optics using photolithography and etching. This work is complementary to our FPM analysis (Paper I) and to previous developments made over recent years in PIAA optics manufacturing (e.g., Balasubramanian et al. 2010, 2011; Guyon et al. 2010; Pluzhnik et al. 2016; Newman et al. 2016; Knight et al. 2017; Martinez et al. 2020). In particular, we use an inexpensive manufacturing technique that differs from former developments for high-precision PIAA optics (diamond turned fabrication). We generalize our analysis of the design and manufacturing process so that it can be applied to other systems. Furthermore, to our knowledge, little has been done so far to evaluate the potential of PIAACMC for segmented telescopes and to explore the manufacturing error propagation with a prototype in laboratory settings, especially in the high-contrast regime.
The paper is structured as follows: in Sect. 2, the PIAACMC design optimization process is detailed in the context of the SPEED testbed environment; in Sect. 3, the manufacturing process and the characterization of the prototypes are presented; Sect. 4 investigates the optical performance of the purpose-built FPM; Sect. 5 investigates the optical performance of the purpose-built PIAA optics; in Sect. 6, the performance of the PIAACMC with the SPEED testbed are presented, where potential improvement through manufacturing error minimization and wavefront control and shaping are evaluated. Finally, in Sect. 7, we draw our conclusions.
2 Design
2.1 The SPEED testbed
The SPEED testbed (Martinez et al. 2022) is an instrumental facility to study high-contrast imaging techniques with a segmented telescope at very short angular separations in view of the next generation of ground- and space-based observatories. Our laboratory bench is installed at the Lagrange laboratory in Nice, France, in an ISO7 clean room environment. It offers an optimal environment for studying small IWA coronagraphy, control and shaping of the wavefront, and fine correction of cophasing error by considering the effects, disturbances, and instabilities generated by pupil fragmentation. The scientific emphasis of the SPEED project is on some of the main instrumental challenges fundamental to the discovery of low-mass planets in very tight orbits, ultimately reaching the habitable zone around M-dwarfs, with ELTs, for example.
The testbed as depicted in Fig. 1 offers two different optical paths: (1) in the optical domain for fine cophasing, and (2) in the NIR for high-contrast imaging. SPEED combines a source module, a telescope simulator (orange line), and a dichroic that reflects the visible light to cophasing optics (blue line), and transmits the NIR light (red line) toward wavefront shaping, coronagraphy, and a science camera. Figure 1 presents the laboratory bench layout and hardware.
The common path includes all the optics to feed the beam to the cophasing and science paths. The telescope simulator consists of the combination of (i) an active segmented mirror (ASM, from IRIS AO vendor) with 163 segments controlled in piston and tip-tilt, and (ii) a physical mask fixed magnetically on the structure of the tip/tilt mirror (TTM, for beam stability control) to simulate the presence of a large central obscuration and secondary support structures mimicking the ESO/ELT pupil (see Fig. 2, left image).
The NIR path (H-band, red line) includes a wavefront control and shaping module made of two Kilo-C deformable mirrors (DMs) of 952 actuators (DM1 and DM2, from Boston Micromachines) separated by free-space propagation. Both DMs are in the out-of-pupil plane, enabling efficient correction of both phase and amplitude errors at short angular separations (Beaulieu et al. 2017, 2020). The targeted field of view (FoV) for the dark hole is set between 1 and 4 λ/D (small IWA and FoV). The coronagraph is a PIAACMC combining two mirrors (M1/M2) for pupil apodization, a focal plane mask (FPM2), and a Lyot stop (LS). The science camera is an infrared camera (InGaAs sensor, air-cooled) from NIT vendor that works at 1.65 µm with an internal H-band filter. The SPEED entrance pupil (Fig. 2, left image) is the main obstacle for high-contrast imaging. It exhibits enough segments to mimic a complexity in the pupil that is very similar to that of the ESO/ELT primary mirror. There are five times fewer segments in the pupil compared to the ESO/ELT but they are still four and nine times more numerous than for the Keck telescope and the James Webb space telescope (JWST), respectively. The pupil exhibits a 30% central obscuration with six spiders separated by 60 degrees, similar to the ESO/ELT secondary mirror architecture.
The bench rests on a 1.5 × 2.4 m table with active vibration isolation supports and protection panels forming an almost closed box. The area around the optical table is isolated from vibrations originating from the surrounding building. The bench also accommodates two separated coronagraphic testbeds (Fig. 1, hatched area) for controlling performance evaluations of the PIAA optics and FPMs individually before inserting them into the SPEED optical path. These coronagraphic benches have the same entrance pupil (PIAA optics testbed) or a similar f-number at the coronagraphic focus (FPM testbed) to the SPEED bench, and use the star simulator of the SPEED bench (they get the light from the SPEED fiber). In addition, we use a ZYGO interferometer (Fig. 1) for metrological or alignment purposes.
Non-common path aberrations (NCPAs) are present to some extent in all high-contrast imaging observing sequences. These contribute to an additional speckle noise, which is strongest at small angular separations and is therefore detrimental to coronagraphic performance. For SPEED, these aberrations contribute to an average wavefront error of approximately 40 nm RMS (Fig. 2, middle). In addition, an offline differential optical transfer function wavefront sensor compensation procedure (dOTF, Codona 2013) was used to reduce these NCPAs down to 28 nm RMS using the ASM for the correction (Fig. 2, right). The SPEED testbed NIR arm exhibits a Strehl ratio of >98% at 1650 nm (NCPA corrected, Martinez et al. 2022).
In the bench (see Fig. 1), the role of any off-axis parabolas (OAPs) is to transform the beam from collimated to converging, or diverging to collimated, so that any pupil or image planes can be easily identified. The first pupil plane is at the TTM plane at the early stage of the bench. Pupil conjugates are then localized at the ASM plane, at 200 mm after DM1 plane (between DM1 and DM2), at the PIAA-M1 plane, and at the Lyot stop (LS) plane. Image conjugates are localized at FM1, FPM1, APOGEE camera, FM3, FM4, FPM2, and NIT camera planes.
 |
Fig. 1 Three-dimensional CAO view of the SPEED testbed. Color code: telescope simulator and common path (orange), visible path (blue), and NIR path (red). Acronyms: TTM – tip/tilt mirror, OAP – off-axis parabola, ASM – active segmented mirror, DM – deformable mirror, FM – flat mirror, DIC – dichroic, L – lens, SCC-PS – self-coherent camera-phasing sensor, FPM – focal plane mask, PIAA-M1 and PIAA-M2 – phase induced amplitude apodization mirrors 1 and 2, LS – Lyot stop, APOGEE – visible camera, NIT – near-infrared camera, Basler – pupil camera (VIS and NIR), FF – flip flop mirror, FW – filter wheel. |
 |
Fig. 2 SPEED pupil structure and PSF quality. Left: SPEED telescope simulator pupil as assumed for the PIAACMC development. PSF in H-band without correction of non-common path aberrations (middle) and with correction (right). |
2.2 Design optimization
In this section, we briefly describe the design drivers and optimization process of our PIAACMC for SPEED. We account for the following design guidelines: the coronagraph has to accommodate to the SPEED pupil architecture and targeted FoV, to provide a contrast requirements after post-processing of <10−6 at IWA with an IWA of the order of 1λ/D, to be made of reflective optics, and to make the use of a unique Lyot stop. In addition, we wish to respect certain SPEED optical design constraints: a pupil size of 7.7 mm, a distance between PIAA-M1 (in the pupil plane) and PIAA-M2 (out of the pupil plane but in a collimated beam) of 150 mm, a coronagraphic F-number of 78, and an operating wavelength of 1.65 µm.
The PIAACMC optimization code developed by O. Guyon and written in C uses a numerical propagator specifically developed for propagation through PIAA optics (Pueyo et al. 2009) and uses matrix Fourier transform (Soummer et al. 2007) for the FPM. It only considers the PIAACMC optics, that is, a classical coronagraphic propagation process is computed independently from the SPEED testbed. The shape of the optics assumes nominal flat optics (collimated beam in, collimated beam out). In particular, in the SPEED bench, the nonzero beam angle of incidence for the PIAACMC components is omitted during the design process and has no impact on the performance (see Sect. 5.2 for more details). Various regularization parameters are tuned to constrain the optics shape and FPM sag. Regularization coefficients are applied on the FPM to exclude extreme sag values, restrict sag depth to a limited peak-to-valley (PV) range, or to penalize sag excursions that are out of the IWA within the FPM effective area. We forced the PIAA-M1 and PIAA-M2 shapes to remain centrally symmetric in order to simplify the manufacturing of the mirrors. While the departure from central symmetry can be of the same order as or even lower than the fabrication errors, we noticed that going below a contrast of 10−6 breaks the central symmetry in the shape of the optics and in this regime the PIAA optics start to perform as a wavefront control system by creating a dark hole in the image at the cost of noticeable high-frequency ripples in the optics phase profile. A trade-off is necessary between the authority given to the coronagraph and that given to the wavefront control system. We adopt the philosophy of avoiding as many ripples as possible and advocate central symmetry in the shape of the optics to ease the manufacturing process. Further details of the numerical design optimization process are provided in Paper I.
At the end of the optimization, the performance (contrast, IWA, throughput, PSF field dependence) obtained with the down-selected design is verified with an independent coronagraphic code written in IDL including Fresnel propagation (Beaulieu et al. 2018). This code is used for a tolerance analysis of the PIAACMC components (optics and FPM) in order to define the specification for the manufacturer (Martinez et al. 2018). A last numerical code is used independently to guarantee that the PIAACMC design is in step with the SPEED optical contrast design; namely the end-to-end SPEED modeling code (SPEED e2e, Beaulieu et al. 2017), which incorporates Fresnel diffraction propagation using PROPER (Krist 2007) within a realistic system model (SPEED) with simulated wavefront sensing and control, including as-built optics with measured wavefront errors.
2.3 Layout and specifications
In a PIAACMC architecture, starlight suppression is achieved by combining four elements: (i) a lossless apodization with aspheric mirrors to provide a point-spread function (PSF) with attenuated bright diffraction rings: the first mirror, namely PIAA-M1, compresses the beam into the desired pupil apodization profile and the second mirror, PIAA-M2, corrects optical path length errors that are introduced by the remapping; (ii) a complex focal plane mask that induces destructive interference inside the downstream pupil; (iii) a Lyot stop stage that blocks diffracted light, and (iv) an inverse PIAA optics stage that undistorts the wavefront, because the wavefront remapping of PIAA-M2 usually introduces a significant off-axis distortion of the field PSF.
Nonetheless, in small IWA PIAACMC, because the majority of diffraction suppression is obtained by the small phase-shifting FPM, the apodization delivered by the pair of optics is relaxed to relatively moderate sags, which reduces the off-axis PSF distortion. In PIAA optics, there is a field dependence in the PSF, but for weak apodization, the field PSF varies by a small amount. For our application, inverse PIAA is omitted due to the weak apodization resulting from a small IWA and a small FoV of interest. In SPEED, the PSF field dependence is negligible in the targeted dark hole FoV.
Our resulting PIAACMC design gathers PIAA mirrors, a reflective FPM, and a single Lyot stop. The sag depth of the PIAA mirrors is ~5 µm. The FPM is made of hexagonal tiling and includes 20 concentric rings extending to a diameter of 4 λ/D in 498 hexagons of 25 µm diameter (circumscribed diameter). The hexagons exhibit a sag that varies by a maximum of 0.4 µm relative to the outer region of the mask. The PIAACMC IWA is 1.3 λ/D (Fig. 3 of Paper I). The raw contrast delivered is better than 10−5 at IWA and better than 10−6 from 3λ/D and in the SPEED FoV. The system throughput is high (~50%), and the PSF shape remains unchanged over the FoV (Fig. 5 of Paper I).
 |
Fig. 3 Pictures and observations made of the PIAACMC components (M1, M2, and FPM) through various microscope magnifications. |
3 Manufacturing
3.1 Manufacturing process
Our PIAACMC was manufactured by SILIOS Technologies. Both FPM and PIAA M1/M2 used microtechnology processes in a cleanroom environment, where the basic principle for encoding the phase maps is to apply several successive individual steps of photolithography and etching. A maximum of 2N phase levels is achieved through N individual etching steps, which either cumulate or do not. In the specific case of the FPM, 128 (27) levels are generated with seven photolithography and etching steps. For PIAA mirrors, 256 (28) levels are generated with eight photolithography and etching steps.
All the components were manufactured into specific fused-silica substrates (Corning FPHS 7980), where the diameter of the substrates was 100 mm in order to fit with the four-inch semiconductor standards adapted to the SILIOS microtechnology equipment. The thickness was 3 mm, and the substrates were polished to reach a wavefront roughness of less than λ/20 PV at 633 nm over a surface of 15 × 15 mm2. The components were extracted from the substrate via a dicing process (diamond saw) with a centering accuracy of ±50 µm.
The etching process uses a reactive ion etching (RIE) reactor, which generates plasma (from fluoride precursor gases) in the chamber where the substrate is installed. The RIE process is based on chemical and physical etching steps. The chemical etching consists of etching the SiO2 surface with the fluoride ions, whereas the physical etching involves the sputtering of the SiO2 surface due to the accelerated ions. Both have advantages and drawbacks regarding roughness quality and the isotropy or anisotropy of the process, and a trade-off is needed to guarantee low roughness of the etched surface and pattern definition (minimizing under-etching issues).
Based on private communication with former PIAA development teams, as well as tolerance studies (Martinez et al. 2018; Beaulieu et al. 2018), our FPM sag-averaged local deviation specification is 5 nm RMS, whereas it is <50 nm RMS for the PIAA mirrors (with the best achievement being <25 nm RMS). The expected height of the discretization step is 6.25 nm (FPM) and 20 nm (PIAA mirrors). For PIAA mirrors, while the minimum resolution possible with the technology (radial discretization width) is 2 µm, we specify 15 µm, which was sufficient (Martinez et al. 2018).
3.2 Prototype characterization
Because we reported an extensive metrological characterization of the FPM in Paper I, we mainly restrict and concentrate our description on the PIAA mirror characterization. However, for the sake of clarity, we start to briefly recall the main results from the FPM control evaluation treated in Paper I in the following subsection.
3.2.1 Focal plane mask
We use a binocular microscope (Fig. 3) and an interferential microscope (WYKO NT9100) for the metrology inspection of the FPM. The cosmetic analysis shows very few artifacts or defects outside the effective area (the hexagonal tiling area), with micron-scale size and no expected impact considering the surface of the artifacts relative to the overall surface of the FPM pattern. Our manufactured FPM exhibits: (i) outstanding low-depth errors, which are independent from the zone position within the mask, (ii) high surface quality, and (iii) proper, steeply sloped transition regions. We find that the depth of the manufactured FPM zones matches the design profile with an average error of 3 nm and a standard deviation of 6 nm RMS. Our measurements provide a model of the FPM that demonstrates the expected coronagraphic performance given the manufacturing errors in simulation. We show that our purpose-built FPM (from the complete mapping of measured FPM, we numerically modeled a purpose-built 2D map of the FPM) has a limited impact on the raw coronagraphic contrast, where most of the contrast degradation occurs at short angular separations, and in particular at the IWA. As the depth errors involved are of the order of a few nanometers, which is comparable to the wavefront error on optics, we concluded that wavefront control can compensate for them and thus recover the theoretical FPM performance. However, in Paper I, we did not confirm this analysis empirically; in particular we did not confirm that (1) performance degradation was limited, as expected from simulations, (2) nor that wavefront control could effectively correct for these manufacturing errors in a laboratory setting. This aspect is treated in the present paper and presented in the following sections, along with a quality control of the PIAA mirrors.
 |
Fig. 4 Metrological control of PIAACMC mirrors. Top row: 2D map of Ml and M2 obtained with a ZYGO interferometer (12 mm diameter). Middle row: Residual errors (specification map subtracted from measurement map) for M1 and M2 over the pupil area (7.7 mm). Bottom row: Corresponding measured 1D azimuthally averaged radial profile (blue line) compared to specification (black line) for M1 (left) and M2 (right). |
3.2.2 PIAA mirrors
The PIAA mirrors are a challenging component of the system in terms of their manufacture because the departure of their shape from a flat surface is usually of the order of many waves, and they have to be manufactured very precisely. The sag depth of our PIAA mirrors is ~5 µm, which corresponds to three times the operating wavelength. Figure 3 presents an inspection of our mirrors with a binocular microscope for different magnification values, where light scattering is observable. In these images, we observe transitions instead of steps (light scattering comes from transition). The greater the number of individual levels of photolithography and etching, the brighter the transition. However, the number of individual steps is not directly proportional to the sag (if the sag follows a linear progression, the number of levels used to produce it does not follow a linear progression). We cannot therefore compare M1/M2 sags measured with a FIZEAU interferometer (Fig. 4, top raw images) and the brightness of the image obtained with the microscope (Fig. 3). While transition repartition over the mirror is inhomogeneous for that reason and because of mask repositioning errors during the individual etching steps, the mirror pattern appears relatively circularly symmetric, as specified. Mask-to-mask repositioning errors are variable from one level of photolithography to another. For this reason, the repositioning and therefore the brightness of the edges can be inhomogeneous. The transition width was measured to 3 µm and the smallest observable steps to 15 µm, which is in agreement with specifications. While light scattering might be detrimental to high-contrast imaging, we expect that it impacts performance at contrast levels way below our requirements.
Our microscope inspection allows cosmetic and dimension control of the mirrors, where a few defects or artifacts are observable but are principally outside the useful areas of the mirrors. As far as sag is concerned, we use a FIZEAU interferometer (hereafter, ZYGO Verifire xpz) combined with a 4 in. to 25 mm aperture converter from Zygo Corp. In Fig. 4, we present measured 2D maps of M1 and M2 sags (top row images), as well as azimuthally averaged radial profiles (blue lines) compared to specifications (black lines) for both mirrors (bottom row images). These latter plots show the deviation from the flat surface expressed in micrometers as a function of radius in the unit of pupil radius (3.85 mm), and the correspondence between the two is relatively accurate. The dashed line (Fig. 4) indicates the pupil radius. The interferometer sampling is 16 µm per pixel. In these conditions, transitions and the smallest etching steps are unresolved. Measured sags presented in Fig. 4 (top and bottom raw images) visually match the specified sags, even in the area of the surface where ripples in the profiles are present. The 2D M1 and M2 sag deviations from the specification are presented in Fig. 4 (middle raw images). These maps correspond to the subtraction of the measured M1/M2 maps with the ZYGO from the specification maps. Errors in M1 are relatively homogeneous, while errors in M2 appear to be affected by an asymmetry in the diagonal that does not result from the subtraction of the specified and measured maps. Indeed, measured data were first corrected for hot pixels and biased data, and subpixel recentering algorithms were applied prior to the subtraction. M1 and M2 error maps highlight errors on individual levels due to the concentric circles that are observables.
Figure 5 presents the difference between specified sags and measured sags for M1 (green curve) and M2 (purple curve) obtained from the 2D maps (Fig. 4, middle raw images) but in the form of an azimuthally averaged radial profile. Obviously, azimuthally averaged radial profiles present reduced PV errors compared to the profile presented in Fig. 4 (middle raw images). In Fig. 5, by excluding the area covered by the central obscuration (30%, identified by the dashed black line), the sag error deviation can be as high as ~100 nm PV (M2) and ~70 nm PV (M1). These are non-negligible PV errors, particularly for M2, where high PV errors dominate. Deviations of less than 10 nm (PV) are expected for targets on individual levels and on the accumulations. These measurements, which were made by the manufacturer for process control using a mechanical profilometer, were based on test areas arranged around components whose dimensions are larger than the dimensions of the actual structures of the M1/M2 pattern (resulting from a constraint of the measurement tool).
While the sag-averaged local deviation specification was 50 nm RMS, we estimated the error to be 25 nm RMS (M1) and 66 nm RMS (M2). PIAA M2 is therefore not to specification (evaluated through the pupil diameter beam footprint, including the area covered by the central obscuration). Manufacturing improvements are further discussed in Sect. 6.
 |
Fig. 5 M1 and M2 sag errors. Here we show 1D radial profiles corresponding to the subtraction of measurement data from the specification for each mirror. |
4 FPM optical efficiency
4.1 Test apparatus
The first separated optical testbed presented in Fig. 6 (most of the acronyms in this section refer to this figure) is designed to test FPMs in ideal conditions. This laboratory setting implements only the necessary elements for the performance evaluation of the optical efficiency of the FPM (with fewer optics than in the SPEED testbed in order to reduce uncertainties in the analysis). The optical design thus only successively implements an entrance pupil plane, a focal plane for the FPM, a Lyot stop plane, and a detector plane. In practice, the light comes and deviates from the SPEED testbed using a flat mirror (FM), before the SPEED telescope simulator, and after OAP0 in a collimated beam. A similar pupil to the SPEED pupil but downsized from 7.7 mm to 2.6 mm (without any segmentation) is inserted into the optical train in a mount before L1 (see Fig. 6). The pupil stop (Lyot stop) mimics our PIAACMC Lyot stop but is rescaled to the 2.6 mm entrance pupil. The entrance aperture and Lyot stop masks are in a laser-cut stainless steel sheet. The FPM is at an F/78 beam, which is similar to the coronagraphic focus of the SPEED bench. The coronagraphic testbed uses achromatic doublets (L1, L2, L3) of 200 mm in focal length. We use a super-continuum white-light source (SPEED light module source) combined with an IR narrow band filter (central wavelength of 1.65 µm). The camera is a NIR camera (from NiT vendor).
4.2 Performance
This first test intends to demonstrate the correct behavior of the FPM on the PSF. In Fig. 7, we compare the coronagraphic PSF (red line) without apodization (no M1/M2) to the noncoronagraphic and nonapodized PSF (black line), and the expected performance of the FPM alone from numerical simulation (green line) and assuming the purpose-built FPM (yellow line). The nominal PIAACMC curve is provided for reference only (blue line). Even though the M1/M2 module is missing, a coronagraphic effect is observable. The on-axis rejection rate is ~1250. By comparing, for instance, the blue line to the green line, Fig. 7 provides insight into the respective roles or impacts of the FPM and M1/M2 on the performance. Red, yellow, and green curves are similar, which indicates that the FPM optical efficiency is as expected. Both metrological inspection (Paper I) and laboratory evaluation convey optimal FPM efficiency. At this point, we are confident that the FPM is of excellent optical quality and coronagraphic efficiency.
 |
Fig. 6 Optical test apparatus for the FPM performance evaluation. Top: picture of the coronagraphic test bed for testing the individual performance of the FPM. Acronyms are as in Fig. 1 and ND and LP stand for neutral density and lens for pupil imaging mode, respectively. Bottom: simplified and in-line optical schematic design. For the sake of clarity, pupil and image conjugates are identified. |
 |
Fig. 7 Performance evaluation on the coronagraphic testbed compared with expected performances based on numerical simulations. |
5 PIAA optics efficiency
5.1 Test apparatus
The second separated optical testbed presented in Fig. 8 (most of the acronyms in this section refer to this figure) is developed to test the M1/M2 optics in ideal conditions. The laboratory setting implements the necessary optics for the performance evaluation of the optical efficiency of apodization with M1/M2 (with fewer elements than in the SPEED testbed in order to reduce uncertainties in the analysis). The optical design thus only successively implements an entrance pupil plane to install the M1/M2 module, a focal plane, and a second pupil plane where the camera is installed for pupil imaging. The light is picked up in the SPEED testbed using a flat mirror, FM(a), but this time after the SPEED telescope simulator, at the output of OAP2 and before DM1, in a collimated beam. By doing so, the pupil is the SPEED pupil (including segmentation). The PIAA M1 is aligned with the beam and is in the pupil plane. At 150 mm beyond M2, we place an achromatic doublet (L1, 500 mm focal length), and a second doublet (L2, same focal length) is installed so that the pupil is recovered after FM(c) where the camera (NiT) is placed. We use a super-continuum white-light source (SPEED light module source) combined with an IR narrow-band filter (central wavelength of 1.65 µm) directly inserted in the camera. The testbed is designed to control the impact of M1/M2 optics on the pupil structure in the relayed geometrical pupil and compare with simulations.
 |
Fig. 8 Optical test apparatus for the mirror performance evaluation. Top: picture of the coronagraphic test bed for testing the individual performance of the PIAA mirrors M1 and M2. Acronyms are as in Fig. 1. Bottom: simplified and in-line optical schematic design. Pupil and image conjugates are identified for the sake of clarity. |
 |
Fig. 9 PIAA M1/M2 opto-mechanical mount. Left: with alignment calibration wedge in white. Right: 3D CAO view with alignment calibration wedge in blue and beam alignment targets in green. |
5.2 Implementation and alignment
The PIAA-M1 is placed in a pupil plane and installed in three manual rotation stages (tip/tilt and rotation around its axis). The PIAA-M2, being out of the pupil plane (in a collimated beam), is installed in an opto-mechanical mount with six degrees of freedom for the alignment (all nonmotorized): Three rotations (tip/tilt, and rotation around its axis) and three translations (x-, y-, and z-). Figure 9 (left image) presents the opto-mechanical mount of the PIAA mirrors, where the separation between M1 and M2 is 150 mm. In practice, M1/M2 separation is guaranteed using a 3D-printed calibration wedge (see Fig. 9, the left and right images, in white and blue, respectively).
We use a ZYGO interferometer and alignment targets (see Fig. 9, in green) for the pre-alignment of the module (beam angle and M1/M2 parallelism). Alignment of the M1/M2 module in any optical testbed (SPEED or the testbed presented in Fig. 8) is a two-step alignment: the first step uses a ZYGO interferometer and guarantees alignment of the module in the optical train of the bench (see Fig. 10, top images), while the second step corresponds to a fine-tuning on the basis of the PSF quality recorded by the science detector (see Fig. 10, bottom images). When tested with the SPEED bench, we regularly monitor pupil quality using the available pupil-imaging mode of the testbed (SPEED offers a pupil-imaging mode using CMOS detectors (cameras from Basler vendor; see Fig. 1). These implementation details and alignment steps are important because (1) the PIAACMC design is the result of an optimization process that includes optical and physical parameters (beam angle, M1/M2 separation, etc.) that must be respected in practice when installed in a bench; (2) we focus on component error impact on performance and we must ensure that performance degradation is not alignment related; and (3) some physical aspects have been neglected and their potential impact had to be fairly estimated. In particular, considering (3), the design process discussed in Sect. 2.2, the aim of which is to optimize the PIAA-M1 and M2 shapes, assumes a nonphysical on-axis, unfolded collimated configuration. In the SPEED testbed, the beam angle to the PIAA mirrors is 5° (similarly to the beam angle with the FPM; see Fig. 1, where the beam is in red). Converting the PIAACMC design to an off-axis physical configuration in agreement with the SPEED optical layout is not trivial (Pluzhnik et al. 2016), and so an estimation of the impact of the 5° angle on the on-axis PIAACMC design has been investigated. We use simulations to evaluate the contrast degradation considering the beam angle. To this end, we use the sag map times cos (5°) instead of using the sag map only. This emulates the first-order effect of the beam angle on the optics: reduced optical path lengths due to non-normal incidence. We observe a negligible impact for the optics and no impact at all for the FPM (Martinez et al. 2018). A second-order effect of the off-axis term is a shape distortion, as the viewing angle changes (rotation of a 3D shape is not the same as just collapsing it by a factor of the cosine of 5°). The effect is, in principle, small because the slopes on the mirror are small.
An upper bound to the associated sag error will be equal to [sin(5°) × max sag] × max slope. The first term, sin(5°), is the maximum lateral displacement of the intersection between a light ray and the 3D optical surface. For ~ 5µm max sag (for the optics), this corresponds to a ~ 0.4 µm lateral displacement. The maximum slope value is 0.0022, corresponding to 5 µm sag over 2.3 mm. The maximum sag change over the 0.4 µm lateral displacement is therefore (5 µm/2.3 mm) × 0.4 µm = 0.9 nm. This second-order off-axis effect therefore only leaves subnanometric residuals. Both first- and second-order terms induce an almost achromatic low-order aberration term, and we conclude that wavefront aberration terms associated with translating the on-axis PIAACMC to off-axis PIAACMC for SPEED can be omitted.
 |
Fig. 10 PIAACMC control images obtained during the alignment process. Top row: PIAA M1/M2 alignment with a ZYGO interferometer, which takes measurements during (left) and at the end (right) of the alignment. Bottom row: PSF recorded at the end of the alignment procedure with the ZYGO interferometer (left) and after fine-tuning based on the PSF quality using the science detector (right). |
5.3 Performance
This second test is designed to demonstrate the correct behavior of the M1/M2 module on the pupil. With PIAA optics, the apodized pupil is created by geometric redistribution of the light rather than selective absorption. The M1/M2 module does not absorb light (PIAA is a lossless beam apodization) and preserves the sensitivity and angular resolution of the telescope. While pupil apodization by creating a soft-edged pupil reduces the Airy rings, PIAA apodization modifies the pupil structure.
For instance, our M1/M2 module impacts the pupil structure by reducing its central obscuration ratio from 30% to 22%. By doing so, it changes the relative peak diffraction intensity and the longitudinal extension of the diffraction pattern of the PSF. Our test setup is therefore designed to evaluate the pupil central obscuration modification and control pupil cosmetics. In Fig. 11, we compare our laboratory measurement (right image) to expectations based on simulations (middle image). Precise diameter measurements show that the central obscuration effectively reduces from 30% to 22%, as expected by design. We can also confirm that, as expected from the simulation, as one moves away from the centre of the pupil, the thickness of the spider widens. Some artifacts are present in the top left area of our measured image (Fig. 11, right image) and correspond to locked segments in the ASM and are of no relation to M1/M2.
However, in our laboratory data (Fig. 11, right image) we observe various bright and dark concentric rings within the pupil area that are unexpected based on simulations (middle image). When we use the M1/M2 map measured with our ZYGO in simulation (left image), these structures in the pupil are observable. Pupil structure modification occurs, as expected, but along with abnormal light distribution in the form of concentric rings.
At this point, and despite unexpected artifacts in the pupil, we are confident that M1/M2 optical apodization is efficient. Further, we compared apodized PSFs recorded in the SPEED bench and compared them to expectations from simulations; the two PSFs match at first glance (see Fig. 12). In the following section, we discuss the tests performed with the SPEED testbed.
6 Performance with the SPEED testbed
In this section, we report results from tests of the FPM and M1/M2 mirrors with the SPEED bench. We first tested the FPM alone – where M1and M2 are replaced by blank mirrors – in order to evaluate the performance of the FPM only and compare it to numerical simulations. When using M1/M2, it is then possible to assess the apodization on the noncoronagraphic PSF (off-axis PSF) and the coronagraphic performance of the whole PIAACMC (on-axis PSF).
6.1 Performance and analysis
The first test is designed to evaluate the FPM efficiency alone (no M1/M2). Figure 13 presents the PSF obtained with SPEED (dashed black line) and the one obtained from numerical simulations (dashed and dotted black line); both are nonapodized. The blue curve presents the PIAACMC nominal (including M1/M2 theoretical apodization) contrast level for reference only. The contrast curve obtained with SPEED is the red curve to compare with the expectation from the simulation (green curve). We observe good agreement between these two. Our simulation assumes a SPEED-like configuration with expected WFE; we see agreement when comparing the measured PSF to the simulated PSF. This result, presented in Fig. 13, indicates that the FPM is working correctly and as suggested from the initial analysis presented in Paper I, and as expected from the complementary results shown in Sect. 4 of this paper.
The second test is designed to evaluate the efficiency of the complete PIAACMC. Figure 14 presents the results, where the blue curve stands for the PIAACMC nominal contrast level for reference only, the red curve is the measured PIAACMC contrast (Fig. 12, right image is the recorded PIAACMC image), the green curve is the expected contrast level assuming the purpose-built PIAACMC (FPM and M1/M2, Fig. 12, third image from the left is the simulated PIAACMC image), and the yellow curve is similar to the green curve but includes the expected SPEED configuration (WFE). Finally, the black curves are off-axis PSFs:
(1) recorded on the bench (dashed line), (2) theoretical for reference only (solid line), (3) and as expected from a SPEED-like simulation (dashed and dotted line). Analysis of these results and comparison with our former result (Fig. 13) indicates that the PIAACMC-measured contrast level is not in line with our desired specification (nominal contrast level in blue). Considering the complete former analysis presented in previous sections, the degradation can only be explained by the optical quality of the M1/M2 (Fig. 4). The M1 and M2 residual error pattern presented in Fig. 4 are identified as the origin of the contrast loss. Further analysis demonstrates that M2 is predominant in the degradation of performance. In simulations, when only the purpose-built M1 is considered (M2 is left ideal), the contrast curve evolves from 10−3 to 10−4 between the on-axis position and 10 λ/D, while when only the purpose-built M2 is considered (M1 is left ideal), the contrast curve evolves from 10−2 to 10−3 at the same angular separation. In the following two subsections, we show that both manufacturing improvement and wavefront control can act to recover the nominal performance.
 |
Fig. 11 Geometric apodized pupil images by M1/M2. Left: from simulation using theoretical M1/M2 maps. Middle: from simulations using measured M1/M2 maps. Right: from laboratory data using M1/M2 prototypes. |
 |
Fig. 12 From left to right: NIR (H-band) apodized PSF from simulation data using theoretical M1 and M2 maps, from laboratory measurements with the SPEED testbed, PIAACMC image from simulation data, and PIAACMC image as recorded on the SPEED bench. The color scales of all images are log-stretch. |
 |
Fig. 13 Performances obtained with the SPEED testbed using the FPM only (no apodization) and compared to simulations. |
6.2 Improving contrast: Reducing manufacturing errors
While the depth errors involved for the FPM are of the order of a few nanometers only, the depth errors involved for the PIAA mirrors are more significant and represent a PV of a few hundred nanometers. Because FPM and M1/M2 present sag and pattern differences, it is critical that we understand the origin of the manufacturing errors and that we assess whether or not they can be corrected. By comparing the manufacturing quality and optical efficiency of the components, we can derive some basic conclusions and define some manufacturing guidelines: (i) the FPM is operating as expected because its optical quality is within the specification, and (ii) the PIAA mirrors, because they exhibit sag deviation that is not in line with our desired specification, have a severely impacted performance.
The FPM sag local deviation is at an average error of 3 nm and standard deviation of 6 nm RMS (Paper I, based on a histogram of the difference between measured and specified segment depths). This optical quality meets our expectations (based on measurements made by the manufacturer on test components). The optical efficiency of the FPM is confirmed by experimental and numerical evaluations. The characteristic size of the FPM features is 25 µm, with depths ranging over ±0.4 µm.
The M1/M2 sag local deviation reaches maximum errors of 73 nm and 236 nm, and standard deviations of 25 nm RMS and 66 nm RMS, for M1 and M2, respectively. We observe a difference between the measurement carried out by the manufacturer using a mechanical profilometer in test components for process control (less than 10 nm PV) and the actual depths in the patterns of our components. We suspect that the etching behavior differs from expectations when multilevel and deep sag patterns are involved. The effects of variations on the local behavior of the etching process – which depends on the geometries, characteristic sizes, and the local environment of the engraved pattern – could be the origin of this discrepancy. In particular, the etch levels of annular geometry may participate in this phenomenon. Improving the accuracy of the realization of the M1/M2 mirrors requires that we (i) set up a procedure to iteratively control etching depths (sag levels) of the prototype during manufacturing and no longer in test patterns (at least for the two or three deepest levels of engraving, which benefit from the least narrow geometries) and to include test patterns outside of the M1/M2 useful areas; (ii) assess the impact of different etch geometries by comparing the values measured in the test areas and the values actually engraved in the useful pattern; (iii) revise the specification regarding the lateral discretization of the M1/M2 pattern (the thinnest rings measured on our M1/M2 have a width of about 15 µm, which is 10 µm smaller than the characteristic size of the FPM features); and finally (iv) refine the M1/M2 sag deviation specification based on our reliable error map models.
For (iii), and based on former simulation analysis (Martinez et al. 2018), we find that the 15 µm formerly specified can be revised to 25 µm or 50 µm, considering that the SPEED wave-front error budget is better settled and that the purpose-built FPM impact is known. For (iv), we propose to refine the specifications regarding the surface quality on M1 and M2. The objective is threefold: (i) characterize the impact of individual mirror errors (as a function of the sag deviation from specification) on the contrast (M1 is in the pupil plane, M2 is an out-of-pupil plane mirror); (ii) define an accurate specification regarding the manufacturing process for both mirrors; and (iii) assess the contrast evolution when the local deviation of the sag is below 10 nm (PV), which is the deviation initially expected for the manufacturing process. Our analysis is based on numerical simulations, where the M1/M2 error patterns presented in Fig. 4 (middle row images) are used to model a representative error map of 1 nm RMS that can be added to the theoretical M1/M2 maps to emulate scalable manufacturing errors. From these M1/M2 error maps, which are scaled down to a wavefront error of 1 nm RMS over the pupil area, we can assess the impact of errors of various amplitudes, namely from 1 nm RMS to 100 nm RMS, when applied independently to M1 and M2. Our simulations use a code written in IDL that includes Fresnel propagation using PROPER (Krist 2007), and a matrix Fourier transform (Soummer et al. 2007) for the FPM and the SPEED pupil. While it is difficult to translate RMS to PV error, we can empirically estimate from our modeled error maps of M1/M2 that the PV error is higher than the RMS error by a factor of 7 (M1) and 5 (M2). Therefore, 1 nm RMS is approximately equivalent to 7 nm PV (M1) and 5 nm PV (M2).
Several metrics can be used to quantify the capability of a coronagraph, and we base our analysis on the contrast between the star peak and an average intensity in an annular region of the focal plane where an off-axis companion is expected. The metric reads as
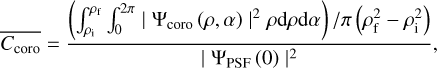 (1)
(1)
where ρ and α are the radial and angular coordinates, respectively, ρi and ρf are the inner and outer radii of the annular region considered, respectively, | ΨPSF (0) |2 is the maximum intensity of the star image (at the center) on the detector (without the FPM, but the term includes the M1/M2 mirrors), and | ΨCORO(ρ, α) |2 is the intensity of the coronagraphic image on the detector. We use this metric to study the variation in performance of the PIAACMC concerning the M1/M2 errors in nm RMS.
We note that this metric for contrast estimation does not include the effects of reduced Strehl ratio or throughput for off-axis sources. It is a common choice for such a metric and all the more because in small-IWA PIAACMC, the off-axis PSF distortion is reduced (see Paper I, Sect. 2.1 and Fig. 5).
The area of calculation in the focal plane for 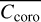 can be matched to the instrumental parameters. The width of the ring can be modified to match SPEED requirements. For most results presented hereafter, the search area is bounded at ρi = 1.3λ/D for short radii (IWA requirement) and at ρf = 10λ/D for large radii (hereafter, region 1). Alternatively,
can be matched to the instrumental parameters. The width of the ring can be modified to match SPEED requirements. For most results presented hereafter, the search area is bounded at ρi = 1.3λ/D for short radii (IWA requirement) and at ρf = 10λ/D for large radii (hereafter, region 1). Alternatively, 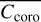 is evaluated at IWA in a ring of width λ/D (hereafter, region 2).
is evaluated at IWA in a ring of width λ/D (hereafter, region 2).
Figure 15 shows 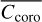 in the form of a contour plot as a function of M1 and M2 errors, both expressed in nm RMS. The images in the top row present
in the form of a contour plot as a function of M1 and M2 errors, both expressed in nm RMS. The images in the top row present 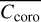 evaluated in region 1 (left image) and in region 2 (right image) when errors in the mirrors deviate from specification by up to 50 nm RMS. Bottom-row images present similar results but for errors in mirrors deviating from specification by up to 10 nm RMS only. From these plots, we can make several observations:
evaluated in region 1 (left image) and in region 2 (right image) when errors in the mirrors deviate from specification by up to 50 nm RMS. Bottom-row images present similar results but for errors in mirrors deviating from specification by up to 10 nm RMS only. From these plots, we can make several observations:
Independently from the region considered,
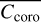 is highly sensitive to M1/M2 errors, even for a small amount of deviation from our desired specification. For instance, for Ml and M2 errors of 10 nm RMS, contrast drops from 5 × 10−7 to 10−5 (region 1) and from 2 × 10−6 to 9 × 10−5, respectively (see Fig. 15, bottom row images).
is highly sensitive to M1/M2 errors, even for a small amount of deviation from our desired specification. For instance, for Ml and M2 errors of 10 nm RMS, contrast drops from 5 × 10−7 to 10−5 (region 1) and from 2 × 10−6 to 9 × 10−5, respectively (see Fig. 15, bottom row images).When
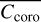 is evaluated in region 1 (at large angular separation and wide area), M1 has a greater impact on contrast than M2 (left column images). For instance, for a contrast level of 6 × 10−5 (top left image), mirrors can accept 28 nm RMS (M1) and 36 nm RMS (M2).
is evaluated in region 1 (at large angular separation and wide area), M1 has a greater impact on contrast than M2 (left column images). For instance, for a contrast level of 6 × 10−5 (top left image), mirrors can accept 28 nm RMS (M1) and 36 nm RMS (M2).When
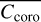 is evaluated in region 2 (at IWA), M2 has a greater impact on contrast than M1 (right column images). For a contrast level of 6 × 10−5 (bottom right image), mirrors can accept 12 nm RMS (M1) and 8 nm RMS (M2).
is evaluated in region 2 (at IWA), M2 has a greater impact on contrast than M1 (right column images). For a contrast level of 6 × 10−5 (bottom right image), mirrors can accept 12 nm RMS (M1) and 8 nm RMS (M2).
These results indicate that where sag errors are concerned, and based on realistic error models for M1/M2 mirrors, PIAACMC degrades significantly and rapidly with increasing error levels. In addition, Fig. 15 (bottom row images) provides insight into the performance that can be expected to be obtained if deviations of below 10 nm RMS are achieved. Translating the FPM evaluated quality (6 nm RMS) to the M1/M2 realization would provide a significant improvement on the contrast currently reached by our prototypes, that is, toward levels that are in line with the SPEED raw coronagraphic specifications.
 |
Fig. 14 Performances obtained with the SPEED testbed using the PIAACMC and compared to simulations. |
 |
Fig. 15 Contour plots presenting contrast evaluated from IWA to OWA (left images) and at IWA in a ring of λ/D (figures on the right) as a function of M1 and M2 errors expressed in nm RMS. Color bars are given as an indication only. To convert RMS to PV errors, in our modeled error maps, PV error is higher than the RMS error by a factor of 7 for M1 and 5 for M2. |
6.3 Improving the contrast: Wavefront control
In Paper I, we suggest that because the depth errors involved for the FPM are of the order of a few nanometers, which is comparable to the wavefront errors on the optics, wavefront control can compensate for them and thus recover the theoretical FPM performance. Because the amplitude of the errors in the fabricated PIAA mirrors is larger than that of the error on the FPM, while remaining within the wavefront control dynamic range, the question is even more timely. Because wavefront shaping at small angles is generally more difficult than at greater angular separations, it is important to evaluate the capacity of our dual-DM system to compensate for the PIAACMC optics errors.
For this purpose, we use the SPEED end-to-end (e2e) numerical code. SPEED e2e is a high-fidelity performance end-to-end simulator of the bench that is designed for specification, contrast analysis, and system verification (Beaulieu et al. 2017, 2020). It incorporates Fresnel diffraction propagation using PROPER (Krist 2007) combined with a realistic system model, and is up to date with the bench optical design. It uses simulated wavefront sensing and control, including as-built optics with measured wavefront errors, and guarantees that the emulator is in agreement with the SPEED bench optical contrast design. The SPEED e2e reproduces the reality of optics positioning and wavefront errors on optical surfaces far from the pupil plane (considering Talbot length), which translates through Fresnel propagation into chromatic phase and amplitude perturbations. The code also includes a dark hole algorithm using DM1 and DM2, our two out-of-pupil deformable mirrors.
The algorithm generating the zone of high contrast in the science image is based on a linear approach and minimizes the energy inside the dark hole. The dark hole algorithm is implemented and described in detail in separate papers (Beaulieu et al. 2017, Beaulieu et al. 2020). Briefly, the electric field conjugation (EFC) approach is implemented and defined by first computing the total energy at the image plane with one DM and then generalized to the case with two DMs. This method uses setup matrix representation to compute the DM coefficients, where these coefficients allow the energy inside a dark region – the so-called dark hole – to be minimized. The interaction matrix, which represents the system response of each DM actuator, is computed by (1) adding a poke to each actuator, (2) propagating the wavefront all along the setup, and (3) recording the complex electric field at the focal plane.
We define a nominal case as a basis for comparison so that we may assess the relative impact of the optical quality of M1 and M2. This nominal case corresponds to a setup of 25 optics (SPEED testbed) containing: (i) an obscured mask with spiders located on a tip-tilt mirror, (ii) an imperfectly phased segmented mirror (the ASM with 163 segments, assuming 5 nm RMS piston errors, 5 nm RMS tip/tilt errors, and 10 nm RMS focus errors), and (iii) a PIAACMC coronagraph (purpose-built FPM and either purpose-built M1/M2 maps or M1/M2 theoretical maps with modeled errors, as described in the previous subsection), and (iv) two DMs (34 × 34 actuators) with a finite stroke of 1.5 µm (but infinite stroke precision: an actuator stroke is encoded with an infinite precision, i.e., using ideal drive electronics) located 1.5 and 0.2 m from the pupil plane. The nominal case assumes 5 nm rms aberration with a PSD in ƒ−3 for each passive and active optic including the dichroic (8 nm RMS) and the DM windows (10 nm RMS). The total aberration level of the setup is 30 nm RMS, which corresponds to the SPEED wave-front error level after correction of NCPA. For statistical analysis, 128 phase realizations are defined per optic and the performance is computed for each of these cases. The statistical validity of using 128 realizations has been verified (Beaulieu et al. 2017). The numerical pupil diameter size is 225 pixels corresponding to the 7.7 mm pupil diameter for a grid size of 1024 pixels. The simulation is monochromatic at the wavelength of 1.65 µm.
Figure 16 shows the contrast ratio histogram for the nominal case in black (perfect M1/M2, purpose-built FPM), representing the number of realizations (ordinate) that reach a given 5σ contrast (abscissa, in logarithm scale) defined as the median of the contrast computed within a dark hole from 0.8 to 4 λ/D from the optical axis. For instance, in Fig. 16, the red curve provides the number of realizations that reach a given 5σ contrast in the dark hole assuming the purpose-built FPM and M1/M2. The degradation with respect to the nominal case (including ideal M1/M2 and purpose-built FPM) is obvious and reveals the impact of the M1/M2 manufacturing errors discussed above.
By using the modeled M1/M2 error maps of 1 nm RMS scaled to various amplitude values, we found that the departure from the nominal case occurs at error levels of between 30 and 40 nm RMS. Assuming that these M1/M2 errors are reduced equally to 30 nm RMS, the performance represented by the orange curve brings the 5σ contrast in the dark hole to the same level as the nominal case. In other words, manufacturing errors of the order of 30 nm RMS per mirror are correctable by our wavefront control system. Error levels higher than that (40 nm RMS for instance) impact the capability of our wave-front shaping to dig into the dark hole. Because the location of the DM is critical in a PIAA system, this simulation shows that despite the pupil remapping effect of the PIAA optics (with no inverse PIAA in our system), a dual-DM wavefront control and shaping system architecture – ahead of the PIAA mirrors and optimized to short angular separations – is operating at a level that is adequate for generating a dark zone and for compensating for PIAACMC manufacturing errors. However, because our simulations assume a perfect wavefront sensor, a perfect detector (no readout and current noises), and preclude amplitude and temporal errors, the algorithm reaches – in this ideal regime that is free of various source uncertainties – very high-contrast dynamics; that is, a nominal 5σ contrast ratio of below 10−9, which is well below what SPEED will achieve. This nominal contrast ratio serves as a reference, helping us to define an upper bound limit on the M1/M2 manufacturing error. Specifications must be tighter in reality. Further, because it is generally advised that the load on the wavefront control system be reduced by as much as possible, improving the manufacturing process is essential, and should be made a priority.
 |
Fig. 16 5σ PIAACMC contrast (median) ratio histogram for aberrated mirrors (M1/M2) considering as-built mirrors (red), 20 nm RMS per mirror (blue), 30 nm RMS per mirror (orange), 40 nm RMS per mirror (cyan), and with no aberrations (black). |
7 Conclusions
In this paper, we evaluate a PIAACMC prototype designed for a segmented telescope and manufactured using photolithography and an etching technique, and assess the impact of manufacturing errors. We demonstrate the feasibility of manufacturing high-quality PIAACMC optics with high performance for the FPM (a complex phase-shifting optical element), and milder efficiency for the mirrors (phase-induced amplitude apodization). The purpose-built FPM shows a limited impact on the raw coronagraphic contrast, where most contrast degradation occurs at short angular separations and at the IWA. Despite accurate sag profiles, the purpose-built mirrors impact the raw coronagraphic performance where the contrast level is more sensitive to M2 errors than M1 errors at short angular separations. We expect that PIAA mirrors will be made with similar optical quality to the FPM by improving the manufacturing process and component specifications. Our measurements provide a model of the FPM and PIAA mirrors, which, when used in simulations, sets the expected coronagraphic performance given the manufacturing errors. Because the depth of the errors involved is within the dynamic range of the wavefront control, this latter can compensate for them and thus recover most of the theoretical PIAACMC performance, despite the fact that no inverse PIAA system is implemented within SPEED. This was verified with complex simulations. It is critical that we evaluate the capacity of our dual-DM system to experimentally correct these errors. It is also mandatory that we assess its ability to operate adequately, correct for manufacturing errors, and generate a small field dark hole at short angular separations. These aspects will be studied on the SPEED facility in future work. We will also oversee the manufacture of a second generation of PIAA mirrors using photolithography and the etching process. A direct comparison between different manufacturing processes (e.g., photolithography and etching vs. diamond turning) is not trivial (see a discussion about the FPM in Paper I, Sect. 3.3 and 3.4). Our results demonstrate that the combination of photolithography and etching is a relevant and inexpensive manufacturing technique for producing PIAACMC components, particularly for ground-based and segmented observatories. However, as contrast requirements become more challenging (e.g., space-based application), the manufacturing process will become more complex, requiring cycling between optical testing and polishing and etching iterations, which has not yet been explored. Further, the discretization steps would need to be reduced.
Acknowledgements
This activity received funding from CNES (the French space agency) under contract 4500063765/DIA094.
Appendix A M1 and M2 spare prototypes
Spare PIAA M1 and M2 prototypes were evaluated similarly, and they demonstrate similar manufacturing quality and thus highlight the consistency of the process. Figure A.1 presents the error maps, while Fig. A.2 presents the measured 1D azimuthally averaged radial profile that can be compared to specifications. We estimated the error to be 23 nm RMS (M1 ref-1906), 31 nm RMS (M1 ref-1907), 53 nm RMS (M2 ref-1909), and 60 nm RMS (M2 ref-1910).
 |
Fig. A.1 Residual errors (specification map subtracted from measurement map obtained with a ZYGO interferometer) for M1 and M2 over the pupil area (7.7 mm) for various spare prototypes. |
 |
Fig. A.2 Azimuthally averaged radial profile (blue line) obtained from measurements compared to specification (black line) for M1 and M2 spares. |
References
- Balasubramanian, K., Shaklan, S. B., Pueyo, L., Wilson, D. W., & Guyon, O. 2010, SPIE Conf. Ser., 7731, 77314U [NASA ADS] [Google Scholar]
- Balasubramanian, K., Cady, E., Pueyo, L., et al. 2011, Proc. SPIE, 8151, 815105 [NASA ADS] [CrossRef] [Google Scholar]
- Beaulieu, M., Abe, L., Martinez, P., et al. 2017, MNRAS, 469, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Beaulieu, M., Martinez, P., Abe, L., et al. 2018, SPIE Conf. Ser., 10700, 107003O [NASA ADS] [Google Scholar]
- Beaulieu, M., Martinez, P., Abe, L., et al. 2020, MNRAS, 498, 3914 [NASA ADS] [CrossRef] [Google Scholar]
- Belikov, R., Pluzhnik, E., Connelley, M. S., et al. 2009, SPIE Conf. Ser., 7440, 74400J [NASA ADS] [Google Scholar]
- Codona, J. L. 2013, Opt. Eng., 52, 097105 [CrossRef] [Google Scholar]
- de Zeeuw, T., Tamai, R., & Liske, J. 2014, The Messenger, 158, 3 [NASA ADS] [Google Scholar]
- France, K., Fleming, B., West, G., et al. 2017, SPIE Conf. Ser., 10397, 1039713 [Google Scholar]
- Gaudi, B. S., Seager, S., Mennesson, B., et al. 2020, ArXiv e-prints [arXiv: 2001.06683] [Google Scholar]
- Guyon, O. 2003, A&A, 404, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guyon, O., Pluzhnik, E. A., Kuchner, M. J., Collins, B., & Ridgway, S. T. 2006, ApJS, 167, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Pluzhnik, E., Martinache, F., et al. 2010, PASP, 122, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Kern, B., Belikov, R., et al. 2012, Am. Astron. Soc. Meeting Abstracts, 219, 155.15 [NASA ADS] [Google Scholar]
- Guyon, O., Hinz, P. M., Cady, E., Belikov, R., & Martinache, F. 2014, ApJ, 780, 171 [Google Scholar]
- Hartman, C. 2022, in 44th COSPAR Scientific Assembly, Held 16–24 July, 44, 1884 [Google Scholar]
- Kasper, M., Cerpa Urra, N., Pathak, P., et al. 2021, The Messenger, 182, 38 [Google Scholar]
- Kern, B., Guyon, O., Give’on, A., Kuhnert, A., & Niessner, A. 2011, SPIE Conf. Ser., 8151, 815104 [NASA ADS] [Google Scholar]
- Knight, J. M., Brewer, J., Hamilton, R., et al. 2017, SPIE Conf. Ser., 10400, 104000N [NASA ADS] [Google Scholar]
- Krist, J. E. 2007, Proc. SPIE, 6675, 66750P [NASA ADS] [CrossRef] [Google Scholar]
- Lozi, J., Martinache, F., & Guyon, O. 2009, PASP, 121, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, P., Beaulieu, M., Guyon, O., et al. 2018, SPIE Conf. Ser., 10702, 1070243 [NASA ADS] [Google Scholar]
- Martinez, P., Beaulieu, M., Barjot, K., et al. 2020, A&A, 635, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, P., Beaulieu, M., Gouvret, C., et al. 2022, SPIE Conf. Ser., 12184, 121843W [NASA ADS] [Google Scholar]
- Mawet, D., Pueyo, L., Lawson, P., et al. 2012, in Proc. SPIE, 8442, 844204 [Google Scholar]
- Mennesson, B., Bailey, V. P., Zellem, R., et al. 2022, SPIE Conf. Ser., 12180, 121801W [NASA ADS] [Google Scholar]
- Newman, K., Conway, J., Belikov, R., & Guyon, O. 2016, PASP, 128, 055003 [NASA ADS] [CrossRef] [Google Scholar]
- Pluzhnik, E., Guyon, O., Belikov, R., & Bendek, E. 2016, J. Astron. Telescopes Instrum. Syst., 2, 011018 [NASA ADS] [CrossRef] [Google Scholar]
- Pueyo, L., Shaklan, S., Give’on, A., & Krist, J. 2009, Proc. SPIE, 7440, 74400E [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, G. H. 2013, J. Astrophys. Astron., 34, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Sidick, E., Lou, J. Z., Shaklan, S., & Levine, M. 2009, Proc. SPIE, 7440, 74400I [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Pueyo, L., Sivaramakrishnan, A., & Vanderbei, R. J. 2007, Opt. Express, 15, 15935 [CrossRef] [Google Scholar]
- Stark, C. C., Roberge, A., Mandell, A., et al. 2015, ApJ, 808, 149 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Three-dimensional CAO view of the SPEED testbed. Color code: telescope simulator and common path (orange), visible path (blue), and NIR path (red). Acronyms: TTM – tip/tilt mirror, OAP – off-axis parabola, ASM – active segmented mirror, DM – deformable mirror, FM – flat mirror, DIC – dichroic, L – lens, SCC-PS – self-coherent camera-phasing sensor, FPM – focal plane mask, PIAA-M1 and PIAA-M2 – phase induced amplitude apodization mirrors 1 and 2, LS – Lyot stop, APOGEE – visible camera, NIT – near-infrared camera, Basler – pupil camera (VIS and NIR), FF – flip flop mirror, FW – filter wheel. |
| In the text | |
 |
Fig. 2 SPEED pupil structure and PSF quality. Left: SPEED telescope simulator pupil as assumed for the PIAACMC development. PSF in H-band without correction of non-common path aberrations (middle) and with correction (right). |
| In the text | |
 |
Fig. 3 Pictures and observations made of the PIAACMC components (M1, M2, and FPM) through various microscope magnifications. |
| In the text | |
 |
Fig. 4 Metrological control of PIAACMC mirrors. Top row: 2D map of Ml and M2 obtained with a ZYGO interferometer (12 mm diameter). Middle row: Residual errors (specification map subtracted from measurement map) for M1 and M2 over the pupil area (7.7 mm). Bottom row: Corresponding measured 1D azimuthally averaged radial profile (blue line) compared to specification (black line) for M1 (left) and M2 (right). |
| In the text | |
 |
Fig. 5 M1 and M2 sag errors. Here we show 1D radial profiles corresponding to the subtraction of measurement data from the specification for each mirror. |
| In the text | |
 |
Fig. 6 Optical test apparatus for the FPM performance evaluation. Top: picture of the coronagraphic test bed for testing the individual performance of the FPM. Acronyms are as in Fig. 1 and ND and LP stand for neutral density and lens for pupil imaging mode, respectively. Bottom: simplified and in-line optical schematic design. For the sake of clarity, pupil and image conjugates are identified. |
| In the text | |
 |
Fig. 7 Performance evaluation on the coronagraphic testbed compared with expected performances based on numerical simulations. |
| In the text | |
 |
Fig. 8 Optical test apparatus for the mirror performance evaluation. Top: picture of the coronagraphic test bed for testing the individual performance of the PIAA mirrors M1 and M2. Acronyms are as in Fig. 1. Bottom: simplified and in-line optical schematic design. Pupil and image conjugates are identified for the sake of clarity. |
| In the text | |
 |
Fig. 9 PIAA M1/M2 opto-mechanical mount. Left: with alignment calibration wedge in white. Right: 3D CAO view with alignment calibration wedge in blue and beam alignment targets in green. |
| In the text | |
 |
Fig. 10 PIAACMC control images obtained during the alignment process. Top row: PIAA M1/M2 alignment with a ZYGO interferometer, which takes measurements during (left) and at the end (right) of the alignment. Bottom row: PSF recorded at the end of the alignment procedure with the ZYGO interferometer (left) and after fine-tuning based on the PSF quality using the science detector (right). |
| In the text | |
 |
Fig. 11 Geometric apodized pupil images by M1/M2. Left: from simulation using theoretical M1/M2 maps. Middle: from simulations using measured M1/M2 maps. Right: from laboratory data using M1/M2 prototypes. |
| In the text | |
 |
Fig. 12 From left to right: NIR (H-band) apodized PSF from simulation data using theoretical M1 and M2 maps, from laboratory measurements with the SPEED testbed, PIAACMC image from simulation data, and PIAACMC image as recorded on the SPEED bench. The color scales of all images are log-stretch. |
| In the text | |
 |
Fig. 13 Performances obtained with the SPEED testbed using the FPM only (no apodization) and compared to simulations. |
| In the text | |
 |
Fig. 14 Performances obtained with the SPEED testbed using the PIAACMC and compared to simulations. |
| In the text | |
 |
Fig. 15 Contour plots presenting contrast evaluated from IWA to OWA (left images) and at IWA in a ring of λ/D (figures on the right) as a function of M1 and M2 errors expressed in nm RMS. Color bars are given as an indication only. To convert RMS to PV errors, in our modeled error maps, PV error is higher than the RMS error by a factor of 7 for M1 and 5 for M2. |
| In the text | |
 |
Fig. 16 5σ PIAACMC contrast (median) ratio histogram for aberrated mirrors (M1/M2) considering as-built mirrors (red), 20 nm RMS per mirror (blue), 30 nm RMS per mirror (orange), 40 nm RMS per mirror (cyan), and with no aberrations (black). |
| In the text | |
 |
Fig. A.1 Residual errors (specification map subtracted from measurement map obtained with a ZYGO interferometer) for M1 and M2 over the pupil area (7.7 mm) for various spare prototypes. |
| In the text | |
 |
Fig. A.2 Azimuthally averaged radial profile (blue line) obtained from measurements compared to specification (black line) for M1 and M2 spares. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


