EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A72 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A72
Number of page(s) 10
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/202347676
Published online 09 November 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Following the discovery of HD 140283 and HD 19445 by Chamberlain & Aller (1951), the search for metal-poor stars proceeded serendipitously or by selecting stars with anomalous kinematics with regard to the Galactic rotation (Bessell & Norris 1984). A breakthrough came in the 1980s with the H&K survey of Beers et al. (1985), who identified many metal-poor candidates with [Fe/H] ≈ −4 that were later confirmed by means of high-resolution follow-ups (Molaro & Castelli 1990; Molaro & Bonifacio 1990). The H&K survey revealed that a large fraction of metal-poor stars were enriched in carbon, the so-called carbon-enriched metal-poor (CEMP) stars. CEMP stars show the presence of neutron-capture (n-capture) elements, revealing the imprint of asymptotic giant branch (AGB) contamination. A puzzling CEMP star without any detectable presence of elements formed by the slow n-capture process, CS 22957-27, was found by Norris et al. (1997) and Bonifacio et al. (1998). These papers were submitted a few days apart. Other CEMP stars without signs of n-capture elements were found by Aoki et al. (2002), and Christlieb et al. (2004) discovered the remarkable HE 0107–5240 giant with [Fe/H] = −5.4, [C/Fe] > 3.9, and no detectable n-capture elements, from the Hamburg/ESO objective prism survey. These stars were grouped into the CEMP-no class, where the ‘no’ indicates the absence of n-capture elements, defined as stars with [C/Fe] > 0.7, originally >1.0, and [Ba/Fe]< 0.0; the more common stars with [Ba/Fe] > 1 are called CEMP-s, where‘s’ indicates the presence of n-capture elements (Beers & Christlieb 2005).

Spite et al. (2013) noted that [C/Fe] increases with decreasing iron, which implies a constant carbon abundance, and suggested two different nucleosynthetic origins for the carbon in the CEMP-no and CEMP-s stars. While in CEMP-s stars carbon is coming from an AGB companion along with the n-capture elements, in the CEMP-no stars the carbon was presumably already present in the gas from which the star formed (Spite et al. 2013; Bonifacio et al. 2015). Radial velocity studies have found that almost all CEMP-s stars are in binary systems, unlike CEMP-no stars, which supports this idea (Hansen et al. 2015, 2016).

Subsequent surveys such as the Sloan Digital Sky Survey (York et al. 2000) and its extensions SEGUE (Yanny et al. 2009) and SEGUE-2 (Rockosi et al. 2022), AEGIS (Keller et al. 2007), LAMOST (Deng et al. 2012), Pristine (Starkenburg et al. 2017), and TOPoS (Caffau et al. 2013) increased the number of known CEMP-no stars, showing that they dominate the low-metallicity tail. Metal-poor stars are defined as ultra metal-poor (UMP), hyper metal-poor (HMP), and mega metal-poor (MMP), corresponding to [Fe/H] < −4, [Fe/H] < −5, and [Fe/H] < −6, respectively. There are two MMP stars and seven HMP stars known to date, all of which are CEMP-no. There are also five known UMP stars with [Fe/H] < −4.5, three of which are CEMP-no and two are normal stars with approximately solar-scaled abundances (see Aguado et al. 2023 and references therein). Cooling of the gas by fine-structure line emission of singly ionised carbon or neutral atomic oxygen could have allowed the formation of CEMP-no stars earlier than those with normal carbon levels (Bromm & Loeb 2003). CEMP-s stars are seen only for [Fe/H] > -4.5, and this is likely because CEMP-s stars require the time necessary for the companion to evolve into an AGB star. It was also determined that CEMP-no stars are found primarily in the outer halo (Carollo et al. 2012), while a significant dearth of CEMP-no stars in the Galactic Bulge is interpreted as a signature of pair instability supernovae (SNe; Pagnini et al. 2023). Zepeda et al. (2023) found evidence that CEMP-no stars form chemo-dynamically tagged groups with a low dispersion in their [C/Fe] abundances.

The extremely low iron abundance of MMP and HMP stars suggests that only a few and perhaps just one single progenitor polluted the gas out of which they formed. The C enhancement could originate from faint SNe with energies of 1051 erg together with mixing and fallback (Umeda & Nomoto 2003, 2005; Nomoto et al. 2013; Tominaga et al. 2007, 2014). With a large amount of fallback, faint SNe eject a lot of carbon and a small amount of Fe. This produces ejecta with large [C/Fe] abundance ratios. An alternative model to explain the CEMP-no stars is represented by massive, low-metallicity fast-rotating stars called spinstars, with efficient mixing and mass loss (Meynet et al. 2006; Chiappini et al. 2008; Maeder et al. 2015; Limongi & Chieffi 2018). Therefore, the identification of the progenitors of CEMP-no stars has important bearings on the nature of the first stars (Frebel & Norris 2015). The elemental abundance pattern includes a limited number of elements, and the progenitors are poorly constrained. Thanks to their carbon enhancement, CEMP-no stars offer a unique opportunity to explore the behaviour of 12C/13C at the lowest metallicities. At low metallicities, very high 12C/13C ratios, greater than 103, are expected due to the secondary nature of 13C (Chiappini et al. 2008; Romano & Matteucci 2003; Romano 2022; Kobayashi et al. 2020a). Aguado et al. (2022, 2023) derived significant bounds to the isotopic ratio 12C/13C in HE 0107–5240 and SMSS J1605–1443, with [Fe/H] = −5.8 and −6.2, respectively. In this paper we extend this analysis to four additional known extremely metal-poor (EMP) CEMP-no stars. We also reconsider the previous analysis of SMSS J1605–1443, for which new observations have since been conducted, and turn the bound into a value. We then discuss the results in the context of 12C/13C determinations in other CEMP-no stars, highlighting some implications that had until now been overlooked.

2 Observations and data reduction

Observations of some of the most metal-poor stars known have been taken with the ESPRESSO, the Echelle SPectrograph for Rocky Exoplanets and Stable Spectroscopic Observations, at the Very Large Telescope within the ESO Guaranteed Time Observations (GTO) programme on EMP stars (PI: Paolo Molaro). The stars are SMSSJ0313–6708, HE 1327-2326, HE 1313-0019 (also known as 2MASS J13132688-0019415), and HE 0233-0343 (also known as SDSS J002314.00+030758.0). Since a few additional observations for SMSS J1605–1443 were taken after the Aguado et al. (2023) analysis, we also revised the carbon isotopic ratio estimation for this star. The journal of the observations is given in Table 1 together with the ESPRESSO observing mode and the exposure times. The ESPRESSO spectrograph has two fibres, one for the target and one for the sky, with diameter of 140 µm that corresponds to a 1.″O aperture on sky and provides a spectral coverage from 380.0 to 780.0 nm (Pepe et al. 2021). The CCD was binned by either 4 × 2 pixels (i.e. 4 pixels binned in the spatial direction and 2 in the spectral one) or by 2 × 1 pixels, as reported in the third column of Table 1. The corresponding resolution was R = λ/δλ ≈ 140.000 for both binnings. The observations were performed in service mode with individual exposure times of the order of 3000 s. The precise exposure times and the signal-to-noise ratio per pixel measured at 4300 nm are provided in the last two columns of Table 1.

The automatic Data Reduction Software, DRS 3.0, of the ESPRESSO pipeline was used for the data reduction, which includes bias, flat-fielding correction, and sky subtraction, with the sky taken from the second fibre. The wavelength calibration combines a ThAr lamp with a Fabry-Pérot étalon as described in Pepe et al. (2013).

Table 1

Journal of observations.

3 Analysis

3.1 The programme stars

In order to study the 12C/13C isotopic ratio at the beginning of chemical evolution, we selected some of the most metal-poor stars known. The sample includes the giant SMSS J0313–6708, discovered by Keller et al. (2014); with [Fe/H] < −7.3, it is the most iron-poor star presently known. We note that the inferred iron abundances are significantly higher in 3D non-local thermodynamic equilibrium than in ID thermodynamic equilibrium, by 0.8 dex (Nordlander et al. 2017). The second most metal-poor giant is SMSS J1605–1443, first detected by the SkyMapper telescope; its iron abundance is measured at [Fe/H] = −6.2 by Nordlander et al. (2019). HE 1327–2326 with [Fe/H] = −5.60 is the most metal-poor turn-off star. It was discovered by Frebel et al. (2005, 2008) and studied by Aoki et al. (2006). The star has [Zn/Fe] = 0.8, and a 25 M⊙ aspherical SN model exploding with E = 5× 1051 erg has been suggested to provide the best match with the high zinc abundance (Ezzeddine et al. 2020). Our programme sample also includes the giant SDSS J1313–0019 with a measured metallicity of [Fe/H] = −5.0 ± 0.1. This star was discovered by Allende Prieto et al. (2015) and studied by Frebel et al. (2015) and Aguado et al. (2017). Allende Prieto et al. (2015) and Frebel et al. (2015) suggested that SDSS J1313–0019 could be a binary system. Finally, the sample includes another turn-off star, HE 0233–0343, with [Fe/H] = −4.68 ± 0.2 dex (Beers et al. 2007; García Pérez et al. 2008; Hansen et al. 2014). The carbon abundance in all these stars is A(C) ≈ 6–7, falling in the low-C band; although their barium abundance limits are not sensitive enough to match the condition [Ba/Fe] < 0, all of them can be classified as CEMP-no stars.

3.2 Carbon isotopic ratio 12C/13C

Deriving 12C/13C ratios in metal-poor stars is challenging due to the weakness of the 13C lines. However, the high carbon abundance of CEMP stars and the hundreds of lines of the G band collectively provide sufficient information (Masseron et al. 2014). Portions of the combined ESPRESSO spectra of the programme stars corresponding to the strongest 13C lines are shown in Fig. 1. We computed stellar models using the ATLAS model atmosphere code assuming stellar parameters such as effective temperature (Teff), surface gravity (log ɡ), metallicity ([Fe/H]), and total carbon abundance, A(C). This code employs an opacity distribution function corresponding to a metallicity of −5.01.

The stellar parameters used in our analysis are those obtained from the most complete studies of the stars under study since there is no way to verify or improve them. The adopted stellar parameters for SMSS J0313–6708 are Teff = 5125 ± 100 K and log ɡ = 2.3 ± 0.2, as derived from low-resolution spectrophotometry by Keller et al. (2014). Those of HE 1327–2326 are Teff = 6180 ± 100 K and log ɡ = 3.70 ± 0.3, from Aoki et al. (2006). We note that Aoki et al. (2006) also find a solution for a slightly higher surface gravity of log ɡ = 4.5 ± 0.3 with an almost equal probability that the star is a dwarf or a subgiant, though the Gaia parallax favours the subgiant solution. For HE 0233–0343, Hansen et al. (2015) obtained Teff = 6100 ± 100 K and log ɡ = 3.4 ± 0.3 dex, but the Gaia parallax suggests Teff = 6230 and log ɡ = 4.43. SDSS J1313–0019 has Teff = 5200 ± 150 K and log ɡ = 26 ± 0.5 ± according to Frebel et al. (2015). The stellar parameters of SMSS J1605–1443 are Teff = 4850 ± 100 and log ɡ = 2.0 ± 0.2 dex as derived by Nordlander et al. (2019). These stellar parameters are summarised in Table 2. We adopted an [α/Fe] ratio of +0.4 and microturbulences of 1.8, 2.0, 1.5, 1.5, and 1.5 km s−1 for SMSS J1605–1443, SMSS J0313–6708, SDSS J1313–0019, HE 0233–0343, and HE 1327–2326, respectively. It should be noted that line intensities of isotopic molecules originate from identical or very similar rotational and vibrational levels, making the isotope ratio relatively insensitive to uncertainties in the atmospheric parameters.

With this model atmosphere, we generated a grid of synthetic spectra using the SYNTHE code (Kurucz 2005; Sbordone 2005). We adopted the solar carbon abundance of A(C)⊙ = 8.46 from Asplund et al. (2021). For each set of stellar parameters corresponding to our targets, we computed models with varying 12C/13C ratios: 2.2, 5.3, 11.6, 24.1, 49.1, 99.0, and 198.6. These ratios were specifically chosen to capture the largely non-linear behaviour of 12C/13C ratios. With the SYNTHE stellar models, a grid in a format compatible with the FERRE code was constructed (Allende Prieto et al. 2006)2. We generated one grid per target, allowing the FERRE code to read and process the data seamlessly.

In Aguado et al. (2023) we tested a Markov chain Monte Carlo (MCMC) technique that enables the derivation of 12C/13C ratios even with marginal detections of the 13C lines. This methodology is described in Appendix B of Aguado et al. (2023). In short, we identified the spectral regions of the G band near 430.0 nm, where the 13C information is maximum, by subtracting two theoretical models with high and low 12C/13C, respectively. This enabled us to concentrate the fitting procedure of the code exclusively on the pertinent regions while disregarding other features or minor artefacts present in the data. After a 300-pixel running-mean normalisation, the code employs an MCMC self-adaptive randomised subspace sampling algorithm for the fitting, which is described in Vrug et al. (2009). Ten chains of 5000 experiments each were run following this MCMC methodology. Based on our experience with the code, experiments from the initial chain can encounter a blockage. To address this, we allowed the algorithm to ignore the first 500 iterations. Finally, the code provides us with the most probable result and the samples from the Markov chains, following the approach used in Aguado et al. (2023). The sample distributions of the MCMC experiments versus the most likely 12C/13C value are shown in Fig. 2. In Fig. 1 the best FERRE fits are compared with the data in the region around ~422.5 nm at the edge of the G band, where the strongest 13C absorptions are.

We successfully measured the 12C/13C ratios in the three relatively cool giants. For the two MMP stars – SMSS J0313 –6708 and HE 1605−1443 – the 12C/13C ratios are 98.5 ± 5.5 and 67.3 ± 1.0, respectively. Previously, Aguado et al. (2023) had set a lower limit of 12C/13C > 60 for HE 1605−1443. In the HMP SDSSJ1313–0019, the 12C/13C ratio is 39.1 ± 0.6. For the two relatively warm and unevolved stars, HE 1327–2326 and HE 0233–0343, the code provides 12C/13C ratios of 68.9 ± 7.3 and 78.9 ± 5.4, respectively. However, in the spectrum of HE 1327-2326, only very faint evidence of the 13C lines can be observed by eye in Fig. 1. Thus, we conservatively considered a lower limit of 47 for this star at the 3cr confidence level (CL). Overall, all the CEMP-no stars investigated in this study exhibit 12C/13C values or lower limits in the range 39 < 12C/13C < 100, providing evidence of primary production of 13C at the dawn of chemical evolution.

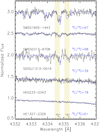thumbnail Fig. 1

Portion of the combined ESPRESSO spectra of the HMP stars, with a focus on the strongest lines of 13C in the G band. The best fit derived with FERRE using an MCMC algorithm is displayed in magenta.
Table 2

Abundance data for the CEMP-no stars grouped in bins of iron metallicity.

thumbnail Fig. 2

Distribution of the MCMC experiments versus the most likely 12C/13C value for each of the targets. The mean value and typical deviation are displayed to provide a summary of the results.

4 Discussion

The 12C/13C ratio is a solid indicator of the presence of CNO-cycle-processed material at the surface of a star. This processed material could come from the interior of the star or from the progenitors that polluted the gas from which the star formed. 12C is formed in the triple-α process during hydrostatic helium burning and is a primary product of stellar nucleosynthesis. The stable13C isotope is produced in the hydrogen-burning shell when the CN cycle converts pre-existing 12C into 13C via proton capture followed by ß decay. The 12C/13C is not locked to the C abundance and provides independent information on either the evolution of the star or the nature of the progenitor.

As a star evolves off the main sequence, the outer convective envelope expands inwards into the CN-cycle-processed regions. This mixing episode, called the ‘first dredge-up’, lowers the 12C/13C ratio from the original value (Iben & Renzini 1984).

Mixing also occurs in the thermal pulses of intermediate-mass stars that become AGB stars. This could lead to a CN-cycle equilibrium ratio of about 12C/13C ~3.4, and in fact ratios as small as 6 are observed in the atmospheres of red supergiants (Lambert & Sneden 1977; Dearborn et al. 1975).

Nova explosions at temperatures >108 K can produce 13C in a hot CNO cycle. Pre-nova white dwarfs are rich in CNO nuclei, and the hot CNO cycle triggers the explosion and transmutes CNO into 13C, 15N, and 17O with enhancement factors of 100 times the solar values (Starrfield et al. 1972; José & Hernanz 1998). All stars as small as 1 solar mass can thus release matter enriched in 13C into the interstellar medium via stellar wind or at the end of their evolution. Therefore, chemical evolution models predict a monotonie decrease in the isotopic ratio 12C/13C with time (Romano & Matteucci 2003; Kobayashi et al. 2020b). In fact, the value found in the interstellar medium and in young molecular clouds is 12C/13C ~ 60–70, which is lower than the solar ratio, 12C/13C = 91 ± 1.3 (Goto et al. 2003; Ayres et al. 2013). Moreover, relatively low values of about 24 have been derived in the Galactic centre by Halfen et al. (2017), and a gradient is observed as a function of galactocentric distances that clearly shows the secondary nature of 13C (Yan et al. 2023).

At low metallicities or before the birth of the Solar System, the 12C/13C is predicted to be higher than solar (Romano & Matteucci 2003; Chiappini et al. 2008; Kobayashi et al. 2020a; Romano 2022). This prediction is difficult to verify because there are few observations that can measure ratios higher than, or even close to, solar. Botelho et al. (2020) in 63 solar twins found a value close to solar with a mild increase in the metallicity range −0.2 < [Fe/H] < −0.0, which is opposite to what is expected. By contrast, Crossfield et al. (2019) measured 12C/13C = 296 ± 45 and 224 ± 26 in the two components of the brown dwarf system GJ 745 at [Fe/H] = −0.48, which are too high for the Galactic chemical evolution models. At lower metallicities, the isotopic ratio in metal-poor giants is found in the range 30–50 and in the metal-poor dwarf HD 140283 is 12C/13C=33−6+12${{^{12}{\rm{C}}} \mathord{\left/ {\vphantom {{^{12}{\rm{C}}} {^{13}{\rm{C}}}}} \right. \kern-\nulldelimiterspace} {^{13}{\rm{C}}}} = 33_{ - 6}^{ + 12}$ (Spite et al. 2006, 2021). Overall, observations do not provide a comprehensive evolutionary curve of the 12C/13C in the Galaxy.

In Fig. 3 we compile the existing 12C/13C measurements or significant limits of CEMP-no stars from the literature. Data are from Bonifacio et al. (1998), Aoki et al. (2002), Masseron et al. (2012), Norris et al. (2013b), Hansen et al. (2015), and Aguado et al. (2022, 2023). Only lower limits in 12C/13C greater than 15, which help in differentiating between low and high isotopes ratios, are shown. The majority of the CEMP-no stars in Fig. 3 have low 12C/13C values. The CEMP-no supergiants have 12C/13C < 10, and the second dredge-up could have internally synthesised 13C. However, quite remarkably there are low values in four dwarfs that have not gone through the first or second dredge-up. They are CS 22958-042 with 12C/13C = 4.5 measured by Sivarani et al. (2006), CS 22887-048 with 12C/13C = 3.7 measured by Aoki et al. (2002), CS 22956-028 with 12C/13C = 4.3 measured by Masseron et al. (2010), and G77-61 with 12C/13C = 5 measured by Plez & Cohen (2005). A chemical transfer from a possible massive companion can be ruled out since all these stars are single or belong to non-interacting binaries, and unless they are wrongly classified as CEMP-no stars, the enhancement of 13C needs to come from their progenitors. This is probably also true for some giants that show very low 12C/13C values that cannot be the result of the first dredge-up. Already in the CEMP-no prototype CS 22957-027, the 12C/13C ratio is 10 ± 5, and Bonifacio et al. (1998) pointed out that the star’s low luminosity means that the13 C could not come from self-polluting dredge-up processes and that the absence of n-capture elements is evidence against mass transfer from an AGB companion.

We note that these measurements point to a complex Galactic behaviour for the ratio 12C/13C. If it is very low at metallicities −3.5 <[Fe/H]<−2, then it needs to rise to match the solar value. This implies that the sources of primary 13C should cease their contribution around [Fe/H] ≈ −2. If so, when the 12C abundance increases by two orders of magnitude, the 12C/13C ratio would also increase by the required two orders of magnitude. Unfortunately, the lack of 12C/13C ratio measurements in the range −2.0 < [Fe/H] < 0 prevents us from verifying this prediction. These measurements would have to be extended to other CEMP-no main-sequence stars to see if the low isotope ratios are common at low metallicities and trace the rise of the isotope ratio until it reaches the solar value.

Remarkably, all the MMP and HMP CEMP-no stars have12 C/13 C > 40, while the majority of other CEMP-no have values <30. There is also a hint of a smooth decrease in the values going from the MMP to the HMP stars and then to the UMP stars. In the sample of UMP and EMP stars, there are 30 CEMP-no stars and all but two of them show low 12C/13C ratios, in a few cases close to the CNO equilibrium value. The exceptions are Seque1–7 and CS31080-095, which have values of 12C/13C > 50 and 40, respectively, which is comparable to the more metal-poor stars.

The extremely low iron abundance of MMP and HMP stars suggests that only a few and perhaps only a single progenitor polluted the gas out of which they formed. The carbon might originate from faint SNe with energies of 1051 erg (Umeda & Nomoto 2003). With mixing and a large amount of fallback, faint SNe eject a lot of carbon and a small amount of Fe, thus producing ejecta with large [C/Fe] abundance ratios. Supernovae with stellar masses of 10–20 M⊙ and low explosion energies of about 1051 erg have been shown to be able to reproduce the pattern of chemical abundances of CEMP-no stars (Tominaga et al. 2014; Almusleh et al. 2021). Tominaga et al. (2007) successfully reproduced the observed abundance pattern of the CEMP-no star CS 29498-043 (Aoki et al. 2004) with a 25 M⊙ faint SN model. Almusleh et al. (2021) suggest that weak SN progenitors with stellar masses of 11–22 M⊙ and explosion energies in the range 0.3–1.8 × 1051 erg could be the progenitors of the chemical abundances of five CEMP-no stars. However, models are not unique, and, for instance, several different kinds of progenitors with masses in the range 12–60 M⊙ (Ishigaki et al. 2014; Nordlander et al. 2017) have been proposed to explain the abundances of the most iron-poor star known, SMSS J0313–6708. Moreover, a large dispersion in the [Fe/Ca] values is predicted by fallback models, which is not observed (Ishigaki et al. 2014). A variant model includes a double source with the CNO elements synthesised by faint SNe and the heavier elements made by conventional core-collapse SNe (Limongi et al. 2003; Bonifacio et al. 2015).

An alternative, potentially complementary, model for the progenitors of CEMP-no stars is massive low-metallicity, fast-rotating stars in the range 40–120 M⊙, the so-called spinstars, which may experience efficient mixing and significant mass loss (Meynet et al. 2006; Chiappini et al. 2008; Maeder et al. 2015; Limongi & Chieffi 2018). Mixing is driven by rapid rotation, and the diffusion of matter between the H- and He-burning zones largely increases the abundance of 13C. If 13C flows into the convective core, it is transported to the surface and delivered into the interstellar medium by winds (Meynet et al. 2006; Chiappini et al. 2008; Maeder et al. 2015; Limongi & Chieffi 2018). In the spinstar model, the mixing occurs progressively during the evolutionary stages and 13C is lost through stellar winds, while in the faint SN model the mixing that produces 13C should occur in the explosion and is unconstrained.

High 12C/13C values imply partial or very mild mixing that occurred either within the star itself or in the progenitor. For the unevolved stars HE 1327–2326 and HE 0233–0343, all the 13C is coming from the parent cloud. Generalising this result to the giants, it follows that the parent generation of the most metal-poor stars, likely the first stars, synthesised significant amounts of primary 13C. A transition seems to occur at [Fe/H] ≈ −4 and suggests the presence of different progenitors for the two groups of stars. The first generation of massive stars that polluted the gas seems to have made less 13C than later generations.

Primordial faint SN models do not make specific predictions concerning the production of 13C, while significant quantities of 13C are expected from massive, low-metallicity, fast-rotating stars with 12C/13C ratios between 30 and 300 (Chiappini et al. 2008). In the zero-metallicity non-rotating stars models by Limongi & Chieffi (2012), the production of primary 13C, and all CNO isotopes more generally, occurs in a restricted mass range between 25 and 35 M⊙, where the convective shell of He, in which 12C is produced from the He burning, incorporates the H shell. Once the He shell begins to engulf H, it extends considerably. The maximum extension of the shell is for a star of 25 M⊙; for more massive stars it decreases and therefore the abundance of 13C also decreases. Stars of 20 M⊙ or 50 M⊙ do not have this mixing and there is no production of 13C. This picture could explain the observed trend with the more massive stars being the parents of the HMP stars and progressively lower-mass stars progenitors of the UMP stars. However, the presence of significant rotation could drive extra mixing in layers that are otherwise in radiative equilibrium. A rotational-driven mixing could bring the 12C synthesised in the He convective core up into the tail of the H-burning shell, where it is converted into 13C. However, the production is not monotonie due to a complex interplay between rotation and convection (Limongi 2023, priv. comm.). We note that similar processes necessary to produce 13C are also invoked to explain the primary N behaviour at very low metallicities in damped Lyα galaxies (Molaro 2003; Molaro et al. 2004; Zafar et al. 2014).

thumbnail Fig. 3

12C/13C–[Fe/H] plane for CEMP-no stars. The value for HE 0107–5240 is taken from Aguado et al. (2022). Only lower limits greater than 15 are shown since the smaller ones do not provide useful information. Errors in [Fe/H] are omitted for clarity. Red triangles are dwarfs with log ɡ > 3.5. Blue star-symbols are stars on the first ascent to the red giant branch, with 2 < log ɡ < 3.5. Orange squares are super-giants with log ɡ < 2. The 12C/13C = 30 value that splits stars with evidence of internal mixing from the others according to Spite et al. (2006) is also shown; the background above this value is yellow and below is peach coloured.

4.1 n-capture elements

The CEMP-no classification does not imply a complete absence of n-capture elements, only that [Ba/Fe] < 0 (Christlieb et al. 2004). For the most iron-poor stars (i.e. [Fe/H] < −5), this condition is difficult to fulfil and limits are much less stringent. There are several cases where neither Ba nor Fe can be measured, leaving the [Ba/Fe] unconstrained. For instance, for SMSS J0313-6708 we can place [Ba/H] < −5.6 and [Sr/H] < −5.8, but the [Ba,Sr/Fe] ratios remain unbound. For these stars, the criterion for CEMP-no membership is necessarily restricted to the absolute carbon abundance, which for CEMP-no stars is around A(C) ≈ 6.8 ± 0.5 (Bonifacio et al. 2015). For SMSSJ1605–1443, which has [Fe/H] = −6.21, Nordlander et al. (2019) in their discovery paper derived [Sr/Fe] < 0.2 and [Ba/Fe] < 1.0. With our ESPRESSO data we slightly improve upon these limits, placing an upper bound of [Sr/Fe] < 0.18 and [Ba/Fe] < 0.6 at the 3σ CL. In HE 1327-2326 and HE 0233–0343, strontium has been measured and found to be relatively abundant, with [Sr/Fe] = 1.04 and 0.3, respectively (Frebel et al. 2005; Hansen et al. 2014). The portion of the ESPRESSO spectrum of HE 1327-2326 corrected for a radial velocity of 63.681 km s−1 around the Ball 455.40 nm line is shown in Fig. 4; it shows a hint of a line at the expected position. The abundance would be [Ba/Fe] = 1.3. Strictly speaking, this abundance violates the condition of [Ba/Fe] < 0.0. However, the star shows an absolute carbon abundance of A(C) = 6.96, similar to the other CEMP-no stars. Indeed, there is a small group of CEMP-no stars with measurable Sr, and some of them also have barium measured. With the present detection, HE 1327-2326 would be the CEMP-no star with the highest barium abundance relative to iron. The existence of this group of stars shows that n-capture elements sometimes need to be synthesised at a solar ratio relative to iron from the very beginning. This may favour the scenario that foresees the additional contribution from core-collapse SNe in addition to faint SNe, though the latter are required to provide the seed nuclei. For high rotation velocities, the mixing processes with successive back and forth motions between the He- and H-burning layers may also lead to the 22Ne(α,n)25Mg reaction that produces s-elements by n-captures on seed heavy elements. In this way, a substantial number of s-elements of the first peak, such as Sr, corresponding to the magic number of neutrons N = 50, are formed, as are a few elements of the second peak, such as Ba, corresponding to the magic number of N = 82; nothing of the third peak is formed (Frischknecht et al. 2016).

thumbnail Fig. 4

ESPRESSO spectrum of HE 1327-2326 around the Ba II 455.40 nm line. Three different synthetic models computed with SYNTHE are also shown.

4.2 Lithium in the CEMP-no stars

In the sample of stars with [Fe/H] < − 4.5, there are six unevolved stars with effective temperatures between 5800 and 6345 K. As noted by Sbordone et al. (2010), they should lie on the Spite and Spite plateau at metallicities below [Fe/H] = −3. The HMP and UMP stars follow this trend and magnify the meltdown, showing more Li-depleted stars at the lowest-metallicity end. Below [Fe/H] < −4.0 there are no stars with Li abundances strictly on the plateau, and about half of them show no detectable Li at all. This is in contrast with the recent suggestion by Heger & Woosley (2020), of significant Li production by neutrino-induced spallation during the explosion of very compact zero-metal core-collapse SNe. The 12C/13C values could also help in interpreting the origin of Li depletion. A clear correlation between 12C/13C and Li abundance is observed in a large sample of disk giants, with the low values in the isotopic ratio showing the highest Li depletion (Takeda et al. 2019). Stars with evidence of mixing also show Li depletion since Li is burned in the mixing process. This seems to also hold for the CEMP-no stars. One example is the CEMP-no dwarf CS 22958-042 with 12C/13C = 9 and A (Li) < 0.6 (Sivarani et al. 2006). However, HE 1327–2326 has A (Li) < 0.62 according to Frebel et al. (2005), which is considerably below the plateau value of A(Li) ≈ 2.2, but has a relatively high value of 12C/13C. This suggests that the mechanism behind the Li depletion is not mixing in the progenitor. Matsuno et al. (2017) also measured Li at the Spite plateau level in two CEMP-no stars with metallicities of about -3.0, arguing that the nature of neither the CEMP-no stars nor their progenitors can explain the higher fraction of Li depletion at low metallicities. The mechanism seems more related to the metallicity, rather than the nature, of the CEMP-no stars or their progenitors.

A similar argument can also be made for the giants. Mucciarelli et al. (2022) find a thin Li plateau at A(Li) = 1.09 ± 0.01 in the giants following the Li dilution, which occurs when the star leaves the main sequence. It is quite remarkable that in SMSS J0313–6708, the most iron-poor star presently known, we measure A(Li) = 0.70 ± 0.15, see Fig. 5, in agreement with the 0.7 quoted by Keller et al. (2012). After correcting this value using the dilution factor from Mucciarelli et al. (2022), the original Li becomes 0.39 dex below the primordial value, regardless of whether this is at the Planck value of A(Li) ≈ 2.7 or at the halo stars’ value of A(Li) ≈ 2.2. Thus, Li values below Mucciarelli’s plateau indicate the presence of effective Li depletion. In the case of SMSS J1605–1443, we could place 3σ upper limits at A(Li) < 0.0, see Fig. 5, improving upon the A(Li) < 0.48 limit from Nordlander et al. (2019), as illustrated in Fig. 6 in the three giants with high 12C/13C, Li is observed at A(Li) < 0.6; this is below the Mucciarelli plateau, indicating Li depletion in excess of dilution.

Fu et al. (2015) suggest a stellar fix to the cosmological Li problem that involves a substantial pre-main-sequence depletion partially compensated for by gas accretion with a primordial Li composition of A(Li) = 2.7, as inferred from standard Big Bang nucleosynthesis, once the baryon density from the cosmic microwave background power spectrum or the D/H extragalactic measurements is adopted. The presence of overshooting, which is required by helioseismology, leads to a substantial Li burning in the pre-main-sequence evolution, which needs to be compensated for with a later accretion (Fu et al. 2015). An accretion rate of 10−8 M0 yr−1 at the birth line that then decays exponentially until it is halted by photo-evaporation provides a self-regulating mechanism able to reproduce a Li plateau for a range of stellar masses. The MMP and HMP stars are smaller and hotter, and the tenuous accretion disk could be dissipated before the restoration of the initial Li is completed. Thus, a break of this self-regulating mechanism could explain, at least qualitatively, the increased scatter of the lithium abundances at very low metallicities.

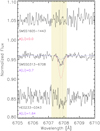thumbnail Fig. 5

ESPRESSO spectra for three representative stars around the Li 670.7 nm position. Radial velocities given in Aguado et al. (2022) have been subtracted.
thumbnail Fig. 6

Lithium abundances for CEMP-no stars from Table 2. The two plateaux for dwarfs and giants observed at higher metallicities are shown in red and blue, respectively. The former is from Sbordone et al. (2010), and the latter is at A(Li) = 1.09 ± 0.01 and is from Mucciarelli et al. (2022). Red triangles are for warm dwarfs, Teff > 5800 K and log ɡ > 3.4. Blue stars are for giants, log ɡ < 3.0. Supergiants with log ɡ < 2.0 are not shown.

5 Conclusions

By means of high-resolution spectra acquired with the ESPRESSO spectrograph at the VLT, we succeeded in measuring the 12C/13C ratio in four of the lowest-metallicity stars known: the MMP giant SMSS J0313–6708, with [Fe/H] < −7.1; the HMP dwarf HE 1327–2326, [Fe/H] = −5.8; the giant SDSS J1313–0019, [Fe/H] = −5.0; and the UMP subgiant HE 0233–0343, [Fe/H] = −4.7. We also revised the value for the star SMSS J1605–1443, [Fe/H] = −6.2, turning a lower limit into a value. Our main results are the following:

  • For the three cool giants SMSS J0313–6708, SMSS J1605–1443, and SDSS J1313–0019, we derive a12 C/13 C measurement, while for the two warm unevolved stars we provide a measurement for HE 0233–0343 and a lower limit for the dwarf HE 1327–2326. Measurements or limits are all in the range 39 < 12C/13C < 100, with a monotonic decrease going from the more metal-poor stars to the less metal-poor ones. The values derived for the 12C/13C ratio provide evidence of mixing between the He- and H-burning layers in the progenitors and a primary production of13C at the dawn of chemical evolution.

  • For the CEMP-no dwarf stars with 12C/13C values in the literature, we find that very low isotopic values, even close to the CNO cycle equilibrium value, are common. In particular, they are also found in a few dwarfs. Both the literature 12C/13C values and those obtained here show a monotonic decrease, reaching the lowest values at metallicities in the range [Fe/H] ≈ −4, −3. This could mark a real difference between the progenitor 3C pollution captured by stars with different metallicities. In particular, the decrease in the 12C/13C values with metallicity could reflect an increase in 13C production by less massive stars (Limongi & Chieffi 2012).

  • The ESPRESSO spectrum of HE 1327-2326 shows a hint of a Ba II line. If present, the abundance would be [Ba/Fe] = 1.3, making HE 1327-2326 the CEMP-no star with the highest barium abundance. Such an abundance violates the [Ba/Fe] < 0.0 criterion since HE 1327-2326 also has a carbon abundance characteristic of the CEMP-no stars. Indeed, there is a small group of CEMP-no stars with measured Sr values, of which four also have Ba measurements. The existence of this group of stars within the CEMP-no category indicates a very early synthesis of n-capture elements.

  • A general correlation between 12C/13C values and Li abundance holds. Since the fragile Li is burned in the mixing process, low carbon isotopic ratios are generally associated with the largest Li depletions (Takeda et al. 2019). This is not observed in our stars, and Li depletion is observed for relatively high 12C/13C values, suggesting that neither mixing in the progenitor nor the CEMP-no nature of the stars is responsible for the Li depletion.

The study of the isotope ratio in low-mass halo stars has revealed the presence of significant synthesis of 13C in the most massive stars of the very first stellar generations that contaminated the gas from which they formed. A synthesis that can only occur through the mixing of the helium and hydrogen burning layers, thus providing important information on the structure of the first stars. Future observations will have to ascertain how the values observed in low metallicity stars can be traced back to the high values observed in stars with solar abundances.

Acknowledgements

P.M. acknowledges important discussions with Marco Limongi about the 13C production by massive zero metal stars. D.A. also acknowledges financial support from the Spanish Ministry of Science and Innovation (MICINN) under the 2021 Ramón y Cajal program MICINN RYC2021-032609. E.C. acknowledges support from the French National Research Agency (ANR) funded project Pristine (ANR-18-CE31-0017). J.I.G.H., C.A.P., A.S.M. and R.R. acknowledge financial support from the Spanish Ministry of Science and Innovation (MICINN) project PID2020-117493GB-I00. M.R.Z.O. acknowledges financial support from the Spanish Ministry of Science and Innovation through project PID2019-109522GB-C51. A.S.M. acknowledges financial support from the Spanish Ministry of Science and Innovation (MICINN) under 2018 Juan de la Cierva program IJC2018-035229-I. A.S.M. acknowledges financial support from the Government of the Canary Islands project ProID2020010129. F.P.E., C.L.O., and T.M.S. would like to acknowledge the Swiss National Science Foundation (SNSF) for supporting research with ESPRESSO through the SNSF grants nr. 140649, 152721, 166227, 184618, and 193689. The ESPRESSO Instrument Project was partially funded through SNSF’s FLARE Programme for large infrastructures. D.M. is also supported by the INFN PD51 INDARK grant. This work was financed by FCT - Fundação para a Ciência e a Tec-nologia under projects UIDB/04434/2020 & UIDP/04434/2020, CERN/FIS-PAR/0037/2019, PTDC/FIS-AST/0054/2021, PTDC 2022.04048(Phi in the Sky). C.J.M. also acknowledges FCT and POCH/FSE (EC) support through Investigador FCT Contract 2021.01214.CEECIND/CP1658/CT0001. M.T.M. acknowledges the support of the Australian Research Council through Future Fellowship grant FT180100194.

References

  1. Aguado, D. S., Allende Prieto, C., González Hernández, J. I., Rebolo, R., & Caffau, E. 2017, A & A, 604, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Aguado, D. S., González Hernández, J. I., Allende Prieto, C., & Rebolo, R. 2018, ApJ, 852 L20 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aguado, D. S., González Hernández, J. I., Allende Prieto, C., & Rebolo, R. 2019, ApJ, 874, L21 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aguado, D., Molaro, P., Caffau, E., et al. 2022, A & A, 668, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Aguado, D. S., Caffau, E., Molaro, P., et al. 2023, A & A, 669, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Allen, D. M., Ryan, S. G., Rossi, S., Beers, T. C., & Tsangarides, S. A. 2012, A & A, 548, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Allende Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
  8. Allende Prieto, C., Fernández-Alvar, E., Aguado, D. S., et al. 2015, A & A, 579, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Almusleh, N. A., Taani, A., Özdemir, S., et al. 2021, Astron. Nachr., 342, 625 [NASA ADS] [CrossRef] [Google Scholar]
  10. Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2002, ApJ, 567, 1166 [Google Scholar]
  11. Aoki, W., Norris, J. E., Ryan, S. G., et al. 2004, ApJ, 608, 971 [NASA ADS] [CrossRef] [Google Scholar]
  12. Aoki, W., Frebel, A., Christlieb, N., et al. 2006, ApJ, 639, 897 [Google Scholar]
  13. Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A & A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Ayres, T. R., Lyons, J. R., Ludwig, H. G., Caffau, E., & Wedemeyer-Böhm, S. 2013, ApJ, 765, 46 [NASA ADS] [CrossRef] [Google Scholar]
  15. Beers, T. C., & Christlieb, N. 2005, ARA & A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
  16. Beers, T. C., Preston, G. W., & Shectman, S. A. 1985, AJ, 90, 2089 [NASA ADS] [CrossRef] [Google Scholar]
  17. Beers, T. C., Flynn, C., Rossi, S., et al. 2007, ApJS, 168, 128 [Google Scholar]
  18. Bessell, M. S., & Norris, J. 1984, ApJ, 285, 622 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bonifacio, P., Molaro, P., Beers, T. C., & Vladilo, G. 1998, A & A, 332, 672 [Google Scholar]
  20. Bonifacio, P., Caffau, E., Spite, M., et al. 2015, A & A, 579, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Bonifacio, P., Caffau, E., Spite, M., et al. 2018, A & A, 612, A65 [CrossRef] [EDP Sciences] [Google Scholar]
  22. Botelho, R. B., Milone, A. D. C., Meléndez, J., et al. 2020, MNRAS, 499, 2196 [CrossRef] [Google Scholar]
  23. Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [Google Scholar]
  24. Caffau, E., Bonifacio, P., François, P., et al. 2016, A & A, 542, A51 [Google Scholar]
  25. Caffau, E., Bonifacio, P., Sbordone, L., et al. 2013, A & A, 560, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Caffau, E., Bonifacio, P., Spite, M., et al. 2016, A & A, 595, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
  28. Chamberlain, J. W., & Aller, L. H. 1951, ApJ, 114, 52 [NASA ADS] [CrossRef] [Google Scholar]
  29. Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A & A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Christlieb, N., Gustafsson, B., Korn, A. J., et al. 2004, ApJ, 603, 708 [NASA ADS] [CrossRef] [Google Scholar]
  31. Crossfield, I. J. M., Lothringer, J. D., Flores, B., et al. 2019, ApJ, 871, L3 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dearborn, D. S. P., Lambert, D. L., & Tomkin, J. 1975, ApJ, 200, 675 [NASA ADS] [CrossRef] [Google Scholar]
  33. Deng, L.-C., Newberg, H. J., Liu, C., et al. 2012, Res. Astron. Astrophys., 12, 735 [Google Scholar]
  34. Ezzeddine, R., Rasmussen, K., Frebel, A., et al. 2020, ApJ, 898, 150 [NASA ADS] [CrossRef] [Google Scholar]
  35. Frebel, A., & Norris, J. E. 2015, ARA & A, 53, 631 [NASA ADS] [CrossRef] [Google Scholar]
  36. Frebel, A., Aoki, W., Christlieb, N., et al. 2005, Nature, 434, 871 [CrossRef] [Google Scholar]
  37. Frebel, A., Collet, R., Eriksson, K., Christlieb, N., & Aoki, W. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
  38. Frebel, A., Chiti, A., Ji, A. P., Jacobson, H. R., & Placco, V. M. 2015, ApJ, 810, L27 [NASA ADS] [CrossRef] [Google Scholar]
  39. Frebel, A., Ji, A. P., Ezzeddine, R., et al. 2019, ApJ, 871, 146 [NASA ADS] [CrossRef] [Google Scholar]
  40. Frischknecht, U., Hirschi, R., Pignatari, M., et al. 2016, MNRAS, 456, 1803 [Google Scholar]
  41. Fu, X., Bressan, A., Molaro, P., & Marigo, P. 2015, MNRAS, 452, 3256 [CrossRef] [Google Scholar]
  42. García Pérez, A. E., Christlieb, N., Ryan, S. G., et al. 2008, Phys. Scrip., 133, 014036 [CrossRef] [Google Scholar]
  43. González Hernández, J. I., Aguado, D. S., Allende Prieto, C., Burgasser, A. J., & Rebolo, R. 2020, in XIV.0 Scientific Meeting (virtual) of the Spanish Astronomical Society, 142 [Google Scholar]
  44. Goto, M., Usuda, T., Takato, N., et al. 2003, ApJ, 598, 1038 [NASA ADS] [CrossRef] [Google Scholar]
  45. Halfen, D. T., Woolf, N. J., & Ziurys, L. M. 2017, ApJ, 845, 158 [Google Scholar]
  46. Hansen, T., Hansen, C. J., Christlieb, N., et al. 2014, ApJ, 787, 162 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hansen, T., Hansen, C. J., Christlieb, N., et al. 2015, ApJ, 807, 173 [Google Scholar]
  48. Hansen, C. J., Nordström, B., Hansen, T. T., et al. 2016, A & A, 588, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Heger, A., & Woosley, S. 2020, Mem. Soc. Astron. Ital., 91, 58 [Google Scholar]
  50. Iben, I., & Renzini, A. 1984, Phys. Rep., 105, 329 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ishigaki, M., Tominaga, N., Kobayashi, C., & Nomoto, K. 2014, ApJ, 792, L32 [NASA ADS] [CrossRef] [Google Scholar]
  52. José, J., & Hernanz, M. 1998, ApJ, 494, 680 [Google Scholar]
  53. Keller, S. C., Schmidt, B. P., Bessell, M. S., et al. 2007, PASA, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
  54. Keller, S. C., Skymapper Team, & Aegis Team. 2012, ASP Conf. Ser., 458, 409 [NASA ADS] [Google Scholar]
  55. Keller, S. C., Bessell, M. S., Frebel, A., et al. 2014, Nature, 506, 463 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020a, ApJ, 900, 179 [Google Scholar]
  57. Kobayashi, C., Leung, S.-C., & Nomoto, K. 2020b, ApJ, 895, 138 [CrossRef] [Google Scholar]
  58. Kurucz, R. L. 2005, Mem. Soc. Astron. Ital., 8, 14 [Google Scholar]
  59. Lambert, D. L., & Sneden, C. 1977, ApJ, 215, 597 [CrossRef] [Google Scholar]
  60. Limongi, M., & Chieffi, A. 2012, ApJS, 199, 38 [NASA ADS] [CrossRef] [Google Scholar]
  61. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  62. Limongi, M., Chieffi, A., & Bonifacio, P. 2003, ApJ, 594, L123 [CrossRef] [Google Scholar]
  63. Maeder, A., Meynet, G., & Chiappini, C. 2015, A & A, 576, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A & A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Masseron, T., Johnson, J. A., Lucatello, S., et al. 2012, ApJ, 751, 14 [NASA ADS] [CrossRef] [Google Scholar]
  66. Masseron, T., Plez, B., Van Eck, S., et al. 2014, A & A, 571, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Matsuno, T., Aoki, W., Suda, T., & Li, H. 2017, PASJ, 69, 24 [NASA ADS] [CrossRef] [Google Scholar]
  68. Meynet, G., Ekström, S., & Maeder, A. 2006, A & A, 447, 623 [CrossRef] [EDP Sciences] [Google Scholar]
  69. Molaro, P. 2003, ASP Conf. Ser., 304, 221 [NASA ADS] [Google Scholar]
  70. Molaro, P., & Bonifacio, P. 1990, A & A, 236, L5 [NASA ADS] [Google Scholar]
  71. Molaro, P., & Castelli, F. 1990, A & A, 228, 426 [Google Scholar]
  72. Molaro, P., Centurión, M., D’Odorico, V., & Péroux, C. 2004, in Origin and Evolution of the Elements, eds. A. McWilliam, & M. Rauch (Cambridge: Cambridge University Press), 39 [Google Scholar]
  73. Mucciarelli, A., Monaco, L., Bonifacio, P., et al. 2022, A & A, 661, A153 [CrossRef] [EDP Sciences] [Google Scholar]
  74. Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA & A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
  75. Nordlander, T., Amarsi, A. M., Lind, K., et al. 2017, A & A, 597, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Nordlander, T., Bessell, M. S., Da Costa, G. S., et al. 2019, MNRAS, 488, L109 [Google Scholar]
  77. Norris, J. E., Ryan, S. G., & Beers, T. C. 1997, ApJ, 489, L169 [NASA ADS] [CrossRef] [Google Scholar]
  78. Norris, J. E., Bessell, M. S., Yong, D., et al. 2013a, ApJ, 762, 25 [NASA ADS] [CrossRef] [Google Scholar]
  79. Norris, J. E., Yong, D., Bessell, M. S., et al. 2013b, ApJ, 762, 28 [NASA ADS] [CrossRef] [Google Scholar]
  80. Pagnini, G., Salvadori, S., Rossi, M., et al. 2023, MNRAS, 521, 5699 [NASA ADS] [CrossRef] [Google Scholar]
  81. Pepe, F., Cristiani, S., Rebolo, R., et al. 2013, The Messenger, 153, 6 [NASA ADS] [Google Scholar]
  82. Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A & A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Plez, B., & Cohen, J. G. 2005, A & A, 434, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Rockosi, C. M., Lee, Y. S., Morrison, H. L., et al. 2022, ApJS, 259, 60 [CrossRef] [Google Scholar]
  85. Romano, D. 2022, A & ARv, 30, 7 [NASA ADS] [Google Scholar]
  86. Romano, D., & Matteucci, F. 2003, MNRAS, 342, 185 [Google Scholar]
  87. Sbordone, L. 2005, Mem. Soc. Astron. Ital., 8, 61 [NASA ADS] [Google Scholar]
  88. Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A & A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Sivarani, T., Beers, T. C., Bonifacio, P., et al. 2006, A & A, 459, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Spite, M., Cayrel, R., Hill, V., et al. 2006, A & A, 455, 291 [CrossRef] [EDP Sciences] [Google Scholar]
  91. Spite, M., Caffau, E., Bonifacio, P., et al. 2013, A & A, 552, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Spite, M., Spite, F., & Barbuy, B. 2021, A & A, 652, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [Google Scholar]
  94. Starkenburg, E., Martin, N., Youakim, K., et al. 2017, MNRAS, 471, 2587 [NASA ADS] [CrossRef] [Google Scholar]
  95. Starrfield, S., Truran, J. W., Sparks, W. M., & Kutter, G. S. 1972, ApJ, 176, 169 [NASA ADS] [CrossRef] [Google Scholar]
  96. Takeda, Y., Omiya, M., Harakawa, H., & Sato, B. 2019, PASJ, 71, 119 [NASA ADS] [CrossRef] [Google Scholar]
  97. Tominaga, N., Umeda, H., & Nomoto, K. 2007, ApJ, 660, 516 [NASA ADS] [CrossRef] [Google Scholar]
  98. Tominaga, N., Iwamoto, N., & Nomoto, K. 2014, ApJ, 785, 98 [NASA ADS] [CrossRef] [Google Scholar]
  99. Umeda, H., & Nomoto, K. 2003, Nature, 422, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  100. Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
  101. Vrug, A., ter Braak, C., Dicks, C., et al. 2009, Int. J. Nonlinear Sci. Numer. Simulation, 10, 273:290 [Google Scholar]
  102. Yan, Y. T., Henkel, C., Kobayashi, C., et al. 2023, A & A, 670, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [Google Scholar]
  104. York, D. G., Adelman, J., John E., Anderson J., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  105. Zafar, T., Centurión, M., Péroux, C., et al. 2014, MNRAS, 444, 744 [NASA ADS] [CrossRef] [Google Scholar]
  106. Zepeda, J., Beers, T. C., Placco, V. M., et al. 2023, ApJ, 947, 23 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Journal of observations.

In the text
Table 2

Abundance data for the CEMP-no stars grouped in bins of iron metallicity.

In the text

All Figures

thumbnail Fig. 1

Portion of the combined ESPRESSO spectra of the HMP stars, with a focus on the strongest lines of 13C in the G band. The best fit derived with FERRE using an MCMC algorithm is displayed in magenta.
In the text
thumbnail Fig. 2

Distribution of the MCMC experiments versus the most likely 12C/13C value for each of the targets. The mean value and typical deviation are displayed to provide a summary of the results.
In the text
thumbnail Fig. 3

12C/13C–[Fe/H] plane for CEMP-no stars. The value for HE 0107–5240 is taken from Aguado et al. (2022). Only lower limits greater than 15 are shown since the smaller ones do not provide useful information. Errors in [Fe/H] are omitted for clarity. Red triangles are dwarfs with log ɡ > 3.5. Blue star-symbols are stars on the first ascent to the red giant branch, with 2 < log ɡ < 3.5. Orange squares are super-giants with log ɡ < 2. The 12C/13C = 30 value that splits stars with evidence of internal mixing from the others according to Spite et al. (2006) is also shown; the background above this value is yellow and below is peach coloured.
In the text
thumbnail Fig. 4

ESPRESSO spectrum of HE 1327-2326 around the Ba II 455.40 nm line. Three different synthetic models computed with SYNTHE are also shown.
In the text
thumbnail Fig. 5

ESPRESSO spectra for three representative stars around the Li 670.7 nm position. Radial velocities given in Aguado et al. (2022) have been subtracted.
In the text
thumbnail Fig. 6

Lithium abundances for CEMP-no stars from Table 2. The two plateaux for dwarfs and giants observed at higher metallicities are shown in red and blue, respectively. The former is from Sbordone et al. (2010), and the latter is at A(Li) = 1.09 ± 0.01 and is from Mucciarelli et al. (2022). Red triangles are for warm dwarfs, Teff > 5800 K and log ɡ > 3.4. Blue stars are for giants, log ɡ < 3.0. Supergiants with log ɡ < 2.0 are not shown.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.