EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 678 (October 2023) A&A, 678 (2023) A32 Full HTML
Open Access
Issue
A&A
Volume 678, October 2023
Article Number A32
Number of page(s) 19
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202347058
Published online 29 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open access funding provided by Max Planck Society.

1. Introduction

The solar atmosphere is predominantly governed by loops of different sizes and heights in the quiet Sun and active regions. They are also occasionally found in coronal holes, which are dominated by open magnetic flux. When it is observed in emission from plasma at around 1.0 MK, the quiet Sun reveals an abundance of these loops. The brighter of them were named coronal bright points (CBPs; for review see Madjarska 2019) and are also known as X-ray bright points (XBPs). The fainter loops appear to build up most of or eventually all of the background diffused emission at 1.25 MK that is recorded in the 193 Å channel of the Atmospheric Imaging Assembly (AIA) on board the Solar Dynamics Observatory (SDO).

The loops seen at coronal temperatures composing the CBPs (from various methods, except for magnetic field extrapolation; see Sect. 3.5 of Madjarska 2019) are found to have average heights of 6500 km (from 5000 to 10 000 km). They connect magnetic fluxes of opposite polarities (Krieger et al. 1971; Golub et al. 1974; Harvey et al. 1975) and have enhanced emission at coronal temperatures (and also transition-region temperatures) because they confine higher-density and higher-temperature plasma than the background atmosphere (Madjarska 2019).

Golub et al. (1977) reported the first in-depth study of the magnetic properties of CBPs. The newly emerging bipolar regions, named ephemeral regions (ERs; first introduced by Dodson 1953), in magnetograms taken at the Kitt Peak National Observatory were compared with XBPs recorded by an X-ray telescope on board Skylab. The study reported the relation of XBPs to bipole flux emergence, that is, ERs, and evolution, and the contribution of XBPs to the total emerging flux on the Sun. ERs are described to have sizes of up to ∼20″, a total magnetic flux of ∼1020 Mx, and lifetimes shorter than a day. From data taken with the Imaging Magnetograph Experiment (IMaX; Martínez Pillet et al. 2011), Guglielmino et al. (2012) reported ERs with magnetic fluxes as low as 1016 Mx and a magnetic flux growth rate of 2.6 × 1015 Mx s−1. The average lifetime of ERs was estimated to be 1–2 days (Harvey & Martin 1973) or shorter. The newly emerging and decaying XBPs were found to have only one polarity (Golub et al. 1977). Because loops are always rooted in magnetic fluxes of different polarities, the lack of one detectable polarity arises because loops typically connect magnetic fluxes with different strengths (for details, see Wiegelmann et al. 2010), and if one is weaker or below the instrumental resolution, it cannot be detected. During magnetic flux emergence or just before a CBP disappearance, one of the polarities is quite weak and dispersed and may therefore not be seen because its strength is below the resolving power of the observing instrument (especially for ground-based instrumentation in the 1970s).

Golub et al. (1977) found that only 49% of the ERs have corresponding XBPs (36 out of 73 XBPs). A large number of the ERs linked to non-XBPs were associated with diffuse (rather than bright compact) X-ray emission obscured by large coronal structures, and therefore, they could not be identified as XBPs. The limited correspondence of XBPs to ERs might be related to the evolutionary history of XBPs or CBPs. CBPs can attain X-ray temperatures (e.g., as high as 3.5 MK) for a short period of time during their lifetimes, as was found from EUV and X-ray co-observations (Zhang et al. 2001) or only during the duration of microflares that often take place in CBPs or XBPs (Mou et al. 2018; Madjarska et al. 2020, 2022, and references therein).

Harvey (1984) and Harvey et al. (1994) found that 70%–80% of the XBPs were associated with a chance encounter of magnetic flux, while just 20%–30% were linked to ERs. From data obtained with the Helioseismic Magnetic Imager (HMI) on board the SDO, Mou et al. (2016, 2018) reported that more than 50% of the CBPs result from an emergence of magnetic flux.

The total magnetic flux of XBPs was found to be in the range from 1019 to 1020 Mx (Krieger et al. 1971; Golub et al. 1974; Harvey et al. 1975), with typical values of 2–5 × 1019 Mx. Golub et al. (1976) estimated the total magnetic flux emerging on the Sun per day associated with XBPs to be 1.2 × 1022 to 3.6 × 1022 Mx. When only latitudes outside the active region belt (±30°) are considered, the emerged total magnetic flux was estimated to be between 6 × 1021 and 1.2 × 1022 Mx per day. Only XBPs associated with a flux emergence were investigated in this study. A typical XBP has been found to have a photospheric magnetic flux growth rate of 1.5 × 1019 Mx s−1 for a lifetime of 8 h (in X-rays), reaching a total unsigned flux of 2.0 × 1019 Mx (Golub et al. 1977). In active regions, the bipolar magnetic flux of XBPs was found to emerge rapidly and to decay more gradually.

While there are several qualitative studies describing the bipole evolution associated with CBPs, only (very) few studies made quantitative estimations of the magnetic flux, for instance, Brown et al. (2001) and Mou et al. (2016). Preś & Phillips (1999) studied a few CBPs recorded in EUV imaging and magnetic field data from the extreme-ultraviolet imaging telescope (EIT) and the Michelson Doppler Imager (MDI) on board the Solar Heliospheric Observatory (SoHO), respectively. The EUV emission from the CBPs was found to correlate with the variation in the associated total unsigned magnetic flux. This was confirmed in a study by Madjarska et al. (2003) of a CBP in a coronal hole that was also recorded by SoHO/EIT and MDI data and in a study by Chandrashekhar et al. (2013) using SDO/AIA and HMI data. Preś & Phillips (1999) measured the total unsigned magnetic flux of one CBP at the intensity peak to be 5.0 × 1019 Mx, while Madjarska et al. (2003) obtained 2.0 × 1020 Mx for a coronal-hole CBP. Similar values were found by Kwon et al. (2012). Longcope et al. (2001) reported a median flux of 1.3 × 1019 Mx for a large set of CBPs.

This overview shows that the magnetic properties of CBPs in the photosphere and the corona are not sufficiently covered by previous studies. The present study provides a long-overdue quantitative statistical study on the magnetic and coronal emission properties of small-scale loop systems and their evolution in the quiet Sun. It is not limited to bright loop systems, the so-called X-ray or coronal bright points, but also investigates faint loops, which might be the main contributors to the background emission at coronal temperatures. This statistical study also focuses on the evolutionary properties of the photospheric magnetic field and its coronal response as recorded in the Fe XII 193 Å channel of SDO/AIA. We examine the complexity of the photospheric magnetic flux, the coronal events, and features resulting from this evolving complexity. We report on the lifetimes of faint and bright SSLSs in Sect. 3.2 and on the photospheric magnetic flux range in Sect. 3.3. The intensity range and evolution (Sect. 3.4) are also examined, with special attention to spikes in the intensity. The corellation of photospheric magnetic flux and intensity is provided in Sect. 3.5. In Sect. 3.6 we report on the measurements of the footpoint separation for some of the SSLSs at the start and end of their lifetimes. A discussion of the results is presented in Sect. 4. The summary and conclusions are provided in Sect. 5. In a follow-up paper (Madjarska et al., in prep.), we will address the properties of the coronal magnetic field obtained using an automatic linear magnetohydrostatic field extrapolation tool developed by Wiegelmann & Madjarska (2023).

2. Observational data

The observations used in this study were taken over a time period of 48 h starting on 2019 September 15 at 00:00 UT and comprise imaging data from AIA (Lemen et al. 2012) on board SDO (Pesnell et al. 2012), taken in the 193 Å channel (hereafter AIA 193) and HMI line-of-sight magnetograms (Scherrer et al. 2012). We purposely selected the AIA 193 channel because it samples emission from plasma at ∼1.25 MK best, in which CBPs are known to have a dominant emission in the corona. A detailed description of the response of the AIA 193 channel is given in Mou et al. (2018). The AIA EUV data have a 12 s cadence and 0.6″ × 0.6″ pixel size. We downloaded and processed 14 400 images. To increase the signal-to-noise ratio, we binned every three consecutive images. We used HMI line-of-sight magnetograms taken at a 45 s cadence. The HMI data have a 0.5″ × 0.5″ pixel size, but were rescaled to the AIA pixel size of 0.6″ using the hmi_prep.pro procedure. To increase the signal-to-noise ratio, we binned eight consecutive magnetograms. The AIA 1600 Å images were used to align the HMI data with those from AIA. All images were derogated to 00:00 UT on September 16, 2019. The final dataset consists of a selection of quasi-temporal 480 AIA and HMI binned images taken approximately 6 min apart. A square field of view (FOV) that covers −400″ to 400″ from the disc centre (or 1334 × 1334 px2) was extracted from the processed images. 1″ equals 720 km. The noise level of the 45 s cadence HMI magnetograms is 10.2 G (Liu et al. 2012).

3. Analysis and results

We investigated the magnetic properties of small-scale loops employing AIA 193 and HMI data taken during the most recent minimum of the solar activity cycle, that is, in 2019, when the visible solar disc was free of active regions. The dates were selected after we investigated each day of the solar minimum period so that only a quiet Sun was present in the solar disc centre. The solar atmosphere was dominated by small-scale loops, some of them bright (CBPs), but there were also numerous faint loops. Loops with a projected length from ∼5″ to ∼60″ and heights 10 km at most (determined from indirect measurements) were considered to have a small scale (for details, see Sects. 3.4 and 3.5 in Madjarska 2019). Figure 1 shows the selected FOV. We selected 90 loop systems in total for the present analysis. Their locations are shown in Fig. 1. Some of the SSLSs may not be clearly distinguishable in the shown frame or are not present at all because their lifetimes fall into different periods of the selected time range of 48 h. The enumeration is given in the order they were selected for this study. Case 40 was investigated as a separate event, but it is also part of case 24, which is a typical case of a multiple magnetic flux emergence that led to complex magnetic connectivities. We first selected SSLSs in frame 240 (from 480), then in frame 300, and last in frame 100. The data cover the full lifetime of the SSLSs in only 38 of these 90 SSLSs. For the rest, either the beginning or the end of their lifetime is missing. This is noted with an asterisk before or after the lifetime duration in Table 1.

thumbnail Fig. 1.

Analysed AIA and HMI fields of view. The images were taken at heliocentric x and y coordinates of 0″, 0″. The white rectangles represent the FOVs of the SSLSs. The enumeration indicates each studied case as noted in the tables and figures. The pixel size of both images is 0.6″. The HMI magnetogram is saturated at ±50 G.

Table 1.

Photospheric magnetic properties of small-scale loops in the quiet Sun.

While some loop systems appear bright for most of their lifetime, the so-called CBPs, others have weak emission that changes little during their lifetime and does not reach the brightness of CBPs. The aim of this study and the follow-up study (Madjarska et al., in prep.) is to investigate both types of loops because to the best of our knowledge, the properties of the latter have not been considered so far. These loops might be the main contributor to the diffuse coronal emission (also called background emission). It was challenging to select and follow the intensity and magnetic flux evolution of faint SSLSs (see below for details). Only seven such loop systems are therefore presented here.

To determine the FOV that covers an SSLS (either bright or faint) during its entire lifetime, we ensured that the magnetic polarities remained in the selected FOV during the entire lifetime of the SSLS and avoided contamination by magnetic fluxes that were not involved in the SSLS. Moreover, the SSLS loops had to remain continuously in the FOV, and the contamination by other coronal phenomena intruding in the FOV had to be minimised. Some SSLSs, although located at the very disc centre, can have very tilted loops, which means that the footpoints do not lie directly below the bright loops, but are positioned on their side. In addition, the footpoints of loops may not lie simply at either end of the bright feature seen in the coronal emission because the structure of some SSLSs can be rather complex: the magnetic flux concentrations are randomly distributed. Thus, we decided to visually determine square FOVs and obtain both the intensity and the magnetic flux in these FOVs. When an SSLS was selected in a frame, a larger FOV was chosen and an animation was created. Then the animation was visually inspected and the FOV changed until an optimum solution of its size was found. It is noticeable (see the provided animations) that for some of the cases, parts of the SSLSs may occasionally appear to extend beyond the chosen FOV, such as during the formation of sigmoid-like loops during microflaring and eruptions with jets or mini coronal mass ejections (mini-CMEs) ejected at large distances. These are cases of very complex SSLSs (see below). In this situation, we had to decide whether to restrict the FOV to prevent inclusion of other features in the surroundings in the measurements or to miss some temporarily appearing structures that do not contribute significantly to the derived physical parameters. The described approach brings certain errors in the estimation of magnetic and intensity fluxes, but the dynamic evolution of the studied phenomena, as seen in the provided animations, left no other choice. A contour based on the intensity threshold either of a fixed value or with a changing value cannot comprise the SSLSs for their entire lifetime. Small-scale compact brightenings, for instance, called ‘microflares’ here, which occur in the FOV and may or may not be related to the SSLSs, would influence this approach strongly.

To demonstrate the extent of the challenge in isolating a loop system, we show the emission from plasma heated to around 1 MK recorded in the 193 Å channel of AIA in Fig. 2 (part of the studied FOV shown in Fig. 1), while in the middle panel, we present the structure of the coronal magnetic field obtained from potential field extrapolation based on the magnetogram shown in the bottom panel. We assume that this potential extrapolation model approximately reproduces the connectivities of the coronal magnetic field. We have to note that for presentation purposes, the images in Fig. 2 are rotated at 180° with respect to the images in Fig. 1. To plot the field lines, we used 500 randomly seeded footpoints, biased towards the strong magnetic field regions. Numerated arrows point at corresponding loop system regions (i.e. SSLSs). The bright-loop system counterparts are easily noticeable, and they are associated with magnetic field lines that are rooted in the stronger magnetic flux concentrations, as expected. A large loop indicated by arrow 7 in the extrapolation image cannot be found in the AIA 193 image. The loop, however, is visible in the cooler AIA channel Fe IX/X 171 Å (not shown here). This is expected because short loops rooted in a stronger magnetic field confine plasma at higher temperatures (SSLSs 1, 2, 3, 4, and 5). In contrast, longer loops rooted in a weaker field tend to be less bright because their plasma is cooler (e.g., arrow 6 points at a faint loop). This has been determined from observational studies (e.g., Xie et al. 2017, and references therein), but also from modelling studies (e.g., Dahlburg et al. 2018). The magnetic loops in the AIA 193 channel typically confine plasma with a temperature of ∼1.25 MK. Our investigation here and in Madjarska et al. (in prep.) focuses on providing information about the magnetic properties of these loops, while another forthcoming study will investigate small-scale loops that confine plasma at various temperatures from the chromosphere to the corona.

thumbnail Fig. 2.

Quiet Sun photospheric magnetic flux and associated coronal magnetic structures. Top panel: an AIA 193 image (rotated at 180 degrees with respect to the image in Fig. 1). Middle panel: magnetic field lines from a potential field model overplotted with VAPOR on an HMI LOS magnetogram. Bottom panel: HMI LOS magnetogram. Arrows numbered 1, 2, 3, 4, and 5 point at bright small-scale loop systems. Arrow 6 indicates a faint loop, and arrow 7 (shown only in the middle panel) points at a large loop that is not detectable in AIA 193, but can be seen in AIA 171 (not shown here).

Table 1 lists some of the obtained results. Although the meaning of the column abbreviations is given in the notes to the table, we give a slightly more extended explanation here. Column 1 lists the case number, which, as mentioned above, is assigned by the selection order. Column 2 reports the lifetimes of SSLSs, which were determined by visually inspecting the animations for the appearance and disappearance of the loop system in the AIA 193 images (discussed in detail in Sect. 3.2). The horizontal lines ending with arrows in Figs. 3–11 and the two vertical lines show the selected lifetime period. The same type of figures is also provided online1. for all 90 cases. In Col. 3, we list the minimum and maximum values of the total unsigned magnetic flux during the lifetime of the SSLSs (m(st)mmfl; Sect. 3.3). The marking (st) denotes that for the cases with full lifetime coverage, we report the values at the start of the lifetime of the SSLSs rather than the minimum values of the magnetic flux. In Col. 4, we list the peak of the maximum intensity (Peak int) during the lifetimes of the SSLSs. We chose to use the maximum intensity because it depicts the flaring activity related to the dynamic nature of the ‘quiet’ solar corona very well. In Col. 5 we report the minimum and maximum total intensity during the lifetime of the SSLSs (mmifl; discussed in Sect. 3.4), followed in Col. 6 by the Pearson correlation coefficient of the total unsigned magnetic flux and the total intensity of the SSLSs (Sect. 3.5). The footpoint distance determined from the centre of mass of each polarity is noted in Col. 7 (Sect. 3.6). In the following subsections, we report the results of these physical quantities. The last Col. 8 describes the evolutionary properties and features of the photospheric magnetic field of SSLSs, including emergence, coalescence, convergence, divergence, cancellation, and the level of complexity (anything more than a simple bipole configuration), and whether microflares have occurred in the SSLS.

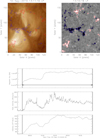thumbnail Fig. 3.

Intensity and photospheric magnetic flux properties of an SSLS associated with a flux emergence. The top row shows the AIA 193 image and quasi-temporal HMI magnetogram for case 24 (see the online animation bp024.mov). The contours outline the ±25 and ±50 G magnetic flux concentrations. The evolution of the total magnetic flux is shown in the second row, and the maximum (peak) intensity and the total intensity flux evolution taken from the selected FOV are given in the third and fourth rows of Table 1. The two vertical thick lines together with the arrowed horizontal line (only shown in the top panel) indicate the SSLS lifetime.

thumbnail Fig. 4.

Same as Fig. 3 for case 34 (see the online animation bp034.mov).

thumbnail Fig. 5.

Same as Fig. 3 for case 40 (see the online animation bp040.mov).

thumbnail Fig. 6.

Same as Fig. 3 for case 58, also showing multiple bipolar magnetic flux emergences (see the online animation bp058.mov).

thumbnail Fig. 7.

Same as Fig. 3 for case 3, which is an example of an SSLS formation from a magnetic flux coalescence. The sigmoid-like loop is related to a mini-eruption as in Madjarska et al. (2022) (see the online animation bp003.mov).

thumbnail Fig. 8.

Same as Fig. 3 for case 13, which is an SSLS that formed as a result of flux coalescence and convergence. This is one out of two cases in which one of the polarities rotates with respect to the other polarity of the opposite sign while the two converge (see the online animation bp013.mov).

thumbnail Fig. 9.

Same as Fig. 3 for case 33, which is a faint SSLS that formed as a result of flux coalescence, with loops stretching above two supergranulation cells (see the online animation bp033.mov).

thumbnail Fig. 10.

Same as Fig. 3 for case 89, which is an example of a faint loop system (see the online animation bp089.mov).

thumbnail Fig. 11.

Same as Fig. 3 for case 64, which is related to a bipolar magnetic flux emergence (see the online animation bp064.mov).

3.1. Evolutionary properties

We start with the last column of Table 1, where, as mentioned above, we list the processes, events, and observed features that were visually identified during the temporal evolution of the selected loop systems. Seven out of 90 SSLSs are marked as faint (F), while the rest reached the brightness typically associated with CBPs. It is important to mention that some faint small-scale elongated features have the appearance of loops, but it was impossible to identify or follow their associated magnetic fluxes, possibly due to the insufficient resolution and sensitivity of HMI (see Fig. 1). Therefore, so few faint loops were selected. The data cover the start of the lifetime of 53 out of 90 SSLSs. In the investigated period, we followed the full lifetimes of 38 SSLSs. Only four of these represent faint loop systems.

Twenty-nine cases are associated with magnetic flux emergence, none of which is related to faint loop systems, that is, approximately 55%. In some cases, newly emerging magnetic flux coalesces with pre-existing flux to form a new SSLS. The same results were found by Mou et al. (2016, 2018), while earlier studies that investigated CBPs in X-ray observations suggested that only 20–30% result from a magnetic flux emergence (see Sect. 1 for more information). Figure 3 and the associated animation show a case of a magnetic flux emergence. This case is a typical representation of the emergence of multiple close-by bipoles. In addition, magnetic flux coalescence leads to what can be described as three CBPs in which loops appear to connect the positive magnetic flux concentrations with a negative polarity situated in a relatively central position with respect to the positive fluxes in the FOV. The dark lane at the location of the negative flux is related to the obscuration of coronal emission by spicules rooted at the same location. Some of the chromospheric phenomena also evolve along the legs of the SSLSs (for a more detailed explanation, see Bose et al. 2023; Madjarska et al. 2021; Tsiropoula et al. 2012). The magnetic flux evolution in the second panel (from the top) clearly displays the two episodes of flux emergence. The AIA 193 intensity flux evolution clearly shows the delay in the appearance of loops heated to coronal temperatures. Other similar cases are noted with Em (emergence) and mEm (multiple bipole emergence) in the last column of Table 1.

This emission delay in response to the magnetic flux emergence has a simple explanation. After rising above the photosphere, the emerging loops initially confine cool plasma, which causes them to appear in absorption in the coronal 193 Å channel (see the animations of the cases associated with magnetic flux emergence; e.g., case 24). After a few minutes, as it takes some time for the newly emerging loops to reach coronal heights, the heating process commences and the plasma is heated to coronal temperatures. Then, bright loops become visible in the coronal emission channels or spectrometers that record spectral lines with high formation temperatures. Mou et al. (2018) found a delay of 30–60 min in the detection of CBPs following a magnetic flux emergence.

Figures 4 and 5 present two more examples of CBPs that formed from a magnetic flux emergence. We were able to follow their entire lifetime of 20.88 h and 17 h, respectively, as they fall into the chosen observing window. Case 34 is an example of a very small loop system with a maximum footpoint separation of only 9 Mm. The CBP is still detectable at coronal temperatures when the footpoint separation is only 2.5 Mm close to the end of its lifetime. Unless the loop is highly elliptical, it implies a very low-lying loop of 1.25 Mm, which is considered ‘chromospheric height’, confining plasma heated to coronal temperatures. Loop shapes and heights will be reported and analysed in the follow-up paper by Madjarska et al. (in prep.).

Case 40 (shown in Fig. 5) is an example of a magnetic flux emergence that occurred close by the footpoint of one of the polarities of a pre-existing loop system (composed of two loops that are visible at the start of the 48 h time series). The polarities of the emerging flux have the same orientation as the pre-existing one, which leads to the build-up of a larger and brighter-growing loop system. Case 58 (Fig. 6) is another very clear example of a double close-by magnetic flux emergence. During the emergence period, the negative fluxes of the two bipoles move towards the same location, which gives the SSLS a fan-like appearance.

A typical formation and evolution of SSLSs associated with magnetic flux emergence follows to a large extent one and the same scenario. At the start, bipolar flux appears as two patches with a clear polarity-inversion area (PIA). Although typically, the term polarity-inversion line (PIL) is used in the literature, ‘area’ describes the observation more correctly, at least during the emergence period. A polarity inversion line is better suited to describe elongated narrow regions between converging and cancelling magnetic fluxes. Each of the patches seen at the HMI spatial resolution is formed by small concentrations of magnetic flux of the same polarity. At the beginning of the emergence, there is occasionally no clear PIA, and some of the rising flux concentrations have slightly different bipole orientations. As these polarities are pushed together in the crowded area of the flux emergence, compact emission brightenings appear that cover the area of a few pixels. They are related to microflares caused by magnetic reconnection in the low solar atmosphere (similar to Ellerman bombs (Ellerman 1917) in the active regions). This causes some of the emerging flux to vanish, that is, the so-called magnetic flux cancellation. While the bipole magnetic flux continues to emerge, the polarities start to diverge. When they reach their maximum separation, which also coincides with the maximum intensity of the CBPs, the polarities start to converge. For some SSLSs, the intensity and magnetic flux curves level out at maximum values (e.g., case 24 in Fig. 3 and case 33 in Fig. 9 from those shown in the text) or little change at maximum values (e.g., case 13 in Fig. 8 and case 34 in Fig. 4), while the footpoints of the SSLSs remain at relatively the same location. Only one faint loop system, case 15 (shown in the additional material), is related to a weak magnetic flux emergence that occurs later in the lifetime. The newly emerging flux has the bipole orientation of the pre-existing one, which leads to the formation of a brighter loop system. When the emerging bipole does not have the orientation of the pre-existing one, the convergence of the opposite fluxes leads to microflares, some of which trigger mini-eruptions (Madjarska et al. 2022, and references therein).

The bipole convergence is always associated with a decrease in the total unsigned magnetic flux. We refer to it as the decay phase. During this phase, magnetic flux cancellation (magnetic flux that vanishes while the polarities visibly touch along the polarity inversion line) appears to play an important role in removing magnetic flux. Magnetic flux cancellation is typically associated with microflares and eruptions of the SSLS loops (jets or mini-CMEs) that confine hotter but also cooler plasma, as well as mini-filaments (Madjarska et al. 2022, and references therein). Occasionally but rarely, the SSLSs disappear simply due to magnetic flux decrease while the polarities are at their maximum separation or due to further flux divergence. This is observed in both the flux-emergence and flux-coalescence cases.

Twenty-four cases out of 53 (i.e. slightly fewer than 50% from all cases with a recorded start of the lifetime) do not form from a magnetic flux emergence. As small patches of magnetic flux of the same polarity group together (coalesce), the newly built-up magnetic flux concentration eventually creates a connecting loop (closed magnetic field line) with another polarity located at a certain distance, the so-called chance encounter of magnetic flux. We refer to these cases hereafter as ‘coalescence cases’ (CoalC). Magnetic reconnection in the corona between converging fluxes of opposite polarities is thought to be the process leading to the formation of these closed-field lines, and consequently, their confined plasma is heated to corona temperatures, forming bright loops seen in extreme-ultraviolet (EUV) and X-ray emission. Several models that aim to explain this formation of SSLSs (XBPs and CBPs) have been proposed since the 1990s (for a review, see Sect. 9 in Madjarska 2019), and the most recent is by Syntelis et al. (2019), Nóbrega-Siverio & Moreno-Insertis (2022, which is not yet included in the review).

The end of life of CoalC follows similar scenarios as in the magnetic flux emergence cases, that is, convergence and magnetic flux disappearance, or more rarely, magnetic flux divergence. Magnetic flux cancellation is often observed between the main polarities, typically towards the end of the lifetime of the SSLSs. Figures 7 and 8 show two examples of SSLSs (CBPs) that formed from magnetic flux coalescence. The magnetic flux and intensity curves increase more slowly, in contrast to the sharp rise of the magnetic flux when it is due to a magnetic flux emergence.

The last two examples shown in Figs. 9 and 10 represent the group of faint loops. The polarities of these loops typically form from magnetic flux coalescence, and their maximum total intensity is weaker than those of the CBPs. Their intensity curves are hard to separate from the background coronal emission. These loops also show very stable footpoint locations (see Sect. 3.6). Their total unsigned magnetic flux cannot be obtained unambiguously because this flux is close to other non-loop-associated fluxes, which results in a low to negative Pearson cross-correlation coefficient (for details, see Sect. 3.5). In all cases, we observe magnetic flux cancellation involving small-scale magnetic flux weak background-flux polarities and the main bipoles at almost any time (see more results on this in Mou et al. 2016, 2018).

Small-scale loop systems always connect magnetic fluxes of opposite polarities, although previous studies mention that CBPs are occasionally associated with a single polarity at the start or close to the end of their lifetimes. This typically arises when one of the polarities is too weak and falls below the resolution capabilities of the observing instrument (see Sect. 4.1 of Madjarska 2019). These bipolar fluxes, especially in CoalC cases, can be randomly located in the network and often create SSLSs with complex appearances. It is rare for the SSLSs to show a simple bipolar structure (two patches of opposite magnetic flux on either side of a PIA), such as case 40 shown in Fig. 5. Even in this case, the polarities are quite dispersed and thus form loops at different lengths and heights. In the cases of flux emergence, the morphology at least in the early stages of the SSLS lifetime tends to be simpler, but often, as the SSLS evolves, it can lead to the formation of bright loops with close-by pre-existing fluxes or the loss of its simple appearance due to the divergence and dispersal of the emerging magnetic flux. When SSLSs form by chance encounter as magnetic flux is swept towards the network junctions, loops with various connectivity can form, and these SSLSs more often have a complex structure.

In two cases, 13 and 64 (see the additional material), we observed a rotation of one polarity with respect to the other. This behaviour is obviously rare, and in both cases, the displacement of the polarity was due to the emergence and evolution of new supergranular cells that moved the polarity from its location. The rotation did not lead to any dynamic activity in the SSLSs.

3.2. Lifetimes of SSLSs

Although several studies have reported the lifetimes of CBPs (see Sect. 3.2 in Madjarska 2019), for the further analysis of the obtained results, we also report and discuss the lifetimes of the SSLSs selected for the present study. As mentioned above, we estimated the lifetime of the SSLSs by visually establishing when they become visible and when they vanish in the AIA 193 channel (emission at ∼1.25 MK). We then produced two sets of animations that cover the lifetime of each loop system, adding ten frames before and after the disappearance of the SSLS. One set of animations uses the original magnetograms, and one set the masked magnetic field images. The latter was also used to obtain the total unsigned magnetic flux. Both sets of animations are provided online2.

In the second column of Table 1, we give the obtained lifetimes, and in Fig. 12a, we show their distribution. The stars before or after the lifetimes (in Table 1) indicate that the SSLS was already visible at the beginning of the time series (48 h) or remained visible at the end of the series. The lifetimes of only 38 SSLSs were fully covered by the selected observing window. The average (median) lifetime as determined from the AIA 193 channel of the SSLSs is 23.65 (23.5) h, with a minimum of 3.8 h and a maximum of 47.7 h. It should be noted here that longer-living SSLSs can exist, although they are rare. Madjarska et al. (2020) reported on an SSLS (CBP) in a coronal hole with a lifetime of 7 days.

thumbnail Fig. 12.

Histograms of the physical quantities. Panel a shows the lifetimes of SSLSs for 38 cases whose lifetimes are fully covered. The maximum total unsigned magnetic flux for all 90 cases is given in panel b; see Table 1, Col. 3. The maximum peak intensities associated with microflares of SSLSs for all 90 cases are shown in panel c; see Table 1, Col. 5. The maximum total intensity flux of SSLSs for all 90 cases is provided in panel d; see Table 1, Col. 6.

Small-scale loop systems with a duration shorter than 8 h are only formed from magnetic flux coalescence. Hereafter, we refer to them as ‘coalescence cases’. SSLSs related to a magnetic flux emergence tend to have longer lifetimes with an average of 28.3 h (based on 17 cases). The lifetime duration is indicated with two vertical thick lines in all plots (e.g., Figs. 3–10), while an arrowed horizontal line is only plotted on the magnetic flux curve. Faint SSLSs appear to have longer lifetimes than bright loop systems associated with similar magnetic fluxes because the distance between the two opposite polarities tends not to converge. When magnetic bipoles converge, as for many cases of CBPs, this causes the formation of quasi-separatrix layers (QSL; Démoulin et al. 1996; Titov 2007) where magnetic reconnection can occur (Mou et al. 2018; Galsgaard et al. 2019; Madjarska et al. 2020, 2022). The product of the reconnection process is a sudden energy release, which has both thermal and kinetic components, resulting in the observation of microflares and jets or mini-eruptions. This leads to a fast(er) exhaustion of the total magnetic flux and a shorter lifetime of the SSLSs, similar to solar flares in active regions (e.g., Castellanos Durán et al. 2018; see below, Sect. 4 on the relation between magnetic fluxes and lifetimes of SSLSs). In the cases of faint loops, polarity convergence is not observed because their footpoints are separated by one or more supergranular cells. Cancellation of small-scale parasite polarities with the main polarities of the bipole is seen at almost any time, but their effect on the main bipole total magnetic flux (the whole SSLS) is quite negligible. Some of them also cause microflares, but often without detectable eruptive phenomena seen at the AIA spatial resolution.

3.3. Photospheric magnetic flux range and evolution

We estimated the total unsigned magnetic flux and its evolution from the selected square FOVs of the SSLSs (see the top right panel in Figs. 3–11). This assumes that the photospheric magnetic flux in the FOVs is involved in the build-up of the magnetic skeleton of the SSLSs. However, as the images of Figs. 3–11 and the animation material show, this is not always the case because the magnetic flux connectivity is complex. When the FOV is seeded with small patches of flux concentrations with a strength close to the strength at the footpoints of the SSLS, the errors of the measured magnetic flux can become relatively large. This affects the estimation of the total unsigned magnetic flux for small CBPs or faint SSLSs associated with weaker magnetic flux.

We masked the background magnetic flux up to ±20 G. Higher background values appear to remove the magnetic flux involved with small or faint SSLSs. We did not correct for the line-of-sight effect because it is negligible for the selected FOV (±25°). We should also point out that we cannot use HMI vector magnetograms because they are not reliable in the quiet Sun: the level of the signal-to-noise ratio of the transverse component is too low (Hoeksema et al. 2014).

In the third column of Table 1, we list the minimum and maximum total unsigned magnetic flux density for the SSLSs during their lifetimes. When we covered the full lifetime of the SSLSs, we instead list the minimum of the magnetic flux at the start of the lifetime, which is the minimum flux in most cases. The distribution of the maximum total unsigned magnetic flux density is given in panel b of Fig. 12. A few examples of the magnetic flux evolution are shown in the top panels of Figs. 3–11. The magnetic flux curves are smoothed with a three-pixel running average. As mentioned above, the lifetime of a loop system was determined by investigating its appearance in the coronal AIA 193 channel. The footpoints of some (especially larger) loops that are highly tilted with respect to the radial direction do not necessarily lie below the projected intensity area of the SSLSs even at a disc-centre location (this is discussed in more detail in Sect. 3.1).

The results show that the minimum magnetic flux density associated with a small-scale loop system that confines plasma around a million degrees is 3 × 1018 Mx and the maximum is 1.8 × 1020 Mx (case 24 is excluded from the statistics as it is composed by two emerging bipoles). Thus, small-scale coronal loop systems are associated with magnetic fluxes that scale over almost two orders of magnitude.

Figure 3 shows an example of an SSLS that is also formed by magnetic flux emergence. The maximum magnetic flux of this SSLS is one of the highest, but it should be noted that it is composed of what we would normally count as two to three CBPs (two of them related to magnetic flux emergence). Some of the footpoints of the small-scale loops are obscured by spicules that are rooted in the same polarities (the negative polarity). Before the second flux emergence, the maximum flux is ∼1.1 × 1020 Mx. Case 64 (Fig. 11 and corresponding animations) has the strongest magnetic flux of a complex bipole. It reaches the highest intensity and has the fastest emergence rate (see Sect. 3.7 for more details).

3.4. Intensity range, spikes, and evolution

Our analysis of the image animations indicated highly dynamic intensity evolution of the SSLSs with spikes in intensity either in loops (loop brightenings) or in small compact regions with a size of a few pixels in the area of the SSLSs. When we produced curves of the maximum intensity from the selected FOV of each SSLS, we were surprised to find many intensity spikes, almost all related to microflares. In 77 out of 90 SSLS cases, these compact transient brightenings were associated with microflares. The curves are shown in the middle panels of Figs. 3–11. We purposely did not smooth these curves to demonstrate the very short duration of the microflares, which in some cases are close to the data cadence of 6 min. In Col. 4 of Table 1, we list the peak of the maximum intensity, which is the largest intensity spike during the lifetime of an SSLS. The intensity distribution of these peaks is shown in a histogram in Fig. 12c. These events are not different from the microflares explored in our previous studies on dynamic activities in CBPs (Mou et al. 2018; Galsgaard et al. 2019; Madjarska et al. 2020, 2022). We should note here that in these studies, we were solely interested in microflares that trigger eruptions, either jets or mini CMEs. Not all of the microflares found here appear to trigger mini-eruptions on the scale of those investigated in our previous studies. The intensity spikes are often associated with magnetic flux cancellation, that is, magnetic bipoles converging and vanishing. For some cases, the flux cancellation was hardly distinguishable as the flux involved was at the HMI noise level. Even in these cases, the associated microflares displayed very high-intensity increases (e.g., see cases 34, 3, and 89 in Figs. 4, 7, and 10, respectively). Some weaker spikes are due to an increase in loop intensity, but whether they are also related to microflares is hard to establish at the spatial resolution of the AIA and HMI data. We will investigate these important details using data from Solar Orbiter (Müller et al. 2020), the high-resolution Extreme-Ultraviolet Imager (EUI; Rochus et al. 2020) and the Polarimetric and Helioseismic Imager (PHI; Solanki et al. 2020).

We found that regions of SSLSs with more complex photospheric fields produced more microflares. The intensity increase occurs in an area of a few pixels and ranges between 113 DN/px/s and 2043 DN/px/s, with an average value of 571 DN/px/s and a median of 499 DN/px/s. No pixel saturation was detected. The intensity flux of the peaks is in the range from 200 to 1000 DN/px/s in 88% of the cases (see panel c in Fig. 12). We also calculated the intensity ratio of these peaks with respect to the minimum and maximum mean intensity of the SSLSs to estimate the level of increase. The relative intensity increase with respect to the minimum mean intensity ranges from 4 to 42 times (average 13; Fig. 13, top panel), while with respect to the maximum mean intensity, the increase is between 3 and 18 times (average 8; Fig. 13, bottom panel). The minimum mean intensity is very close to the background intensity. The maximum intensity increase registered in the studied cases is 2043 DN/px/s. A unique event registered by NuSTAR on 2019 April 26, peaking at about 02:06 UT (Iain Hannah, priv. comm.), had a peak intensity in the brightest pixel of 9138 DN/px/s.

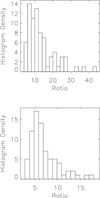thumbnail Fig. 13.

Histograms of intensity ratios. The top panel shows the ratio of the microflare-associated intensity peaks with respect to the minimum-mean intensity (close to the quiet-Sun background intensity), and in the bottom panel, we show the ratio with respect to the maximum mean intensity in the FOV of the SSLSs.

We also show in the bottom panels of Figs. 3–11, the total intensity flux of the SSLSs. It was obtained by summing the intensity in the selected FOV of the SSLSs. In Table 1, Col. 5, we list the minimum and maximum total intensity of the SSLSs. The distribution of the maximum total intensities is shown in panel d of Fig. 12. The SSLSs have an average (median) maximum total intensity flux 46(38) × 104 DN/s ranging from 2.8 × 104 to 212 × 104 DN/s.

3.5. Linear Pearson correlation coefficient

The intensity evolution of SSLSs shows a strong correlation with the magnetic flux when only SSLS cases are considered that are negligibly contaminated by magnetic and intensity fluxes in the FOVs that are not related to the SSLS. We obtained the linear Pearson correlation coefficient (CC) of the logarithm of total unsigned magnetic flux (log Φ) and the total intensity flux during the lifetime (log F) of the SSLSs in the selected FOVs. Only for 35 out of 90 cases is CC equal to or above 0.8. The total maximum unsigned magnetic flux for those with CC above 0.8 is 5.7 × 1019 Mx, and those with a CC below 0.5 have an average maximum total unsigned magnetic flux of 3.9 × 1019 Mx. Smaller correlation coefficients or negative ones (shown with an en-dash in Table 1) are due to contamination in the FOV of either magnetic flux that is not involved in the build-up of the SSLSs or to brighter features that temporarily contaminate the selected FOV. Thus, for SSLSs associated with stronger magnetic fluxes, the contamination will have a lower effect on the correlation.

3.6. SSLS footpoint separation

Next, we attempted to obtain the footpoint displacement during the SSLS lifetimes. To do this, we used the centre of mass of each polarity and removed the points where the centre of mass was not located at the flux concentration associated with the detectable (bright or faint) loop system. The complexity of magnetic flux in the photosphere often prevented us from following the footpoint displacement because the centres of mass change their locations in time. Nevertheless, we succeeded in obtaining an estimate of this evolution for 51 cases, that is, for more than half of the cases. The data in these cases cover the entire lifetime of only 19 SSLSs, for 6 of which, the end-of-life is related to magnetic flux divergence, and for 11 of which it is related to convergence and cancellation. In two cases, the distance of the footpoints does not change with time. Both cases are associated with faint loops, for one of which the largest distance was measured, 56 Mm. In all faint loop cases, the footpoint separation typically either does not change or the change is very small in comparison to the bright SSLSs (CBPs). In only one faint SSLS case is magnetic flux divergence observed. This is excpected because the observations show that in the case of faint loops, they are separated by at least two supergranulation cells. If all 51 cases are considered, magnetic flux convergence is the dominant behaviour towards the end of the lifetime of CBPs, while faint loops, as mentioned above, have their footpoints at a constant distance until the magnetic flux is fully exhausted. The minimum distance between bipole footpoints is 1.8 Mm, and the largest distance is 37 Mm. From 50 cases (we removed one measurement of a faint loop system with an exceptionally large footpoint separation, case 33), the average maximum distance combining both cases of convergence and divergence is ∼36 Mm. The average small footpoint separation based on 12 cases of flux separation is 2.2 Mm (cases related to flux convergence alone).

3.7. Magnetic flux emergence and decay rates

We obtained the magnetic flux emergence and decay duration and rates for 29 cases. They are given in Table 2. For the emergence period, we chose the steepest part of the magnetic flux curve to measure the emergence rate. As shown in Kontogiannis et al. (2020), the magnetic flux emerges at various rates during the emergence period. We find that a faster flux emergence is observed initially more frequently, followed by a slower emergence. We were able to estimate all four parameters for 11 out of 29 cases. We visually selected the obvious periods of faster emergence and decay period from the magnetic flux curve. The decay-time period was determined as the time of obvious decrease in the magnetic flux. We were able to estimate the emergence duration for 22 cases, 2 of which represent consecutive emergence in the same SSLS, case 24 (noted in Table 2 as 24em1 and 24em2). The emergence duration ranged from 83 to 503 min, with an average value of 219.2 min (median – 185 min). The emergence rate and corresponding errors were obtained from a linear fit of the selected emergence curve. They are in the range between 1.2 and 5.7 × 1015 Mx s−1, with an average of 2.8 × 1015 Mx s−1 (median of 2.3 × 1015 Mx s−1). We note that the lowest and highest rates of 0.8 × 1015 Mx s−1 and 7.8 × 1015 Mx s−1 were excluded from these calculations.

Table 2.

Magnetic flux emergence duration (Em dur), emergence rate (Em rate), and decay duration (Dec dur) and rate (Dec rate) for SSLSs associated with flux emergence.

We also estimated the decay duration and rate for 18 cases, some of which are formed from magnetic flux coalescence (CoalC). Their decay durations (removing one excessive value of 1349 min) range from 143 to 875 min, with an average value of 466.5 min (median – 360). Again, after removing the highest and the lowest values of 1.95 and 0.19, respectively, we find a decay-rate range between 0.3 and 1.6 × 1015 Mx s−1, with an average of 0.8 × 1015 Mx s−1 and a median of 0.9 × 1015 Mx s−1. The average (median) emergence rate is 3.4 (2.5) times higher than the decay rate. From the presented example, the duration and emergence rate of case 24, which is composed of two newly emerging loop systems (forming three CBPs) shown in Fig. 3, are 126 and 203 min, with an emergence rate of 5.5 × 1015 Mx s−1 and 5.7 × 1015 Mx s−1, respectively.

4. Discussion

The assertion that loops are the main building blocks of the solar atmosphere may sound overstated, but this description reflects the true nature of the magnetic structure of the solar atmosphere. Closed magnetic field lines with various lengths and heights form the skeleton of these loops. When the plasma that is confined along these field lines becomes denser and hotter than the surrounding atmosphere, the loops become visible in emission from plasma with various temperatures. The plasma-heating mechanism of loops in active regions has been studied very intensively over the past few decades. For a review on coronal loops, see Reale (2014) and the most recent observational and theoretical studies by Kucera et al. (2019), Ugarte-Urra et al. (2019), Brooks et al. (2021) and van Ballegooijen et al. (2017), Shi et al. (2019), Li et al. (2022), for example. Bright small-scale loop systems known as coronal bright points (CBPs) have also been covered by numerous studies (for a review, see Madjarska 2019) but many important details were missed or poorly investigated. As shown in the example image in Fig. 1, the solar atmosphere of the quiet Sun is entirely dominated by small-scale loops, especially during the minimum of the solar activity cycle, and it is evident that understanding their nature is equally (and even more) important as the plasma heating of large loops in active regions (ARs). When we assume that the same heating mechanism is in operation in both the AR large and the QS small loops, then investigating small-scale loops carries more advantages than limitations, especially in a time of unprecedentedly high-resolution data from Solar Orbiter EUI and the forthcoming Multi-slit Solar Explorer (MUSE; De Pontieu et al. 2020) and the Extreme Ultraviolet High-Throughput Spectroscopic Telescope Epsilon Mission (Solar-C EUVST; Suematsu et al. 2021) spectrometers. These loops are a great choice for studying the heating mechanism of magnetically confined plasma because we can follow the formation and evolution of both bright (CBPs) and faint loop systems from their emergence or formation stage until their full disappearance because their lifetimes are short. They are generally less complex than active regions, and their modelling is less computationally expensive. We find that in 50% of the cases, the loop formation is due to the chance encounter of magnetic fluxes, which is explored in numerous models. The most recent were reported by Wyper et al. (2018), Syntelis et al. (2019), and Nóbrega-Siverio & Moreno-Insertis (2022). The heating of small-scale loops due to magnetic flux emergence might be produced by the same physical mechanism, but this is still to be explored with both the MURaM (e.g., Vögler et al. 2005; Rempel 2014) and Bifrost (Gudiksen et al. 2011) codes.

The last comprehensive study that statistically and qualitatively investigated the photospheric magnetic field of small-scale loops (only bright loops observed in X-ray observations, the so-called X-ray bright points (for a review, see Madjarska 2019) was by Golub et al. (1977). Our motivation for pursuing this research project (i.e. photospheric and coronal properties of the magnetic field of small-scale loops and related coronal activity) comes from the needs of the modelling community for model constraint and validation on the heating mechanism and associated activities of small-scale loops.

The evolutionary behaviour of CBPs has been covered by a very limited number of studies (e.g., Golub et al. 1974; Mou et al. 2016). Some quantitive measurements were reported by Mou et al. (2016), although the study concentrated rather on the evolutionary description of the photospheric magnetic flux associated with CBPs alone. The results obtained here complement these studies by following the evolution of the magnetic fluxes in the photosphere of the loop systems in full detail, investigating both bright and faint loop systems. Magnetic flux emergence in earlier studies is found in two-thirds of the cases (for a review, see Madjarska 2019), while the present study and the study by Mou et al. (2018) find that 50% of bright loop systems (CBPs) form as a result of magnetic bipole emergence. None of the faint loop systems was found to be related to magnetic flux emergence because the main formation mechanism suggests that the build-up of most of the faint (background) coronal emission happens through random (chance) encounters of magnetic polarities. We find that magnetic and intensity fluxes increase slowly and gradually during the plasma heating of loops that are formed by a chance encounter, in contrast to the sharp rise of the magnetic flux and intensity due to magnetic flux emergence. This indicates that a different input of energy per time unit is put into the different processes. In the flux emergence cases, a large amount of flux reaches the corona, and consequently, a large amount of plasma is heated quickly to coronal temperatures, suggesting loop-top heating as in the null-point reconnection models of Wyper et al. (2018) and Nóbrega-Siverio & Moreno-Insertis (2022), rather than footpoint heating. Heating that initially occurs on loop tops and is driven by heat conduction towards the lower part of the loops has also been found both in observations Madjarska et al. (2021) and explored in several models by Wyper et al. (2018) and Nóbrega-Siverio & Moreno-Insertis (2022), for instance.

The lifetimes of magnetically driven phenomena is an important parameter that may give an additional indication as to which physical mechanism is at work in heating of plasma to temperatures that are at least two orders of magnitude higher than the background corona. We examined the (log, log) relation of the total (over the entire lifetime) unsigned magnetic flux and intensity in the AIA 193 channels and the lifetime duration of SSLSs. Both parameters, as shown in the top row panels of Fig. 14, show a linear correlation with the lifetime duration of SSLSs. Only 38 cases for which the full lifetimes were covered by the data were included. The correlation coefficient for the magnetic flux versus lifetime is 0.87, and the intensity flux versus lifetime is 0.85.

thumbnail Fig. 14.

Scatter plots. The log10 of the maximum total unsigned (over lifetime) magnetic flux vs. the lifetime duration of SSLSs is shown in the top left panel. The log10 of the maximum total intensity flux (over lifetime) vs. lifetime duration of SSLSs is shown in the top right panel, while the log10 of the maximum total intensity flux (over lifetime) vs. the log10 of the maximum total unsigned magnetic flux is shown in the bottom left panel. The two top panels include only full-lifetime covered cases, and the bottom left panel includes all 90 cases. The bottom right panel shows the peak intensity associated with microflares vs. the log10 of the maximum total unsigned magnetic flux. The abbreviation MF in the last column of Table 1 indicates the identified 77 cases.

The examination of the lifetime of SSLSs revealed an interesting fact, namely that bright loop systems (CBPs) with lifetimes shorter than 8 h are only formed from magnetic flux coalescence and convergence, while the average lifetime of CBPs formed by flux emergence is 28.3 h. Thus, random walks of magnetic flux in the network can sporadically lead to loop formation. Random loop formation can also occur during bipole flux emergence and a chance encounter with parasite fluxes of opposite polarity. Faint loop systems (we only examined seven such systems) do not show short lifetimes, but this is expected because their footpoints remain at large and almost constant distances in comparison to their bright counterparts. This behaviour of the photospheric flux means that the bipole polarities are less likely to interact, and microflares occur in consequence, which contributes to the faster exhaustion of the magnetic flux.

The detection of numerous intensity spikes in the region of SSLSs shows that the quiet Sun is anything but quiet. Here, we refer to these events as microflares, but the estimation of thermal energies of small flares in CBPs by Kotani et al. (2023) gives a range from 1024 to 1027 erg, indicating a wider range that is covered by both nanoflares (1024–1025 erg) and microflares (> 1026 erg). The authors estimated that the magnetic field strength involved in these small flares is in the range of 5–15 G. The temperature and density temporal evolution suggested that chromospheric evaporation plays an essential role in the thermal properties of some of the small flares in the quiet Sun, similarly to large flares.

By examining the maximum intensity variation during the lifetime of the SSLSs, we found a larger number of microflares than previously expected. The series of microflares is related to the main bipole system or/and one of the polarities and a parasite one of an opposite sign. We find that the more complex the background field, the higher the probability for numerous microflares to occur, leading to a higher decay rate of the SSLSs. Mou et al. (2018) concluded that CBPs are sources of at least one eruption during their lifetime. When only the main bipole is involved, the eruptions always occur towards the end of the lifetime of the CBPs, and they are always related to microflares. The eruptions were also associated with the ejection of cool material, which often has an elongated structure that is thought to be a minifilament whose magnetic flux rope has built up during the convergence and cancellation of the opposite polarities of the bipoles. Not all of the microflares observed here appear to result in eruptive events (as far as the AIA resolution permits us to detect), but they certainly contribute to the sudden energy release, heating, and faster decay of the SSLSs.

A study by Mondal et al. (2023) used radio co-observations from the Very Large Array (VLA) and the Expanded Owens Valley Solar Array (EOVSA) to detect transient events in the corona of the quiet Sun in the microwave (GHz) domain, including those related to CBPs. The larger bandwidth of the combined VLA and EOVSA observations in comparison with past observations (Habbal et al. 1986), allowed the quantification of the non-thermal energy associated with two transients, one of which has a source region in a CBP located in a coronal hole. The event associated with the CBP is identical to the intensity spikes (microflares) found in the present study. The presence of non-thermal electrons provides further evidence that the dynamic events in the SSLSs studied here result from magnetic reconnection. In Fig. 14, bottom right panel, we present the relation of the peak intensity (due to microflares) during the SSLSs time and the total unsigned magnetic flux. We find a weak correlation of only 0.37. This is not surprising as the build-up of free energy in the corona does not entirely depend on the photospheric magnetic flux, but rather on its random motions and connectivity patterns.

The present study reports for the first time the full magnetic flux range of small-scale loop systems. We selected a wide range of small-scale loop systems from the smallest to the largest and from the faintest to the brightest possible, following their entire lifetime. We find that a total unsigned magnetic flux as small as 3 × 1018 Mx can sustain a loop system with plasma reaching a million degrees. The highest magnetic flux reaches 1.8 × 1020 Mx. This brings up the question of whether this upper limit can be exceeded and whether a CBP can evolve into an active region (a magnetic bipole region that contains pore(s) and sunspot(s)). A forthcoming case study will discuss the properties of these regions and will provide further qualitative information about the possible upper boundary of SSLSs before they become an active region. Previous studies mention only an upper limit of 1019 Mx and 1020 Mx for CBPs (see Sect. 1) typically concerning X-ray CBPs. As discussed in Madjarska (2019), only CBPs associated with strong magnetic fluxes or during microflaring phase can be observed in X-rays. Most of the CBPs seem not to reach X-ray temperatures. The most recent study by Mou et al. (2016) reported that the total unsigned magnetic flux of CBPs at the peak of the intensity of CBPs is in the range between 1 × 1019 Mx – 2.0 × 1020 Mx, which is in accordance with the values obtained here. We find that the loop systems that form from a flux emergence (19 cases with fully covered lifetime) have a higher magnetic flux by 74% on average than those formed from coalescence and a follow-up chance encounter of magnetic fluxes (22 cases). Similarly, the intensity of emerging SSLSs is higher by 64% on average.

Similar to Mou et al. (2016), Pevtsov et al. (2003), and Toriumi et al. (2022), we obtained the relation of the total unsigned magnetic flux and the total intensity flux of the SSLSs. The linear Pearson correlation coefficient (CC) of the total unsigned magnetic flux and intensity in the FOV of the SSLSs during their lifetime were reported in Sect. 3.5. For only 35 cases did we obtain a CC above 0.8. A smaller or negative CC was found to be caused by contamination in the FOV by either magnetic flux that is not related to the magnetic connectivities of the SSLS or by bright emission that is also unrelated to the SSLS. To further investigate this relation, we then used the total unsigned magnetic flux and intensity summed over the entire lifetime of the SSLSs. Mou et al. (2016) obtained the power-law index using the relation of the total unsigned magnetic flux at the peak of the CBP radiation. Our initial attempt to derive the power-law index as in Mou et al. (2016) showed high dispersion of the relation values. This can easily be explained by the fact that the corona responds with delay to the variations in the photospheric magnetic flux, and if high-cadence data are used, the corresponding variations will not occur simultaneously. The results are shown in the bottom left panel of Fig. 14. We obtain a power-law index α for the linear fit log F ∝ α log Φ, where F is the total intensity flux and Φ is the total unsigned magnetic flux during the entire SSLS lifetimes. Our results are best compared to the work of Toriumi et al. (2022), where for wavelengths of Fe XII 193–195 Å, the study finds a power-law index α of 1.14 ± 0.03, while the present study finds 1.10 ± 0.02. The similarities of the obtained values indicate that the plasma heated to the formation temperatures of Fe XII, which dominates the AIA 193 channels, is entirely confined in small-scale magnetic loops. Here, the correlation coefficient of log F and log Φ is 0.98. The power-law index obtained by Mou et al. (2016) is 1.37; the difference might come from the different approaches in the two works. Toriumi & Airapetian (2022) found a dependence of the power-law index α on the solar activity cycle. Given the results obtained in the present study, a future statistically extensive work covering all phases of the solar cycle and loop systems of all scales (including active region loops) and possibly employing machine learning may help explain this dependence.

The emergence of magnetic bipoles, also referred to as ephemeral regions, is observed everywhere on a photospheric level. Possibly all of them form small loops that are visible in images sampling a wide range of temperatures from the chromosphere to the corona. We therefore discuss some of the results obtained here in the context of the findings on ephemeral regions. Numerous studies report the total unsigned magnetic flux of ephemeral regions as well as their emergence rate (Schrijver et al. 1998; Chae et al. 2001; Zhao & Li 2012; Yang & Zhang 2014; Wang 1988). These studies give a mean magnetic flux of ephemeral regions ranging from 9.27 × 1018 Mx to 3.3 × 1019 Mx. For a single case of small emerging bipolar magnetic flux associated with a CBP, Kontogiannis et al. (2020) reported a mean unsigned magnetic flux of ∼5 × 1018 Mx. The photospheric magnetic flux range found in the present study ranges from 3 × 1018 Mx–1.8× to 1020 Mx, which includes this magnetic flux range. This indicates that it is highly probable that all ERs in the magnetic flux range found here could give rise to a magnetic small-scale system that confines plasma heated to coronal temperatures. Investigating this will be the subject of a future study. The emergence rates obtained in the present study also comply with the emergence rate of ERs. Yang & Zhang (2014) found a mean value of 2.6 × 1015 Mx s−1, while here, we find an average emergence rate of 3.0 × 1015 Mx s−1. Norton et al. (2017) presented in their Fig. 5 the magnetic flux emergence rate as a function of the maximum total unsigned magnetic flux for active regions, penumbra, and ERs. The SSLS-associated fluxes studied here are in the range of ERs from the studies of Hagenaar (2001) and Yang & Zhang (2014). We find that decay rates above 1.0 × 1015 Mx s−1 are typically related to SSLSs with strong microflares occurring towards the end of the lifetime of the SSLSs.

5. Summary and conclusions

We investigated both qualitatively and quantitatively the photospheric magnetic properties of bright and faint small-scale loop systems (SSLSs) from SDO/HMI magnetograms and associated coronal intensities as recorded in SDO/AIA 193 images. Faint loop systems that to the best of our knowledge have not been studied before were analysed, and their properties were compared with bright SSLSs (also known as CBPs). We used 48 h of AIA and HMI co-observations taken at a 6 min cadence and studied 90 SSLSs, 7 of which are faint. We derived a range of physical parameters that can be used to validate theoretical models. We can confirm that ∼50% of the SSLSs form either from magnetic flux emergence or by magnetic flux coalescence, followed by the chance encounter of close-by magnetic flux concentrations of opposite polarities. We find that faint loop systems only form by a chance encounter of magnetic flux. We provide for the first time the full range of the photospheric magnetic field associated with bright and faint loops, which for the data sample used here ranges from 3 × 1018 Mx to 1.8 × 1020 Mx. We obtained an average lifetime of SSLSs of 23.65 h, ranging from 3.8 h to 47.7 h. The maximum intensity variation during the lifetime of SSLSs reveals numerous intensity spikes from a few pixel size areas, which are identified as microflares, even though their energies as found by Kotani et al. (2023) range from 1024 to 1027 erg, that is, both nanoflare and microflare energies. Loop brightenings are also observed, but it is unclear whether these brightenings are also related to nano- or microflares. The relative intensity increase in these spikes with respect to the minimum mean intensity (close to the background emission) in the SSLS FOV ranges from 4 to 42 times (average 13), while with respect to the maximum mean intensity in the FOV, this is between 3 and 18 times (average 8). A follow-up dedicated study that employs an identification code for intensity spikes (adopted from our previous studies by Subramanian et al. 2010, 2018) on the same dataset but at a cadence of 45 s will report in full detail about the duration, location, full intensity range, and occurrence rate. This study will also investigate the role of transient sporadic heating events to plasma heating in SSLSs.

The linear Pearson correlation coefficient of the total unsigned magnetic flux and total intensity is higher than 0.9 for SSLSs associated with a strong magnetic field (with respect to the background magnetic field). Lower Pearson coefficients are caused by the contamination from background magnetic flux that is not involved in the magnetic connectivities of the SSLSs. For SSLSs that are formed by magnetic flux emergence, the emergence durations range from 83 to 503 min, with an average value of 219.2 min (median – 185 min). The emergence rate is in the range between 1.2 and 5.7 × 1015 Mx s−1, an average of 2.8 × 1015 Mx s−1 (median of 2.3 × 1015 Mx s−1). We also estimated the decay duration and rate for 18 cases, including SSLSs formed by magnetic flux coalescence and chance encounters of the magnetic flux. Their decay durations range from 143 to 875 min, with an average value of 466.5 min (median – 360). The decay-rate range is between 0.3 and 1.6 × 1015 Mx s−1, with an average of 0.82 × 1015 Mx s−1 and a median of 0.9 × 1015 Mx s−1. The average (median) emergence rate is found to be 3.4 (2.5) times higher than the decay rate. A linear correlation is found between the total unsigned magnetic flux and lifetimes as well as coronal intensity and lifetime, with coefficients of 0.86 and 0.85, respectively.

The power-law index α of the logarithm of the total unsigned magnetic flux and the total intensity for the full lifetime of SSLSs is 1.10 ± 0.02, which is similar to the findings by Toriumi et al. (2022) of 1.14 ± 0.03, indicating that the emission of the corona of the quiet Sun at ∼1.25 MK is presumably mostly confined to small-scale loops (some brighter, others fainter). Therefore, it is imperative to understand the mechanism that heats the plasma in these loops. Various models have successfully produced small-scale loops that confine plasma heated to million degrees (Wyper et al. 2018; Chen et al. 2022; Nóbrega-Siverio & Moreno-Insertis 2022). The validity of these models can only be tested if the physical properties of these modelled loop systems are compared with observations. This study is the first of a series of studies aiming to deliver some of these physical properties. Our follow-up study will report on the coronal magnetic field parameters of some of the small-scale loops studied here by employing the new algorithm based on a magnetohydrostatic model developed by Wiegelmann & Madjarska (2023). The algorithm computes the magnetic field in the solar atmosphere and automatically matches individual magnetic field lines with observed structures that appear with enhanced emission in extreme-ultraviolet (EUV) images.

Movies

Movie 1 associated with Fig. 3 (bp024) Access here

Movie 2 associated with Fig. 4 (bp034) Access here

Movie 3 associated with Fig. 5 (bp040) Access here

Movie 4 associated with Fig. 6 (bp058) Access here

Movie 5 associated with Fig. 7 (bp003) Access here

Movie 6 associated with Fig. 8 (bp013) Access here

Movie 7 associated with Fig. 9 (bp033) Access here

Movie 8 associated with Fig. 10 (bp089) Access here

Movie 9 associated with Fig. 11 (bp064) Access here

Acknowledgments

The authors thank the anonymous referee very much for their helpful and important comments. M.M. and T.W. acknowledge DFG-grant WI 3211/8-1. This research is partially supported by the Bulgarian National Science Fund, grant No KP-06-N44/2. T.W. is also supported by DLR grant 50 OC 2301. The HMI and AIA data are provided courtesy of NASA/SDO science teams. The HMI and AIA data have been retrieved using the Stanford University’s Joint Science Operations Centre/Science Data Processing Facility. The use of UCAR’s VAPOR software (Li et al. 2019; Pearse et al. 2023) is gratefully acknowledged.

References

  1. Bose, S., Nóbrega-Siverio, D., De Pontieu, B., & Rouppe van der Voort, L. 2023, ApJ, 944, 171 [NASA ADS] [CrossRef] [Google Scholar]
  2. Brooks, D. H., Warren, H. P., & Landi, E. 2021, ApJ, 915, L24 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brown, D. S., Parnell, C. E., Deluca, E. E., Golub, L., & McMullen, R. A. 2001, Sol. Phys., 201, 305 [NASA ADS] [CrossRef] [Google Scholar]
  4. Castellanos Durán, J. S., Kleint, L., & Calvo-Mozo, B. 2018, ApJ, 852, 25 [Google Scholar]
  5. Chae, J., Martin, S. F., Yun, H. S., et al. 2001, ApJ, 548, 497 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chandrashekhar, K., Krishna Prasad, S., Banerjee, D., Ravindra, B., & Seaton, D. B. 2013, Sol. Phys., 286, 125 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chen, F., Rempel, M., & Fan, Y. 2022, ApJ, 937, 91 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dahlburg, R. B., Einaudi, G., Ugarte-Urra, I., Rappazzo, A. F., & Velli, M. 2018, ApJ, 868, 116 [CrossRef] [Google Scholar]
  9. Démoulin, P., Priest, E. R., & Lonie, D. P. 1996, J. Geophys. Res., 101, 7631 [Google Scholar]
  10. De Pontieu, B., Martínez-Sykora, J., Testa, P., et al. 2020, ApJ, 888, 3 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dodson, H. W. 1953, PASP, 65, 256 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ellerman, F. 1917, ApJ, 46, 298 [NASA ADS] [CrossRef] [Google Scholar]
  13. Galsgaard, K., Madjarska, M. S., Mackay, D. H., & Mou, C. 2019, A&A, 623, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Golub, L., Krieger, A. S., Silk, J. K., Timothy, A. F., & Vaiana, G. S. 1974, ApJ, 189, L93 [NASA ADS] [CrossRef] [Google Scholar]
  15. Golub, L., Krieger, A. S., & Vaiana, G. S. 1976, Sol. Phys., 50, 311 [NASA ADS] [CrossRef] [Google Scholar]
  16. Golub, L., Krieger, A. S., Harvey, J. W., & Vaiana, G. S. 1977, Sol. Phys., 53, 111 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Guglielmino, S. L., Martínez Pillet, V., Bonet, J. A., et al. 2012, ApJ, 745, 160 [NASA ADS] [CrossRef] [Google Scholar]
  19. Habbal, S. R., Ronan, R. S., Withbroe, G. L., Shevgaonkar, R. K., & Kundu, M. R. 1986, ApJ, 306, 740 [Google Scholar]
  20. Hagenaar, H. J. 2001, ApJ, 555, 448 [NASA ADS] [CrossRef] [Google Scholar]
  21. Harvey, K. L. 1984, in The Hydromagnetics of the Sun, eds. T. D. Guyenne, & J. J. Hunt, ESA Spec. Pub., 220, (Paris) [Google Scholar]
  22. Harvey, K. L., & Martin, S. F. 1973, Sol. Phys., 32, 389 [NASA ADS] [CrossRef] [Google Scholar]
  23. Harvey, K. L., Harvey, J. W., & Martin, S. F. 1975, Sol. Phys., 40, 87 [NASA ADS] [Google Scholar]
  24. Harvey, K. L., Strong, K. S., Nitta, N., & Tsuneta, S. 1994, ASP Conf. Ser., 68, 377 [NASA ADS] [Google Scholar]
  25. Hoeksema, J. T., Liu, Y., Hayashi, K., et al. 2014, Sol. Phys., 289, 3483 [Google Scholar]
  26. Kontogiannis, I., Tsiropoula, G., Tziotziou, K., et al. 2020, A&A, 633, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Kotani, Y., Ishii, T. T., Yamasaki, D., et al. 2023, MNRAS, 522, 4148 [NASA ADS] [CrossRef] [Google Scholar]
  28. Krieger, A. S., Vaiana, G. S., & van Speybroeck, L. P. 1971, IAU Symp., 43, 397 [NASA ADS] [Google Scholar]
  29. Kucera, T. A., Young, P. R., Klimchuk, J. A., & DeForest, C. E. 2019, ApJ, 885, 7 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kwon, R.-Y., Chae, J., Davila, J. M., et al. 2012, ApJ, 757, 167 [Google Scholar]
  31. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  32. Li, S., Jaroszynski, S., Pearse, S., Orf, L., & Clyne, J. 2019, Atmosphere, 10, 488 [NASA ADS] [CrossRef] [Google Scholar]
  33. Li, B., Chen, S.-X., & Li, A.-L. 2022, ApJ, 928, 33 [NASA ADS] [CrossRef] [Google Scholar]
  34. Liu, Y., Hoeksema, J. T., Scherrer, P. H., et al. 2012, Sol. Phys., 279, 295 [Google Scholar]
  35. Longcope, D. W., Kankelborg, C. C., Nelson, J. L., & Pevtsov, A. A. 2001, ApJ, 553, 429 [NASA ADS] [CrossRef] [Google Scholar]
  36. Madjarska, M. S. 2019, Liv. Rev. Sol. Phys., 16, 2 [Google Scholar]
  37. Madjarska, M. S., Doyle, J. G., Teriaca, L., & Banerjee, D. 2003, A&A, 398, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Madjarska, M. S., Galsgaard, K., Mackay, D. H., Koleva, K., & Dechev, M. 2020, A&A, 643, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Madjarska, M. S., Chae, J., Moreno-Insertis, F., et al. 2021, A&A, 646, A107 [EDP Sciences] [Google Scholar]
  40. Madjarska, M. S., Mackay, D. H., Galsgaard, K., Wiegelmann, T., & Xie, H. 2022, A&A, 660, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [Google Scholar]
  42. Mondal, S., Chen, B., & Yu, S. 2023, ApJ, 949, 56 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mou, C., Huang, Z., Xia, L., et al. 2016, ApJ, 818, 9 [Google Scholar]
  44. Mou, C., Madjarska, M. S., Galsgaard, K., & Xia, L. 2018, A&A, 619, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
  46. Nóbrega-Siverio, D., & Moreno-Insertis, F. 2022, ApJ, 935, L21 [CrossRef] [Google Scholar]
  47. Norton, A. A., Jones, E. H., Linton, M. G., & Leake, J. E. 2017, ApJ, 842, 3 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pearse, S., Li, S., clyne, et al. 2023, https://doi.org/10.5281/zenodo.7779648 [Google Scholar]
  49. Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
  50. Pevtsov, A. A., Fisher, G. H., Acton, L. W., et al. 2003, ApJ, 598, 1387 [Google Scholar]
  51. Preś, P., & Phillips, K. H. J. 1999, ApJ, 510, L73 [CrossRef] [Google Scholar]
  52. Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
  53. Rempel, M. 2014, ApJ, 789, 132 [Google Scholar]
  54. Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
  56. Schrijver, C. J., Title, A. M., Harvey, K. L., et al. 1998, Nature, 394, 152 [NASA ADS] [CrossRef] [Google Scholar]
  57. Shi, M., Li, B., Huang, Z., & Chen, S.-X. 2019, ApJ, 883, 196 [NASA ADS] [CrossRef] [Google Scholar]
  58. Solanki, S. K., del Toro Iniesta, J. C., Woch, J., et al. 2020, A&A, 642, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Subramanian, S., Madjarska, M. S., & Doyle, J. G. 2010, A&A, 516, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Subramanian, S., Kashyap, V. L., Tripathi, D., Madjarska, M. S., & Doyle, J. G. 2018, A&A, 615, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Suematsu, Y., Shimizu, T., Hara, H., et al. 2021, SPIE Conf. Ser., 11852, 118523K [NASA ADS] [Google Scholar]
  62. Syntelis, P., Priest, E. R., & Chitta, L. P. 2019, ApJ, 872, 32 [NASA ADS] [CrossRef] [Google Scholar]
  63. Titov, V. S. 2007, ApJ, 660, 863 [Google Scholar]
  64. Toriumi, S., & Airapetian, V. S. 2022, ApJ, 927, 179 [NASA ADS] [CrossRef] [Google Scholar]
  65. Toriumi, S., Airapetian, V. S., Namekata, K., & Notsu, Y. 2022, ApJS, 262, 46 [NASA ADS] [CrossRef] [Google Scholar]
  66. Tsiropoula, G., Tziotziou, K., Kontogiannis, I., et al. 2012, Space Sci. Rev., 169, 181 [Google Scholar]
  67. Ugarte-Urra, I., Crump, N. A., Warren, H. P., & Wiegelmann, T. 2019, ApJ, 877, 129 [NASA ADS] [CrossRef] [Google Scholar]
  68. van Ballegooijen, A. A., Asgari-Targhi, M., & Voss, A. 2017, ApJ, 849, 46 [Google Scholar]
  69. Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
  70. Wang, H. 1988, Sol. Phys., 116, 1 [CrossRef] [Google Scholar]
  71. Wiegelmann, T., & Madjarska, M. S. 2023, Sol. Phys., 298, 3 [NASA ADS] [CrossRef] [Google Scholar]
  72. Wiegelmann, T., Solanki, S. K., Borrero, J. M., et al. 2010, ApJ, 723, L185 [NASA ADS] [CrossRef] [Google Scholar]
  73. Wyper, P. F., DeVore, C. R., Karpen, J. T., Antiochos, S. K., & Yeates, A. R. 2018, ApJ, 864, 165 [NASA ADS] [CrossRef] [Google Scholar]
  74. Xie, H., Madjarska, M. S., Li, B., et al. 2017, ApJ, 842, 38 [NASA ADS] [CrossRef] [Google Scholar]
  75. Yang, S., & Zhang, J. 2014, ApJ, 781, 7 [Google Scholar]
  76. Zhang, J., Kundu, M. R., & White, S. M. 2001, Sol. Phys., 198, 347 [NASA ADS] [CrossRef] [Google Scholar]
  77. Zhao, J., & Li, H. 2012, Res. Astron. Astrophys., 12, 1681 [CrossRef] [Google Scholar]

All Tables

Table 1.

Photospheric magnetic properties of small-scale loops in the quiet Sun.

In the text
Table 2.

Magnetic flux emergence duration (Em dur), emergence rate (Em rate), and decay duration (Dec dur) and rate (Dec rate) for SSLSs associated with flux emergence.

In the text

All Figures

thumbnail Fig. 1.

Analysed AIA and HMI fields of view. The images were taken at heliocentric x and y coordinates of 0″, 0″. The white rectangles represent the FOVs of the SSLSs. The enumeration indicates each studied case as noted in the tables and figures. The pixel size of both images is 0.6″. The HMI magnetogram is saturated at ±50 G.
In the text
thumbnail Fig. 2.

Quiet Sun photospheric magnetic flux and associated coronal magnetic structures. Top panel: an AIA 193 image (rotated at 180 degrees with respect to the image in Fig. 1). Middle panel: magnetic field lines from a potential field model overplotted with VAPOR on an HMI LOS magnetogram. Bottom panel: HMI LOS magnetogram. Arrows numbered 1, 2, 3, 4, and 5 point at bright small-scale loop systems. Arrow 6 indicates a faint loop, and arrow 7 (shown only in the middle panel) points at a large loop that is not detectable in AIA 193, but can be seen in AIA 171 (not shown here).
In the text
thumbnail Fig. 3.

Intensity and photospheric magnetic flux properties of an SSLS associated with a flux emergence. The top row shows the AIA 193 image and quasi-temporal HMI magnetogram for case 24 (see the online animation bp024.mov). The contours outline the ±25 and ±50 G magnetic flux concentrations. The evolution of the total magnetic flux is shown in the second row, and the maximum (peak) intensity and the total intensity flux evolution taken from the selected FOV are given in the third and fourth rows of Table 1. The two vertical thick lines together with the arrowed horizontal line (only shown in the top panel) indicate the SSLS lifetime.
In the text
thumbnail Fig. 4.

Same as Fig. 3 for case 34 (see the online animation bp034.mov).
In the text
thumbnail Fig. 5.

Same as Fig. 3 for case 40 (see the online animation bp040.mov).
In the text
thumbnail Fig. 6.

Same as Fig. 3 for case 58, also showing multiple bipolar magnetic flux emergences (see the online animation bp058.mov).
In the text
thumbnail Fig. 7.

Same as Fig. 3 for case 3, which is an example of an SSLS formation from a magnetic flux coalescence. The sigmoid-like loop is related to a mini-eruption as in Madjarska et al. (2022) (see the online animation bp003.mov).
In the text
thumbnail Fig. 8.

Same as Fig. 3 for case 13, which is an SSLS that formed as a result of flux coalescence and convergence. This is one out of two cases in which one of the polarities rotates with respect to the other polarity of the opposite sign while the two converge (see the online animation bp013.mov).
In the text
thumbnail Fig. 9.

Same as Fig. 3 for case 33, which is a faint SSLS that formed as a result of flux coalescence, with loops stretching above two supergranulation cells (see the online animation bp033.mov).
In the text
thumbnail Fig. 10.

Same as Fig. 3 for case 89, which is an example of a faint loop system (see the online animation bp089.mov).
In the text
thumbnail Fig. 11.

Same as Fig. 3 for case 64, which is related to a bipolar magnetic flux emergence (see the online animation bp064.mov).
In the text
thumbnail Fig. 12.

Histograms of the physical quantities. Panel a shows the lifetimes of SSLSs for 38 cases whose lifetimes are fully covered. The maximum total unsigned magnetic flux for all 90 cases is given in panel b; see Table 1, Col. 3. The maximum peak intensities associated with microflares of SSLSs for all 90 cases are shown in panel c; see Table 1, Col. 5. The maximum total intensity flux of SSLSs for all 90 cases is provided in panel d; see Table 1, Col. 6.
In the text
thumbnail Fig. 13.

Histograms of intensity ratios. The top panel shows the ratio of the microflare-associated intensity peaks with respect to the minimum-mean intensity (close to the quiet-Sun background intensity), and in the bottom panel, we show the ratio with respect to the maximum mean intensity in the FOV of the SSLSs.
In the text
thumbnail Fig. 14.

Scatter plots. The log10 of the maximum total unsigned (over lifetime) magnetic flux vs. the lifetime duration of SSLSs is shown in the top left panel. The log10 of the maximum total intensity flux (over lifetime) vs. lifetime duration of SSLSs is shown in the top right panel, while the log10 of the maximum total intensity flux (over lifetime) vs. the log10 of the maximum total unsigned magnetic flux is shown in the bottom left panel. The two top panels include only full-lifetime covered cases, and the bottom left panel includes all 90 cases. The bottom right panel shows the peak intensity associated with microflares vs. the log10 of the maximum total unsigned magnetic flux. The abbreviation MF in the last column of Table 1 indicates the identified 77 cases.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.