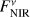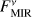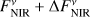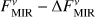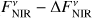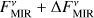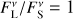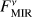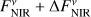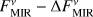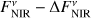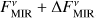How much large dust could be present in hot exozodiacal dust systems?

T. A. Stuber; F. Kirchschlager; T. D. Pearce; S. Ertel; A. V. Krivov; S. Wolf

doi:10.1051/0004-6361/202346109

Home

All issues

Volume 678 (October 2023)

A&A, 678 (2023) A121

Full HTML

Open Access

Issue		A&A Volume 678, October 2023


Article Number		A121
Number of page(s)		18
Section		Interstellar and circumstellar matter
DOI		https://doi.org/10.1051/0004-6361/202346109
Published online		13 October 2023

A&A, 678, A121 (2023)

How much large dust could be present in hot exozodiacal dust systems?

T. A. Stuber¹, F. Kirchschlager², T. D. Pearce³, S. Ertel⁴^,5, A. V. Krivov³ and S. Wolf¹

¹ Institut für Theoretische Physik und Astrophysik, Christian-Albrechts-Universität zu Kiel, Leibnizstr. 15, 24118 Kiel, Germany
e-mail: tstuber@astrophysik.uni-kiel.de
² Sterrenkundig Observatorium, Ghent University, Krijgslaan 281-S9, 9000 Gent, Belgium
³ Astrophysikalisches Institut und Universitätssternwarte, Friedrich-Schiller-Universität Jena, Schillergässchen 2–3, 07745 Jena, Germany
⁴ Department of Astronomy and Steward Observatory, The University of Arizona, 933 North Cherry Ave, Tucson, AZ 85721, USA
⁵ Large Binocular Telescope Observatory, The University of Arizona, 933 North Cherry Ave, Tucson, AZ 85721, USA

Received: 9 February 2023
Accepted: 19 July 2023

Abstract

Context. An infrared excess over the stellar photospheric emission of main-sequence stars has been found in interferometric surveys, commonly attributed to the presence of hot exozodiacal dust (HEZD). While submicrometer-sized grains in close vicinity to their host star have been inferred to be responsible for the found near-infrared excesses, the presence and amount of larger grains as part of the dust distributions are weakly constrained.

Aims. We quantify how many larger grains (above-micrometer-sized) could be present in addition to submicrometer-sized grains, while being consistent with observational constraints. This is important in order to distinguish between various scenarios for the origin of HEZD and to better estimate its observational appearance when observed with future instruments.

Methods. We extended a model suitable to reproduce current observations of HEZD to investigate a bimodal size distribution. By deriving the characteristics of dust distributions whose observables are consistent with observational limits from interferometric measurements in the K and N bands we constrained the radii of sub- and above-micrometer-sized grains as well as their mass, number, and flux density ratios.

Results. In the most extreme cases of some of the investigated systems, large grains ≳10 µm might dominate the mass budget of HEZD while contributing up to 25 % of the total flux density originating from the dust at a wavelength of 2.13 µm and up to 50 % at a wavelength of 4.1 µm; at a wavelength of 11.1 µm their emission might clearly dominate over the emission of small grains. While it is not possible to detect such hot-dust distributions using ALMA, the ngVLA might allow us to detect HEZD at millimeter wavelengths.

Conclusions. Large dust grains (above-micrometer-sized) might have a more important impact on the observational appearance of HEZD than previously assumed, especially at longer wavelengths.

Key words: circumstellar matter / interplanetary medium / infrared: planetary systems / submillimeter: planetary systems / methods: numerical

© The Authors 2023

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Interferometric observations of main-sequence stars in the photometric bands H to L revealed an excess emission over the stellar photosphere. It was found across spectral types G to A and over diverse stellar ages with an incidence rate of around 10 % (Ertel et al. 2014) to 30 % (Absil et al. 2013). This excess emission has been attributed to the presence of hot circumstellar dust distributions (e.g., Absil et al. 2006; Di Folco et al. 2007; Defrère et al. 2011), called hot exozodiacal dust or hot exozodis (HEZD, for a review, see Kral et al. 2017). In contrast, the corresponding excess measured in the mid-infrared (MIR) N band is weaker and often not even detected (Millan-Gabet et al. 2011; Mennesson et al. 2014)¹.

Further analyses show the need for small (submicrometer-sized) dust grains in close (sub-au) vicinity of their host star to explain the measured near-infrared (NIR) excess. While carbonaceous grains are consistent with the observations, a dominant contribution of silicate grains can be excluded because the weak MIR excess would be inconsistent with the otherwise expected strong N band emission feature (e.g., Absil et al. 2006; Akeson et al. 2009; Kirchschlager et al. 2017).

The physical processes behind the phenomenon of HEZD are not yet well-constrained. While the classical dust replenishment by a steady-state collisional cascade in an in situ debris belt is unlikely (Wyatt et al. 2007; Lebreton et al. 2013), submicrometer motes should be repelled by radiation pressure and rapidly blown out of the system, in particular around luminous stars of spectral type A (Burns et al. 1979; Backman & Paresce 1993). Multiple alternative solutions to this problem have been proposed to date, such as dust migration and pile-up by the combination of Poynting-Robertson (P–R) drag and sublimation (Belton 1966; Mukai et al. 1974; Krivov et al. 1998; Kobayashi et al. 2009, 2010, 2011; van Lieshout et al. 2014b; Sezestre et al. 2019, see also Poynting 1904; Robertson 1937; Wyatt & Whipple 1950; Burns et al. 1979 for work on the P–R drag); in situ delivery by exocomets (Bonsor & Wyatt 2012; Bonsor et al. 2012, 2014; Raymond & Bonsor 2014; Marboeuf et al. 2016; Faramaz et al. 2017; Sezestre et al. 2019; Pearce et al. 2022); or trapping of dust grains by gas (Lebreton et al. 2013; Pearce et al. 2020), magnetic fields (Czechowski & Mann 2010; Su et al. 2013; Rieke et al. 2016; Stamm et al. 2019; Kimura et al. 2020), or the differential Doppler effect (Burns et al. 1979; Rusk 1987; Sezestre et al. 2019). However, none of these scenarios provides a comprehensive explanation for the transport of the dust to the inner regions nor how it can survive there or be replenished efficiently (see overview in Pearce et al. 2022).

While it was possible to constrain the grain size and location of small dust grains (i.e., ≲1 µm), the deducible constraints on dust grains much larger than the NIR and MIR observing wavelengths are limited. Paired with studies that tried to explain the MIR excess by a second cooler dust distribution farther out (e.g., Lebreton et al. 2013), this led to the picture that the hot inner HEZD distributions consist solely of small submicrometer-sized grains (or dust populations with an extremely steep grain size distribution). Constraints on the prevalence or lack of larger grains in HEZD distributions would have significant implications on the theoretical models explaining the phenomenon. For example, if hot dust originates farther out in the system and is deposited close to the star, its size distribution upon arrival would depend on the transportation process; the size distribution of grains released close to a star by star-grazing comets (e.g., Sekanina & Miller 1973; Hanner 1984; Harker et al. 2002; Blum et al. 2017) may differ considerably to that of grains originating in an asteroid belt, migrating in under P–R drag and experiencing collisions on the way in (e.g., Rigley & Wyatt 2020). Hence the transportation mechanism would set the ratio of large to small grains arriving at the hot-emission region. Similarly, many hot-dust models posit that some mechanisms trap grains close to the star; mechanisms such as gas trapping or magnetic trapping would preferentially trap grains of certain sizes (generally trapping smaller grains more efficiently), again affecting the ratio of large to small grains near the star. Consequently, if there is an unjustified bias toward denying the presence of larger grains, this bias transfers to unified theories seeking to provide a thorough explanation of the enigmatic phenomenon of HEZD around main-sequence stars. Furthermore, constraints on HEZD distributions are important for exoplanetary studies because the radiation scattered and emitted by the HEZD would potentially interfere with that of close-in exoplanets.

In this study we derived constraints on large (≳1 µm) dust grains in HEZD distributions from existing observations. For this purpose we revisited interferometric observations in both the NIR and MIR wavelength ranges of the targets that were analyzed by Kirchschlager et al. (2017). They utilized a model with dust of a single grain size distributed in a thin ring around a central star to constrain the HEZD characteristics; we expanded their model to contain two dust grain sizes. We present the stellar sample and our modeling approach in Sect. 2 and the derived constraints on HEZD parameters in Sect. 3. In Sect. 4, we discuss our modeling approach and findings. Furthermore, we conduct a study of feasibility to detect large grain distributions at sub-millimeter/millimeter wavelengths. We close with a summary in Sect. 5.

2 Methods

A single population of submicrometer-sized grains was shown to reproduce the inferred NIR K band (hereafter NIR) excesses, while being consistent with the inferred smaller MIR N band (hereafter MIR) excesses (Kirchschlager et al. 2017). The emissivity of such small grains drops steeply with increasing wavelength, as derived from Mie theory (Mie 1908), leading to a steep decrease in the emission spectrum from the NIR to the MIR wavelength regime which is consistent with the observations. In that wavelength range, larger grains (above-micrometer-sized) show a less drastic decrease in emissivity and are mostly cooler at the same stellocentric distance, and thus they produce an emission spectrum shallower than that inferred from observations. Therefore, the possible amount of these larger grains is limited. However, beyond this qualitative argumentation, it is unknown what amount of larger grains can be added to the already inferred submicrometer-sized grain population without violating the observational constraints. To derive these upper limits on the amount of larger grains in HEZD distributions, we searched for combinations of populations of smaller and larger grains whose radiation reproduces the inferred flux density both in the NIR and MIR wavelength range.

2.1 Stellar sample and observations

We investigated nine hot-dust targets with interferometric measurements both in the NIR and MIR wavelength range that are compiled in Group I in Kirchschlager et al. (2017, see there for more information about the sample selection criteria). The stellar parameters and references are listed in Table 1. In the NIR all targets were part of a survey performed by Absil et al. (2013) using the Fiber Linked Unit for Optical Recombination (FLUOR, Coudé du Foresto et al. 1997, 1998; Mérand et al. 2006) at the Center for High Angular Resolution Astronomy (CHARA) Array (Coudé du Foresto et al. 2003; ten Brummelaar et al. 2005) except HD 216956 (Fomalhaut), which was investigated by Absil et al. (2009) using archival data obtained with the Very Large Telescope Interferometer (VLTI, Schöller et al. 2003; Schöller & Glindemann 2003; Richichi & Percheron 2005) using the VLT Interferometer Commissioning Instrument (VINCI, Kervella et al. 2000, 2003). For all NIR measurements, also for that of VLTI/VINCI, we assumed an effective observing wavelength of the K band to be λ = 2.13 µm, as given by Absil et al. (2013). In the MIR, all targets were part of a survey by Mennesson et al. (2014, central bin wavelength of λ = 8.5 µm) using the Keck Interferometer mid-infrared Nulling instrument (KIN, Serabyn et al. 2012; Colavita et al. 2013).

Due to the new HIPPARCOS reduction (van Leeuwen 2007) and the Gaia Early Data Release 3 (Gaia Collaboration 2021) the parallaxes of several targets changed compared to those used in the literature, which slightly affects the determined stellar properties. As these changes are usually small compared to uncertainties originating from observational and modeling effects, we used the stellar parameters that appear in the literature.

2.2 Inferred values of flux density

Absil et al. (2009, 2013) and Mennesson et al. (2014) inferred the radiation originating from the circumstellar environment relative to the contribution of the central star alone. We transformed these relative measures to values of the flux density originating from the circumstellar dust distributions by multiplying by the stellar flux density 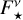$F_{⋆}^{v}$ $F_ \star ^v$ obtained from the Planck function that corresponds to the effective temperature T_★ of the respective host star. For the NIR measurements, the flux density of the circumstellar emission is computed as 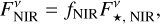$F_{NIR}^{v} = f_{NIR} F_{⋆, INR}^{v},$ $F_{{\rm{NIR}}}^v = {f_{{\rm{NIR}}}}F_{ \star ,{\rm{INR}}}^v,$ (1)

with the disk-to-star flux ratio f_NIR taken from Table 2 of Absil et al. (2009) and Table 4 of Absil et al. (2013 denoted there as f_CSE). For the MIR measurements, we computed the flux density of the circumstellar emission following Kirchschlager et al. (2017) as 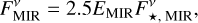$F_{MIR}^{v} = 2.5 E_{MIR} F_{⋆, MIR}^{v},$ $F_{{\rm{MIR}}}^v = 2.5{E_{{\rm{MIR}}}}F_{ \star ,{\rm{MIR}}}^v,$ (2)

with E_MIR being the measured excess leak in the 8 to 9 µm bin from Table 2 of Mennesson et al. (2014, denoted there as E_8–9) and the factor of 2.5 compensating for the radiation not transferred through the KIN transmission pattern. To compute the corresponding uncertainties of the derived flux densities, denoted by ΔF_NIR and ΔF_MIR, we took the mostly probabilistic uncertainties of the measured excesses Δf_NIR (denoted as σ_f in Absil et al. 2013) and ΔE_MIR (denoted as σ_8–9 in Mennesson et al. 2014) into account; we neglected uncertainties of the stellar flux density 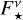$F_{⋆}^{v}$ $F_ \star ^v$ in Eqs. (1) and (2). The derived flux densities and corresponding quantities for all considered sources are listed in Table 2.

Table 1

Stellar parameters of investigated targets (Group I from Kirchschlager et al. 2017).

Table 2

Measurements and inferred flux densities in the NIR and MIR wavelength range of investigated targets.

2.3 Model of hot exozodiacal dust

2.3.1 Motivation: underlying observational constraints

The available observational data on the investigated targets are strongly limited. They typically consist of a significant detection in the NIR and an additional photometric upper limit in the MIR plus the constraint that the radiation has to originate from the region inside the respective working angles of the instruments. Consequently, those data are not overly constraining regarding characteristics of HEZD. To date there is no consistent theory explaining the dynamics of hot dust nor how the dust is delivered and trapped in the close vicinity of the central star. Therefore, due to the limited constraints on possible models, the use of a simple model is indicated.

A thin ring with a flat surface density seen face-on that consists of dust with a single grain size represents such a simple model. It has been proven to explain the rich data set of observations of HEZD for the target HD 7788 (κ Tuc), including L band interferometric measurements obtained with the Multi AperTure mid-Infrared SpectroScopic Experiment (MATISSE, Lopez et al. 2014, 2022) at the VLTI (Kirchschlager et al. 2020). Compared to a broad ring, this model allows dust temperatures to be more easily interpreted, especially in the context of sublimation. Furthermore, it allows the results from this study and previous results to be directly compared (Kirchschlager et al. 2017, 2018, 2020). As motivated above, the observational data hardly justify a more detailed model, nor would the observations allow us to well constrain more parameters.

To be able to constrain the amount of above-micrometer-sized grains that are in agreement with the two photometric data points, we expanded the single grain size description used in Kirchschlager et al. (2017) to include a second larger grain size. Due to the interplay of different dust transport and trapping mechanisms that most efficiently deliver or trap grains of certain sizes, a bimodal grain size distribution could be produced that differs from the continuous power law shapes classically used in debris disk models. Consequently, the use of a bimodal size distribution leads to conclusions on the possible interplay of different dust delivery and trapping mechanisms. While there is no known trapping mechanism that traps grains of different sizes at the same radial location that would correspond to this model, there is also no mechanism fully explaining the observations of HEZD, and hence the dust dynamics. In summary, the application of a simple model is indicated by both the limited observational constraints and the uncertainty with regard to the underlying physical mechanisms that are responsible for the HEZD phenomenon.

2.3.2 Model setup and simulated observations

Given the considerations presented in Sect. 2.3.1, we chose the following description of HEZD. As in Kirchschlager et al. (2017, the dust is distributed in a wedge-shaped ring with a half-opening angle of 5 º, radially restricted by an inner and outer radius R_out = 1.5 R_in; the number density of the dust grains is assumed to decrease with increasing distance to the star R as n (R) ∝ R⁻¹, resulting in a flat surface density. The overall dust distribution is assumed to be optically thin and seen in face-on orientation; it consists of two single dust populations at the same location, but with different grain radii, denoted by a_S (S : smaller) and a_L (L: larger).

To compute the surface brightness maps of the dust rings, we used an extended version of the numerical tool Debris disks around Main-sequence Stars (DMS, Kim et al. 2018), considering both thermal dust emission and scattered stellar radiation. To obtain dust absorption and scattering cross sections, and the scattering phase function, we used the numerical tool miex (Wolf & Voshchinnikov 2004) based on Mie theory. The single-mode fiber interferometers FLUOR and VINCI showed a sensitivity over the field of view of a Gaussian shape with full width at half maximum (FWHM) of 0.8 as and 1.6 as, respectively. We took this into account when simulating the brightness of dust configurations in the NIR by multiplying the maps of surface brightness with two-dimensional circular Gaussian distributions centered on the host star with peak intensity of unity and with the respective FWHM. This decreases the contribution of the outer disk regions to the total flux density along with increasing stellocentric distance. From these brightness distributions we computed values of total flux density by summing the flux densities of the entire map.

2.4 Constraining parameters of hot exozodiacal dust

In their approach to constraining parameters of HEZD, Kirchschlager et al. (2017) considered the mostly insignificant MIR measurements as upper limits. Single-sized grains with radii in the submicrometer range then allowed them to reproduce the observed NIR excess. In our study we aimed to put constraints on the amount and characteristics of larger (≳1 µm) grains as constituents of HEZD that are nonetheless consistent with the present upper limits represented by the MIR measurements. For this purpose, we assumed the MIR measurements to be the true values.

To constrain the possible number of dust grains with certain radii, the two dust populations with grain radii a_S and a_L, respectively, are assumed to produce the entire NIR and MIR radiation of the HEZD. With the observed NIR-to-MIR flux density ratio 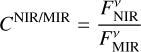$C^{NIR / MIR} = \frac{F_{NIR}^{v}}{F_{MIR}^{v}}$ ${C^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}}} = {{F_{{\rm{NIR}}}^v} \over {F_{{\rm{MIR}}}^v}}$ (3)

and the ratios of the simulated flux densities 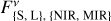$F_{{S, L}, {NIR, MIR}}^{v}$ $F_{\left\{ {{\rm{S}},{\rm{L}}} \right\},\,\left\{ {{\rm{NIR}},\,{\rm{MIR}}} \right\}}^v$ originating from the grain populations of the smaller and larger grains in the NIR and MIR wavelength range, respectively, 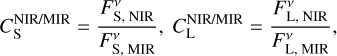$C_{S}^{NIR / MIR} = \frac{F_{S,NIR}^{v}}{F_{S,MIR}^{v}}, C_{L}^{NIR / MIR} = \frac{F_{L,NIR}^{v}}{F_{L,MIR}^{v}},$ $C_{\rm{S}}^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}} = {{F_{{\rm{S,NIR}}}^v} \over {F_{{\rm{S,MIR}}}^v}},C_{\rm{L}}^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}} = {{F_{{\rm{L,NIR}}}^v} \over {F_{{\rm{L,MIR}}}^v}},$ (4)

a dust configuration with a certain parameter combination of disk radius and grain radii can reproduce the flux densities as inferred from the observations if the condition $\begin{matrix} C_{S}^{NIR / MIR} < C^{NIR / MIR} < C_{L}^{NIR / MIR} \\ or \\ C_{S}^{NIR / MIR} > C^{NIR / MIR} > C_{L}^{NIR / MIR} \end{matrix}$ $\matrix{ {C_{\rm{S}}^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}} > {C^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}}} > C_{\rm{L}}^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}}} \cr {{\rm{or}}} \cr {C_{\rm{S}}^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}} > {C^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}}} > C_{\rm{L}}^{{{{\rm{NIR}}} \mathord{\left/ {\vphantom {{{\rm{NIR}}} {{\rm{MIR}}}}} \right. \kern-\nulldelimiterspace} {{\rm{MIR}}}}}} \cr }$ (5)

is fulfilled. In this case, the respective dust masses of the simulated populations can be scaled such that the flux densities inferred from observations are matched simultaneously at the NIR and MIR wavelengths. This is achieved by solving the system of two linear equations 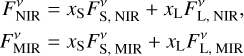$\begin{array}{l} F_{NIR}^{v} = x_{S} F_{S,NIR}^{v} + x_{L} F_{L,NIR}^{v}, \\ F_{MIR}^{v} = x_{S} F_{S,MIR}^{v} + x_{L} F_{L,MIR}^{v} \end{array}$ $\matrix{ {F_{{\rm{NIR}}}^v = {x_{\rm{S}}}F_{{\rm{S,NIR}}}^v + {x_{\rm{L}}}F_{{\rm{L,NIR}}}^v,} \hfill \cr {F_{{\rm{MIR}}}^v = {x_{\rm{S}}}F_{{\rm{S,MIR}}}^v + {x_{\rm{L}}}F_{{\rm{L,MIR}}}^v} \hfill \cr }$ (6)

for the scaling factors x_{{S, L}}. With the obtained scaling factors we yielded the dust masses of the two grain populations M_S and M_L (see Fig. 1).

We investigated the impact of the interferometric measurement uncertainties on the derived constraints on HEZD parameters. As the valid parameter combinations are determined by the observed NIR-to-MIR flux density ratio (Eq. (5)), we considered the cases of the largest and smallest value thereof possible within the observational uncertainties. This is achieved for the two cases (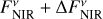 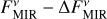$F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) and vice versa ( 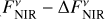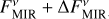$F_{NIR}^{v} - Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v - {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} + Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v + {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ), respectively, for which we repeat the computation of dust masses with Eq. (6).

Additionally to the discussed observations in the NIR and MIR wavelength range, all investigated stellar systems have been observed at longer wavelengths λ ≥ 24 µm. We collected those measurements from the literature and used them as upper limits for valid dust configurations at the respective wavelengths (see Table A.1). For observations with the Atacama Large Millimeter/submillimeter Array (ALMA, Kurz et al. 2002) at wavelengths of 870 µm and 1300 µm (we assumed a wavelength of 1300 µm for all observations with ALMA band 6) and for the observation of HD 216956 with the Herschel Space Observatory (Pilbratt et al. 2010) by Acke et al. (2012) we used the inferred flux density of the central unresolved point source including stellar photospheric emission. For all other observations we used the entire flux density measured in the field of view, and thus the measurements possibly include contributions of cold-dust emission originating from larger stellocentric distances. Therefore, all of these measurements pose conservative upper limits, and we neglected the corresponding measurement uncertainties in this investigation.

Fig. 1

Flux density F^v originating from hot dust for the system HD 172167 (Vega). The black crosses denote the values inferred from the observations (see Table 2). The orange line shows the radiation of a carbonaceous dust ring reproducing the observed flux densities with an inner disk radius of R_in = 0.18 au, a population of grains with radius a_S = 0.2 µm and a dust mass of M_S ≈ 6.2 × 10⁻¹⁰ M_⊕, and a population of larger grains with radius a_L = 10 µm and a dust mass of M_L ≈ 8.9 × 10⁻¹⁰ M_⊕; the dashed lines in blue and red denote the respective contributions of the two grain populations. For comparison, the solid green line depicts the radiation of a dust ring at the same location comprised of grains made of astronomical silicate with a grain radius of a = 0.2 µm; the dust mass is scaled such that the flux density matches the value inferred from observations at λ = 2.13 µm. This dust ring does not reproduce the observations due to the high predicted flux density in the MIR wavelength range.

2.5 Parameter space

In the following we present the investigated parameter space of hot-dust configurations.

Disk radii. We varied the disk inner and outer radii within the interval corresponding to the angular on-sky region the instruments FLUOR, VINCI, and KIN were sensitive to. In contrast to classical imaging instruments, additionally to an outer working angle (OWA) set by the field of view, interferometric instruments also possess an inner working angle (IWA) within which radiation is strongly attenuated. Thus, constraints on dust distributions with an angular size smaller than the IWA or larger than the OWA of any of the instruments cannot be derived using our modeling approach. The KIN possessed an IWA of 6 mas (Mennesson et al. 2014), which is larger than the IWAs of CHARA/FLUOR and VLTI/VINCI derived by Kirchschlager et al. (2017). At the same time, the KIN OWA was 200 mas, which is smaller than those of CHARA/FLUOR and VLTI/VINCI. Therefore, for each of the investigated systems, we can only constrain dust configurations with R_in ≥ 6 mas and R_out ≤ 200 mas. The corresponding length scales depend on the stellar distance d and are individual for each target (see Table 1).

Dust radii. We investigated dust grains with radii a between 1 nm and 1 mm, logarithmically sampled with 103 values². From this sample we built mutually exclusive pairs of grain radii for the combinations of a_S and a_L, for a total of 5253 pairs.

Dust material. We investigated two different dust materials using values of the wavelength-dependent complex refractive index derived by Draine (2003), astronomical silicate with a bulk density of ρ = 3.8 g cm⁻³ and graphite with a bulk density of ρ = 2.2 g cm⁻³. For the latter we used the catalog of complex refractive indices that were computed for an assumed grain radius of a = 0.1 µm and the 1/3–2/3 assumption to combine parallel- and perpendicular-oriented grains (Draine & Malhotra 1993).

Such small dust grains in such close vicinity to their host star can reach equilibrium temperatures high enough to sublimate. To decide whether a dust grain of a specific material and size at a specific distance from the host star is sublimated, we compute the equilibrium temperature at constant distance while taking the wavelength-dependent absorption cross section into account, and compare it to the sublimation temperatures T_sub = 1200 K for astronomical silicate and T_sub = 2000 K for graphite (Kobayashi et al. 2009). We considered every dust distribution with any grains exceeding the sublimation temperature to be invalid to reproduce the observations.

3 Results

From the procedure described in Sect. 2 we obtained a set of valid dust distributions, whose simulated observable quantities are consistent with the observations.

3.1 Systems where not all analyses were possible due to MIR observations

Due to the measured excess leaks in the MIR (E_MIR in Table 2), which can be negative due to instrumental noise (Mennesson et al. 2014), all combinations of inferred flux density and corresponding uncertainty are non-positive for the system HD 56537 as E_MIR = −ΔE_MIR. Thus, this system could not be constrained as our modeling approach requires a positive flux density. 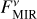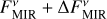For the same reason, not all combinations of inferred flux density and corresponding uncertainties could be investigated for any system as E_MIR ≤ ΔE_MIR; for the systems HD 177724 and HD 203280 we were only able to investigate dust parameters for the cases of inferred flux densities of $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ and $F_{MIR}^{v} + Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v + {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ; for the system HD 10700 only for the case of $F_{MIR}^{v} + Δ F_{MIR}^{v}$ $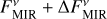F_{{\rm{MIR}}}^v + {\rm{\Delta }}F_{{\rm{MIR}}}^v$ .

3.2 Dust composition

For grains composed of pure astronomical silicate, there is no viable combination of grain radii and disk radii in the entire investigated parameter space (the lack of a significant contribution of silicate grains was already pointed out by, e.g., Absil et al. 2006; Akeson et al. 2009; Lebreton et al. 2013; Kirchschlager et al. 2017). This is an expression of the fact that the characteristic N band silicate emission feature always results in a too high emission at λ ≈ 10 µm (see Fig. 1); none of the investigated sizes of the silicate grains at none of the investigated disk radii fulfills the condition given in Eq. (5). Therefore, the following discussions will refer solely to carbonaceous grains.

3.3 No constraints from observations at wavelengths λ ≥ 24 µm

Of those carbonaceous dust configurations able to reproduce the flux densities inferred from observations in the NIR and MIR wavelength range, none showed flux densities at longer wavelengths (i.e., λ = 24… 1300 µm), which exceed any of the photometric measurements listed in Table A.1. Thus, the results are constrained solely by the interferometric measurements at λ = 2.13 µm and λ = 8.5 µm.

3.4 Constraints on hot exozodiacal dust parameters

For each stellar system we derived constraints on all parameters of hot dust set by the smallest and largest value out of all valid parameter sets. The results are displayed in Fig. 2; the numerical values are listed in Table B.1.

However, there are systems and combinations of observational uncertainties for which there are no carbonaceous dust distributions in the investigated parameter space that are able to reproduce the observations, either because the condition given in Eq. (5) cannot be fulfilled or all the dust grains exceed their sublimation temperature: HD 187642 in the case of inferred flux densities of (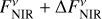 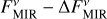$F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) and ( 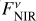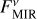$F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ), HD 203280 in the case of ( 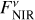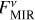$F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ), and HD 172167 and HD 216956 in the case of ( $F_{NIR}^{v} + Δ F_{NIR}^{v}$ $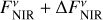F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $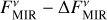F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ).

The derived constraints on the inner disk radius and grain radius of the small grain population are generally similar to those derived by Kirchschlager et al. (2017). This was expected because our modeling approaches are similar (see Sect. 4.2 for a discussion about the deviations and a comparison of the modeling approaches). In the following, we present and discuss the results for all parameters individually.

3.4.1 Inner disk radius R_in

For the systems HD 10700, HD 22484, and HD 177724, the smallest possible inner disk radius R_in (first panel of Fig. 2) coincides with the smallest considered value, which is the IWA of the KIN, and therefore remains unconstrained. However, relaxing the need of MIR data and using solely data obtained with CHARA/FLUOR that provided higher angular resolution, the innermost dust location can be further constrained (Kirchschlager et al. 2017). For the systems with lower limits on the inner disk radius R_in we found the same trend of values increasing with increasing stellar luminosity. On the upper end all inner disk radii are constrained to values smaller than ~ 1 au.

3.4.2 Dust mass M

The constraints on the total dust mass in the systems (second panel of Fig. 2) encompass grains up to a grain radius of a = 1 mm. For all investigated systems, except HD 10700, the possible dust masses are constrained to values of ~10⁻¹⁰… 10⁻⁶ M_⊕ without any obvious trend with stellar luminosity. For HD 10700, the dust masses are constrained to values of ~2.5 × 10⁻¹¹… 3.0 × 10⁻⁹ M_⊕ when taking observational uncertainties into account. In each case the dust distributions with the highest masses are those with the largest possible grain radius of the population of large grains, that is a = 1 mm. The relative contribution of the larger grains to the total mass is barely constrained; values of M_L/M ~ 0.01… 99.99 % are allowed.

3.4.3 Larger grain radius a_L

The condition given in Eq. (5) sets lower limits on the grain radius of the population of larger grains a_L (third panel of Fig. 2).

It is constrained to values larger than ≈0.004…0.17µm. On the upper end, a_L is unconstrained because above a certain distance from the central star arbitrarily large particles show a NIR-to-MIR flux density ratio (Eq. (4)) smaller than that derived from observations (Eq. (3)). For every system these constraints allow grains with radii smaller and larger than the blowout grain radius. An illustration can be seen of the parameter space of valid combinations of the grain radius a_L and the inner disk radius R_in for all possible values of a_S for the example system HD 172167 in the right panel of Fig. 3 (see Fig. B.1 for all other investigated targets).

Fig. 2

Constraints on HEZD parameters of inner disk radius R_in, total dust mass M, and grain radius of the populations of larger and smaller grains, a_L and a_S. Three approaches were used to deal with observational uncertainties: no uncertainties ( $F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ) in blue; plus NIR, minus MIR uncertainty ( $F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in gold; and minus NIR, plus MIR uncertainty ( $F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in red. No markers are displayed when the respective quantity could not be constrained because the MIR excess leak was non-positive due to instrumental noise (see Sect. 3.1), no viable dust distribution was found in the investigated parameter space that is able to reproduce the observations (see Sect. 3.4), or the boundary of the chosen simulated parameter space (see Sect. 2.5) was reached (for R_in, a_L, or a_S). In addition, the first panel shows the location of the habitable zones (as defined in Sect. 2.5 of Kirchschlager et al. 2017) and the inner and outer working angles of the KIN at the respective system distances that represent the borders of the parameter space of disk radii used in the simulations. The second panel shows the total dust mass M with possible grain radii shown in the third and fourth panel. When no further restrictions were possible, the boundaries of the parameter space apply (i.e., is grain radii from 1 nm to 1 mm).

Fig. 3

Parameter combinations of inner disk radius R_in and the radii of the smaller and larger grains a_S, a_L for the system HD 172167 (see the Fig. B.1 for all other investigated targets). The blue sections enclose all parameter combinations able to reproduce the flux densities inferred from observations in the NIR and MIR wavelength ranges. The red sections indicate parameter combinations that cannot reproduce the observations. The upper boundary of possible values of R_in is given by the distance, where the radiation originating from the grain population of smaller grains no longer shows a NIR-to-MIR flux density ratio (Eq. (4)) higher than the observed value (Eq. (3)). The lower boundary is given by the physical scale corresponding to the IWA of the KIN, which is depicted by the solid black line. The dashed black line depicts the sublimation radii for different grain sizes. The intersecting set of parameter values for which, on the one hand, the dust configurations can reproduce the observations and, on the other hand, the dust grains of the respective grain sizes do not sublimate is indicated by the dashed area. Right: parameter space of R_in and a_L for all possible values of a_S. Left: parameter space of R_in and a_S with the value of a_L fixed to a_L ∈ {10 µm, 100 µm, 1000 µm}; valid parameter combinations of R_in and a_S are the same for these three values.

3.4.4 Smaller grain radius a_S

For the grain radius of the population of smaller grains aS (fourth panel of Fig. 2) Eq. (5) sets upper limits; values are constrained to be smaller than ≈0.2… 0.9 µm. For every system the upper value is smaller than the respective blowout grain radius, which shows the need for submicrometer-sized, sub-blowout grains to reproduce the NIR excess. We found lower limits being constrained to values of ≈0.08… 0.15 µm around the systems, HD 10700, HD 187642, HD 216956, and HD 172167.

3.5 Impact of observational uncertainties on derived constraints

The consideration of observational uncertainties does not alter the qualitative nature of the resulting parameter constraints while the exact values thereof change. The lower constraint of the stellocentric distance is mostly invariant to changes in the inferred MIR flux density as it is, if interferometrically resolved, set by the sublimation radii in our model. As the largest possible stellocentric distance is set by the distance where no grain of the population of smaller grains can produce a NIR-to-MIR flux density ratio higher than the one observed, this constraint increases with increasing true MIR excess and shrinks for smaller true MIR excess. The possible dust masses increase with decreasing NIR-to-MIR flux density ratio. At a fixed stellocentric distance, a smaller MIR excess, and hence a higher NIR-to-MIR flux density ratio, would typically require hotter, and thus smaller grains, while a larger MIR excess would require colder, thus larger grains, effectively shifting the constraints on the grain radii a_S and a_L in the respective directions. However, exceptions from this general trend with grain temperature can arise as the emission spectrum of a dust grain depends on the complex interplay of the wavelength-dependent intensity of the stellar light and wavelength, grain size, and material dependent absorption (emission) efficiency of the respective dust grain. Such exceptions occur for the systems HD 102647, HD 216956, and HD 172167 for which the case of (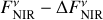 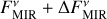$F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) permits smaller values of a_L than the case of ( 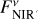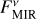$F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ) (see third panel of Fig. 2).

3.6 Dust distributions with larger grains of the radii a_L = 10 µm, 100 µm, 1000 µm

To explore the nature of valid dust distributions with large grain radii a_L > 1 µm, we selected subsets of all valid parameter combinations with the population of larger grains having a grain radius of a_L ∈ {10 µm, 100 µm, 1000 µm}. These grain radii are larger than the blowout radii for each system. The constraints on the inner disk radius R_in are the same as for the full parameter set, grains of all three sizes at locations as shown in Fig. 2 are consistent with the observational constraints. The same is true for the grain radius of the population of smaller grains a_S except for the system HD 177724 without observational uncertainties, there is now a lower limit of a_S = 0.004 µm. For the example system HD 172167 the combinations of R_in and a_S of all dust distributions with a_L ∈ {10 µm, 100 µm, 1000 µm} that are able to reproduce the observations are shown for illustration in the left panel of Fig. 3 (see Fig. B.1 for all other investigated targets).

From the mass and grain radius of each grain population we inferred the number of grains making up each population, N_S and N_L, and computed the number ratio of larger to smaller grains N_L /N_S. The constraints on this quantity together with that on the total dust mass M and the relative contribution of the population of larger grains to the total dust mass M_L/M are displayed in Fig. 4 (for all possible values of R_in and a_S). Constraints are shown without taking observational uncertainties into account, except for the systems HD 10700, HD 187642, and HD 203280 for which no other constraints could be derived (see Sects. 3.1 and 3.4). Consistent across the investigated stellar systems, along with increasing grain radius a_L the values of N_L/N_S decrease: from a logarithmic mid value of the parameter intervals of N_L/N_S ≈ 3 × 10⁻⁹… 8 × 10⁻⁷ for a_L = 10 µm, over N_L/N_S ≈ 3 × 10⁻¹¹… 8 × 10⁻⁹ for a_L = 100 µm to N_L/N_S ≈ 3 × 10⁻¹³… 9 × 10⁻¹¹ for a_L = 1000 µm.

Along with an increasing larger grain radius a_L, the total dust mass increases as larger and more massive grains contribute disproportionately to the total mass budget. The dust distributions with the largest overall grain radius a_L = 1000 µm are the most massive ones in the overall set of valid dust distributions (cf. Fig. 2). Furthermore, the relative contribution of the population of larger grains to the overall mass budget M_L/M increases: from M_L/M ≈ 0.3% … 96.2% for a_L = 10 µm, over M_L/M ≈ 3.3% … 99.6% for a_L = 100 µm to M_L/M ~ 26.7% … 99.96% for a_L = 1000 µm. For each of the three investigated grain radii, there are valid dust distributions for which the relative contribution to the total disk mass of the population of larger grains exceeds that of the population of smaller grains (red dashed line in bottom panel of Fig. 4). The other HEZD parameters of those dust distributions show the whole range of possible values. This finding illustrates that the dust configurations for which the mass is dominated by grains with radii ≥10 µm are not located in isolated parts of the parameterspace.

To investigate the possible impact of the presence of larger grains in HEZD systems on observable quantities, we computed the ratio of flux density 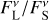$F_{L}^{v} / F_{S}^{v}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}}$ originating from the larger grains of sizes a_L ∈ {10 µm, 100 µm, 1000 µm} to that originating from the population of smaller grains with any possible grain radius a_S (see Fig. 5). For a quantitative analysis we chose four example observing wavelengths. At first we selected λ = 2.13 µm as the adopted wavelength for the CHARA/FLUOR sample that is also accessible with GRAVITY (GRAVITY Collaboration 2017) at the VLTI. Toward longer wavelengths, the impact of the larger grains increases due to their lower temperatures and increasing emission efficiency. For this wavelength range we chose λ = 4.1 µm, which is the central wavelength of the L&M band arm of VLTI/MATISSE and λ = 11.1 µm, which is the central wavelength of the N′ filter of the Large Binocular Telescope Interferometer (LBTI, Hinz et al. 2016; Ertel et al. 2020b), that was used to perform the survey Hunt for Observable Signatures of Terrestrial Systems (HOSTS, Ertel et al. 2018a,b, 2020a). Finally, we selected λ = 870 µm as the most promising ALMA band to observe larger grains in HEZD (see Sect. 4.4 for a feasibility investigation regarding ALMA).

At the chosen wavelengths of 2.13 µm, 4.1 µm, and 11.1 µm, the ratio of flux densities are constrained to similar values for all three grain radii. This can be explained by the fact that the large grains are equally inefficient emitters at the respective wavelengths ≲a. Consequently, at the wavelength 870 µm we see a split. There the grains with radius a_L = 100 µm are the most efficient emitters of the three investigated sizes, followed by the grains with radius a_L = 1000 µm. Across all stellar systems and all three grain radii, the ratio of flux densities is constrained to values on the order of 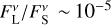$F_{L}^{v} / F_{S}^{v} \sim 10^{- 5}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} \sim {10^{ - 5}}$ to at most ≈0.35 at a wavelength of λ = 2.13 µm, to values of 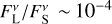$F_{L}^{v} / F_{S}^{v} \sim 10^{- 4}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} \sim {10^{ - 4}}$ at a wavelength of λ = 4.1 µm, and to values of 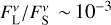$F_{L}^{v} / F_{S}^{v} \sim 10^{- 3}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} \sim {10^{ - 3}}$ at λ = 11.1 µm. At λ = 870 µm, we found 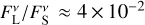$F_{L}^{v} / F_{S}^{v} \app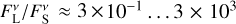rox 4 \times 10^{- 2}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} \approx 4 \times {10^{ - 2}}$ for a_L = 10 µm, $F_{L}^{v} / F_{S}^{v} \approx 3 \times 10^{- 1} \dots 2 \times 10^{3}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} \approx 3 \times {10^{ - 1}} \ldots 2 \times {10^3}$ for a_L = 100 µm, and intermediate values of 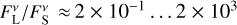$F_{L}^{v} / F_{S}^{v} \approx 2 \times 10^{- 1} \dots 2 \times 10^{3}$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} \approx 2 \times {10^{ - 1}} \ldots 2 \times {10^3}$ for a_L = 1000 µm. Across all four wavelengths, we generally found the ratios of flux density to be more tightly constrained around closer systems, but without a clear monotonic trend with stellar distance. Even at a wavelength of 4.1 µm, there are dust configurations consistent with the observations, for which the population of larger grains with a grain radius of a_L ≥ 10 µm contributes as much to the total dust emission as the population of smaller grains or even dominates it.

Fig. 4

Constraints for dust distributions with grain radius of the population of larger grains of a_L = 10 µm (gold), a_L = 100 µm (orange), and a_L = 1000 µm (dark red) on the HEZD parameters number ratio of larger to smaller grains N_L/N_S, total dust mass M, and relative contribution of the population of larger grains to the total dust mass M_L/M. The horizontal dashed red line denotes the case when the mass of the population of larger grains would make up half of the total dust mass (i.e., M_L/M = 0.5); for higher values of M_L/M the large grains dominate the mass budget. Constraints are computed without taking observational uncertainties into account, except for the systems HD 10700, HD 187642, and HD 203280 for which no other constraints could be derived (see Sects. 3.1 and 3.4).

Fig. 5

Constraints on the ratio of flux density originating from the population of larger grains with the grain radius a_L = 10 µm (gold), a_L = 100 µm (orange), and a_L = 1000 µm (dark red) to that originating from the population of smaller grains with any possible grain radius a_S for the four observing wavelengths 2.13 µm, 4.1 µm, 11.1 µm, and 870 µm. The horizontal dashed red lines denote equal contribution of the two grain populations to the total flux density (i.e., $F_{L}^{v} / F_{S}^{v} = 1$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} = 1$ ). Constraints are computed without taking observational uncertainties into account, except for the systems HD 10700, HD 187642, and HD 203280 for which no other constraints could be derived (see Sects. 3.1 and 3.4).

4 Discussion

4.1 Employed model of hot exozodiacal dust

Above-micrometer-sized grains as constituents of HEZD have already been inferred by Lebreton et al. (2013) to model inter-ferometric observations of the system HD 216956. They used a different dust description and assumed a two-ring model. This approach is based on the work of Mennesson et al. (2013); using only one dust ring in the modeling they were not able to reasonably fit their whole data set of MIR observations obtained with the KIN. However, they modeled the grain size distribution with a single continuous power law. To reproduce the high NIR excess, the minimum grain size was found to lie in the sub-micrometer range and the slope of the power law was found to be extremely steep; however, this model was unable to reproduce the rising slope of the MIR excess. They solved this issue by invoking a second ring with a second grain size distribution; this ring was found to have a larger radius and to contain a dust distribution with above-micrometer-sized grains, although again with an extremely steep slope of the grain size distribution. Using this model together with a new treatment of grain sublimation Lebreton et al. (2013) then confirmed these general results (see Sect. 4.2 for a comparison of their findings to ours). However, the need for two independent (i.e., in the two rings) power-law grain size distributions, each with an extremely steep slope, may also be interpreted as an indication of a bimodal grain size distribution as applied in this work. As the distance from the central star is degenerate with the grain size in its effect on the grain temperature and hence emission spectrum of the dust, the two-ring description in the modeling approach of Mennesson et al. (2013) and Lebreton et al. (2013) has a similar impact on the resulting spectral distribution of flux density as a bimodal or at least broken grain size distribution.

The use of different dust descriptions in our investigation would not cause qualitative changes of the derived parameter constraints, in particular of the main result: large amounts of above-micrometer-sized grains are consistent with current observations of HEZD and can dominate the dust mass budget. However, quantitative changes would arise, and in the following we discuss the individual model assumptions of this study in detail.

4.1.1 Thin dust ring seen face-on

We assumed the HEZD to be distributed in a thin ring with R_in = 1.5R_out. A broader ring would allow for grains at larger stellocentric distances, and hence lower equilibrium temperatures. On the one hand, the presence of lower dust temperatures would result in a lower NIR-to-MIR flux density ratio of the emission of both grain populations, decreasing the possible relative number of large grains. On the other hand, it would result in a generally lower emission power of the dust grains, leading to higher dust masses to compensate for the lower emissivity. The relative impact of these effects on the overall emission spectrum depends on the radial dependency of the density distribution.

We considered the dust to be seen in face-on orientation. For an optically thin system of spherical particles, different spatial dust configurations and orientations with respect to the line of sight change the amount of stellar light scattered toward the observer, while the amount of observed thermal emission remains unchanged (neglecting minor effects of dust coverage by the host star). However, if the total dust radiation (thermal emission and scattered stellar light) is inferred from interfero-metric observations, most of the forward-scattered light typical of Mie scattering is strongly attenuated due to the IWAs of the instruments. Consequently, for a dust configuration comprising solely grains of a specific grain size, a dust ring seen edge-on and a spherical dust shell do not result in clearly different constraints on the dust characteristics compared to a ring seen face-on (Kirchschlager et al. 2017). Furthermore, for the A-type star HD 56537 the relative contribution of scattered stellar light to the total brightness peaks in the NIR wavelength regime for grains with radii in the range 0.2.… 1 µm (Kirchschlager et al. 2017, see their Fig. 4). Thus, for our dust configurations additionally comprising grains up to a radius of 1 mm, the impact of scattered stellar light and hence the impact of the spatial dust configuration and orientation is negligible in the NIR wavelength regime. Lebreton et al. (2013) also note that in their modeling of the inner debris disk of HD 216956 the contribution of scattered stellar light is always negligible in the NIR-MIR wavelength range. At an observing wavelength of 870 µm, large grains of the size ~100 µm can be efficient in scattering stellar light, while the dust thermal emission is weaker because of lower equilibrium temperatures of the dust grains. However, at such long wavelengths the stellar emission is also weaker, and the contribution of scattered stellar emission to the total dust radiation remains negligible.

4.1.2 Bimodal grain size distribution

We modeled the grain size distribution with two distinct grain sizes. The use of grains with single radii a can cause interference in the spectral distribution of radiation due to the shape of the wavelength-dependent cross sections derived from Mie theory; the effect can be mitigated by the use of a narrow grain size distribution centered around a so the interference cancel each other out (e.g., Kirchschlager et al. 2019). The effect of this interference on our model results is small and we refrained from using narrow grain size distributions around the distinct grain sizes for easier comparison with the results of Kirchschlager et al. (2017).

When replacing our two grain sizes in the model by a continuous distribution ranging from the smaller to the larger grain size, the constraints on the stellocentric distance of the HEZD as derived would be weakly affected; the inner boundary is determined by the modeled dust sublimation and the outer boundary is determined by the distance beyond which no grain of any size produces radiation with a NIR-to-MIR flux density ratio higher than the one observed. The constraints on the smaller grain radius would transform to constraints on the minimum grain radius of the continuous distribution and remain qualitatively unaltered as they are set predominantly by the large observed NIR-to-MIR flux density ratio. This is supported by the findings of Kirchschlager et al. (2017), who used only one grain radius in the modeling of various HEZD systems, and by Lebreton et al. (2013), who modeled the HEZD around HD 216956 using a continuous grain size distribution; both showed constraints on the size of smallest grains similar to ours (see Sect. 4.2). The amount of the largest grains would be reduced as the grain size regime between the minimum and maximum grain size would then be populated by dust motes contributing to the total radiation that is constrained by the observations. This effect would be strongest in the case of the most separated smaller and larger grain sizes. Nonetheless, while a continuous, single power-law size distribution is a conventional choice to model cold debris disks, in the case of HEZD it is doubtful as possibly different dust transport and trapping mechanisms might shape the size distribution (see Sects. 1 and 2.3.1).

4.1.3 Dust composition

We used graphite as a proxy for a carbonaceous material; other possible choices include amorphous carbon (e.g., Rouleau & Martin 1991; Jäger et al. 1998). While those different materials do not produce a strongly different spectral distribution of flux density (see Fig. 6 in Kirchschlager et al. 2017 or the similar fit results in Kirchschlager et al. 2020 for different carbonaceous materials) their bulk densities differ from our choice, which would result in a linear re-scaling of our presented absolute mass estimates.

With grains composed of graphite we can reproduce the NIR and MIR measurements, while with grains composed of astronomical silicate we cannot as such grains generate MIR emission that is far too high, due to their ~ 10 µm spectral feature. This was also found by Kirchschlager et al. (2017) and indicated by previous observational analyses (e.g., Absil et al. 2006; Akeson et al. 2009; Lebreton et al. 2013). Across all grain radii and investigated targets the graphite grains of our valid dust distributions show temperatures ranging from ~450 K up to the assumed sublimation temperature of 2000 K. Based on Kobayashi et al. (2009), who indicate a sublimation temperature of silicates of 1200 K, this temperature range allows silicates to survive. Therefore, a dust configuration with carbonaceous grains that incorporate at least some amount of silicates is possible (also indicated by Lebreton et al. 2013). Furthermore, with decreasing stellocentric distance to the central star the silicate components could sublimate, leaving potentially porous carbonaceous grains (see below).

We assumed compact and hence non-porous dust grains. Analyses of the aftermath of the collision created during the Deep Impact mission (A’Hearn et al. 2005a,b; Meech et al. 2005) showed that the upper layer of comets (which are discussed as suppliers of HEZD grains) can be highly porous (Kobayashi et al. 2013), which increases the blowout grain size (Arnold et al. 2019). Furthermore, from investigations of porous silicate grains it was concluded that porous dust grains show a lower equilibrium temperature at a fixed stellocentric distance (Kirchschlager & Wolf 2013; Brunngräber et al. 2017). With the caveat of a non-silicate material, in our modeling approach lower grain temperatures would result in lower NIR-to-MIR flux density ratios and reduce the sublimation radii, allowing grains to survive closer to the central star. While the exact equilibrium temperature and emissivity of porous grains depends on the individual combination of stellar spectrum, grain size and porosity, compared to our results we expect an increase in the grain number density with a roughly conserved absolute dust mass for low porosity values. Highly porous grains are generally disfavored due to the large blowout sizes, and hence the difficulty to define reasonable supply and trapping mechanisms to explain the permanent nature of the phenomenon of HEZD. Lebreton et al. (2013) suggested that the submicrometer-sized population around HD 216956 is composed of solid residuals from the disruption of larger particles. Following this idea, a dust distribution with two phases is also possible, for example a population of highly porous large grains supplied by comet layers that get disrupted and create a second population of solid submicrometer-sized grains. In the case of a complete disintegration of a porous aggregate into its constituents (Blum & Münch 1993) this would cause a discontinuous grain size distribution similar to that used in our model. Nonetheless, as the available scarce observational data result in a highly degenerate set of possible dust parameters, more observational constraints are needed to conclude on the porosity of HEZD.

4.1.4 Stellar model

We modeled the central stars as spherical blackbody emitters with a specific effective temperature, luminosity, and radius. This assumption neglects the rapid rotator nature of some A-type stars (see Royer et al. 2007 for a compilation of rotational velocities of A-type stars). The rapid spinning can produce a rather oblate shape of the star and a varying surface brightness across the stellar surface, which has been shown for the following stars from our sample: HD 172167 (e.g., Gulliver et al. 1994; Peterson et al. 2006b; Aufdenberg et al. 2006a,b; Monnier et al. 2012), HD 177724 (Zhao et al. 2009), HD 187642 (e.g., van Belle et al. 2001; Peterson et al. 2006a), and HD 203280 (van Belle et al. 2006). This deviation from a spherical blackbody emitter can change our results depending on the dust morphology and its orientation with respect to the stellar rotation axis as a different surface brightness of the stellar surface changes the equilibrium temperatures of the dust grains, and hence their sublimation radii and emitted radiation, and the characteristics of the scattered stellar emission as well. As the true dust morphology is not constrained for any of the known HEZD systems, this issue persists until stronger observational constraints are available. However, we do not expect a major influence on the results by this as the general characteristics of our findings are consistent across the investigated targets, which include A-type stars with different orientations of their rotational axis as well as a G- and an F-type star.

4.1.5 Dust sublimation

The derived constraints on the minima of stellocentric distance and dust grain radii depend on the assumed fixed sublimation temperature of 2000 K for graphite (Kobayashi et al. 2009). The assumption of a fixed temperature for the phase change, which is in fact a continuous process, is justified as the process becomes rapid once a certain temperature is reached (Lamy 1974), and we neglected grain dynamics in our modeling (for a more thorough treatment of dust grain sublimation, see, e.g., Lamy 1974; Kobayashi et al. 2008, 2009; Lebreton et al. 2013; van Lieshout et al. 2014a,b; Pearce et al. 2022). Lebreton et al. (2013) found that the additional consideration of the processes collisions, PR-drag, and blowout by radiation pressure (but no trapping mechanism) alters the sublimation distances around HD 216956 only for grains with radii smaller than 10 µm. Thus, our results for large grains ≥ 10 µm would be not affected. Furthermore, the constraints on the grain radii are mainly determined by the observed ratio of NIR-to-MIR flux density.

However, the lower constraint on the inner disk radius R_in is determined by the particular choice of the sublimation temperature as it defines the stellocentric distance inside which no grains of a certain size can survive. Consequently, a higher value of the assumed sublimation temperature would lead to smaller possible inner disk radii and vice versa.

4.2 Derived constraints on parameters of hot exozodiacal dust

We constrained the stellocentric distance of the hot dust to ≲ 1 au and the grain radius of one dust grain population to ≲1 µm, similarly to what was found by Kirchschlager et al. (2017). Deviations arise due to a different treatment of observational uncertainties and due to the way to include the MIR observations in the modeling; while our aim was to reproduce the inferred MIR flux densities as measured and explore the uncertainties separately, Kirchschlager et al. (2017) used the significance limits (except for HD 102647 for which the excess leak was measured significantly) and considered these MIR measurements solely as upper limits. Furthermore, we modeled only dust distributions with an angular scale larger than the IWA of the KIN which is larger than the IWAs of CHARA and VINCI, and thus did not consider dust at smaller stellocentric distances as Kirchschlager et al. (2017) did. For the systems with lower limits on the inner disk radius R_in we found the same rough trend of increasing values along with stellar luminosity as Kirchschlager et al. (2017); using the stellar ages given in their Table 1, we also found no clear trend for the dust mass. We found dust masses of ~10⁻¹¹… 10⁻⁶ M_⊕, similar to the results of Kirchschlager et al. (2017, their Fig. 7).

Lebreton et al. (2013) found the inner dust distribution around HD 216956 to be located inside 0.1… 0.3 au, which closely matches our constraints on the inner disk radius of R_in = 0.1… 0.22 au. They determined the dust mass up to grain radii of 1 mm to be 2.5 × 10⁻¹⁰ M_⊕ (2.6 × 10⁻¹⁰ M_⊕ with a different modeling approach). This is consistent with the low mass end of our results 2.2 × 10⁻¹⁰… 6.1 × 10⁻⁸ M_⊕, which is defined by dust distributions where large grains do not dominate the mass budget. The grain size distribution of the inner ring appears extremely steep with a minimum grain radius of 0.01 … 0.5 m, similar to our constraints on the grain radius of the population of smaller grains a_S = 0.08… 0.3 µm. In addition to the population of submicrometer-sized carbonaceous grains, their modeling approach also required above-micrometer-sized grains (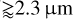 $\underset{\approx}{>} 2.3 μm$ $\mathop > \limits_ \approx 2.3\,{\rm{\mu m}}$ or 3.5 µm, depending on the exact modeling approach); the composition was assumed to be half silicate and half carbonaceous. This second grain population resides by design in a second ring that was constrained to be located at a stellocentric distance of ~2 au with a mass of ~10⁻⁶ M_⊕ up to grain radii of 1 mm. Both distance and dust mass are greater than the upper limits we found on the inner disk radius, 0.22 au, and dust mass, 6.1 × 10⁻⁸ M_⊕ (0.58 au and 3.8 × 10⁻⁷ Me in the case of 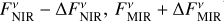$F_{NIR}^{v} - Δ F_{NIR}^{v}, F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{NIR}}}^v - {\rm{\Delta }}F_{{\rm{NIR}}}^v,\,F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ). However, in our modeling approach the population of large grains shares the same location with the small grains.

In principle, the presence of arbitrarily large grains a ≫ 1 µm in HEZD systems is consistent with the present observational constraints because arbitrarily large particles at a sufficient distance from the central star produce a NIR-to-MIR flux density ratio lower than that derived from observations. The relative mass contribution of the large grain population (a_L ≤ 1 mm) is in the range ~0.01… 99.99 %. Thus, above-micrometer-sized grains might indeed dominate the HEZD mass budget. Furthermore, these larger grains might contribute up to ~25% to the total radiation originating from the HEZD at a wavelength of 2.13 µm (e.g., CHARA/FLUOR, VLTI/GRAVITY) and up to ~50% at a wavelength of 4.1 µm (e.g., VLTI/MATISSE); at a wavelength of 11.1 µm (e.g., LBTI) they might even clearly dominate the total radiation with a contribution ten times larger than that of smaller submicrometer-sized grains (see Sect. 3.6). However, a possible large relative contribution of these large grains to the total dust mass and radiation budgets has only been identified within a rather limited fraction of the investigated parameter space in the case of about half of the investigated systems. Nevertheless, in future attempts to explain the HEZD phenomenon it must be considered that large grains (i.e., above-micrometer-sized), might have a significant impact on the mass budget and observational appearance of HEZD distributions.

4.3 Significance of the MIR observations and use in the modeling approach

The stellar set compiled in Group I of Kirchschlager et al. (2017) that we investigated further in this study represents the complete ensemble of systems with detected NIR excess and additional interferometric MIR measurements with a sufficiently small IWA (excluding the variable HEZD system HD 7788 A). We investigated what amount of above-micrometer-sized grains is still consistent with the mostly insignificant flux densities inferred from the MIR observations. For this purpose, we assumed the measured excess leaks in the MIR at the wavelengths bin of 8 to 9 µm (Mennesson et al. 2014) to be true values.

Out of the set of systems, only HD 102647 shows a significant MIR excess with a measured excess significance (ratio of the measured excess to its uncertainty) higher than three, with the caveat that this excess could mainly originate from the outer regions of the KIN field of view (see below). However, Mennesson et al. (2014) note that from statistical considerations not all measurements with an excess significance between 1 and 2 can be produced by instrumental noise, hinting at true dust emission. This is supported by the fact that the excess measurements presented by Mennesson et al. (2014) are averaged values from multiple observations. The intensity of the radiation originating from the circumstellar environment that is transferred through the nulling transmission pattern depends on the source morphology and its orientation with respect to the transmission pattern during observation, which also changes with time as the source traverses the sky. Therefore, for an asymmetric dust configuration, for example a disk seen edge-on, there is a statistical error of the excess values resulting from averaging the measurements of observations performed at different hour angles. Nonetheless, as the HEZD is not safely detected by the KIN, the results of this study as presented provide upper limits of the presence and impact of above-micrometer-sized grains in HEZD distributions.

From the measured excess leaks we inferred values of flux density originating from circumstellar dust. The applied factor of 2.5 to rectify for the circumstellar radiation not transmitted through the KIN transmission pattern is an approximation suitable for an average system, while the true factor again depends on the source morphology and its orientation with respect to the transmission pattern (see above). Therefore, the true MIR radiation from any of the observed systems can deviate in both directions from the inferred values. This would alter the observed NIR-to-MIR flux density ratio, causing the same effects on the derived HEZD parameter constraints as when taking observational uncertainties into account (see Sect. 3.5).

For the special case of HD 102647, with recent LBTI measurements (Ertel et al. 2020a) a similar excess to that found with the KIN was inferred. As the LBTI possesses an IWA of ~70mas (Ertel et al. 2018a), and thus larger than that of the KIN (6 mas), this indicates that most of the excess inferred with the KIN originated from the outer parts of its field of view ≳70mas, and hence less radiation originates from the on-sky region in the range 6… 70 mas. Thus, the total flux density inferred from KIN measurements (listed in Table 2) cannot be attributed to hot dust at locations corresponding to the angular scale of 6… 70 mas around HD 102647 (Pearce et al. 2022). This would result in a higher NIR-to-MIR flux density ratio derived from the observations. However, to maintain uniformity of the analyzed data set, we decided not to use these recent LBTI measurements.

Altogether, our results emphasize the need for a larger number of high sensitivity MIR measurements of systems, with already significantly detected HEZD distributions in the NIR wavelength regime, to either verify the MIR detections or to derive robust upper limits. As the LBTI has an IWA of ~70 mas, too large to investigate the innermost circumstellar regions, to date, VLTI/MATISSE is the only instrument worldwide providing the required instrument capabilities (Lopez et al. 2014, 2022; Kirchschlager et al. 2018, 2020). Possible future capabilities to observe HEZD may be offered by the Nulling Observations of Exoplanets and Dust (NOTT, formerly Hi-5, Defrère et al. 2018a,b, 2022; Laugier et al. 2023) which is proposed to work as part of the Asgard suite (Martinod et al. 2022, 2023) at the VLTI.

4.4 Feasibility to observe large grains at submillimeter and millimeter wavelengths

To date, HEZD has only been convincingly detected with interferometers operating in the H, K, and L bands. However, in this study we showed that a non-negligible contribution to the total mass of HEZD distributions by above-micrometer-sized grains is consistent with the existing observations. While the confirmation of the presence of such large grains appears infeasible in the NIR and MIR wavelength range, observations with comparable angular resolution in the far-infrared (FIR) and submillimeter/millimeter wavelength regimes are more appropriate to measure the emission of such large grains. Currently, there are no observatories providing such a high angular resolution in the FIR; however, in the submillimeter/millimeter wavelength regime there is ALMA.

To explore the general feasibility of observing HEZD that partly consists of larger grains using ALMA, we assumed an unresolved observation and compared the maximum flux densities produced by dust thermal emission and scattered stellar light (in the face-on case) of all valid dust distributions to the sensitivity of ALMA for a source at zenith in all bands (see Fig. 6). We estimated the instrument sensitivity as three times the root mean square (RMS) for exposure times of t_exp = 1 h and 8 h; these values were obtained from the ALMA sensitivity calculator³.

The system with the highest possible flux density in any ALMA band is HD 102647, followed by HD 22484 and HD 172167. Before bands 6 and 8, the most promising one is band 7 at an observing wavelength of 870 µm. For HD 102647 and taking no observational uncertainties into account, the maximum flux density of all valid dust distributions is ≈3 times smaller than the sensitivity for an exposure time of t_exp = 8 h; when taking observational uncertainties into account it is ≈2 times smaller. As this is the most favorable case in our investigation, detecting HEZD with ALMA seems to be infeasible. Across all other systems, the dust mass and hence the flux density would have to be one to two orders of magnitude higher to enable detections with ALMA.

A future instrument with sufficient resolving power is the ngVLA (Selina et al. 2018). Performance estimates from December 2021⁴ are given with a continuum RMS of 0.40 µJy beam⁻¹ at an observing frequency of 93 GHz (corresponding to a wavelength of λ ≈ 3.22 mm) for an exposure time of t_exp = 1 h. Assuming all HEZD emission is collected in one beam, the possible presence of some of the brightest dust distributions containing larger grains could be tested with the ngVLA (see Fig. 6, bottom panel).

4.5 Implications on HEZD theories

Better constraints on the dust populations responsible for the excess emission over the stellar photosphere are essential if we are to understand this phenomenon. Until now such populations were generally considered to comprise only small grains, and one of the major technical difficulties encountered by theoretical models is explaining how such sub-blowout grains can exist in large quantities close to stars. If a significant fraction of the dust mass could actually be hidden in larger (non-blowout) grains, as our work suggests, then this would allow for a broader range of dynamical possibilities that could make it easier to find a viable mechanism. Similarly, some existing models (e.g., cometary supply) predict that grains would be present at all sizes, while other models (e.g., gas trapping) suggest that the size distribution is dominated by dust at a single size. Our work has shown that it is possible (though by no means guaranteed) that large grains are present, which unfortunately means that we cannot exclude different models from our current large-grain constraints at the moment. However, we showed that future observations, for example with the ngVLA, could directly measure the large-grain component (see Sect. 4.4), which would allow us to exclude various dynamical models.

Fig. 6

Maximum flux density of all valid dust distributions at observing wavelengths corresponding to ALMA bands 10 to 3 and the ngVLA at an observing frequency of 93 GHz (λ ≈ 3220 µm). Three approaches were used to deal with the observational uncertainties: no uncertainties ( $F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ) in blue; plus NIR, minus MIR uncertainty ( $F_{NIR}^{v} - Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v - {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in gold; and minus NIR, plus MIR uncertainty ( $F_{NIR}^{v} - Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v - {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} + Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v + {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in red. Dashed horizontal lines indicate instrument sensitivity as three times the RMS for exposure times of t_exp = 1 h (green) and 8 h (red).

4.6 Implications on exoplanetary science

We were able to constrain dust configurations with the largest extent matching the OWA of the KIN. As shown in Fig. 2, for the system HD 22484 this completely covers the habitable zone (as defined in Sect. 2.5 of Kirchschlager et al. 2017), while a partial coverage results for HD 10700 and HD 177724. The habitable zones of the other systems did not fall in the sensitivity window of the KIN. However, the radii were constrained to be smaller than the OWA. Thus, in the case that any additional dust reservoirs are present outside the OWA and inside the habitable zone, these are not connected to the HEZD populations in view of the sensitivities of the KIN. However, Ahlers et al. (2022) showed that the habitable zones around rapid rotators (see Sect. 4.1.4) can reside closer to the host star than for an equivalent non-rotating star, which we assumed in our modeling. Furthermore, as we used a simple approximation of a blackbody in thermal equilibrium for a potential celestial body to compute the location of the habitable zones, a more thorough treatment of this topic including effects such as light scattering in a potential atmosphere or off the surface, the greenhouse effect, or inner heating sources might result in deviating locations of the habitable zones.

In the case of exoplanet transit observations any additional source of emission, such as hot circumstellar dust, causes an offset of the monitored light curve, both before and during the transit, which translates into the planetary radius being determined too small. In the H and K bands, the dust-to-star flux ratio of HEZD distributions can be as high as several percent (Absil et al. 2013; Ertel et al. 2014) and in the L band as high as 5… 7 % (Kirchschlager et al. 2020), comparable to achievable precision in the determination of stellar radii (e.g., Baines et al. 2009; Torres et al. 2010; White et al. 2013; Ligi et al. 2016).

In addition to HEZD as contributor to the net flux of extrasolar planetary systems, we also have to take into account that the radiation disseminating from an exoplanet is partially polarized. This is the result of different light scattering processes, such as stellar light scattering off the planetary atmosphere (e.g., Kattawar & Adams 1971; Seager et al. 2000; Stam et al. 2004; Stam 2008; Buenzli & Schmid 2009; Fluri & Berdyugina 2010; Zugger et al. 2010, 2011a,b; Karalidi et al. 2011, 2012, 2013; Karalidi & Stam 2012; Lietzow & Wolf 2022), an ocean surface (e.g., Stam 2008; Williams & Gaidos 2008; Zugger et al. 2010), or circumplanetary rings (e.g., Lietzow et al. 2021; Lietzow & Wolf 2023), and by the scattering of planetary thermal emission in the planetary atmosphere (e.g., de Kok et al. 2011; Stolker et al. 2017), with periodically changing magnitudes of the total scattered flux and polarization degree thereof as the planet orbits its host star and rotates around its own axis. This effect has been used to search for exoplanets and the first exoplanet detected in this way, HD 189733b, was reported by Berdyugina et al. (2008. However, the large amplitude of the periodic polarization signal, also reported by Berdyugina et al. (2011), was not confirmed by Wiktorowicz et al. (2015) and Bott et al. (2016), and according to Bailey et al. (2021) could also be caused by the magnetic activity of the host star. In addition to magnetic activity of the host star, a co-existing HEZD distribution could also produce a polarization signal by scattering the stellar light. The signal can be variable in time in the case of an asymmetric HEZD distribution, which could be produced for example by dust clumps formed by interaction with the close-by exoplanet or a stochastic dust delivery process such as the disintegration of star grazing comets. As the true dust morphology of any of the known HEZD systems is unknown so far, HEZD must be considered as an additional radiation source in the efforts to detect and characterize exoplanets via polarimetric observations.

5 Summary

Using a bimodal grain size distribution we investigated how many large (above-micrometer-sized) dust grains in addition to the already inferred submicrometer-sized dust grains could be present in HEZD systems, while still being consistent with inter-ferometric observations in the K and N bands. In confirmation of previous findings, we found that while dust grains consisting of pure silicates are ruled out due to their high N band emission, carbonaceous grains are consistent with the observational constraints. We constrained the dust location to be ≲1 au, consistent with previous findings and, given our bimodal grain size model, also constrained the number ratios of larger to smaller grains. In the most extreme systems and dust configurations, large grains ≳10 µm might dominate the mass budget of the considered HEZD systems while contributing up to 25% to the total flux density originating from the dust at a wavelength of 2.13 µm, up to 50% at a wavelength of 4.1 µm, and clearly dominating at a wavelength of 11.1 µm. While it is not possible to detect the radiation stemming from such hot-dust distributions with ALMA, the ngVLA could potentially allow us to detect HEZD at millimeter wavelengths.

Acknowledgements

We thank the anonymous referee for various suggestions that helped to improve the presentation and discussion of our results, particularly in the context of previous studies. The author T.S. thanks all members of the Astrophysics Department Kiel for discussions and comments about this work in general. This research has made use of NASA’s Astrophysics Data System Bibliographic Services, a modified A&A bibliography style file for the preprint version of the article (https://github.com/yangcht/AA-bibstyle-with-hyperlink), Ipython (Perez & Granger 2007), Jupyter notebooks (Kluyver et al. 2016), Astropy (https://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018), Matplotlib (Hunter 2007), and Numpy (Harris et al. 2020). This work was supported by the Research Unit FOR 2285 “Debris Disks in Planetary Systems” of the Deutsche Forschungsgemeinschaft (DFG). The authors T.S. and S.W. acknowledge the DFG for financial support under grant WO 857/15-2, T.D.P. and A.V.K. under grants KR 2164/14-2 and KR 2164/15-2. F.K. has received funding from the European Research Council (ERC) under the EU’s Horizon 2020 research and innovation programme DustOrigin (ERC-2019-StG-851622). S.E. is supported by the National Aeronautics and Space Administration through the Exoplanet Research Program (Grant No. 80NSSC21K0394).

Appendix A Photometrie measurements at wavelengths λ ≥ 24 µm

The photometric measurements from the literature at wavelengths λ≥24 µm are presented in Table A.1.

Table A.1

Photometric values at specified observing wavelengths from the literature.

Appendix B Constraints on hot exozodiacal dust parameters

The values of all constraints shown in Fig. 2 are listed in Table B.1. Figure B.1 shows the same as Fig. 3, but for all other investigated systems.

Table B.1

Full set of constraints on hot exozodiacal dust parameters, as shown in Fig. 2.

Fig. B.1

Same as Fig. 3, but for all other investigated targets.

References

Absil, O., di Folco, E., Mérand, A., et al. 2006, A & A, 452, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Absil, O., di Folco, E., Mérand, A., et al. 2008, A & A, 487, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Absil, O., Mennesson, B., Le Bouquin, J.-B., et al. 2009, ApJ, 704, 150 [NASA ADS] [CrossRef] [Google Scholar]
Absil, O., Defrère, D., Coudé du Foresto, V., et al. 2013, A & A, 555, A104 [Google Scholar]
Acke, B., Min, M., Dominik, C., et al. 2012, A & A, 540, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
A’Hearn, M. F., Belton, M. J. S., Delamere, A., & Blume, W. H. 2005a, Space Sci. Rev., 117, 1 [CrossRef] [Google Scholar]
A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2005b, Science, 310, 258 [Google Scholar]
Ahlers, J. P., Fromont, E. F., Kopparappu, R., Cauley, P. W., & Haqq-Misra, J. 2022, ApJ, 928, 35 [NASA ADS] [CrossRef] [Google Scholar]
Akeson, R. L., Ciardi, D. R., Millan-Gabet, R., et al. 2009, ApJ, 691, 1896 [NASA ADS] [CrossRef] [Google Scholar]
Arnold, J. A., Weinberger, A. J., Videen, G., & Zubko, E. S. 2019, AJ, 157, 157 [NASA ADS] [CrossRef] [Google Scholar]
Astropy Collaboration (Robitaille, T. P., et al.) 2013, A & A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006a, ApJ, 651, 617 [NASA ADS] [CrossRef] [Google Scholar]
Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006b, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]
Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]
Bailey, J., Bott, K., Cotton, D. V., et al. 2021, MNRAS, 502, 2331 [NASA ADS] [CrossRef] [Google Scholar]
Baines, E. K., McAlister, H. A., ten Brummelaar, T. A., et al. 2009, ApJ, 701, 154 [NASA ADS] [CrossRef] [Google Scholar]
Belton, M. J. S. 1966, Science, 151, 35 [Google Scholar]
Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2008, ApJ, 673, L83 [NASA ADS] [CrossRef] [Google Scholar]
Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2011, ApJ, 728, L6 [NASA ADS] [CrossRef] [Google Scholar]
Blum, J., & Münch, M. 1993, Icarus, 106, 151 [Google Scholar]
Blum, J., Gundlach, B., Krause, M., et al. 2017, MNRAS, 469, S755 [Google Scholar]
Bonsor, A., & Wyatt, M. C. 2012, MNRAS, 420, 2990 [Google Scholar]
Bonsor, A., Augereau, J. C., & Thébault, P. 2012, A & A, 548, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bonsor, A., Raymond, S. N., Augereau, J.-C., & Ormel, C. W. 2014, MNRAS, 441, 2380 [Google Scholar]
Bott, K., Bailey, J., Kedziora-Chudczer, L., et al. 2016, MNRAS, 459, L109 [NASA ADS] [CrossRef] [Google Scholar]
Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [Google Scholar]
Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [Google Scholar]
Brunngräber, R., Wolf, S., Kirchschlager, F., & Ertel, S. 2017, MNRAS, 464, 4383 [CrossRef] [Google Scholar]
Buenzli, E., & Schmid, H. M. 2009, A & A, 504, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [Google Scholar]
Churcher, L. J., Wyatt, M. C., Duchêne, G., et al. 2011, MNRAS, 417, 1715 [NASA ADS] [CrossRef] [Google Scholar]
Colavita, M. M., Wizinowich, P. L., Akeson, R. L., et al. 2013, PASP, 125, 1226 [Google Scholar]
Coudé du Foresto, V., Ridgway, S., & Mariotti, J. M. 1997, A & AS, 121, 379 [Google Scholar]
Coudé du Foresto, V., Perrin, G., Ruilier, C., et al. 1998, SPIE Conf. Ser., 3350, 856 [Google Scholar]
Coudé du Foresto, V., Borde, P. J., Merand, A., et al. 2003, SPIE Conf. Ser., 4838, 280 [Google Scholar]
Czechowski, A., & Mann, I. 2010, ApJ, 714, 89 [Google Scholar]
Defrère, D., Absil, O., Augereau, J. C., et al. 2011, A & A, 534, A5 [CrossRef] [EDP Sciences] [Google Scholar]
Defrère, D., Absil, O., Berger, J. P., et al. 2018a, Exp. Astron., 46, 475 [CrossRef] [Google Scholar]
Defrère, D., Ireland, M., Absil, O., et al. 2018b, SPIE Conf. Ser., 10701, 107010U [Google Scholar]
Defrère, D., Bigioli, A., Dandumont, C., et al. 2022, SPIE Conf. Ser., 12183, 121830H [Google Scholar]
de Kok, R. J., Stam, D. M., & Karalidi, T. 2011, ApJ, 741, 59 [Google Scholar]
Di Folco, E., Thévenin, F., Kervella, P., et al. 2004, A & A, 426, 601 [CrossRef] [EDP Sciences] [Google Scholar]
Di Folco, E., Absil, O., Augereau, J. C., et al. 2007, A & A, 475, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Draine, B. T. 2003, ApJ, 598, 1026 [Google Scholar]
Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [Google Scholar]
Ertel, S., Absil, O., Defrère, D., et al. 2014, A & A, 570, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ertel, S., Defrère, D., Hinz, P., et al. 2018a, AJ, 155, 194 [Google Scholar]
Ertel, S., Kennedy, G. M., Defrère, D., et al. 2018b, SPIE Conf. Ser., 10698, 106981V [Google Scholar]
Ertel, S., Defrère, D., Hinz, P., et al. 2020a, AJ, 159, 177 [Google Scholar]
Ertel, S., Hinz, P. M., Stone, J. M., et al. 2020b, SPIE Conf. Ser., 11446, 1144607 [Google Scholar]
Faramaz, V., Ertel, S., Booth, M., Cuadra, J., & Simmonds, C. 2017, MNRAS, 465, 2352 [NASA ADS] [CrossRef] [Google Scholar]
Fluri, D. M., & Berdyugina, S. V. 2010, A & A, 512, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gaia Collaboration (Brown, A. G. A., et al.) 2021, A & A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gáspár, A., Rieke, G. H., & Balog, Z. 2013, ApJ, 768, 25 [CrossRef] [Google Scholar]
GRAVITY Collaboration (Abuter, R., et al.) 2017, A & A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gray, R. O., & Garrison, R. F. 1989, ApJS, 70, 623 [NASA ADS] [CrossRef] [Google Scholar]
Gray, R. O., Corbally, C. J., Garrison, R. F., McFadden, M. T., & Robinson, P. E. 2003, AJ, 126, 2048 [Google Scholar]
Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [Google Scholar]
Greaves, J. S., Wyatt, M. C., Holland, W. S., & Dent, W. R. F. 2004, MNRAS, 351, L54 [Google Scholar]
Gulliver, A. F., Hill, G., & Adelman, S. J. 1994, ApJ, 429, L81 [NASA ADS] [CrossRef] [Google Scholar]
Habing, H. J., Dominik, C., Jourdain de Muizon, M., et al. 2001, A & A, 365, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hanner, M. S. 1984, Adv. Space Res., 4, 189 [NASA ADS] [CrossRef] [Google Scholar]
Harker, D. E., Wooden, D. H., Woodward, C. E., & Lisse, C. M. 2002, ApJ, 580, 579 [CrossRef] [Google Scholar]
Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]
Hindsley, R. B., & Harrington, R. S. 1994, AJ, 107, 280 [NASA ADS] [CrossRef] [Google Scholar]
Hinz, P. M., Defrère, D., Skemer, A., et al. 2016, SPIE Conf. Ser., 9907, 990704 [Google Scholar]
Holland, W. S., Matthews, B. C., Kennedy, G. M., et al. 2017, MNRAS, 470, 3606 [NASA ADS] [CrossRef] [Google Scholar]
Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
Jäger, C., Mutschke, H., & Henning, T. 1998, A & A, 332, 291 [Google Scholar]
Karalidi, T., & Stam, D. M. 2012, A & A, 546, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Karalidi, T., Stam, D. M., & Hovenier, J. W. 2011, A & A, 530, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Karalidi, T., Stam, D. M., & Hovenier, J. W. 2012, A & A, 548, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Karalidi, T., Stam, D. M., & Guirado, D. 2013, A & A, 555, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kattawar, G. W., & Adams, C. N. 1971, ApJ, 167, 183 [NASA ADS] [CrossRef] [Google Scholar]
Keenan, P. C., & McNeil, R. C. 1989, ApJS, 71, 245 [Google Scholar]
Kervella, P., Coudé du Foresto, V., Glindemann, A., & Hofmann, R. 2000, SPIE Conf. Ser., 4006, 31 [NASA ADS] [Google Scholar]
Kervella, P., Gitton, P. B., Segransan, D., et al. 2003, SPIE Conf. Ser., 4838, 858 [NASA ADS] [Google Scholar]
Kim, M., Wolf, S., Löhne, T., Kirchschlager, F., & Krivov, A. V. 2018, A & A, 618, A38 [Google Scholar]
Kimura, H., Kunitomo, M., Suzuki, T. K., et al. 2020, Planet. Space Sci., 183, 104581 [NASA ADS] [CrossRef] [Google Scholar]
Kirchschlager, F., & Wolf, S. 2013, A & A, 552, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kirchschlager, F., Wolf, S., Krivov, A. V., Mutschke, H., & Brunngräber, R. 2017, MNRAS, 467, 1614 [NASA ADS] [Google Scholar]
Kirchschlager, F., Wolf, S., Brunngräber, R., et al. 2018, MNRAS, 473, 2633 [NASA ADS] [CrossRef] [Google Scholar]
Kirchschlager, F., Bertrang, G. H. M., & Flock, M. 2019, MNRAS, 488, 1211 [NASA ADS] [CrossRef] [Google Scholar]
Kirchschlager, F., Ertel, S., Wolf, S., Matter, A., & Krivov, A. V. 2020, MNRAS, 499, L47 [NASA ADS] [CrossRef] [Google Scholar]
Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, Jupyter Notebooks – A Publishing Format for Reproducible Computational Workflows, eds. F. Loizides, & B. Schmidt (Netherlands: IOS Press), 87 [Google Scholar]
Kobayashi, H., Watanabe, S.-I., Kimura, H., & Yamamoto, T. 2008, Icarus, 195, 871 [NASA ADS] [CrossRef] [Google Scholar]
Kobayashi, H., Watanabe, S.-I., Kimura, H., & Yamamoto, T. 2009, Icarus, 201, 395 [NASA ADS] [CrossRef] [Google Scholar]
Kobayashi, H., Kimura, H., Yamamoto, S., Watanabe, S. I., & Yamamoto, T. 2010, Earth Planets Space, 62, 57 [NASA ADS] [CrossRef] [Google Scholar]
Kobayashi, H., Kimura, H., Watanabe, S.I., Yamamoto, T., & Müller, S. 2011, Earth Planets Space, 63, 1067 [NASA ADS] [CrossRef] [Google Scholar]
Kobayashi, H., Kimura, H., & Yamamoto, S. 2013, A & A, 550, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kral, Q., Krivov, A. V., Defrère, D., et al. 2017, Astron. Rev., 13, 69 [NASA ADS] [Google Scholar]
Krivov, A., Kimura, H., & Mann, I. 1998, Icarus, 134, 311 [Google Scholar]
Kurz, R., Guilloteau, S., & Shaver, P. 2002, The Messenger, 107, 7 [NASA ADS] [Google Scholar]
Lamy, P. L. 1974, A & A, 35, 197 [NASA ADS] [Google Scholar]
Laugier, R., Defrère, D., Woillez, J., et al. 2023, A & A, 671, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Laureijs, R. J., Jourdain de Muizon, M., Leech, K., et al. 2002, A & A, 387, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lawler, S. M., Di Francesco, J., Kennedy, G. M., et al. 2014, MNRAS, 444, 2665 [Google Scholar]
Lebreton, J., van Lieshout, R., Augereau, J. C., et al. 2013, A & A, 555, A146 [Google Scholar]
Lietzow, M., & Wolf, S. 2022, A & A, 663, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lietzow, M., & Wolf, S. 2023, A & A, 671, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lietzow, M., Wolf, S., & Brunngräber, R. 2021, A & A, 645, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ligi, R., Creevey, O., Mourard, D., et al. 2016, A & A, 586, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lopez, B., Lagarde, S., Jaffe, W., et al. 2014, The Messenger, 157, 5 [NASA ADS] [Google Scholar]
Lopez, B., Lagarde, S., Petrov, R. G., et al. 2022, A & A, 659, A192 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
MacGregor, M. A., Lawler, S. M., Wilner, D. J., et al. 2016, ApJ, 828, 113 [Google Scholar]
Mamajek, E. E. 2012, ApJ, 754, L20 [Google Scholar]
Marboeuf, U., Bonsor, A., & Augereau, J. C. 2016, Planet. Space Sci., 133, 47 [CrossRef] [Google Scholar]
Martinod, M.-A., Defrère, D., Ireland, M. J., et al. 2022, SPIE Conf. Ser., 12183, 1218310 [NASA ADS] [Google Scholar]
Martinod, M.-A., Defrère, D., Ireland, M., et al. 2023, J. Astron. Telescopes Instrum. Syst., 9, 025007 [NASA ADS] [Google Scholar]
Matrà, L., Dent, W. R. F., Wilner, D. J., et al. 2020, ApJ, 898, 146 [CrossRef] [Google Scholar]
Meech, K. J., Ageorges, N., A’Hearn, M. F., et al. 2005, Science, 310, 265 [NASA ADS] [CrossRef] [Google Scholar]
Mennesson, B., Absil, O., Lebreton, J., et al. 2013, ApJ, 763, 119 [NASA ADS] [CrossRef] [Google Scholar]
Mennesson, B., Millan-Gabet, R., Serabyn, E., et al. 2014, ApJ, 797, 119 [Google Scholar]
Mérand, A., Coudé du Foresto, V., Kellerer, A., et al. 2006, SPIE Conf. Ser., 6268, 62681F [Google Scholar]
Mie, G. 1908, Ann. Phys., 330, 377 [Google Scholar]
Millan-Gabet, R., Serabyn, E., Mennesson, B., et al. 2011, ApJ, 734, 67 [NASA ADS] [CrossRef] [Google Scholar]
Monnier, J. D., Che, X., Zhao, M., et al. 2012, ApJ, 761, L3 [NASA ADS] [CrossRef] [Google Scholar]
Mukai, T., Yamamoto, T., Hasegawa, H., Fujiwara, A., & Koike, C. 1974, PASJ, 26, 445 [NASA ADS] [Google Scholar]
Pearce, T. D., Krivov, A. V., & Booth, M. 2020, MNRAS, 498, 2798 [Google Scholar]
Pearce, T. D., Kirchschlager, F., Rouillé, G., et al. 2022, MNRAS, 517, 1436 [NASA ADS] [CrossRef] [Google Scholar]
Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006a, ApJ, 636, 1087 [NASA ADS] [CrossRef] [Google Scholar]
Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006b, Nature, 440, 896 [CrossRef] [Google Scholar]
Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A & A, 518, A1 [Google Scholar]
Poynting, J. H. 1904, Philos. Trans. Roy. Soc. London A, 202, 525 [NASA ADS] [CrossRef] [Google Scholar]
Raymond, S. N., & Bonsor, A. 2014, MNRAS, 442, L18 [NASA ADS] [CrossRef] [Google Scholar]
Richichi, A., & Percheron, I. 2005, A & A, 434, 1201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rieke, G. H., Gáspár, A., & Ballering, N. P. 2016, ApJ, 816, 50 [Google Scholar]
Rigley, J. K., & Wyatt, M. C. 2020, MNRAS, 497, 1143 [NASA ADS] [CrossRef] [Google Scholar]
Robertson, H. P. 1937, MNRAS, 97, 423 [NASA ADS] [Google Scholar]
Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
Royer, F., Zorec, J., & Gómez, A. E. 2007, A & A, 463, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rusk, E. T. 1987, ApJ, 320, 315 [NASA ADS] [CrossRef] [Google Scholar]
Schöller, M. & Glindemann, A. 2003, Earths: DARWIN/TPF and the Search for Extrasolar Terrestrial Planets, eds. M. Fridlund, T. Henning, & H. Lacoste, ESA Special Publication, 539, 109 [Google Scholar]
Schöller, M., Gitton, P. B., Argomedo, J., et al. 2003, SPIE Conf. Ser., 4838, 870 [Google Scholar]
Seager, S., Whitney, B. A., & Sasselov, D. D. 2000, ApJ, 540, 504 [NASA ADS] [CrossRef] [Google Scholar]
Sekanina, Z., & Miller, F. D. 1973, Science, 179, 565 [NASA ADS] [CrossRef] [Google Scholar]
Selina, R. J., Murphy, E. J., McKinnon, M., et al. 2018, SPIE Conf. Ser., 10700, 107001O [NASA ADS] [Google Scholar]
Serabyn, E., Mennesson, B., Colavita, M. M., Koresko, C., & Kuchner, M. J. 2012, ApJ, 748, 55 [NASA ADS] [CrossRef] [Google Scholar]
Sezestre, É., Augereau, J. C., & Thébault, P. 2019, A & A, 626, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sibthorpe, B., Vandenbussche, B., Greaves, J. S., et al. 2010, A & A, 518, A130 [Google Scholar]
Sibthorpe, B., Kennedy, G. M., Wyatt, M. C., et al. 2018, MNRAS, 475, 3046 [Google Scholar]
Spitzer Science Center (SSC) & Infrared Science Archive (IRSA) 2021, VizieR Online Data Catalog: II/368 [Google Scholar]
Stam, D. M. 2008, A & A, 482, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Stam, D. M., Hovenier, J. W., & Waters, L. B. F. M. 2004, A & A, 428, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Stamm, J., Czechowski, A., Mann, I., Baumann, C., & Myrvang, M. 2019, A & A, 626, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Stolker, T., Min, M., Stam, D. M., et al. 2017, A & A, 607, A42 [CrossRef] [EDP Sciences] [Google Scholar]
Su, K. Y. L., Rieke, G. H., Stansberry, J. A., et al. 2006, ApJ, 653, 675 [Google Scholar]
Su, K. Y. L., Rieke, G. H., Malhotra, R., et al. 2013, ApJ, 763, 118 [NASA ADS] [CrossRef] [Google Scholar]
Su, K. Y. L., Rieke, G. H., Defrére, D., et al. 2016, ApJ, 818, 45 [NASA ADS] [CrossRef] [Google Scholar]
ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [Google Scholar]
Thureau, N. D., Greaves, J. S., Matthews, B. C., et al. 2014, MNRAS, 445, 2558 [NASA ADS] [CrossRef] [Google Scholar]
Torres, G., Andersen, J., & Giménez, A. 2010, A & ARv, 18, 67 [Google Scholar]
van Belle, G. T., & von Braun, K. 2009, ApJ, 694, 1085 [NASA ADS] [CrossRef] [Google Scholar]
van Belle, G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., & Lada, E. A. 2001, ApJ, 559, 1155 [NASA ADS] [CrossRef] [Google Scholar]
van Belle, G. T., Ciardi, D. R., ten Brummelaar, T., et al. 2006, ApJ, 637, 494 [NASA ADS] [CrossRef] [Google Scholar]
van Leeuwen, F. 2007, A & A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
van Lieshout, R., Dominik, C., Kama, M., & Min, M. 2014a, A & A, 571, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
van Lieshout, R., Min, M., & Dominik, C. 2014b, A & A, 572, A76 [CrossRef] [EDP Sciences] [Google Scholar]
White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]
White, J. A., Boley, A. C., Dent, W. R. F., Ford, E. B., & Corder, S. 2017, MNRAS, 466, 4201 [NASA ADS] [Google Scholar]
Wiktorowicz, S. J., Nofi, L. A., Jontof-Hutter, D., et al. 2015, ApJ, 813, 48 [NASA ADS] [CrossRef] [Google Scholar]
Williams, D. M., & Gaidos, E. 2008, Icarus, 195, 927 [NASA ADS] [CrossRef] [Google Scholar]
Wolf, S., & Voshchinnikov, N. V. 2004, Comput. Phys. Commun., 162, 113 [Google Scholar]
Wyatt, S. P., & Whipple, F. L. 1950, ApJ, 111, 134 [NASA ADS] [CrossRef] [Google Scholar]
Wyatt, M. C., Smith, R., Greaves, J. S., et al. 2007, ApJ, 658, 569 [NASA ADS] [CrossRef] [Google Scholar]
Zhao, M., Monnier, J. D., Pedretti, E., et al. 2009, ApJ, 701, 209 [NASA ADS] [CrossRef] [Google Scholar]
Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2010, ApJ, 723, 1168 [NASA ADS] [CrossRef] [Google Scholar]
Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2011a, ApJ, 739, 55 [NASA ADS] [CrossRef] [Google Scholar]
Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2011b, ApJ, 739, 12 [NASA ADS] [CrossRef] [Google Scholar]

¹

The only significant excess detection in the N band has been observed in the system of HD 102647 (β Leo). However, this is in doubt due to recent observations (see Sect. 4.3).

²

With 103 values the grain radii a = 10 µm, 100 µm, and 1000 µm investigated in Sect. 3.6 are present in the grid exactly.

³

https://almascience.eso.org/proposing/sensitivity-calculator

⁴

https://ngvla.nrao.edu/page/performance

All Tables

Table 1

Stellar parameters of investigated targets (Group I from Kirchschlager et al. 2017).

In the text

Table 2

Measurements and inferred flux densities in the NIR and MIR wavelength range of investigated targets.

In the text

Table A.1

Photometric values at specified observing wavelengths from the literature.

In the text

Table B.1

Full set of constraints on hot exozodiacal dust parameters, as shown in Fig. 2.

In the text

All Figures

Fig. 1

Flux density F^v originating from hot dust for the system HD 172167 (Vega). The black crosses denote the values inferred from the observations (see Table 2). The orange line shows the radiation of a carbonaceous dust ring reproducing the observed flux densities with an inner disk radius of R_in = 0.18 au, a population of grains with radius a_S = 0.2 µm and a dust mass of M_S ≈ 6.2 × 10⁻¹⁰ M_⊕, and a population of larger grains with radius a_L = 10 µm and a dust mass of M_L ≈ 8.9 × 10⁻¹⁰ M_⊕; the dashed lines in blue and red denote the respective contributions of the two grain populations. For comparison, the solid green line depicts the radiation of a dust ring at the same location comprised of grains made of astronomical silicate with a grain radius of a = 0.2 µm; the dust mass is scaled such that the flux density matches the value inferred from observations at λ = 2.13 µm. This dust ring does not reproduce the observations due to the high predicted flux density in the MIR wavelength range.

In the text

Fig. 2

Constraints on HEZD parameters of inner disk radius R_in, total dust mass M, and grain radius of the populations of larger and smaller grains, a_L and a_S. Three approaches were used to deal with observational uncertainties: no uncertainties ( $F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ) in blue; plus NIR, minus MIR uncertainty ( $F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in gold; and minus NIR, plus MIR uncertainty ( $F_{NIR}^{v} + Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v + {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in red. No markers are displayed when the respective quantity could not be constrained because the MIR excess leak was non-positive due to instrumental noise (see Sect. 3.1), no viable dust distribution was found in the investigated parameter space that is able to reproduce the observations (see Sect. 3.4), or the boundary of the chosen simulated parameter space (see Sect. 2.5) was reached (for R_in, a_L, or a_S). In addition, the first panel shows the location of the habitable zones (as defined in Sect. 2.5 of Kirchschlager et al. 2017) and the inner and outer working angles of the KIN at the respective system distances that represent the borders of the parameter space of disk radii used in the simulations. The second panel shows the total dust mass M with possible grain radii shown in the third and fourth panel. When no further restrictions were possible, the boundaries of the parameter space apply (i.e., is grain radii from 1 nm to 1 mm).

In the text

Fig. 3

Parameter combinations of inner disk radius R_in and the radii of the smaller and larger grains a_S, a_L for the system HD 172167 (see the Fig. B.1 for all other investigated targets). The blue sections enclose all parameter combinations able to reproduce the flux densities inferred from observations in the NIR and MIR wavelength ranges. The red sections indicate parameter combinations that cannot reproduce the observations. The upper boundary of possible values of R_in is given by the distance, where the radiation originating from the grain population of smaller grains no longer shows a NIR-to-MIR flux density ratio (Eq. (4)) higher than the observed value (Eq. (3)). The lower boundary is given by the physical scale corresponding to the IWA of the KIN, which is depicted by the solid black line. The dashed black line depicts the sublimation radii for different grain sizes. The intersecting set of parameter values for which, on the one hand, the dust configurations can reproduce the observations and, on the other hand, the dust grains of the respective grain sizes do not sublimate is indicated by the dashed area. Right: parameter space of R_in and a_L for all possible values of a_S. Left: parameter space of R_in and a_S with the value of a_L fixed to a_L ∈ {10 µm, 100 µm, 1000 µm}; valid parameter combinations of R_in and a_S are the same for these three values.

In the text

Fig. 4

Constraints for dust distributions with grain radius of the population of larger grains of a_L = 10 µm (gold), a_L = 100 µm (orange), and a_L = 1000 µm (dark red) on the HEZD parameters number ratio of larger to smaller grains N_L/N_S, total dust mass M, and relative contribution of the population of larger grains to the total dust mass M_L/M. The horizontal dashed red line denotes the case when the mass of the population of larger grains would make up half of the total dust mass (i.e., M_L/M = 0.5); for higher values of M_L/M the large grains dominate the mass budget. Constraints are computed without taking observational uncertainties into account, except for the systems HD 10700, HD 187642, and HD 203280 for which no other constraints could be derived (see Sects. 3.1 and 3.4).

In the text

Fig. 5

Constraints on the ratio of flux density originating from the population of larger grains with the grain radius a_L = 10 µm (gold), a_L = 100 µm (orange), and a_L = 1000 µm (dark red) to that originating from the population of smaller grains with any possible grain radius a_S for the four observing wavelengths 2.13 µm, 4.1 µm, 11.1 µm, and 870 µm. The horizontal dashed red lines denote equal contribution of the two grain populations to the total flux density (i.e., $F_{L}^{v} / F_{S}^{v} = 1$ ${{F_{\rm{L}}^v} \mathord{\left/ {\vphantom {{F_{\rm{L}}^v} {F_{\rm{S}}^v}}} \right. \kern-\nulldelimiterspace} {F_{\rm{S}}^v}} = 1$ ). Constraints are computed without taking observational uncertainties into account, except for the systems HD 10700, HD 187642, and HD 203280 for which no other constraints could be derived (see Sects. 3.1 and 3.4).

In the text

Fig. 6

Maximum flux density of all valid dust distributions at observing wavelengths corresponding to ALMA bands 10 to 3 and the ngVLA at an observing frequency of 93 GHz (λ ≈ 3220 µm). Three approaches were used to deal with the observational uncertainties: no uncertainties ( $F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v$ ) in blue; plus NIR, minus MIR uncertainty ( $F_{NIR}^{v} - Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v - {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} - Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v - {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in gold; and minus NIR, plus MIR uncertainty ( $F_{NIR}^{v} - Δ F_{NIR}^{v}$ $F_{{\rm{NIR}}}^v - {\rm{\Delta }}F_{{\rm{NIR}}}^v$ , $F_{MIR}^{v} + Δ F_{MIR}^{v}$ $F_{{\rm{MIR}}}^v + {\rm{\Delta }}F_{{\rm{MIR}}}^v$ ) in red. Dashed horizontal lines indicate instrument sensitivity as three times the RMS for exposure times of t_exp = 1 h (green) and 8 h (red).

In the text

	Fig. B.1 Same as Fig. 3, but for all other investigated targets.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Absil, O., di Folco, E., Mérand, A., et al. 2006, A & A, 452, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[2] Absil, O., di Folco, E., Mérand, A., et al. 2008, A & A, 487, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[3] Absil, O., Mennesson, B., Le Bouquin, J.-B., et al. 2009, ApJ, 704, 150 [NASA ADS] [CrossRef] [Google Scholar]

[4] Absil, O., Defrère, D., Coudé du Foresto, V., et al. 2013, A & A, 555, A104 [Google Scholar]

[5] Acke, B., Min, M., Dominik, C., et al. 2012, A & A, 540, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[6] A’Hearn, M. F., Belton, M. J. S., Delamere, A., & Blume, W. H. 2005a, Space Sci. Rev., 117, 1 [CrossRef] [Google Scholar]

[7] A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2005b, Science, 310, 258 [Google Scholar]

[8] Ahlers, J. P., Fromont, E. F., Kopparappu, R., Cauley, P. W., & Haqq-Misra, J. 2022, ApJ, 928, 35 [NASA ADS] [CrossRef] [Google Scholar]

[9] Akeson, R. L., Ciardi, D. R., Millan-Gabet, R., et al. 2009, ApJ, 691, 1896 [NASA ADS] [CrossRef] [Google Scholar]

[10] Arnold, J. A., Weinberger, A. J., Videen, G., & Zubko, E. S. 2019, AJ, 157, 157 [NASA ADS] [CrossRef] [Google Scholar]

[11] Astropy Collaboration (Robitaille, T. P., et al.) 2013, A & A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[12] Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]

[13] Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006a, ApJ, 651, 617 [NASA ADS] [CrossRef] [Google Scholar]

[14] Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006b, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]

[15] Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]

[16] Bailey, J., Bott, K., Cotton, D. V., et al. 2021, MNRAS, 502, 2331 [NASA ADS] [CrossRef] [Google Scholar]

[17] Baines, E. K., McAlister, H. A., ten Brummelaar, T. A., et al. 2009, ApJ, 701, 154 [NASA ADS] [CrossRef] [Google Scholar]

[18] Belton, M. J. S. 1966, Science, 151, 35 [Google Scholar]

[19] Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2008, ApJ, 673, L83 [NASA ADS] [CrossRef] [Google Scholar]

[20] Berdyugina, S. V., Berdyugin, A. V., Fluri, D. M., & Piirola, V. 2011, ApJ, 728, L6 [NASA ADS] [CrossRef] [Google Scholar]

[21] Blum, J., & Münch, M. 1993, Icarus, 106, 151 [Google Scholar]

[22] Blum, J., Gundlach, B., Krause, M., et al. 2017, MNRAS, 469, S755 [Google Scholar]

[23] Bonsor, A., & Wyatt, M. C. 2012, MNRAS, 420, 2990 [Google Scholar]

[24] Bonsor, A., Augereau, J. C., & Thébault, P. 2012, A & A, 548, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[25] Bonsor, A., Raymond, S. N., Augereau, J.-C., & Ormel, C. W. 2014, MNRAS, 441, 2380 [Google Scholar]

[26] Bott, K., Bailey, J., Kedziora-Chudczer, L., et al. 2016, MNRAS, 459, L109 [NASA ADS] [CrossRef] [Google Scholar]

[27] Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [Google Scholar]

[28] Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [Google Scholar]

[29] Brunngräber, R., Wolf, S., Kirchschlager, F., & Ertel, S. 2017, MNRAS, 464, 4383 [CrossRef] [Google Scholar]

[30] Buenzli, E., & Schmid, H. M. 2009, A & A, 504, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[31] Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [Google Scholar]

[32] Churcher, L. J., Wyatt, M. C., Duchêne, G., et al. 2011, MNRAS, 417, 1715 [NASA ADS] [CrossRef] [Google Scholar]

[33] Colavita, M. M., Wizinowich, P. L., Akeson, R. L., et al. 2013, PASP, 125, 1226 [Google Scholar]

[34] Coudé du Foresto, V., Ridgway, S., & Mariotti, J. M. 1997, A & AS, 121, 379 [Google Scholar]

[35] Coudé du Foresto, V., Perrin, G., Ruilier, C., et al. 1998, SPIE Conf. Ser., 3350, 856 [Google Scholar]

[36] Coudé du Foresto, V., Borde, P. J., Merand, A., et al. 2003, SPIE Conf. Ser., 4838, 280 [Google Scholar]

[37] Czechowski, A., & Mann, I. 2010, ApJ, 714, 89 [Google Scholar]

[38] Defrère, D., Absil, O., Augereau, J. C., et al. 2011, A & A, 534, A5 [CrossRef] [EDP Sciences] [Google Scholar]

[39] Defrère, D., Absil, O., Berger, J. P., et al. 2018a, Exp. Astron., 46, 475 [CrossRef] [Google Scholar]

[40] Defrère, D., Ireland, M., Absil, O., et al. 2018b, SPIE Conf. Ser., 10701, 107010U [Google Scholar]

[41] Defrère, D., Bigioli, A., Dandumont, C., et al. 2022, SPIE Conf. Ser., 12183, 121830H [Google Scholar]

[42] de Kok, R. J., Stam, D. M., & Karalidi, T. 2011, ApJ, 741, 59 [Google Scholar]

[43] Di Folco, E., Thévenin, F., Kervella, P., et al. 2004, A & A, 426, 601 [CrossRef] [EDP Sciences] [Google Scholar]

[44] Di Folco, E., Absil, O., Augereau, J. C., et al. 2007, A & A, 475, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[45] Draine, B. T. 2003, ApJ, 598, 1026 [Google Scholar]

[46] Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [Google Scholar]

[47] Ertel, S., Absil, O., Defrère, D., et al. 2014, A & A, 570, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[48] Ertel, S., Defrère, D., Hinz, P., et al. 2018a, AJ, 155, 194 [Google Scholar]

[49] Ertel, S., Kennedy, G. M., Defrère, D., et al. 2018b, SPIE Conf. Ser., 10698, 106981V [Google Scholar]

[50] Ertel, S., Defrère, D., Hinz, P., et al. 2020a, AJ, 159, 177 [Google Scholar]

[51] Ertel, S., Hinz, P. M., Stone, J. M., et al. 2020b, SPIE Conf. Ser., 11446, 1144607 [Google Scholar]

[52] Faramaz, V., Ertel, S., Booth, M., Cuadra, J., & Simmonds, C. 2017, MNRAS, 465, 2352 [NASA ADS] [CrossRef] [Google Scholar]

[53] Fluri, D. M., & Berdyugina, S. V. 2010, A & A, 512, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[54] Gaia Collaboration (Brown, A. G. A., et al.) 2021, A & A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[55] Gáspár, A., Rieke, G. H., & Balog, Z. 2013, ApJ, 768, 25 [CrossRef] [Google Scholar]

[56] GRAVITY Collaboration (Abuter, R., et al.) 2017, A & A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[57] Gray, R. O., & Garrison, R. F. 1989, ApJS, 70, 623 [NASA ADS] [CrossRef] [Google Scholar]

[58] Gray, R. O., Corbally, C. J., Garrison, R. F., McFadden, M. T., & Robinson, P. E. 2003, AJ, 126, 2048 [Google Scholar]

[59] Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [Google Scholar]

[60] Greaves, J. S., Wyatt, M. C., Holland, W. S., & Dent, W. R. F. 2004, MNRAS, 351, L54 [Google Scholar]

[61] Gulliver, A. F., Hill, G., & Adelman, S. J. 1994, ApJ, 429, L81 [NASA ADS] [CrossRef] [Google Scholar]

[62] Habing, H. J., Dominik, C., Jourdain de Muizon, M., et al. 2001, A & A, 365, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[63] Hanner, M. S. 1984, Adv. Space Res., 4, 189 [NASA ADS] [CrossRef] [Google Scholar]

[64] Harker, D. E., Wooden, D. H., Woodward, C. E., & Lisse, C. M. 2002, ApJ, 580, 579 [CrossRef] [Google Scholar]

[65] Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]

[66] Hindsley, R. B., & Harrington, R. S. 1994, AJ, 107, 280 [NASA ADS] [CrossRef] [Google Scholar]

[67] Hinz, P. M., Defrère, D., Skemer, A., et al. 2016, SPIE Conf. Ser., 9907, 990704 [Google Scholar]

[68] Holland, W. S., Matthews, B. C., Kennedy, G. M., et al. 2017, MNRAS, 470, 3606 [NASA ADS] [CrossRef] [Google Scholar]

[69] Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]

[70] Jäger, C., Mutschke, H., & Henning, T. 1998, A & A, 332, 291 [Google Scholar]

[71] Karalidi, T., & Stam, D. M. 2012, A & A, 546, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[72] Karalidi, T., Stam, D. M., & Hovenier, J. W. 2011, A & A, 530, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[73] Karalidi, T., Stam, D. M., & Hovenier, J. W. 2012, A & A, 548, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[74] Karalidi, T., Stam, D. M., & Guirado, D. 2013, A & A, 555, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[75] Kattawar, G. W., & Adams, C. N. 1971, ApJ, 167, 183 [NASA ADS] [CrossRef] [Google Scholar]

[76] Keenan, P. C., & McNeil, R. C. 1989, ApJS, 71, 245 [Google Scholar]

[77] Kervella, P., Coudé du Foresto, V., Glindemann, A., & Hofmann, R. 2000, SPIE Conf. Ser., 4006, 31 [NASA ADS] [Google Scholar]

[78] Kervella, P., Gitton, P. B., Segransan, D., et al. 2003, SPIE Conf. Ser., 4838, 858 [NASA ADS] [Google Scholar]

[79] Kim, M., Wolf, S., Löhne, T., Kirchschlager, F., & Krivov, A. V. 2018, A & A, 618, A38 [Google Scholar]

[80] Kimura, H., Kunitomo, M., Suzuki, T. K., et al. 2020, Planet. Space Sci., 183, 104581 [NASA ADS] [CrossRef] [Google Scholar]

[81] Kirchschlager, F., & Wolf, S. 2013, A & A, 552, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[82] Kirchschlager, F., Wolf, S., Krivov, A. V., Mutschke, H., & Brunngräber, R. 2017, MNRAS, 467, 1614 [NASA ADS] [Google Scholar]

[83] Kirchschlager, F., Wolf, S., Brunngräber, R., et al. 2018, MNRAS, 473, 2633 [NASA ADS] [CrossRef] [Google Scholar]

[84] Kirchschlager, F., Bertrang, G. H. M., & Flock, M. 2019, MNRAS, 488, 1211 [NASA ADS] [CrossRef] [Google Scholar]

[85] Kirchschlager, F., Ertel, S., Wolf, S., Matter, A., & Krivov, A. V. 2020, MNRAS, 499, L47 [NASA ADS] [CrossRef] [Google Scholar]

[86] Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, Jupyter Notebooks – A Publishing Format for Reproducible Computational Workflows, eds. F. Loizides, & B. Schmidt (Netherlands: IOS Press), 87 [Google Scholar]

[87] Kobayashi, H., Watanabe, S.-I., Kimura, H., & Yamamoto, T. 2008, Icarus, 195, 871 [NASA ADS] [CrossRef] [Google Scholar]

[88] Kobayashi, H., Watanabe, S.-I., Kimura, H., & Yamamoto, T. 2009, Icarus, 201, 395 [NASA ADS] [CrossRef] [Google Scholar]

[89] Kobayashi, H., Kimura, H., Yamamoto, S., Watanabe, S. I., & Yamamoto, T. 2010, Earth Planets Space, 62, 57 [NASA ADS] [CrossRef] [Google Scholar]

[90] Kobayashi, H., Kimura, H., Watanabe, S.I., Yamamoto, T., & Müller, S. 2011, Earth Planets Space, 63, 1067 [NASA ADS] [CrossRef] [Google Scholar]

[91] Kobayashi, H., Kimura, H., & Yamamoto, S. 2013, A & A, 550, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[92] Kral, Q., Krivov, A. V., Defrère, D., et al. 2017, Astron. Rev., 13, 69 [NASA ADS] [Google Scholar]

[93] Krivov, A., Kimura, H., & Mann, I. 1998, Icarus, 134, 311 [Google Scholar]

[94] Kurz, R., Guilloteau, S., & Shaver, P. 2002, The Messenger, 107, 7 [NASA ADS] [Google Scholar]

[95] Lamy, P. L. 1974, A & A, 35, 197 [NASA ADS] [Google Scholar]

[96] Laugier, R., Defrère, D., Woillez, J., et al. 2023, A & A, 671, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[97] Laureijs, R. J., Jourdain de Muizon, M., Leech, K., et al. 2002, A & A, 387, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[98] Lawler, S. M., Di Francesco, J., Kennedy, G. M., et al. 2014, MNRAS, 444, 2665 [Google Scholar]

[99] Lebreton, J., van Lieshout, R., Augereau, J. C., et al. 2013, A & A, 555, A146 [Google Scholar]

[100] Lietzow, M., & Wolf, S. 2022, A & A, 663, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[101] Lietzow, M., & Wolf, S. 2023, A & A, 671, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[102] Lietzow, M., Wolf, S., & Brunngräber, R. 2021, A & A, 645, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[103] Ligi, R., Creevey, O., Mourard, D., et al. 2016, A & A, 586, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[104] Lopez, B., Lagarde, S., Jaffe, W., et al. 2014, The Messenger, 157, 5 [NASA ADS] [Google Scholar]

[105] Lopez, B., Lagarde, S., Petrov, R. G., et al. 2022, A & A, 659, A192 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[106] MacGregor, M. A., Lawler, S. M., Wilner, D. J., et al. 2016, ApJ, 828, 113 [Google Scholar]

[107] Mamajek, E. E. 2012, ApJ, 754, L20 [Google Scholar]

[108] Marboeuf, U., Bonsor, A., & Augereau, J. C. 2016, Planet. Space Sci., 133, 47 [CrossRef] [Google Scholar]

[109] Martinod, M.-A., Defrère, D., Ireland, M. J., et al. 2022, SPIE Conf. Ser., 12183, 1218310 [NASA ADS] [Google Scholar]

[110] Martinod, M.-A., Defrère, D., Ireland, M., et al. 2023, J. Astron. Telescopes Instrum. Syst., 9, 025007 [NASA ADS] [Google Scholar]

[111] Matrà, L., Dent, W. R. F., Wilner, D. J., et al. 2020, ApJ, 898, 146 [CrossRef] [Google Scholar]

[112] Meech, K. J., Ageorges, N., A’Hearn, M. F., et al. 2005, Science, 310, 265 [NASA ADS] [CrossRef] [Google Scholar]

[113] Mennesson, B., Absil, O., Lebreton, J., et al. 2013, ApJ, 763, 119 [NASA ADS] [CrossRef] [Google Scholar]

[114] Mennesson, B., Millan-Gabet, R., Serabyn, E., et al. 2014, ApJ, 797, 119 [Google Scholar]

[115] Mérand, A., Coudé du Foresto, V., Kellerer, A., et al. 2006, SPIE Conf. Ser., 6268, 62681F [Google Scholar]

[116] Mie, G. 1908, Ann. Phys., 330, 377 [Google Scholar]

[117] Millan-Gabet, R., Serabyn, E., Mennesson, B., et al. 2011, ApJ, 734, 67 [NASA ADS] [CrossRef] [Google Scholar]

[118] Monnier, J. D., Che, X., Zhao, M., et al. 2012, ApJ, 761, L3 [NASA ADS] [CrossRef] [Google Scholar]

[119] Mukai, T., Yamamoto, T., Hasegawa, H., Fujiwara, A., & Koike, C. 1974, PASJ, 26, 445 [NASA ADS] [Google Scholar]

[120] Pearce, T. D., Krivov, A. V., & Booth, M. 2020, MNRAS, 498, 2798 [Google Scholar]

[121] Pearce, T. D., Kirchschlager, F., Rouillé, G., et al. 2022, MNRAS, 517, 1436 [NASA ADS] [CrossRef] [Google Scholar]

[122] Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]

[123] Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006a, ApJ, 636, 1087 [NASA ADS] [CrossRef] [Google Scholar]

[124] Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006b, Nature, 440, 896 [CrossRef] [Google Scholar]

[125] Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A & A, 518, A1 [Google Scholar]

[126] Poynting, J. H. 1904, Philos. Trans. Roy. Soc. London A, 202, 525 [NASA ADS] [CrossRef] [Google Scholar]

[127] Raymond, S. N., & Bonsor, A. 2014, MNRAS, 442, L18 [NASA ADS] [CrossRef] [Google Scholar]

[128] Richichi, A., & Percheron, I. 2005, A & A, 434, 1201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[129] Rieke, G. H., Gáspár, A., & Ballering, N. P. 2016, ApJ, 816, 50 [Google Scholar]

[130] Rigley, J. K., & Wyatt, M. C. 2020, MNRAS, 497, 1143 [NASA ADS] [CrossRef] [Google Scholar]

[131] Robertson, H. P. 1937, MNRAS, 97, 423 [NASA ADS] [Google Scholar]

[132] Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]

[133] Royer, F., Zorec, J., & Gómez, A. E. 2007, A & A, 463, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[134] Rusk, E. T. 1987, ApJ, 320, 315 [NASA ADS] [CrossRef] [Google Scholar]

[135] Schöller, M. & Glindemann, A. 2003, Earths: DARWIN/TPF and the Search for Extrasolar Terrestrial Planets, eds. M. Fridlund, T. Henning, & H. Lacoste, ESA Special Publication, 539, 109 [Google Scholar]

[136] Schöller, M., Gitton, P. B., Argomedo, J., et al. 2003, SPIE Conf. Ser., 4838, 870 [Google Scholar]

[137] Seager, S., Whitney, B. A., & Sasselov, D. D. 2000, ApJ, 540, 504 [NASA ADS] [CrossRef] [Google Scholar]

[138] Sekanina, Z., & Miller, F. D. 1973, Science, 179, 565 [NASA ADS] [CrossRef] [Google Scholar]

[139] Selina, R. J., Murphy, E. J., McKinnon, M., et al. 2018, SPIE Conf. Ser., 10700, 107001O [NASA ADS] [Google Scholar]

[140] Serabyn, E., Mennesson, B., Colavita, M. M., Koresko, C., & Kuchner, M. J. 2012, ApJ, 748, 55 [NASA ADS] [CrossRef] [Google Scholar]

[141] Sezestre, É., Augereau, J. C., & Thébault, P. 2019, A & A, 626, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[142] Sibthorpe, B., Vandenbussche, B., Greaves, J. S., et al. 2010, A & A, 518, A130 [Google Scholar]

[143] Sibthorpe, B., Kennedy, G. M., Wyatt, M. C., et al. 2018, MNRAS, 475, 3046 [Google Scholar]

[144] Spitzer Science Center (SSC) & Infrared Science Archive (IRSA) 2021, VizieR Online Data Catalog: II/368 [Google Scholar]

[145] Stam, D. M. 2008, A & A, 482, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[146] Stam, D. M., Hovenier, J. W., & Waters, L. B. F. M. 2004, A & A, 428, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[147] Stamm, J., Czechowski, A., Mann, I., Baumann, C., & Myrvang, M. 2019, A & A, 626, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[148] Stolker, T., Min, M., Stam, D. M., et al. 2017, A & A, 607, A42 [CrossRef] [EDP Sciences] [Google Scholar]

[149] Su, K. Y. L., Rieke, G. H., Stansberry, J. A., et al. 2006, ApJ, 653, 675 [Google Scholar]

[150] Su, K. Y. L., Rieke, G. H., Malhotra, R., et al. 2013, ApJ, 763, 118 [NASA ADS] [CrossRef] [Google Scholar]

[151] Su, K. Y. L., Rieke, G. H., Defrére, D., et al. 2016, ApJ, 818, 45 [NASA ADS] [CrossRef] [Google Scholar]

[152] ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [Google Scholar]

[153] Thureau, N. D., Greaves, J. S., Matthews, B. C., et al. 2014, MNRAS, 445, 2558 [NASA ADS] [CrossRef] [Google Scholar]

[154] Torres, G., Andersen, J., & Giménez, A. 2010, A & ARv, 18, 67 [Google Scholar]

[155] van Belle, G. T., & von Braun, K. 2009, ApJ, 694, 1085 [NASA ADS] [CrossRef] [Google Scholar]

[156] van Belle, G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., & Lada, E. A. 2001, ApJ, 559, 1155 [NASA ADS] [CrossRef] [Google Scholar]

[157] van Belle, G. T., Ciardi, D. R., ten Brummelaar, T., et al. 2006, ApJ, 637, 494 [NASA ADS] [CrossRef] [Google Scholar]

[158] van Leeuwen, F. 2007, A & A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[159] van Lieshout, R., Dominik, C., Kama, M., & Min, M. 2014a, A & A, 571, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[160] van Lieshout, R., Min, M., & Dominik, C. 2014b, A & A, 572, A76 [CrossRef] [EDP Sciences] [Google Scholar]

[161] White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [Google Scholar]

[162] White, J. A., Boley, A. C., Dent, W. R. F., Ford, E. B., & Corder, S. 2017, MNRAS, 466, 4201 [NASA ADS] [Google Scholar]

[163] Wiktorowicz, S. J., Nofi, L. A., Jontof-Hutter, D., et al. 2015, ApJ, 813, 48 [NASA ADS] [CrossRef] [Google Scholar]

[164] Williams, D. M., & Gaidos, E. 2008, Icarus, 195, 927 [NASA ADS] [CrossRef] [Google Scholar]

[165] Wolf, S., & Voshchinnikov, N. V. 2004, Comput. Phys. Commun., 162, 113 [Google Scholar]

[166] Wyatt, S. P., & Whipple, F. L. 1950, ApJ, 111, 134 [NASA ADS] [CrossRef] [Google Scholar]

[167] Wyatt, M. C., Smith, R., Greaves, J. S., et al. 2007, ApJ, 658, 569 [NASA ADS] [CrossRef] [Google Scholar]

[168] Zhao, M., Monnier, J. D., Pedretti, E., et al. 2009, ApJ, 701, 209 [NASA ADS] [CrossRef] [Google Scholar]

[169] Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2010, ApJ, 723, 1168 [NASA ADS] [CrossRef] [Google Scholar]

[170] Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2011a, ApJ, 739, 55 [NASA ADS] [CrossRef] [Google Scholar]

[171] Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2011b, ApJ, 739, 12 [NASA ADS] [CrossRef] [Google Scholar]

How much large dust could be present in hot exozodiacal dust systems?

1 Introduction

2 Methods

2.1 Stellar sample and observations

2.2 Inferred values of flux density

2.3 Model of hot exozodiacal dust

2.3.1 Motivation: underlying observational constraints

2.3.2 Model setup and simulated observations

2.4 Constraining parameters of hot exozodiacal dust

2.5 Parameter space

3 Results

3.1 Systems where not all analyses were possible due to MIR observations

3.2 Dust composition

3.3 No constraints from observations at wavelengths λ ≥ 24 µm

3.4 Constraints on hot exozodiacal dust parameters

3.4.1 Inner disk radius Rin

3.4.2 Dust mass M

3.4.3 Larger grain radius aL

3.4.4 Smaller grain radius aS

3.5 Impact of observational uncertainties on derived constraints

3.6 Dust distributions with larger grains of the radii aL = 10 µm, 100 µm, 1000 µm

4 Discussion

4.1 Employed model of hot exozodiacal dust

4.1.1 Thin dust ring seen face-on

4.1.2 Bimodal grain size distribution

4.1.3 Dust composition

4.1.4 Stellar model

4.1.5 Dust sublimation

4.2 Derived constraints on parameters of hot exozodiacal dust

4.3 Significance of the MIR observations and use in the modeling approach

4.4 Feasibility to observe large grains at submillimeter and millimeter wavelengths

4.5 Implications on HEZD theories

4.6 Implications on exoplanetary science

5 Summary

Acknowledgements

Appendix A Photometrie measurements at wavelengths λ ≥ 24 µm

Appendix B Constraints on hot exozodiacal dust parameters

References

All Tables

All Figures

3.4.1 Inner disk radius R_in

3.4.3 Larger grain radius a_L

3.4.4 Smaller grain radius a_S

3.6 Dust distributions with larger grains of the radii a_L = 10 µm, 100 µm, 1000 µm