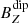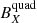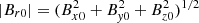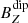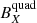| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 8 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245517 | |
| Published online | 15 September 2023 | |
HCS background magnetic field study HYTARO+
Dpt. of Physics and Mathematics, University of Alcalá, Alcalá de Henares, Spain
e-mail: david.arrazola@uah.es
Received:
21
November
2022
Accepted:
24
July
2023
Context. HYTARO+ is an analytical model developed to evaluate the influence of the solar magnetic dipole in the topology of the local structure of the heliospheric current sheet (HCS).
Aims. Statistical methods such as MVA, which are typically used in the study of the HCS come with two limitations. On one hand, they do not provide any information about the physical properties of the current sheet and, on the other, they do not offer the possibility of defining the local structure of the HCS from the physical conditions that prevail in the two sectors that separate the sheet. HYTARO model describes the interaction between the magnetic field that defines the structure of the current sheet and the plasma confined within it. HYTARO+ goes deeper into the study of the background magnetic field that is included in the HYTARO model with the aim of identifying its source.
Methods. Multipole expansion is used to provide a general approach to any physical phenomenon of some system, thereby allowing for a potential function representation. In our case, we considered the dipolar and quadrupolar Sun magnetic field contribution in the HCS.
Results. In the development of the HYTARO+ model, we estimated the components of the dipole and quadrupole magnetic fields at 1 AU. In the present study, we establish that the Z component of the dipole field and the X component of the quadrupole field are the more relevant terms of the background field present in the data that correspond to the discontinuities. A summary of the contribution of the multipolar components along the 23 solar cycle is incorporated.
Key words: Sun: heliosphere / Sun: magnetic fields / solar wind / Sun: activity
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The heliospheric current sheet (HCS) is observed as a sector boundary in the ecliptic plane and its orientation and structure have been studied intensively (Smith 2001). It divides the heliosphere into regions with opposite magnetic polarities. Analyses of its local structure at 1 AU enable studies of the HCS as a magnetic directional discontinuity supported by a current sheet (CS).
The potential field source surface (PFSS) is a model that extrapolates the photospheric magnetic field to an imaginary surface called the source surface, which marks the boundary beyond which the magnetic field points in the radial direction are due solely and exclusively to the solar wind. The PFSS model provides a reasonable estimate of the structure of the coronal field. Models of the coronal magnetic field have been developed from observations and data acquired from the interplanetary magnetic field (IMF) and, in turn, based on the boundary conditions of the solar photospheric magnetic field obtained from photospheric magnetograms. The modelling of the large-scale structure of the expansion of the solar wind is an area of development in plasma physics mainly driven by the uncertainty in setting the boundary conditions. The strong spatial and temporal variability of the solar magnetic field and the short-term effects of the solar activity (Hale et al. 1919; Parker 1958, 1969) further complicate the problem. Even with the limitations of the model, their usefulness in advancing the understanding of the expansion of the solar corona has been demonstrated since they were first proposed. In fact, the main success of the source surface lies in the location and characterization of the neutral line (NL), which is the contour that separates the magnetic fields leaving the photosphere from the incoming fields. The existence of the NL anticipates the existence of magnetic sectors in the interplanetary medium and marks the origin of the HCS in the solar corona.
Historically, description of the HCS was based on the premise that the magnetic field of the Sun could be described as a dipole. Therefore, if there are two hemispheres (or sectors) with the magnetic field in opposite directions, there must be a magnetic discontinuity between them that represents a neutral line in the Sun and a sheet in the solar wind (Wilcox & Ness 1965; Alfvén 1977; Schwadron & McComas 2005). The solar origin of the sector structure of the interplanetary magnetic field (IMF) was corroborated with the first data obtained via satellite (Ness & Wilcox 1964). Antonucci and Svalgaard defined the HCS as an extension of the solar magnetic equator, namely, the NL, from the equator of the solar magnetic field into the heliosphere (Antonucci & Svalgaard 1974). In addition, the relationship between the position of the NL on the Sun and the position of the HCS in the heliosphere was studied (Behannon et al. 1981).
In recent years, observational data have confirmed that the HCS is not the only current sheet on large spatial and temporal scales. Research by Kislov (e.g., Kislov et al. 2019) also points in this direction. In the development of the radial expansion of coronal models, the solar magnetic field has been approximated to a dipole. However, the complexity of the solar magnetic field over the solar cycle implies the need to include higher order components. Kislov develops a model based on a multipolar analysis to conclude that there is a possibility, depending on the solar cycle and the region of the Sun analyzed, more current sheets appear in the heliosphere, similarly to the HCS. The fact that the HCS is not the only large-scale, long-lived current sheet in the solar wind has been confirmed by observations of long-lived, conical current sheets located within polar coronal holes. These cone-shaped structures were evaluated on the basis of in situ measurements (Khabarova et al. 2017). These conical neutral surfaces can be interpreted as extensions of local neutral lines, formed in the polar regions as a result of the superposition of the dipole and the quadrupole. On the other hand, consecutive magnetic field polarity inversions are observed and a unique HCS crossing cannot be clearly identified. These observations have been interpreted in terms of propagating waves in the HCS, local waviness or multiple parallel CS located at the sector boundary region (Arrazola et al. 2012). When studying the local structure of the HCS, it is usual to find wide HCS crossings that is related with a complex internal structure, including multiple HCS crossings that are consecutive on the order of minutes (Blanco et al. 2006). Other studies show that HCS could be perturbed or disrupted by transient structures in the solar wind such as shocks and CMEs (Liu et al. 2009).
Statistical methods, such as the minimum variance method (MVA) or the coplanarity variance method (CVA), do not provide any information on the physical properties of the analyzed CS, and cannot identify the local structure of the CS from the physical conditions prevailing in the two sectors separating the sheet. The MVA method is the classical approach used to determine the normal direction of a magnetic discontinuity. It assumes that the structure is flat and the possible time variations that may affect the discontinuity during a satellite crossing are negligible. For its part, CVA analyzes the degeneracy of the eigenvalue of the covariance matrix present in planar structures to find a normal vector consistent with the plane of coplanarity.
On the other hand, analytical models take into account the physical conditions of the structure to be analyzed, for instance, HYTARO. It includes a background field (Bx0, By0, Bz0) assuming the existence of additional fields to the one existing in the CS itself. In the improvements published to the HYTARO model (Arrazola et al. 2022), the background field was calculated from the mean values of the magnetic field components provided by the satellite data.
In this paper, based on experimental data, we identify one of the possible sources of this background field that has led us to define a new analytical model, that is, HYTARO+. The influence of the solar magnetic field in the interplanetary medium is postulated as the main candidate for this purpose. Firstly, the dipolar behavior of the IMF was confirmed by the Ulysses satellite (1990–2009), describing the first polar orbit around the Sun between 1994 and 1995, where it confirmed the results obtained by satellites orbiting close to the Earth on the polarity of the Sun’s surface (Forsyth et al. 1996). Secondly, interplanetary magnetic field lines originating from the Sun are swept away by the solar wind, creating two regions of opposite magnetic polarity at solar longitudes, separated by the HCS located near the plane of the solar equator (latitude 0°). Observations provided by Ulysses showed that the waviness of the HCS reached ±20° (Forsyth et al. 1996). Four magnetic sectors were identified in the equatorial plane that rotate around solar longitudes.
An examination of the geometry of the multipole analysis of the IMF has been analyzed and explained in term of tendencies of the IMF components (Obridko et al. 2004). It is feasible to express a complex source, namely, a solar magnetic field, as a sum of elementary parts. A multipole analysis method approaches the expansion by performing a binomial expansion and allows us to evaluate the decomposition of the complex source term by term. Thus, it can be written in terms of an infinite series of elementary sources.
In a multipolar expansion applied to the interplanetary medium, the relationship between consecutive terms can be expressed as a function of the speeds of rotation and propagation of the solar wind, R⊙ω/vSW, where R⊙ and ω are the radius and the angular speed solar, and vSW is the speed of the solar wind. This relation, assuming a value of vSW ∼ 450 km s−1, is of the order of ∼1/200. Since this ratio is small, the effects of higher-order moments of the solar magnetic field on the structure of the current sheet are also small. This is the reason why Kaburaki (Kaburaki & Yoshii 1979) worked only with the solar dipole moment. Now, there is an exception whereby the quadrupole moment can contribute significantly and it therefore becomes necessary to include it in the multipole expansion. This exception occurs when it is assumed that the dipole axis coincides with the axis of rotation, in this case, the dipole moment and the angular velocity of rotation are vectors parallel to each other (m ∥ ω).
The existence of a background field present in the HCS crossings, identified by the analytical studies carried out with HYTARO, has led us to further study the background field and to search for its physical meaning, which is defined by the components of the solar dipole and quadrupole magnetic field, namely, HYTARO+. In the approach taken to develop the HYTARO+ model, we have assumed that the solar dipole axis is coincident with the GSE Z axis, which leads us to include the quadrupole term.
The quadrupolar magnetic field has been closely linked to the study of the interplanetary medium since observations at 1 AU of four sectors of the IMF were associated with the existence of the quadrupolar magnetic field (Schulz 1973; Girish & Prabhakaran Nayar 1988), although Svalgaard showed that a wavy shape of the solar magnetic equator could produce the same observational effect (Svalgaard et al. 1974). This last approximation is better correlated with the observations (Korzhov 1978). Furthermore, the study of the quadrupole component has led to the conclusion that it could not be neglected, for example, during periods of high solar activity (Sanderson et al. 2003). Later studies concluded that higher order components, such as the octupole, could also appear throughout a solar cycle, which has complicated the study of the solar magnetic field and its extension to the heliosphere (DeRosa et al. 2012).
2. HYTARO+
HYTARO+ is an analytical model that identifies the interplanetary magnetic field as the origin of the background field inside any CS crossings. Its starting point is a similar approach as HYTARO model (Blanco et al. 2006): the HCS is locally a plane whose local system is defined with the y-component being the direction perpendicular to the own plane and the other two components are contained in the HCS plane. The HYTARO model (see Eq. (1)) was a pure tangential discontinuity model where the constant background (Bx0, By0, Bz0) is present.
HYTARO, in addition to obtaining the CS local orientation, determines the inversion point (y0), the semi-width of the CS (L), and the magnetic field amplitude (B0). The assumption that the magnetic field is described by Eq. (1) is supported by the statistical methods; the magnetic field varies along the maximum variance direction, while remaining almost constant along the other two directions (Blanco et al. 2006; Liou & Wu 2021).
Bx0, By0, and Bz0 are the magnetic field components just out of the HCS plane. Nevertheless, when a spacecraft crosses the HCS, its magnetometer detects a simple magnetic structure as described previous one Eq. (1) but rotated with respect the spacecraft trajectory. This assumption implies to apply two consecutive rotations (α, β).
On-board instruments on satellites take sequential measurements of the solar wind conditions at a specific point in space. It is accepted as a valid approximation that satellites are at rest with respect to the solar wind and the structures that move in the solar wind (the order of magnitude of the velocities of a satellite is 1 km s−1, while the solar wind has velocities of the order of 300 km s−1 or higher). From a kinematical point of view, the variation time of the HCS is longer than the time it takes to cross the satellite position. This allows to interpret the time measurements as a spatial sweep assuming that the transit velocity is the solar wind velocity. Thus, in order to evaluate an HCS crossing, we must take into consideration the crossing time (t) and the solar wind speed (vSW) at the crossing to be able to spatially evaluate the event. Then, we need to adapt the parametric expression of the magnetic field topology associated with a CS that we defined in spatial terms (Eq. (1)) to an expression that takes into account the time dependence of the data acquired by the satellites. For this purpose, we define a term associated with the velocity, taking into account that the satellite velocity is assumed to be negligible compared to the solar wind velocity. We then take the velocity components provided by the satellite data (GSE system) and transfer them to the local system. Having defined the normal direction along the y-axis, we take the velocity along that direction in the local system and arrive at the following expression:
The final expression is then:
Subsequent revisions updated the model and the last version determined the background field present at CS crossings from the mean value of the magnetic field data supplied by the instruments on board the satellites (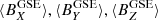 ), adding the orientations of the CS (Eq. (4)). This relationship (Eq. (4)) was obtained after determining the temporal mean value for a symmetric interval around t0, (Arrazola et al. 2022). The superscripts refers to the Geocentric Solar Ecliptic coordinate system (GSE).
), adding the orientations of the CS (Eq. (4)). This relationship (Eq. (4)) was obtained after determining the temporal mean value for a symmetric interval around t0, (Arrazola et al. 2022). The superscripts refers to the Geocentric Solar Ecliptic coordinate system (GSE).
The HYTARO+ model includes the background magnetic field present at a CS crossing by defining it on the basis of the dipole and quadrupole terms obtained from the multipole expansion. The multipolar expansion of the solar magnetic field by overlapping the magnetic dipole and the quadrupole terms (Fig. 1) allows to identify the contribution of each term in the topology of the magnetic structures analyzed. The positional dependence of the model is intrinsic to multipolar expansion. In our case, the study of the HCS at 1 AU identified in the vicinity of the ecliptic plane let us to anticipate a dominant Bz component for the dipolar term, while for the quadrupolar term, the dominant component should be Bx. The quadrupolar component of the solar magnetic field is responsible of the existence of polarity imbalances and their manifestation in the HCS, and the non uniformity in the distribution of magnetic activity (Mordvinov 2006).
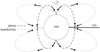 |
Fig. 1. Sketch of the dipole and quadrupole modes of the solar magnetic field. HCS region is identify as a black line. |
We assume an ideal dipole in which the magnetic field decreases with the inverse cube of the distance. Then the magnetic dipole moment (Eq. (5)) depends on the magnetic field at the solar surface, Bs, and the solar radius, R⊙:
This assumption obliges to fix a magnetic field at the solar surface. We take as reference the solar dynamo. The developed solar dynamo models point in the direction of the existence of an oscillating dipole (Parker 1993) with which the poloidal field is maintained throughout the solar sphere. In addition, the large-scale solar magnetic field near the poles is essentially dipolar, with a strength of about 10−3 T. However, publications assume a mean magnetic field at the solar surface of 10−4 T (Babcock 1961). Note that the structure of a large-scale dipole magnetic field is distorted by several effects. From a global point of view, by the rotation of the Sun and the solar wind, and from a local point of view, by sunspots and active bipolar regions in mid-latitudes where magnetic activity occurs on relatively short time scales (months, years...; Brants & Zwaan 1982). Besides, differential rotation implies that the speed of rotation depends on the latitude, in the vicinity of the solar equator, the period of rotation is approximately 24 days, while at the poles, the period is ∼30 days. All those values of these parameters (intensity on the solar surface and rotational speed) show a high level of uncertainty in their determination.
The configuration of the dipole field is specified by its vector potential A (Eq. (6)):
where the multipolar expansion of the magnetic vector potential A, obtains an expression that is valid for distant points from the source and the associated current density. From the vector potential calculated, we can obtain the corresponding magnetic field. To do it, the vector potential associated with a current loop and far from the source is calculated. The components of the dipole magnetic field are then:
where r is equal to 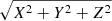 , and X, Y, Z are the spatial positions of the observation point, in this case the CS crossing with respect to the source, that is, the Sun, expressed in GSE coordinates (X = 1 AU–XGSE; Y = YGSE; Z = ZGSE).
, and X, Y, Z are the spatial positions of the observation point, in this case the CS crossing with respect to the source, that is, the Sun, expressed in GSE coordinates (X = 1 AU–XGSE; Y = YGSE; Z = ZGSE).
We have the frame (GSE coordinate system) and we identify the background field within that frame, but with respect to the source (the Sun). At this point, the model has a background field dipolar components in GSE coordinates (Eq. (7)) and a magnetic structure proposed to identify CS in a local system (LS), as per Eq. (1). It is necessary to relate both expressions in the same coordinate system. To that end, we applied two consecutive rotations to the background field components once we have defined the quadrupole term (Eq. (12)). At this point, it should be noted that the GSE coordinate system has its origin at the center of the Earth and that the X coordinate indicates the distance from the Sun to the satellite. Also, M is a parameter related with the magnetic dipole moment, m, evaluating the impact that the solar magnetic field has in spatial terms on the background field identified in CS crossings (Eq. (8)). It is necessary to take into account the rotation of the Sun, by that, the magnetic moment associated with a rotating sphere is calculated assuming a constant angular velocity, ω, of the sphere around the Z axis. The parameter M associated with the rotating sphere is then:
where R⊙ is the Sun radius, μ0 is the vacuum magnetic permeability, and C1 is an additional parameter related to the dipole components whose purpose is to absorb, on the one hand, the indetermination in the definition of the magnetic dipole moment and, secondly, the deviations presented by the ideal expressions of a dipolar field compared to the experimental data obtained via satellite.
The asymmetry of the solar magnetic field and its effects in the IMF entails to incorporate the quadrupolar term, it may be the dominant term in the periods of the solar cycle in which the Sun’s magnetic field reverses. Besides the quadrupole term is the main contribution to the non-dipole field and (unlike the centered dipole) describes the directional change of the solar magnetic field. The effects of the asymmetry of the solar magnetic field has been related to a shift of the global HCS (Smith et al. 2000). These studies led us to conclude that part of the background field identified in the CS crossings should have a contribution linked to the quadrupole term. In fact, an analysis that included only the contribution of the dipole component (Fig. 2a) showed that the displacement of the Bx and By components of the magnetic field of the CS cannot be evaluated with respect to the inversion point. The dipolar field in the ecliptic plane is residual and the contribution of the 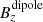 component does not identify the displacement of the background magnetic field in CS. The superposition of the dipole and quadrupole terms clearly improves the results previously obtained. In Fig. 2b, we show the fit including the quadrupole term. It is remarkable that the main contributors in terms of multipolar components are
component does not identify the displacement of the background magnetic field in CS. The superposition of the dipole and quadrupole terms clearly improves the results previously obtained. In Fig. 2b, we show the fit including the quadrupole term. It is remarkable that the main contributors in terms of multipolar components are 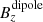 and
and 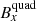 as the theoretical configuration (shown in Fig. 1) indicates. The contribution of the dipole term to the background magnetic field is very similar in both fits, without, (a), and with, (b) the quadrupole term.
as the theoretical configuration (shown in Fig. 1) indicates. The contribution of the dipole term to the background magnetic field is very similar in both fits, without, (a), and with, (b) the quadrupole term.
 |
Fig. 2. Dipole and quadrupole magnetic field components in GSE coordinates for July 31, 1995. Fit lines (in red) are included. Fitting excluding the contribution of the quadrupole component of the field (C2 = 0) (a) and including it (b). |
Thus, we could establish the field of a linear quadrupole. This can be obtained from a dipole by adding another dipole of opposite sign, infinitesimally displaced from the first and of such magnitude that the product of the dipole momentum and the displacement will be constant as the displacement approaches zero. To fix the coordinates with which to describe the linear magnetic quadrupole, we start with two coils, each of radius R, where the currents flow in opposite directions and are separated by a distance, d. This linear quadrupole has axial and azimuthal symmetry because all elements are colinear along the z axis
The quadrupolar components are calculated from two current loops. The vector potential associated to the quadrupolar term are then:
The magnetic quadrupole moment tensor, ⃡Qm, is a mathematical tool for describing the field. It is a tensor of the second rank, real, symmetric and with zero trace. Being real and symmetric, it can be diagonalized it and its three eigenvectors correspond to the main directions of the field. Its zero trace implies that only two of its components are independent. In our model, we have worked with a linear magnetic quadrupole defined along the Z axis. The components of the quadrupolar magnetic field is then:
where Q is related with the quadrupolar moment and again X, Y, and Z are the spatial positions of the observation point.
As with dipolar contribution, an additional parameter, C2, is included, in this case referring to the quadrupole component. The relation between the dipolar and quadrupolar moment let us to relate it to the M parameter (Eq. (11)). Then, the expression used in the model is:
The background field is defined for each of the components as shown below. Each of the components of the background field has a contribution of the dipolar and the quadrupolar magnetic field. Taking into account that the magnetic structure detected by spacecrafts when a CS crossing is rotated with respect to the plane magnetic structure defined by the model, it is necessary to apply two consecutive rotations (α, β angles) to obtain definitive background magnetic field components, (Eq. (12)). We note that the background magnetic field is calculated from the multipole components whose values are obtained from the fitting parameters C1 and C2 (Eqs. (8) and (11)). Therefore the background field components for HYTARO+ are summarized as follows:
The basic parameters of the model are seven. Three related with the local topology of the CS, independent of the background magnetic field, (reversal time (t0), amplitude (B0), half-width (L), two angular terms associated with rotation (α, β)), and two parameters (C1 and C2) related to the dipolar and quadrupolar terms of the solar magnetic field respectively.
We need to adapt the parametric expression of the topology of the magnetic field associated with a CS crossing that we define in spatial terms (Eq. (1)) to an expression that takes into account the time dependency shown by the satellite data (Eq. (13)). For this, we defined a term associated with the speed, taking into account that the speed of the satellite is assumed to be negligible compared to the speed of the solar wind (v).
3. Analysis
The period analyzed in this work has covered part of cycle 22 (from January 1995 to August 1996) and the whole cycle 23 (from August 1996 to December 2008). Cycle 23 was characterized by having an unusually low level activity in its minimum and by the fact that the polar fields were about 40% weaker than during the previous three minima (Schrijver & Liu 2008). If we consider that the polar coronal holes provide most of the open magnetic flux in the period of minimum solar activity, a weakening in the intensity of the interplanetary magnetic field was observed during this cycle (Smith & Balogh 2008). On the other hand, in terms of solar wind, the observations made by Ulysses showed that the solar wind at high latitudes was slower (∼3%) and less dense (∼17%) in the period of minimum activity than in the same period for the previous cycle (McComas et al. 2008).
Then, a set of 100 CS crossings were identified and analyzed. Data from the MFI instrument (Lepping et al. 1995) averaged over 3 s and from both the SWE instrument (Ogilvie et al. 1995) and on board WIND satellite were used. The criteria used to identify a CS crossing are the following: a minimum in the magnetic field intensity, a reversal polarity and that the electron flow in the solar wind reverses its sign (Blanco et al. 2006).
HYTARO+ is based on the premise concerning the local structure that defines the HYTARO model and is shown in Eq. (1), namely, a current sheet is a simple structure that is rotated with respect to a reference frame. The CS crossings have been analyzed with both models with similar results for the parameters describing the local topology of the current sheet.
HYTARO+ incorporates the physical meaning to the background magnetic field present in the crossing of the current sheet, allowing us to identify the effect of the dipolar and quadrupole field components on it. If there is only one dipole field, we can identify two effects: one that is stretched out by the solar wind that define the topology of the CS, along with a second one, which still has the classical form of a dipole even at 1 AU (background magnetic field).
In Fig. 3, we give an example of application of HYTARO+. This CS was detected by WIND instrumentation on 17 of April of 2006. The magnetic field components, BX and BY, showed a change in its directions with a minimum in its strength inside a slow solar wind region. During this event, plasma beta parameter (ratio of the plasma pressure to the magnetic pressure) shows an increment of its value. It is included the electron pitch angle distribution where the reversal is shown.
 |
Fig. 3. Wind instrumentation data at 1 AU from 2006, April 17. From top to bottom: 38.68 eV electron pitch angle distribution, plasma β, magnetic field intensity, and GSE magnetic field coordinates. |
Magnetic field component in GSE components and fit lines (continuous lines) obtained after fitting the magnetic field to theoretic magnetic topology for the local structure of the CS crossing using HYTARO+ is shown in Fig. 4, including the dipole and quadrupole components calculated. The fit parameters are included on Table 1.
 |
Fig. 4. WIND spacecraft observation of a CS crossing on April 17, 2006. The background magnetic field is decomposed in the dipolar and quadrupolar components in GSE coordinates and the results of them are presented in this figure. In figure, dots represent the magnetic field components measured by MFI/WIND, and the solid lines represent the fit curve. |
Figure 5 shows the histograms generated for the dipolar and quadrupolar components after analysing the 100 crossings. The magnetic field components (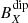 ,
, 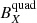 in green,
in green, 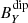 ,
, 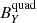 in blue, and
in blue, and 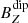 ,
, 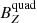 in yellow) are shown. This extensive analysis of the contribution by components of the dipole and quadrupole fields shows the
in yellow) are shown. This extensive analysis of the contribution by components of the dipole and quadrupole fields shows the 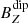 component is the most relevant component in dipole term with a mean value of around 1 nT, while the contribution of the
component is the most relevant component in dipole term with a mean value of around 1 nT, while the contribution of the 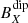 and
and 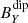 components, contained in the ecliptic plane, are residuals (10−4 nT and 10−7 nT respectively), as shown in Fig. 5a. The quadrupole field (Fig. 5b) shows a significant contribution of the
components, contained in the ecliptic plane, are residuals (10−4 nT and 10−7 nT respectively), as shown in Fig. 5a. The quadrupole field (Fig. 5b) shows a significant contribution of the 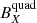 component (green columns on the right of the figure), whose average magnitude is around 1 nT, while the contribution of the other two components is negligible, in this case, with both the
component (green columns on the right of the figure), whose average magnitude is around 1 nT, while the contribution of the other two components is negligible, in this case, with both the 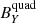 and
and 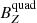 components with an average value of 10−4 nT. As expected, the multipole expansion shows the position dependence that the expressions for the dipole (Eq. (7)) and quadrupole (Eq. (10)) components indicate. However, the positional dependence of the multipole components does not seem to be present in the background magnetic field calculated from the model. After all, the background magnetic field (Bx0, By0, Bz0) is calculated taking into account the contribution of all the components of the dipole and the quadrupole terms (Eq. (12)).
components with an average value of 10−4 nT. As expected, the multipole expansion shows the position dependence that the expressions for the dipole (Eq. (7)) and quadrupole (Eq. (10)) components indicate. However, the positional dependence of the multipole components does not seem to be present in the background magnetic field calculated from the model. After all, the background magnetic field (Bx0, By0, Bz0) is calculated taking into account the contribution of all the components of the dipole and the quadrupole terms (Eq. (12)).
 |
Fig. 5. Histograms with the contribution of each of the components of the dipole (a) and the quadrupole (b) fields evaluating the magnitude B(T) of each of them. Histograms are generated after analyzing 100 CS crossings. The major contribution for the background field in the vicinity of a CS crossing are the dipolar Z (yellow) and quadrupolar X (green) components. |
Figure 6 shows the results obtained for 20 of 100 randomly selected CS crossings. The background magnetic field components are represented with the main multipolar contributors (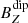 ,
, 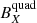 ). On the other hand, the quadrupole component does not show a direct correlation with any of the components of the background magnetic field. Although the background magnetic field is calculated using the multipolar components (as expected) the positional dependence of the multipole components does not seem to be reflected in the background field calculated from the model.
). On the other hand, the quadrupole component does not show a direct correlation with any of the components of the background magnetic field. Although the background magnetic field is calculated using the multipolar components (as expected) the positional dependence of the multipole components does not seem to be reflected in the background field calculated from the model.
 |
Fig. 6. Magnitude values of the background components (Bx0, By0, Bz0) are shown (squares). In addition, |
If we evaluate the contribution of each of the components of the background field (Fig. 7), Bz0 is the main term. For the other two components, the contribution of Bx0 magnitude could be slightly larger than By0 in most of the cases analyzed. The Bz0 component (Eq. (12)) does not depend on the 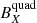 , major contributor of the quadrupole term (Fig. 5b), which leads us to conclude that its larger contribution to the background field is motivated by the
, major contributor of the quadrupole term (Fig. 5b), which leads us to conclude that its larger contribution to the background field is motivated by the 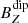 component.
component.
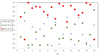 |
Fig. 7. Contribution of each of the components of the background magnetic field (Bx0, By0, Bz0). They are evaluated with respect to Br0 defined as |
It is worth highlighting in Fig. 7 two cases in which the Bz0 component becomes the component with the smallest weight, while the By0 component becomes the component with the largest contribution. In both cases, the magnitude of the quadrupole component is larger than the dipole one.
Hereafter, an analysis of the CS crossings in each of the regions of interest along the solar cycle has been achieved. Solar cycle 23 begins in August 1996 and ends in January 2008. The minimum between cycles 22 and 23 was identified between 1995 and the end of 1997. Then, the ascent phase begins until it reaches the maximum in the year 2001. The period of maximum activity is framed between the years 2000 and 2002. The descent phase culminates around 2005 when a new period of minimum solar activity begins until January 2008, starting cycle 24.
We developed the analysis by component throughout cycle 23 by grouping the CS crossings analyzed by year. Figure 8 shows the average values per year for the amplitude B0, and the multipolar components whose contribution is greater throughout the analyzed cycle: 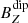 and
and 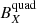 . In the figure the quadrupolar component reaches its maximum in the period of maximum solar activity of cycle 23, coinciding with the maximum intensity. This result could be in agreement with the idea of the major contribution of the quadrupole term of the solar magnetic field happens in the inversion polarity periods (Sanderson et al. 2003). In addition, the average values of the quadrupole and the intensity until the descent phase of the cycle show similar behavior.
. In the figure the quadrupolar component reaches its maximum in the period of maximum solar activity of cycle 23, coinciding with the maximum intensity. This result could be in agreement with the idea of the major contribution of the quadrupole term of the solar magnetic field happens in the inversion polarity periods (Sanderson et al. 2003). In addition, the average values of the quadrupole and the intensity until the descent phase of the cycle show similar behavior.
 |
Fig. 8. Dipole ( |
The dipolar component shows an oscillation during the first half of the cycle, reaching its maximum in the descent phase in 2003; however, during this cycle, the years 2000, 2001, and 2003 were years of high solar activity.
The analysis of the B0 amplitude versus the multipole components shows that the periods in which the contribution of the quadrupole component is more significant coincide with the B0 maximum, while the maximum contribution of the dipolar component coincides with the B0 minimum value that occurs in the downward phase.
HYTARO+ has helped to advance our development of a tool to evaluate the influence of the dipole and quadrupole fields throughout the solar cycle and identify their contribution by analyzing local CS crossings.
4. Conclusions
There have been comparative studies between solar and heliospheric magnetic fields by a number of authors, pointing out the global effects on the HCS. Multipole analyses have shown cyclic changes in the magnetic flux imbalance and it was corroborated that the solar magnetic field asymmetry is present in the interplanetary magnetic field. This fact was associated with the quadrupole term. In any case, all these studies pointed to a remarkable contribution of the dipole and quadrupole components in the interplanetary medium that we assume to be a background field with effects on the HCS. The existence of this global background field led us to try to identify the effects at the local level by focusing on the analysis of HCS crossings, thus giving rise to the HYTARO+ model.
The background field components were already included in the HYTARO model, however, the physical meaning of this was not clear. With HYTARO+, we can identify two effects of the solar dipole field: one that is stretched out by the solar wind that define the topology of the CS and a second one that still has the classical form of a dipole even at 1 AU (background magnetic field). With that, in addition to providing information regarding the local topology of the CS, HYTARO+ identifies the physical meaning of the background field present at CS crossings and allows the evaluation of the dipolar and quadrupole field component contribution by means of a multipolar analysis.
To substantiate the improvement of HYTARO+ compared to previous models and studies, the analysis of 100 CS crossings at 1 AU covering solar cycle 23 has been carried out.
In the development of the HYTARO+ model, we have had to calculate the components of the dipole and quadrupole magnetic fields at 1 AU, which has allowed us (among other things) to identify the Z magnitude of the dipole field and the X magnitude of the quadrupole field as the terms that contribute most to the background field present in the analyzed crossings, something that is expected once the topology of both contributions to the magnetic field is observed (Fig. 1). The HYTARO+ is a model, in addition to helping characterize the topology of a CS crossing, that is poised to advance our understanding of the solar magnetic field and its influence on the interplanetary medium. The fact that the results obtained by HYTARO+ on the 100 crossings analyzed at 1 AU in the plane of the ecliptic are in line with what is expected from the topology of the magnetic field lines of a dipole (Fig. 1) leads us to conclude that HYTARO+ is a promising model for analysing the interplanetary magnetic field in the vicinity of a CS crossing, as well as to further characterise the topology of crossings. These results motivate us to address further studies focusing on the latitudinal and longitudinal influence of the background field by including data from new satellites.
A preliminary analysis of the background magnetic field shows Bz0 as the main contributor of the magnetic field just in the borders of the CS. Furthermore, the contribution of the multipolar components throughout the solar cycle has been analyzed with HYTARO+, showing a certain dependence on the phase of the cycle, although the study should be extended to more solar cycles. Finally, HYTARO+ can help in understanding the behavior of the interplanetary magnetic field through the local analysis of the HCS, a structure that is present throughout the heliosphere.
Acknowledgments
The authors thank the teams of WIND/MFI and WIND/SWE instruments for the use of key parameters data. Part of this work was supported by PID2019-107806GB-I00 project funded by Ministerio de Economía y Competitividad and by the European Regional Development Fund, FEDER.
References
- Alfvén, H. 1977, Rev. Geophys. Space Phys., 15, 271 [CrossRef] [Google Scholar]
- Antonucci, E., & Svalgaard, L. 1974, Sol. Phys., 36, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Arrazola, D., Blanco, J. J., Rodríguez-Pacheco, J., & Hidalgo, M. A. 2012, Sol. Phys., 281, 263 [Google Scholar]
- Arrazola, D., Blanco, J., & Hidalgo, M. 2022, A&A, 660, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Behannon, K. W., Neubauer, F. M., & Barnstorf, H. 1981, J. Geophys. Res. Space Phys., 86, 3273 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, J., Rodriguez-Pacheco, J., Hidalgo, M., & Sequeiros, J. 2006, J. Atmos. Sol.-Terr. Phys., 68, 2173 [NASA ADS] [CrossRef] [Google Scholar]
- Brants, J., & Zwaan, C. 1982, Sol. Phys., 80, 251 [NASA ADS] [CrossRef] [Google Scholar]
- DeRosa, M. L., Brun, A. S., & Hoeksema, J. T. 2012, ApJ, 757, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Forsyth, R., Balogh, A., Horbury, T., et al. 1996, A&A, 316, 287 [NASA ADS] [Google Scholar]
- Girish, T. E., & Prabhakaran Nayar, S. R. 1988, Sol. Phys., 116, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, G. E., Ellerman, F., Nicholson, S. B., & Joy, A. H. 1919, ApJ, 49, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Kaburaki, O., & Yoshii, Y. 1979, Sol. Phys., 64, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Khabarova, O. V., Zank, G. P., Malandraki, O. E., et al. 2017, Sun Geosph., 12, 23 [NASA ADS] [Google Scholar]
- Kislov, R. A., Khabarova, O. V., & Malova, H. V. 2019, ApJ, 875, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Korzhov, N. P. 1978, AZh, 55, 96 [NASA ADS] [Google Scholar]
- Lepping, R., Acũna, M., Burlaga, L., et al. 1995, Space Sci. Rev., 71, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Liou, K., & Wu, C.-C. 2021, ApJ, 920, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Luhmann, J. G., Lin, R. P., et al. 2009, ApJ, 698, L51 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D., Ebert, R., Elliott, H., et al. 2008, Geophys. Res. Lett., 35, L18103 [NASA ADS] [CrossRef] [Google Scholar]
- Mordvinov, A. V. 2006, Astron. Rep., 50, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, N. F., & Wilcox, J. M. 1964, Phys. Rev. Lett., 13, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Obridko, V., Golyshev, S., & Levitin, A. 2004, Geomagnet. Aeron., 44, 410 [Google Scholar]
- Ogilvie, K., Chornay, D., Fritzenreiter, R., et al. 1995, Space Sci. Rev., 71, 55 [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Parker, E. N. 1969, Space Sci. Rev., 9, 325 [NASA ADS] [Google Scholar]
- Parker, E. 1993, ApJ, 407, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, T., Appourchaux, T., Hoeksema, J., & Harvey, K. 2003, J. Geophys. Res. Space Phys., 108, 7 [CrossRef] [Google Scholar]
- Schrijver, C. J., & Liu, Y. 2008, Sol. Phys., 252, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, M. 1973, Ap&SS, 24, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N., & McComas, D. 2005, Geophys. Res. Lett., 32 [CrossRef] [Google Scholar]
- Smith, E. J. 2001, J. Geophys. Res. Space Phys., 106, 15819 [Google Scholar]
- Smith, E. J., & Balogh, A. 2008, Geophys. Res. Lett., 35, L22103 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, E. J., Jokipii, J. R., Kóta, J., Lepping, R. P., & Szabo, A. 2000, ApJ, 533, 1084 [Google Scholar]
- Svalgaard, L., Wilcox, J. M., & Duvall, T. L. 1974, Sol. Phys., 37, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wilcox, J., & Ness, N. 1965, J. Geophys. Res., 70, 5793 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Sketch of the dipole and quadrupole modes of the solar magnetic field. HCS region is identify as a black line. |
| In the text | |
 |
Fig. 2. Dipole and quadrupole magnetic field components in GSE coordinates for July 31, 1995. Fit lines (in red) are included. Fitting excluding the contribution of the quadrupole component of the field (C2 = 0) (a) and including it (b). |
| In the text | |
 |
Fig. 3. Wind instrumentation data at 1 AU from 2006, April 17. From top to bottom: 38.68 eV electron pitch angle distribution, plasma β, magnetic field intensity, and GSE magnetic field coordinates. |
| In the text | |
 |
Fig. 4. WIND spacecraft observation of a CS crossing on April 17, 2006. The background magnetic field is decomposed in the dipolar and quadrupolar components in GSE coordinates and the results of them are presented in this figure. In figure, dots represent the magnetic field components measured by MFI/WIND, and the solid lines represent the fit curve. |
| In the text | |
 |
Fig. 5. Histograms with the contribution of each of the components of the dipole (a) and the quadrupole (b) fields evaluating the magnitude B(T) of each of them. Histograms are generated after analyzing 100 CS crossings. The major contribution for the background field in the vicinity of a CS crossing are the dipolar Z (yellow) and quadrupolar X (green) components. |
| In the text | |
 |
Fig. 6. Magnitude values of the background components (Bx0, By0, Bz0) are shown (squares). In addition, |
| In the text | |
 |
Fig. 7. Contribution of each of the components of the background magnetic field (Bx0, By0, Bz0). They are evaluated with respect to Br0 defined as |
| In the text | |
 |
Fig. 8. Dipole ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



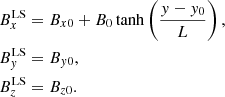
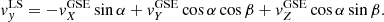
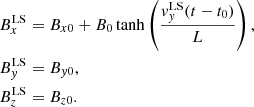
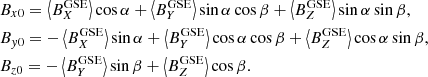
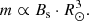
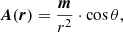
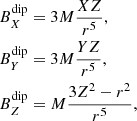
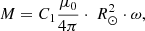
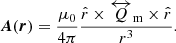
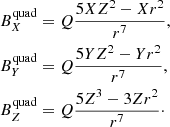
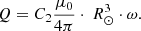
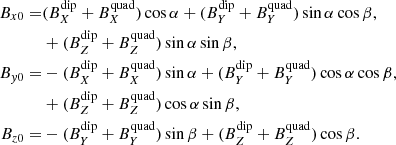
![$$ \begin{aligned} \begin{aligned}&B^\mathrm{GSE}_X = \left[ B_{x0}+ B_0 \tanh \left( \frac{v(t-t_0)}{L}\right) \right]\cos {\alpha } - B_{{ y}0}\sin {\alpha }, \\&B^\mathrm{GSE}_Y = \left\{ \left[ B_{x0} + B_0 \tanh \left( \frac{v(t-t_0)}{L}\right) \right]\sin {\alpha } + B_{{ y}0}\cos {\alpha } \right\} \cos {\beta } \\&\qquad \qquad - B_{z0}\sin {\beta }, \\&B^\mathrm{GSE}_Z = \left\{ \left[ B_{x0}+ B_0 \tanh \left( \frac{v(t-t_0)}{L}\right) \right]\sin {\alpha } + B_{{ y}0}\cos {\alpha } \right\} \sin {\beta } \\&\qquad \qquad + B_{z0}\cos {\beta }. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/09/aa45517-22/aa45517-22-eq18.gif)