| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 9 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245688 | |
| Published online | 23 August 2023 | |
Propagation of a dome-shaped, large-scale extreme-ultraviolet wave in the solar corona
1
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: GMann@aip.de
2
Institute of Physics, University of Graz, Universitätsplatz 5, 8010 Graz, Austria
3
Kanzelhöhe Observatory for Solar and Environmental Research, University of Graz, Kanzelhöhe 19, 9521 Treffen, Austria
Received:
14
December
2022
Accepted:
23
June
2023
Context. The first observation of a dome-shaped extreme-ultraviolet (EUV) wave was recorded by the EUVI instrument on board the STEREO-B spacecraft on January 17, 2010. This observation has allowed us to study the three-dimensional propagation of a large-scale EUV wave in the solar corona, which is considered to be a manifestation of a large-amplitude magnetohydrodynamic (MHD) wave.
Aims. These unique observations by EUVI offer the opportunity to compare the theory of large-amplitude MHD waves with observations.
Methods. Nonlinear MHD equations were employed for describing large-amplitude fast magnetosonic waves in terms of so-called simple waves.
Results. Measuring the velocity of the EUV wave across the solar surface allows us to determine the quiet Sun’s magnetic field to be ≈3.2 G. This magnetic field can be extrapolated to the corona by means of magnetic flux conservation. Then, the height dependence of the Alfvén velocity can be calculated, adopting an isothermal, gravitationally stratified density model with a temperature of 1.4 MK for the quiet corona. The Alfvén velocity has a local maximum of ≈680 km s−1 at a height of ≈1030 Mm above the photosphere. The observations show that the EUV wave initially steepens and subsequently decays during its further evolution along the solar surface. This behavior can be aptly explained in terms of simple MHD waves. Initially, the wave front steepens due to nonlinear effects. Since the EUV waves are circularly or spherically propagating waves in the corona, their amplitudes are decreasing during the evolution. Hence, the wave steepening vanishes at the final state of the evolution of the EUV wave, which is consistent with the observations. In reality, the nature of the considered EUV wave is a combination of that of a circular and a spherical wave in the corona.
Conclusions. The propagation of this dome-shaped EUV wave can be well described by the theory of large amplitude (simple) MHD waves.
Key words: Sun: corona / Sun: flares / Sun: coronal mass ejections (CMEs)
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Extreme Ultraviolet Imaging Telescope (EIT; Delaboudinière et al. 1995) aboard the ESA/NASA SOHO spacecraft has discovered a new wave phenomenon in the solar corona (Moses et al. 1997; Thompson et al. 1998), hereafter referred to as “EIT waves” (also as “large-scale EUV waves” or “large-scale coronal bright fronts”).
Large-scale EUV waves appear as a bright rim (sometimes nearly circular) propagating as a large-scale disturbance over substantial regions of the Sun. In extreme cases, they can even propagate over the full Sun, like the event associated with the strong X8.2 flare/CME on 10 September 2017 (Liu et al. 2018; Veronig et al. 2018). They are reminiscent of Moreton waves (Moreton & Ramsey 1960), which are observed in the solar chromosphere using filtergrams recorded in the Hα spectral line sensitive to a temperature of about 104 K. Moreton waves are often accompanied by solar type II radio bursts (Kai 1970; Warmuth et al. 2004b) as signatures of coronal shock waves (Wild et al. 1959). Because of this relationship, Moreton waves and the type II radio burst related shock waves are believed to be caused by the same origin, namely by a solar eruption (Uchida 1968; Vršnak et al. 2016). In contrast to Moreton waves, large-scale EUV waves are visible in the EUV spectral lines formed at coronal temperatures in the range of T ≈ (1 − 2)×106 K (e.g., Zhukov & Auchère 2004; Vanninathan et al. 2015). Furthermore, the velocities of Moreton waves (e.g., Warmuth et al. 2004a) are (on average) much higher than those of the EUV waves, which lie mostly in the range 200–500 km s−1 (Klassen et al. 2000; Thompson & Myers 2009; Warmuth & Mann 2011; Muhr et al. 2014), though in some cases also speeds of the order of 1000 km s−1 have been reported (Nitta et al. 2013; Liu et al. 2018; Veronig et al. 2018).
According to Mann et al. (1999a), a flare and/or coronal mass ejection (CME) excites a fast magnetosonic wave in the corona, which is observed as a EUV wave when it propagates along the surface of the Sun. If it enters into the corona, it steepens to a shock wave observed as type II radio bursts. This scenario explains the relationship between EUV waves and solar type II radio bursts as reported by Klassen et al. (2000). Adopting this consideration, a magnetic field strength of ≈3 G is deduced for the quiet Sun. The Alfvén-Mach number of the type II radio burst associated shocks is found to be well above 1.6 (Mann et al. 1999a).
Because of the low cadence of 12–15 min of the SOHO/EIT instrument, it has not been possible to properly study the evolution of EUV waves. This limitation was overcome by the Extreme Ultraviolet Imager (EUVI; Howard et al. 2008) on board the twin spacecraft of the Solar-Terrestrial Relations Observatory (STEREO; Kaiser et al. 2008). For studying large-scale coronal waves, the STEREO EUVI observations have the advantage of having a large field of view, high sensitivity, and higher cadence while carrying out simultaneous observations from two well-separated vantage points in space, which have enabled studies of the three-dimensional (3D) evolution of EUV waves and the wave-driver relationship, as well as detailed comparisons with MHD simulations of solar eruptions (e.g., Long et al. 2008; Veronig et al. 2008; Kienreich et al. 2009; Patsourakos & Vourlidas 2009, 2012; Cohen et al. 2009; Downs et al. 2011; Ma et al. 2011; Muhr et al. 2011, 2014; Delannée et al. 2014; Podladchikova et al. 2019). The simultaneous ultra high-cadence observations (12 s) in six different EUV filters by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) have brought about new advances in the study of large-scale EUV waves, by allowing for plasma and temperature diagnostics by differential emission measure (DEM) analyses, along with spectroscopic observations from Hinode/EIS and detailed observations and modeling of the interaction (reflection, transmission) of EUV waves through coronal holes and active regions with related seismology of the coronal field, as well as refined stack plot analysis that enable in-depth studies of the speed evolution of the wave and its relation to the driver, namely, the CME and its expanding flanks (e.g., Schrijver et al. 2011; Veronig et al. 2011; Harra et al. 2011; Downs et al. 2012; Cheng et al. 2012; Olmedo et al. 2012; Vanninathan et al. 2015; Liu et al. 2018; Hu et al. 2019; Hou et al. 2022).
The physical nature of EUV waves has been a subject of intense scientific debate and has been summarized from different viewpoints in a number of reviews (Vršnak & Cliver 2008; Wills-Davey & Attrill 2009; Gallagher & Long 2011; Zhukov 2011; Patsourakos & Vourlidas 2012; Warmuth 2015; Long et al. 2017). To search for evidence of potentially different classes of EUV waves, Warmuth & Mann (2011) analysed a sample of 176 EUV wave events with respect to their kinematics. Their study revealed three different classes of EUV waves (see Fig. 8 therein):
-
Their initial velocity is > 320 km s−1 and they show a pronounced deceleration during propagation.
-
They propagate with a nearly constant speed of 170−320 km s−1.
-
They have slow speeds (< 130 km s−1) and show a rather erratic motion.
The first class is interpreted as large-amplitude magnetohydrodynamic (MHD) waves or shocks. The propagation speed of these types of events is faster than the local fast magnetosonic speed. Due to the amplitude decrease during propagation, its local speed is decreasing. The dependence of the propagation speed of the wave on its amplitude is a typical nonlinear effect. The second class is considered to be linear waves traveling at the local fast magnetosonic speed. The third class is regarded as disturbances caused by magnetic reconfigurations (Warmuth & Mann 2011). Muhr et al. (2014) found the same basic characteristics of the EUV wave kinematics and speed relations for the first two classes. This suggests that the first and second class of EUV waves represent freely propagating waves in the corona (Warmuth & Mann 2011).
Veronig et al. (2010) reported the first observation of a full dome-shaped EUV wave, which occurred on January 17, 2010 over the time range of 3:52–4:36 UT (see Fig. 1). Further studies on this EUV wave include Grechnev et al. (2011), Zhao et al. (2011), Temmer et al. (2013). Interestingly, this EUV wave-dome event was also associated with one of the first wide-spread solar energetic particle events (SEPs) reported that covered over almost 360° in longitude in the heliosphere (Dresing et al. 2012). Further examples of EUV wave domes are presented in Kozarev et al. (2011) and Francile et al. (2016).
 |
Fig. 1. Direct (top) and 5-min running difference (bottom) image of the dome-shaped EIT wave at 3:56:02 UT on January 17, 2010 as recorded by the 195 Å filter of the EUVI instrument aboard STEREO-B. |
Such observations of the full EUV wave dome are important as they allow us to study the 3D evolution of such a wave in high-cadence EUV imaging, especially with respect to the evolution of its velocity, amplitude, and pulse width. These measurements of a dome-shaped EUV wave therefore provide us with the opportunity to compare the observations with the theory of nonlinear MHD waves. A summary of the properties of the dome-shaped EUV wave of January 17, 2010 is given in Sect. 2. Because of its kinematics, it belongs to the first and/or second class of EUV waves according to Warmuth & Mann (2011). Hence, it is considered to be a freely propagating fast mode MHD wave, and its propagation velocity is determined by the fast magnetosonic speed (Mann et al. 1999a). This characteristic speed depends on the magnetic field, the density, and the temperature of the ambient medium. Therefore, models of the magnetic field, the density, and the temperature of the corona are developed in Sect. 3, resulting in a model of the Alfvén speed distribution in the corona. Adopting these results, the spatio-temporal evolution of the dome-shaped EUV wave is studied (Sect. 4). It is well known that fast magnetosonic waves with large amplitudes can change their wave pulse profile due to nonlinear effects such as wave steepening. Thus, the evolution of such a wave pulse is theoretically studied and compared with the measurements in Sect. 5. The results of the paper are summarized in Sect. 6.
2. Observations
In this section, we provide a summary of the observations of the dome-shaped EUV wave that occurred on 2010 January 17 that are relevant for this study, based on the results from Veronig et al. (2010). The wave was best observed in the 195 Å filter of the STEREO-B/EUVI instrument, which has a peak temperature response at 1.5 MK (Wuelser et al. 2004). The center of origin of the wave is located at a meridional distance of 57° East from the STEREO-B view, and 36° behind the Eastern limb from observatories in the Sun-Earth line (Veronig et al. 2010).
Running difference images were created to determine the distance of the wave front from the center of the wave on the solar surface and, consequently, the kinematics of the wave front (see Fig. 2). The deduced wave velocity is vEUV, ∥ = 283 ± 27 km s−1, as measured along the solar surface. This horizontal propagation of the wave could be followed up to a distance of about 950 Mm from the center of the wave, and was found to be homogeneous, namely, displaying a constant velocity. The upward motion of the wave dome was followed up to a height of ≈1000 Mm above the photosphere by combining measurements from the EUVI instrument and the COR1 white-light coronagraph onboard STEREO-B. The velocity of the upward motion of the wave dome projected onto the plane-of-sky was found to be vEUV, ⊥ ≈ 650 km s−1, which is much faster than the EUV wave speed along the solar surface, vEUV, ∥ ≈ 280 km s−1 (see Fig. 2). The horizontal motion was measured at a height of approximately 10 Mm above the photosphere.
 |
Fig. 2. Kinematics of the vertical (red) and horizontal (black) motion of the EUV wave on 2010 January 17 (adapted from Fig. 4 in Veronig et al. 2010, © AAS, reproduction with permission). |
Figure 3 shows the spatio-temporal behaviour of the EUV wave in terms of its intensity profile with respect to its horizontal motion. In the early phase, namely, 03:56–04:01 UT, the amplitude is increasing. This can be interpreted, that the wave is externally driven, for instance, by an eruptive magnetic disturbance. After 04:01 UT, the EUV wave behaves as a freely propagating one with an amplitude decreasing during its propagation.
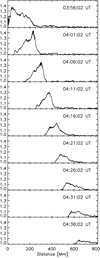 |
Fig. 3. STEREO-B/EUVI 195 Å intensity profiles of the EUV wave on 2010 January 17 with respect to its horizontal motion (adapted from Fig. 5 in Veronig et al. 2010, © AAS, reproduction with permission). |
3. Model of the Alfvén speed in the corona
The velocity of a fast magnetosonic wave is given by:
with θ as the angle between the propagation direction and the ambient magnetic field B (Priest 1982). Here, vA = B/(4πρ)1/2 and cs = (γp/ρ)1/2 denote the Alfvén- and sound speed, respectively, (B, magnitude of the magnetic field B; ρ, mass density; p, pressure; γ, ratio between specific heats). For θ = 0° and 90°, the expression (Eq. (1)) for the wave speed reduces to V = vA and 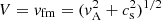 , respectively. Also, vfm is usually known as the fast magnetosonic speed.
, respectively. Also, vfm is usually known as the fast magnetosonic speed.
Since both B and ρ are varying in the corona with the distance r from the center of the Sun, the characteristic speeds, namely, vA, cs, and V, also depend on r. Hence, models of the radial behaviour of the density and the magnetic field are necessary, in order to derive a model of the radial dependence of the Alfvén speed.
An isothermal, gravitationally stratified atmosphere can be descibed by the stationary momentum equation of MHD
in spherical symmetry (γG as the gravitational constant and M⊙ as the mass of the Sun). The mass density is defined by 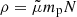 (mp as the proton mass), with
(mp as the proton mass), with 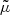 as the mean molecular weight and N as the full particle number density. The pressure, p, is related to N via the equation of state p = NkBT (kB, Boltzmann’s constant), with temperature, T (Priest 1982). Assuming that the plasma of the corona consists of electrons, protons, and doubly ionized Helium, N is related to the electron and proton number density by N = 1.92Ne = 2.27Np (Mann et al. 1999b). Here,
as the mean molecular weight and N as the full particle number density. The pressure, p, is related to N via the equation of state p = NkBT (kB, Boltzmann’s constant), with temperature, T (Priest 1982). Assuming that the plasma of the corona consists of electrons, protons, and doubly ionized Helium, N is related to the electron and proton number density by N = 1.92Ne = 2.27Np (Mann et al. 1999b). Here, 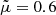 is taken as a typical value for the mean molecular weight in the corona (Priest 1982). The differential equation (Eq. (2)) can be integrated to:
is taken as a typical value for the mean molecular weight in the corona (Priest 1982). The differential equation (Eq. (2)) can be integrated to:
with NS = N(r = R⊙) as the full particle number density at the bottom of the corona, and
with 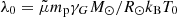 . Taking
. Taking 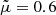 and T0 = 1 MK, it results in λ0 = 13.83. Hence, the barometric scale height hbhs is given by hbhs = R⊙/λ, as it is usually defined. For instance, we would get hbhs = 70 Mm for a temperature of 1.39 MK.
and T0 = 1 MK, it results in λ0 = 13.83. Hence, the barometric scale height hbhs is given by hbhs = R⊙/λ, as it is usually defined. For instance, we would get hbhs = 70 Mm for a temperature of 1.39 MK.
The white-light observations of the corona by Koutchmy (1994) showed that the radial behavior of the electron number density, Ne, can be fitted by an α-fold Newkirk (1961) model as follows:
with N0 = 4.2×104 cm−3. As presented in Fig. 1 in Koutchmy (1994), the electron number density in the solar corona can vary over a broad range of 107–1010 cm−3. However, its radial behaviour can be described by α = 1, 4, and 10 in an appropriate manner for quiet equatorial regions, dense loops and extremely dense loops, respectively.
Since EUV waves are propagating mostly outside active regions, namely, through the quiet Sun region, a one-fold Newkirk model (i.e., α = 1) is a good choice for describing the radial density behaviour in the quiet corona. Comparing Eq. (5) with Eq. (3), the Newkirk model corresponds to a barometric density model with a temperature of T = 1.39 MK in the quiet corona. A one-fold Newkirk model corresponds to an electron number density NS, e = 8.775×108 cm−3 and a full particle number density of NS = 1.687×109 cm−3 at the base of the corona. The temperature of T = 1.39 MK leads to a value of 179 km s−1 for the sound speed 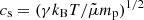 (with γ = 5/3) in the quiet corona.
(with γ = 5/3) in the quiet corona.
As mentioned above, EUV waves are travelling mainly outside active regions, where the magnetic field is substantially lower than in active regions. This quiet Sun’s magnetic field is nearly radially directed (see Fig. 16 in Wedemeyer-Böhm et al. 2009 and the discussion therein). According to the conservation of the magnetic flux, it can be extrapolated from the photosphere into the corona via (see also Mann et al. 2003 and Warmuth & Mann 2005):
By inserting Eqs. (3) and (6) into the definition of the Alfvén speed,
we get:
with 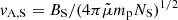 . The radial behavior of the Alfvén speed (see Fig. 4) shows a local maximum at rmax = (λ/4)⋅R⊙. We note that the location of this maximum only depends on the temperature and for increasing temperature shifts towards the Sun. Then, λ = 9.95 is obtained for a temperature of 1.39 MK. Hence, the maximum appears at rmax = 1727 Mm from Sun center or at a height of 1031 Mm above the photosphere (see Fig. 4).
. The radial behavior of the Alfvén speed (see Fig. 4) shows a local maximum at rmax = (λ/4)⋅R⊙. We note that the location of this maximum only depends on the temperature and for increasing temperature shifts towards the Sun. Then, λ = 9.95 is obtained for a temperature of 1.39 MK. Hence, the maximum appears at rmax = 1727 Mm from Sun center or at a height of 1031 Mm above the photosphere (see Fig. 4).
 |
Fig. 4. Height dependence of the local Alfvén speed in the quiet corona. |
4. Propagation of a fast magnetosonic wave in the corona
The dome-shaped EUV wave observed on January 17, 2010 was initially excited by an eruptive flare or CME event in the vicinity of an active region. Figure 3 shows that after 04:01:02 UT, the EUV wave is a freely propagating wave. At this time, its vertical position is at 576 Mm above the photosphere. Hence, this part of the EUV wave is considered as a fast magnetosonic wave travelling through the corona.
The horizontal motion of the EUV wave appears mainly in quiet Sun regions. At the bottom of the corona, the observed EUV wave velocity is VEUV, ∥ = 283 km s−1. The temperature in the corona is not isothermal, but the distribution of the differential emission measure of quiet Sun regions shows that the temperature is in the range 1.2−2.0 MK (Brosius et al. 1996). Large-scale EUV waves are best seen in the 195 Å filter of the STEREO-B/EUVI instrument, which has a peak temperature response at 1.5 MK (Wuelser et al. 2004). A coronal temperature of 1.39 MK was derived from the radial behavior of the electron number density (see Koutchmy 1994 and the discussion in Sect. 3). Hence, a temperature of 1.39 MK is justified to be assumed in the corona above quiet equatorial regions, leading to a sound speed of cs = 179 km s−1. The horizontal motion of EUV waves is observed near the bottom of the corona above quiet Sun regions. There, the magnetic field is directed nearly vertical (see Fig. 16 in Wedemeyer-Böhm et al. 2009 and the discussion therein).
Hence, the wave propagates nearly perpendicularly to the ambient magnetic field, namely, θ ≈ 90°. In this case, V is reduced to vfm (see Eq. (1)). Consequently, the EUV wave velocity can be identified with the fast magnetosonic speed, that is: 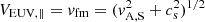 . Because of VEUV, ∥ = 283 km s−1 and cs = 179 km s−1, it leads to vA, S = 219 km s−1 as the Alfvén speed at the bottom of the corona. Adopting for NS = 1.687 × 109 cm−3 (see Sect. 3), one finds BS = 3.19 G for the quiet Sun magnetic field at the bottom of the corona. This is a typical value for this quantity (Schrijver & De Rosa 2003). The radial behaviour of the local Alfvén speed in the quiet corona is given completely by Eq. (8), with NS = 1.687 × 109 cm−3 and BS = 3.19 G. This is illustrated in Fig. 4. As can be seen, it has a maximum of 680 km s−1 at a height of 1031 Mm above the photosphere.
. Because of VEUV, ∥ = 283 km s−1 and cs = 179 km s−1, it leads to vA, S = 219 km s−1 as the Alfvén speed at the bottom of the corona. Adopting for NS = 1.687 × 109 cm−3 (see Sect. 3), one finds BS = 3.19 G for the quiet Sun magnetic field at the bottom of the corona. This is a typical value for this quantity (Schrijver & De Rosa 2003). The radial behaviour of the local Alfvén speed in the quiet corona is given completely by Eq. (8), with NS = 1.687 × 109 cm−3 and BS = 3.19 G. This is illustrated in Fig. 4. As can be seen, it has a maximum of 680 km s−1 at a height of 1031 Mm above the photosphere.
The employment of Eq. (2) requires a stationary atmosphere. This is justified for regions well below the critical radius rc according to Parker (1958) solar wind model. The critical radius rc is defined by 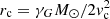 with the critical velocity
with the critical velocity 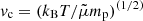 , which is the sound speed for an isothermal plasma (Priest 1982). According to this approach, the solar wind speed exceeds the speed vc at the critical radius rc. For a temperature of T = 1.39 MK, the critical radius rc is 4.94 R⊙. Since the location of the maximum of the local Alfvén speed (see Fig. 4) is well below the critical radius, Eqs. (2) and (8) are appropriate to describe the behaviour of the density and Alfvén speed in the solar corona, respectively.
, which is the sound speed for an isothermal plasma (Priest 1982). According to this approach, the solar wind speed exceeds the speed vc at the critical radius rc. For a temperature of T = 1.39 MK, the critical radius rc is 4.94 R⊙. Since the location of the maximum of the local Alfvén speed (see Fig. 4) is well below the critical radius, Eqs. (2) and (8) are appropriate to describe the behaviour of the density and Alfvén speed in the solar corona, respectively.
In the following, the vertical motion of the dome-shaped EUV wave is considered. It travels with the speed V given in Eq. (1). Then, the radial propagation of the EUV wave can be described by:
with hi = h(t = t0). Since the vertical motion happens above an active region, the magnetic field topology can vary between a parallel and a perpendicular one. Therefore, in Eq. (9) a mean value of vA and vfms is employed for the velocity V, namely, V = (vA + vfms)/2.
To compare the kinematic description (Eq. (9)) with the observations, hi = h(t = 0) = 576 Mm and t0 = 675 are chosen. In Fig. 5, t = 0 corresponds to 03:50:18 UT in Fig. 2. Here, we consider the wave is a freely propagating one after 04:01:02 UT, as argued in Sect. 2. At this time, the wave front is located at a height of 576 Mm above the photosphere.
 |
Fig. 5. Height–time diagram (full line) of the radial motion of a fast magnetosonic wave according to Eq. (9) by adopting vA, S = 219 km s−1 and a coronal temperature of 1.39 MK (i.e., λ = 9.88). The crosses show the radial motion of the dome-shaped EUV wave from measurements according to Fig. 2. Here, t = 0 corresponds to 03:50:18 UT in Fig. 2. |
The numerical solution of Eq. (9) that is found in this way is presented in Fig. 5. The crosses show the vertical motion of the dome-shaped EUV wave derived from the observations (see Fig. 3). Figure 5 shows that the theoretical description agrees well with the observations for heights above 500 Mm. That can be explained by the following manner: The EUV wave is initially excited by a sudden energy release (flare or CME) in an active region. There, the magnetic field is strong and the density is enhanced. Nevertheless, the motion of the EUV wave can be described well by means of the behaviour of the Alfvén speed above quiet Sun regions (see Eq. (8)). Hence, the influence of the active region can be neglected with respect to the density and magnetic field for heights ≥500 Mm above the photosphere. For illustration, the Alfvén speed in the height range 500–1000 km above the photosphere is about 600 km s−1 (see Fig. 4). That results in vfms = 626 km s−1 with cs = 179 km s−1 and V = (vA + vfms)1/2 = 613 km s−1, namely, V ≈ vA. Hence, V is not crucially depending on the angle θ and, hence, on the local magnetic field topology. This means that the magnetic field of the quiet Sun dominates at heights above 500 Mm, and the local Alfvén speed can appropriately be described by Eq. (8) in the corona at heights above 500 Mm.
5. Nonlinear MHD waves
Figure 3 shows the evolution of the intensity profile of the EUV wave during its horizontal evolution, which was derived from the EUVI-A 195 Å filtergrams. As mentioned above, after 04:01 UT the EUV wave is a freely propagating one. The wave profile shows an initial steepening of the leading edge and a subsequent (i.e., after 04:16 UT) decay during its further evolution. The maximum intensity enhancement is Imax/I0 = 1.45, which corresponds to a maximum density enhancement of ≈1.2 for optically thin emission lines (Veronig et al. 2010). Wave steepening is a typical property of nonlinear waves. Therefore, nonlinear MHD wave theory (Mann 1995) must be employed.
In order to study the evolution of the wave profile, for instance, wave steepening, the approach of so-called “simple waves” (Landau & Lifshitz 1987) is employed. The disturbances associated with the wave are travelling along the x-axis. All varying quantities are assumed to be depending only on the spatial and temporal coordinates x and t. The ideal MHD equations are conveniently written in terms of Lagrangian coordinates (see Eq. (3) in Mann 1995). In the framework of simple waves, there are well defined relationships between the disturbed quantities. In MHD, these quantities are the density, the magnetic field, and the flow velocity. The relationships between them are described in terms of ordinary differential equations (see Eq. (4) in Mann 1995):
with
Here, the full particle number density N, the magnitude of the magnetic field b and all velocities (i.e., the Alfvén speed, vA, the sound speed, cs, the phase velocity, V, and the flow velocity, vx) are normalized to the full particle number density, N0, the magnetic field, B0, and the Alfvén speed, 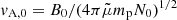 in the undisturbed plasma. Then, vA, x, vA, and cs are given by:
in the undisturbed plasma. Then, vA, x, vA, and cs are given by:
with 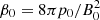 as the ratio between the thermal and the magnetic pressure. b(N = 1) = 1 and vx(N = 1) = 0 are the initial conditions of Eqs. (10) and (11). Here, the x-component of the magnetic field bx is a constant and is related to the angle θ between the ambient magnetic field and the x-axis by bx = cos θ.
as the ratio between the thermal and the magnetic pressure. b(N = 1) = 1 and vx(N = 1) = 0 are the initial conditions of Eqs. (10) and (11). Here, the x-component of the magnetic field bx is a constant and is related to the angle θ between the ambient magnetic field and the x-axis by bx = cos θ.
Since EUV waves are propagating nearly perpendicular to the ambient magnetic field at the bottom of the corona, the angle θ = 90° has to be chosen leading to vA, x = 0. Then, Eq. (12) provides 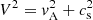 , and after inserting Eq. (14) into Eq. (11), Eq. (11) is reduced to
, and after inserting Eq. (14) into Eq. (11), Eq. (11) is reduced to
With the initial conditions, this leads to b(N) = N. Finally, Eq. (12) can be written as
By means of Eqs. (17), (10) can then be expressed as:
Figure 6 shows the numerical solutions of Eqs. (17) and (18) with β0 = 0.8 (i.e., 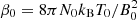 , N0 = NS = 1.687 × 109 cm−3, T0 = 1.39 MK, and B0 = BS = 3.19 G) and γ = 5/3. Both, V and vx are functions monotonically increasing with N.
, N0 = NS = 1.687 × 109 cm−3, T0 = 1.39 MK, and B0 = BS = 3.19 G) and γ = 5/3. Both, V and vx are functions monotonically increasing with N.
 |
Fig. 6. Functions V(N)+vx(N) (full line), V(N) (dashed-dotted line), and vx(N) (dashed line) as solutions of Eqs. (17) and (18). |
In MHD, it is well known that a fast magnetosonic wave is accompanied with a density enhancement. However, a density enhancement is also related to an increase in the temperature:
The EUV wave under study is related to a density enhancement of 1.2 and, hence, to a maximum temperature of 1.57 MK according to Eq. (19). Here, the value of T0 = 1.39 MK has been used. This may explain why the EUV wave is best seen in the EUVI 195 Å passband. However, it also indicates that ≈1.4 MK is a good choice for the temperature of the quiet corona.
Next, the evolution of a fast magnetosonic wave pulse is considered (see Fig. 7). The local propagation velocity within the simple wave is given by W = V + vx. Since W is monotonically increasing with N (see Fig. 6), the part at the top of the wave, where the density has its maximum Nmax, is propagating faster than at the wings, where N = 1. This results in a steepening of the wave at its leading edge as illustrated in Fig. 7.
 |
Fig. 7. Sketch of a simple wave propagating to the right. |
The length between the top of the EUV wave and the wings is derived from the observations as Δs0 = 60 Mm (see Fig. 3). The relative velocity between the top and the wing of the EUV wave is given by ΔW = Wtop − Wwing. For Nmax = 1.2, inspection of Fig. 6 provides Wtop = 1.65 and Wwing = 1.29 leading to a relative velocity of (1.65 − 1.29)×vA = 78 km s−1. Since the evolution of the EUV wave during its propagation along the solar surface is studied here, vA = 219 km s−1 must be taken for the Alfvén velocity (see Sect. 3). Then, a wave steepening should appear if the top of the wave pulse overtakes the wing of the leading edge. That should occur after a time tsteepening = Δs/(ΔWvA) = 60 Mm/78 km s−1 = 769 s (≈13 min). Yet this does not happen, as seen in Fig. 3. In this estimation, the amplitude at the top of the wave pulse is regarded to be constant, but this is not the case for real EUV waves. Since these waves travel as nearly circular waves over the Sun, their amplitude is decreasing, in the typical way of a circular or spherical wave. Consequently, the velocity Wmax at the top of the wave pulse is also decreasing, leading to a prevention of the wave steepening.
In order to investigate this subject, the motion of the top stop and the wing swing of the wave pulse is considered according to:
and
with W0 = W(N = 1) = 1.29, vA = 219 km s−1, Nmax = 1.2, and Δs0 = 60 Mm, respectively. The evolution of the density is described by an iterative manner. At the time ti, the top of the wave is located at ri. There, it has an enhanced particle number density Nmax, i. Hence, it propagates with the velocity W(Nmax, i)vA. After the time step Δt, the top of the wave travels up to ri + 1 = ri + W(Nmax, i)vA ⋅ Δt. During this time step, the density at the top is diminished to Nmax, i + 1 according to:
with δ = 1 and 2 for a circular and spherical wave, respectively. As already mentioned, the EUV wave is fully developed at 4:01:02 UT. At that time, the top of the EUV wave pulse is 357 Mm away from the center of the wave (see Fig. 3). This region is sufficiently far away from the active region, so that the quiet Sun magnetic field is the dominant one there. Consequently, r0 is taken to be 357 Mm. Now, Eq. (20) can numerically be solved by means of Eq. (22) in an iterative manner. Δt = 100 s and Nmax, i = 0 = 1.2 are chosen.
In Fig. 8, the result is presented in terms of Δs = stop − swing. Complete wave steepening occurs, if the top of the wave pulse overtakes its leading wing, namely, Δs = 0. This is the case after 1100 s (≈18 min) for δ = 1, as seen in Fig. 8. Within this timeframe, the density at the top diminishes from 1.2 to 1.094. Then, a shock with a density compression of 1.094 and an Alfvén Mach number 1.461 can be established. However, it is a weak shock that is formed. For the other case, that is, δ = 2, the dotted line approaches continuously zero, but it will never cross zero (see Fig. 8). This means that the wave initially steepens and, subsequently, the steepening stops due to the decrease of the amplitude at the top of the wave pulse. Such an evolution can indeed be observed, as demonstrated in Fig. 3.
 |
Fig. 8. Temporal behaviour of the distance Δs path-time diagram between the top and the wing of the wave pulse according to Eqs. (20) and (21) for δ = 1 (dashed line) and δ = 2 (dotted line). |
Figure 9 plots the decrease of the maximum density enhancement (N − 1) at the top of the wave pulse during its evolution for the two cases, namely, a circular (δ = 1) and a spherical (δ = 2) wave. It shows that in the initial phase the horizontal motion of the EUV wave can be aptly described as a circular wave, whereas for the later phase, a spherical wave is a better description. This finding can be explained as follows: on the one hand, the dome-shaped EUV wave under study should be regarded as a spherical wave (i.e., δ = 2); on the other hand, the density in the corona is radially stratified, namely, the highest density is at the bottom of the corona. Thus, the dome-shaped EUV wave is in reality a mixture between a circular and a spherical wave. The observations show that during the evolution of the EUV wave its maximum intensity, Imax, is decreasing according to ∝r−2.5 ± 0.3 (Veronig et al. 2010).
 |
Fig. 9. Decrease in the maximum enhancement N − 1 of the particle number density during the evolution of a simple MHD wave according to Eq. (22). The dashed and dotted lines represents the cases δ = 1 and δ = 2, respectively. The crosses represents the data of the EUVI measurements for the January 17, 2010 wave from Veronig et al. (2010). |
In the case of optically thin EUV line emission, the intensity of the emitted radiation is depending on both the temperature, T, and the density, N, in the source region (see Eqs. (2.8.6) and (2.8.7) in Aschwanden 2005). In case that the temperature variation is small in large-scale EUV waves1 (e.g., Vanninathan et al. 2015), the density dependence can be approximated by Imax/I0 ∝ N2 (I0, intensity of the background). Hence, in the event under study, the density, N, is decreasing according to ∝r−1.25. This means that the EUV wave under study is indeed a mixture between a circular and spherical wave.
As already mentioned, Fig. 6 shows that the propagation velocity depends on the density compressions of N that accompany the wave, which is a purely nonlinear property. In the case of N → 1, the propagation velocity continuously approaches the linear value. As discussed above, the EUV wave starts with the velocity Wtop = 1.65 (361 km s−1) at the top, whereas the wings have the velocity Wwing = 1.29 (i.e., 283 km s−1). In Sect. 3, the linear wave velocities (see Eq. (1)) are employed to derive plasma properties from the velocities of the EUV wave under discussion. The error of that is of the order of 12% (because of (Wtop − Wwing)/(Wtop + Wwing)). Such an error can be accepted, since the EUV measurements are also connected with errors and the model of simple MHD waves is a simple model, that is to say that it neglects the large scale inhomogeneity of the corona, for instance. Nevertheless, the presented approach is able to describe the propgation of a dome-shaped, large-scale EUV wave in the corona in a quantitative manner.
6. Summary
The observation of a dome-shaped EUV wave by the EUVI instrument onboard STEREO-B on January 17, 2010 (Veronig et al. 2010) allows us to study the 3D evolution of such a wave in the corona. This EUV wave can be regarded as a freely propagating, large-amplitude fast magnetosonic wave. These complete and comprehensive observations of the full wave dome offer a unique opportunity to link the nonlinear MHD wave theory with observations.
Although large-scale EUV waves are initially excited by a solar eruption (e.g., Veronig et al. 2008, 2018; Patsourakos & Vourlidas 2009; Kienreich et al. 2009; Shen & Liu 2012), they mostly travel outside active regions, namely, in quiet Sun regions. The measurements of the spatio-temporal behavior of the 17 January, 2010 EUV wave reveal that the wave is travelling with a nearly constant speed of about 280 km s−1 along the solar surface. If it is identified with the fast magnetosonic speed, the quiet Sun’s magnetic field at the bottom of the corona can be estimated to be ≈3.2 G. This magnetic field is extrapolated into the corona by using the conservation of the magnetic flux. With this knowledge of the radial behavior of the magnetic field and the assumption of a barometric model for the density behaviour, the radial behavior of the local Alfvén speed for the quiet corona can be derived (see Fig. 2). It shows a local maximum of ≈680 km s−1 at a height of ≈1030 Mm above the photosphere. With this characteristic of the Alfvén speed, the vertical motion of the EUV wave can be calculated. The resulting height-time diagram agrees well with the observations, as can be seen in Fig. 5. This agreement demonstrates that the presented approach aptly describes the kinematics of a radially propagating EUV wave and that the models of the density, the magnetic field, and Alfvén speed are an appropriate choice for the quiet solar corona.
The evolution of large-amplitude MHD waves can be described in terms of simple MHD waves as developed by Mann (1995). This theoretical study shows that the wave is initially steepening. Subsequently, this steepening stops due to the decrease of the wave amplitude during its further evolution. Such a decrease of the amplitude occurs for a circular and/or spherical wave during its propagation (see Figs. 8 and 9). We emphasize that this behavior, namely, the initial wave steepening and subsequent decay, is indeed observed in the case of the dome-shaped EUV wave under study (see Fig. 3).
These results confirm that nonlinear MHD wave theory provides a valid description of the 3D evolution of freely propagating, large-amplitude EUV waves in the corona.
A density compression is also connected with an adiabatically enhancement of the temperature as discussed with Eq. (19).
Acknowledgments
The authors express their thanks to Hakan Önel for his assistance for the numerical evaluation of Eqs. (17) and (18) by mathematica. A. V. acknowledges the Austrian Science Fund (FWF): P24092-N16.
References
- Aschwanden, M. J. 2005, Physics of the Solar Corona. An Introduction with Problems and Solutions, 2nd edn. (Berlin: Springer) [Google Scholar]
- Brosius, J. W., Davila, J. M., Thomas, R. J., & Monsignori-Fossi, B. C. 1996, ApJS, 106, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, X., Zhang, J., Olmedo, O., et al. 2012, ApJ, 745, L5 [Google Scholar]
- Cohen, O., Attrill, G. D. R., Manchester, W. B., & Wills-Davey, M. J. 2009, ApJ, 705, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Delaboudinière, J. P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [Google Scholar]
- Delannée, C., Artzner, G., Schmieder, B., & Parenti, S. 2014, Sol. Phys., 289, 2565 [CrossRef] [Google Scholar]
- Downs, C., Roussev, I. I., van der Holst, B., et al. 2011, ApJ, 728, 2 [Google Scholar]
- Downs, C., Roussev, I. I., van der Holst, B., Lugaz, N., & Sokolov, I. V. 2012, ApJ, 750, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Dresing, N., Gómez-Herrero, R., Klassen, A., et al. 2012, Sol. Phys., 281, 281 [NASA ADS] [Google Scholar]
- Francile, C., López, F. M., Cremades, H., et al. 2016, Sol. Phys., 291, 3217 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, P. T., & Long, D. M. 2011, Space. Sci. Rev., 158, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Afanasyev, A. N., Uralov, A. M., et al. 2011, Sol. Phys., 273, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Harra, L. K., Sterling, A. C., Gömöry, P., & Veronig, A. 2011, ApJ, 737, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, Z., Tian, H., Wang, J.-S., et al. 2022, ApJ, 928, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space. Sci. Rev., 136, 67 [CrossRef] [Google Scholar]
- Hu, H., Liu, Y. D., Zhu, B., et al. 2019, ApJ, 878, 106 [CrossRef] [Google Scholar]
- Kai, K. 1970, Sol. Phys., 11, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space. Sci. Rev., 136, 5 [Google Scholar]
- Kienreich, I. W., Temmer, M., & Veronig, A. M. 2009, ApJ, 703, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Klassen, A., Aurass, H., Mann, G., & Thompson, B. J. 2000, A&AS, 141, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koutchmy, S. 1994, AdSpR, 14, 29 [NASA ADS] [Google Scholar]
- Kozarev, K. A., Korreck, K. E., Lobzin, V. V., Weber, M. A., & Schwadron, N. A. 2011, ApJ, 733, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics (New York: Pergamon Press) [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Liu, W., Jin, M., Downs, C., et al. 2018, ApJ, 864, L24 [Google Scholar]
- Long, D. M., Gallagher, P. T., McAteer, R. T. J., & Bloomfield, D. S. 2008, ApJ, 680, L81 [Google Scholar]
- Long, D. M., Bloomfield, D. S., Chen, P. F., et al. 2017, Sol. Phys., 292, 7 [CrossRef] [Google Scholar]
- Ma, S., Raymond, J. C., Golub, L., et al. 2011, ApJ, 738, 160 [CrossRef] [Google Scholar]
- Mann, G. 1995, J. Plasma Phys., 53, 109 [CrossRef] [Google Scholar]
- Mann, G., Aurass, H., Klassen, A., Estel, C., & Thompson, B. J. 1999a, in 8th SOHO Workshop: Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, eds. J. C. Vial, & B. Kaldeich-Schü, ESA Spec. Publ., 446, 477 [Google Scholar]
- Mann, G., Jansen, F., MacDowall, R. J., Kaiser, M. L., & Stone, R. G. 1999b, A&A, 348, 614 [NASA ADS] [Google Scholar]
- Mann, G., Klassen, A., Aurass, H., & Classen, H. T. 2003, A&A, 400, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moreton, G. E., & Ramsey, H. E. 1960, PASP, 72, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, D., Clette, F., Delaboudinière, J. P., et al. 1997, Sol. Phys., 175, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Muhr, N., Veronig, A. M., Kienreich, I. W., Temmer, M., & Vršnak, B. 2011, ApJ, 739, 89 [Google Scholar]
- Muhr, N., Veronig, A. M., Kienreich, I. W., et al. 2014, Sol. Phys., 289, 4563 [NASA ADS] [CrossRef] [Google Scholar]
- Newkirk, G., Jr 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, N. V., Schrijver, C. J., Title, A. M., & Liu, W. 2013, ApJ, 776, 58 [Google Scholar]
- Olmedo, O., Vourlidas, A., Zhang, J., & Cheng, X. 2012, ApJ, 756, 143 [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Patsourakos, S., & Vourlidas, A. 2009, ApJ, 700, L182 [Google Scholar]
- Patsourakos, S., & Vourlidas, A. 2012, Sol. Phys., 281, 187 [NASA ADS] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Podladchikova, T., Veronig, A. M., Dissauer, K., Temmer, M., & Podladchikova, O. 2019, ApJ, 877, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1982, Geophys. Astrophys., 21, 19 [Google Scholar]
- Schrijver, C. J., & De Rosa, M. L. 2003, Sol. Phys., 212, 165 [Google Scholar]
- Schrijver, C. J., Aulanier, G., Title, A. M., Pariat, E., & Delannée, C. 2011, ApJ, 738, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Liu, Y. 2012, ApJ, 754, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Temmer, M., Vrsnak, B., & Veronig, A. M. 2013, Sol. Phys., 287, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, B. J., & Myers, D. C. 2009, ApJS, 183, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, B. J., Plunkett, S. P., Gurman, J. B., et al. 1998, Geophys. Res. Lett., 25, 2465 [Google Scholar]
- Uchida, Y. 1968, Sol. Phys., 4, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Vanninathan, K., Veronig, A. M., Dissauer, K., et al. 2015, ApJ, 812, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Veronig, A. M., Temmer, M., & Vršnak, B. 2008, ApJ, 681, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Veronig, A. M., Muhr, N., Kienreich, I. W., Temmer, M., & Vršnak, B. 2010, ApJ, 716, L57 [Google Scholar]
- Veronig, A. M., Gömöry, P., Kienreich, I. W., et al. 2011, ApJ, 743, L10 [Google Scholar]
- Veronig, A. M., Podladchikova, T., Dissauer, K., et al. 2018, ApJ, 868, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Vršnak, B., & Cliver, E. W. 2008, Sol. Phys., 253, 215 [Google Scholar]
- Vršnak, B., Žic, T., Lulić, S., Temmer, M., & Veronig, A. M. 2016, Sol. Phys., 291, 89 [Google Scholar]
- Warmuth, A. 2015, Liv. Rev. Sol. Phys., 12, 3 [Google Scholar]
- Warmuth, A., & Mann, G. 2005, A&A, 435, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., & Mann, G. 2011, A&A, 532, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A., & Otruba, W. 2004a, A&A, 418, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warmuth, A., Vršnak, B., Magdalenić, J., Hanslmeier, A., & Otruba, W. 2004b, A&A, 418, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., Lagg, A., & Nordlund, Å. 2009, Space. Sci. Rev., 144, 317 [Google Scholar]
- Wild, J. P., Sheridan, K. V., & Trent, G. H. 1959, in URSI Symp. 1: Paris Symposium on Radio Astronomy, 9, 176 [NASA ADS] [Google Scholar]
- Wills-Davey, M. J., & Attrill, G. D. R. 2009, Space. Sci. Rev., 149, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Wuelser, J. P., Lemen, J. R., Tarbell, T. D., et al. 2004, SPIE Conf. Ser., 5171, 111 [NASA ADS] [Google Scholar]
- Zhao, X. H., Wu, S. T., Wang, A. H., et al. 2011, ApJ, 742, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukov, A. N. 2011, J. Atmos. Solar-Terrest. Phys., 73, 1096 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukov, A. N., & Auchère, F. 2004, A&A, 427, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Direct (top) and 5-min running difference (bottom) image of the dome-shaped EIT wave at 3:56:02 UT on January 17, 2010 as recorded by the 195 Å filter of the EUVI instrument aboard STEREO-B. |
| In the text | |
 |
Fig. 2. Kinematics of the vertical (red) and horizontal (black) motion of the EUV wave on 2010 January 17 (adapted from Fig. 4 in Veronig et al. 2010, © AAS, reproduction with permission). |
| In the text | |
 |
Fig. 3. STEREO-B/EUVI 195 Å intensity profiles of the EUV wave on 2010 January 17 with respect to its horizontal motion (adapted from Fig. 5 in Veronig et al. 2010, © AAS, reproduction with permission). |
| In the text | |
 |
Fig. 4. Height dependence of the local Alfvén speed in the quiet corona. |
| In the text | |
 |
Fig. 5. Height–time diagram (full line) of the radial motion of a fast magnetosonic wave according to Eq. (9) by adopting vA, S = 219 km s−1 and a coronal temperature of 1.39 MK (i.e., λ = 9.88). The crosses show the radial motion of the dome-shaped EUV wave from measurements according to Fig. 2. Here, t = 0 corresponds to 03:50:18 UT in Fig. 2. |
| In the text | |
 |
Fig. 6. Functions V(N)+vx(N) (full line), V(N) (dashed-dotted line), and vx(N) (dashed line) as solutions of Eqs. (17) and (18). |
| In the text | |
 |
Fig. 7. Sketch of a simple wave propagating to the right. |
| In the text | |
 |
Fig. 8. Temporal behaviour of the distance Δs path-time diagram between the top and the wing of the wave pulse according to Eqs. (20) and (21) for δ = 1 (dashed line) and δ = 2 (dotted line). |
| In the text | |
 |
Fig. 9. Decrease in the maximum enhancement N − 1 of the particle number density during the evolution of a simple MHD wave according to Eq. (22). The dashed and dotted lines represents the cases δ = 1 and δ = 2, respectively. The crosses represents the data of the EUVI measurements for the January 17, 2010 wave from Veronig et al. (2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



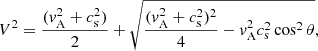
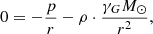
![$$ \begin{aligned} N(r) = N_{\rm S} \cdot \mathrm{e}^{\lambda [(R_{\odot }/r)-1]} ,\end{aligned} $$](/articles/aa/full_html/2023/08/aa45688-22/aa45688-22-eq7.gif)
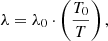
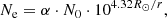
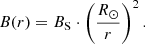
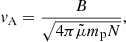
![$$ \begin{aligned} v_{\rm A}(r) = v_{\rm A,S} \cdot \left(\frac{R_{\odot }}{r} \right)^{2} \cdot \mathrm{e}^{-\lambda [(R_{\odot }/r)-1]/2} ,\end{aligned} $$](/articles/aa/full_html/2023/08/aa45688-22/aa45688-22-eq15.gif)
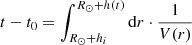
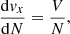
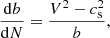
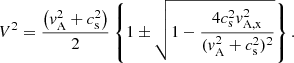
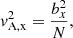
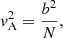
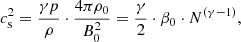
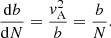
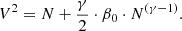
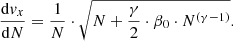
![$$ \begin{aligned} N_{\mathrm{max},i+1} = 1 + \frac{(N_{\mathrm{max},i}-1)}{\left[1 + \frac{W(N_{\mathrm{max},i})v_{\rm A}\Delta t}{r_{i}} \right]^{\delta }} ,\end{aligned} $$](/articles/aa/full_html/2023/08/aa45688-22/aa45688-22-eq37.gif)