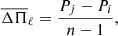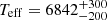| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202141610 | |
| Published online | 10 August 2023 | |
Frequency analysis of the hybrid δ Sct-γ Dor star CoRoT-102314644
1
Astronomical Institute, Czech Academy of Sciences, Fričova 298, 25165 Ondřejov, Czech Republic
e-mail: julieta.sanchez@asu.cas.cz
2
Instituto de Astrofísica La Plata, CONICET-UNLP, Paseo del Bosque s/n, B1900FWA La Plata, Argentina
3
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire, CS 34229, 06304 Nice cedex 4, France
Received:
22
June
2021
Accepted:
8
May
2023
Context. Observations from space missions allowed significant progress due to the absence of atmospheric noise contributions and having uninterrupted data sets. This has been extremely beneficial in asteroseismology because many oscillation frequencies, not observable from the ground, can be detected. One example of this success is the large number of hybrid δ Sct-γ Dor stars discovered. These stars have radial and non-radial p and g modes simultaneously excited, allowing us to probe both the external and near-to-core layers.
Aims. We aim to analyse the light curve of the hybrid δ Sct-γ Dor star CoRoT ID 102314644 and characterise its frequency spectrum. Using the detected frequencies, we intend to perform an initial interpretation developing stellar models.
Methods. The frequency analysis was obtained with a classical Fourier analysis. A detailed analysis of the individual frequencies is performed using phase diagrams and other light curve characteristics. Initial stellar modelling was performed using the Cesam2k and the GYRE code.
Results. We detected 29 γ Dor type frequencies in the [0.32 − 3.66] c/d range and a series of six equidistant periods with a mean period spacing of ΔΠ = 1612 s. In the δ Sct domain, we found 38 frequencies in the [8.63 − 24.73] c/d range and a quintuplet centred on the frequency p1 = 11.39 c/d, which suggests a rotational period of 3.06 d. The frequency analysis suggests the presence of spots. Nevertheless, we could not dismiss the possibility of a binary system. The initial modelling of the frequency data allowed us to refine its astrophysical parameters.
Conclusions. The observed period spacing, a p-mode quintuplet, the possible rotation period, and the analysis of the individual frequencies impose significant constraints on our understanding of differential rotation and magnetic fields operating in A–F-type stars. Nevertheless, it is fundamental to accompany photometric data with spectroscopic measurements to distinguish variations between surface activity from a companion.
Key words: asteroseismology / stars: oscillations / stars: variables: δ Scuti / techniques: photometric
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the last decade, several space missions, such as the COnvection ROtation and planetary Transits (CoRoT) satellite (Auvergne et al. 2009) and NASA’s Kepler space telescope (Borucki 2016), have revolutionised asteroseismology thanks to their high level of precision allowing the detection of very small amplitude modes that are not detectable from ground-based instruments. Indeed, δ Sct stars have been known for many decades now due to the high amplitude of some of their oscillation modes, which reach up to tenths of a magnitude, while γ Dor stars have only been known since 1999 (Kaye et al. 1999) thanks to uninterrupted data from space, which allowed the detection of their low amplitude periodicities near one day (Aerts et al. 2010). The existence of hybrid δ Sct-γ Dor stars has been known since 2002 (Handler et al. 2002). Their unique characteristic of exhibiting both radial and non-radial pressure (p) oscillation modes typical of δ Sct variable stars and gravity (g) pulsation modes characteristic of γ Dor variable stars simultaneously allows one to probe their stellar structure from the core to the envelope.
The δ Sct stars lie on and above the main sequence with masses of approximately 1.5 − 2.5 M⊙ and spectral types between A2 and F5. They exhibit radial and non-radial p and g modes driven by the κ mechanism operating in the He II partial ionisation zone (Baker & Kippenhahn 1962) and the turbulent pressure acting in the hydrogen ionisation zone (Antoci et al. 2014).
The γ Dor variables are generally cooler than δ Sct stars, with Teff centred between 6700 K and 7400 K (spectral types between A7 and F5) and masses in the 1.5 to 1.8 M⊙ range approximately (Catelan & Smith 2015). They pulsate in low-degree, high-order g modes apparently driven by a flux modulation mechanism called convective blocking and induced by the outer convective zone (Guzik et al. 2000; Dupret et al. 2004; Grigahcène et al. 2005). The high-order g modes (n ≫ 1) excited in these stars allow the use of the asymptotic theory (Tassoul 1980) and the departures from uniform period spacing to explore the possible chemical inhomogeneities in the structure of the convective cores (Miglio et al. 2008).
The aforementioned distinction between δ Sct and γ Dor stars is a topic of debate. Diverse studies on samples of δ Sct and γ Dor stars suggest that the hybrid behaviour of these stars is very common (Grigahcène et al. 2010; Uytterhoeven et al. 2011; Bradley et al. 2015; Balona et al. 2015). Moreover, in 2016 Xiong et al. (2016) calculated a theoretical instability strip using a non-local and time-dependent convection theory and concluded that the κ mechanism operates significantly in warm δ Sct and γ Dor stars, while the coupling between convection and oscillations is responsible for excitation in cool stars. Furthermore, the instability strips of δ Sct and γ Dor stars partially overlap in the Hertzprung-Russell (HR) diagram (see, for instance, Fig. 1 of Grigahcène et al. 2010), explaining the existence of hybrid δ Sct-γ Dor stars. As we mentioned, the simultaneous presence of both g and p non-radial, along with radial excited modes, allows one to place strong constraints on the whole interior structure. In addition, some of these objects show rapid rotation, making them excellent targets for modelling stellar structure and testing different physical phenomena such as the effect of angular transport induced by rotation (Aerts et al. 2019; Ouazzani et al. 2019).
Although a significant number of hybrid δ Sct-γ Dor stars are currently known (Grigahcène et al. 2010; Balona 2014), the analysis of low frequencies in A–F stars still represents a challenge due to the different origins that these frequencies can have, for example spots, field stars contaminating the light apertures of the main target, a companion forming a non-eclipsing binary system, Rossby modes usually present in moderate to rapid rotating stars, and more (Li et al. 2019; Chowdhury et al. 2018; Saio et al. 2018). Our aim is to present, for the first time, a complete observational analysis of the light curve and the frequencies of the hybrid δ Sct-γ Dor CoRoT 102314644 along with the corresponding interpretation.
The paper is laid out as follows. Both literature and CoRoT data are presented in Sect. 2, followed by the description of the frequency analysis in Sect. 3. A detailed analysis of the frequencies including their mode identification is then presented and discussed in Sect. 4. An initial interpretation of the oscillation modes with stellar models is presented in Sect. 5, and we conclude in Sect. 6.
2. Literature data
2.1. Known stellar quantities from the literature
CoRoT 102314644 (V ∼ 12.2, α = 6h 10m26.73s and δ = +4° 18′ 12.19″) was observed during the third CoRoT long run, LRa03, which targeted the Galactic anti-centre (see Fig. 1). The observations lasted 148 days from 2009 October 10 to 2010 March 1. The EXODAT database (Deleuil et al. 2009) indicates the star has an A5V spectral type and 2MASS photometry of J = 11.394, H = 11.18, K = 11.131. It also indicates a star with reddening of E(B − V) = 0.4 mag. However, more recently, Lallement et al. (2019) estimated E(B − V) = 0.248 ± 0.079 mag based on the distance of the star1. The sky map given by the CoRoT database is shown in Fig. 1, upper panel, which clearly identifies the target. We also give a wider angle sky map showing our target at the centre and the positions of Gaia Data Release (GDR2/GDR3) identified sources in the lower panel (Gaia Collaboration 2018, 2021, 2023). The photometry and various identifications of the star are given in Table 1.
 |
Fig. 1. CoRoT 102314644 in the sky. Upper: star map showing the star’s position and coordinates from the ExoDAT database. Lower: star map showing a slightly wider view, along with the Gaia DR2 identified sources (red). |
Identification and literature data for CoRoT 102314644.
2.2. Fundamental stellar parameters
Gaia eDR3 also provides additional properties of the star: its parallax π, its radial velocity vrad and photometry G, GBP, and GRP, given in Table 1. For π, we applied the recommended parallax zero-point correction of −0.027 mas based on the magnitude, colour, and sky position of the star (Lindegren et al. 2021). Using the extinction, we dereddened the photometry and used the colour–Teff relations from Casagrande et al. (2021) to derive Teff. To convert the extinction from E(B − V) to other bands, we assumed a reddening law of R = 3.1 and used the coefficients from Danielski et al. (2018). The colour–Teff relations require log g and [Fe/H] as input, so we used log g = 3.9 (see below) and assumed solar metallicity in the absence of literature values. Then, using G, extinction AG, the parallax and a bolometric correction, we calculated the luminosity, L. Using the Stefan-Boltzmann law with these values, we estimated the stellar radius. Finally, using an estimate of mass between 1.7 and 2.1 M⊙, we calculated a surface gravity of 3.9 ± 0.1 using the derived radius.
Teff and L are highly correlated because they both depend on the extinction value. To calculate the uncertainties and correlations in the Teff–L plane, we performed simulations where we perturbed the input values (E(B − V), π, G, GBP, and GBP) by their errors. Then we propagated these perturbed values to the Teff, L, radius, and log g. The values obtained for L and Teff agree with the assumption that the star is a hybrid γ Dor–δ Scuti. The derived values and their 1D uncertainties are L⋆ = 13.6 ± 2.9 L⊙; Teff = 7065 ± 460, and R⋆ = 2.27 ± 0.07 R⊙. In our interpretation of the models in Sect. 5 we used these values as a first approximation to constrain the models2.
2.3. CoRoT light curve
We followed a similar analysis of this CoRoT light curve to that performed in Chapellier et al. (2012) and Chapellier & Mathias (2013). We used the reduced N2 light curves from Auvergne et al. (2009). The light curve consists of a total of 386 381 measurements obtained with a temporal resolution of 32 s. We retained only 342 598 points, those flagged as ‘0’ by the CoRoT pipeline that were not affected by instrumental effects such as stray light or cosmic rays. We then corrected the measurements by long-term trends (systematic trends). Individual measurements considered outliers (primarily high-flux data points caused by cosmic ray impacts) were removed by an iterative procedure. We retained a total of 340 257 measurements, which gives an approximate frequency resolution of 0.008 c/d.
The resulting light curve is represented at different timescales in Fig. 2. The amplitude was calculated by converting from flux to magnitudes and subtracting the mean. The timescale is labelled in units of the CoRoT Julian day (JD), where the starting CoRoT JD corresponds to HJD 2445545.0 (2000 January 1 at UT 12:00:00). In the top panel, we show the full corrected light curve spanning 148 days. In the middle and lower panels, we show twenty-day and five-day time spans, respectively. Here, we can distinguish two kinds of periodic timescales: one corresponding to low frequencies, characteristic of γ Dor stars (middle panel), and one due to higher frequencies, characteristic of the δ Sct star (lower panel).
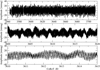 |
Fig. 2. Light curve of the star CoRoT 102314644 corrected for long-term trends and outliers (see main text) for different timescales. From top to bottom, the complete light curve over 148 d, then a set over 20 d, and finally a zoomed-in view of the 5 d subset. |
3. Light-curve analysis
We analysed the frequency content of the light curve using the package Period04 (Lenz & Breger 2005). We searched frequencies in the interval [0;100] c/d. For each detected frequency, the amplitude and the phase were calculated by a least-squares sine fit. The data were then cleaned of this signal (this is known as pre-whitening) and a new analysis was performed on the residuals. This iterative procedure was continued until we reached the signal-to-noise ratio (S/N) equal to 5.2, as recommended (Baran & Koen 2021). The first Fourier transform in the 0−30 c/d range is depicted in Fig. 3, with the y-axis showing amplitude.
 |
Fig. 3. First Fourier transform of CoRoT 102314644. |
We eliminated frequencies lower than 0.25 c/d. These correspond to trends in the CoRoT data (Chapellier et al. 2012) and the satellite orbital frequency (fsat = 13.97213 c/d) along with its harmonics. In addition, small-amplitude frequencies with a separation from large-amplitude frequencies lower than the frequency resolution were ignored. These smaller amplitude frequencies are not real and are due to the spectral window or to amplitude or frequency variability of the pulsations during the observations (Bowman et al. 2016).
As a result, we obtained a total of 68 stellar frequencies. The first ten frequencies with the highest amplitudes are shown in Table 2, and the complete list with uncertainties is given in Table A.1.
First ten frequencies with the highest amplitudes.
We also include an identity for each frequency in Table A.1 (see next section). Briefly, we identified two ranges of frequencies: δ Sct and γ Dor frequency ranges, which are labelled with ‘p’ and ‘g’, respectively; the frequency with the highest amplitude in each range has the sub-index ‘1’, and subsequent frequencies with lower amplitudes are labelled with increasing sub-index.
The uncertainties in the frequencies were calculated by performing Monte Carlo-like simulations on the light curve and recalculating the frequency content of each simulated light curve. More concretely, we created a fake signal sj by adding background noise to the original signal. We calculated the periodogram and then fitted the individual frequencies of the simulated periodogram. The fit to each frequency, fj, i, where i runs over the list of independent frequencies, was retained for each j = 1, …N simulation. We used N = 500 as this provided a good balance between computation time and enough sampling. We then analysed the resulting distributions of each fi, by calculating the 68%, 95%, and 99.7% confidence intervals. We checked first that these values scaled roughly as we expect them to. We report the 99.7% interval (∼ ± 3σ) in the second column in Table A.1.
4. Analysis of extracted frequencies
We analysed the frequencies derived in Sect. 3 and distinguished four main regimes: δ Sct-type frequencies, γ Dor-type periods, a regime with a coupling of ‘p’ and ‘g’ modes, and frequencies whose nature we discussed in terms of surface activity or gravitational effects provoked by a companion. One of the tools we used for the analysis of the frequencies is the phase diagram. The construction of these diagrams consists of taking all the observations and folding the light curve modulo a single standardized period (in time). Each time point is then assigned a phase with respect to this chosen period, and it takes a value of between 0 and 1, (0 < ϕ < 1). All measurements are then plotted with phase as the independent variable.
4.1. Spots or binarity
We noted that the first low frequency F2 = 0.65259 c/d with A = 4.47 mmag has a half-frequency harmonic F8 = 0.32630 c/d with A = 1.37 mmag. Such a combination of a frequency and a lower amplitude half frequency corresponds to a double wave curve typical of spotted or eclipsing stars (see e.g. Paunzen et al. 2017). Figure 4 shows the phase diagram corresponding to F8 = 0.32630 c/d after removing all frequencies corresponding to pulsation modes (see Sects. 4.2 and 4.3). It clearly shows a double wave curve that can be explained in terms of spots or a companion of an ellipsoidal variable, assuming that F8 = 0.32630 c/d is the orbital frequency. In the case of spots, the star appears slightly fainter when a large dark spot is on the visible side, and slightly brighter when it is not. We note that the phase diagram corresponding to the rotation frequency in a regular single star without pulsation frequencies or surface activity should be flat. A similar effect would be produced by a companion in an ellipsoidal variable system. These systems are non-eclipsing close binaries whose components are distorted by their mutual gravitation and the variations observed in the light curve are due to the changing variations are therefore due to the changing cross-sectional areas and surface luminosities that the distorted stars present to the observer at different phases (Morris 1985).
 |
Fig. 4. Phase diagram using rotational frequency frot = 0.326 c/d after removing of all the pulsational frequencies. |
We explored the possibility of being in the presence of one of these systems. We followed the equations in Morris (1985) assuming P = 3.06 d, R1 = 2.27 R⊙ as derived in Sect. 2.2, M1 = 1.75 M⊙, τ = 0.2 and μ = 0.4 from Claret & Bloemen (2011), and Δm = 0. We found possible solutions for a mass companion, making it impossible to dismiss this hypothesis; for example, M2 = 0.7 M⊙, 1.4 M⊙ for A = 12 R⊙, 13 R⊙ respectively, A being the semi-major axis.
To explore the existence of spots, we examined the star’s behaviour over several rotational periods, assuming a rotational frequency equal to F8 = 0.32630 c/d (∼3.06466 d). We binned the light-curve data in groups of ten measurements by assigning the average in time and magnitude to each group, and then we pre-whitened the data with all the pulsational frequencies. The result is presented in Fig. 5 for the duration of three rotational periods, each separated with horizontal lines. Two phenomena are present: amplitude variations from one orbit to another and moving bumps. The moving bumps might be explained by spots located at different latitudes. Additionally, the changes shown in Fig. 5 can be due to spots with a short lifetime. In the Sun, for example, the lifetime of the spots can vary from hours to months, and it is known that they usually migrate (Solanki 2003). Besides this, it has been shown that for hot stars the lifetime tends to decrease, especially for those stars with short rotational periods (Giles et al. 2017), as is the case of CoRoT 102314644. This suggests that CoRoT 102314644 can be a spotted star with a rotation period of Prot = 3.0647 d. Nevertheless, we found frequencies (F49, F55, and F64) that are a linear combination of frot, and this strongly suggests that the origin of frot is not surface activity (Kurtz et al. 2015) but, possibly, the beating of undetected pulsation frequencies. In order to properly determine the origin of these variabilities, spectroscopic measurements are required.
 |
Fig. 5. Extract of light curve corresponding to three rotational periods separated with vertical lines. We used the residuals after removing all pulsational frequencies of the binned data. |
4.2. γ Doradus domain
We found a total of 29 frequencies in the range of 0.3262−3.6631 c/d. From these frequencies, those we consider g-mode oscillations are labelled as ‘g’ modes in Table A.1. The frequency with the highest amplitude in this domain, after F2 = 2frot, is F4 = 1.0059 c/d with A = 2.0 mmag.
Light variabilities from orbital or rotational variation are typically non-sinusoidal; thus, in order to distinguish between possible real g modes and the frequencies corresponding to the spots in this domain, we analysed the phase diagram for each frequency. The phase diagrams for typical g- and p-mode frequencies show a sinusoidal behaviour. For instance, in Fig. 9 we have folded the light curve at the period corresponding to F1, and here we can clearly observe sinusoidal behaviour. This suggests that F1 is an oscillation eigenmode. On the other hand, for F18 = 0.4638 c/d, a non-sinusoidal can be spotted. In Fig. 6, the phase diagram for F18 for different amplitude scales is depicted. It seems that there is a maximum of around 0.1 and a minimum between 0.3 and 0.4. This suggests that F18 may correspond to periods related to spots. Nevertheless, we note that this test only provides hints about the origin of the frequency and is not conclusive. In fact, if F18 were originated by spots, it would imply over 40% in differential rotation, which is a slightly high value for A–F stars (Reinhold et al. 2013).
 |
Fig. 6. Data phased with F18 = 0.46385 c/d, a frequency possibly related to spots in the γ Doradus domain using different scale rages. |
Considering F18 as originated from spots and dismissing the rotational frequency and its harmonics, we retain a total of 26 frequencies in the γ Doradus domain, possibly g modes, depicted in black in Fig. 7. In addition, we searched for frequency combinations in this range, but no frequency couplings or splittings were found among these g modes. We labelled the frequencies ‘Fk’ as a combination of frequencies after finding a fit of at least two significant digits among all the possible combinations of type ‘mFi ± nFj’ for the given frequency ‘Fk’.
 |
Fig. 7. Amplitude versus frequency in γ Dor range of [0−4] c/d. Black lines represent all the g-mode frequencies found in this range. Grey data correspond to the frequency spectrum obtained from the FT. |
Hybrid δ Sct-γ Dor stars, as well as γ Dor stars, are characterised as having high-order g modes. For these modes, with high radial order (k) and long periods, the separation of consecutive periods (|Δk| = 1) becomes nearly constant, and it depends on the harmonic degree (ℓ), given the asymptotic theory of non-radial stellar pulsation (Tassoul 1980) in which the asymptotic period spacing is
with
where r is the distance from the stellar centre, N is the Brunt–Väisälä frequency, and r1 and r2 are the boundaries of the propagation region.
Motivated by this fact, we searched for equidistant γ Dor periods by analysing the differences between all the periods found in the γ Dor domain. We found a series of six equidistant periods with a mean separation of ΔΠ = 1621 s (see Table 3). These periods correspond to g modes of the same harmonic degree ℓ and consecutive radial orders k. The asymptotic series is depicted in Fig. 8. In the top panel of this figure, we show the periods (Π) versus an arbitrary radial order (k). We can see that these periods are almost equally spaced, forming a line. In the bottom panel of this figure, we show the forward period spacing (ΔΠ = Πk + 1 − Πk) versus k, and we denote the corresponding average period spacing with the red horizontal continuous line. According to Van Reeth et al. (2016), the value we found is more likely to correspond to an asymptotic series with ℓ = 2. In this paper, the authors determine values of about 3100 s and 1800 s for the asymptotic period spacing calculated with ℓ = 1 and ℓ = 2, respectively, employing Eqs. (1) and (2). In fact, our models predict a harmonic value ℓ = 2 for this series.
 |
Fig. 8. Asymptotic series found in CoRoT 102314644. Top Panel: period versus an arbitrary radial order for the equally spaced series of periods founded. Bottom panel: forward period spacing versus radial order. The horizontal red line indicates the average period spacing along with the associated error in dashed lines. |
Six periods of the asymptotic series.
4.3. δ Scuti domain
In the δ Scuti domain, we found a total of 38 frequencies in the 8.6−24.73 c/d range (see Table 4). The highest amplitude frequency in this range is F1 = 11.3910 c/d with A = 0.008 mag. A phase diagram folded with this frequency shows sinusoidal behaviour (Fig. 9), thus indicating that F1 is an eigenmode.
 |
Fig. 9. Data phased with F1 = 11.3910 c/d, the highest amplitude frequency in the δ Scuti domain. |
Variable content of the star.
Stellar rotation induces rotational splitting of the frequencies in the pulsation spectra. Considering rigid rotation and the first-order perturbation theory, the components of the rotational multiplets are
where νln is the central mode of the multiplet and Ω/2π is the rotational frequency. We found a quintuplet centred on p1 = F1 (see Table 5), which clearly indicates that this frequency is a non-radial mode with ℓ = 2. The differences between the central mode and the components of the quintuplets are given in the last column of Table 5. Considering Cnl ≈ 0 for p modes, we find a very good agreement with the value for frot = 0.32629 c/d derived in Sect. 4.1. However, this match does not dismiss the possibility of CoRoT 102314644 being an ellipsoidal variable. In fact, an alternative interpretation of this splitting would be tidally deformed oscillation modes that have variable amplitude over the orbit, if 0.32629 c/d is indeed a binary orbital period.
Frequencies of the quintuplet.
We also found four combinations between p modes exclusively, and the harmonics for p1 and p2 (see Table 6). The linear combination between two frequencies yields a third frequency whose amplitude is smaller than those that form it. It is important to distinguish between mode-coupled frequencies and ‘pure’ frequencies because when developing asteroseismic modelling, only frequencies that come from pulsation, i.e. pure frequencies, can be accurately calculated and thus used. Removing the couplings, the harmonics, and the splitting corresponding to p1, we retain a total of 15 independent frequencies in the range of 10.9−21.4 c/d, which are depicted in black in Fig. 10.
 |
Fig. 10. Amplitude versus frequency diagram zoomed into the δ Sct range of [10−25] c/d. Black lines represent the pure p mode frequencies found in this range. Grey data corresponds to the frequency spectrum obtained from the FT. |
Combinations between p modes and harmonics.
4.4. P- and g-mode combinations
The coupling between p and g modes was originally proposed as a way to explore g modes in the Sun (see Kennedy et al. 1993 and, more recently, Fossat et al. 2017). According to these studies, internal solar g modes produce a frequency modulation in p modes, which results in a pair of side lobes symmetrically placed about each p-mode frequency. We explored this feature of g modes in p modes by searching combinations of frequencies in the δ Sct domain. We found these combinations in the form of p1 ± gi, with i = 1, 2, 3 and p1 − g4 and p1 − g7. The list of coupled p and g modes is given in Table 7. This same interaction has also been found in two other hybrid stars, namely CoRoT-100866999 and CoRoT-105733033 studied in detail in Chapellier & Mathias (2013) and Chapellier et al. (2012), respectively. This indicates that the coupling mechanism first proposed by Kennedy et al. (1993) also operates in hybrid δ Sct and γ Dor stars.
p- and g-mode coupling for the highest amplitude frequency.
Is important to notice that the detection of a combination of p and g modes, i.e. pi ± gj, implies that pi and gj originated in the same star. Additionally, we found one frequency between the δ Sct and γ Dor domains, i1 = 5.038 c/d in Table A.1, whose position on the frequency spectrum did not allow us to safely classify it.
5. Interpretation of frequency data
5.1. Rotational period and critical velocity
The analysis of low frequencies in A–F stars is a tricky task. It requires several considerations, especially when analysing hybrid pulsators, and this problem arises not only with CoRoT observations but also with TESS data. Many phenomena can mimic stellar oscillations and additional data than photometry is required to disentangle the possible phenomena (Skarka et al. 2022).
In Sect. 4.1, we interpret the period found, Prot = 3.064 d, or frot = 0.326 c/d, in two different ways: according to the rotational period of the star or the orbital period of a binary system. Given that the splitting found can also be interpreted as tidally deformed oscillation modes that have variable amplitude over the orbit of a binary system, we could not rule out the possibility of CoRoT 102314644 being a binary system.
With the aim of further testing the case of a single star, we calculated the rotational and critical velocities for the values obtained in Sect. 2. By considering the estimated radius, R⋆ ∼ 2.27 R⊙, we obtain a linear rotational velocity (v = 2πR/Prot) of ∼37 km s−1. In this case, the corresponding rotational critical velocity (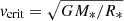 ) for a mass of 1.75 M⋆ would be ∼383 km s−1, meaning that the linear velocity is less than 10% of the critical velocity.
) for a mass of 1.75 M⋆ would be ∼383 km s−1, meaning that the linear velocity is less than 10% of the critical velocity.
The effect of rotation in main-sequence stars varies parameters involved in the modelling of stars such as the mean period spacing and the splitting of p modes, even at linear velocities that are a low percentage of the critical velocity. Nevertheless, in this work we present a preliminary model of CoRoT 102314644 without considering rotation as a first approximation.
5.2. Use of stellar models to constrain the mass and age
With the aim of performing a preliminary modelling of CoRoT 102314644, we first explored the position of this star in the HR diagram for masses and overshooting parameters. The stellar structure and evolution models were calculated with Cesam2k code (Morel & Lebreton 2008)3. We considered masses between 1.5 and 1.8 M⊙ with a mass step of 0.05 M⊙ and overshoot parameters of α = 0.0, 0.1, and 0.3. Overshooting phenomena were considered as an extent of the chemical mixing region around the convective core through the expression for the overshooting distance
where Hp is the local pressure scale height and rS is the Schwarzschild limit of the core.
Figure 11 shows the HR diagram with the evolutionary sequences for different masses and overshooting parameters from the pre-main sequences up to an abundance of H of 10−6 in the core, along with the error boxes centred on the values of log(L/L⊙) and log(Teff) derived in Sect. 2. In order to find a representative model for CoRoT 102314644, we selected different models indicated with circles inside the box shown in Fig. 11, and then we calculated their oscillation modes with GYRE code (Townsend & Teitler 2013). We computed adiabatic radial and non-radial (ℓ = 0, 1 and 2) p and g modes in the [0.3, 23] c/d frequency range, thus encompassing the range of observed frequencies.
 |
Fig. 11. HR diagram showing evolutionary sequences for different stellar masses. Sequences shown in solid lines correspond to cases without overshooting, while those in short-dashed lines have αov = 0.1 and long-dashed lines correspond to evolutionary sequences with αov = 0.3. The box indicates the values of log(Teff) and log(L/L⊙) derived in Sect. 2. Colour-coding shows the age of each evolutionary sequence. Selected models listed in Table 8 are shown by diamonds. The green circle shows the position of our best-fit model (see main text). |
5.3. Asteroseismic analysis
The presence of a series of equidistant periods in CoRoT 102314644 (see Sect. 4.2) provides us with a useful tool for the search of a representative model, 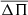 , the mean period spacing of high-order g modes. As stars evolve in the main sequence and consume H in the core, the Brunt–Väisälä (B–V) frequency, which governs the behaviour of g modes, is affected by the change of the convective core. For masses greater than ∼1.5 M⊙, the core shrinks and its edge moves inward as the star evolves. The period can be expressed as
, the mean period spacing of high-order g modes. As stars evolve in the main sequence and consume H in the core, the Brunt–Väisälä (B–V) frequency, which governs the behaviour of g modes, is affected by the change of the convective core. For masses greater than ∼1.5 M⊙, the core shrinks and its edge moves inward as the star evolves. The period can be expressed as
where N is the Brunt–Väisälä frequency, and a and b are the lower and upper boundaries of the propagation zone of the g mode. Thus, during the evolution, the integral increases since it expands toward inner regions resulting in a decreasing period and therefore a decreasing period spacing of g (see Miglio et al. 2008, for example).
We used this parameter as an indicator of the evolutionary status of stars at the main sequence (Saio et al. 2015; Kurtz et al. 2014; Sánchez Arias et al. 2017), which allowed us to place constraints in the search for a representative model. For each model inside the box in Fig. 11, we calculated the mean period spacing of g modes for ℓ = 1, 2, as follows:
where Pj and Pi are the closest periods to the extremes inside the observed interval [90878.5:98984.9] s where the asymptotic series lie, and n is the number of periods found in this range. Table 8 summarizes the mass, the overshooting parameter, the age, 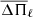 , and the difference between
, and the difference between 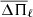 and the value found in Sect. 4.2 for modes with ℓ = 1 and 2 for CoRoT 102314644.
and the value found in Sect. 4.2 for modes with ℓ = 1 and 2 for CoRoT 102314644.
Parameters studied for the models considered.
Another parameter we employed to select our best model is the ratio between the period spacing for ℓ = 1 and ℓ = 2, which should be equal to 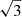 in the asymptotic regime. We also included this value in Table 8 for the selected models. We decided to use this criterion due to the possible deviation from the asymptotic regime with the adopted search. Our model was selected by the one with the lowest Dl = 2 among those ones closest to
in the asymptotic regime. We also included this value in Table 8 for the selected models. We decided to use this criterion due to the possible deviation from the asymptotic regime with the adopted search. Our model was selected by the one with the lowest Dl = 2 among those ones closest to 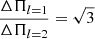 . This model has 1.75 M⊙, no core overshooting, 1241.24 × 106 yr and its luminosity and radius are 11.36 L⊙ and 2.48 R⊙. We notice that mode-trapping or other internal mode-selection mechanisms might prevent us from detecting more periods belonging to the observed asymptotic series resulting in a mean period spacing of g modes apart from the asymptotic value.
. This model has 1.75 M⊙, no core overshooting, 1241.24 × 106 yr and its luminosity and radius are 11.36 L⊙ and 2.48 R⊙. We notice that mode-trapping or other internal mode-selection mechanisms might prevent us from detecting more periods belonging to the observed asymptotic series resulting in a mean period spacing of g modes apart from the asymptotic value.
6. Summary and conclusions
In this work, we present a detailed analysis of the light curve of CoRoT 102314644 and its frequencies. This star exhibits a rich frequency spectrum, with characteristics typical of hybrid δ Sct-γ Dor stars. Such objects offer a great opportunity to explore both the outer regions as well as their deep interiors, due to the simultaneous presence of p and g modes. We performed an in-depth analysis of the frequency and variable content of the time series.
– We detected two separate frequency domains, corresponding to γ Dor domain and δ Sct-type oscillations. We detected 26 pure frequencies in the γ-Dor range of [0.32, 3.66] c/d, and 15 pure frequencies in the δ-Sct range [9.38, 21.39] c/d (Fig. 3 and Table A.1).
– In the γ Dor domain, we found an asymptotic series of six equidistant periods with a mean separation of 1621 s ± 20 s (Fig. 8 and Table 3), which most likely corresponds to ℓ = 2.
– In the δ Sct domain, we found a quintuplet centred in the highest amplitude frequency of this domain, p1. The splitting in the frequencies of this quintuplet suggests that frot = 0.32629 c/d is a rotational frequency (Table 5).
– The phase diagram corresponding to frot (Fig. 4) along with the moving bumps and the amplitude variation from one orbit to another in Fig. 5 suggest the presence of spots in this hybrid star, in the case of frot being a rotational frequency.
– Another remarkable characteristic of this hybrid star is the presence of coupling between p and g modes in the δ Sct domain (Table 7). This phenomenon, probably common among hybrid δ Sct-γ Dor stars, should provide information about their internal structure and the resonant cavities in these kinds of stars.
– We developed a preliminary modelling for CoRoT 102314644 by employing our frequency analysis along with the parameters derived in Sect. 2.2, corrected for extinction. We obtained a mass and age of 1.75 M⊙ and 1241 × 106 yr, without overshooting. The model parameters are L = 11.36 L⊙, Teff = 6726 K, R = 2.48 R⊙, and mean period spacing ΔΠ = 1624 s, which of course reproduce the derived parameters in Sect. 2.2 within their uncertainties.
Finally, we highlight the need to follow up on this star with spectroscopic measurements in order to detect orbital radial velocity deviations from a possible companion or width-line variations over a rotational period from a line corresponding to surface activity in the case of CoRoT 102314644 being a spotted star.
The following physics were considered. The opacities are those from Iglesias & Rogers (1996) and Alexander & Ferguson (1994). We used the equation of state of OPAL project (Rogers et al. 1996) and a nuclear network with the following elements: 1H, 2H, 3He, 4He, 7Li, 7Be, 12C, 13C, and 14N to describe the H (proton-proton chain and CNObi-cycle), and He burning and C ignition with reaction rates extracted from Angulo et al. (1999). In addition, we adopted the classical mixing length theory (MLT; Böhm-Vitense 1958) for convection with a free parameter, α = 1.85. The occurrence of diffusion and mass loss during the evolution was dismissed and the solar metallicity distribution considered Grevesse & Sauval (1998). We used MARCS atmosphere models (Gustafsson et al. 2008). All of our models have initial H and He abundances per mass unit of 0.72 and 0.26, with an initial value of Z/X = 0.0028.
Acknowledgments
J.P.S.A. acknowledges the Henri Poincaré Junior Fellowship Program at the Observatoire de la Côte d’Azur. We thank the referee for their valuable time in reviewing the manuscript and providing suggestions for improvement. The Astronomical Institute Ondřejov is supported by the project RVO:67985815. This paper is dedicated to the memory of Eric Chapellier.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
- Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [Google Scholar]
- Antoci, V., Cunha, M., Houdek, G., et al. 2014, ApJ, 796, 118 [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baker, N., & Kippenhahn, R. 1962, Z. Astrophys., 54, 114 [NASA ADS] [Google Scholar]
- Balona, L. A. 2014, MNRAS, 437, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2015, MNRAS, 452, 3073 [Google Scholar]
- Baran, A. S., & Koen, C. 2021, Acta Astron., 71, 113 [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Borucki, W. J. 2016, Rep. Progr. Phys., 79, 036901 [Google Scholar]
- Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, P. A., Guzik, J. A., Miles, L. F., et al. 2015, AJ, 149, 68 [CrossRef] [Google Scholar]
- Casagrande, L., Lin, J., Rains, A. D., et al. 2021, MNRAS, 507, 2684 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M., & Smith, H. A. 2015, Pulsating Stars (Wiley-VCH) [Google Scholar]
- Chapellier, E., & Mathias, P. 2013, A&A, 556, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapellier, E., Mathias, P., Weiss, W. W., Le Contel, D., & Debosscher, J. 2012, A&A, 540, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chowdhury, S., Joshi, S., Engelbrecht, C. A., et al. 2018, Ap&SS, 363, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danielski, C., Babusiaux, C., Ruiz-Dern, L., Sartoretti, P., & Arenou, F. 2018, A&A, 614, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2004, A&A, 414, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossat, E., Boumier, P., Corbard, T., et al. 2017, A&A, 604, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giles, H. A. C., Collier Cameron, A., & Haywood, R. D. 2017, MNRAS, 472, 1618 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grigahcène, A., Antoci, V., Balona, L., et al. 2010, ApJ, 713, L192 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJ, 542, L57 [Google Scholar]
- Handler, G., Balona, L. A., Shobbrook, R. R., et al. 2002, MNRAS, 333, 262 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Kaye, A. B., Handler, G., Krisciunas, K., Poretti, E., & Zerbi, F. M. 1999, PASP, 111, 840 [Google Scholar]
- Kennedy, J. R., Jefferies, S. M., & Hill, F. 1993, ASP Conf. Ser., 42, 273 [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [Google Scholar]
- Kurtz, D. W., Shibahashi, H., Murphy, S. J., Bedding, T. R., & Bowman, D. M. 2015, MNRAS, 450, 3015 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Babusiaux, C., Vergely, J. L., et al. 2019, A&A, 625, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [Google Scholar]
- Li, G., Bedding, T. R., Murphy, S. J., et al. 2019, MNRAS, 482, 1757 [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [Google Scholar]
- Morris, S. L. 1985, ApJ, 295, 143 [Google Scholar]
- Ouazzani, R.-M., Marques, J. P., Goupil, M.-J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E., Hümmerich, S., Bernhard, K., & Walczak, P. 2017, MNRAS, 468, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [Google Scholar]
- Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
- Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., & Lee, U. 2018, MNRAS, 474, 2774 [Google Scholar]
- Sánchez Arias, J. P., Córsico, A. H., & Althaus, L. G. 2017, A&A, 597, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skarka, M., Žák, J., Fedurco, M., et al. 2022, A&A, 666, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
- Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiong, D. R., Deng, L., Zhang, C., & Wang, K. 2016, MNRAS, 457, 3163 [Google Scholar]
Appendix A: Additional table
Complete list of stellar frequencies.
All Tables
All Figures
 |
Fig. 1. CoRoT 102314644 in the sky. Upper: star map showing the star’s position and coordinates from the ExoDAT database. Lower: star map showing a slightly wider view, along with the Gaia DR2 identified sources (red). |
| In the text | |
 |
Fig. 2. Light curve of the star CoRoT 102314644 corrected for long-term trends and outliers (see main text) for different timescales. From top to bottom, the complete light curve over 148 d, then a set over 20 d, and finally a zoomed-in view of the 5 d subset. |
| In the text | |
 |
Fig. 3. First Fourier transform of CoRoT 102314644. |
| In the text | |
 |
Fig. 4. Phase diagram using rotational frequency frot = 0.326 c/d after removing of all the pulsational frequencies. |
| In the text | |
 |
Fig. 5. Extract of light curve corresponding to three rotational periods separated with vertical lines. We used the residuals after removing all pulsational frequencies of the binned data. |
| In the text | |
 |
Fig. 6. Data phased with F18 = 0.46385 c/d, a frequency possibly related to spots in the γ Doradus domain using different scale rages. |
| In the text | |
 |
Fig. 7. Amplitude versus frequency in γ Dor range of [0−4] c/d. Black lines represent all the g-mode frequencies found in this range. Grey data correspond to the frequency spectrum obtained from the FT. |
| In the text | |
 |
Fig. 8. Asymptotic series found in CoRoT 102314644. Top Panel: period versus an arbitrary radial order for the equally spaced series of periods founded. Bottom panel: forward period spacing versus radial order. The horizontal red line indicates the average period spacing along with the associated error in dashed lines. |
| In the text | |
 |
Fig. 9. Data phased with F1 = 11.3910 c/d, the highest amplitude frequency in the δ Scuti domain. |
| In the text | |
 |
Fig. 10. Amplitude versus frequency diagram zoomed into the δ Sct range of [10−25] c/d. Black lines represent the pure p mode frequencies found in this range. Grey data corresponds to the frequency spectrum obtained from the FT. |
| In the text | |
 |
Fig. 11. HR diagram showing evolutionary sequences for different stellar masses. Sequences shown in solid lines correspond to cases without overshooting, while those in short-dashed lines have αov = 0.1 and long-dashed lines correspond to evolutionary sequences with αov = 0.3. The box indicates the values of log(Teff) and log(L/L⊙) derived in Sect. 2. Colour-coding shows the age of each evolutionary sequence. Selected models listed in Table 8 are shown by diamonds. The green circle shows the position of our best-fit model (see main text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



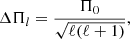
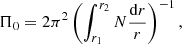
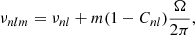
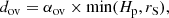
![$$ \begin{aligned} \Pi _n \approx \frac{2 \pi ^2 |n|}{\sqrt{l(l+1)}} \left[\int _a^b\frac{N}{r}\mathrm{d}r\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2023/08/aa41610-21/aa41610-21-eq9.gif)