| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A190 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346676 | |
| Published online | 21 July 2023 | |
Deuterium fractionation across the infrared-dark cloud G034.77−00.55 interacting with the supernova remnant W44
1
Department of Space, Earth and Environment, Chalmers University of Technology,
412 96
Gothenburg, Sweden
e-mail: giuliana.cosentino@chalmers.se
2
Department of Astronomy, University of Virginia,
530 McCormick Road Charlottesville,
22904-4325,
USA
3
Centro de Astrobiología (CSIC/INTA),
Ctra. de Torrejón a Ajalvir km 4,
Madrid, Spain
4
INAF Osservatorio Astronomico di Arcetri,
Largo E. Fermi 5,
50125
Florence, Italy
5
Max Planck Institute for Extraterrestrial Physics,
Giessenbachstrasse 1,
85748
Garching bei München, Germany
6
Astrophysics Research Institute, Liverpool John Moores University,
146 Brownlow Hill,
Liverpool
L3 5RF, UK
7
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
8
European Southern Observatory,
Karl-Schwarzschild-Strasse 2,
85748
Garching, Germany
9
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden, The Netherlands
10
Department of Physics and Astronomy, University College London,
Gower Street,
London,
WC1E 6BT, UK
11
Instituto de Astrofísica de Andalucía, CSIC,
Glorieta de la Astronomía s/n,
18008
Granada, Spain
12
Star and Planet Formation Laboratory, Cluster for Pioneering Research, RIKEN,
2-1 Hirosawa, Wako,
Saitama,
351-0198, Japan
Received:
17
April
2023
Accepted:
31
May
2023
Context. Supernova remnants (SNRs) may regulate star formation in galaxies. For example, SNR-driven shocks may form new molecular gas or compress pre-existing clouds and trigger the formation of new stars.
Aims. To test this scenario, we measured the deuteration of N2H+, DfracN2H+ – a well-studied tracer of pre-stellar cores – across the infrared-dark cloud (IRDC) G034.77-00.55, which is known to be experiencing a shock interaction with the SNR W44.
Methods. We use N2H+ and N2D+J = 1−0 single pointing observations obtained with the 30m antenna at the Instituto de Radioas-tronomia Millimetrica to infer DfracN2H+ towards five positions across the cloud, namely a massive core, different regions across the shock front, a dense clump, an+d ambient gas.
Results. We find DfracN2H+ in the range 0.03−0.1, which is several orders of magnitude larger than the cosmic D/H ratio (~10−5). The DfracN2H+ across the shock front is enhanced by more than a factor of 2 (DfracN2H+ ~ 0.05 - 0.07) with respect to the ambient gas (≤0.03) and simila+r to that measured generally in pre-stellar cores. Indeed, in the massive core and dense clump regions of this IRDC we measure DfracN2H+ ~ 0.01.
Conclusions. We find enhanced deuteration of N2H+ across the region of the shock, that is, at a level that is enhanced with respect to regions of unperturbed gas. It is possible that this has been induced by shock compression, which would then be indirect evidence that the shock is triggering conditions for future star formation. However, since unperturbed dense regions also show elevated levels of deuteration, further, higher-resolution studies are needed to better understand the structure and kinematics of the deuterated material in the shock region; for example, to decipher whether it is still in a relatively diffuse form or is already organised in a population of low-mass pre-stellar cores.
Key words: astrochemistry / ISM: clouds / ISM: supernova remnants / ISM: individual objects: G34.77-00.55 / ISM: individual objects: W44 / stars: formation
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Infrared-dark clouds (IRDCs) are dense (nH ≥ 104 cm−3; Butler & Tan 2012) and cold (T ≤ 20 K; Pillai et al. 2006) regions of the interstellar medium (ISM) that have high column densities and extinctions and can therefore appear dark against the diffuse Galactic mid-infrared background. IRDCs are the densest regions of giant molecular clouds (GMCs) and are known to host the formation of low-, intermediate-, and high-mass stars (e.g. Tan et al. 2013; Foster et al. 2014; Pillai et al. 2019; Moser et al. 2020; Yu et al. 2020). Despite their importance for the stellar content of galaxies (e.g. Tan et al. 2014; Hernandez & Tan 2015; Peretto et al. 2016; Retes-Romero et al. 2020; Morii et al. 2021), it is still unclear as to how star formation is initiated therein.
One possible scenario that may lead to the initiation of star formation in IRDCs involves compression due to internal cloud turbulence (e.g. Krumholz & McKee 2005). Another is rooted in the decay of turbulent and/or magnetic support, perhaps associated with the global collapse of a recently formed GMC (e.g. Vázquez-Semadeni et al. 2011). Yet another scenario is characterised by triggered compression by galactic-shear-driven GMC–GMC collisions (Tan 2000), with various numerical simulation studies of this process carried out by for example Tasker & Tan (2009) and Wu et al. (2015, 2017). The involvement of an external agent to a given GMC, such as collision with another GMC, can help explain the large dispersion in star formation activity in GMC populations (e.g. Tan 2000; Lee et al. 2016). Finally, it has also been proposed that IRDC and star formation are triggered by stellar-feedback-driven shocks, for example in HII regions or supernova remnants (e.g. Inutsuka et al. 2015). In systems like the Milky Way, where the global star formation rate (SFR) is relatively low compared to the amount of dense gas available (Zuckerman & Evans 1974; Krumholz & Tan 2007), stellar-feedback-driven star formation is unlikely to account for the majority of star formation, because if it did, the SFR would grow exponentially to large values. Nevertheless, the process may occur occasionally, and such instances can provide important information; for example, as to whether the star formation process varies when triggered in this way.
There are a number of recent observational studies presenting evidence for instances of IRDC and star formation triggered by SNR-driven shocks (e.g. Cosentino et al. 2019, 2022; Rico-Villas et al. 2020). Cosentino et al. (2019) investigated how the shock driven by the SNR W44 affects the physical conditions of the interacting cloud, the IRDC G034.77-00.55 (hereafter G34.77 or IRDC G from the sample of Butler & Tan 2012). Towards this source, the shock interaction is occurring at the edge of the IRDC, that is, towards an arch-like ridge with no signatures of deeply embedded protostars (Cosentino et al. 2018, 2019; Barnes et al. 2021). Using ALMA images of silicon monoxide (SiO), Cosentino et al. (2019) studied the shocked gas kinematics and inferred a shock velocity of ~20 km s−1, which is compatible with that previously estimated by Sashida et al. (2013), and a shock dynamical age of ~1.5 × 104 yr. From C180 observations, the authors estimated a density enhancement – caused by the shock – of a factor of >10; with post-shocked volume densities of n(H2) > 105 cm−3.
In this paper, we investigate how the SNR-driven shock may be affecting the chemical properties of the molecular gas. A well-studied tracer of the chemical conditions at the onset of star formation is the fraction of deuterium with respect to hydrogen (D/H) measured from N2H+ and N2D+ emission (hereafter 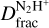 ).
). 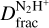 , defined as the ratio of the column densities of the deuterated and non-deuterated species, is highly enhanced in pre-stellar cores (i.e. with values of ~0.1; Crapsi et al. 2005; Caselli et al. 2008; Emprechtinger et al. 2009) compared to the cosmic D/H abundance (of ~1·0−5; Oliveira et al. 2003). This is due to a combination of low temperatures (T ≤ 20 K) and high densities (n(H2) ≥ 104 cm−3), which are typical of the pre-stellar phase, and lead to high levels of CO freeze-out onto dust grains (e.g. Caselli et al. 1999). With the CO largely depleted, reactions between N2 and
, defined as the ratio of the column densities of the deuterated and non-deuterated species, is highly enhanced in pre-stellar cores (i.e. with values of ~0.1; Crapsi et al. 2005; Caselli et al. 2008; Emprechtinger et al. 2009) compared to the cosmic D/H abundance (of ~1·0−5; Oliveira et al. 2003). This is due to a combination of low temperatures (T ≤ 20 K) and high densities (n(H2) ≥ 104 cm−3), which are typical of the pre-stellar phase, and lead to high levels of CO freeze-out onto dust grains (e.g. Caselli et al. 1999). With the CO largely depleted, reactions between N2 and 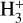 (and its deuterated form H2D+) can efficiently occur, boosting the formation of N2D+ (e.g. Dalgarno & Lepp 1984; Caselli et al. 2002; Walmsley et al. 2004).
(and its deuterated form H2D+) can efficiently occur, boosting the formation of N2D+ (e.g. Dalgarno & Lepp 1984; Caselli et al. 2002; Walmsley et al. 2004).  is therefore considered an optimal tracer of the evolutionary phase of both low- and high-mass star forming objects (Fontani et al. 2011; Tan et al. 2013; Giannetti et al. 2019).
is therefore considered an optimal tracer of the evolutionary phase of both low- and high-mass star forming objects (Fontani et al. 2011; Tan et al. 2013; Giannetti et al. 2019).
Here, we estimate 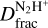 in several regions of the IRDC G34.77. To the best of our knowledge, no previous studies have investigated
in several regions of the IRDC G34.77. To the best of our knowledge, no previous studies have investigated 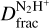 in shocks driven by SNRs. However, previous studies have measured D/H in other species in shocks associated with molecular outflows (e.g. Codella et al. 2013; Fontani et al. 2014; Busquet et al. 2017). In these environments, the shock passage causes the release into the gas phase of deuterated species whose formation occurs on the icy mantle of dust grains; for example, deuterated counterparts of CH3OH and H2CO (Fontani et al. 2014; Busquet et al. 2017). The sputtering and grain–grain collision processes enabled in shocks increase the CO abundance in the gas phase and the formation of N2D+ is therefore expected to be suppressed. However, at the high densities reached in the post-shocked gas, gas-phase chemistry can proceed at a much faster rate and the CO depletion timescales can be shortened (Lis et al. 2002, 2016). This may therefore result in enhanced abundances of N2D+.
in shocks driven by SNRs. However, previous studies have measured D/H in other species in shocks associated with molecular outflows (e.g. Codella et al. 2013; Fontani et al. 2014; Busquet et al. 2017). In these environments, the shock passage causes the release into the gas phase of deuterated species whose formation occurs on the icy mantle of dust grains; for example, deuterated counterparts of CH3OH and H2CO (Fontani et al. 2014; Busquet et al. 2017). The sputtering and grain–grain collision processes enabled in shocks increase the CO abundance in the gas phase and the formation of N2D+ is therefore expected to be suppressed. However, at the high densities reached in the post-shocked gas, gas-phase chemistry can proceed at a much faster rate and the CO depletion timescales can be shortened (Lis et al. 2002, 2016). This may therefore result in enhanced abundances of N2D+.
This article is organised as follows. In Sect. 2, we describe the observations and discuss the selection of positions across the cloud+. In Sect. 3, we describe the method applied to estimate 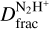 . In Sect. 4, we report and discuss our results. Finally, in Sect. 5, we present our conclusions.
. In Sect. 4, we report and discuss our results. Finally, in Sect. 5, we present our conclusions.
Equatorial coordinates of the five positions analysed in this work.
 |
Fig. 1 Three-colour image of G34.77. Red is 24 µm emission (Spitzer MIPSGAL; Carey et al. 2009), green is 8 µm emission (Spitzer GLIMPSE; Churchwell et al. 2009), and blue is 1 GHz continuum emission (THOR survey; Beuther et al. 2016; black contours from 3 to 27 Jy beam−1 by 6 Jy beam−1 ). The continuum emission probes the gas associated with the expanding shell of the SNR. The magenta contour (AV = 20 mag Kainulainen & Tan 2013) highlights the cloud shape. Superimposed on the map are the five positions of interest (white circles; 34″ IRAM 30 m beam at the N2D+ frequency of 77.112 GHz). The cyan contours correspond to the ALMA SiO contours from Cosentino et al. (2019; from 0.05 to 0.3 Jy beam−1 by 0.05 Jy beam−1). |
2 Observations and target selection
In March 2020, we observed the J = 1 → 0 rotational transitions of N2H+ and N2D+ towards five positions across the IRDC G34.77 (Table 1). These positions (white circles) are shown in Fig. 1 and listed in Table 1. These were selected to probe different environments across G34.77, namely the known massive core G3 characterised by Butler & Tan (2012), unperturbed gas within the cloud (referred to here as ‘Ambient’), a dense clump adjacent to the shock front (‘Clump’; Barnes et al. 2021), and two regions across the shock front seen by ALMA, that is, the ‘Shock’ and the ‘Ridge’ (Cosentino et al. 2019). The core G3, first detected as a point-like source, MM4, in the 1.2 mm images presented by Rathborne et al. (2006), shows no evidence of a central protostellar source. This is indicated by the lack of point-like 8 (Rathborne et al. 2006), 24 µm or 4.5 µm (Chambers et al. 2009) sources or SiO emission (Cosentino et al. 2018). Towards the Clump, Barnes et al. (2021) report no evidence of 3 mm continuum and IR emission, indicating that the region is not harbouring deeply embedded protostars. Therefore, G3 and the Clump may be representative of starless regions. However, we note that since 1.2 mm continuum emission is detected towards G3, this may be at an evolutionary stage that is more advanced than the Clump. The Shock position corresponds to the region where the higher velocity shocked material (SiO at ~44–45 km s−1) is found. The Ridge position corresponds to the low-density structure that is almost detached from the main body of the cloud and into which the shock is plunging (SiO at ~39–40 km s−1). Finally, the Ambient position is representative of dense unperturbed material within the IRDC.
Towards the five positions, we used the 30 m single-dish antenna at Instituto de Radioastronomia Millimetrica (IRAM-30 m, Pico Veleta, Spain) to obtain single-pointing N2H+(1−0) and N2D+(1−0) spectra in position switching mode (off-position RA(J2000) = 18h57m01s, Dec(J2000) = 1d22m25s). The angular resolution of the 30 m antenna is 34″ and 27″ at the N2D+ and N2H+ frequencies, respectively. These correspond to a linear spatial resolution of 0.4–0.5 pc at the distance of G34.77, of namely 2.9 kpc (Rathborne et al. 2006). The FTS spectrometer was used with a frequency resolution of 200 kHz, which corresponds to a velocity resolution of between 0.7 and 0.8 km s−1. Intensities were measured in units of antenna temperature, 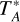 , and converted into main-beam brightness temperature, Tmb, using beam and forward efficiencies of 0.81 and 0.95, respectively. The final spectra were produced using the CLASS software within the GILDAS package1 and have a final velocity resolution of 0.8 km s−1. The achieved rms per channel, σrms, is 7 and 5 mK for the N2H+ and N2D+ spectra, respectively.
, and converted into main-beam brightness temperature, Tmb, using beam and forward efficiencies of 0.81 and 0.95, respectively. The final spectra were produced using the CLASS software within the GILDAS package1 and have a final velocity resolution of 0.8 km s−1. The achieved rms per channel, σrms, is 7 and 5 mK for the N2H+ and N2D+ spectra, respectively.
 |
Fig. 2 N2H+ (black curves, top panels) and N2D+ (black curves, bottom panels) obtained towards the five positions. The IRDC G34.77 central velocity is indicated as a vertical dotted line in all panels. The red curves show the best LTE fitting models obtained by MADCUBA. The green curves show the Gaussian fitting obtained for the isolated component. For the Shock, Ridge, and Clump positions, we report the SiO(2−1) spectra (orange filled) extracted from the ALMA images (Cosentino et al. 2019) towards an angular region consistent with that of our current observations (34″). In the bottom panels, the SiO spectra have been multiplied by 0.2 to allow a more straightforward comparison with the N2D+ spectra. |
3 Method
The N2H+ (top panels) and N2D+ (bottom panels) spectra obtained towards the five positions are shown in Fig. 2. The orange shadows in Fig. 2 correspond to the SiO(2−1) spectra obtained with ALMA in Cosentino et al. (2019). We detect significant N2H+ and N2D+ emission towards all positions except at the Ambient position, where no N2D+ is observed above a threshold of 3 × Arms, where 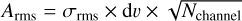 , with dv the velocity resolution of the spectra, and Nchannel ≃ 4 was estimated as the number of channels within a line width of 3 km s−1, which is consistent with that estimated for both the N2H+ and N2D+ emission (see MADCUBA values in Table 4). We note the presence of additional significant line emission at ~35 km s−1 within the N2D+ spectrum towards the Ridge. This component shows a line width of ~2.2 km s−1 (~3 channels), peak intensity of ~0.018 K, and an integrated intensity of ~0.04 K km s−1, that is, ~5 × Arms. We suggest that this line is either due to emission present along the line of sight or to an unknown species.
, with dv the velocity resolution of the spectra, and Nchannel ≃ 4 was estimated as the number of channels within a line width of 3 km s−1, which is consistent with that estimated for both the N2H+ and N2D+ emission (see MADCUBA values in Table 4). We note the presence of additional significant line emission at ~35 km s−1 within the N2D+ spectrum towards the Ridge. This component shows a line width of ~2.2 km s−1 (~3 channels), peak intensity of ~0.018 K, and an integrated intensity of ~0.04 K km s−1, that is, ~5 × Arms. We suggest that this line is either due to emission present along the line of sight or to an unknown species.
From the shown spectra, we estimate 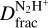 as:
as:
where N(N2D+) and N(N2H+) are the total column densities of these species. To estimate these quantities, we use the software MADCUBA2 (Martin et al. 2019) to fit the hyper-fine structure of the two species. By comparing the line emission with local thermodynamic equilibrium (LTE) models, MADCUBA provides estimates of the species excitation temperature, Tex, column density, N, centroid velocity, vLSR, and line width, Δν. Initially, we fit the N2D+ and N2H+ spectra with just one assumption, namely that the emission fills the beam (filling factor = 1). However, the software is unable to produce reasonable models, as indicated by the high uncertainties in the returned parameters (>200%). This is likely due to the presence of a complex kinematic structure that is not well resolved at the velocity resolution of our observations (0.8 km s−1). We therefore conclude that it is not possible to estimate the excitation temperatures of the two species from a single rotational transition, and assume all lines to have the same Tex = 9 K, as measured from multiple CH3OH transitions detected towards the shock peak in G34.77 (Cosentino et al. 2018). How this assumption affects our results is discussed in Appendix A.
The best LTE fitting models are shown in Fig. 2 (red curves) for the five regions. In Table 3, N(N2D+) and N(N2H+) are reported together with the corresponding 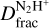 values and the Herschel-derived mass surface densities, Σ, towards the five positions (Lim et al. 2016). The Herschel-derived image has an angular resolution of 18″, but the Σ values listed in Table 3 were extracted from a region with a 34″ aperture, consistent with that of the N2D+ observations.
values and the Herschel-derived mass surface densities, Σ, towards the five positions (Lim et al. 2016). The Herschel-derived image has an angular resolution of 18″, but the Σ values listed in Table 3 were extracted from a region with a 34″ aperture, consistent with that of the N2D+ observations.
We also estimate the N2H+ and N2D+ column densities from Eq. (2), which is Eq. (A4) from Caselli et al. (2002), under the assumption of optically thin emission:
with the partition function, Qrot, defined as:
In Eqs. (2) and (3), ν is the line frequency, Aul is the Einstein coefficient for spontaneous emission and gup is the statistical weight of the upper state. Jv(Tex) and Jv(Tbg) are the equivalent Rayleigh-Jeans excitation and background temperatures (Tbg = 2.73 K), that is Jv(T) = (hv/k)[exp(hv/kT) − 1]−1. J is the rotational state quantum number and EJ = J(J + 1)hB the corresponding state energy, which is calculated from the molecular rotational constant B. Wtot is the integrated intensity of the full rotational transition J = 1−0. Finally, Tex is the line excitation temperature. The spectroscopic quantities for the two species were obtained from the CDMS catalogue3 and are reported in Table 2.
We performed Gaussian fittings of the N2H+ and N2D+ isolated components and calculated the integrated intensity, Wisolated, as the area underneath the Gaussian. We then estimate Wtot by scaling Wisolated for its relative intensity Ri = 1/9. The best Gaussian fitting are reported in Fig. 2 (green curves), while Table 3 lists the N2H+ and N2D+ column densities obtained from Eq. (2) whilst assuming Tex = 9 K (Cosentino et al. 2018) and the associated 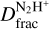 values. The best-fitting parameters obtained with both the MADCUBA and Gaussian fitting analysis are reported in Table 4.
values. The best-fitting parameters obtained with both the MADCUBA and Gaussian fitting analysis are reported in Table 4.
From Table 3, the 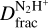 values obtained from the two methods (MADCUBA and Gaussian fitting of isolated components) are in agreement. The only significant discrepancy is found towards the Shock, where the
values obtained from the two methods (MADCUBA and Gaussian fitting of isolated components) are in agreement. The only significant discrepancy is found towards the Shock, where the 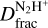 value estimated from the Gaussian fitting method (~0.2) is a factor of 3 larger than that obtained from the MADCUBA analysis (~0.07). Towards this position, the ratio between the intensity of the main and isolated N2D+ components is smaller (~1.2) than that seen towards other positions (~4.5). As a consequence, the N2D+ isolated component towards the Shock is not well reproduced by MADCUBA. This could be due to the isolated component being affected by a random noise spike that coincides with the line position, making it appear enhanced. Alternatively, the N2D+ emission towards the Ridge may need a non-LTE approach, for which the collisional coefficients of N2D+ are not available and multiple rotational transitions are needed. Finally, we exclude the possibility that the N2D+ is blended with another molecular species as no other molecular transitions are found at these frequencies.
value estimated from the Gaussian fitting method (~0.2) is a factor of 3 larger than that obtained from the MADCUBA analysis (~0.07). Towards this position, the ratio between the intensity of the main and isolated N2D+ components is smaller (~1.2) than that seen towards other positions (~4.5). As a consequence, the N2D+ isolated component towards the Shock is not well reproduced by MADCUBA. This could be due to the isolated component being affected by a random noise spike that coincides with the line position, making it appear enhanced. Alternatively, the N2D+ emission towards the Ridge may need a non-LTE approach, for which the collisional coefficients of N2D+ are not available and multiple rotational transitions are needed. Finally, we exclude the possibility that the N2D+ is blended with another molecular species as no other molecular transitions are found at these frequencies.
Finally, in addition to the statistical uncertainty reported by MADCUBA for the N2H+ and N2D+ column densities, we also consider the systematic uncertainty due to the assumption Tex = 9 K. A ± 30% variation of Tex, that is variation within the range of 6–12 K, would result in a 5–10% variation of the N2H+ column density and 3–10% in the N2D+ column densities. Hence, we assume a systematic uncertainty of 10% and add this in quadrature to the statistical errors. The obtained total uncertainties on the column density values are then propagated – with standard Gaussian rules – in order to estimate the uncertainties on 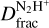 . The final values are reported in Table 3.
. The final values are reported in Table 3.
Spectroscopic information of the targeted species as obtained from the CDMS catalogue.
4 Results and discussion
Towards all positions, we obtain D/H values that are several orders of magnitude larger than the cosmic D/H abundance. We find 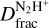 in the range ~0.05–0.1 towards G3, the Shock, the Ridge, and the Clump. For the Ambient gas, we estimate an upper limit of 0.03. These resu+lts are shown in Fig. 3, where we compare the obtained
in the range ~0.05–0.1 towards G3, the Shock, the Ridge, and the Clump. For the Ambient gas, we estimate an upper limit of 0.03. These resu+lts are shown in Fig. 3, where we compare the obtained 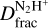 estimates with those typically observed in low-mass starless cores (LMSCs; Crapsi et al. 2005; Fontani et al. 2006; Friesen et al. 2013; Cheng et al. 2021), high-mass starless cores (HMSCs; Fontani et al. 2011; Kong et al. 2016), high-mass protostellar objects (HMPOs; Fontani et al. 2011), low-mass protostellar objects (LMPOs; Emprechtinger et al. 2009; Friesen et al. 2013) and large-scale regions of IRDCs (Miettinen et al. 2011; Gerner et al. 2015; Barnes et al. 2016).
estimates with those typically observed in low-mass starless cores (LMSCs; Crapsi et al. 2005; Fontani et al. 2006; Friesen et al. 2013; Cheng et al. 2021), high-mass starless cores (HMSCs; Fontani et al. 2011; Kong et al. 2016), high-mass protostellar objects (HMPOs; Fontani et al. 2011), low-mass protostellar objects (LMPOs; Emprechtinger et al. 2009; Friesen et al. 2013) and large-scale regions of IRDCs (Miettinen et al. 2011; Gerner et al. 2015; Barnes et al. 2016).
In Fig. 4, we show 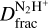 as a function of mass surface density, Σ. From Fig. 4 and Table 3, the Shock and Ridge show an Σ value that is lower than or similar to that found for the Ambient region. Hence,
as a function of mass surface density, Σ. From Fig. 4 and Table 3, the Shock and Ridge show an Σ value that is lower than or similar to that found for the Ambient region. Hence, 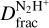 would be expected to be lower than or comparable to that measured towards the Ambient region. However, an opposite trend is seen in Fig. 4. Towards the Shock, the N(N2H+) is similar to that estimated for the Ambient gas, but the N(N2D+) is enhanced by at least a factor of 2. Towards the Ridge, the N2H+ column density is significantly larger than that reported towards the Ambient gas within the uncertainties, indicating the presence of more dense material towards this region. At the same time, the N2D+ column density towards this position is more than a factor of ~3 larger than that measured for the Ambient gas. As a consequence,
would be expected to be lower than or comparable to that measured towards the Ambient region. However, an opposite trend is seen in Fig. 4. Towards the Shock, the N(N2H+) is similar to that estimated for the Ambient gas, but the N(N2D+) is enhanced by at least a factor of 2. Towards the Ridge, the N2H+ column density is significantly larger than that reported towards the Ambient gas within the uncertainties, indicating the presence of more dense material towards this region. At the same time, the N2D+ column density towards this position is more than a factor of ~3 larger than that measured for the Ambient gas. As a consequence, 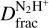 towards the two positions is enhanced (but within the uncertainty) with respect to the unperturbed gas within the cloud. These differences indicate that, towards the Shock and the Ridge, additional processes may be boosting the production of D-bearing species with respect to the unperturbed Ambient gas.
towards the two positions is enhanced (but within the uncertainty) with respect to the unperturbed gas within the cloud. These differences indicate that, towards the Shock and the Ridge, additional processes may be boosting the production of D-bearing species with respect to the unperturbed Ambient gas.
This enhanced 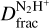 may be produced in the fast-cooling post-shocked gas, where the shock has compressed the gas to densities of n(H2) > 105 cm−3. This high density is expected to shorten the CO depletion timescale and boost the production of N2D+ (Lis et al. 2002, 2016). For the post-shocked density n(H2) ≥ 105 cm−3 measured in Cosentino et al. (2019), the CO depletion timescale is expected to be ≤104 yr (Caselli et al. 1999), which is consistent with the shock dynamical age (Cosentino et al. 2019). On the other hand, as reported by Codella et al. (2013) towards the molecular outflow shock L1157-B1, N2H+ is expected to be a fossil record of the pre-shocked gas that has been compressed. These two effects together result in an enhanced
may be produced in the fast-cooling post-shocked gas, where the shock has compressed the gas to densities of n(H2) > 105 cm−3. This high density is expected to shorten the CO depletion timescale and boost the production of N2D+ (Lis et al. 2002, 2016). For the post-shocked density n(H2) ≥ 105 cm−3 measured in Cosentino et al. (2019), the CO depletion timescale is expected to be ≤104 yr (Caselli et al. 1999), which is consistent with the shock dynamical age (Cosentino et al. 2019). On the other hand, as reported by Codella et al. (2013) towards the molecular outflow shock L1157-B1, N2H+ is expected to be a fossil record of the pre-shocked gas that has been compressed. These two effects together result in an enhanced 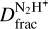 towards the Shock and the Ridge. In accordance with this scenario, the CO depletion factor towards the two positions is in the range of ~4–6. We obtained CO depletion maps obtained towards G34.77 using 13CO(1−0) and C18O(1−0) emission maps from the Green Bank Telescope and these will be presented in a forthcoming paper (Petrova et al., in prep.). We converted the 13CO(1−0) and C18O(1−0) maps into column densities assuming an excitation temperature of 7.5 Κ and using the mass surface density maps derived from Herschel data (Lim et al. 2016).
towards the Shock and the Ridge. In accordance with this scenario, the CO depletion factor towards the two positions is in the range of ~4–6. We obtained CO depletion maps obtained towards G34.77 using 13CO(1−0) and C18O(1−0) emission maps from the Green Bank Telescope and these will be presented in a forthcoming paper (Petrova et al., in prep.). We converted the 13CO(1−0) and C18O(1−0) maps into column densities assuming an excitation temperature of 7.5 Κ and using the mass surface density maps derived from Herschel data (Lim et al. 2016).
Finally, both the N2H+ and N2D+ centroid velocities towards the Ridge (Table 4) are consistent with the velocity of the post-shocked gas (~40 km s−1; Cosentino et al. 2019). Toward the Shock, both the N2H+ and N2D+ emission show higher velocities of ~42 km s−1, but this still consistent with the lowest velocities (which are associated with the most downstream post-shocked gas) reached by the SiO towards that region (Fig. 2). We note that the N2H+ column density towards the Ridge is a factor 1.5 larger than that measured towards the Shock. This may simply reflect the decreasing amount of dense gas at the cloud outskirts (from the Ridge to the Shock) and/or a larger compression of the gas towards the Ridge. Indeed, here the shock velocities probed by SiO reach even lower values (down to 39 km s−1; Cosentino et al. 2019).
The high 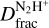 across the shock front may also be explained by the presence of a population of starless cores. In this parallel scenario, we speculate that the denser cooled-down post-shocked material is not diffuse but is rather organised into low-mass cores, whose formation may have been triggered by the shock passage that compresses gas to high densities (Cosentino et al. 2019).
across the shock front may also be explained by the presence of a population of starless cores. In this parallel scenario, we speculate that the denser cooled-down post-shocked material is not diffuse but is rather organised into low-mass cores, whose formation may have been triggered by the shock passage that compresses gas to high densities (Cosentino et al. 2019).
Furthermore, as shown in Fig. 4, the 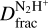 estimates towards the Shock (blue circle) and the Ridge (blue plus) are consistent with those previously measured towards LMSCs (orange circles Crapsi et al. 2005; Fontani et al. 2006; Friesen et al. 2013) and LMPOs (Emprechtinger et al. 2009; Friesen et al. 2013, green circles). However, as no evidence of deeply embedded protostars has been found towards these regions (Cosentino et al. 2019; Barnes et al. 2021), we exclude the possibility that this putative low-mass population could have already reached the protostellar phase.
estimates towards the Shock (blue circle) and the Ridge (blue plus) are consistent with those previously measured towards LMSCs (orange circles Crapsi et al. 2005; Fontani et al. 2006; Friesen et al. 2013) and LMPOs (Emprechtinger et al. 2009; Friesen et al. 2013, green circles). However, as no evidence of deeply embedded protostars has been found towards these regions (Cosentino et al. 2019; Barnes et al. 2021), we exclude the possibility that this putative low-mass population could have already reached the protostellar phase.
We note that the timescale required for a core to reach 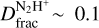 may be as short as 104 yr (Kong et al. 2015) under the physical conditions of density and cosmic ionisation rate similar to those estimated towards the shock in G34.77 (n(H2) ~ 105 cm−3 and ζ ~10−15 s−1; Cosentino et al. 2019) and if the H2 ortho-to-para (OPR) ratio is ≤0.1. However, at the relatively low angular resolution of our observations, it is not possible to distinguish between the two scenarios described above, namely of cooled-down diffuse post-shocked gas or a population of low-mass pre-stellar cores.
may be as short as 104 yr (Kong et al. 2015) under the physical conditions of density and cosmic ionisation rate similar to those estimated towards the shock in G34.77 (n(H2) ~ 105 cm−3 and ζ ~10−15 s−1; Cosentino et al. 2019) and if the H2 ortho-to-para (OPR) ratio is ≤0.1. However, at the relatively low angular resolution of our observations, it is not possible to distinguish between the two scenarios described above, namely of cooled-down diffuse post-shocked gas or a population of low-mass pre-stellar cores.
Towards the Clump, we measure 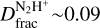 , which is consistent with that measured towards G3 and previously reported towards LMSC, HMSCs, and LMPOs (Fig. 3). The Clump also has a relatively high mass surface density of 0.07 g cm−1 (~60 M⊙ within the 34″ beam), which is consistent with that of G3. Towards this position, Barnes et al. (2021) report a N2H+ emission peak. As the source shows no signatures of point-like emission at 4.5, 8, or 24 µm (Chambers et al. 2009) nor 1 mm (Rathborne et al. 2006) or 3 mm continuum emission (Cosentino et al. 2019; Barnes et al. 2021), we exclude that the Clump may be hosting deeply embedded protostars. Due to its mass, density, lack of IR and mm continuum signatures, and high
, which is consistent with that measured towards G3 and previously reported towards LMSC, HMSCs, and LMPOs (Fig. 3). The Clump also has a relatively high mass surface density of 0.07 g cm−1 (~60 M⊙ within the 34″ beam), which is consistent with that of G3. Towards this position, Barnes et al. (2021) report a N2H+ emission peak. As the source shows no signatures of point-like emission at 4.5, 8, or 24 µm (Chambers et al. 2009) nor 1 mm (Rathborne et al. 2006) or 3 mm continuum emission (Cosentino et al. 2019; Barnes et al. 2021), we exclude that the Clump may be hosting deeply embedded protostars. Due to its mass, density, lack of IR and mm continuum signatures, and high 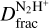 value, we speculate that the Clump may still be evolving into the state of a centrally condensed pre-stellar core. However, it remains to be established whether or not the gas is gravitationally bound or whether or not it will fragment. We note that the Clump is located in the immediate vicinity of the shock front, where the shocked gas seen in SiO (Fig. 1) has already decelerated down to 40 km s−1. However, the N2H+ and N2D+ centroid velocities are not consistent with that of the post-shocked material. They indeed appear more in agreement with those measured towards the inner cloud, that is, G3. We therefore speculate that the Clump may have existed before the interaction with the SNR and has only been marginally affected by the shock.
value, we speculate that the Clump may still be evolving into the state of a centrally condensed pre-stellar core. However, it remains to be established whether or not the gas is gravitationally bound or whether or not it will fragment. We note that the Clump is located in the immediate vicinity of the shock front, where the shocked gas seen in SiO (Fig. 1) has already decelerated down to 40 km s−1. However, the N2H+ and N2D+ centroid velocities are not consistent with that of the post-shocked material. They indeed appear more in agreement with those measured towards the inner cloud, that is, G3. We therefore speculate that the Clump may have existed before the interaction with the SNR and has only been marginally affected by the shock.
The N2H+ and N2D+ line profiles
Table 4 shows the N2H+ and N2D+ centroid velocities, line widths (full width at half maximum) and line peaks obtained from the MADCUBA analysis and the Gaussian fitting method, respectively. The two sets of parameters agree within the velocity resolution of our observations (0.8 km s−1). Figure 5 shows the correlation plots between the N2H+ and N2D+ centroid velocities (left) and line width (right) obtained from the MADCUBA analysis. We see that the centroid velocities of the two species are in agreement within the 0.8 km s−1 velocity resolution. This is also the case for the line widths of the species. The only exception may be represented by the Shock, where the N2H+ emission is slightly broader (3.2 km s−1) than the corresponding N2D+ emission (2.7 km s−1). In the proposed scenarios, this may be due to the fact that the N2H+ also probes gas in the act of being compressed, while the N2D+ does not. These putative complex kinematics are marginally seen in the velocity wings in the N2H+ spectrum, but cannot be fully resolved at the current velocity resolution. The presence of this additional unresolved N2H+ velocity component would result in the N2H+ column density being slightly overestimated. Therefore, the towards the Shock may be even larger than what is reported.
Mass surface density (Σ), Ν2Η+ and N2D+ column densities and deuterium fraction, 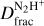 , of the five positions analysed in this work using both the MADCUBA software and Gaussian fittings of the isolated components.
, of the five positions analysed in this work using both the MADCUBA software and Gaussian fittings of the isolated components.
 |
Fig. 3 Column density values from the MADCUBA analysis of N2D+ as a function of N2H+ for all the positions analysed in this work, as well as literature values for LMSCs (Crapsi et al. 2005; Fontani et al. 2006; Friesen et al. 2013; Cheng et al. 2021), HMSCs (Fontani et al. 2011; Kong et al. 2016), HMPOs (Fontani et al. 2011), LMPOs (Emprechtinger et al. 2009; Friesen et al. 2013), and IRDCs (Miettinen et al. 2011; Gerner et al. 2015; Barnes et al. 2016). The average uncertainties associated to the data point from the literature are reported in the bottom right corner. Finally, dotted lines correspond to fixed values of D/H ratios. |
 |
Fig. 4
|
Best-fitting parameters of the N2H+ and N2D+ emission lines obtained using MADCUBA and the Gaussian fitting of the isolated components.
 |
Fig. 5 N2D+ centroid velocities (left) and line widths (right) as a function of the corresponding N2H+ quantities. The Pearson's correlation coefficients are indicated within each panel. |
5 Conclusions
We report observations of the N2H+ and N2D+ J = 1−0 emission towards five positions across the IRDC G34.77, namely a massive core (G3; ‘Core’), different positions across the shock front driven by the nearby SNR W44 (‘Shock’ and ‘Ridge’), a dense clump (‘Clump’), and unperturbed cloud material (‘Ambient’). We measured 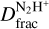 across the cloud and compared the obtained results with those typically measured in star-forming regions at different evolutionary stages. We find that towards the Core, Shock, Ridge, and Clump,
across the cloud and compared the obtained results with those typically measured in star-forming regions at different evolutionary stages. We find that towards the Core, Shock, Ridge, and Clump, 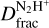 is significantly larger than that measured towards the Ambient region (
is significantly larger than that measured towards the Ambient region (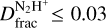 ) and is several orders of magnitu+de greater than the cosmic D/H ratio. We report enhanced
) and is several orders of magnitu+de greater than the cosmic D/H ratio. We report enhanced 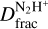 towards both the Shock and the Ridge, where the gas is being compressed by the SNR-driven shock. Towards these regions, we suggest that the N2H+ emission may be a fossil record of the pre-shocked material that is now being compressed by the shock passage. We also suggest that the enhanced N2D+ column densities – with respect to the Ambient region – towards these regions may be associated with the fast-cooling, much denser post-shocked material. Here, the previously reported high densities enable a faster chemistry that quickly causes CO to be depleted and boosts the formation of D-bearing species in the gas phase. We also speculate that the shock passage may have triggered the formation of a low-mass starless core population in the dense post-shocked material. Here, the measured
towards both the Shock and the Ridge, where the gas is being compressed by the SNR-driven shock. Towards these regions, we suggest that the N2H+ emission may be a fossil record of the pre-shocked material that is now being compressed by the shock passage. We also suggest that the enhanced N2D+ column densities – with respect to the Ambient region – towards these regions may be associated with the fast-cooling, much denser post-shocked material. Here, the previously reported high densities enable a faster chemistry that quickly causes CO to be depleted and boosts the formation of D-bearing species in the gas phase. We also speculate that the shock passage may have triggered the formation of a low-mass starless core population in the dense post-shocked material. Here, the measured 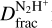 may be produced towards these cores. High-angular resolution images are necessary to distinguish between the possible scenarios. Finally, we measured
may be produced towards these cores. High-angular resolution images are necessary to distinguish between the possible scenarios. Finally, we measured 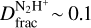 towards the Clump, which is similar to that observed towards starless cores, including G3. The source also has a mass surface density similar to that typically observed in clumps with the potential to harbour star formation. We speculate that this clump may represent a starless core in the making but we find no evidence that this formation was triggered by the shock passage.
towards the Clump, which is similar to that observed towards starless cores, including G3. The source also has a mass surface density similar to that typically observed in clumps with the potential to harbour star formation. We speculate that this clump may represent a starless core in the making but we find no evidence that this formation was triggered by the shock passage.
Acknowledgements
G.C. acknowledges support from the Swedish Research Council (VR Grant; Project: 2021-05589). J.C.T. acknowledges support from ERC project 788829–MSTAR. I.J-.S acknowledges funding from grant No. PID2019-105552RB-C41 awarded by the Spanish Ministry of Science and Innovation/State Agency of Research MCIN/AEI/10.13039/501100011033. J.D.H. gratefully acknowledges financial support from the Royal Society (University Research Fellowship; URF/R1/221620). P.G. acknowledges support from the Chalmers Cosmic Origins postdoctoral fellowship. R.F. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 101032092. R.F. also acknowledges support from the grants Juan de la Cierva FJC2021-046802-I, PID2020-114461GB-I00 and CEX2021-001131-S funded by MCIN/AEI/ 10.13039/501100011033 and by “European Union NextGenerationEU/PRTR”. S.V. acknowledges partial funding from the European Research Council (ERC) Advanced Grant MOPPEX 833460. S.V. and J.C.T acknowledge the support from a Royal Society International Exchanges Scheme grant (IES\R3\170325)
Appendix A The HFS GILDAS fitting method
The HFS method in GILDAS is a fitting procedure that reproduces the N2H+ and N2D+ hyperfine structures in the regime of optically thin and thick lines. In the case of optically thick lines, the excitation temperature can be estimated together with the total line optical depth and the centroid velocity. We applied the HFS method to the N2H+ and N2D+ spectra in Figure 2. For all the N2D+ spectra, the HFS method indicates that the lines are optically thin towards all positions. It is therefore not possible to estimate Tex for this species. For the N2H+ spectra, the HFS method indicates optically thin lines towards all position except the core G3. Furthermore, towards the Shock, Ridge and Clump, the method also returns a poor fit. This is likely due to the presence of a complex kinematic structures not resolved at the low velocity resolution of our observations. As a consequence, it is not possible to estimate Tex of N2H+ towards these positions. The only spectrum for which the HFS is successful is the N2H+ emission towards the core G3, for which we report the best fitting parameters in Table A.1.
Best-fitting parameters from the HFS method in GILDAS applied to the N2H+ spectra towards the core G3.
From these parameters, we estimate the excitation temperature using the following equation (e.g. Punanova et al. 2016):
where ν is the frequency of the component used as a reference in the HFS fitting; Jv(Tbg) is the equivalent Rayleigh-Jeans background temperature (Tbg=2.73 K); and τ is the optical depth of the main component. In the case of optically thick lines, TA × τ is the total optical depth times the difference between the Rayleigh-Jeans equivalent excitation and background temperatures, while for the case of optically thin lines it corresponds to the main beam temperature of the main component. From Equation A.1, we estimate the excitation temperature to be Tex=7 K. This value is consistent with that reported in other low-mass (Friesen et al. 2013) and high-mass cores (Fontani et al. 2011; Kong et al. 2016) and towards other IRDCs (Barnes et al. 2016). Assuming Tex=7 K would lead to 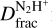 values lower by less than 10% with respect to those reported in Table 3 for Tex = 9 K.
values lower by less than 10% with respect to those reported in Table 3 for Tex = 9 K.
References
- Barnes, A. T., Kong, S., Tan, J. C., et al. 2016, MNRAS, 458, 1990 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, A. T., Henshaw, J. D., Fontani, F., et al. 2021, MNRAS, 503, 4601 [CrossRef] [Google Scholar]
- Beuther, H., Bihr, S., Rugel, M., et al. 2016, A&A, 595, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busquet, G., Fontani, F., Viti, S., et al. 2017, A&A, 604, A20 [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, M. J., & Tan, J. C. 2012, ApJ, 754, 5 [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [Google Scholar]
- Caselli, P., Vastel, C., Ceccarelli, C., et al. 2008, A&A, 492, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, E. T., Jackson, J. M., Rathborne, J. M., & Simon, R. 2009, ApJS, 181, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, Y., Tan, J. C., Caselli, P., et al. 2021, ApJ, 916, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [Google Scholar]
- Codella, C., Viti, S., Ceccarelli, C., et al. 2013, ApJ, 776, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Cosentino, G., Jiménez-Serra, I., Henshaw, J. D., et al. 2018, MNRAS, 474, 3760 [NASA ADS] [Google Scholar]
- Cosentino, G., Jiménez-Serra, I., Caselli, P., et al. 2019, ApJ, 881, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Cosentino, G., Jiménez-Serra, I., Tan, J. C., et al. 2022, MNRAS, 511, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Dalgarno, A., & Lepp, S. 1984, ApJ, 287, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Emprechtinger, M., Caselli, P., Volgenau, N. H., Stutzki, J., & Wiedner, M. C. 2009, A&A, 493, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Caselli, P., Crapsi, A., et al. 2006, A&A, 460, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Palau, A., Caselli, P., et al. 2011, A&A, 529, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontani, F., Sakai, T., Furuya, K., et al. 2014, MNRAS, 440, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, J. B., Arce, H. G., Kassis, M., et al. 2014, ApJ, 791, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Kirk, H. M., & Shirley, Y. L. 2013, ApJ, 765, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Gerner, T., Shirley, Y. L., Beuther, H., et al. 2015, A&A, 579, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Bovino, S., Caselli, P., et al. 2019, A&A, 621, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernandez, A. K., & Tan, J. C. 2015, ApJ, 809, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., Inoue, T., Iwasaki, K., & Hosokawa, T. 2015, A&A, 580, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., & Tan, J. C. 2013, A&A, 549, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kong, S., Caselli, P., Tan, J. C., Wakelam, V., & Sipilä, O. 2015, ApJ, 804, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, S., Tan, J. C., Caselli, P., et al. 2016, ApJ, 821, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
- Krumholz, M. R., & Tan, J. C. 2007, ApJ, 654, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, E. J., Miville-Deschênes, M.-A., & Murray, N. W. 2016, ApJ, 833, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, W., Tan, J. C., Kainulainen, J., Ma, B., & Butler, M. 2016, AAS Meeting Abstracts, 227, 424.06 [Google Scholar]
- Lis, D. C., Gerin, M., Phillips, T. G., & Motte, F. 2002, ApJ, 569, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Wootten, H. A., Gerin, M., et al. 2016, ApJ, 827, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, S., Martín-Pintado, J., Blanco-Sánchez, C., et al. 2019, A&A, 631, A159 [Google Scholar]
- Miettinen, O., Hennemann, M., & Linz, H. 2011, A&A, 534, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morii, K., Sanhueza, P., Nakamura, F., et al. 2021, ApJ, 923, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Moser, E., Liu, M., Tan, J. C., et al. 2020, ApJ, 897, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Oliveira, C. M., Hébrard, G., Howk, J. C., et al. 2003, ApJ, 587, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Lenfestey, C., Fuller, G. A., et al. 2016, A&A, 590, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., & Menten, K. M. 2006, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Kauffmann, J., Zhang, Q., et al. 2019, A&A, 622, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Punanova, A., Caselli, P., Pon, A., Belloche, A., & André, P. 2016, A&A, 587, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [Google Scholar]
- Retes-Romero, R., Mayya, Y. D., Luna, A., & Carrasco, L. 2020, ApJ, 897, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Rico-Villas, F., Martín-Pintado, J., González-Alfonso, E., Martín, S., & Rivilla, V. M. 2020, MNRAS, 491, 4573 [NASA ADS] [CrossRef] [Google Scholar]
- Sashida, T., Oka, T., Tanaka, K., et al. 2013, ApJ, 774, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C. 2000, ApJ, 536, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., Kong, S., Butler, M. J., Caselli, P., & Fontani, F. 2013, ApJ, 779, 96 [Google Scholar]
- Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 149 [Google Scholar]
- Tasker, E. J., & Tan, J. C. 2009, ApJ, 700, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Banerjee, R., Gómez, G. C., et al. 2011, MNRAS, 414, 2511 [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, B., Van Loo, S., Tan, J. C., & Bruderer, S. 2015, ApJ, 811, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, B., Tan, J. C., Nakamura, F., et al. 2017, ApJ, 835, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., Wang, J., & Tan, J. C. 2020, ApJ, 905, 78 [Google Scholar]
- Zuckerman, B., & Evans, N. J. I. 1974, ApJ, 192, L149 [NASA ADS] [CrossRef] [Google Scholar]
MADCUBA is a software developed in the Madrid Center of Astrobiology (INTA-CSIC). https://cab.inta-csic.es/ madcuba/
All Tables
Spectroscopic information of the targeted species as obtained from the CDMS catalogue.
Mass surface density (Σ), Ν2Η+ and N2D+ column densities and deuterium fraction, 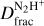 , of the five positions analysed in this work using both the MADCUBA software and Gaussian fittings of the isolated components.
, of the five positions analysed in this work using both the MADCUBA software and Gaussian fittings of the isolated components.
Best-fitting parameters of the N2H+ and N2D+ emission lines obtained using MADCUBA and the Gaussian fitting of the isolated components.
Best-fitting parameters from the HFS method in GILDAS applied to the N2H+ spectra towards the core G3.
All Figures
 |
Fig. 1 Three-colour image of G34.77. Red is 24 µm emission (Spitzer MIPSGAL; Carey et al. 2009), green is 8 µm emission (Spitzer GLIMPSE; Churchwell et al. 2009), and blue is 1 GHz continuum emission (THOR survey; Beuther et al. 2016; black contours from 3 to 27 Jy beam−1 by 6 Jy beam−1 ). The continuum emission probes the gas associated with the expanding shell of the SNR. The magenta contour (AV = 20 mag Kainulainen & Tan 2013) highlights the cloud shape. Superimposed on the map are the five positions of interest (white circles; 34″ IRAM 30 m beam at the N2D+ frequency of 77.112 GHz). The cyan contours correspond to the ALMA SiO contours from Cosentino et al. (2019; from 0.05 to 0.3 Jy beam−1 by 0.05 Jy beam−1). |
| In the text | |
 |
Fig. 2 N2H+ (black curves, top panels) and N2D+ (black curves, bottom panels) obtained towards the five positions. The IRDC G34.77 central velocity is indicated as a vertical dotted line in all panels. The red curves show the best LTE fitting models obtained by MADCUBA. The green curves show the Gaussian fitting obtained for the isolated component. For the Shock, Ridge, and Clump positions, we report the SiO(2−1) spectra (orange filled) extracted from the ALMA images (Cosentino et al. 2019) towards an angular region consistent with that of our current observations (34″). In the bottom panels, the SiO spectra have been multiplied by 0.2 to allow a more straightforward comparison with the N2D+ spectra. |
| In the text | |
 |
Fig. 3 Column density values from the MADCUBA analysis of N2D+ as a function of N2H+ for all the positions analysed in this work, as well as literature values for LMSCs (Crapsi et al. 2005; Fontani et al. 2006; Friesen et al. 2013; Cheng et al. 2021), HMSCs (Fontani et al. 2011; Kong et al. 2016), HMPOs (Fontani et al. 2011), LMPOs (Emprechtinger et al. 2009; Friesen et al. 2013), and IRDCs (Miettinen et al. 2011; Gerner et al. 2015; Barnes et al. 2016). The average uncertainties associated to the data point from the literature are reported in the bottom right corner. Finally, dotted lines correspond to fixed values of D/H ratios. |
| In the text | |
 |
Fig. 4
|
| In the text | |
 |
Fig. 5 N2D+ centroid velocities (left) and line widths (right) as a function of the corresponding N2H+ quantities. The Pearson's correlation coefficients are indicated within each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



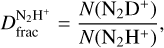
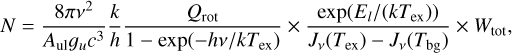
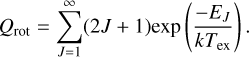
![${T_{{\rm{ex}}}} = {{hv} \over k}\,{\left[ {ln\,\left( {{{\left( {{{hv} \mathord{\left/ {\vphantom {{hv} k}} \right. \kern-\nulldelimiterspace} k}} \right)} \over {{{\left( {{T_A} \times \tau } \right)} \mathord{\left/ {\vphantom {{\left( {{T_A} \times \tau } \right)} {\tau + {J_v}\left( {{T_{{\rm{bg}}}}} \right)}}} \right. \kern-\nulldelimiterspace} {\tau + {J_v}\left( {{T_{{\rm{bg}}}}} \right)}}}} + 1} \right)} \right]^{ - 1}},$](/articles/aa/full_html/2023/07/aa46676-23/aa46676-23-eq47.png)