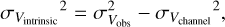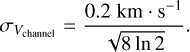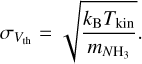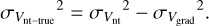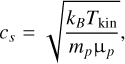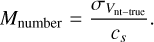EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 674 (June 2023) A&A, 674 (2023) A46 Full HTML
Open Access
Issue
A&A
Volume 674, June 2023
Article Number A46
Number of page(s) 12
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202244525
Published online 29 May 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The formation of high-mass stars (M★ > 8 M⊙) remains a fundamental problem in modern astrophysics. Traditionally, high-mass stars are believed to form in highly turbulent gas (e.g., Larson 1981; Liu et al. 2012; Sánchez-Monge et al. 2013b; Tan et al. 2013). Supersonic turbulence is important to provide the required support against gravitational collapse (McKee & Tan 2003), by maintaining an equivalent "turbulent Jeans mass" that is generally much higher than the thermal Jeans mass (typically on order of 1 M⊙), allowing the formation of massive stars (e.g., Wang et al. 2011, 2014). Observations of giant molecular clouds and massive star-forming regions often reveal supersonic turbulence. Recent examples include interferometric observations of NH3 in a sample of high-mass-star-formation regions (Sánchez-Monge et al. 2013b; Lu et al. 2014, 2018).

However, it is important to note that those NH3 studies, and most of the similar observations toward massive-star-forming regions in the literature, do not actually provide sufficient resolving power to properly study turbulence, which is important for the initial conditions of star formation. Owing to the large distances to typical massive-star-forming regions, observations must meet the following minimum requirements: (1) a high spectral resolution that is sufficient to resolve thermal line widths (sound speed 0.23 km s−1 at 15 K); (2) a high spatial resolution that is sufficient to resolve thermal Jeans length (0.09 pc for a clump of 103 M⊙ in 1 pc diameter, or 3".5 at a distance of 5 kpc); and (3) a flux sensitivity that is sufficient to resolve thermal Jeans mass (typically 1 M⊙).

Notably, several Very Large Array (VLA) observations in NH3 used a correlator setup with a 0.6–0.7 km s−1 channel width, especially for observations taken prior to the JVLA upgrade in 2010 (Perley et al. 2011). In those data, the instrumental broadening is already a few times larger than the thermal broadening and therefore they cannot be used to detect the thermal line width. A special marginal case is presented by Wang et al. (2012), who combined VLA-C configuration NH3 image cubes at 0.2 km s−1 resolution with VLA-D configuration data at 0.6 km s−1 resolution to study clump P1 in the G28.34+0.06 infrared-dark cloud (IRDC). These authors found a supersonic turbulence over the cloud scale. However, all the dense cores showed a much reduced line width in comparison to the clump-scale widths, which is indicative of turbulence dissipation from clump- to core scale.

Only a few studies have achieved observations that meet the three aforementioned requirements (Sokolov et al. 2018; Hacar et al. 2018; Yue et al. 2021; Li et al. 2022), and surprisingly, all of them found that subsonic to transonic turbulence, instead of supersonic turbulence, is dominant. Sokolov et al. (2018) imaged IRDC G035.39-00.33 (G35.39 hereafter) in NH3 (1,1) and (2,2) lines at a spectral resolution of 0.2 km s−1 down to scales of 0.07 pc. The star-forming cores are exclusively located in subsonic regions of the IRDC, and the entire IRDC is dominated by subsonic turbulence. Similar results are observed in the Orion molecular cloud, the nearest high-mass star-forming region (Hacar et al. 2018; Yue et al. 2021), and in NGC 6334S (Li et al. 2022). In particular, Yue et al. (2021) showed that the observed line width is resolution dependent, changing from transonic to subsonic as the spatial resolution increases from 104 AU to 103 AU.

These studies, reported by four independent groups using different analysis methods, suggest that previous similar observations with insufficient spatial and/or spectral resolution may have led authors to believe the turbulence is resolution dependent, and that massive stars are forming in low-turbulence environments in OMC, G35.39, and NGC6334S. Therefore, it is of great interest to study turbulence in massive star-forming regions with both sufficient spatial and spectral resolution in order to further investigate whether supersonic turbulence is necessary to form high-mass stars. In general, a turbulence with low Mach number infers significantly less support from the turbulence than it was previously assumed, and magnetic fields may play a more important role in preventing gravitational collapse in order to form high-mass stars.

In this context, here we present JVLA and ALMA observations of the massive-star-forming region G35.20-0.74 N (G35.20 hereafter). The high spatial and spectral resolution enabled an in-depth investigation of the turbulence. The paper is organized as follows. Section 2 presents observations and data. Section 3 gives an overview of G35.20 with both previous and our new observations. Section 4 describes fitting to NH3 lines and results. Section 5 discusses the implications of our results in the context of star formation. In Sect. 6, we summarize our main findings.

2 Observations and data

2.1 JVLA

In Fig. 1, we observed G35.20-0.74 N (RA (J2000), Dec (J2000): 18:58:13.00, 01:40:36.00) using JVLA in its D configuration at K band on 2013 May 23 (project ID: 13A-373, PI: Ke Wang). The WIDAR correlator (Perley et al. 2011) was tuned to cover NH3 inversion transition lines from (1,1) to (7,7) at approximately 23.7–25.7 GHz, with a spectral resolution of 15.625 kHz (about 0.2 km s−1). At the same time, 15 sub-bands of 128 MHz are used to cover the continuum. The VLA primary beam at K band is about 2'.

Standard bandpass, flux, and gain of the target observation was calibrated by observing 3C454.3, 3C48 (0137+331), and J1851+0035, respectively. Corrections for baseline and atmospheric opacity are performed before calibration in CASA 4.7.2 (Common Astronomy Software Applications, McMullin et al. 2007). Image cubes of NH3 lines are made using the multi-scale CLEAN algorithm (Cornwell 2008) in the CASA task TCLEAN with Briggs weighting and a robust parameter of 0.5. The synthesized beam in NH3 (1,1) is 2.9'' × 1.9'', PA=67.9° with therms noise at 2.8 mJy beam−1. Integrated flux images of NH3 (1,1) to (7,7) lines are presented in Fig. 2. To achieve the same resolution from NH3 (1,1) to (7,7), we smooth all image cubes to the beam of the NH3 (1,1) cubes. The line fitting (Sect. 4.1) is performed on the smoothed image cubes to avoid any artefacts originating from different beam shapes.

Additionally, we made a continuum image by multi-frequency synthesis line-free channels in the sub-bands of 15×128 MHz in width centered on 24.7 GHz, corresponding to 1.2 cm. We used uv-taper and robust weighting during cleaning to reach a synthesized beam of 2.6'' × 1.3'', PA=75°. The image rms noise is 18 μJy beam−1, reaching a dynamical range of better than 230.

2.2. ALMA

We retrieved the 870 μm continuum image of G35.20 from the ALMA science archive (Project Code: 2011.0.00275.S, PI: Cesaroni, Riccardo). Details of the observations can be found in Sánchez-Monge et al. (2013a). The synthesized beam of the continuum image is 0.51'' × 0.46'', PA = 48°, with an rms noise level at 1.8 mJy beam−1. The ALMA primary beam at 350 GHz is about 16'', covering the central part of the VLA field, as marked in the middle panel of Fig.1.

3 G35.20 overview: Dust, NH3, and radio continuum in an evolved IRDC

Located at a parallax distance of 2.19 kpc (Zhang et al. 2009), the G35.20 molecular cloud is actively forming massive stars (Sánchez-Monge et al. 2014). The dense clump coincides with a bright infrared (IR) source IRAS 18556+0136, and has been observed to have a high bolometric luminosity (> 104 L⊙, Gibb et al. 2003; Sánchez-Monge et al. 2013a; Zhang et al. 2013), molecular outflows (Dent et al. 1985; Gibb et al. 2003; Birks et al. 2006; Qiu et al. 2013), radio continuum sources (e.g., Gibb et al. 2003; Beltrán et al. 2016, this work), and masers (e.g., Brebner et al. 1987; Hutawarakorn & Cohen 1999; Surcis et al. 2012; Yan et al. 2013; Beltrán et al. 2016).

Figure 1 presents an overview of the G35.20 molecular cloud as observed by Spitzer, APEX, JVLA, and ALMA. The dense part as traced by the Atacama Pathfinder Experiment (APEX) 870 μm corresponds to 2.9 × 103 M⊙ in a radius of 0.87 pc (Sánchez-Monge et al. 2013a). Infrared extinction is visible in Fig. 1 toward the edges of the cloud (outermost contours of the APEX Telescope Large Area Survey of the Galaxy, ATLAS-GAL in short), which is spatially coincident with the Spitzer dark clouds identified in this region (Peretto & Fuller 2009; Pari & Hora 2020). However, the central part has developed into a "butterfly"-shaped mid-IR nebula consistent with the active molecular outflow (Dent et al. 1985; Lee et al. 2012). Hence, G35.20 represents an evolved IRDC.

Out of the apparently roundish clump seen in the APEX 870 μm image, the JVLA NH3 emission reveals a filament of 0.5 pc in length orientated north-south. The two ends of the filament slightly bend in opposite directions, resembling an integral-shaped filament. The ALMA 870 μm continuum image reveals an almost straight-line filament harboring a string of six regularly spaced compact cores. Following Sánchez-Monge et al. (2014), we label the ALMA cores as A to F in Fig. 1. Physical parameters of the cores are listed in Table 1. The central core B corresponds to an almost edge-on Keplerian disk and a possible binary system (Sánchez-Monge et al. 2013a; Beltrán et al. 2016). We note that we measure core fluxes above 3σ, while Sánchez-Monge et al. (2014) used a 5σ cut, meaning that the core fluxes reported here are slightly higher. We also used updated temperature values to compute the core masses reported in Table 1. The masses are consistent with those listed in Sánchez-Monge et al. (2014), which are in the range of 0.5–11 M⊙. We note that our mass estimates for cores A and B are likely overestimated, because we used lower temperatures compared to the ones measured in Sánchez-Monge et al. (2014; see also Sect. 4.2). In addition, we also calculated the virial parameters of cores and present them in Table 1. Details of the computation process are provided in Sect. 5.1.

The VLA 1.2 cm continuum image reveals a lane of ionized gas misaligned with the NH3 and ALMA dust continuum emission. The angle between the ALMA dust filament and the VLA radio continuum lane is about 37°. The radio lane is consistent with VLA observations at 1.3 cm and 2 cm (Heaton & Little 1988; Beltrán et al. 2016). At this resolution, the 1.2 cm radio continuum emission is condensed to at least five compact sources, which are further resolved at higher resolution by Beltrán et al. (2016). This lane spatially matches with the central part of the butterfly-shaped Spitzer nebula. Gibb et al. (2003) has deduced that the radio lane traces a thermal radio jet and this conjecture was later confirmed by ALMA and VLBA observations (Sánchez-Monge et al. 2013a; Beltrán et al. 2016).

Figure 2 presents flux-integrated maps of JVLA NH3 from (1,1) to (7,7). The NH3 emission reveals an elongated filament of about 0.5×0.1 pc in size, an intermediate scale that bridges the larger spatial scale (clouds) traced in the APEX 870 μm emission and the smaller scale (cores) traced in ALMA data. In the rest of the paper, we refer to this NH3 feature as the "filament/clump". NH3 (1,1) and (2,2) reveal a larger extent of the elongated clump, while higher transitions from (3,3) to (7,7) highlight the central part, suggesting a warm central region surrounded by colder emission, which is further explored in the following section. We also note that NH3 (6,6) emission is stronger than that in the nearby (5,5) and (7,7) lines, likely because the (6,6) transition is in an ortho state. Comparing the ortho state (3,3) and (6,6) with other para states, we can find that the ortho/para ratio in NH3 emission has a complex morphology. We discuss the details of this in Sect. 4.4.

thumbnail Fig. 1

Overview of G35.20-0.74 N imaged by Spitzer, APEX, JVLA, and ALMA at various scales. First row-left: Spitzer 4.6 μm emission (Benjamin et al. 2003) obtained by IRAC overlaid with a green contour map of the 870 μm continuum emission from the ATLASGAL survey (Csengeri et al. 2014). The unit of the color wedge is MJy sr−1 in IRAC map. The APEX 870 μm contours start from 3σ, and are then 6σ, 12σ, and 24 σ, where σ =90 mJy beam−1. The dashed yellow and red circles are of 1' and 2' in diameter, with the latter being the VLA primary beam. First row-right: Same Spitzer 4.6 μm emission overlaid with green contours showing the integrated intensity map of NH3 (1,1) and black contours showing 1.2 cm continuum emission from our observations. The green contours start from 5 σ, and are then 10σ, 15σ, and 20 σ, where 1σ is equal to 1.2 mJy beam−1. The black contours start from 6σ, and are then 20σ, 48σ, 80σ, 130σ, 180σ, and 230 σ, where 1σ is equal to 18 μJy beam−1. Blue arrows show the direction of the CO outflow (Birks et al. 2006). Second row: Same VLA 1.2 cm continuum in color scale overlaid with ALMA 870 μm continuum emission in green contours. The color bar is in units of mJy beam−1. Green contours are from 9 to 230 mJy beam−1 with a step of 1.8 mJy beam−1. Cores A-F are marked following Sánchez-Monge et al. (2014).
thumbnail Fig. 2

Flux-integrated maps of JVLA NH3 lines from (1,1) to (7,7) in G35.20-0.74 N. Upper row: From left to right are NH3 (1,1) to (3,3) shown in the same color bar. Ellipses in the bottom-right corner are synthesized beams of each line image. Contours show the 3σ level of each line-integrated map. Lower row: Similar to the upper row but for lines from (4,4) to (7,7), with a different color bar.
Table 1

Physical parameters of the ALMA cores.

4 NH3 fitting results

4.1 NH3 fitting

We use the Python-based PySpecKit package (Ginsburg & Mirocha 2011) to simultaneously fit the NH3 (1,1) to (7,7) lines. The algorithm models the NH3 lines simultaneously using six fitting parameters, including excitation temperature (Tex), kinetic temperature (Tk), column density, ortho/para ratio (OPR), centroid velocity (VLSR), and velocity dispersion We do not use the cold-ammonia model presented in Lee et al. (2012) because of the relatively high temperature which is more than 50 K (in Fig. 3) toward the center of G35.20.

Pixels with a signal-to-noise ratio (S/N) of higher than 3 are included in our fitting. As shown in Fig. 2, the outer regions are only detected in NH3 (1,1) and (2,2). We tune the PyspecKit to fit lines in those regions by setting nondetected pixels as "NAN" so that the package will set upper limits automatically for all parameters ensuring the peak S/N of high-energy lines is less than 3. To check the influence of this limitation on both derived temperatures and column densities, we visually checked all fitted lines: none of the parameters are underestimated because of the limitation, and based on the low residuals, all fitted lines are reasonable. During the fitting, we check uncertainties and make sure they are under 10%; otherwise we reset the limitation and rerun the fitting.

More specifically, we first make a uniform parameter space to generate equally spaced parameters as the initial guess for the above model. We also adopt a number of criteria for parameters to ensure fitted results are reasonable: the kinetic temperature is from 3 K to 102 K, the OPR is from zero to infinity and the column density is 1014–1017 cm−2. By limiting the range of parameters and using a Monte Carlo Markov-Chain (MCMC) method, we obtain the best fitted result with the lowest relative residuals, with a mean value of about 3%.

We fitted the NH3 data cubes with multiple velocity components, and find that G35.20 is dominated by a single velocity component (detailed in Appendix A). Therefore, we adopt the fitting result from one velocity component throughout this paper. Figure 3 illustrates the fitting results, including kinetic temperature, column density, velocity dispersion, cetroid velocity, and OPR. The fitting error and histograms of the pixel distributions of these parameters are also plotted. The filamentary G35.20 cloud is divided into three regions based on their gas properties, referred to here as the Northern, Central, and Southern regions for simplicity in the following text.

4.2 Temperature and column density: Warm central and cool surroundings

The fitted kinetic temperature of G35.20 is shown in the first row of Fig. 3. The temperature map is highly structured, and features a warm central region up to 60–70 K and an almost uniform temperature of about 25 K across the entire clump, while toward the two ends, the temperature drops to <14 K. The coldest ends of the elongated clump have temperatures comparable to quiescent IRDCs (e.g., Wang et al. 2012), and may retain the initial conditions least affected by the star-formation activities in the central region. However, the vast majority of pixels in G35.20 have higher temperatures than quiescent IRDCs, and are likely heated by the central region. We note that 70 K is clearly not the highest limit of the temperature in G35.20. Sánchez-Monge et al. (2014) used CH3CN and CH3OH, which trace denser gas than NH3, and obtained up to 200 K toward the central cores.

The column density map reveals three distinct dense regions. Each region has a similar NH3 column density at about 1015.3 cm−2. The distribution of pixel values in those three regions is flat, with fitted uncertainty of less than 10−2 dex. These three regions correspond to the North, Central, and Southern regions, respectively.

4.3 Radial velocity and velocity dispersion: Cores decoupled from filament

The centroid velocity map clearly shows two gas streams, one at about 34.5 km s−1 in the Southern region, and another at typically 33 km s−1 in the Central and Northern regions (see Fig. 3). This is also obviously seen in the pixel histograms. Interestingly, toward the innermost part where ALMA cores A and B are located, the velocity shows distinct values of about 31–32 km s−1 higher than the surroundings, suggesting these two cores may have been decoupled from the ambient gas in the Central region. Another similar trend is seen toward the southern end covered by the ALMA data, at core E, where the velocity is distinctly higher than in the surroundings. Similarly, near the northern tip of the clump, a distinct velocity is also observed (blue color in the map), but that region is out of the ALMA field of view, and so the presence of a dense dust continuum core is yet to be observed.

This northern tip corresponds to the lowest velocity dispersion in the entire G35.20 clump (~0.3 km s−1 ), possibly representing the turbulence level of the natal clump unaffected by star formation. The Central region has higher velocity dispersion than the rest of the clump, typically 1.5–2 km s−1, compared to 0.6–0.9 km s−1 in the Southern and Northern regions. Most of the ALMA cores coincide with reduced velocity dispersion compared to the surroundings, which is similar to the findings of Wang et al. (2012). This leads to a lower Mach number (Sect. 4.5) in the inner most Central region.

4.4 NH3 ortho/para ratio (OPR)

The OPR map reveals a rich structure similar to that of the column density (see Fig. 3). The mean OPR across the clump is about 0.2, with higher values mainly concentrated in the Central and Southern regions. The Northern region and the two tips of the filament/clump feature the lowest OPR, down to less than 0.1. We note that the Centarl/Southern regions harbor the ALMA cores, particularly cores A/B with active star formation, where heating and outflows may have increased the OPR as compared to the rest of the clump (e.g., Wang et al. 2014). More detail on this point is discussed in Sect. 5.3.

4.5 Mach number: Calm cores in turbulent gas

To calculate the Mach number, we first correct the line width broadened by the effect from the finite channel width:

(1)

(2)

Here, the 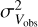is derived from the fitted result (typically in the range 0.56–2.43 km s−1) and the 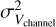is the channel width (in this work is 0.21 km s−1). The channel width contributes 9.79%±3.26% of the intrinsic velocity dispersion. We then calculate the nonthermal velocity dispersion from the fitted temperature and the 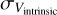. (Myers 1983):

(3)

(4)

The width caused by the (thermal) temperature is derived using Eq. (4), is typically in the range 0.17–0.34 km s−1, and corresponds to 9.63%±2.53% of the intrinsic velocity dispersion. As the correction is based on each pixel, which has a finite resolution, we need to deduct the velocity gradient from the large-scale motion to get the line width purely caused by turbulence. This velocity gradient contributes the extra velocity dispersion at the pixel scale: the slight difference at two opposite edges of one pixel could make the velocity dispersion appear larger (see detailed methodology in Lu et al. 2018). For this reason, we derive the true nonthermal velocity dispersion using:

(5)

The large-scale gradient is about 3.96 km s−1 pc−1, and contributes only about 2.85%±1.79% to the total velocity dispersion, which is a smaller contribution compared to the other components. This is likely because, with our high-spatial resolution observations, we have not detected large velocity gradients in the G35.20 region.

So far, we have carefully subtracted the line-width broadening originated from channel width, thermal motion, and velocity gradient, which respectively contribute about 10%, 10%, and 3% of the observed velocity dispersion. The rest of the broadening is considered to be caused by turbulence. We then proceed to compute the sound speed based on the temperature and the Mach number, making use of the true nonthermal velocity dispersion, using the equations:

(6)

(7)

We note that most previous interferometric NH3 observations had a larger channel width of 0.6 km s−1 (determined by the old VLA correlator), which was larger than the sound speed (e.g., Sánchez-Monge et al. 2013b; Lu et al. 2014, 2018). We stress the necessity to use a spectral resolution of higher than that of thermal broadening; otherwise, nonthermal motions will be overestimated.

The Mach number map is shown in Fig. 4. The mean value of the Mach number is about 3.7, and the pixel distribution peaks at 2.8. The error map is flat with a mean value of 0.016. The Mach number map is highly structured and similar to the velocity dispersion map: the two ends of the G35.20 have a lower Mach number (about 2) and the central region has a higher value (about 6). Interestingly, toward the central cores, the Mach number drops again to less than 3. We discuss this further in Sect. 5.2.

thumbnail Fig. 3

Maps of fitted parameters (left column) with errors (middle column) and histograms of pixel distribution of the Northern, Central, and Southern regions (right column). From top to bottom are the kinetic temperature, column density, velocity dispersion, centroid velocity, and OPR. The black contour is the same as that of the right panel in Fig. 1, which shows the ALMA 870 μm emission. Scale bars on the right share the same units for parameter and fitting error.
thumbnail Fig. 4

Mach number (left) and its pixel distribution (right). The white contours and red crosses mark the ALMA 870 μm emission cores, with contour levels the same as in Fig. 1. The dashed black and red vertical lines mark the typical Mach number in the literature, representative of quiescent and protostellar stages, respectively. The brown histogram corresponds to the brown circle of the central region (covering cores A and B), and the blue histogram is that of the whole G35.2 clump.

4.6 Position-velocity diagram: Wave-like pattern

From the ALMA continuum map, we see that the six cores are distributed at almost regularly intervals along the filament. Separations among these cores are similar and the velocity of each core is slightly different from that of the host filament. Considering this, we make a position-velocity (PV) map (beam by beam) along the direction of the filament (the direction is shown in Fig. 5) from the fitted velocity map to study the possible relationship between those cores and their host filament. The velocity is adopted as the average value of each sampled beam. To investigate the most active region in the central region, we also chose a rectangular region in the central part of G35.20, which corresponds to [−0.12, 0.12 pc] in the complete PV plot (0 point is between core A and B). This rectangular region covers all six cores and we plot the PV plot pixel by pixel, marking the location of cores from A to F. The result is shown in Fig. 5. The six cores seem to belong to three pairs in the ALMA images: cores A and B seem connected, and similarly for C and E, and D and F.

Interestingly, cores A and B have significantly different centroid velocities from the filament, suggesting that they may have been decoupled from the parental clump they are embedded in. This decoupling is also evident in the velocity dispersion and Mach number. The PV diagram in Fig. 5 clearly shows an opposite velocity gradient between cores A+B and the host filament. The distinct velocity gradient in cores A+B is consistent with the kinematics traced by hot molecular lines (Sánchez-Monge et al. 2013a).

As cores A and B have velocities that are clearly different from that of the host filament, we masked pixels around these two cores within one beam size and fit the rest of the data in the PV map with a line. The linear fitting results in a velocity gradient of 3.96 km s−1 pc−1 along the NH3 clump. The fitting result is shown in Fig. 5. This velocity gradient is typical of that measured at core scales (Yue et al. 2021), but it is more than ten times larger than typical velocity gradients measured in longer filaments (Wang et al. 2016; Wang 2018; Ge & Wang 2022).

After removing this global velocity gradient, the PV diagram shows some wave-like patterns. We then performed a Lomb-Scargle method to study the periodicity (method detailed in Wang 2018). The most likely period is 0.025 pc (although other larger periods are also possible), consistent with the average separation of 0.023 pc between the ALMA cores (Sánchez-Monge et al. 2014). This picture is consistent with the toy model proposed by Hacar & Tafalla (2011) to explain the formation of cores in one of the filaments of the L1517 star-forming region. However, the small number of data points in our observations prevented us from making a sophisticated comparison.

thumbnail Fig. 5

Velocity and column density in G35.20. Left: NH3 fitted centroid velocity overlaid with ALMA 870 μm contours as in Fig. 3. The box and arrow indicate how the PV cuts are made on the right panels. Right: The top panel is a PV cut showing the averaged centroid velocity (beam by beam) of the entire NH3 filament along the direction pointed by the arrow in the left panel, starting from the northern end down to the southern end of the NH3 filament shown in the left panel. The zero point is located between cores A and B. The red line is a linear fit excluding data between cores A and B. The middle panel is a pixel-by-pixel (instead of beam by beam) PV cut along the black-box region in the left panel after subtracting a global velocity gradient (red line in top panel). The bottom panel corresponds to the NH3 column density profile. The positions of the six ALMA cores A-F are marked with dashed vertical lines.

5 Discussion

5.1 Fragmentation and stability

We use the APEX and ALMA 870 μm dust-continuum emission data to study the fragmentation of the G35.20 cloud. The APEX 870 μm thermal dust emission (Fig. 1) reveals a clump with a diameter of 0.87 pc, encompassing 119.1 Jy of integrated flux. With an averaged dust temperature of 25.9 K from our fitted results, this flux corresponds to 4.94 × 103M⊙. Assuming a spherical geometry, its volume density is 1.11 × 104 cm−3. Under the derived temperature and density, the thermal Jeans mass is about 11.2 M⊙ and the Jeans length is 0.32 pc. Here the temperature is the current value elevated due to heating from the active star formation in the clump center, and so the Jeans values should be regarded as the current values as well, and so should not be compared to the observed ALMA cores. For a meaningful comparison, we should estimate the Jeans mass and length of the initial G35.20 clump; although we no longer have a direct observation with which to measure these, we can make a reasonable estimation. We assume an initial temperature of 15 K, typical for quiescent IRDCs and in agreement with the currently observed kinetic temperature in the two ends of the G35.20 filament/clump, which are least affected by the central star formation activities. We also assume that the averaged volume density does not change significantly following the initial stage. Then, for 15 K and 1.11 × 104 cm−3, the Jeans mass is 4.95 M⊙, and Jeans length is 0.24 pc. The Jeans mass is comparable to that of the ALMA cores, but the Jeans length is ten times higher than the mean separation between the cores (Table 1).

It is possible that the cores, after initial fragmentation, have drifted toward the center of the gravitational potential well, now at the location of cores A and B. A useful reference is that for a 1 km s−1 velocity; it takes 106 yr to move 1 pc. Assuming a relative velocity of 0.2 km s−1 between the cores (cf. Fig. 5), it takes 106 yr to move 0.2 pc, which is a few times the free-fall timescale of the G35.20 clump (3.5 × 105 yr). However, the spatial distribution of those cores presents a well-aligned filamentray structure, which indicates that the fragmentation most likely happened after the formation of the filament. This drift scenario is highly unlikely. Another possibility is that the filamentary morphology has played a role in fragmentation. The regularly spaced ALMA cores resemble a cylinder fragmentation rather than Jeans fragmentation in homogeneous medium (e.g., Wang et al. 2011, 2014, 2016; Ge & Wang 2022). However, it is difficult to infer the initial conditions of the gas cylinder that fragmented to the ALMA cores. High-resolution observations of quiescent IRDCs sensitive to multiple spatial scales would constitute the best tools to better understand the initial steps of the fragmentation process.

Caution has to be taken for a proper Jeans analysis for fragmentation (cf. recent examples Saha et al. 2022; Xu et al. 2023; Jiao et al. 2023; Zhang et al. 2023). For example, in our above analysis, an underlying assumption is that the observed ALMA cores are directly fragmented from the initial clump. However, hierarchical structure is common in molecular clouds, and it is possible that there is an intermediate structure between the parsec-scale clump and the 0.01 pc scale "cores" (Table 1). It is evident that the six ALMA cores seem to belong to three pairs: A/B, C/E, and D/F (Sect. 4.6). Each of these pairs might have been an original 0.1 pc scale structure that fragmented to form the cores. The density of such 0.1 pc scale structures would be larger, making the corresponding Jeans mass smaller. However, the current ALMA data only cover the central 0.2 pc of the clump. A full mosaic of the clump combining 12m and ACA, and ideally also singled-dish data, would be best suited to study the hierarchical fragmentation (Wang et al. 2011, 2014) in G35.20; this is beyond the scope of this paper, but is critically important to understand the initial conditions for massive-star formation.

We investigate the stability of the clump in G35.20 by studying its virial properties. The virial parameter of the entire clump is <0.2, which was estimated based on the above clump mass and size and the FWHM line width of 3.2 km s−1 measured from Effelsberg NH3 (1,1), (Wienen et al. 2012). A smaller FWHM of 2.6 km s−1 was reported by Urquhart et al. (2011) based on GBT NH3 (1,1). The G35.20 clump, even with the current turbulence level, is therefore gravitationally unstable. Here, we have not taken magnetic fields into account, which may provide additional support against gravity at a similar level as turbulence. However, at the initial stage, the line width may have been even smaller. We can therefore conclude that the virial parameter of the initial clump is much smaller than 1. Similarly, we calculate the virial parameters of the cores based on their fitted column density, size, and velocity dispersion. The result is presented in Table 1. If we use the velocity dispersion measured by Effelsberg (1.4 km s−1 ) or GBT (1.1 km s−1 ) to calculate virial parameters, the result is similar to that from JVLA (1.2 km s−1 ); the differences are in the range of the error. The current ALMA cores have virial parameters of mostly less than 2. Without knowing and counting magnetic fields, four of the six cores are in rough agreement with the "turbulent core" scenario of being in virial equilibrium (McKee & Tan 2002). However, the core masses are far less than the 102 M⊙ massive cores in the scenario, even if they have accreted more mass since the initial stage as evident from the observed outflows. Additionally, the unstable clump has highly fragmented to at least six cores, and these are not in a monolithic structure.

5.2 Supersonic turbulence and its dissipation toward cores

The Mach number map in Fig. 4 provides a snapshot of the current status of the turbulence in G35.20. The spatial distribution of Mach number is highly structured. Overall, the entire clump is mostly supersonic, but the two ends are transonic to subsonic, with Mach number down to 2 or even lower than 1. Toward the central 0.15 pc, where the ALMA dust continuum reveals six dense cores, the Mach number increases up to 7. Interestingly, most of the cores are located in local minima of the Mach number. The cores are therefore relatively "calm" compared to the surrounding turbulence. This spatial configuration has been observed in IRDCs (Zhang & Wang 2011; Wang et al. 2012; Sokolov et al. 2018; Lu et al. 2018). A stark contrast is seen in cores A/B, where the mean Mach number drops from 4.5 in their surroundings to 2.8 in the cores. The cores themselves are still supersonic, with Mach numbers ranging 2.6–5.9 (Table 1). Only in Sokolov et al. (2018) do the cores coincide exclusively with subsonic turbulence.

This "calm cores" picture appears to be consistent with a dissipation of turbulence from the clump scale to core scale. However, another possibility is that the natal clump, with an extent of 0.5 pc roughly traced by VLA NH3 (1,1) emission, is initially subsonic as a result of turbulence dissipation from even larger cloud scale (>1 pc, cf. Wang et al. 2008). The low turbulence allows gravitational collapse to proceed and the clump fragments to cores, where star formation has been launched in the central part, namely cores A/B. The turbulent gas in the clump might be a feedback of the heating and energetic outflows from the forming young stars embedded in cores A/B. Because the outflow direction is roughly perpendicular to the elongated clump/filament (Fig. 1), the two ends are least affected by this feedback, and therefore retain the initial turbulence and temperature.

To compare our results with other observations of massive star formation regions, we draw the histogram of pixel distribution in Mach number in Fig. 4. The peak value of the entire G35.20 clump is at around 2.8, which is similar to that of the Central region. This value closely resembles the values reported by Sánchez-Monge et al. (2013b; 2.2) and Lu et al. (2014; 2–3) in typical protostellar clumps, and much higher than 0.9 reported in IRDC G35.39 (Sokolov et al. 2018). We note here that only Sokolov et al. (2018) reported a high spectral resolution of 0.2 km s−1 as in this work (see Sect. 1). IRDC G35.39 therefore remains the only distant high-mass-star-formation region (other than the Orion molecular cloud; see Sect. 1) where subsonic cores have been observed to dominate the whole region. G35.20, as an evolved IRDC clump, does retain the configuration of "calm cores in turbulent gas", but the cores as well as the clump are supersonic overall. It is of great interest to investigate turbulence at the initial stages – for example in a sample of quiescent clumps like G35.39 – in order to place more stringent constraints on the role turbulence plays in high-mass star formation in theoretical models.

5.3 Diverse NH3 ortho/para ratio (OPR)

The detection of all seven rotational lines of NH3 (1,1) to (7,7), including two ortho lines (3,3) and (6,6), enabled us to derive a reliable OPR for NH3. Many previous NH3 studies only detected one ortho line NH3 (3,3), or even no ortho line, and an OPR of 1 is often assumed to derive NH3 column density (e.g., Wang et al. 2014; Sokolov et al. 2018).

OPR values smaller than unity have been reported in high-mass-star-formation regions (Hermsen et al. 1985, 1988; Persson et al. 2012), as well as in low-mass-star-formation regions (Feng et al. 2022). The low OPR is thought to originate from the gas that formed NH3 molecules (Faure et al. 2013).

On the other hand, OPR values higher than unity (1.1–3.0) have also been reported in Galactic star-formation regions (Goddi et al. 2011; Wang et al. 2014). In IRDC G11.11-0.12, Wang et al. (2014) observed NH3 and find the OPR increases from 1.1 to 3.0 along molecular outflows downstream. These authors interpreted the trend as differential desorption of the ortho- and para-NH3 molecules due to a slight difference in the energy needed for desorption. In G35.20, the outflow is perpendicular to the filament/clump, but the Central and Southern regions are more affected by the outflow than the Northern region. The trend is consisent with that in G11.11-0.12, but the OPR values are much lower.

As our OPR is derived from multiple ortho and multiple para lines, which is a rare accomplishment, it should be more robust. Further, similar investigations with samples of sources are needed to reach conclusive results on the NH3 OPR in star-formation regions (Wang et al., in prep.).

6 Summary

We present high-spatial- and spectral-resolution observations toward the massive-star-formation region G35.20-0.74 N made with ALMA and JVLA. The ALMA 870 μm dust continuum resolves fragmentation, and the JVLA NH3 (1,1) to (7,7) lines and 1.2 cm continuum emission reveal gas properties. By fitting the NH3 line cubes, we obtained maps of kinetic temperature, excitation temperature, NH3 column density, centroid velocity, velocity dispersion, and the ortho/para ratio. Based on these results, we derived a Mach number map due to intrinsic turbulence after subtracting line broadening by channel width (10%), thermal pressure (10%), and velocity gradient (3%). These well-resolved maps provide a unique opportunity to study the dynamical properties of G35.20 in depth. Our main findings are summarized as follows.

  1. The VLA NH3 line emission reveals a filament/clump of 0.5 pc in length, an intermediate scale between the larger dust clump traced by APEX 870 μm image and the six dense cores resolved by ALMA at the central 0.2 pc. The VLA 1.2 cm continuum emission reveals a lane of ionized gas in agreement with a thermal jet. The jet is misaligned with the filament traced by VLA NH3 and ALMA dust cores by 37°.

  2. The turbulence in G35.20 is supersonic overall, with the Mach number pixel distribution peaking at 2.8. However, the spatial distribution of Mach number is highly structured across the 0.5 long filament/clump: the two ends of the filament feature subsonic to transonic turbulence with Mach number down to lower than 2; the bulk of the filament has Mach number in the range of 2–4, toward the Central part of the filament it rises up to 6–7, and on the central dust cores A/B the Mach number drops dramatically to less than 3.

  3. The central cores A/B, which are actively forming stars, appear to have decoupled from the parental filament/clump, which is made evident by an opposite velocity gradient and reduced turbulence as compared to the filament/clump.

  4. The NH3 OPR is 0.1–0.3 across the clump and has a spatial structure similar to that of NH3 column density. Our study presents a rare case in which more than one ortho-NH3 line is used to derive the OPR, calling for more similarly robust measurements to study the OPR in star-formation regions.

Our observations provide a snapshot of the turbulence in G35.20, an evolved IRDC clump with active ongoing star formation in its central part. G35.20 shows supersonic turbulence overall, which is generally consistent with the traditional picture. However, the reduced turbulence toward the central star-forming cores indicates an initial stage with low levels of turbulence, possibly similar to those of the quiescent parts of the filament with subsonic turbulence. Importantly, because G35.20 is evolved, the turbulence is not in a pristine state. In a forthcoming paper (Wang et al., in prep.), we will analyze a sample of IRDCs in order to put more stringent constraints on the role of turbulence in the initial conditions of massive-star formation.

Acknowledgements

We are grateful to the anonymous referee for constructive comments that helped improve the manuscript. We thank Fengwei Xu, Qizhou Zhang, Tapas Baug, Nannan Yue, Siju Zhang, Wenyu Jiao, and Yifei Ge for valuable discussion. We acknowledge support from the National Science Foundation of China (11973013), the China Manned Space Project (CMS-CSST-2021-A09), the National Key Research and Development Program of China (22022YFA1603102, 2019YFA0405100), and the High-performance Computing Platform of Peking University. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.1.00275.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.

Appendix A Comparing one- and multi-velocity component fitting

The G35.20 NH3 clump seems to be well described by a single velocity component. Briefly, fitting two velocity components failed to converge in all but 11 pixels (1.5 beam area) around core A (top row, Figure. A.1).

In the following, we present the NH3 spectral line fitting with one velocity component, and compare the results to those when fitting multiple velocity components. The results of fitting with two velocity components are presented as a representative case because other fittings including more than two velocity components are similar.

First, we ran the one-component fitting on the entire clump. The middle row in Figure. A.1 shows the spectra of NH3 (1,1) and (2,2) extracted toward core A (marked in Figure. 5). The observed data (black) are over-plotted with the fitted line (red) and labeled with the fitted parameters. This particular pixel is chosen to illustrate the complexity in the spectra. Comparing the data and the best-fitted spectra from the top row, we cannot exclude the existence of two or more velocity components in core A because of the two-peak structure in the residuals.

Motivated by the results of the spectral fits toward core A, we then ran a fitting with two components. However, only 11 pixels (about 1.5 beam area) around core A can be successfully fitted: the fitting in the vast majority of the pixels does not converge because of the much poorer residuals under the assumption of two components. The fitting results with two velocity components for the pixel toward core A are shown in the bottom row of Figure. A.1.

Comparing the two fits shown in Figure. A.1, the second run results in better residuals for the pixels around core A, yet the fitting is only valid in 1.5 beam area around this core, and the vast majority of the NH3 clump cannot be fitted. Nevertheless, in core A, the main velocity component (with VLSR = 32.09 km s−1) from the two-component fitting is similar to the one-component fitting (with VLSR = 32.11 km s−1). The centroid velocity maps are therefore similar and both are around 32 km s−1 (in Figure. A.1). The Mach number derived from the one-component fitting is about 3.1 in core A, while the two-component fitting results are 3.1 (for the main component at VLSR = 32.09 km s−1 ) and 3.3 (for the secondary component at VLSR = 32.19 km s−1). The secondary component contributes 0.7% to the difference in Mach number (less than the uncertainty from the fitting).

In summary, our comparison shows that while core A can be better described with two components, there is mainly one component in the rest of the G35.20 clump. Even in core A, the one-component fitting results can reproduce the properties of the main component in the two-component fitting. As an example, we show one of the six fitting parameters, namely centroid velocity, from the one- and two-component fitting in the top row of Figure. A.1, demonstrating the robustness of the one-component fitting. Therefore, we adopt the one-component fitting throughout the paper.

thumbnail Fig. A.1

Fitting results of one/two velocity components. Upper row: Fitted centroid velocity maps from the one-component fitting (left), and that of the main and secondary component from the two-component fitting (middle, right). The red crosses mark the six ALMA 870 μm cores A-F, as in Figure. 1. Across the entire clump, which is well fitted by a single component, only a tiny portion around core A can be properly fitted with two-component fitting. Middle row: One velocity component fitting. NH3 (1,1) and (2,2) spectra (black) extracted from the peak of core A, overlaid with fitting results (red) and residuals. Fitted parameters are labeled on the spectra plots. Bottom row: Same as the middle row, but for a two-velocity-component fitting.

References

  1. Beltrán, M. T., Cesaroni, R., Moscadelli, L., et al. 2016, A & A, 593, A49 [CrossRef] [EDP Sciences] [Google Scholar]
  2. Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [Google Scholar]
  3. Birks, J. R., Fuller, G. A., & Gibb, A. G. 2006, A & A, 458, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Brebner, G. C., Heaton, B., Cohen, R. J., & Davies, S. R. 1987, MNRAS, 229, 679 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cornwell, T. J. 2008, IEEE J. Sel. Top. Signal Process., 2, 793 [Google Scholar]
  6. Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A & A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Dent, W. R. F., Little, L. T., Sato, S., Ohishi, M., & Yamashita, T. 1985, MNRAS, 217, 217 [NASA ADS] [CrossRef] [Google Scholar]
  8. Faure, A., Hily-Blant, P., Le Gal, R., Rist, C., & Pineau des Forêts, G. 2013, ApJ, 770, L2 [NASA ADS] [CrossRef] [Google Scholar]
  9. Feng, S., Liu, H. B., Caselli, P., et al. 2022, ApJ, 933, L35 [CrossRef] [Google Scholar]
  10. Ge, Y., & Wang, K. 2022, ApJS, 259, 36 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gibb, A. G., Hoare, M. G., Little, L. T., & Wright, M. C. H. 2003, MNRAS, 339, 1011 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ginsburg, A., & Mirocha, J. 2011, Astrophysics Source Code Library [record ascl:1189.881] [Google Scholar]
  13. Goddi, C., Greenhill, L. J., Humphreys, E. M. L., Chandler, C. J., & Matthews, L. D. 2011, ApJ, 739, L13 [CrossRef] [Google Scholar]
  14. Hacar, A., & Tafalla, M. 2011, A & A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Hacar, A., Tafalla, M., Forbrich, J., et al. 2018, A & A, 610, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Heaton, B. D., & Little, L. T. 1988, A & A, 195, 193 [NASA ADS] [Google Scholar]
  17. Hermsen, W., Wilson, T. L., Walmsley, C. M., & Batrla, W. 1985, A & A, 146, 134 [NASA ADS] [Google Scholar]
  18. Hermsen, W., Wilson, T. L., Walmsley, C. M., & Henkel, C. 1988, A & A, 201, 285 [NASA ADS] [Google Scholar]
  19. Hutawarakorn, B., & Cohen, R. J. 1999, MNRAS, 303, 845 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jiao, W., Wang, K., Pillai, T. G. S., et al. 2023, ApJ, 945, 81 [NASA ADS] [CrossRef] [Google Scholar]
  21. Larson, R. B. 1981, MNRAS, 194, 809 [Google Scholar]
  22. Lee, H.-T., Takami, M., Duan, H.-Y., et al. 2012, ApJS, 200, 2 [NASA ADS] [CrossRef] [Google Scholar]
  23. Li, S., Sanhueza, P., Lee, C. W., et al. 2022, ApJ, 926, 165 [NASA ADS] [CrossRef] [Google Scholar]
  24. Liu, H. B., Quintana-Lacaci, G., Wang, K., et al. 2012, ApJ, 745, 61 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lu, X., Zhang, Q., Liu, H. B., Wang, J., & Gu, Q. 2014, ApJ, 790, 84 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lu, X., Zhang, Q., Liu, H. B., et al. 2018, ApJ, 855, 9 [Google Scholar]
  27. McKee, C. F., & Tan, J. C. 2002, Nature, 416, 59 [CrossRef] [Google Scholar]
  28. McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [Google Scholar]
  29. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
  30. Myers, P. C. 1983, ApJ, 270, 105 [Google Scholar]
  31. Pari, J., & Hora, J. L. 2020, PASP, 132, 054301 [NASA ADS] [CrossRef] [Google Scholar]
  32. Peretto, N., & Fuller, G. A. 2009, A & A, 505, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Perley, R. A., Chandler, C. J., Butler, B. J., & Wrobel, J. M. 2011, ApJ, 739, L1 [Google Scholar]
  34. Persson, C. M., De Luca, M., Mookerjea, B., et al. 2012, A & A, 543, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Qiu, K., Zhang, Q., Menten, K. M., Liu, H. B., & Tang, Y.-W. 2013, ApJ, 779, 182 [NASA ADS] [CrossRef] [Google Scholar]
  36. Saha, A., Tej, A., Liu, H.-L., et al. 2022, MNRAS, 516, 1983 [NASA ADS] [CrossRef] [Google Scholar]
  37. Sánchez-Monge, Á., Cesaroni, R., Beltrán, M. T., et al. 2013a, A & A, 552, A10 [Google Scholar]
  38. Sánchez-Monge, Á., Palau, A., Fontani, F., et al. 2013b, MNRAS, 432, 3288 [CrossRef] [Google Scholar]
  39. Sánchez-Monge, Á., Beltrán, M. T., Cesaroni, R., et al. 2014, A & A, 569, A11 [CrossRef] [EDP Sciences] [Google Scholar]
  40. Sokolov, V., Wang, K., Pineda, J. E., et al. 2018, A & A, 611, A3 [Google Scholar]
  41. Surcis, G., Vlemmings, W. H. T., van Langevelde, H. J., & Hutawarakorn Kramer, B. 2012, A & A, 541, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Tan, J. C., Kong, S., Butler, M. J., Caselli, P., & Fontani, F. 2013, ApJ, 779, 96 [Google Scholar]
  43. Urquhart, J. S., Morgan, L. K., Figura, C. C., et al. 2011, MNRAS, 418, 1689 [NASA ADS] [CrossRef] [Google Scholar]
  44. Wang, K. 2018, RNAAS, 2, 52 [NASA ADS] [Google Scholar]
  45. Wang, K., Zhang, Q., Wu, Y., & Zhang, H. 2011, ApJ, 735, 64 [Google Scholar]
  46. Wang, K., Zhang, Q., Wu, Y., Li, H.-B., & Zhang, H. 2012, ApJ, 745, L30 [NASA ADS] [CrossRef] [Google Scholar]
  47. Wang, K., Zhang, Q., Testi, L., et al. 2014, MNRAS, 439, 3275 [Google Scholar]
  48. Wang, K., Testi, L., Burkert, A., et al. 2016, ApJS, 226, 9 [NASA ADS] [CrossRef] [Google Scholar]
  49. Wang, Y., Zhang, Q., Pillai, T., Wyrowski, F., & Wu, Y. 2008, ApJ, 672, L33 [NASA ADS] [CrossRef] [Google Scholar]
  50. Wienen, M., Wyrowski, F., Schuller, F., et al. 2012, A & A, 544, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Xu, F.-W., Wang, K., Liu, T., et al. 2023, MNRAS, 520, 3259 [NASA ADS] [CrossRef] [Google Scholar]
  52. Yan, Q.-Z., Zhang, B., Tang, Z.-H., & Zheng, X.-W. 2013, Res. Astron. Astrophys., 13, 815 [Google Scholar]
  53. Yue, N.-N., Li, D., Zhang, Q.-Z., et al. 2021, Res. Astron. Astrophys., 21, 024 [CrossRef] [Google Scholar]
  54. Zhang, B., Zheng, X. W., Reid, M. J., et al. 2009, ApJ, 693, 419 [Google Scholar]
  55. Zhang, Q., & Wang, K. 2011, ApJ, 733, 26 [Google Scholar]
  56. Zhang, S., Wang, K., Liu, T., et al. 2023, MNRAS, 520, 322 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zhang, Y., Tan, J. C., De Buizer, J. M., et al. 2013, ApJ, 767, 58 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Physical parameters of the ALMA cores.

In the text

All Figures

thumbnail Fig. 1

Overview of G35.20-0.74 N imaged by Spitzer, APEX, JVLA, and ALMA at various scales. First row-left: Spitzer 4.6 μm emission (Benjamin et al. 2003) obtained by IRAC overlaid with a green contour map of the 870 μm continuum emission from the ATLASGAL survey (Csengeri et al. 2014). The unit of the color wedge is MJy sr−1 in IRAC map. The APEX 870 μm contours start from 3σ, and are then 6σ, 12σ, and 24 σ, where σ =90 mJy beam−1. The dashed yellow and red circles are of 1' and 2' in diameter, with the latter being the VLA primary beam. First row-right: Same Spitzer 4.6 μm emission overlaid with green contours showing the integrated intensity map of NH3 (1,1) and black contours showing 1.2 cm continuum emission from our observations. The green contours start from 5 σ, and are then 10σ, 15σ, and 20 σ, where 1σ is equal to 1.2 mJy beam−1. The black contours start from 6σ, and are then 20σ, 48σ, 80σ, 130σ, 180σ, and 230 σ, where 1σ is equal to 18 μJy beam−1. Blue arrows show the direction of the CO outflow (Birks et al. 2006). Second row: Same VLA 1.2 cm continuum in color scale overlaid with ALMA 870 μm continuum emission in green contours. The color bar is in units of mJy beam−1. Green contours are from 9 to 230 mJy beam−1 with a step of 1.8 mJy beam−1. Cores A-F are marked following Sánchez-Monge et al. (2014).
In the text
thumbnail Fig. 2

Flux-integrated maps of JVLA NH3 lines from (1,1) to (7,7) in G35.20-0.74 N. Upper row: From left to right are NH3 (1,1) to (3,3) shown in the same color bar. Ellipses in the bottom-right corner are synthesized beams of each line image. Contours show the 3σ level of each line-integrated map. Lower row: Similar to the upper row but for lines from (4,4) to (7,7), with a different color bar.
In the text
thumbnail Fig. 3

Maps of fitted parameters (left column) with errors (middle column) and histograms of pixel distribution of the Northern, Central, and Southern regions (right column). From top to bottom are the kinetic temperature, column density, velocity dispersion, centroid velocity, and OPR. The black contour is the same as that of the right panel in Fig. 1, which shows the ALMA 870 μm emission. Scale bars on the right share the same units for parameter and fitting error.
In the text
thumbnail Fig. 4

Mach number (left) and its pixel distribution (right). The white contours and red crosses mark the ALMA 870 μm emission cores, with contour levels the same as in Fig. 1. The dashed black and red vertical lines mark the typical Mach number in the literature, representative of quiescent and protostellar stages, respectively. The brown histogram corresponds to the brown circle of the central region (covering cores A and B), and the blue histogram is that of the whole G35.2 clump.
In the text
thumbnail Fig. 5

Velocity and column density in G35.20. Left: NH3 fitted centroid velocity overlaid with ALMA 870 μm contours as in Fig. 3. The box and arrow indicate how the PV cuts are made on the right panels. Right: The top panel is a PV cut showing the averaged centroid velocity (beam by beam) of the entire NH3 filament along the direction pointed by the arrow in the left panel, starting from the northern end down to the southern end of the NH3 filament shown in the left panel. The zero point is located between cores A and B. The red line is a linear fit excluding data between cores A and B. The middle panel is a pixel-by-pixel (instead of beam by beam) PV cut along the black-box region in the left panel after subtracting a global velocity gradient (red line in top panel). The bottom panel corresponds to the NH3 column density profile. The positions of the six ALMA cores A-F are marked with dashed vertical lines.
In the text
thumbnail Fig. A.1

Fitting results of one/two velocity components. Upper row: Fitted centroid velocity maps from the one-component fitting (left), and that of the main and secondary component from the two-component fitting (middle, right). The red crosses mark the six ALMA 870 μm cores A-F, as in Figure. 1. Across the entire clump, which is well fitted by a single component, only a tiny portion around core A can be properly fitted with two-component fitting. Middle row: One velocity component fitting. NH3 (1,1) and (2,2) spectra (black) extracted from the peak of core A, overlaid with fitting results (red) and residuals. Fitted parameters are labeled on the spectra plots. Bottom row: Same as the middle row, but for a two-velocity-component fitting.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.