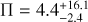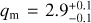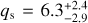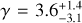| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202040267 | |
| Published online | 23 May 2023 | |
Understanding the trans-Neptunian Solar System
Reconciling the results of serendipitous stellar occultations and the inferences from the cratering record
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris,
5 place Jules Janssen,
92195
Meudon, France
e-mail: quentin.kral@obspm.fr
Received:
31
December
2020
Accepted:
27
March
2023
The most pristine remnants of the Solar System planet formation epoch orbit the Sun beyond Neptune. These are the small bodies of the trans-Neptunian object populations. The bulk of the mass is distributed in ~100 km objects, but objects at smaller sizes have undergone minimum collisional processing. The New Horizons mission recently revealed that the body (486958) Arrokoth, with its effective diameter of ~20 km, appears to be a primordial body and not a collisional fragment. This indicates that bodies at these (and perhaps smaller) sizes retain a record of how they were formed, and they are the most numerous record of this epoch. However, it is impractical to find these bodies with optical surveys because their brightnesses are very low. Their presence can be inferred from the observed cratering record of Pluto and Charon, and it can be directly measured by serendipitous stellar occultations. These two methods produce contradicting results: occultations measure roughly ten times the number of about kilometer-size bodies as are inferred from the cratering record. We used numerical models to explore how these observations can be reconciled with evolutionary models of the outer Solar system. We find that models in which the initial size of the bodies decreases with increasing semimajor axis of formation and models in which the surface density of the bodies increases beyond the 2:1 mean-motion resonance with Neptune can produce both sets of observations, but a comparison to various observational tests favours the former mechanism. We discuss how the astrophysical plausibility of these solutions can be evaluated, and we conclude that extended serendipitous occultation surveys with a broad sky coverage are the most practical approach.
Key words: Kuiper belt: general / occultations
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The Solar system beyond Neptune is thought to contain the least collisionally evolved population of small bodies in the Solar system. Owing to their relatively unevolved state, observations of these bodies thus give the best direct constraints of how planetesimals formed and evolved at sizes of ~1 ~ 100 km. There is an observed turnover in the size-number distribution around a radius of s = 50 ~ 70 km (Bernstein et al. 2004; Fraser et al. 2014). Although it was originally suspected that this might be of collisional origin, further work has shown that it is far more likely to be of primordial origin (Vitense et al. 2012) because the size is far too large to be produced in even the most optimistic models of collisional evolution (Pan & Sari 2005). Similar conclusions have been reached about the size-number distribution of the asteroids (Morbidelli et al. 2009). The conclusion that the turnover in the size-number distribution of trans-Neptunian objects (TNOs) is not collisional is strongly re-enforced by New Horizons observations of the body (486958) Arrokoth, whose effective diameter is about 20 km, and which appears to be a primordial body rather than a collisional fragment (Stern et al. 2019). This may also be true of the Jupiter family comet1 67P/Churyumov-Gerasimenko (Massironi et al. 2015), with its diameter of about 4 km, although this interpretation has been contested (Jutzi & Benz 2017). Morbidelli et al. (2021) estimated from the survival of (486958) Arrokoth that the size at which bodies transition from being mostly primordial to mostly collisional fragments may be ~1 km. Further evidence of the low degree of collisional evolution of TNOs comes from the survival of ultra-wide binaries in the cold classical Kuiper belt (Parker & Kavelaars 2012).
The evidence of minimum collisional evolution in the populations of TNOs applies most clearly to the cold classical Kuiper belt. In the usual population classification scheme (Gladman et al. 2008), the cold classicals are known to exist mainly within the main classical Kuiper belt, between the 3:2 and 2:1 mean motion resonances with Neptune. A few appear to exist beyond the 2:1 mean motion resonance (Bannister et al. 2018), but the properties of the belt are less clear there, and Nesvorny (2020) suggested they may have been implanted from primordial orbits closer to the Sun. The cold classicals formed close to their current orbits (Dawson & Murray-Clay 2012; Nesvorný 2015), which isolated them from much of the Solar system evolution. The various hot populations (resonant, hot classicals, scattering, and detached) formed closer to the Sun before they were pushed to their current orbits (Malhotra 1993; Levison et al. 2008; Brasil et al. 2014; Volk & Malhotra 2019), and could have undergone significant early collisional evolution (Charnoz & Morbidelli 2007; Campo Bagatin & Benavidez 2012; Shannon et al. 2019), depending on the timing and details of the outer Solar system evolution (Gomes et al. 2005; Morbidelli et al. 2018; Nesvorný et al. 2018). The observational evidence of the collisional evolution of the hot population is rather unclear. The hot populations lack ultra-wide binaries (Grundy et al. 2019), but these may have been lost by a non-collisional process (Parker & Kavelaars 2010). A few of the largest bodies show evidence of giant impacts (Canup 2005; Brown et al. 2007), but it appears that these may have occurred at low speeds (Canup 2011; Proudfoot & Ragozzine 2019; Pike et al. 2020), and thus they reflect accretional collisions rather than destructive collisions. This question remains far from settled, however.
Thus, well-constrained measurements of the size-number distribution of TNOs, especially of cold classicals, at sizes clearly smaller than ~50 km could provide strong support for models of their formation. Planetesimal formation via the streaming instability (Youdin & Goodman 2005; Johansen et al. 2007) is currently generally seen as the most promising mechanism for forming planetesimals at these sizes (Raymond & Morbidelli 2022), and makes clear predictions for the expected size-number distribution below the primordial break in the size-number distribution (Simon et al. 2016, 2017). Conversely, these measurements might instead provide evidence of a competing mechanism, such as fluffy aggregate growth (Arakawa & Nakamoto 2016), collisional pebble agglomeration (Shannon et al. 2016), or turbulent clustering (Cuzzi et al. 2010, 2016; Hartlep & Cuzzi 2020).
At sizes below tens of kilometres, however, it is prohibitively difficult to strongly constrain the size-number distribution with reflected-light surveys (Bernstein et al. 2004; Fraser et al. 2014). Two techniques can be employed to measure the size-number distribution down to sizes of several hundred meters. Small TNOs can be detected by serendipitous occultations of stars (Roques et al. 2003; Schlichting et al. 2009) and by counting the size-number distribution of craters on Pluto and Charon seen by New Horizons to infer the size-number distribution of the impactors (Robbins et al. 2017). So far, four experiments have reported detections of serendipitous occultations (Schlichting et al. 2012; Liu et al. 2015; Arimatsu et al. 2019; Doressoundiram et al. 2020), and at least one more experiment is under construction (Lehner et al. 2019), while others provided upper limits (Bickerton et al. 2008; Bianco et al. 2009; Wang et al. 2010; Chang et al. 2013; Zhang et al. 2013).
The serendipitous occultation surveys have found results that are generally compatible with one another. They report the number of objects with a size of about one kilometer to be 10 ~ 100× as numerous as inferred from the cratering record (Singer et al. 2019; Fig. 1). Reconciling these two sets of observations may be possible because the observations do not necessarily sample the same populations of bodies: the occultations measure the present-day population along the line of sight, and the craters are a time-integrated record of bodies that overlap the orbit of Pluto-Charon. Here we investigate whether a hypothetical extension of the cold populations to larger semimajor axes can be consistent with both sets of observations, allowing for the possibility that the characteristic formation size of bodies might decrease (or increase) with their semimajor axis of formation. In Sect. 2 we outline the method we used to model the evolution of the trans-Neptunian populations and compare them to observations. In Sect. 3 we present the results of the modelling. In Sect. 4 we discuss the implications of the results and how they can be validated. In Sect. 5 we present our conclusions.
 |
Fig. 1 Existing measurements of the size-number distribution of small bodies in the outer Solar system. We compare the results of occultation surveys (upper limits: Bickerton et al. 2008; Bianco et al. 2009; Wang et al. 2010; Chang et al. 2013; Zhang et al. 2013; and detections: Schlichting et al. 2012; Liu et al. 2015; Arimatsu et al. 2019; Doressoundiram et al. 2020), optical surveys (Fraser et al. 2014), and crater counting (Singer et al. 2019), which are converted into a population number using the dynamical model of Greenstreet et al. (2015). Because the different types of surveys use different measurements, they can only be directly compared in a somewhat model-dependent way. Thus, the apparent disagreement may represent a disagreement of the observations, or an incorrect assumption in the modelling. |
2 Methods
2.1 Single-model evaluation
To simulate the collisional and dynamical evolution of the outer Solar system, we used a statistical particle-in-a-box approach in which bodies of similar masses and orbital elements are grouped together (Safronov 1969). Our code is derived from the code presented in Shannon et al. (2015, 2016), with several modifications to make it suitable for the problem at hand.
While Shannon et al. (2015, 2016) considered only a single radial zone, we considered four unique, mutually interacting, dynamical populations: the cold classical Kuiper belt, the hot classical Kuiper belt, the scattered disk, and the resonant disk. Each population contains multiple semimajor axis bins so that bodies at different distances from the Sun can be represented. Most of the bin position choices do not significantly affect the evolution. They were set to divide the modelled population in a uniform way while keeping the total number of bins small enough to keep computations tractable. The innermost bin of the cold classical Kuiper belt was set to have an outer end near 50 au to accommodate our assumption that a discontinuity in the surface density of cold classicals there is possible. Based on this, we set the cold classical to have six bins at 42 au < a < 52 au, 52 au < a < 62 au, 62 au < a < 72 au, 72 au < a < 82 au, 82 au < a < 92 au, and 92 au < a < 102 au. The first bin covers the known cold classicals, and the subsequent bins cover our hypothetical extention. The hot classicals have two bins for objects with 36 au < a < 48 au and 48 au < a < 60 au. For the scattered disk, we use two bins, one bin for objects with 35 au < a < 62.5 au, and one bin for 62.5 au < a < 100 au. Although there are scattered objects with larger semimajor axes, the low surface density and long orbital periods render them relatively unimportant for any collisional evolution. The resonant disk has three bins to represent the populations of the 3:2 MMR from 39 to 40 au, 2:1 from 47.3 to 48.3 au, and the 5:2 from 54.9 to 55.9 au. For the resonant populations, the eccentricity rather than semimajor axis bin width sets the radial extent of the population, and therefore, the choice of bin width is largely unimportant. Each semimajor axis bin was assigned a single eccentricity and inclination, neither of which evolved. All cold classical bins were assigned e = 0.04 and i = 2.5° (Petit et al. 2011), all hot classical bins were assigned e = 0.2 and i = 14.5° (Petit et al. 2017). Scattered bins were assigned i = 14.5°, and the eccentricities were chosen so that the pericentre was q = 30 au. For the resonant objects, the 3:2 MMR populations were assigned e = 0.175 and i = 12°, the 2:1 MMR populations were assigned e = 0.28 and i = 4.0°, and the 5:2 MMR populations were assigned e = 0.35 and i = 10° (Volk et al. 2016).
Each semimajor axis bin contained 90 mass bins covering masses from 1010 to 1025 grams that initially were spaced equally in log(mass). The bin masses were not exactly fixed, but were allowed to float to improve the resolution (as in e.g. Kenyon & Luu 1998, and our implementation was tested in detail in Shannon et al. 2015). To keep computation times down, but accurately model the collisional evolution of the smaller bins and avoid edge effects, bodies from 10−12 to 1010 grams were represented with non-evolving bins, whose evolution was not calculated, and whose size-number distribution was forced to obey dn/ds ∝ s−35 (Dohnanyi 1969), with the normalisation fixed by the lowest-mass evolving bin (somewhat analogous to the procedure used in e.g. Kenyon & Bromley 2008). Within the evolving bins, the initial size distribution is a doubly broken power law, with the large size slope qL, and the large break size sL set to their observed values, and the small break size sS set by inference from the cratering record of Charon, while the medium size slope qm and the small size slope qs are free parameters that we introduced to fit the model. Kenyon & Bromley (2020) explored producing sL and sS analogues by collisional evolution and reported that producing these breaks in the cold classicals would require a high total mass that is unlikely to be plausible for this population. We therefore take it to be the case that these breaks may be primordial. For the hot classicals, the scattering, and the resonant populations, the large size slope was set to qL = −5.5 (Volk et al. 2016) and the large break size was set to sL = 55 km (Fraser et al. 2014). Setting these three populations to the same values is partially motivated by the idea that they formed from a single parent population that originated closer to the Sun (Levison et al. 2008). For the cold classicals, the large size slope was set to qL = −8.5 and the large size break was set to sL = 70 km for a < 50 au (Fraser et al. 2014). Within our model. we chose to allow the large break size to scale with semimajor axis as
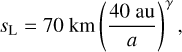 (1)
(1)
where γ is a free parameter that we introduced to characterise our supposition that the characteristic size of formation may vary with orbital distance. We fitted this γ to the data. The resulting initial size-number distribution that was used in our model is sketched in Fig. 2.
To model the evolving dynamical history of the Solar system, we depleted the unstable populations exponentially, with timescales of 1 Gyг for the scattered disk (Duncan & Levison 1997), 3.43 Gyгs for the 3:2 resonant objects, and 2.37 Gyгs for the 2:1 resonant objects (Tiscareno & Malhotra 2009).
To set the normalisation in each bin, we first assumed that the surface density of objects varies as a−1.5 (Weidenschilling 1977), then we set the total number of large objects to match the present-day populations from Fraser et al. (2014) for the cold and hot classicals, and the Outer Solar System Origins Survey (OSSOS) from Volk et al. (2016) for the resonant populations, and from Lawler et al. (2018b) for the scattering population. We accounted for the imposed dynamical depletion and assumed that collisional deletion for objects at ≳50 km is negligible. The latter assumption is predicted by theory (Pan & Sari 2005; Vitense et al. 2012) and is now supported by various lines of observational evidence (Parker & Kavelaars 2012; McKinnon et al. 2020). In the case of the cold classicals, the observational normalisation was set for the first bin alone, from 42 to 52 au, where the main cold classical belt is located, and which covers the known objects. Beyond this, we posit that the cold classical belt may be extended to much larger semimajor axes. We wished to allow for the possibility that the primordial surface density may have discontinuously changed with radial distance. We therefore multiplied the surface density by a factor Π, which we introduced to quantify this change, and which we fit to the data. If the size-number distribution is constant as a function of semimajor axis, then Π must be ≪1 to be consistent with the small number of large (≳100 km) bodies detected by surveys in the optical (Bannister et al. 2016). However, because we also let the large break size (sL) be a function of semimajor axis, Π can be greater than one if the characteristic size of large bodies decreases with semimajor axis (i.e. if γ > 0, Eq. (1)). We therefore restrict its value to be only Π ≥ 0. We motivate Π > 1 cases partially by the argument that the sweeping of the 2:1 MMR may have depleted the original population interior to its current location (Nesvorný 2015; Fraser et al. 2017), and partly by the observation that the surface density in solids is not a monotonically decreasing function of distance in protoplanetary disks (ALMA Partnership 2015; Andrews et al. 2018).
The number of bodies in all bins evolved by mutual collisions. The bodies in one semimajor axis and mass bin collided with those in all other bins with a frequency of nσυ, where n is the volume density of these bodies, σ is the cross section for a collision, given by π (s1 + s2)2, where s1 and s2 are the radii of the two objects, and υ is the random velocity between the two bins, given by (Wetherill & Stewart 1993)
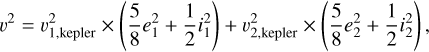 (2)
(2)
where e1 and e2 are the eccentricities of the two bins, i1 and i2 are the inclinations of the two bins, and υ1,kepler and υ1,kepler are the Keplerian velocities in the middle of the two bins. When two bins overlap partially, the interaction rate was decreased by the fractional overlap of the two bins, as outlined in Krivov et al. (2005). Collisional outcomes were determined using the prescription of Leinhardt & Stewart (2012) for collisional outcomes, including disruption, super-catastrophic disruption, and hit-and-run collisions. Our choice of model parameters prevents merging collisions. We slightly simplified the calculations by always setting the impact angle to the median value of 60°. We used the material parameters from Stewart & Leinhardt (2009) fit to weak low-density rock or sand with their parameters µ = 0.4, ϕ = 7, qs = 500 (their qs, different from our qs), qg = 10−4, and a material density ρ = 1 g cm−3.
To explore the combinations of parameters that can produce the currently observed Solar system, we employed the MCMC code of Foreman-Mackey et al. (2013). The model was allowed to explore four free parameters: the medium-size slope qm and the small-size slope change qs, which determine the primordial size-number distribution of the bodies in all populations; γ, a power-law exponent that scales the large break size of the primordial size number distribution of cold classical objects with the formation distance; and Π, the scaling factor for the surface density of cold classical bodies beyond 50 au. The goodness of fit for each trial was determined by comparisons to the observations described below:
The cratering record of Charon as reported in Singer et al. (2019). We parametrised their relative (R) plot of the surface density of craters as R (s = 100 m) = 0.004 ± 0.002, R (s = 500 m) = 0.05 ± 0.025, and R (s = 7.5 km) = 0.05 ± 0. 025, where these values are estimated approximately from the dispersion within that work. The volume density of TNOs in space was converted into R using the impact probabilities for each population onto Charon calculated by Greenstreet et al. (2015).
The on-sky surface density of occulting bodies with r > 250 m in the ecliptic today from the observations of Schlichting et al. (2012), who found
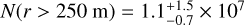 deg−2.
deg−2.The on-sky surface density of occulting bodies with r > 530 m in the ecliptic today compared to the observations of Doressoundiram et al. (2020), who found
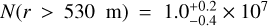 deg−2.
deg−2.The pencil-beam optical survey of Bernstein et al. (2004), who surveyed 0.019 square degrees in the ecliptic, with a modelled detection efficiency of ~100% for m < 28.4 and ~50% for 28.4 < m < 28.6. They discovered three objects in the classical populations, which we assigned an uncertainty of
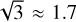 objects (Bernstein et al. 2006).
objects (Bernstein et al. 2006).
Because the direct observations and occultations measure bodies that are in the ecliptic, all populations are measured in it, with more highly inclined populations contributing a smaller fraction of their bodies to these measures. Cratering requires the orbits of a population to overlap that of Pluto-Charon. All populations except the cold classicals beyond 50 au contribute to the cratering, and the 3:2 resonance overlaps most strongly. Other possible observational tests exist, but we chose not to employ them. We used the OSSOS results to set the input, rather than evaluate the output, to keep the number of free parameters reasonably low, and because we are primarily interested in smaller (~1 km) bodies, which are not well measured by that survey. In Fig. 3 we use the OSSOS simulator (Lawler et al. 2018a) to understand which cold classical objects might be detected by optical surveys. For this calculation, we used a uniform flat distribution of the eccentricity from e = 0 to e = 0.04. The default model employed by OSSOS increases in eccentricity with the semimajor axis (Petit et al. 2011), but whether this should be expected to continue to larger semimajor axes is unclear (e.g. see Batygin et al. 2011). We therefore instead considered a cold population that remained dynamically cold at all semimajor axes. The exact conversion of the absolute magnitude to sizes depends on the albedo of the bodies, which is known to have varied with the semimajor axis of formation (Fraser et al. 2014), and is poorly constrained observationally beyond ~46 au. For reference, however, comets have a typical albedo of 0.04, small hot classicals of 0.06, and cold classicals of 0.15. For a spherical body with a diameter of 100 km, this corresponds to H ≈ 9.1, 8.7, and 7.7. Although the 2:1 mean-motion resonance with Neptune is sometimes associated with the outer boundary of the cold classical Kuiper belt, Bannister et al. (2018) identified four apparent detections of cold classical bodies beyond the 2:1 mean-motion resonance at 47.8 au. They identified these bodies by selecting objects with q > 40 au and inclinations of a few degrees at most. The exact choice for cutoff parameters can slightly affect the count. For instance, their object o5d052, with a = 53.7 au, i = 4.5°, but e = 0.29, q = 38.2 au, is classified by their criteria as a detached object, but it might be better associated with the cold classicals. Although these are only a handful of objects, the outerlimits of the cold classicalbeltare notwellestablished, and limits depend on the assumptions made about the properties of the bodies in the population.
We converted the bodies from the model populations into an expected number of objects within β of the ecliptic following Fraser et al. (2014),
![$ F\left( { > \beta } \right) = {\textstyle{2 \over \pi }}\,{\sin ^{ - 1}}\,\left( {\min \,\left[ {{{\sin \beta } \over {\sin \,i}},1} \right]} \right), $](/articles/aa/full_html/2023/05/aa40267-20/aa40267-20-eq6.png) (3)
(3)
which allowed us to calculate the fraction of the time for which a body with an inclination i is within β of the ecliptic. We compared this to our observational tests.
 |
Fig. 2 Example sketch of how we parametrised the initial size-number distribution in our simulations. Bodies in the solid-line region are logarithmically placed in bins with six bins per decade of mass. The intermediate-size slope is parametrised as −qs − qm, so that the qs parameter measures the need for a break in the slope of the size-number distribution. Bodies within the dotted line are included as impactors, but they are not evolved, but are forced to obey a collisional equilibrium power law from the smallest evolving bin (see text). |
 |
Fig. 3 Fraction of bodies in a cold disk detected by the OSSOS survey simulator, calculated using the method outlined in Lawler et al. (2018a), as a function of absolute magnitude H and semimajor axis a. Each point considered one million hypothetical objects. The 0.000 line therefore represents a chance of discovery lower than 0.0001%. |
 |
Fig. 4 Autocorrelation time estimates for two different sets of MCMC chains for the qm parameter, estimated in two different ways, using the method of Goodman & Weare (2010) and of Foreman-Mackey et al. (2013). The four estimates are slightly different, but all indicate a correlation time of ≲102. The other parameters also have autocorrelation times of O (τ) ~ 102, with τγ a factor of 2 ~ 3 larger. |
2.2 Ensemble-model evaluation
We initialised our default case with 16 walkers searching the phase space, initially dispersed around the point Π = 1, qm = 3, qs = 4, and γ = 4. The values were chosen to fit observational constraints and were found to produce plausible model fits in initial evaluations. In some other cases, parameter choices can result in models that are both poor fits to the observational tests and extremely computationally onerous to evaluate. These can prevent initialisations from converging in a reasonable computation time, but are not a significant problem later on, as they are found to be much poorer fits later in searches. The walkers therefore typically revert to their previous step location. To randomise the walkers, we began the search with the 16 walkers spread around the starting point by randomly perturbing the initial values by 0.1. The searches were constrained to the space defined by 0 ≤ Π ≤ 100, 0.0 ≤ qm ≤ 6.0, −10.0 ≤ qs ≤ 10, and −5 ≤ γ ≤ 15.
Examination of the autocorrelation times (Fig. 4) in the Markov chains using the approaches suggested in Foreman-Mackey et al. (2013) suggest a typical value of 𝒪 102. Because the model is multidimensional and non-linear, there are local minimums in the parameter space at which the walkers can become stuck for more extended periods (Fig. 5). For our model evaluation, we ran the chains for 13 500 steps and discarded the first 9000. Because our chains are significantly longer than the autocorrelation times, the chains converged well.
Our starting point for the Markov chain Monte Carlo walkers was physically and observationally motivated, but we wish to be confident that it does not represent some kind of local minimum within the parameter space. To test this, we randomly and uniformly initialised a run of 32 walkers across the allowed search space (0 ≤ Π ≤ 100, 0.0 ≤ qm ≤ 6.0, −10.0 ≤ qs ≤ 10, and −5 ≤ γ ≤ 15). Initial computations are slow, but within ~102 iterations, roughly half the walkers are within the converged solution space (Fig. 6). The remaining walkers continue to converge towards the best-fit solutions, but the convergence slows and the increased computation times at some of the sticky points prevented us from running this case to complete convergence. Nonetheless, the results here give us confidence that our choice of initial conditions produce a good coverage of the applicable solution phase space.
 |
Fig. 5 MCMC chains for the model parameter γ after the chains converged well. The walkers mostly stay near the median value of 3.6, but some of the excursions to higher or lower values are somewhat sticky, reflecting local minima in the probability space. |
3 Results
The results of the full chains are plotted in Fig. 7. The best-fit values of the model parameters are 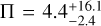 ,
, 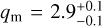 ,
, 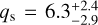 , and
, and 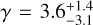 . The best-fit Π does not indicate whether the model has a preference for a jump in the surface density, as an examination of the distribution of values shows they are clustered near 1, with a long tail to high values, whereas negative values were disallowed as unphysical. The lower bounds on qs are produced by the model, but the upper bounds appear to be produced by the choice that values of qs > 10 were prohibited. We did not reconsider this limit, as we expect and confirmed that very high values quickly converge in behaviour by collisional evolution. The four free parameters do not show significant correlations, except in the region of large Π and small/negative γ (Fig. 7 bottom left panel), which are disfavoured but not entirely excluded by the model. In these cases, the total mass increases with distance, but this mass is largely in a small number of very large bodies, resulting in a poor but not completely excluded fit by the model. It might be possible to further exclude this area with the addition of further observational tests that are sensitive to small numbers of large objects (e.g. shallow all-sky surveys like Brown et al. 2015), but as these represent similar models at the roughly 100 m to ~1 km sizes we are interested in, we chose not to pursue these complications.
. The best-fit Π does not indicate whether the model has a preference for a jump in the surface density, as an examination of the distribution of values shows they are clustered near 1, with a long tail to high values, whereas negative values were disallowed as unphysical. The lower bounds on qs are produced by the model, but the upper bounds appear to be produced by the choice that values of qs > 10 were prohibited. We did not reconsider this limit, as we expect and confirmed that very high values quickly converge in behaviour by collisional evolution. The four free parameters do not show significant correlations, except in the region of large Π and small/negative γ (Fig. 7 bottom left panel), which are disfavoured but not entirely excluded by the model. In these cases, the total mass increases with distance, but this mass is largely in a small number of very large bodies, resulting in a poor but not completely excluded fit by the model. It might be possible to further exclude this area with the addition of further observational tests that are sensitive to small numbers of large objects (e.g. shallow all-sky surveys like Brown et al. 2015), but as these represent similar models at the roughly 100 m to ~1 km sizes we are interested in, we chose not to pursue these complications.
To better understand the solution, we plot an example of the evolution for the best-fit parameters in Fig. 8. The figure shows that the model meets the various observational criteria. The size of the largest bodies that formed decreases with distance from the Sun, keeping the number of large bodies that could be seen in optical surveys small. Even though the total mass in each radial bin decreases with distance from the Sun (except for a small bump after the first bin), the number of bodies at a few hundred meter sizes increases because the mass is distributed there, rather than in largerbodies. This produces large numbers of bodies with sizes of a few hundred meters that can be detected in serendipitous occultation surveys. These bodies at a greater distance from the Sun do not produce a cratering record on Pluto or Charon because their orbits do not overlap. In this way, the parameters produced from the model can be tied to specific observables, for instance the Π parameter only affects bodies that do not produce a cratering record on Pluto or Charon, so that an observational test does not favour any particular value for Π (Fig. 9). In contrast, the pencil-beam HST survey of Bernstein et al. (2004) disfavours high values of Π (Fig. 10) because that survey is sensitive to bodies with radii as small as 10 km at 50 au. Bodies smaller than ~100 m do not appear in any of the observations, so that the effective slope measured for the smallest bodies is approximately −2. If smaller bodies were measurable, we should expect them to have a more negative slope as our fit needs a positive qs, which is driven primarilyby theobservation of craters at 200 m. However, as with all parameters, the interaction between the four input parameters and six observations is complex. We can also compare the simulated size distribution of bodies in the main Kuiper belt (dark blue line in Fig. 8) to that obtained from the Charon cratering record (light blue curve in Fig. 1) for the smallest sizes, that is, between radii of 100 and 500 m. We note that the simulations show a dip at ~500 m before they transition to the −3.5 slope at smaller sizes. This dip may explain the shallower slope in −1.7 that is observed between 100 and 500 m from the Charon cratering record. However, the dip does not extend to a wide range of radii and apparently fails to fully explain the observations. The simulations show the end state of the collisional evolution, but it is expected that the dip was much deeper in the youth of the Solar system (see the dashed line in Fig. 8), when most impacts occurred with Charon. Because the cratering record with Charon is integrated over the whole history of the Solar system and the simulation is at a given time, we should not directly compare the two figures, but the dip (which was even deeper early on when most impacts occurred) apparently goes in the correct direction to explain this observed shallower slope in −1.7.
In the example evolution, the initial conditions are fairly similar to the present-day conditions, and in this case, significant collisional evolution only occurs at sizes of a few hundred meters and smaller, where the more numerous, smaller bodies collide more frequently. With a steep size-number distribution, the transition from where the chance of a catastrophic collision is ≫ 1 to where it is ≪1 is quite sharp. This low degree of collisional evolution is consistent with the observation that (486958) Arrokoth is not significantly collisionally evolved (Spencer et al. 2020), which also holds for the ultra-wide binaries of the cold classicals (Parker & Kavelaars 2012).
We noted that examination of the distributions suggests that our choice to restrict qs ≤ 10.0 likely excludes higher values of qs that would give acceptable fits. This example evolution shows that because qs governs the size distribution below 500 m, which is significantly filled in simulations that begin with very few small bodies, it is likely that there is no upper limit for this parameter. If qs + qm ≳ 0, smaller bodies are less numerous than larger bodies (Fig. 2), and thus the larger bodies drive the collisional evolution, which causes all these models to converge quickly. It is therefore safe to exclude values of qs here.
 |
Fig. 6 Example showing a run for which we randomly and uniformly initialised 32 walkers across the full allowed space 0 ≤ Π ≤ 100, 0.0 ≤ qm ≤ 6.0, −10.0 ≤ qs ≤ 10, and −5 ≤ γ ≤ 15. The walkers converged towards the same qm ~ 2.9 as in the longer run, but the model evaluation times for some points far from the good solutions can be exceedingly long, making it computationally difficult to fully evaluate these chains. Because of this, we prefer to start walkers near our default solution. |
4 Discussion
4.1 Variation in formation size with formation distance
In the streaming instability model, simulations find that the formation size of planetesimals varies with distance (Simon et al. 2016). In a simple minimum mass solar nebula model (Weidenschilling 1977), this size increases slowly with formation distance, but this simple model may not reflect reality (Desch 2007; Carrera et al. 2017; Andrews 2020), so that this remains a possibility. Klahr & Schreiber (2020) reported that for their assumptions about disk evolution, the formation size slowly increased with distance, but turned over and quickly decreased at 10s of au. Krivov & Wyatt (2021) suggested that large populations of small (~ km) without accompanying large (~100 km) bodies might be able to resolve some issues in the debris disk models that otherwise infer implausibly high masses. If this interpretation is correct, it would be natural to expect that a similar population could exist around the Sun.
4.2 Detection of small, distant bodies
Fundamentally, a model that can fit all the observations is not a demonstration that the model represents the astrophysical reality. This concern is perhaps particularly strong in a case like this, in which the model has tunable parameters that give it significant flexibility. This poses the question whether we can demonstrate that the detections are of astrophysically occulting objects and are not some kind of noise of the instruments or artefacts of the data reduction.
Occulting objects are far too small to be followed up (with expected apparent magnitudes ≳35), even in the most optimistic cases for LUVOIR (The LUVOIR Team 2019). The most straightforward evidence would be to demonstrate that the occultations preferentially occur in the ecliptic. Previous occultation surveys have been limited in their ability to do this. Schlichting et al. (2012) reported two detections using the Hubble Space Telescope fine-guiding sensors. They reported detections at 6.6°, 14.4°, and a possible detection at 81.5° from a sample that was roughly uniform across the sky. These detections are concentrated towards the ecliptic, but this result is not statistically significant. Arimatsu et al. (2019) reported the detection of a single object at 0.2°, but imaged only stars within 0.8° of the ecliptic, and thus the detection has insufficient statistical power to demonstrate that the detections are concentrated towards the ecliptic. Liu et al. (2015) reported 13 possible detections in CoRoT fields around 20 ± 8° from the ecliptic, which again limited their ability to measure the inclination distribution of the potential detections. Doressoundiram et al. (2020) reported five detections in fields from 0° to 90°, but the searched fields are concentrated towards the ecliptic, and thus the detections do not have the statistical power to convincingly demonstrate that they are not uniform across the sky.
The large TNOs generally follow an inclination of the form Brown (2001)
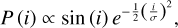 (4)
(4)
with two components with σ ≈ 16° and σ ≈ 2.6°, with the former component about 20 times more massive than the latter (Fraser et al. 2014). However, this does not perfectly fit the distribution, and a small number of bodies can be found at very high inclinations as a result of various mechanisms (Gomes 2011; Chen et al. 2016), so that a single detection at very high inclination is not sufficient to demonstrate that this is not astrophysical. Nonetheless, we can estimate the number of objects we would need to detect to be positive that the potential events are indeed occultations by objects within the Solar system. In Fig. 11 we plot the Kolmogorov-Smirnov statistics of a Monte Carlo suite of realisations of MIOSOTYS surveys that detect N real TNOs, compared to non-physical detections that are randomly and uniformly distributed across the survey area. For each N, we realised 100 surveys, all using the same search areas on the sky as the MIOSOTYS survey presented in Doressoundiram et al. (2020), to understand the distribution. In this plot, we assume that the σ ≈ 16° and σ ≈ 2.6° components have equal numbers of bodies at sizes of a few hundred meters, reflecting the model presented in this work. The figure shows that we would typically expect to need 15–20 detections to be 99% confident that the distribution is not uniform on the sky. When the hot population outnumbers the cold population by a factor of ~20, four to five times as many detections are needed to exclude a uniform distribution at the same confidence. Although we used the MIOSOTYS footprint, the details of the survey implementation are not too important; a survey that spent half its time in the ecliptic and half its time on the ecliptic pole would only need half as many detections to obtain the same level of confidence that the signal was astrophysical, but would need twice as much survey time to obtain the detections because only the observations in the ecliptic would produce detections.
For future proposed missions to the outer Solar system (e.g. McNutt et al. 2019; Heller et al. 2020; Turyshev et al. 2021), it might be possible to detect an extended cold belt. If the mission is close to the ecliptic, the brightest member would have an apparent magnitude of ~13 in the best-fit model. New Horizons detected TNOs to m ~ 19 (Verbiscer et al. 2019), which means that aspirations like this are plausible. However, any space mission is virtually assured to be far more costly than an extended MIOSOTYS or similar programme. The latter will therefore remain the plausible approach.
 |
Fig. 7 Corner plot of the results of the MCMC search of the viable parameter space. The contour plots show the correlations between parameters, and the histograms show the one-parameter distribution within the model evaluation. The best-fit values of the model parameters are |
 |
Fig. 8 Initial (dashed lines) and final (solid lines) size-number distributions of the cold bodies from a simulation that begins with Π = 4.4, qm = 2.9, qs = 6.3, and γ = 3.6. The simulation also includes hot, resonant, and scattering populations, which are not plotted here for clarity, but for which the overall evolution is similar. Collisional evolution is largely confined to sizes smaller than ~500 m. The number of small bodies increases in bins that lie farther out, even as the total mass declines as the γ parameter pushes the mass distribution towards smaller sizes. The Π parameter creates the larger discontinuity between the first and second radial bins. |
 |
Fig. 9 Log probability contributed by the cratering record at 15 km from various models runs, plotted against the upfactor Π. The scatter is induced as these are the results from calculations from the full model, and thus also span a range of qm, qs, and γ. Because Π dictates the size-number distribution at larger semimajor axis, it has a negligible influence on the cratering record of Charon. |
 |
Fig. 10 Log probability contributed by the pencil-beam survey of Bernstein et al. (2004) from various models runs, plotted against the upfactor Π. The pencil beam survey disfavours high values of Π, as large numbers of s ~ 10 km bodies at 50+ au would be detectable in that survey. |
 |
Fig. 11 Box-and-whiskers plot of the distribution of the Kolmogorov-Smirnov statistics comparing astrophysical detections to sky-uniform detections, with 100 realisations of surveys of the MIOSOTYS survey area that report N candidate detections for N from 2 to 50. The red boxes contain 50% of the data points, and the whiskers contain 96% of the data points, which the other trials plotted as outlier points. |
4.3 All the observations in one plot
The apparent contradiction of Fig. 1 can be understood by placing the directly observed, cratering, and occulting populations in the same plot. We then implicitly (or explicitly) think of them as coming from the same population. The radial sensitivity of the three observations are very different, however and perhaps it is wiser to start from a place of skepticism towards them representing the same population. If the model presented here is correct, the observations should not be presented side by side.
5 Conclusions
We considered models in which the cold classical Kuiper belt extended to larger semimajor axes than the known objects, and the size at which the bodies form was allowed to change with their formation distance. We find that models in which the formation size decreases with increasing semimajor axis can produce both the relatively high number of bodies with sizes of a few hundred meters that are seen in occultation surveys and the relatively low number inferred from the cratering record on Pluto/Charon. The most promising method of testing the astrophysical reality of these models is extend occultation surveys with a broad inclination coverage so that sufficient events can be obtained to measure their inclination distribution across the sky.
Acknowledgements
We wish to thank the anonymous referee for a thoughtful review that improved the paper. We thank Philippe Thébault for useful discussions. This work received funding from the European Research Council under the European Community’s H2020 2014-2020 ERC Grant Agreement No. 669416 “Lucky Star”.
References
- ALMA Partnership (Brogan, C. L., et al.) 2015, ApJ, 808, L3 [Google Scholar]
- Andrews, S. M. 2020, ARA&A, 58, 483 [Google Scholar]
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Arakawa, S., & Nakamoto, T. 2016, ApJ, 832, L19 [CrossRef] [Google Scholar]
- Arimatsu, K., Tsumura, K., Usui, F., et al. 2019, Nat. Astron., 3, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Bannister, M. T., Kavelaars, J. J., Petit, J.-M., et al. 2016, AJ, 152, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Bannister, M. T., Gladman, B. J., Kavelaars, J. J., et al. 2018, ApJS, 236, 18 [CrossRef] [Google Scholar]
- Batygin, K., Brown, M. E., & Fraser, W. C. 2011, ApJ, 738, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ, 128, 1364 [Google Scholar]
- Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2006, AJ, 131, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, F. B., Protopapas, P., McLeod, B. A., et al. 2009, AJ, 138, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Bickerton, S. J., Kavelaars, J. J., & Welch, D. L. 2008, AJ, 135, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Brasil, P. I. O., Nesvorný, D., & Gomes, R. S. 2014, AJ, 148, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E. 2001, AJ, 121, 2804 [Google Scholar]
- Brown, M. E., Barkume, K. M., Ragozzine, D., & Schaller, E. L. 2007, Nature, 446, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. E., Bannister, M. T., Schmidt, B. P., et al. 2015, AJ, 149, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Campo Bagatin, A., & Benavidez, P. G. 2012, MNRAS, 423, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2005, Science, 307, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2011, AJ, 141, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Gorti, U., Johansen, A., & Davies, M. B. 2017, ApJ, 839, 16 [Google Scholar]
- Chang, H.-K., Liu, C.-Y., & Chen, K.-T. 2013, MNRAS, 429, 1626 [NASA ADS] [CrossRef] [Google Scholar]
- Charnoz, S., & Morbidelli, A. 2007, Icarus, 188, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-T., Lin, H. W., Holman, M. J., et al. 2016, ApJ, 827, L24 [Google Scholar]
- Cuzzi, J. N., Hogan, R. C., & Bottke, W. F. 2010, Icarus, 208, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Hartlep, T., & Estrada, P. R. 2016, Lunar Planet. Sci. Conf., 1903, 2661 [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. 2012, ApJ, 750, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J. 2007, ApJ, 671, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [Google Scholar]
- Doressoundiram, A., Roques, F., Liu, C.-Y., et al. 2020, MNRAS, submitted [Google Scholar]
- Duncan, M. J., & Levison, H. F. 1997, Science, 276, 1670 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fraser, W. C., Brown, M. E., Morbidelli, A., Parker, A., & Batygin, K. 2014, ApJ, 782, 100 [Google Scholar]
- Fraser, W. C., Bannister, M. T., Pike, R. E., et al. 2017, Nat. Astron., 1, 0088 [Google Scholar]
- Gladman, B., Marsden, B. G., & Vanlaerhoven, C. 2008, Nomenclature in the Outer Solar System, eds. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, A. Morbidelli, & R. Dotson (Tucson: University of Arizona Press), 43 [Google Scholar]
- Gomes, R. S. 2011, Icarus, 215, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Greenstreet, S., Gladman, B., & McKinnon, W. B. 2015, Icarus, 258, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Grundy, W. M., Noll, K. S., Roe, H. G., et al. 2019, Icarus, 334, 62 [CrossRef] [Google Scholar]
- Hartlep, T., & Cuzzi, J. N. 2020, ApJ, 892, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Heller, R., Anglada-Escudé, G., Hippke, M., & Kervella, P. 2020, A&A, 641, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Jutzi, M., & Benz, W. 2017, A&A, 597, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2008, ApJS, 179, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2020, Planet. Sci. J., 1, 40 [CrossRef] [Google Scholar]
- Kenyon, S. J., & Luu, J. X. 1998, AJ, 115, 2136 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Schreiber, A. 2020, ApJ, 901, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V., & Wyatt, M. C. 2021, MNRAS, 500, 718 [Google Scholar]
- Krivov, A. V., Sremčević, M., & Spahn, F. 2005, Icarus, 174, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, S. M., Kavelaars, J. J., Alexandersen, M., et al. 2018a, Front. Astron. Space Sci., 5, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, S. M., Shankman, C., Kavelaars, J. J., et al. 2018b, AJ, 155, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Lehner, M., Wang, S.-Y., Reyes-Ruiz, M., et al. 2019, EPSC-DPS Joint Meeting, 13, 1089 [Google Scholar]
- Leinhardt, Z. M., & Stewart, S. T. 2012, ApJ, 745, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Morbidelli, A., Van Laerhoven, C., Gomes, R., & Tsiganis, K. 2008, Icarus, 196, 258 [Google Scholar]
- Liu, C.-Y., Doressoundiram, A., Roques, F., et al. 2015, MNRAS, 446, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1993, Nature, 365, 819 [CrossRef] [Google Scholar]
- Massironi, M., Simioni, E., Marzari, F., et al. 2015, Nature, 526, 402 [NASA ADS] [CrossRef] [Google Scholar]
- McKinnon, W. B., Richardson, D. C., Marohnic, J. C., et al. 2020, Science, 367, aay6620 [NASA ADS] [CrossRef] [Google Scholar]
- McNutt, R. L., Wimmer-Schweingruber, R. F., Gruntman, M., et al. 2019, Acta Astron., 162, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Bottke, W. F., Nesvorný, D., & Levison, H. F. 2009, Icarus, 204, 558 [Google Scholar]
- Morbidelli, A., Nesvorny, D., Laurenz, V., et al. 2018, Icarus, 305, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Nesvorny, D., Bottke, W. F., & Marchi, S. 2021, Icarus, 356, 114256 [CrossRef] [Google Scholar]
- Nesvorný, D. 2015, AJ, 150, 68 [CrossRef] [Google Scholar]
- Nesvorny, D. 2020, ApJ, 908, L47 [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., Bottke, W. F., & Levison, H. F. 2018, Nat. Astron., 2, 878 [Google Scholar]
- Pan, M., & Sari, R. 2005, Icarus, 173, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H., & Kavelaars, J. J. 2010, ApJ, 722, L204 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H., & Kavelaars, J. J. 2012, ApJ, 744, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, J. M., Kavelaars, J. J., Gladman, B. J., et al. 2011, AJ, 142, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, J. M., Kavelaars, J. J., Gladman, B. J., et al. 2017, AJ, 153, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Pike, R. E., Proudfoot, B. C. N., Ragozzine, D., et al. 2020, Nat. Astron., 4, 89 [Google Scholar]
- Proudfoot, B. C. N., & Ragozzine, D. 2019, AJ, 157, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., & Morbidelli, A. 2022, Astrophys. Space Sci. Lib., 466, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Robbins, S. J., Singer, K. N., Bray, V. J., et al. 2017, Icarus, 287, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Roques, F., Moncuquet, M., Lavillonière, N., et al. 2003, ApJ, 594, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1969, Evoliutsiia doplanetnogo oblaka (USA: NASA) [Google Scholar]
- Schlichting, H. E., Ofek, E. O., Wenz, M., et al. 2009, Nature, 462, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichting, H. E., Ofek, E. O., Sari, R., et al. 2012, ApJ, 761, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, A., Wu, Y., & Lithwick, Y. 2015, ApJ, 801, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, A., Wu, Y., & Lithwick, Y. 2016, ApJ, 818, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Shannon, A., Jackson, A. P., & Wyatt, M. C. 2019, MNRAS, 485, 5511 [CrossRef] [Google Scholar]
- Simon, J. B., Armitage, P. J., Li, R., & Youdin, A. N. 2016, ApJ, 822, 55 [Google Scholar]
- Simon, J. B., Armitage, P. J., Youdin, A. N., & Li, R. 2017, ApJ, 847, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Singer, K. N., McKinnon, W. B., Gladman, B., et al. 2019, Science, 363, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., Stern, S. A., Moore, J. M., et al. 2020, Science, 367, aay3999 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Weaver, H. A., Spencer, J. R., et al. 2019, Science, 364, aaw9771 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, S. T., & Leinhardt, Z. M. 2009, ApJ, 691, L133 [NASA ADS] [CrossRef] [Google Scholar]
- The LUVOIR Team 2019, ArXiv e-prints [arXiv:1912.06219] [Google Scholar]
- Tiscareno, M. S., & Malhotra, R. 2009, AJ, 138, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Turyshev, S., Helvajian, H., Friedman, L. D., et al. 2021, BAAS, 53, 039 [Google Scholar]
- Verbiscer, A. J., Porter, S., Benecchi, S. D., et al. 2019, AJ, 158, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Vitense, C., Krivov, A. V., Kobayashi, H., & Löhne, T. 2012, A&A, 540, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Volk, K., & Malhotra, R. 2019, AJ, 158, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Volk, K., Murray-Clay, R., Gladman, B., et al. 2016, AJ, 152, 23 [Google Scholar]
- Wang, J. H., Protopapas, P., Chen, W. P., et al. 2010, AJ, 139, 2003 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
- Wetherill, G. W. & Stewart, G. R. 1993, Icarus, 106, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Zhang, Z. W., Lehner, M. J., Wang, J. H., et al. 2013, AJ, 146, 14 [NASA ADS] [CrossRef] [Google Scholar]
With a probable origin in the trans-Neptunian belt (Duncan & Levison 1997).
All Figures
 |
Fig. 1 Existing measurements of the size-number distribution of small bodies in the outer Solar system. We compare the results of occultation surveys (upper limits: Bickerton et al. 2008; Bianco et al. 2009; Wang et al. 2010; Chang et al. 2013; Zhang et al. 2013; and detections: Schlichting et al. 2012; Liu et al. 2015; Arimatsu et al. 2019; Doressoundiram et al. 2020), optical surveys (Fraser et al. 2014), and crater counting (Singer et al. 2019), which are converted into a population number using the dynamical model of Greenstreet et al. (2015). Because the different types of surveys use different measurements, they can only be directly compared in a somewhat model-dependent way. Thus, the apparent disagreement may represent a disagreement of the observations, or an incorrect assumption in the modelling. |
| In the text | |
 |
Fig. 2 Example sketch of how we parametrised the initial size-number distribution in our simulations. Bodies in the solid-line region are logarithmically placed in bins with six bins per decade of mass. The intermediate-size slope is parametrised as −qs − qm, so that the qs parameter measures the need for a break in the slope of the size-number distribution. Bodies within the dotted line are included as impactors, but they are not evolved, but are forced to obey a collisional equilibrium power law from the smallest evolving bin (see text). |
| In the text | |
 |
Fig. 3 Fraction of bodies in a cold disk detected by the OSSOS survey simulator, calculated using the method outlined in Lawler et al. (2018a), as a function of absolute magnitude H and semimajor axis a. Each point considered one million hypothetical objects. The 0.000 line therefore represents a chance of discovery lower than 0.0001%. |
| In the text | |
 |
Fig. 4 Autocorrelation time estimates for two different sets of MCMC chains for the qm parameter, estimated in two different ways, using the method of Goodman & Weare (2010) and of Foreman-Mackey et al. (2013). The four estimates are slightly different, but all indicate a correlation time of ≲102. The other parameters also have autocorrelation times of O (τ) ~ 102, with τγ a factor of 2 ~ 3 larger. |
| In the text | |
 |
Fig. 5 MCMC chains for the model parameter γ after the chains converged well. The walkers mostly stay near the median value of 3.6, but some of the excursions to higher or lower values are somewhat sticky, reflecting local minima in the probability space. |
| In the text | |
 |
Fig. 6 Example showing a run for which we randomly and uniformly initialised 32 walkers across the full allowed space 0 ≤ Π ≤ 100, 0.0 ≤ qm ≤ 6.0, −10.0 ≤ qs ≤ 10, and −5 ≤ γ ≤ 15. The walkers converged towards the same qm ~ 2.9 as in the longer run, but the model evaluation times for some points far from the good solutions can be exceedingly long, making it computationally difficult to fully evaluate these chains. Because of this, we prefer to start walkers near our default solution. |
| In the text | |
 |
Fig. 7 Corner plot of the results of the MCMC search of the viable parameter space. The contour plots show the correlations between parameters, and the histograms show the one-parameter distribution within the model evaluation. The best-fit values of the model parameters are |
| In the text | |
 |
Fig. 8 Initial (dashed lines) and final (solid lines) size-number distributions of the cold bodies from a simulation that begins with Π = 4.4, qm = 2.9, qs = 6.3, and γ = 3.6. The simulation also includes hot, resonant, and scattering populations, which are not plotted here for clarity, but for which the overall evolution is similar. Collisional evolution is largely confined to sizes smaller than ~500 m. The number of small bodies increases in bins that lie farther out, even as the total mass declines as the γ parameter pushes the mass distribution towards smaller sizes. The Π parameter creates the larger discontinuity between the first and second radial bins. |
| In the text | |
 |
Fig. 9 Log probability contributed by the cratering record at 15 km from various models runs, plotted against the upfactor Π. The scatter is induced as these are the results from calculations from the full model, and thus also span a range of qm, qs, and γ. Because Π dictates the size-number distribution at larger semimajor axis, it has a negligible influence on the cratering record of Charon. |
| In the text | |
 |
Fig. 10 Log probability contributed by the pencil-beam survey of Bernstein et al. (2004) from various models runs, plotted against the upfactor Π. The pencil beam survey disfavours high values of Π, as large numbers of s ~ 10 km bodies at 50+ au would be detectable in that survey. |
| In the text | |
 |
Fig. 11 Box-and-whiskers plot of the distribution of the Kolmogorov-Smirnov statistics comparing astrophysical detections to sky-uniform detections, with 100 realisations of surveys of the MIOSOTYS survey area that report N candidate detections for N from 2 to 50. The red boxes contain 50% of the data points, and the whiskers contain 96% of the data points, which the other trials plotted as outlier points. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.