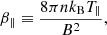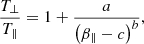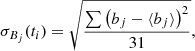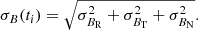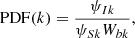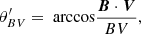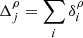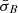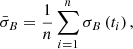EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) L4 Full HTML
Issue
A&A
Volume 672, April 2023
Solar Orbiter First Results (Nominal Mission Phase)
Article Number L4
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202345965
Published online 31 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The solar wind is a nearly collisionless plasma and as such exhibits non-equilibrium conditions that lead to the creation of micro-instabilities (Matteini et al. 2012; Alexandrova et al. 2013; Klein et al. 2018). Linear and quasi-linear Vlasov–Maxwell theory predicts that kinetic-scale instabilities driven by temperature anisotropy with respect to the magnetic field restore the plasma towards thermal equilibrium (Hollweg & Völk 1970; Gary et al. 1976; Gary 1993). These theoretical descriptions often assume a constant background on which the unstable fluctuations are added as a perturbation. However, the real, turbulent solar wind does not provide such a constant background, with the presence of inhomogeneities across the spatial and temporal scales over which the instabilities are predicted to act (Bruno & Carbone 2013; Matthaeus et al. 2014; Verscharen et al. 2019).

The effective action of proton temperature anisotropy-driven instabilities in the solar wind is often inferred in the literature from comparisons of the distribution of observed data and its constraints in the T⊥/T∥–β∥ parameter space, where

(1)

B is the magnitude of the magnetic field, n is the proton number density, kB is the Boltzmann constant, T⊥ is the proton temperature perpendicular to the magnetic field, and T∥ is the proton temperature parallel to the magnetic field (e.g., Marsch et al. 2004; Hellinger et al. 2006; Bale et al. 2009; Chen et al. 2016; Opie et al. 2022). The thresholds of the anisotropy-driven instabilities set limits to the distribution of the data in T⊥/T∥–β∥ parameter space (Gary 1992; Gary et al. 2001; Kasper et al. 2002).

A common analytical approximation for the thresholds of the anisotropy-driven instabilities is given in the parametric form

(2)

where a, b, and c are fit parameters with values specific to each instability and to a given maximum growth rate γm (Hellinger et al. 2006). The oblique fire-hose and the mirror-mode instabilities, which we consider here, approximately provide outer boundaries to the distribution of stable data both in observations (Hellinger et al. 2006; Gary 2015) and in simulations (Servidio et al. 2014; Hellinger et al. 2015; Riquelme et al. 2015).

Solar wind turbulence is mostly non-compressive with a minor component of compressive fluctuations that contribute a relative magnetic energy (δ|B|/B0)2 of a few percent to the turbulent cascade (Chen 2016). Turbulent dissipation of energy is a candidate mechanism to explain the observed anisotropic heating of the solar wind (Isenberg 1984; Marsch 1991; Cranmer et al. 2007; Maruca et al. 2011; Howes 2015). In the context of the expanding solar wind, local heating and the response of the solar wind to the turbulent fluctuations create non-equilibrium features that displace the plasma into unstable regions of the T⊥/T∥–β∥ parameter space, beyond the threshold of the instabilities (Matteini et al. 2006, 2012; Schekochihin et al. 2008; Bott et al. 2021). However, it is unclear how instabilities and turbulence interact at kinetic scales.

Kinetic plasma simulations show that instabilities can regulate the thermal energetics of the plasma, and that turbulence in the expanding solar wind can both raise and lower anisotropy measured with respect to the magnetic field (Matteini et al. 2006; Hellinger & Trávníçek 2008; Kunz et al. 2014; Hellinger et al. 2015, 2017; Riquelme et al. 2015; Markovskii et al. 2020; Bott et al. 2021; Markovskii & Vasquez 2022). The oblique fire-hose instability produces Alfvénic modes with zero frequency, linear polarisation, and finite compressivity (δn ≠ 0 and δ|B|≠0), and so it creates both compressive and non-compressive fluctuations at ion scales (Hellinger & Matsumoto 2000; Hellinger & Trávníçek 2008). Observations and simulations show that the mirror-mode instability generates compressive fluctuations on kinetic scales (Bale et al. 2009; Hellinger et al. 2017). Therefore, both compressive and non-compressive kinetic-scale fluctuations can be attributed to the instabilities themselves or to cascaded background turbulence at these scales (or, in fact, a combination of both), and consequently caution must be exercised in their interpretation (Bale et al. 2009; Chandran et al. 2009; Salem et al. 2012; Chen et al. 2013; Gary 2015).

In this work, we examine non-compressive fluctuations in the magnetic-field direction at scales corresponding to the small-scale end of the inertial range of the turbulence (Kolmogorov 1941; Tu & Marsch 1995). We assume that these fluctuations predominantly represent local Alfvénic fluctuations. By combining magnetic-field measurements with measurements of the proton parameters, we investigate the action of the oblique fire-hose and mirror-mode instabilities in this turbulent background.

2. Data analysis

2.1. The magnetic-field variability measure σB

We developed a measure, σB, for the directional variability of the magnetic field B using Solar Orbiter data. We used the 8 vectors/s magnetic-field data from the magnetometer (MAG; Horbury et al. 2020) in conjunction with ≈106 data points at a cadence of 4 s from the Proton-Alpha Sensor (PAS) of the Solar Wind Analyser (SWA; Owen et al. 2020). These data are coincident with the dataset presented by Opie et al. (2022) and represent predominantly slow solar wind. We did not identify or remove structures such as shocks, coronal mass ejections, or current sheets in the dataset which was taken over eight separate periods totalling 53 days at an average heliocentric distance of ∼0.85 au.

We first derived the magnetic-field unit vector b = B/|B| for each measurement vector B in Radial, Tangential and Normal (RTN) coordinates. PAS derives the proton moments based on a sampling of 1 s duration, every 4 s. We defined the centre of the PAS sampling interval as the time ti. We associated all b measurements in the interval [ti − 2 s,ti + 2 s] with the PAS interval at time ti. We calculated the standard deviation of the unit-vector component bj for time interval ti as

(3)

where the sum was taken over all 32 magnetic-field measurements associated with the PAS measurement at ti, ⟨ ⋅ ⟩ is the average over this time interval of 4 s duration, and the index j = (R, T, N) marks the field component in RTN coordinates. We then combined the components to

(4)

The quantity σB is a measure of the variability of the magnetic-field direction (i.e., excluding changes in magnitude) at the 4 s scale for each combined interval in our SWA/PAS dataset. The mean solar wind bulk velocity for our dataset is 427 km s−1. Therefore, the 4 s temporal scale represents a convected spatial scale of ∼1700 km. The mean gyroradius for our dataset is 51.5 km. Thus, σB represents fluctuations at the small-scale end of the inertial range, in the transition region approaching ion scales (Kiyani et al. 2015).

2.2. Definition of probability density function (PDF)

We define a data point as ‘unstable’ if it lies above the threshold given by Eq. (2) for the given instability. We emphasise that the presence of data in the regions unstable to the oblique fire-hose and mirror-mode instabilities is a rare occurrence in our overall dataset, representing ∼3% and ∼0.5%, respectively, of the total dataset. Consequently, we define the probability density function (PDF) as the normalised density bin count for each individual dataset – in other words separated by oblique fire-hose unstable (OF), mirror-mode unstable (M), and stable (S) datasets:

(5)

where k ∈ [OF, M, S], ψIk is the raw individual bin count of data points in dataset k, ψSk is the total bin count of dataset k summed across all bins, and Wbk is the bin width. In using Eq. (5), the distributions for each individual dataset have been normalised so that ∑(Wbk PDF(k)) = 1 for each k ∈ [OF, M, S].

3. Results

3.1. σB and its distribution in T⊥/T∥–β∥ parameter space

In Fig. 1a, we show the binned distribution of data points in the T⊥/T∥–β∥ parameter space. Each bin is colour-coded with its average value (∑σB)/ψI of σB on a logarithmic scale. For the instability thresholds, we use Eq. (2) with fit parameters for a maximum growth rate of γm = 10−2Ωp, where Ωp is the proton gyrofrequency, given by Verscharen et al. (2016). Higher values of σB occur in the stable data distribution approaching the instability thresholds. In the regions above the thresholds, which overall constrain the data distribution, we see the highest values of the averaged σB.

thumbnail Fig. 1.

Observed data for σB plotted as: (a) distribution of σB binned and averaged by the bin count in T⊥/T∥–β∥ parameter space. The instability thresholds for the oblique fire-hose (OF) and mirror-mode (M) instabilities are shown as labelled. (b) PDFs of σB for oblique fire-hose unstable (magenta), mirror-mode unstable (blue), and stable (green) points in our dataset. The vertical lines denote the ensemble mean [ ⋅ ] of each dataset.

In Fig. 1b, we show the PDF according to Eq. (5) of σB for data defined as stable or unstable to either the oblique fire-hose or mirror-mode instability. We have plotted the ensemble mean values of σB for each of the three distributions as vertical lines. The lowest observed values of σB for the unstable data are higher than for the stable data. The PDFs for the unstable datasets are biased towards higher values of σB relative to the PDF for the stable dataset. We find that [σBM] is greater than [σBF], and [σBF] is greater than [σBS], where [ ⋅ ] is the ensemble mean.

3.2. σB and its relation to θBV parameter space

In Fig. 2, we show PDFs of our data in σB–θBV parameter space, where θBV is the angle between the magnetic field B and the solar wind proton bulk velocity V for each measurement point, given as a value between 0° and 360° measured clockwise from V in the V − B plane when looking down on the V − B plane from the north. To obtain θBV, we first calculated the cone angle between B and V using the complete 3D vectors in RTN coordinates as

(6)

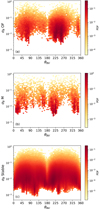thumbnail Fig. 2.

PDF of data in σB–θBV parameter space for (a) oblique fire-hose unstable, (b) mirror-mode unstable, and (c) stable data points.

where V is the bulk velocity of the protons. We defined the complex numbers b ≡ BR + iBT and v ≡ VR + iVT. We then calculated the angle ϕv = arg(v), where arg(⋅)∈[0, 2π) is the polar angle in the complex plane. After rotating b by −ϕv in the complex plane, we defined the difference angle between b and v as ϕbv = 180°  arg(be−iϕv)/π. If 0 < ϕbv ≤ 180°, we set 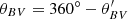. Otherwise, we set 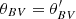(Opie et al. 2022).

The distribution of data identified as oblique fire-hose unstable in Fig. 2a is clustered around values of θBV ≈ 75° and θBV ≈ 255°, which represents a quasi-perpendicular alignment between B and V (which is consistent with the geometry found by Opie et al. 2022). The distribution of data identified as mirror-mode unstable in Fig. 2b exhibits four clusters at θBV ≈ 20° ,160° ,220° , and 340°, which represent a quasi-parallel or quasi-anti-parallel alignment between B and V (see also Opie et al. 2022). The distribution of stable data in Fig. 2c assumes its maximum values in the range 0.001 ≲ σB ≲ 0.1, largely independent of θBV.

3.3. σB and its relation to the persistence of unstable intervals

Figure 3 panels a and b show PDFs according to Eq. (5) of data in 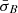–Δρ parameter space, where Δρ is the spatial persistence of consecutive unstable 4 s intervals in units of the proton gyroradius. As discussed by Opie et al. (2022), we calculated Δρ using Taylor’s hypothesis (Taylor 1938). We identified an interval, i, with each unstable data point in the dataset for both oblique fire-hose and mirror-mode instabilities. We calculated the length scale li = Viτ for each unstable interval i, where Vi is the proton bulk velocity of interval i and τ = 4 s is the PAS sampling cadence. Using the proton gyroradius ρpi for each individual interval i, we then calculated the dimensionless length scale 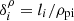. We then defined

(7)

thumbnail Fig. 3.

PDF of data in –Δρ parameter space for (a) oblique fire-hose unstable and (b) mirror-mode unstable data distributions. Panel (c) shows the same PDF for equivalent persistence intervals sampled from the stable data. The vertical lines shown in (a) and (b) denote the breakpoints previously identified by Opie et al. (2022).

as the normalised persistence interval for each occurrence of the respective instability as measured at the spacecraft.

We defined the average σB over consecutive unstable 4 s intervals as

(8)

where n is the number of temporally consecutive 4 s intervals ti in each unstable persistence interval of size Δρ. We then binned the data in 2D histograms in 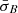–Δρ space. We show plots for both oblique fire-hose (Fig. 3a) and mirror-mode (Fig. 3b) unstable data.

In Fig. 3c, we show a similar plot for consecutive intervals sampled from the stable dataset. We selected all intervals of P consecutive points where P ∈ [2, 3, 4, …, 14, 15] and calculated 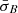and Δρ for the stable data intervals in the same way as for the unstable persistence intervals.

Opie et al. (2022) identify the breakpoints 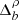of the Δρ distribution as the minimum spatial scales required for these instabilities to act. We have overplotted 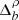as vertical dashed lines in Figs. 3a and b. For both unstable modes, the 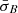value associated with the maximum of the PDF decreases with increasing Δρ. The distributions exhibit a lower bound at 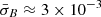for the oblique fire-hose instability and at 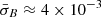for the mirror-mode instability. The maximum of the PDF lies near this lower bound at 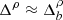for each of the unstable modes.

4. Discussion and interpretation

4.1. Distributions in parameter space

Figure 1a shows a clear dependence of σB on β∥, consistent with previous results using |δ⃗B|/B0 instead of σB, where B0 is the averaged background magnetic field (Kasper et al. 2002; Bale et al. 2009; Servidio et al. 2014). Higher values of β∥ often imply lower values of B0 due to their explicit interdependence in Eq. (1). This interdependence creates a correlation between δB/B0 and β∥ even if δB is constant, which is consistent with the overall β∥ dependence of σB in Fig. 1a. In our analysis, we take this dependence as an inherent feature of the T⊥/T∥–β∥ parameter space and focus on the observed values of σB relating to the partition of the space between stable and unstable data.

The joint dependency of the data distributions on σB and θBV shown in Fig. 2 is consistent with our previous work that shows that the θBV-dependent anisotropy is opposite to the expectations from adiabatic expansion alone (Opie et al. 2022). The observed distributions are also consistent with the PDFs in Fig. 1b which show that the distributions of σB are skewed towards higher values for data in the unstable parameter regimes and that they have a higher ensemble mean compared with the stable data distribution. These statistical properties indicate that the relative level of fluctuations on the 4 s scale, whether from instabilities or background turbulence, is greater in the regions of parameter space unstable to the oblique fire-hose and mirror-mode instabilities than in the stable regime. The conjunction between Fig. 2 and our previous work (Opie et al. 2022) points towards a potential role for the fluctuations represented by σB in raising the tangential and normal temperatures TT and TN relative to the radial temperature TR. We postpone a more detailed discussion of this aspect to future work.

4.2. Instabilities in a turbulent background

Our σB measure captures non-compressive fluctuations at a 4 s timescale by calculating the full directional variability of the magnetic field. We note that σB includes fluctuations both from the background turbulence and from the instabilities, as long as the fluctuations have a directional component (e.g., Alfvénic). Previous work interprets an enhanced level of small-scale fluctuations (|δB|/B0) at and beyond the instability thresholds as evidence of the growing fluctuations of the instabilities (Bale et al. 2009). Comparing our Fig. 1a with the second panel of Fig. 1 by Bale et al. (2009), we find that both measures agree quite closely for the oblique fire-hose instability. In the case of the mirror-mode instability, however, our measure identifies a lower level of enhanced fluctuations than the measure used by Bale et al. (2009), particularly at lower β∥. We attribute this difference to the predominantly compressive polarisation of the mirror-mode instability that we intentionally did not capture. We infer that the fluctuations measured by σB include a significant contribution from background turbulence.

We make the assumption that turbulent fluctuations create non-equilibrium features (Marsch 1991; Matteini et al. 2006, 2012; Schekochihin et al. 2008; Maruca et al. 2011), while instabilities – once triggered and effective – reduce non-equilibrium features (Gary 1992; Gary et al. 2001; Kasper et al. 2002; Hellinger et al. 2006; Bale et al. 2009). This assumption suggests that the observed persistence of data in the regions of unstable T⊥/T∥–β∥ parameter space is evidence that (a) there is insufficient spatial scale for the instabilities to act effectively (Opie et al. 2022), or that (b) the instabilities cannot immediately overcome the turbulent driving of anisotropy (Osman et al. 2013). A combination of both cases is possible.

In the ongoing competition between the turbulent driving and the instabilities, the relevant timescales for the opposing processes are important for deciding the outcome. Under stable solar wind conditions, non-linear processes are effective on timescales that are shorter than the linear timescales associated with the instabilities (Matthaeus et al. 2014; Klein et al. 2018). However, in the unstable regions of the T⊥/T∥–β∥ parameter space, the plasma assumes conditions in which the linear timescales associated with the instabilities are equivalent to or shorter than the non-linear timescales associated with the turbulent driving (Bandyopadhyay et al. 2022). This inversion of the relevant timescales allows the instabilities to provide an effective boundary to non-equilibrium conditions in the solar wind.

4.3. The interactions between instabilities and turbulence

If the observed fluctuations measured by σB were ergodic, which we define as ⟨σB⟩=[σB], we would not expect 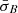to exhibit dependency on Δρ (Matthaeus & Goldstein 1982). The reason for this expectation is that the time-averaged amplitude of the fluctuations at the 4 s scale, if the fluctuations were ergodic, would not depend on the persistence length Δρ of the intervals over which σB is averaged1. For the stable dataset, the distribution of 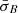does not depend on the averaging length, as shown in Fig. 3c. We verified that ⟨σBP⟩≈[σB] ≈ 0.032, where ⟨σBP⟩ is the mean value of σB for stable intervals of length P and [σB] is the ensemble mean for the complete dataset of stable data points, taken as representative of the statistical properties of the stable solar wind. Subject to our definition, the condition ⟨σBP⟩≈[σB] indicates ergodicity. However, in Figs. 3a and b, the distribution of the data in 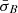–Δρ parameter space indicates an interdependency between 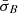and Δρ for both oblique fire-hose and mirror-mode unstable data. This interdependency suggests that σB is not ergodic for the unstable intervals and therefore that the unstable intervals are statistically disjoint from the stable intervals (Matthaeus & Goldstein 1982; Walters 2000). We infer that the interdependency is indicative of processes that are only relevant to the unstable regimes. From our previous assumption, these processes relate either to the creation of non-equilibrium features by background turbulence or to the action of instabilities to reduce non-equilibrium features. In both cases, the process concerned must disrupt the ergodicity of the turbulent fluctuations measured by σB for the stable regime.

The distributions in Figs. 3a and b show that unstable intervals are more likely to be larger in units of Δρ when 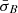is lower. The highest probability densities of the distribution of unstable data are observed and maintained for values of 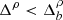, which we have identified as the persistence intervals in which instabilities do not act effectively (Opie et al. 2022). In these intervals, higher 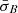implies shorter residence time for the plasma in any particular unstable regime of T⊥/T∥–β∥ parameter space, largely independently of the action of instabilities.

The interdependency continues when 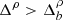, which we have identified as the persistence intervals in which instabilities do act effectively (Opie et al. 2022). For these intervals, Fig. 3 shows that longer unstable intervals (in terms of Δρ) are more likely to have a lower value of 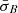than shorter unstable intervals.

We interpret the value of 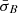as a measure for turbulent ‘activity’. Likewise, we interpret a lower PDF value for unstable intervals as an indication of the more efficient action of the instabilities. In this interpretation, the observed likelihood trend suggests that the efficiency of instabilities to reduce temperature anisotropy is greater in larger and more active intervals than in shorter and less active intervals. Therefore, the competition between the linear relaxation time and the non-linear time not only depends on 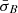(i.e., a measure for the non-linear time), but also on Δρ.

4.4. Limitations of our analysis

In our analysis, we do not include the roles of the parallel fire-hose or ion-cyclotron instabilities. In general, the non-propagating oblique fire-hose and mirror-mode instabilities are more effective in constraining temperature anisotropy (Gary 1993, 2015; Gary et al. 1997; Kunz et al. 2014; Rincon et al. 2015). The thresholds for these instabilities were calculated from linear theory under the assumption of conditions that do not exactly apply to the turbulent solar wind (Matthaeus et al. 2014). Nonetheless, observational studies have shown that these thresholds usefully define the boundaries of the stability of the plasma (Hellinger et al. 2006; Bale et al. 2009; Gary 2015; Chen et al. 2016). It remains an open question as to why the non-propagating thresholds provide better constraints to the data distribution in T⊥/T∥–β∥ parameter space even when the propagating instabilities have lower theoretical thresholds (Gary 2015; Markovskii et al. 2019; Verscharen et al. 2019).

The directional variations measured by σB have an impact on the measurement of T⊥ and T∥. The relevant timescale for this measurement is the 1 s SWA/PAS sampling interval. The typical directional variation in B over one second is ∼3.4° for our dataset and thus small compared to the angular resolution of PAS. However, at large σB ≳ 0.5, the deflections are potentially significant. Therefore, caution must be exercised when defining the instability of intervals at large σB ≳ 0.5.

5. Conclusions

We show that non-compressive magnetic field variability, σB, is a useful measure for evaluating the interplay between turbulence and instabilities in the solar wind. Background magnetic field fluctuations cascade to the small-scale end of the inertial range where they have the ability to increase the temperature anisotropy. If the anisotropy is sufficiently large, the plasma becomes unstable.

The distribution of the data in 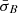–Δρ parameter space shows that 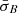and Δρ are interdependent only for the unstable plasma intervals. The competition between the action of the turbulence and the instabilities in these unstable intervals depends on both the level of turbulent activity and the spatial persistence of conditions that define the oblique fire-hose and mirror-mode instabilities. Our analysis suggests that the turbulent solar wind does not provide a simple homogeneous background as assumed by classical linear theory. In fact, a complex interaction between turbulent fluctuations and kinetic instabilities ultimately regulates the proton-scale energetics of the solar wind.

1

In our definition of ergodicity, we rely on the assumption, common to other studies, (e.g., Hellinger et al. 2006; Bale et al. 2009), that the size of our complete dataset is sufficient to be representative of the statistical properties of solar-wind processes, irrespective of the actual sample size. At the spatial scales we consider here, this assumption is justified (Matthaeus & Goldstein 1982).

Acknowledgments

We appreciate very valuable discussions with Matt Kunz. For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising. S. O. is supported by the Natural Environment Research Council (NERC) grant NE/S007229/1. D. V. is supported by the Science and Technology Facilities Council (STFC) Ernest Rutherford Fellowship ST/P003826/1. D. V. and C. J. O. are supported by STFC Consolidated Grants ST/S000240/1 and ST/W001004/1. C. H. K. C. is supported by UKRI Future Leaders Fellowship MR/W007657/1 and STFC Consolidated Grant ST/T00018X/1. P. A. I. is supported by NASA grant 80NSSC18K1215 and by National Science Foundation (NSF) grant AGS2005982. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. Solar Orbiter Solar Wind Analyser (SWA) data are derived from scientific sensors which have been designed and created, and are operated under funding provided in numerous contracts from the UK Space Agency (UKSA), STFC, the Agenzia Spaziale Italiana (ASI), the Centre National d’Etudes Spatiales (CNES), the Centre National de la Recherche Scientifique (CNRS), the Czech contribution to the ESA PRODEX programme and NASA. Solar Orbiter SWA work at UCL/MSSL is currently funded under STFC grants ST/T001356/1 and ST/S000240/1. The Solar Orbiter magnetometer was funded by UKSA grant ST/T001062/1. This work was discussed at the ISSI Team ‘Ion Kinetic Instabilities in the Solar Wind in Light of Parker Solar Probe and Solar Orbiter Observations’, led by L. Ofman and L. Jian.

References

  1. Alexandrova, O., Chen, C. H. K., Sorriso-Valvo, L., Horbury, T. S., & Bale, S. D. 2013, Space Sci. Rev., 178, 101 [Google Scholar]
  2. Bale, S. D., Kasper, J. C., Howes, G. G., et al. 2009, Phys. Rev. Lett., 103, 211101 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bandyopadhyay, R., Qudsi, R. A., Gary, S. P., et al. 2022, Phys. Plasmas, 29, 102107 [Google Scholar]
  4. Bott, A. F. A., Arzamasskiy, L., Kunz, M. W., Quataert, E., & Squire, J. 2021, ApJ, 922, L35 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bruno, R., & Carbone, V. 2013, Liv. Rev. Sol. Phys., 10, 2 [Google Scholar]
  6. Chandran, B. D. G., Quataert, E., Howes, G. G., Xia, Q., & Pongkitiwanichakul, P. 2009, ApJ, 707, 1668 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chen, C. H. K. 2016, J. Plasma Phys., 82, 6 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chen, C. H. K., Boldyrev, S., Xia, Q., & Perez, J. C. 2013, Phys. Rev. Lett., 110, 225002 [Google Scholar]
  9. Chen, C. H. K., Matteini, L., Schekochihin, A. A., et al. 2016, ApJ, 825, L26 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cranmer, S. R., Ballegooijen, A. A. V., & Edgar, R. J. 2007, ApJS, 171, 520 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gary, S. P. 1992, J. Geophys. Res., 97, 8519 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gary, S. P. 1993, Theory of Space Plasma Microinstabilities, Cambridge Atmospheric and Space Science Series (Cambridge: Cambridge University Press) [Google Scholar]
  13. Gary, S. P. 2015, Phil. Trans. R. Soc. A, 373, 20140149 [CrossRef] [Google Scholar]
  14. Gary, S. P., Montgomery, M. D., Feldman, W. C., & Forslund, D. W. 1976, J. Geophys. Res., 81, 1241 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gary, S. P., Wang, J., Winske, D., & Fuselier, S. A. 1997, J. Geophys. Res.: Space Phys., 102, 27159 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gary, S. P., Skoug, R. M., Steinberg, J. T., & Smith, C. W. 2001, Geophys. Res. Lett., 28, 2759 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hellinger, P., & Matsumoto, H. 2000, J. Geophys. Res.: Space Phys., 105, 10519 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hellinger, P., & Trávníçek, P. M. 2008, J. Geophys. Res. Space Phys., 113, A10 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hellinger, P., Trávníèek, P., Kasper, J. C., & Lazarus, A. J. 2006, Geophys. Res. Lett., 33, 9 [CrossRef] [Google Scholar]
  20. Hellinger, P., Matteini, L., Landi, S., et al. 2015, ApJ, 811, L32 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hellinger, P., Landi, S., Matteini, L., Verdini, A., & Franci, L. 2017, ApJ, 838, 158 [Google Scholar]
  22. Hollweg, J. V., & Völk, H. J. 1970, J. Geophys. Res. (1896–1977), 75, 5297 [CrossRef] [Google Scholar]
  23. Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Howes, G. G. 2015, Phil. Trans. R. Soc. A, 373, 20140145 [NASA ADS] [CrossRef] [Google Scholar]
  25. Isenberg, P. A. 1984, J. Geophys. Res.: Space Phys., 89, 6613 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 20 [Google Scholar]
  27. Kiyani, K. H., Osman, K. T., & Chapman, S. C. 2015, Phil. Trans. R. Soc. A, 373, 20140155 [Google Scholar]
  28. Klein, K., Alterman, B., Stevens, M., Vech, D., & Kasper, J. 2018, Phys. Rev. Lett., 120, 205102 [Google Scholar]
  29. Kolmogorov, A. N. 1941, Akademiia Nauk SSSR Doklady, 32, 16 [NASA ADS] [Google Scholar]
  30. Kunz, M. W., Schekochihin, A. A., & Stone, J. M. 2014, Phys. Rev. Lett., 112, 205003 [NASA ADS] [CrossRef] [Google Scholar]
  31. Markovskii, S. A., & Vasquez, B. J. 2022, ApJ, 924, 111 [NASA ADS] [CrossRef] [Google Scholar]
  32. Markovskii, S. A., Vasquez, B. J., & Chandran, B. D. G. 2019, ApJ, 875, 125 [NASA ADS] [CrossRef] [Google Scholar]
  33. Markovskii, S. A., Vasquez, B. J., & Chandran, B. D. G. 2020, ApJ, 889, 7 [NASA ADS] [CrossRef] [Google Scholar]
  34. Marsch, E. 1991, in Reviews in Modern Astronomy, ed. G. Klare (Berlin: Springer), 145 [Google Scholar]
  35. Marsch, E., Ao, X.-Z., & Tu, C.-Y. 2004, J. Geophys. Res., 109, A04102 [NASA ADS] [Google Scholar]
  36. Maruca, B. A., Kasper, J. C., & Bale, S. D. 2011, Phys. Rev. Lett., 107, 201101 [NASA ADS] [CrossRef] [Google Scholar]
  37. Matteini, L., Landi, S., Hellinger, P., & Velli, M. 2006, J. Geophys. Res.: Space Phys., 111, A10 [CrossRef] [Google Scholar]
  38. Matteini, L., Hellinger, P., Landi, S., Trávníèek, P. M., & Velli, M. 2012, Space Sci. Rev., 172, 373 [CrossRef] [Google Scholar]
  39. Matthaeus, W. H., & Goldstein, M. L. 1982, J. Geophys. Res., 87, 10347 [NASA ADS] [CrossRef] [Google Scholar]
  40. Matthaeus, W. H., Oughton, S., Osman, K. T., et al. 2014, ApJ, 790, 155 [NASA ADS] [CrossRef] [Google Scholar]
  41. Opie, S., Verscharen, D., Chen, C. H. K., Owen, C. J., & Isenberg, P. A. 2022, ApJ, 941, 176 [NASA ADS] [CrossRef] [Google Scholar]
  42. Osman, K. T., Matthaeus, W. H., Kiyani, K. H., Hnat, B., & Chapman, S. C. 2013, Phys. Rev. Lett., 111, 201101 [Google Scholar]
  43. Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
  44. Rincon, F., Schekochihin, A. A., & Cowley, S. C. 2015, MNRAS, 447, L45 [NASA ADS] [CrossRef] [Google Scholar]
  45. Riquelme, M. A., Quataert, E., & Verscharen, D. 2015, ApJ, 800, 27 [NASA ADS] [CrossRef] [Google Scholar]
  46. Salem, C. S., Howes, G. G., Sundkvist, D., et al. 2012, ApJ, 745, L9 [NASA ADS] [CrossRef] [Google Scholar]
  47. Schekochihin, A. A., Cowley, S. C., Kulsrud, R. M., Rosin, M. S., & Heinemann, T. 2008, Phys. Rev. Lett., 100, 081301P [Google Scholar]
  48. Servidio, S., Osman, K. T., Valentini, F., et al. 2014, ApJ, 781, L27 [NASA ADS] [CrossRef] [Google Scholar]
  49. Taylor, G. I. 1938, Proc. R. Soc. A, 164, 476 [NASA ADS] [Google Scholar]
  50. Tu, C.-Y., & Marsch, E. 1995, Space Sci. Rev., 73, 1 [Google Scholar]
  51. Verscharen, D., Chandran, B. D. G., Klein, K. G., & Quataert, E. 2016, ApJ, 831, 128 [NASA ADS] [CrossRef] [Google Scholar]
  52. Verscharen, D., Klein, K. G., & Maruca, B. A. 2019, Liv. Rev. Sol. Phys., 16, 1 [NASA ADS] [CrossRef] [Google Scholar]
  53. Walters, P. 2000, An Introduction to Ergodic theory, Graduate Texts in Mathematics No. 79 (Berlin: Springer) [Google Scholar]

All Figures

thumbnail Fig. 1.

Observed data for σB plotted as: (a) distribution of σB binned and averaged by the bin count in T⊥/T∥–β∥ parameter space. The instability thresholds for the oblique fire-hose (OF) and mirror-mode (M) instabilities are shown as labelled. (b) PDFs of σB for oblique fire-hose unstable (magenta), mirror-mode unstable (blue), and stable (green) points in our dataset. The vertical lines denote the ensemble mean [ ⋅ ] of each dataset.
In the text
thumbnail Fig. 2.

PDF of data in σB–θBV parameter space for (a) oblique fire-hose unstable, (b) mirror-mode unstable, and (c) stable data points.
In the text
thumbnail Fig. 3.

PDF of data in –Δρ parameter space for (a) oblique fire-hose unstable and (b) mirror-mode unstable data distributions. Panel (c) shows the same PDF for equivalent persistence intervals sampled from the stable data. The vertical lines shown in (a) and (b) denote the breakpoints previously identified by Opie et al. (2022).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.