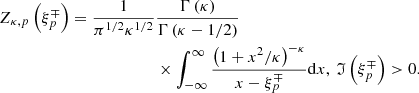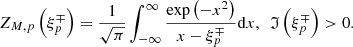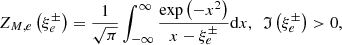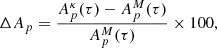| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202348780 | |
| Published online | 29 October 2024 | |
Numerical simulations of temperature anisotropy instabilities stimulated by suprathermal protons
1
Department of Physics and Materials Sciences, College of Arts and Sciences, Qatar University, 2713 Doha, Qatar
2
Research Center in the intersection of Plasma Physics, Matter, and Complexity (P 2mc), Comisión Chilena de Energía Nuclear, Casilla 188-D, Santiago, Chile
3
Departamento de Ciencias Físicas, Facultad de Ciencias Exactas, Universidad Andres Bello, Sazié 2212, Santiago 8370136, Chile
4
Institute for Theoretical Physics IV, Faculty for Physics and Astronomy, Ruhr-University Bochum, 44780 Bochum, Germany
5
Centre for Mathematical Plasma Astrophysics, Dept. of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
6
Institute of Physics, University of Maria Curie-Skłodowska, Pl. Marii Curie-Skłodowskiej 1, 20-031 Lublin, Poland
⋆ Corresponding author; s.m.shaaban88@gmail.com
Received:
29
November 2023
Accepted:
19
August 2024
Context. The new in situ measurements of the Solar Orbiter mission contribute to the knowledge of the suprathermal populations in the solar wind, especially of ions and protons whose characterization, although still in the early phase, seems to suggest a major involvement in the interaction with plasma wave fluctuations.
Aims. Recent studies point to the stimulating effect of suprathermal populations on temperature anisotropy instabilities in the case of electrons already being demonstrated in theory and numerical simulations. Here, we investigate anisotropic protons, addressing the electromagnetic ion-cyclotron (EMIC) and the proton firehose (PFH) instabilities.
Methods. Suprathermal populations enhance the high-energy tails of the Kappa velocity (or energy) distributions measured in situ, enabling characterization by contrasting to the quasi-thermal population in the low-energy (bi-)Maxwellian core. We use hybrid simulations to investigate the two instabilities (with ions or protons as particles and electrons as fluid) for various configurations relevant to the solar wind and terrestrial magnetosphere.
Results. The new simulation results confirm the linear theory and its predictions. In the presence of suprathermal protons, the wave fluctuations reach increased energy density levels for both instabilities and cause faster and/or deeper relaxation of temperature anisotropy. The magnitude of suprathermal effects also depends on each instability’s specific (initial) parametric regimes.
Conclusions. These results further strengthen the belief that wave-particle interactions govern space plasmas. These provide valuable clues for understanding their dynamics, particularly the involvement of suprathermal particles behind the quasi-stationary non-equilibrium states reported by in situ observations.
Key words: instabilities / plasmas / waves / methods: numerical / Sun: corona / solar wind
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Plasmas are hot and diluted in many astrophysical contexts, so particle-particle collisions cannot restore thermal equilibrium (Schlickeiser 2002; Marsch 2006). Eloquent examples are the solar wind and planetary environments, where in situ measurements reveal non-equilibrium velocity distributions (VDs) of plasma particles (e.g., electrons and protons as major species), which cannot be reproduced by isotropic Maxwellian models specific to thermal equilibrium. The relevant features are deviations from isotropy (usually relative to the direction of the local magnetic field), such as field-aligned beams and temperature anisotropies, as well as enhanced high-energy or suprathermal tails, modelled by Kappa (or κ-) power-law distributions (Christon et al. 1991; Collier et al. 1996; Maksimovic et al. 2005; Štverák et al. 2008; Pierrard & Lazar 2010; Anderson et al. 2012; Wang et al. 2015; Lazar et al. 2017; Maruca et al. 2018; Wilson et al. 2019; Berčič et al. 2019; Ďurovcová et al. 2021).
Measured with a cadence lower than the characteristic frequencies of the kinetic (self-generated) instabilities, the anisotropies reveal quasi-stable states, which are, however, sufficiently well shaped by the threshold conditions, suggesting that these instabilities are at work (Kasper et al. 2002; Maksimovic et al. 2005; Samsonov et al. 2007; Štverák et al. 2008; Bale et al. 2009; Wicks et al. 2013; Lacombe et al. 2014; Maruca et al. 2018; Shaaban et al. 2019a,b; Berčič et al. 2019; Huang et al. 2020). In addition, the suprathermal populations are specific not only to electrons but also to protons and heavier ions (Christon et al. 1989; Gloeckler et al. 1995; Collier et al. 1996; Lario et al. 2019; Yang et al. 2023), and seem to be the most involved in the mutual interactions with wave fluctuations and plasma instabilities. There is also observational evidence for the formation of these suprathermal populations in processes of energization and dispersion by wave fluctuations, self-generated and/or enhanced by kinetic instabilities (Maksimovic et al. 2005; Marsch 2006; Berčič et al. 2019; Yang et al. 2023). With the new missions, Parker Solar Probe and Solar Orbiter, in situ measurements seek to uncover possible coronal sources of suprathermal ions (Bale et al. 2021), as well as their involvement as seed populations in acceleration processes (and, e.g., generation of energetic particles) as well by waves and plasma turbulence (Wimmer-Schweingruber et al. 2021; Mason et al. 2023; Yang et al. 2023).
In turn, the suprathermal populations present in the plasma system modify the excitation conditions and the properties of kinetic instabilities, leading, for instance, to the stimulation of those generated by temperature anisotropy (Shaaban et al. 2021a; Lazar et al. 2022), or to the inhibition of beam instabilities, in particular, of electrostatic instabilities triggered by electron beams (Lazar et al. 2023). Working with non-equilibrium Kappa models is, however, not straightforward. It requires physically appropriate and observationally consistent approaches to produce quantitative assessments of suprathermal populations and their contributions, from the contrast with the low-energy Maxwellian (core) populations (Lazar et al. 2015; Lazar & Fichtner 2021). In the case of instabilities generated by temperature anisotropy, that is A = T⊥/T∥ ≠ 1 (where ∥, ⊥ are gyrotropic directions relative to the magnetic field), it is interesting that the suprathermal populations generally have a systematic stimulating effect (Shaaban et al. 2021a; Lazar et al. 2022). Regardless of the nature of the instabilities, whether electrons or protons generate them, or that they are electromagnetic (EM) cyclotron or mirror modes destabilized by A > 1, or firehose instabilities induced by A < 1, linear theory predicts enhanced growth rates and increased ranges of unstable wave-numbers due to suprathermals (Viñas et al. 2015; Lazar et al. 2015, 2019; Shaaban et al. 2018, 2019c, 2021b,c; López et al. 2023). Implicitly, the anisotropy thresholds of all these instabilities are also reduced. In the case of electrons, these predictions are also confirmed by theory and nevertheless by numerical simulations, which indicate increases in the wave energy density and a more pronounced effect of fluctuations on the anisotropy relaxation (Lazar et al. 2019, 2022; López et al. 2019; Moya et al. 2020).
In this paper, we present new results from numerical simulations of protons with anisotropic bi-Kappa distributions in an attempt to confirm theoretical predictions for both the EM ion cyclotron (EMIC) and proton firehose (PFH) instabilities (Shaaban et al. 2021b,c). EMIC modes are destabilized by protons (subscript p) with Ap = T⊥/T∥ > 1, and the parallel (or periodic) PFH instability is triggered by an opposite anisotropy, Ap < 1. Linear and QL properties of these two instabilities have been intensively investigated, especially when triggered by bi-Maxwellian (idealized) protons, such as, for instance, core proton populations in space plasmas, see Davidson & Ogden (1975), Seough & Yoon (2012), Yoon & Seough (2012), Astfalk & Jenko (2018), Shaaban et al. (2021d) and relevant references in the textbook of Gary (1993), to name just a few. Furthermore, numerical simulations can confirm those parametric regimes when these parallel modes are dominant (developing much faster than other instabilities predicted by linear theory), and their effectiveness in relaxing the temperature anisotropy can also be assessed (Gary et al. 1997; Shoji et al. 2009; Yoon 2017; Micera et al. 2020; López et al. 2022). Particle-in-cell (PIC) simulations are, however, very demanding in terms of computational resources and have therefore been limited to bi-Maxwellian protons and often unrealistically low proton-to-electron mass ratios, such as mp/me = 25, 50, 100 (Gary & Saito 2003; Seough et al. 2014, 2015; Micera et al. 2020; López et al. 2022). In the present analysis, we use hybrid simulations, which require much less resources and computing time (Gary et al. 1998).
The results are expected to change markedly under the influence of suprathermal protons modelled with bi-Kappa distributions (Thorne & Summers 1991; Dasso et al. 2003; Shaaban et al. 2021a,b,c; Lazar et al. 2022). On the one hand, linear theory predicts a systematic stimulation of both instabilities under the influence of suprathermal protons by enhanced growth rates and lower anisotropy thresholds. On the other hand, quasilinear (QL) approaches confirm higher levels of fluctuations reached the saturation and a faster and deeper relaxation of temperature anisotropy (Shaaban et al. 2021c,b; Lazar et al. 2022; López et al. 2023). However, numerical simulations still have no definitive confirmation of these effects. Recent 2D hybrid simulations of EMIC instability assumed bi-Kappa protons to test a new 2D moment-based QL approach, aiming to capture the interplay with the oblique mirror modes (Yoon et al. 2023; López et al. 2023). The dominance of EMIC or mirror instabilities depends on the beta parameter, both for bi-Maxwellian (Shaaban et al. 2018) and bi-Kappa protons (Yoon et al. 2023). Thus, we restrict the analysis to the EMIC dominance conditions (when their growth rates exceed those of the mirror instability), that is, for βp∥ < 5, predominant in the solar wind (Wicks et al. 2013) and also relevant for the terrestrial magnetosphere (Maruca et al. 2018). The regimes of PFH instabilities are also more favourable to parallel modes (Micera et al. 2020; López et al. 2022), which motivates our restriction to 1D simulations. This is supported by the observations, which link the parallel-propagating fluctuations at proton scales to instabilities driven by temperature anisotropies and relative ion drifts. In contrast, the oblique fluctuations are consistent with the anisotropic turbulent cascade (Woodham et al. 2019). The simulations of EMIC instability in López et al. (2023) prove its stimulation by suprathermal protons but only for a limited regime of moderate plasma beta (see definition below), that is βp, ∥ = 1. Here, we survey various regimes of parallel-propagating instabilities of extended relevance in space plasmas, such as the solar wind and planetary environments.
In Section 2.1, we explicitly introduce VD models used to describe anisotropic protons and isotropic electrons. The contribution of suprathermal protons to the instability is highlighted by contrasting the results obtained for the bi-Kappa distributed protons with those derived for the bi-Maxwellian limit (κ → ∞), reproducing the low-energy core without suprathermal tails (Lazar et al. 2015, 2016). Our parameterization relies therefore on the observations featuring the highly dense core, for instance, temperature anisotropy and beta parameter (Kasper et al. 2002; Samsonov et al. 2007; Wicks et al. 2013; Maruca et al. 2018; Huang et al. 2020). The suprathermal protons do not yet benefit from a detailed and systematic characterization (due to limited measurement efficiency and low count statistics). However, ongoing studies provide plausible estimates for the power-law exponent of the Kappa distributions used in our analysis (Nicolaou et al. 2018; Lario et al. 2019; Yang et al. 2023). Corresponding to the anisotropic models, the linear equations of wave dispersion and stability from kinetic theory are briefly presented in Section 2.2. The unstable solutions of the dispersion relations must describe the instabilities of interest, wave frequencies, and growth rates as functions of wavenumber. The illustrative results obtained from the simulations for the time evolution of EMIC and PFH instabilities are then discussed in Section 3. We analyze the effects of suprathermal protons on the resulting enhanced fluctuations during their growth and saturation. Also of interest is the reaction of these fluctuations back on the relaxation of the anisotropic distributions. In the last section (Section 4), we draw the main conclusions of the present study.
2. Wave dispersion and stability
2.1. Velocity distributions
We assume collisionless and homogeneous quasi-neutral electron-proton plasmas, with initially anisotropic protons (subscript p), described by the bi-Kappa distribution function (Lazar et al. 2015)
This is defined in terms of the (normalizing) velocities θp ∥ ,⊥(t), which vary with time (t) in simulations (see below), and are related to the anisotropic temperature components (for any κ > 3/2)
as given by the second-order moments of the bi-Kappa distribution. Here mp is the proton mass, and kB is the Boltzmann constant. Tp ⊥ ,∥ approximate the temperature components of the lower energy protons in a bi-Maxwellian core (without suprathermal tails)
which is recovered from Eq. (1) in the limit of large κ → ∞ (Lazar et al. 2015). The results obtained for bi-Kappa distributed protons thus allow a straightforward comparison with those derived in the absence of suprathermal protons in the (bi-)Maxwellian limit, and the difference even characterizes the effects of the suprathermal component (Lazar et al. 2015, 2016).
In linear theory, we can assume electrons (subscript e) to be isotropic and Maxwellian-distributed
with thermal velocity θe linked to temperature Te = meθe2/(2kB), where me is the electron mass.
2.2. Linear dispersion relations
For the plasma configuration described above, the instantaneous dispersion relation for the transverse modes propagating parallel to the background magnetic field reads (Shaaban et al. 2021b,c)
Here 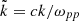 is the normalized wave-number k, c is the light speed, ωpp = (4πnpe2/mp)1/2 is the proton plasma frequency (proportional to the number density np = n0),
is the normalized wave-number k, c is the light speed, ωpp = (4πnpe2/mp)1/2 is the proton plasma frequency (proportional to the number density np = n0), 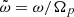 is the normalized wave frequency ω, Ωj = eB0/mjc is the non-relativistic gyro-frequency of the plasma species j (with elementary charge e), βj∥ = θj∥2ωpj2/(c2Ωj2) = 8πn0kBTj∥/B02 are the corresponding parallel plasma beta parameters (in the Maxwellian limit, i.e., not depending on κ), Aj ≡ θj⊥2/θj∥2 ≡ Tj⊥κ/Tj∥κ ≡ Tj⊥/Tj∥ ≡ βj⊥/βj∥ is the temperature anisotropy of the plasma species j, μ = mp/me is the proton to electron mass ratio. In the proton term “∓” denotes the circular left-handed (LH) or right-handed (RH) polarization, respectively, and
is the normalized wave frequency ω, Ωj = eB0/mjc is the non-relativistic gyro-frequency of the plasma species j (with elementary charge e), βj∥ = θj∥2ωpj2/(c2Ωj2) = 8πn0kBTj∥/B02 are the corresponding parallel plasma beta parameters (in the Maxwellian limit, i.e., not depending on κ), Aj ≡ θj⊥2/θj∥2 ≡ Tj⊥κ/Tj∥κ ≡ Tj⊥/Tj∥ ≡ βj⊥/βj∥ is the temperature anisotropy of the plasma species j, μ = mp/me is the proton to electron mass ratio. In the proton term “∓” denotes the circular left-handed (LH) or right-handed (RH) polarization, respectively, and
is the modified dispersion function for Kappa-distributed plasmas (Lazar et al. 2008) of argument 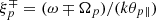 . In the Maxwellian limit
. In the Maxwellian limit 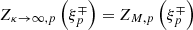 we recover the standard plasma dispersion function (Fried & Conte 1961)
we recover the standard plasma dispersion function (Fried & Conte 1961)
In the dispersion relation (5), “±” in the electron term corresponds to circular LH or RH polarization, respectively (due to the opposite sign of the electric charge), with a similar (standard) dispersion function
of argument 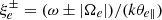 .
.
In the absence of suprathermal protons (i.e., κ → ∞), the modified dispersion function Zκ, p converges to the standard dispersion function ZM, p. Consequently, in this limit, the linear dispersion relation (5) reduces to the standard linear equation that describes the instabilities of the (cooler) bi-Maxwellian core (Gary 1993; Shaaban et al. 2021d). The results from linear theory show the effects of suprathermal protons on the wave frequency and growth rates of EMIC and PFH instabilities. For instance, growth rates are displayed for each case of interest in Sections 3.1 and 3.2, and wave frequencies are shown in Section 3.3 to demonstrate the agreement of the simulations with predictions from linear theory.
3. Hybrid simulations
We have used 1D explicit hybrid simulations to examine the two unstable EM modes: the parallel EMIC and PFH instabilities. In the simulations, protons are modelled as particles with suprathermal, (bi-)Kappa tails and temperature anisotropies Ap ≠ 1, whereas electrons are considered a massless charge-neutralizing fluid with a constant temperature. This code is based on the Winske & Omidi (1993) code. Protons are advanced using the Boris scheme (Boris 1970a,b), and the fields are computed explicitly following the iterative scheme as in Horowitz et al. (1989). The initial proton (bi-)Kappa distribution is loaded using the acceptance-rejection method; see details in (López et al. 2023). For all investigated cases, we assume isotropic electrons with βe = 0.5. The simulation box contains 4 096 000 protons within a length L = 502.65 vA/Ωp and 4096 grid points, and for the normalized time τ = Ωpt a step of δτ = 0.01 is used. The constant background magnetic field is set in the z-direction.
Tables 1 and 2 contain values of the key plasma parameters, Ap and βp∥, used in our simulations. These values are inspired by solar wind observations, mainly proton core data reported from various heliocentric distances by various spacecraft (Kasper et al. 2002; Wicks et al. 2013; Shaaban et al. 2017; Huang et al. 2020), whose relevance can also extend to the terrestrial magnetosphere (Samsonov et al. 2007; Maruca et al. 2018). Moreover, our parameterization is generally favourable to parallel propagating instabilities (see the motivations in Section 1). Observations are quasi-steady states confined to a rhombic-shaped outer boundary known as (Ap, βp∥)–parameter space. Due to a limited measurement cadence, the observed anisotropies are relatively small, specific to quasi-stable states below the thresholds of instabilities. Larger deviations from isotropy (Ap = 1) may exist. Still, they cannot be observed (for now) because they are rapidly relaxed by our instabilities, whose growth rates and relaxation effects increase with the initial anisotropy. This motivates the values we invoke for temperature anisotropies, which can be at or even above the upper limits of the observations.
Parameterization adopted in the hybrid simulations of the EMIC instability, in terms of initial values (τ = 0) for four distinct runs.
Parameterization adopted in the hybrid simulations of the PFH instability, in terms of initial values (τ = 0) for four distinct runs.
3.1. EMIC instability
First, we discuss the results obtained for the EMIC instability for four distinct cases, explained in Table 1 in terms of the plasma parameters’ initial (τ = 0) values. According to Eq. (2), the (initial) proton anisotropy Ap does not depend on the distribution model, as it happens with the (initial) plasma beta parameters. Such that, for initial bi-Kappa distributed protons with κ = 3 parallel plasma beta becomes two times higher than that for quasi-thermal bi-Maxwellian protons (κ → ∞), that is, 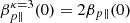 . Corresponding EMIC solutions are displayed in Fig. 1, with red and blue lines, respectively.
. Corresponding EMIC solutions are displayed in Fig. 1, with red and blue lines, respectively.
 |
Fig. 1. EMIC unstable solutions for bi-Kappa protons (red) and the corresponding bi-Maxwellian core (blue) for all four cases in Table 1 with initial proton parameters also indicated in the panels. Comparison of growth rates from linear theory (left panels) and temporal evolution from simulations for the wave energy density (middle panels) and the temperature anisotropy (right panels). |
Left panels in Fig. 1 display the normalized growth rates (γ/Ωp) derived from linear theory, which show a systematic enhancement, with higher peaks and larger ranges of unstable wavenumbers in the presence of suprathermal protons (red). These results agree with previous linear approaches of EMIC instability in plasmas with bi-Kappa protons (and refs. therein Shaaban et al. 2021a). Corresponding to these two (linear) solutions, panels in the middle column also compare the time evolution of the wave energy densities (Wt = δB2/B02), as obtained from simulations. The right column shows the time relaxation of the temperature anisotropy, providing the same comparison between the solutions derived for bi-Kappa (red) and bi-Maxwellian (blue) protons.
First, it should be emphasized that the simulations confirm the linear theory predictions for a wide variety of cases studied (including those not discussed here). Namely, for higher growth rates of EMIC instability in the presence of suprathermal protons (red lines), with markedly higher peaks of maximum growth rates (γm > 0), the resulting wave fluctuations reach a much higher level of energy density at the saturation (middle panels). The increase rate in wave energy density is roughly given by 2γm (see, for instance, Section 3.3). In the presence of suprathermal bi-Kappa protons, it can thus reach saturation values up to several times higher, see cases 2 and 3. More intense wave fluctuations can also cause and explain the faster and deeper relaxation of the temperature anisotropy shown in the right panels. Also, the onset times of the increase in fluctuations and relaxation of the anisotropy can be noticeably shorter. This is due to the suprathermal protons and the additional energy they contribute, which is partially converted into EMIC waves.
Initial values of the main parameters, namely the plasma beta and temperature anisotropy, affect the evolution of the instability. Higher values of the proton beta and anisotropy mean more free energy in the system, leading to higher growth rates of the EMIC instability and larger intervals of unstable wavenumbers. This is proven by a direct comparison between runs 1 and 2, which start from the same low βp∥(0) = 0.1, but different anisotropies, respectively, Ap(0) = 6 and Ap(0) = 3. Higher initial anisotropy in run 1 determines higher levels of fluctuations (quantified by the wave energy density) and deeper relaxation of the temperature anisotropy as time evolves. Similar effects are obtained when the anisotropy is kept the same. Still, the initial plasma beta increases, for instance, if we compare runs 2, 3, and 4, for which we start with the same Ap(0) = 3, but different βp∥(0) = 0.1, 0.5, and 1, respectively. Moreover, we find that all these effects are stimulated by the presence of suprathermal populations, which contribute to the increase of kinetic energy (temperature) of protons and implicitly to an increase of the beta parameter. Thus, growth rates are enhanced, the wave energy density of the resulting EMIC fluctuations is increased, and the relaxation of proton anisotropy is deeper, approaching closer to the isotropy condition.
Up to this point, the impact of suprathermal protons on temperature anisotropy relaxation has not yet been quantified. Therefore, in Fig. 2, we examine the instantaneous relative difference of the proton anisotropy (in %)
 |
Fig. 2. Instantaneous relative difference of the proton anisotropy, ΔAp(τ) (in %, see definition in the text), induced by the presence of suprathermal protons for all EMIC runs in Fig. 1. |
as a function of different initial plasma parameters for all cases in Fig. 1. Apκ(τ) and ApM(τ) represent the instantaneous temperature anisotropies for bi-Kappa and bi-Maxwellian cases. In Fig. 2, it is evident that the instantaneous relative difference ΔAp(τ) reaches minima at the early stages, specifically at τ ∈ [30–40], for runs 1, 3, and 4 with highest levels of wave fluctuations. These minima indicate that the relaxation of temperature anisotropy starts much earlier due to suprathermal protons and becomes significant even before Maxwellian protons begin to relax. Conversely, in run 2, the fluctuations reach only lower levels, and the decrease in ΔAp (blue line) starts around τ ≃ 80. For run 1 with Ap(0) = 6 and βp∥(0) = 0.1 (red line), ΔAp decreases to its minimum value of −31% at τ ≃ 30 before eventually reaching a value of −16% at τ ≃ 500. This means the relaxation of the temperature anisotropy in the presence of suprathermal (Kappa) protons is 31% deeper already at τ ≃ 30, and this difference is reduced to 16% later at τ ≃ 500.
Runs 3 (black) and 4 (green) with higher initial betas, that is, with βp∥(0) = 0.5 and 1.0, respectively, show similar behaviour as time evolves but with lower differences ΔAp. For instance, in case 3 ΔAp = −21.5% at τ ≃ 40 and −11% at τ ≃ 500, whereas for case 4 ΔAp = −25.2% at τ ≃ 29 and −7% at τ ≃ 500. One conclusion to draw here is that as proton plasma beta increases, the effects of suprathermal populations on the resulting fluctuations, and implicitly on the temperature anisotropy relaxation. This influence also becomes evident even with low levels of wave fluctuations, such as in run 2 (blue line); that is, the instantaneous difference ΔAp = −25% at τmax is larger than all the other cases at final stages. The EMIC instability is typical of magnetized plasmas, so variations of βp∥ have a greater impact on the growth rate and fluctuation levels in highly magnetized plasma (with low βp∥) than in weakly magnetized plasmas (with high βp∥). This is also reflected in the contribution of suprathermal protons.
Fig. 3 displays the simulated proton VDs, namely, snapshots of fp(v∥, v⊥), which enable us to identify the deformations that eventually appear compared to the initial shape of these distributions as time evolves, in response to the growth of EMIC fluctuations. The upper two rows of panels show the bi-Maxwellian (κ → ∞) and bi-Kappa (κ = 3) protons for run 1 in Fig. 1 (Ap(0) = 6 and βp∥(0) = 0.1), at four times: τ = 0, 30, 100, 500 (including saturation and extending by the end of the simulation). The initial shape of these distributions, either bi-Kappa or bi-Maxwellian, is generally preserved, although these distributions are subjected to the relaxation of temperature anisotropy. To capture the differences introduced by the suprathermal protons on the VD evolution, the time step τ = 30 is carefully selected in correspondence with the observed minimum in Fig. 2 (red line). At τ = 30, one can see that the initial bi-Maxwellian VD undergoes a small deformation, mainly in the sense of relaxation. In contrast, the initial bi-Kappa distribution shows stronger relaxation towards isotropization. The cyclotron resonant particles are pitch-angle and energy-scattered. As the time progresses to saturation, that is, at τ ≃ 100, the main response of the EMIC fluctuation to the VD is completed. The anisotropic bi-Kappa relaxes faster than the bi-Maxwellian, showing a less elliptical asymmetry. After saturation towards the end of the simulation (i.e., at τ = 500), the particle diffusion in velocity space continues, but less prominently, though the VDs in both cases become more isotropic. The lower panels in Fig. 3 are intended for a similar comparison but for run 2 (blue line in Fig. 2). The contrast between bi-Kappa and bi-Maxwellian distributions becomes evident after τ ≃ 100 increases as time evolves. The results for the bi-Maxwellian protons are consistent with those in Gary & Saito (2003). A comparison of the results from runs 1 and 2 reveals that VDs associated with intense wave fluctuations (run 1) relax faster and more efficiently to approach the isotropy than those associated with lower levels of fluctuations (run 2).
 |
Fig. 3. VDs from the simulations of EMIC instability for cases 1 and 2 from Fig. 1, computed for four time steps, and for both bi-Maxwellian (κ → ∞) and bi-Kappa (κ = 3) distributed protons, as indicated in the panels. |
3.2. PFH instability
In this section, we discuss the proton firehose (PFH) instability for four cases parameterized in Table 2, in terms of the initial values of the plasma beta parameter, both βp∥(0) for bi-Maxwellian and 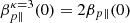 for bi-Kappa protons, and the temperature anisotropy Ap(0) < 1 (not depending on the distribution model). Reasonable growth rates of firehose instabilities (γm/Ωp ≥ 0.01) generally require overdense or weakly magnetized plasmas (i.e., βp∥ ≥ 1), and if the parallel beta is not very high, for instance, βp∥ < 10, PFH instability is triggered by the anomalous resonance of protons (Gary et al. 1998; Astfalk & Jenko 2018). The PFH solutions are displayed in Fig. 4 for both bi-Kappa (red) and bi-Maxwellian (blue) models, using the same structure from Fig. 1. The normalized (linear) growth rates (γ/Ωp) are shown in the left column and exhibit a similar enhancement in the presence of suprathermal protons. Their stimulation is more significant at low values of the beta parameter, leading to increases of 3 or even 4 times the maximum growth rate if, for example, βp∥(0) = 2.0 (case 1, top panel). However, this effect decreases rapidly with increasing beta parameter, suggesting a lower involvement of the suprathermal component. Such that for βp∥(0) = 6, the suprathermal influence remains noticeable only at low wave numbers k ≤ km (case 4, bottom panel), where km corresponds to the mode with the fastest growth, and peaking growth rate γm.
for bi-Kappa protons, and the temperature anisotropy Ap(0) < 1 (not depending on the distribution model). Reasonable growth rates of firehose instabilities (γm/Ωp ≥ 0.01) generally require overdense or weakly magnetized plasmas (i.e., βp∥ ≥ 1), and if the parallel beta is not very high, for instance, βp∥ < 10, PFH instability is triggered by the anomalous resonance of protons (Gary et al. 1998; Astfalk & Jenko 2018). The PFH solutions are displayed in Fig. 4 for both bi-Kappa (red) and bi-Maxwellian (blue) models, using the same structure from Fig. 1. The normalized (linear) growth rates (γ/Ωp) are shown in the left column and exhibit a similar enhancement in the presence of suprathermal protons. Their stimulation is more significant at low values of the beta parameter, leading to increases of 3 or even 4 times the maximum growth rate if, for example, βp∥(0) = 2.0 (case 1, top panel). However, this effect decreases rapidly with increasing beta parameter, suggesting a lower involvement of the suprathermal component. Such that for βp∥(0) = 6, the suprathermal influence remains noticeable only at low wave numbers k ≤ km (case 4, bottom panel), where km corresponds to the mode with the fastest growth, and peaking growth rate γm.
 |
Fig. 4. PFH unstable solutions for bi-Kappa protons (red) and the corresponding bi-Maxwellian core (blue) for all three cases in Table 2 with initial proton parameters also indicated in the panels. Comparison of growth rates from linear theory (left panels) and temporal evolution from simulations for the wave energy density (middle panels) and the temperature anisotropy (right panels). |
Corresponding to the PFH solutions for bi-Maxwellian (blue) and bi-Kappa (red) protons, in the other panels of Fig. 4 we compare the time evolution of the wave energy density (Wt(τ), middle column), and the time relaxation of the temperature anisotropy (Ap(τ), right column), as obtained from simulations. The effect of suprathermal protons also translates into faster increases of energy density Wt(τ) and higher values reached saturation, and even after, in the asymptotic decreasing profiles. In the presence of suprathermal protons, the anisotropy relaxation is not significantly faster but deeper or closer to isotropy (right panels). These differences depend on the initial values of the main parameters and are generally conditioned by the anisotropy and the plasma beta parameter. In case 3, the intense wave fluctuations obtained for bi-Kappa protons with Ap(0) = 0.1 and βp∥(0) = 6.0 are very efficient in the relaxation process leading to very small deviations from isotropy (Ap ≲ 1), with asymptotic values of only Ap(τ → ∞) = 0.8. The results for bi-Maxwellian protons are very similar to those obtained from PIC simulations with a reduced (unrealistic) proton-electron mass ratio (Seough et al. 2015), suggesting a minor dependence on this parameter, as Seough et al. (2015) also claimed.
For the same initial value of the temperature anisotropy, the linear properties and the evolution of the instability are conditioned by the beta parameter and the suprathermal exponent κ. For a low initial plasma beta, for instance, βp∥(0) = 2 in case 1, the wave energy density reached in the presence of suprathermal bi-Kappa (κ = 3) protons is much higher (one order of magnitude higher) than for bi-Maxwellian protons. As an effect of the enhanced fluctuations, the temperature anisotropy also relaxes faster and deeper. Comparisons between runs 1, 2, and 3 show that these differences introduced by suprathermals in the time evolution of wave fluctuations and temperature anisotropy decrease with increasing the initial plasma beta, for instance, βp, ∥(0) = 4.0 and 6.0. The explanation can also be found because this instability is specific to magnetized plasmas. This means that at low βp∥, where the effects of the magnetic field are more pronounced, the growth rates and, implicitly, the level of fluctuations increase significantly with the increase of βp∥, also reflected in the presence of suprathermal populations. Conversely, in weakly magnetized plasmas with high βp∥, the consequences of the same variations of this parameter become less significant.
To quantify the back effect of the enhanced fluctuations on the relaxation of anisotropic protons, we use again the relative difference in the temperature anisotropy ΔAp, defined in Eq. (9). Fig. 5 displays the time variation for each run in the right column of Fig. 4. This also enables us to examine the impact of the chosen initial plasma parameters, including the indirect influence of suprathermal protons on the relaxation of temperature anisotropy. The instantaneous relative differences ΔAp (%) increase as time evolves, reaching the first peaks at the early stages, specifically at τ ∈ [20–35], and continuing to fluctuate until the end of the simulations. The first peaks indicate that for suprathermal protons, the relaxation of temperature anisotropy starts faster than that for less energetic protons. For run 1 (red line) with a low initial plasma beta βp∥(0) = 2, the first peak ΔAp ≈ 185% appears at τ = 35, before ΔAp grows and eventually reaches 235% at τ = 150. In other words, in the presence of suprathermal protons, the relaxation of the temperature anisotropy is 185% and 235% deeper at, respectively, τ = 35 and τ = 150. The subfigure (left corner) in Fig. 5 shows the saturation from longer runs of τmax = 1570, at about ΔAp(τmax)≈416%, and Ap(τmax)≈0.6, concurrent with instability saturation (not shown here). With increasing the initial βp∥(0), the contrast introduced by the suprathermal population is reduced for the abovementioned reasons. For instance, in run 2 with βp∥(0) = 4, ΔAp displays its first peak of value 103% at τ = 24, before eventually reaching the value 80% at τ = 150. Furthermore, for βp∥(0) = 6 in run 3 the first peak of ΔAp reduces to 38% at τ = 22, before reaching a lower value of 29% at τ = 150. Suprathermal populations have their highest potential at lower plasma beta. The initial plasma parameters in run 4 are similar to those of run 3 but with lower anisotropy (two times lower). In this case, the time evolution of ΔAp is similar to that in run 3, especially at later stages (e.g., at τ > 30), reaching a value of 28% at τ = 150.
 |
Fig. 5. Instantaneous relative difference of the proton anisotropy, ΔAp(τ) (in %, see definition in the text), induced by the presence of suprathermal protons for all PFH runs in Fig. 4. |
Fig. 6 displays snapshots of proton VDs from the simulations, which enable us to trace, as time evolves, the deformations undergone by the distributions by comparison to their initial (τ = 0) shape in response to the exponential growth of PFH fluctuations. We follow the same structure as in Fig. 3, and the upper two rows of panels contrast the bi-Maxwellian (κ → ∞) and bi-Kappa (κ = 3) protons from run 1 in Fig. 2 (i.e., for βp∥ = 2 and 6). In these cases, the initial shape of the bi-Maxwellian or bi-Kappa distributions may not be preserved during the relaxation of temperature anisotropy. The departure from the initial shape of VD is a dumbbell-like deformation in the parallel direction, with the excess of kinetic energy (T∥ > T⊥). These deformations are more prominent for bi-Maxwellian distributed protons, and those low-beta protons, see the upper panels in Fig. 6. Dumbbell-like deformations were also reported by Matteini et al. (2006) and Seough et al. (2015) from the simulations of the PFH instability of similar low-beta bi-Maxwellian protons. Even in bi-Kappa distributions, the dumbbell-like deformation can persist longer for low-energy protons in the core of the VD, similar to the low-beta population. A plausible explanation invoked by Matteini et al. (2006) is the distinctive resonance of the growing fluctuations with the proton populations, shaping only part of the VD. The diffusion of more energetic particles (and implicitly less magnetized particles) is much faster and has fewer significant deformations. This is reflected both in the distributions of high-beta protons, compare, for instance, runs 1 and 3 in Fig. 6, but also in the (initial) bi-Kappa distributions contrasting with bi-Maxwellian (κ → ∞). In this sense, the case of bi-Kappa protons with βp∥ = 6 (lower panels) show the most pronounced relaxation as time evolves.
 |
Fig. 6. VDs from the simulations of PFH instability for cases 1 and 3 from Fig. 4, computed for four time steps, and for both bi-Maxwellian (κ → ∞) and bi-Kappa (κ = 3) distributed protons, as indicated in the panels. |
3.3. Simulations vs. linear theory
Here, we use two methods to test the numerical simulation results against the linear theory predictions for both instabilities. On the one hand, Fig. 7 presents examples of magnetic fluctuation spectra obtained from simulations in the ω − k space, by computing the fast Fourier transforms in space and time as |FFT(x, t){δ(Bx + iBy)/B0}|2, for EMIC instability cases 1 and 2 (upper panels), and for PFH instability cases 1 and 3 (lower panels). The results for bi-Maxwellian protons are in the left panels, and for bi-Kappa in the right panels. In this way, the left-handed polarized fluctuations of EMIC instability are shown in the first quadrant [ω > 0, k > 0]. In contrast, the right-handed ones of PFH instability appear in the fourth quadrant [ω < 0, k > 0]. The suprathermal protons enhance peak intensities associated with the triggered instabilities; see the right panels. Moreover, these intensities align to the dispersion curves ωr(k) derived from linear theory (over-plotted dashed lines), showing satisfactory agreement for all cases.
 |
Fig. 7. Magnetic fluctuations from simulations, for EMIC cases 1 and 2 (upper panels) and PFH instability cases 1 and 3 (lower panels), resemble linear dispersion (dashed lines) in the ω − k space and are enhanced in the presence of suprathermals (right panels). The colour scale indicates the normalized magnetic wave energy density. |
On the other hand, we can also examine the time variation of magnetic fluctuation spectra, computed as the spatial Fourier transforms |FFTx{δ(Bx + iBy)/B0}|2 for two distinct modes of EMIC instability, in, for example, cases 1 and 2 shown in Fig. 8, and for other two modes of PFH instability in cases 1 and 3 displayed in Fig. 9. The wave numbers of these modes, distinguished by blue and black lines, are indicated in the legends. The purple lines have slopes given by the growth rates of the same wave modes obtained from linear theory, that is, ∝exp(2γt), with growth rate γ/Ωp given in Figs. 1 and 4 (also indicated along the purple lines). For both instabilities in Figs. 8 and 9, as well as for both bi-Maxwellian and bi-Kappa distributed protons, the initial growth of the magnetic fluctuation is sufficiently well predicted by these growth rates from linear theory.
 |
Fig. 8. Time variation of magnetic fluctuation spectra for two EMIC modes corresponding to distinct wave numbers (see the legend), in cases 1 and 2. Computed as the spatial Fourier transform, |FFTx{δ(Bx + iBy)/B0}|2. |
 |
Fig. 9. Time variation of magnetic fluctuation spectra for two PFH modes corresponding to distinct wave numbers (see the legend), in cases 1 and 3. |
4. Conclusions
This paper reports the first comprehensive results from simulations of EM instabilities triggered by protons with anisotropic temperatures modelled by bi-Kappa distributions. Suprathermal plasma populations, electrons and protons enhance the high-energy (bi-)Kappa tails of the velocity or energy distributions measured in situ in space plasmas. Still, their effect is often ignored, limiting the analysis to the quasi-thermal population in the low-energy (bi-)Maxwellian core. Recent comparative analyses, summarized for instance in Shaaban et al. (2021a) and Lazar et al. (2022), show that suprathermal populations stimulate instabilities generated by temperature anisotropy, such as the EM ion cyclotron (EMIC) and proton firehose (PFH) instabilities. This appears to be a systematic effect, which has already been demonstrated in theory and numerical simulations for electrons.
Here, we have added culminating results to this series of investigations, this time using hybrid simulations that confirm that suprathermal protons indeed stimulate both EMIC and PFH instabilities. The effects are also consistent from a theoretical point of view because the suprathermal protons contribute to an increase in the kinetic energy density and, therefore, to an increase in the beta parameter. For both instabilities, the resulting wave fluctuations can reach significantly enhanced levels of wave energy density at saturation, and the effects of suprathermal protons are most striking when the proton beta parameter is low. Both the EMIC and PFH instabilities are typical of magnetized plasmas, meaning that in a low proton beta regime (i.e., βp ≲ 1 for EMIC), these instabilities respond with larger variations in growth rate and wave energy levels than in the regimes of weakly magnetized plasmas with a high plasma beta (i.e., βp > 1 for EMIC). The enhanced levels of fluctuations obtained in the presence of suprathermal protons, in turn, cause faster and/or deeper relaxation of the temperature anisotropy. Anisotropic protons with bi-Kappa distributions generally show such a fast and deeper relaxation, and it contrasts markedly with the relaxation of the bi-Maxwellian core when the involvement of the suprathermal component is neglected. The PFH instabilities tend to distort the bi-Kappa distributions of protons with the same dumbbell-like deformations previously shown for the bi-Maxwellian distributions. However, these deformations are less prominent for bi-Kappa protons, and the relaxation is more uniform.
At first glance, 1D simulations seem to have a major limitation, but parallel propagating instabilities are the fastest relaxation channels for the chosen regimes. Thus, for protons with anisotropy A > 1 and βp∥ < 5, the parallel EMIC develops with higher growth rates than the oblique modes, including the mirror mode (Gary et al. 1976; Yoon & Seough 2012; Yoon et al. 2023; Shaaban et al. 2018). Although limited to only one set of parameters, a recent result confirms higher EMIC growth rates also in the presence of suprathermal protons (López et al. 2023). Instead, we presented extensive results from analysing different regimes varying the relevant parameters. Moreover, the parallel PFH instability triggered by A < 1 benefits from regimes of extended relevance when their growth rate exceeds that of the oblique modes (Micera et al. 2020; López et al. 2022). The parametric regimes in Table 2 are all favorable to parallel PFH instability, see Figure 3 (left panel) from López et al. (2022). Note that in our case 1, the presence of suprathermal protons shifts from the dominance of oblique PFH to that of parallel PFH instability due to the increase in plasma beta. Restricting our analysis to parallel-propagating instabilities is supported by theory and solar wind observations of proton-scale fluctuations (Woodham et al. 2019), as explained in the introduction.
As we have examined here, these conclusions are valid for multiple regimes with varied parameters, conferring extended relevance not only in space plasmas such as the solar wind and planetary magnetospheres but very likely in other similar astrophysical contexts as well. Moreover, such numerical analyses offer realistic perspectives for modelling the dynamics of non-equilibrium plasmas, in which the suprathermal populations are an essential component intimately connected with the kinetic wave fluctuations. At the same time, these results should motivate further, more detailed investigations of the complete spectra covering the 2D space of the wave vectors to clarify the possible involvement of the other oblique modes under the influence of the suprathermal populations. Future studies could also use improved hybrid simulations, with, for example, particle test methods (Trotta & Burgess 2019), to elucidate, for instance, the potential role of the (enhanced) proton instabilities in the acceleration of electrons from interplanetary shocks, where suprathermal protons are ubiquitous (Lario et al. 2019; Yang et al. 2023).
Acknowledgments
The authors acknowledge support from the Ruhr-University Bochum, the Katholieke Universiteit Leuven, and Qatar University. These results were also obtained in the framework of the projects C16/24/010 (C1 project Internal Funds KU Leuven), G002523N (FWO-Vlaanderen), 4000145223 (SIDC Data Exploitation (SIDEX2), ESA Prodex), Belspo project B2/191/P1/SWiM. Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (CCSS210001). We thank the anonymous reviewer for constructive criticism and suggestions.
References
- Anderson, B. R., Skoug, R. M., Steinberg, J. T., & McComas, D. J. 2012, J. Geophys. Res.: Space Phys., 117, A04107 [NASA ADS] [Google Scholar]
- Astfalk, P., & Jenko, F. 2018, J. Geophys. Res.: Space Phys., 123, 7153 [NASA ADS] [CrossRef] [Google Scholar]
- Bale, S. D., Kasper, J. C., Howes, G. G., et al. 2009, Phys. Rev. Lett., 103, 211101 [NASA ADS] [CrossRef] [Google Scholar]
- Bale, S. D., Horbury, T. S., Velli, M., et al. 2021, ApJ, 923, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Berčič, L., Maksimović, M., Landi, S., & Matteini, L. 2019, MNRAS, 486, 3404 [Google Scholar]
- Boris, J. P. 1970a, Proc. Fourth Conf. Num. Sim. Plasmas, 3 [Google Scholar]
- Boris, J. 1970b, The Acceleration Calculation From a Scalar Potential (Princeton University Plasma Physics Laboratory) [Google Scholar]
- Christon, S. P., Williams, D. J., Mitchell, D. G., Frank, L. A., & Huang, C. Y. 1989, J. Geophys. Res.: Space Phys., 94, 13409 [NASA ADS] [CrossRef] [Google Scholar]
- Christon, S. P., Williams, D. J., Mitchell, D. G., Huang, C. Y., & Frank, L. A. 1991, J. Geophys. Res.: Space Phys., 96, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Collier, M. R., Hamilton, D., Gloeckler, G., Bochsler, P., & Sheldon, R. 1996, Geophys. Res. Lett., 23, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Gratton, F. T., & Farrugia, C. J. 2003, J. Geophys. Res.: Space Phys., 108, 1149 [NASA ADS] [Google Scholar]
- Davidson, R. C., & Ogden, J. M. 1975, Phys. Fluids, 18, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Ďurovcová, T., Šafránková, J., & Němeček, Z. 2021, ApJ, 923, 170 [CrossRef] [Google Scholar]
- Fried, B., & Conte, S. 1961, The Plasma Dispersion Function (New York: Academic Press) [Google Scholar]
- Gary, S. P. 1993, Theory of Space Plasma Microinstabilities (Cambridge University Press) [Google Scholar]
- Gary, S. P., & Saito, S. 2003, J. Geophys. Res.: Space Phys., 108, 1194 [NASA ADS] [Google Scholar]
- Gary, S. P., Montgomery, M. D., Feldman, W. C., & Forslund, D. W. 1976, J. Geophys. Res., 81, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Wang, J., Winske, D., & Fuselier, S. A. 1997, J. Geophys. Res., 102, 27159 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Li, H., O’Rourke, S., & Winske, D. 1998, J. Geophys. Res.: Space Phys., 103, 14567 [NASA ADS] [CrossRef] [Google Scholar]
- Gloeckler, G., Roelof, E. C., Ogilvie, K. W., & Berdichevsky, D. B. 1995, Space Sci. Rev., 72, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, E. J., Shumaker, D. E., & Anderson, D. V. 1989, J. Comput. Phys., 84, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J., Kasper, J. C., Vech, D., et al. 2020, ApJS, 246, 70 [Google Scholar]
- Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 20-1 [CrossRef] [Google Scholar]
- Lacombe, C., Alexandrova, O., Matteini, L., et al. 2014, ApJ, 796, 5 [Google Scholar]
- Lario, D., Berger, L., Decker, R. B., et al. 2019, ApJ, 158, 12 [CrossRef] [Google Scholar]
- Lazar, M., & Fichtner, H. 2021, Kappa Distributions: From Observational Evidences Via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas, Astrophysics and Space Science Library (Springer) https://link.springer.com/book/10.1007/978-3-030-82623-9 [Google Scholar]
- Lazar, M., Schlickeiser, R., & Shukla, P. K. 2008, Phys. Plasmas, 15, 042103 [NASA ADS] [CrossRef] [Google Scholar]
- Lazar, M., Poedts, S., & Fichtner, H. 2015, A&A, 582, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazar, M., Fichtner, H., & Yoon, P. H. 2016, A&A, 589, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazar, M., Pierrard, V., Shaaban, S. M., Fichtner, H., & Poedts, S. 2017, A&A, 602, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazar, M., López, R. A., Shaaban, S. M., Poedts, S., & Fichtner, H. 2019, Astrophys. Space Sci., 364, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Lazar, M., López, R. A., Shaaban, S. M., et al. 2022, Front. Astron. Space Sci., 8, 249 [CrossRef] [Google Scholar]
- Lazar, M., López, R. A., Poedts, S., & Shaaban, S. M. 2023, Phys. Plasmas, 30, 082106 [NASA ADS] [CrossRef] [Google Scholar]
- López, R. A., Lazar, M., Shaaban, S. M., et al. 2019, ApJ, 873, L20 [CrossRef] [Google Scholar]
- López, R. A., Micera, A., Lazar, M., et al. 2022, ApJ, 930, 158 [CrossRef] [Google Scholar]
- López, R. A., Yoon, P. H., Viñas, A. F., & Lazar, M. 2023, ApJ, 954, 191 [CrossRef] [Google Scholar]
- Maksimovic, M., Zouganelis, I., Chaufray, J. Y., et al. 2005, J. Geophys. Res.: Space Phys., 110, A09104 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E. 2006, Liv. Rev. Sol. Phys., 3, 1 [Google Scholar]
- Maruca, B. A., Chasapis, A., Gary, S. P., et al. 2018, ApJ, 866, 25 [Google Scholar]
- Mason, G. M., Ho, G. C., Allen, R. C., et al. 2023, A&A, 673, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteini, L., Landi, S., Hellinger, P., & Velli, M. 2006, J. Geophys. Res.: Space Phys., 111, A10101 [NASA ADS] [CrossRef] [Google Scholar]
- Micera, A., Boella, E., Zhukov, A. N., et al. 2020, ApJ, 893, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Moya, P. S., Lazar, M., & Poedts, S. 2020, Plasma Phys. Control. Fusion, 63, 025011 [Google Scholar]
- Nicolaou, G., Livadiotis, G., Owen, C. J., Verscharen, D., & Wicks, R. T. 2018, ApJ, 864, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Pierrard, V., & Lazar, M. 2010, Sol. Phys., 267, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Samsonov, A. A., Alexandrova, O., Lacombe, C., Maksimovic, M., & Gary, S. P. 2007, Ann. Geophys., 25, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin: Springer) [CrossRef] [Google Scholar]
- Seough, J., & Yoon, P. H. 2012, J. Geophys. Res.: Space Phys., 117, A08101 [NASA ADS] [CrossRef] [Google Scholar]
- Seough, J., Yoon, P. H., & Hwang, J. 2014, Phys. Plasmas, 21, 062118 [NASA ADS] [CrossRef] [Google Scholar]
- Seough, J., Yoon, P. H., & Hwang, J. 2015, Phys. Plasmas, 22, 012303 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S. M., Lazar, M., Poedts, S., & Elhanbaly, A. 2017, Ap&SS, 362, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S. M., Lazar, M., Astfalk, P., & Poedts, S. 2018, J. Geophys. Res.: Space Phys., 123, 1754 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S. M., Lazar, M., Yoon, P. H., & Poedts, S. 2019a, A&A, 627, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaaban, S. M., Lazar, M., Yoon, P. H., & Poedts, S. 2019b, ApJ, 871, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S. M., Lazar, M., López, R. A., Fichtner, H., & Poedts, S. 2019c, MNRAS, 483, 5642 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S. M., Lazar, M., López, R. A., Yoon, P. H., & Poedts, S. 2021a, Advanced Interpretation of Waves and Instabilities in Space Plasmas (Cham: Springer International Publishing) [Google Scholar]
- Shaaban, S., Lazar, M., & Schlickeiser, R. 2021b, Phys. Plasmas, 28, 022103 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S., Lazar, M., Wimmer-Schweingruber, R., & Fichtner, H. 2021c, ApJ, 918, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Shaaban, S. M., Lazar, M., López, R. A., & Wimmer-Schweingruber, R. F. 2021d, MNRAS, 503, 3134 [NASA ADS] [CrossRef] [Google Scholar]
- Shoji, M., Omura, Y., Tsurutani, B. T., Verkhoglyadova, O. P., & Lembege, B. 2009, J. Geophys. Res.: Space Phys., 114, A10203 [NASA ADS] [CrossRef] [Google Scholar]
- Štverák, Š., Trávníček, P., Maksimovic, M., et al. 2008, J. Geophys. Res.: Space Phys., 113, A03103 [Google Scholar]
- Thorne, R. M., & Summers, D. 1991, J. Geophys. Res., 96, 217 [CrossRef] [Google Scholar]
- Trotta, D., & Burgess, D. 2019, MNRAS, 482, 1154 [NASA ADS] [CrossRef] [Google Scholar]
- Viñas, A. F., Moya, P. S., Navarro, R. E., et al. 2015, J. Geophys. Res.: Space Phys., 120, 3307 [CrossRef] [Google Scholar]
- Wang, L., Yang, L., He, J., et al. 2015, ApJ, 803, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Wicks, R. T., Matteini, L., Horbury, T. S., Hellinger, P., & Roberts, D. A. 2013, AIP Conf. Ser., 1539, 303 [NASA ADS] [Google Scholar]
- Wilson, L. B., Chen, L.-J., Wang, S., et al. 2019, ApJS, 243, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Wimmer-Schweingruber, R. F., Janitzek, N. P., Pacheco, D., et al. 2021, A&A, 656, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winske, D., & Omidi, N. 1993, Computer Space Plasma Physics: Simulation Techniques and Software (Tokyo: Terra Scientific Publishing Company) [Google Scholar]
- Woodham, L. D., Wicks, R. T., Verscharen, D., et al. 2019, ApJ, 884, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, L., Heidrich-Meisner, V., Berger, L., et al. 2023, A&A, 673, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, P. H. 2017, Rev. Mod. Plasma Phys., 1, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H., & Seough, J. 2012, J. Geophys. Res.: Space Phys., 117, A08102 [NASA ADS] [Google Scholar]
- Yoon, P. H., López, R. A., & Zaheer, S. 2023, ApJ, 950, 131 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameterization adopted in the hybrid simulations of the EMIC instability, in terms of initial values (τ = 0) for four distinct runs.
Parameterization adopted in the hybrid simulations of the PFH instability, in terms of initial values (τ = 0) for four distinct runs.
All Figures
 |
Fig. 1. EMIC unstable solutions for bi-Kappa protons (red) and the corresponding bi-Maxwellian core (blue) for all four cases in Table 1 with initial proton parameters also indicated in the panels. Comparison of growth rates from linear theory (left panels) and temporal evolution from simulations for the wave energy density (middle panels) and the temperature anisotropy (right panels). |
| In the text | |
 |
Fig. 2. Instantaneous relative difference of the proton anisotropy, ΔAp(τ) (in %, see definition in the text), induced by the presence of suprathermal protons for all EMIC runs in Fig. 1. |
| In the text | |
 |
Fig. 3. VDs from the simulations of EMIC instability for cases 1 and 2 from Fig. 1, computed for four time steps, and for both bi-Maxwellian (κ → ∞) and bi-Kappa (κ = 3) distributed protons, as indicated in the panels. |
| In the text | |
 |
Fig. 4. PFH unstable solutions for bi-Kappa protons (red) and the corresponding bi-Maxwellian core (blue) for all three cases in Table 2 with initial proton parameters also indicated in the panels. Comparison of growth rates from linear theory (left panels) and temporal evolution from simulations for the wave energy density (middle panels) and the temperature anisotropy (right panels). |
| In the text | |
 |
Fig. 5. Instantaneous relative difference of the proton anisotropy, ΔAp(τ) (in %, see definition in the text), induced by the presence of suprathermal protons for all PFH runs in Fig. 4. |
| In the text | |
 |
Fig. 6. VDs from the simulations of PFH instability for cases 1 and 3 from Fig. 4, computed for four time steps, and for both bi-Maxwellian (κ → ∞) and bi-Kappa (κ = 3) distributed protons, as indicated in the panels. |
| In the text | |
 |
Fig. 7. Magnetic fluctuations from simulations, for EMIC cases 1 and 2 (upper panels) and PFH instability cases 1 and 3 (lower panels), resemble linear dispersion (dashed lines) in the ω − k space and are enhanced in the presence of suprathermals (right panels). The colour scale indicates the normalized magnetic wave energy density. |
| In the text | |
 |
Fig. 8. Time variation of magnetic fluctuation spectra for two EMIC modes corresponding to distinct wave numbers (see the legend), in cases 1 and 2. Computed as the spatial Fourier transform, |FFTx{δ(Bx + iBy)/B0}|2. |
| In the text | |
 |
Fig. 9. Time variation of magnetic fluctuation spectra for two PFH modes corresponding to distinct wave numbers (see the legend), in cases 1 and 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} f_{\kappa ,{p}}\left({ v}_{\parallel }, { v}_{\perp }\right) = \frac{1}{\pi ^{3/2} \theta _{{p} \parallel } \theta _{{p} \perp }^{2}}&\, \frac{\Gamma \left( \kappa +1\right)}{\kappa ^{3/2}\Gamma \left( \kappa -1/2\right)}\nonumber \\&\times \left[ 1+\frac{{ v}_{\parallel }^{2}}{\kappa \theta _{{p} \parallel }^{2}} +\frac{{ v}_{\perp }^{2}}{\kappa \theta _{{p} \perp }^{2}}\right] ^{-\kappa -1}. \end{aligned} $$](/articles/aa/full_html/2024/11/aa48780-23/aa48780-23-eq1.gif)
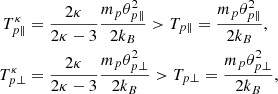
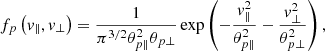
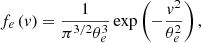
![$$ \begin{aligned} \tilde{k}^2&= \mu \left[A_{e}-1+\frac{A_{e}~\tilde{\omega } \pm \left(A_{e}-1\right)\mu }{\tilde{k} \sqrt{\mu \beta _{{e} \parallel }}} Z_{M, {e}}\left(\frac{\tilde{\omega }\pm \mu }{\tilde{k} \sqrt{\mu \beta _{{e} \parallel }}}\right)\right] \nonumber \\&\quad +A_{p}-1+\frac{A_{p}~\tilde{\omega } \mp \left(A_{p}-1\right)}{\tilde{k} \sqrt{\beta _{{p} \parallel }}}Z_{\kappa ,{p}}\left(\frac{\tilde{\omega }\mp 1}{\tilde{k} \sqrt{\beta _{{p} \parallel }}}\right). \end{aligned} $$](/articles/aa/full_html/2024/11/aa48780-23/aa48780-23-eq5.gif)