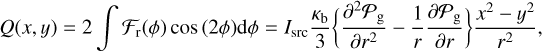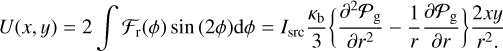| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 17 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202245744 | |
| Published online | 31 March 2023 | |
Polarisation leakage due to errors in track reconstruction in gas pixel detectors
1
INAF – Osservatorio Astrofisico di Arcetri,
Largo Enrico Fermi 5,
50125
Firenze, Italy
e-mail: niccolo.bucciantini@inaf.it
2
Dipartimento di Fisica e Astronomia, Università degli Studi di Firenze,
via G. Sansone 1,
Sesto F.no (FI), Italy
3
INFN – Sezione di Firenze,
via G. Sansone 1,
Sesto F.no (FI), Italy
4
Department of Physics and Kavli Institute for Particle Astrophysics and Cosmology, Stanford University,
452 Lomita Mall,
Stanford, CA
94305, USA
5
INFN – Sezione di Pisa,
Largo Bruno Pontecorvo 3,
56127
Pisa (PI), Italy
6
Dipartimento di Fisica, Università di Pisa,
Largo Bruno Pontecorvo 3,
56127
Pisa (PI), Italy
7
University of Maryland, Baltimore County,
Baltimore,
620 W. Lexington St.,
MD 21250, USA
8
NASA Goddard Space Flight Center,
8800 Greenbelt Rd.,
Greenbelt, MD
20771, USA
9
Center for Research and Exploration in Space Science and Technology, NASA/GSFC,
8800 Greenbelt Rd.,
Greenbelt, MD
20771, USA
10
NASA Marshall Space Flight Center,
4600 Rideout Rd.,
Huntsville, AL
35812, USA
Received:
21
December
2022
Accepted:
1
February
2023
X-ray polarimetry based on gas pixel detectors (GPDs) has reached a high level of maturity thanks to the Imaging X-ray Polarimeter Explorer (IXPE) providing the first-ever spatially resolved polarimetric measurements. However, as this a new technique, a few unexpected effects have emerged in the course of in-flight operations. In particular, it was almost immediately found that, the unpolarized calibration sources on-board were showing radially polarized halos. The origin of these features was recognized in a correlation between the error in reconstructing the absorption point of the X-ray photon and the direction of its electric field vector. Here, we present and discuss this effect in detail, showing that it is possible to provide a simple and robust mathematical formalism to handle it. We further show its role and relevance for the recent IXPE measures as well as for the use of GPD-based techniques in general. We also illustrate how to model it in the context of studying extended sources.
Key words: instrumentation: detectors / instrumentation: polarimeters / techniques: polarimetric / X-rays: general / polarization
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Since the launch of the first X-ray satellites in the 1960s (Kalemci 2018), X-ray astronomy has provided a unique window to investigate high-energy astrophysical environments, such as pulsars (Walter & Ferrigno 2017), magnetars (Mereghetti et al. 2015), pulsar wind nebulae (Kargaltsev & Pavlov 2008), supernova remnants (Vink 2012), black holes (Singh 2013; Bachetti 2016), clusters (Sarazin 1986), and accretion disks (Inoue 2022). The X-ray emission in many of those systems is typically a mixture of thermal and non-thermal components, with the latter essentially due to synchrotron radiation from accelerated particles (pairs) in the strong local magnetic field. Pulsar wind nebulae and supernova remnants are resolved sources that exhibit such emission. One of the key features of synchrotron emission is its high level of polarization (Bucciantini 2018). Polarization might also arise in thermal environments due to plasma propagation effect and in strongly magnetized systems, such as magnetars, due to quantum electrodynamics (Turolla et al. 2015).
Unfortunately, while X-ray imaging and spectral instruments have been operating for a long time, this is not the case for polarimetry. Until very recently, the only X-ray source where X-ray polarimetric measurements have been firmly established was the Crab Nebula (Weisskopf et al. 1978). With the recent launch of the Imaging X-ray Polarimeter Explorer (IXPE, Weisskopf et al. 2022), this gap has finally been filled, offering us a unique opportunity to obtain space-resolved polarimetric observations of several extended Galactic sources, along with some extra-Galactic objects as well.
The polarization sensitive gas pixel detectors (GPDs) on board IXPE (and previously used by PolarLight, Feng et al. 2019) exploit the properties of the photoelectric effect (Costa et al. 2001): the photon, focused by a mirror system and collimated onto the sensitive detector area, converts into a low-Z gas of pure dimethyl ether and emits a photoelectron (PE) that produces an ionization track. This process is quite sensitive to photon polarization given that the initial direction of emitted PE is preferentially in the direction of the photon electric field (polarization vector, EVPA) and has large cross-sections in the low energy range of [2–10] keV, where many of the most interesting astrophysical X-ray sources shine.
The key to deriving the polarization of the X-ray photon is to reconstruct the initial direction of the PE track. This is, however, prone to lead to spurious effects whenever the photo-electron tracks are not perfectly reconstructed. In particular, failure to reconstruct the exact conversion point (the absorption site) of the incoming photon can create false polarization patterns that are particularly prominent for sources characterized by sharp edges. This first feature emerged clearly, soon after the launch of the IXPE satellite, as a radial polarization pattern seen around bright compact unpolarized (on-board) calibration sources, especially in the low intensity wings of the sources themselves, and later found also in unpolarized sky point sources.
In this work, we discuss this phenomenon and present a mathematical formalization to show that – analogously to what is done in radio astronomy, where the polarization leakage is mainly due to well-known non-ideality of the antennas (Hales 2017) – it is possible to model it in terms of Stokes-dependent point spread functions (PSFs), which can be related to the Mueller Matrix elements (Tinbergen 1996) that provide the full imaging response of an instrument to polarized radiation.
In Sect. 2, we review the working of a GPD, and how tracks are reconstructed. In Sect. 3, we present an heuristic explanation of the origin of polarization leakage. In Sect. 4, we introduce a mathematical formalization of the effects and verify the limits of our formalism in predicting these effects, which we later compare with either true IXPE data or Monte Carlo simulations of the GPD in Sect. 5. In Sect. 6, we illustrate how the analysis can be framed in terms of Mueller matrix elements and we offer some applications. We present our conclusions in Sect. 7.
 |
Fig. 1 Example of a photoelectron track generated by a 7 keV photon (left panel) and a 3.5 keV photon (right panel). The dashed lines and the black points represent respectively the simulated PE emission direction and X-ray impact point. The simulated photoelectron path is reported as well. Ionization charges created along the photoelectron path are reported as small cyan dots. The color scale, going from white to dark red, represents the amount of charge collected in each pixel. |
2 Track reconstructions in gas pixel detectors
X-ray polarimetry exploiting the high dependence of the photoelectric effect on the polarization of the incident radiation can be substantially more efficient than previously adopted techniques – as seen in Bragg reflection and Thomson scattering, which suffer from limitations (Soffitta et al. 2003) coming from the energy band width and lack imaging capabilities or offer a low effective area. An example of detector design based on this property has been proposed and developed in early 2000 (Costa et al. 2001) and reached a mature state with the selection of IXPE (Weisskopf et al. 2022). This instrument combines good imaging capabilities and unprecedented polarization sensitivities exploiting a GPD (Bellazzini et al. 2006) design.
An X-ray photon is absorbed in the gas gap of the GPD and a photoelectron is ejected in the direction (θ, ϕ), which preferably lies on the oscillation plane of the electric field of the incoming X-ray (namely the polarization direction). Here, θ is the angle between the incident X-ray direction and the PE emission direction, while ϕ is the azimuthal PE emission direction (Sabbatucci & Salvat 2016). The photoelectron interacts with the gas atoms through ionizing collisions, losing energy and changing direction due to multiple scattering, with the energy losses that increase at each collision1. Such interactions generate a pattern of ions-e− that mark the path followed by the PE before it loses all its energy and is reabsorbed in the gas. Such a pattern, typically a few hundred micron across, is called a “track.” The ions-e− charges are amplified by a gas electron multiplier (GEM) and collected on a plane of hexagonal pixels in an honeycomb configuration. A track, therefore, is a pixelated image containing useful information about the PE, and, as a consequence, about the X-ray that generated that same PE. Two examples of a PE track image for two different X-ray energies are reported in Fig. 1.
The event reconstruction consists of an estimation of the properties of the incoming X-ray photon we are interested in, from the PE track image. In particular, the total collected charge is proportional to the energy of the X-ray, the starting point of the track gives the impact point of the photon and the azimuthal angle ϕ of the PE initial emission direction (before it gets deviated by multiple interactions in the gas) carries the imprint of the X-ray polarization direction. As shown in Fig. 1, the track morphology depends on the energy of the absorbed X-ray; in general, it becomes more challenging to reconstruct the initial PE direction for low-energy X-rays due to the nearly circular shape of the track.
The event reconstruction is typically done analytically, processing the track image to estimate both the impact point of the X-ray and the PE initial direction. A detailed description of the analytic algorithm used in IXPE event reconstruction can be found in Bellazzini et al. (2002). In short, after a zero suppression and clustering stage to identify and isolate the main track, the reconstruction algorithm proceeds with a moment analysis of the two-dimensional (2D) charge distribution. The whole procedure is iterative and, after the initial determination of the barycenter and the principal axis of the track, the moment analysis is run again, this time focusing on the head of the track that supposedly contains the impact point. Most of the energy is indeed released at the end of the photoelectron track (Bragg peak) and thus the projection of the charge distribution along the principal axis allows us to distinguish the head and the tail of track. As an alternative to the analytic algorithm, machine learning techniques can be used. In particular, convolutional neural networks (CNNs) have been explored and tested on simulated data, showing promising results (Kitaguchi et al. 2019; Moriakov et al. 2020; Peirson et al. 2021; Peirson & Romani 2021).
In Fig. 2, we illustrate a typical example of mistakes that can take place in the reconstruction of the property of a track. In this case, the absorption point of the incoming X-ray photon has been reconstructed at the end of the track, close to the Bragg peak, and not at its beginning (due to the intrinsically 3D nature of the PE emission process, some of the ambiguity in the inferred absorption point could be due to initial photo-electron coming out in a more vertical direction). This often occurs when an Auger electron deposits substantial energy near the conversion point. In fact, the error in the conversion point is generally largest along the major axis of the track, which correlates with the EVPA. As we discuss in the next section, it is this kind of error that leads to the polarization leakage, which was first observed in IXPE calibration data. We also note that the reconstructed polarization plane does not correspond to the true direction. This is due in part to the fact that the PE is only generally aligned with the photon electric field and this is in part due to errors in properly reconstructing the track shape. The fact that the reconstructed polarization plane matches the true polarization plane only on average implies that the efficiency of the polarized response of a GPD based detector, the so called modulation factor, can be substantially smaller than unity.
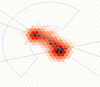 |
Fig. 2 Example of a wrongly reconstructed absorption point. The black dot is the real absorption point, the green one is the reconstructed absorption point and the blue one is the barycenter. Note: the reconstructed polarization plane (blues dashed line) differs from the true one (black dashed line) Colors have the same meaning as in Fig. 1. |
3 Heuristic explanation
In order to briefly explain how reconstruction errors in the absorption point lead to polarization leakage, we consider a source characterized by a sharp edge (see Fig. 3). First, we recall that the GPD merely measures the charge collected along the full track: both the impact point and the polarization direction are reconstructed. In a source with a sharp edge, as in Fig. 3, there will be tracks that extend beyond the edge and for these, there will be a chance of reconstructing the impact point outside the true source boundary. This not only will assign a photon to a region where there should be none, thus blurring the edge, but will systematically assign to those photons a polarization direction normal to the boundary. This will cause an excess of orthogonally polarized photon outside the edge and, consequently, an excess of tangentially polarized photons inside it. We note that this effect does not change the inferred polarization plane of the photon overall, given that the impact point is typically misplaced along the photo-electron track (the principal axis of the track, which is correlated with the incoming photon polarization plane).
Even if a source does not have such a sharp boundary, but a simple gradient of the flux instead, which changes significantly along the scale length of the typical extent of the tracks, there will be a polarization gradient. The result is a polarized “halo” around any source, even if there is no intrinsic polarization. For point sources, these radial polarization gradients average out to no net polarization when integrated around the source at all azimuths. However, for extended sources, or faint sources near bright sources, these induced polarization structures can corrupt the true polarization signal.
We note that this effect is intrinsic of any polarization measure based on track reconstruction, as long as there is a correlation between the offset of the absorption point from its true position and the inferred polarization direction. This is inevitable given that any position uncertainty will be largest along the long axis of the track. Since this axis (especially for well-measured higher energy photons) is along the estimated EVPA, there is naturally a strong correlation between the position offset direction and the inferred polarization.
By looking at Fig. 3, it is clear that for simple sources, characterized by edges, it might be possible to discriminate between a true intrinsic polarization and a polarized feature due to polarization leakage. For a truly polarized signal, the chance of a PE track having an azimuthal angle ϕ is the same as having an azimuthal angle of ϕ ± π (due to the very nature of the PE emission) and the distribution function of the azimuthal angles of the tracks will be dominated by a m = 2 mode. In a polarized halo due to polarization leakage all tracks will tend to point toward the edge (anti-aligned to intensity gradients) and the distribution function of the azimuthal angles of the tracks will be dominated by a m = 1 mode. However, for real sources, characterized by complex intensity patterns, such a simple characterization might not apply. Unfortunately this information is completely lost when transforming from the PE azimuthal angle ϕ to the photon Stokes parameters given that Q(ϕ) = Q(ϕ ± π) – and the same for U. This is an issue when working with IXPE level 2 files given that they only provide the event Stokes parameters (IXPE processing corrects instrument effects in Q, U space; it is not easy to correct the inferred electron track provided in the level 1 files) and not the original PE angle.
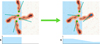 |
Fig. 3 Schematic picture of polarization leakagefoг an unpolarized source with a sharp edge. The light-blue region represents the portion of the GPD corresponding to the source. Four events, close to the edge of the source image, are represented with their respective PE tracks. The green dots represent the true absorption points and the blue segments are the reconstructed polarization planes of the original photons. On the left, all absorption points are correctly reconstructed in their true positions: all events are inside the edge and none remain outside (bottom panel represents the event count); there are as many PEs with tracks tangential as orthogonal to the edge so no net polarization is assigned to the source. On the right the absorption point of the track extending outside the source edge has been wrongly reconstructed at the end of the track (blue dot): there are less events reconstructed inside the edge and more outside (bottom panel represents the event count); there are more PEs reconstructed with tracks tangential than orthogonal to the edge inside the source region, while there are PE events with tracks orthogonal to the edge outside. This leads to a blurring of the edge and to a polarization pattern tangential inside the edge and orthogonal outside. |
4 Formalization
In principle, the offset of the reconstructed absorption point from the true absorption point will feature components both along and transverse to the reconstructed polarization plane. In order to simplify the analysis, we assume that the offset is only along the reconstructed polarization plane (purely 1D). A more general treatment can be found in Appendix A, where a generic correlation is assumed. Interestingly, as the comparison with the more general results shows, our simplified model captures very well the properties of the polarization leakage to the point that it provides reliable estimates of true data.
4.1 1D displacement
We start with the assumption that a photon, from a point source, located at Psrc (see Fig. 4), interacts with the detector at a point Pi on the detector plane and produces a photo-electron track in the direction, n. The photo-electron direction represents the measured polarization plane of the photon. We then consider a reference frame centered on the position of the point source and with the x-axis aligned with the direction n. In this reference frame, the interaction point (the absorption or impact point) will be located at Pi = (xi, yi;). The chance of finding a photon at a location (x, y) is the point spread function (PSF) of the instrument Pg(x, y), where we use the subscript “g” to imply that this is the “geometrical PSF,” namely, the PSF of a light ray. It might happen that due to uncertainties in the reconstruction of the track shape, the interaction point of the photon – instead of being reconstructed in its true position Pi– is reconstructed at a position displaced along n. In our reference frame, the reconstructed impact point will be located at Pr = (xi + δx, yi). We set 𝒫f (δx) as the probability distribution function of the absorption point displacement due to reconstruction errors, which can be safely assumed to be independent of the impact position. It is also safe to assume that 𝒫f (δx) = 𝒫f(−δx), namely, that there is no preference in the sign of the displacement due to the very nature of the photo-electron emission process.
Then one can define a total PSF arising from the combined geometrical and polarization-shifting offsets. The total chance of reconstructing a photon impact point at a location (x, y) will be:
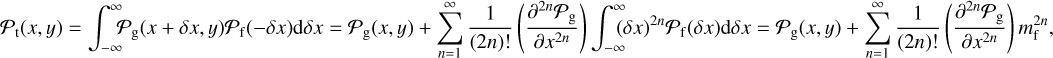 (1)
(1)
where 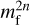 is the central moment of order 2n of 𝒫f(δx), whereby
is the central moment of order 2n of 𝒫f(δx), whereby 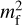 is, by definition, the central variance of the distribution
is, by definition, the central variance of the distribution 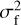 . For examples related to the case in which 𝒫f (δx) is a Gaussian with a variance of
. For examples related to the case in which 𝒫f (δx) is a Gaussian with a variance of 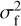 , then we have:
, then we have:
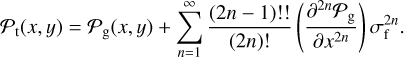 (2)
(2)
If one further assumes that the geometrical PSF is also a Gaussian with the variance, σg, then we find:
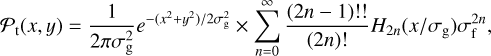 (3)
(3)
where H2n(x) is the Hermite polynomial of order 2n.
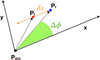 |
Fig. 4 Schematic representation of the geometry involved in the absorption point displacement due to reconstruction errors. Here, Psrc is the location of the point source whence the photon come from; Pi is the true impact (absorption) point of the photon, displaced due to the mirror PSF, while the orange double-headed arrow represents the photo-electron direction, n; Pr is the reconstructed impact point displaced by an amount δx along the photo-electron direction plane. Then x−y are coordinate axes chosen such that x is parallel to the photo-electron direction plane, while ∆ϕ is the polar angle of the reconstructed impact point in the same reference frame, describing the azimuthal distribution of photons due to the mirror PSF. |
4.2 Linearized theory
In the limit of σf ≪ 𝒫g/|∇𝒫g|, we can approximate:
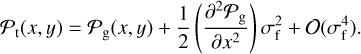 (4)
(4)
If the geometrical-PSF is radially symmetric 𝒫g(x, y) = 𝒫g(r) with 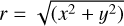 , then we have:
, then we have:
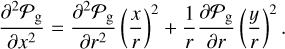 (5)
(5)
Introducing the relative angle, ∆ϕ, between the vector-position of the measured impact point, Pr, and the photo-electron direction, n, (which describes the azimuthal spread of photons due to the mirror PSF and, as such, is totally uncorrelated with the displacement due to reconstruction error), we have:
![$ \matrix{ {{{{\partial ^2}{P_g}} \over {\partial {x^2}}} = {{{\partial ^2}{P_g}} \over {\partial {r^2}}}{{\cos }^2}\left( {\Delta \phi } \right) + {1 \over r}{{\partial {P_g}} \over {\partial r}}{\sin}^2 \left( {\Delta \phi } \right) = {{{\partial ^2}{P_g}} \over {\partial {r^2}}}{{1 + \cos \left( {2\Delta \phi } \right)} \over 2} + {1 \over r}{{\partial {P_g}} \over {\partial r}}{{1 - \cos \left( {2\Delta \phi } \right)} \over 2}} \cr { = {1 \over 2}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right] + {1 \over 2}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]\cos \left( {2\Delta \phi } \right),} \cr } $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq11.png) (6)
(6)
where x = r cos (∆ϕ) and y = r sin (∆ϕ). The effect of misplacing the absorption point is twofold: on the one hand, it modifies the radially symmetric part of the PSF; on the other, it adds a modulation along the photo-electron polarization plane. The total PSF is now a function also of the polarization properties of the photon being considered.
4.2.1 Unpolarized sources
Let us now consider an unpolarized point sources. The chance that a photon has a measured impact point at location (x, y) is:
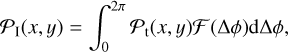 (8)
(8)
where ℱ(∆ϕ) is the photo-electron direction distribution function of the photons coming from the source, that is, the chance that a photon from the point sources has a polarization plane at an angle ∆ϕ (in the range [0,2π]) with respect to the vector position defined by (x, y). For an unpolarized source ℱ(∆ϕ) = 1/2π, and we obtain:
![$ {P_{\rm{I}}}\left( {x,y} \right) = {P_{\rm{I}}}\left( r \right) = {P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right] + 𝒪 \left( {\sigma _{\rm{f}}^4} \right), $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq14.png) (9)
(9)
which represents the PSF of the intensity field of an unpolarized point source. An unpolarized point source with intensity Isrc, will give, to first order in 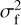 , an image with an intensity of:
, an image with an intensity of:
![$ I\left( {x,y} \right) = {I_{{\rm{src}}}}\left\{ {{P_g}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]} \right\}, $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq16.png) (10)
(10)
showing that this effect leads to an additional blurring of the image.
We can also take a look at the Stokes parameters, Q and U. This, however, requires us to choose an absolute reference frame (Q and U are always defined with respect to an absolute frame). We set x = r cos (ϕı) and y = r sin (ϕı), such that ∆ϕ = ϕı − ϕ where ϕ is the photo-electron angle measured in the same absolute frame. The value of the Stokes parameters at a point (x, y) can then be computed according to:
 (11)
(11)
where 𝒫Q and 𝒫U can be thought of as the PSF for the Stokes parameters, thus generalizing the definition of PSF that typically refers solely to the intensity.
We find to an accuracy of 𝒪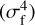 the following:
the following:
![$ \matrix{ {{P_{\rm{Q}}}\left( {x,y} \right) = 2\int_0^{2\pi } {{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]} \cos \left( {2\phi } \right)\cos \left( {2\left( {{\phi _1} - \phi } \right)} \right){1 \over {2\pi }}{\rm{d}}\phi {\rm{ = }}{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]\cos \left( {2{\phi _1}} \right)} \cr { = {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]{{{x^2} - {y^2}} \over {{r^2}}},} \cr } $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq19.png) (12)
(12)
which is exactly what is expected for a pattern of radial and/or tangential polarization. In particular, we would expect a radial versus tangential polarization, depending of the sign of the term in square brackets.
4.2.2 Polarized sources
What we investigated in the previous section was the effect the displacement of the absorption point due to reconstruction errors, on the Intensity distribution and the Stokes U and Q distributions, for an unpolarized point source. In a similar fashion one can repeat the computation for a polarized point source.
For polarized sources, it is more convenient to always use an absolute reference frame. As before, we took an absolute reference frame where x = r cos (ϕı) and y = r sin (ϕı), and ∆ϕ = ϕı − ϕ where ϕ is the photo-electron angle measured in the same absolute frame. A polarized source will have a photo-electron distribution given by:
![$ {{{\cal F}\left( \phi \right) = \left[ {1 + {a_{{\rm{src}}}}\cos \left( {2\left( {\phi - {\phi _{\rm{o}}}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{{\cal F}\left( \phi \right) = \left[ {1 + {a_{{\rm{src}}}}\cos \left( {2\left( {\phi - {\phi _{\rm{o}}}} \right)} \right)} \right]} {2\pi .}}} \right. \kern-\nulldelimiterspace} {2\pi .}} $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq21.png) (14)
(14)
The Stokes parameters of the source are defined as:
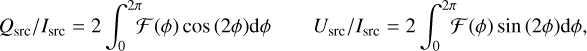 (15)
(15)
which provides the following relation between the amplitude of the modulation, asrc, and the Stokes parameters: 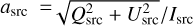 , with Qsrc/Isrc = asrc cos (2ϕo), and Usrc/Isrc = asrc sin (2ϕo).
, with Qsrc/Isrc = asrc cos (2ϕo), and Usrc/Isrc = asrc sin (2ϕo).
Then we find, to an accuracy of 𝒪 :
:
![$ {P_{\rm{I}}}\left( {x,y} \right) = {P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right] + \int_0^{2\pi } {{a_{{\rm{src}}}}} {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]\,\cos \left( {2\left( {{\phi _1} - \phi } \right)} \right){{\cos \,\left( {2\left( {\phi - {\phi _{\rm{o}}}} \right)} \right)} \over {2\pi }}{\rm{d}}\phi , $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq25.png) (16)
(16)
![$ = {P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right] + {{{a_{{\rm{src}}}}} \over 2}{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]\,\cos \left( {2\left( {{\phi _1} - {\phi _{\rm{o}}}} \right)} \right), $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq26.png) (17)
(17)
which, in terms of the source Stokes parameters, is expressed as:
![$ {P_{\rm{I}}}\left( {x,y} \right) = {P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right] + {{\sigma _{\rm{f}}^2} \over 8}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]{{\left[ {{Q_{{\rm{src}}}}\cos \left( {2{\phi _1}} \right) + {U_{{\rm{src}}}}\sin \left( {2{\phi _1}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{Q_{{\rm{src}}}}\cos \left( {2{\phi _1}} \right) + {U_{{\rm{src}}}}\sin \left( {2{\phi _1}} \right)} \right]} {{I_{{\rm{src}}}}}}} \right. \kern-\nulldelimiterspace} {{I_{{\rm{src}}}}}}. $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq28.png) (19)
(19)
Now, we have sin (2ϕ1) = 2xy/r2 while cos (2ϕ1) = x2/r2 − y2/r2, which finally allows us to write:
![$ {P_{\rm{I}}}\left( {x,y} \right) = {P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right] + {{\sigma _{\rm{f}}^2} \over 8}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]\left[ {{{{Q_{{\rm{src}}}}} \over {{I_{{\rm{src}}}}}}{{{x^2} - {y^2}} \over {{r^2}}} + {{{U_{{\rm{src}}}}} \over {{I_{{\rm{src}}}}}}{{2xy} \over {{r^2}}}} \right], $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq29.png) (20)
(20)
which shows that for polarized sources, the PSF is elongated along the direction of the polarization. In general, the PSF is characterized by three contributions: the leading geometrical symmetric PSF, a symmetric term due to unpolarized radiation, and an elongated term associated with the polarized component.
Looking at the Stokes parameters Q and U and recalling that:
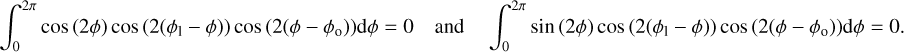 (21)
(21)
we can easily show that for a point source with non-zero Qsrc and Usrc, we have the following:
![$ {P_{\rm{Q}}}\left( {x,y} \right) = {{{Q_{{\rm{src}}}}} \over {{I_{{\rm{src}}}}}}\left\{ {{P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]} \right\} + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]{{{x^2} - {y^2}} \over {{r^2}}}, $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq31.png) (22)
(22)
![$ {P_{\rm{U}}}\left( {x,y} \right) = {{{U_{{\rm{src}}}}} \over {{I_{{\rm{src}}}}}}\left\{ {{P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]} \right\} + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]{{2xy} \over {{r^2}}}. $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq32.png) (23)
(23)
4.2.3 Images of point and extended sources
The effect of polarization-shifting can be formalized introducing different PSFs for each Stokes parameter, Isrc, Qsrc, and Usrc, of a point source located at the coordinates origin, according to the following rules, to first order in the variance, 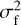 , of the displacement of the absorption point due to reconstruction errors.
, of the displacement of the absorption point due to reconstruction errors.
Its image will display an intensity given by:
![$ I\left( {x,y} \right) = {I_{{\rm{src}}}}\left\{ {{P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]} \right\} + {{\sigma _{\rm{f}}^2} \over 8}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]\left[ {{Q_{{\rm{src}}}}{{{x^2} - {y^2}} \over {{r^2}}} + {U_{{\rm{src}}}}{{2xy} \over {{r^2}}}} \right], $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq35.png) (24)
(24)
and Stokes Q-U maps according to:
![$ Q\left( {x,y} \right) = {Q_{{\rm{src}}}}\left\{ {{P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]} \right\} + {I_{{\rm{src}}}}{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]{{{x^2} - {y^2}} \over {{r^2}}}, $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq36.png) (25)
(25)
![$ U\left( {x,y} \right) = {U_{{\rm{src}}}}\left\{ {{P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]} \right\} + {I_{{\rm{src}}}}{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]{{2xy} \over {{r^2}}}. $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq37.png) (26)
(26)
The fact that different Stokes parameters have different PSFs is akin to what happens in chromatic aberration, where radiations at different wavelengths have different PSFs. For this reason, this phenomena can be thought of as “Stokes chromatism.” The fact that it is manifested in calibration as an excess radial polarization is just a consequence of the geometry of the source and of the profile of the geometrical PSF.
As an example of the possible polarization patterns that this effect can produce, in Fig. 5 we show the results in the case of a uniform disk and a uniform ring adopting for simplicity as geometrical PSF the Gaussian-King model given by Fabiani et al. (2014) at 2.95 keV.
 |
Fig. 5 Intensity (left), Stokes Q (center) and U (right) maps, for a uniform unpolarized disk of unitary surface brightness and radius equal to 15 arcses (upper panel) assuming for the geometrical PSF the one given by Fabiani et al. (2014) at 2.95 keV, and taking σf = 1 arcsec (recall that Q and U scales as |
4.2.4 Limits of the linearized approach
The validity of the linearized approach is limited by two conditions: σf ≪ 𝒫g/|∇𝒫g| and σf must be small enough to allow linearization in transforming from Cartesian to polar coordinartes (see Eqs. (4)–(5)). Both conditions are likely to fail first in the origin, where the geometrical PSF has a sharp peak. Indeed, any centrally peaked geometrical PSF can be expressed as:
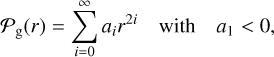 (27)
(27)
which means that the correction to the PSF, in the very center due to the displacement of the absorption point at the linear order is 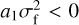 . Obviously, for
. Obviously, for 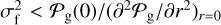 , the resulting total PSF 𝒫I(0) becomes negative in the origin. But even at smaller values of σf, the linear correction can be such that the resulting total PSF displays a minimum in the origin, which would never happen in a full convolution process. In general, we expect that as σf increases, the error associated with the linear approach will also progressively increase, mainly in the central region at r < a few σf. The exact threshold for the validity of the linear approach will depend on the shape of the geometrical PSF 𝒫g(r), as well as on the distribution function describing the chance that the reconstructed absorption point is misplaced.
, the resulting total PSF 𝒫I(0) becomes negative in the origin. But even at smaller values of σf, the linear correction can be such that the resulting total PSF displays a minimum in the origin, which would never happen in a full convolution process. In general, we expect that as σf increases, the error associated with the linear approach will also progressively increase, mainly in the central region at r < a few σf. The exact threshold for the validity of the linear approach will depend on the shape of the geometrical PSF 𝒫g(r), as well as on the distribution function describing the chance that the reconstructed absorption point is misplaced.
Here, we assess this limit, adopting the V11 circular PSF from the ixpeobssim software package (Baldini et al. 2022) as a model for the geometrical PSF 𝒫g(r). This PSF has been optimized to reproduce the results of the IXPE satellite, still retaining the circular symmetry; as such, it provides the best starting point for the application of our formalism to true observational data. Caveats related to this choice will be discussed later. The probability distribution function of the spurious displacement due to reconstruction errors is assumed to be a one-dimensional Gaussian with a variance, σf. We can then numerically perform the full convolution process in Eq. (1) and compute the related PSF for each Stokes parameter, to be compared with the linearized results. We consider the intensity distribution I and the polarized fraction distribution, 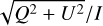 , which for an unpolarized source are just a function of the radial distance. For highly polarized sources, the images will be elongated, and we would have to consider the full image pattern.
, which for an unpolarized source are just a function of the radial distance. For highly polarized sources, the images will be elongated, and we would have to consider the full image pattern.
In Fig. 6, we compare the total PSF of the intensity I, for σf = 1,3,5 arcsec, together with the polarized fraction as a function of the distance from the origin, where the point source is supposedly located. Variations of the total PSF for I are small, mostly concentrated either in the origin, where for σf = 3 arcsec, we begin to observe for the PSF computed in the linearized regime, the profile inversion we discussed before; otherwise, they are located in the low-intensity wings at r > 50 arcsec. We can safely claim that for σf ≤ 3 arcsec, the polarization leakage leads to marginal changes in the intensity distribution of unpolarized sources. The linearized approach, however, tends to lead to an excessive suppression of the intensity in the central region, which has important implications in the estimate of the polarized fraction. By looking at the polarized fraction distribution, we see that for σf ≤ 3 arcsec, the linearized approach matches the results of the full nonlinear convolution quite well. For σf > 3 arcsec, the discrepancy in the central region, r < 5 arcsec, becomes progressively stronger. In the linearized approach a double peak structure emerges, that is partly present also in the full convolution but showing an inner peak that grows much more and that is in large part associated to the error in the intensity profile. There is a much better agreement at r > 10–12 arcsec for σf up to 5 arcsec. For higher values of σf, even beyond 15 arcsec, the agreement is quite poor: at σf = 7 arcsec, the maximum polarized fraction with the full convolution is found to be 0.38 at 36 arcsec, while in the linearized approach, it is 0.33 at 33 arcsec. This is not, however, surprising given that at σf = 7 arcsec, the displacement due to error reconstruction becomes comparable with the one due to the geometric PSF.
In Fig. 6, we also show the elongation of the image, for a source with 100% polarization, defined as the difference between the intensity profile in the direction aligned with the polarization of the source, with respect to the intensity of an unpolarized source. Interestingly, even in the full nonlinear case, the elongation is correctly described by a cos (2ϕ1) pattern. It is just the radial profile that changes with σf. We see that this is similar to what happen for the PSF of unpolarized sources, whereby the linear approximation tends to overestimate the polarization leakage at smaller radii, while converging to the nonlinear results at r > 20 arcsec. In general, however, this effect is quite small and likely to be appreciable only for larger values of σf and only for highly polarized sources. Given the typical polarization of sky sources <20%, this effect can safely be neglected.
 |
Fig. 6 Comparison of the PSF computed with the linearized approach and fully nonlinear approach for various values of σf for an unpolarized point source (left). Comparison of the radial polarization as a function of distance from the source position computed with the linearized approach and fully nonlinear approach for the same values of σf (center). Elongation of the PSF for a fully (100%) polarized point source computed with the linearized approach and fully nonlinear approach (right). In all cases, 𝒫g(r) is given by the V11 PSF of ixpeobssim, and 𝒫f is assumed to be a 1D Gaussian. |
5 Comparisons with the data and GPD simulations
Here, we compare our simple formalism in the fully nonlinear regime with both the results of a full GPD simulation using the GEANT4 simulator (Agostinelli et al. 2003) and of an IXPE observation of a bright unpolarized point source (Cygnus X-1). We do not expect our simplified approach to exactly match the true response of the instrument, but this comparison offers us a way to better characterize its strengths and weaknesses. For the GEANT4 simulation, we considered a point source with a photon distribution described by a simple power-law with photon index of −2. The GEANT4 simulator is coupled with the ixpeobssim/ixpesim software (Baldini et al. 2022; Di Lalla 2019)2, which provides the optical response of the IXPE satellite, using the V11 PSF for 𝒫g(r). This approach is, at this time, the best available in order to simulate the true response of the IXPE satellite. There are, however, a few important caveats in this approach: the V11 PSF is circular, while the IXPE calibration shows that the various mirror modules have PSFs with significant non circular features; the V11 PSF is optimized to reproduce the circular average intensity of an IXPE point source within its half-power diameter; as such, it already factors in the widening of the PSF due to the polarization leakage. Using the V11 PSF amounts to double counting the polarization leakage. The GEANT4 simulation and the IXPE observation are reduced using ixpeobssim with the same pipeline. The energy band band considered here is the operating IXPE band [2–8] keV.
In Fig. 7, we show a comparison of the GEANT4 simulation with our formalism, as described in Sect. 4.2.4, where we have again assumed that the probability distribution function of the spurious displacement due to reconstruction errors is a one-dimensional Gaussian with a variance of σf. By looking at the profiles from the GEANT4 simulation, we see that the effect of polarization leakage on the PSF is clearly present, with the wings of the PSF typically twice as bright as expected. However, the dependence on the energy is small. The amount of radial polarization is instead quite large, reaching up to 45%. Interestingly, there is a clear dependence of the radial polarization profile on the selected energy range, with a double-peak structure in the lower energy range that is not present at higher energies. This is most likely an indication that the probability distribution function of the spurious displacement does not have the same functional form at all energies – as we assume in our formalism when we adopt a Gaussian for which the only parameter that one can adjust is the variance.
If we model the polarization leakage using our simplified nonlinear formalism, we get results that (in terms of radial polarization profile) are in fair agreement with the GEANT4 simulation, if we assume σf = 8 arcsec. Both the amount of polarization and the location of the peak between 30 and 40 arcsec are recovered. However, as discussed above, we cannot reproduce the change of the polarization profile with energy and we do not get the inner peak. Moreover, by looking at the intensity profile, we notice that results using σf = 8 arcsec tend to over-predict the widening of the PSF by about a factor of 2. This is not unexpected, given that the probability distribution function of the spurious displacement is not 1D (it might even turn out not to be centrally peaked), which breaks the one-to-one relation between the level of radial polarization and the PSF widening. We notice that we can get a much better agreement of the PSF if we set σf = 5 arcsec, which, however, leads to an underprediction by a factor of 2 with regard to the level of radial polarization. It appears that the GEANT4 simulation is well reproduced, on average, in the full energy range, if we model the polarization leakage with σf = 5 arcsec, but then increase the amount of radial polarization by a factor of 2. In this case both the intensity and polarization profile are recovered. This is referred in the following as our fiducial nonlinear approach and formalism.
In Fig. 7, we show the radial profile, averaged over circular annuli, of the intensity and radial polarization observed by IXPE for Cygnus X-1. Ideally one would like to select a very bright and unpolarized source. In practice, however, a low level of intrinsic polarization (as long as it is small enough to neglect higher order effects such as image distortion) is not a problem, given that once averaged over an annulus, its contribution to the radial polarization pattern vanishes (the polarized fraction of Cygnus X-1 is just a few percents). By looking at the intensity profile, we can immediately see that the results are not in agreement with either the V11 PSF or the GEANT4 simulations. In particular, the GEANT4 simulation appears to overpredict the intensity in the central region at r < 30 arcsec by about 20% and, in addition it tends to greatly underpredict it at larger distances, up to a factor of 2. This is a clear indication that the V11 PSF that is used in the GEANT4 simulation, despite having been optimized on calibration data, does not allow us to reproduce the true intensity profile. Part of the problem is due to the fact that the V11 was calibrated on data already affected by polarization leakage and, as such, its use in a GEANT4 simulation ends up double-counting it. This is likely to be the origin of the over-prediction in the central region. The fact that the wings of the PSF at r > 30 arcsec are under-predicted is most likely due to either poor calibration in this low intensity region or possible differences between calibration data and flight performances. What might appear more significant are the differences in the profiles of radial polarization. The maximum amount of radial polarization is ~40%, similar to what is found in the GEANT4 simulation, however, in Cygnus X-1, there is no evidence of any double peaked structure. In addition, the radial polarization tend to peak much closer to the source: at 20 arcsec in the [2–4] keV and at 30 arcsec in the [2–8] keV energy bands. Part of this difference might be attributed to the already discussed difference in the intensity profiles due to the incorrect use of the V11 PSF.
We have tried to see if it was possible to modify the geometrical PSF 𝒫g(r) with respect to the V11 in order to reproduce both the intensity and radial polarization profiles. We did so with our fiducial nonlinear formalism, which has proved to provide a reliable approximation of the results of the GEANT4 simulation, but could not find a satisfactory solution. It is easy to modify the geometrical PSF to match the observation, but we could not recover the radial polarization profile. This could be due to an intrinsic limitation of our formalism, for instance, the assumption that the probability distribution function of the spurious displacement due to reconstruction errors is a 1D Gaussian; however, we cannot exclude the possibility that the presence of non-circular patterns in the IXPE PSF might somehow be important. There is also the chance that the GEANT4 simulation of an idealized GPD, does not fully capture the reality of the true GPD on board of the satellite. This is not unexpected given that we already know of spurious effects that cannot be reproduced in the GEANT4 (Rankin et al. 2022).
While the GEANT4 simulation and our formalism get consistent results, there are still significative differences with respect to real IXPE observations of point sources. However, as we will show in the next section, for real extended sources, this effect is only mildly dependent on the details of the radial profile for a point source, making this approach more robust that what could be gleaned from just the simple point-source analysis.
 |
Fig. 7 Intensity profile (in various energy bands) of a point source, with photon index = −2 simulated with the GEANT4, and assuming the V11 ixpeobssim PSF as input geometrical PSF, compared both with the V11 PSF itself, and with the intensity profile computed with our fiducial nonlinear formalism for two different values of the variance σf (upper-left). Comparison of the profile of radial polarization (in various energy bands between the same GEANT4 simulation and our fiducial nonlinear formalism, where the σf = 5 case has been multiplied by a factor of 2 (upper-right). The same as the above is shown in the lower panels, but for Cygnus X-1 as observed by the IXPE satellite. |
6 Mueller matrix formalism
The generalization of the PSF for polarized observations is carried out by the so-called Mueller matrix, M (Tinbergen 1996), whose elements represent the images of a polarized point source in the Stokes plane, as a function of its intrinsic Stokes parameters: Isrc, Qsrc, and Usrc. Its diagonal elements describe how each Stokes parameter of the source is turned into an image in the same Stokes parameter, while off-diagonal elements describe polarization leakage from one Stokes parameter to another.
For example, the terms in curly brackets in Eqs. (24)–(26) represent the diagonal elements, ℳII, ℳQQ, and ℳUU, respectively, while the terms in square brackets represent the off-diagonal terms, ℳIQ, ℳIU, ℳUI, and ℳQI. It can be shown that the spurious displacement of the reconstructed absorption point due to reconstruction errors does not cause any mixing between U and Q (ℳQU = 0). Moreover, it can easily be shown that in our case, we have ℳIQ = ℳIU and ℳUI = ℳQI.
As long as the geometrical PSF 𝒫g(r) is circular, Eqs. (24)–(26), can be generalized as follows:
![$ I\left( {x,y} \right) = {I_{{\rm{src}}}}{\cal G}\left( r \right) + {\cal F}\left( r \right)\left[ {{Q_{{\rm{src}}}}{{{x^2} - {y^2}} \over {{r^2}}} + {U_{{\rm{src}}}}{{2xy} \over {{r^2}}}} \right], $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq42.png) (28)
(28)
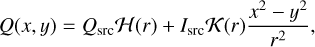 (29)
(29)
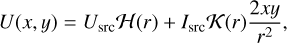 (30)
(30)
where 𝒢(r), ℱ(r), ℋ(r), 𝒦(r) are the Mueller matrix elements. The determination of these functions allows us to compute the image of any source (polarized or unpolarized) in each Stokes parameter. In Sect. 4.2, we show how to derive these functions from the optical PSF at first-order in the variance of the probability distribution function of the spurious displacement due to reconstruction errors, which provides a good approximation as long as the maximum amount of radial polarization does not exceed 15%. For larger values, we would need to use the fully nonlinear approach. It is also possible to derive those functions by directly fitting either the results of a full GEANT4 simulation or even the observation of a bright point source. We have shown that in the case of IXPE, the nonlinear approach based on the assumption that the probability distribution function of the spurious displacement due to reconstruction errors is a 1D Gaussian, can be easily tuned to reproduce the result of a GEANT4 simulation very accurately. Thus, we expect these two approaches to lead to equivalent results. On the other hand, we have noticed important differences in comparison with a true observation of Cygnus X-1.
Our investigations have shown that 𝒢(r) = ℋ(r) and that ℱ(r) can be safely neglected, given that its contribution to the source elongation is small and that typically the intrinsic polarization of X-ray sources does not exceed 20%. On the other hand, a correct determination of 𝒦(r) is quite important because otherwise it can easily lead to false detection. In general, this is not an issue for isolated point sources, but in extended sources, it can lead to complex polarization patterns, which, in case of small intrinsic polarization, can dominate over the true one.
A typical way to evaluate this effect, for IXPE observation, is to simulate a full IXPE observation of an extended source by coupling the ixpeobssim/ixpesim software, which provide the optical response of the various mirror modules, with a GEANT4 simulation that gives the response of the GPD. This allows us to process the resulting tracks with the same data reduction software that is used on the true date to get Level 2 files that are then analyzed again as true data are. This can prove extremely time-consuming and generally requires a huge statistics in order to keep Poisson counting noise under control and it also still suffers from the limitations discussed in Sect. 5 (foremost 𝒫g(r) is not known).
A much easier approach would be to derive the functions 𝒢(r) and 𝒦(r), either from a GEANT4 simulation, or from true on-flight data and use them to compute the Mueller matrix elements. Then computing a polarization map of any source can be reduced to a simple and numerically inexpensive convolution. In Fig. 8, we show the Mueller matrix elements (of an unpolarized source), obtained by fitting 𝒢(r) and 𝒦(r) to the GEANT4 simulation results (but we get equivalent maps using our fiducial nonlinear formalism) and to the IXPE observation of Cygnus X-1. There are some differences, with the true data giving Q and U maps that are more peaked toward the center.
In Fig. 9, we show the application of the Mueller matrix formalism with the functions 𝒢(r) and 𝒦(r) computed using different approaches to the case of a real extended source, namely: the Crab nebula. We took a map of the intensity in the [2–8] keV band derived from a Chandra observation (OsbId 16364) as our fiducial intrinsic source and we assumed the source to be fully unpolarized (not true for the Crab nebula) to see what kind of polarization pattern will arise from polarization leakage. We also performed a full ixpeobssim/ixpesim plus GEANT4 simulation, which is also shown for comparison. Results obtained with 𝒢(r) and 𝒦(r) derives either by fitting the GEANT4 simulation of an unpolarized source or using our fiducial nonlinear formalism agree very well between them and with the full ixpeobssim plus GEANT4 simulation, showing that they provide a reliable substitute of the former, more cumbersome approach. Figure 9 clearly shows that despite the evident difference in the radial polarization profile of an unpolarized point source between the GEANT4 simulation and the Cygnus X-1 data, once applied to extended sources with complex intensity map, the method gives only very marginal differences in the results.
 |
Fig. 8 Maps of I, U and Q for a point source computed according to Eqs. (28)–(30) with functions 𝒢(r) and 𝒦(r), fitted on a GEANT4 simulation of an unpolarized point source (upper panels). The same is shown in the lower panels, but for functions 𝒢(r) and 𝒦(r) fitted on the Cygnus X-1 observation by the IXPE satellite. The reference frame is chosen such that Q is positive for polarization aligned along the x-axis. |
 |
Fig. 9 Image in I, Q/I and U/I of the Crab nebula in the [2–8] keV band, assuming fully unpolarized radiation and computed using a full ixpeobssim plus GEANT4 simulation (upper panel). Data were reduced using a standard ixpeobssim data analysis tool. Gaussian smoothing was applied to reduce Poisson noise. The original source input file was the Chandra ObsId 16364. Lower rows show the same above, but computed by convolution of the Mueller matrix element with the intensity map of Chandra ObsId. In order, from the second to the fourth row, the functions 𝒢(r) and 𝒦(r) were derived as: nonlinear formalism (second row), fit of the results from a GEANT4 point source simulation (third row), and fit of the Cygnus X-1 data (forth row). The reference frame is chosen such that Q is positive for polarization aligned along the north-south direction. |
7 Conclusions
X-ray polarimetry based on gas pixel detectors offers a new observational window that has enabled novel spatially resolved polarimetric studies of Galactic and extra-Galactic extended sources, unveiling otherwise inaccessible properties. The first instrument to successfully adopt this technique is IXPE. As such, its analysis also pioneers our understanding of this new technology and a correct assessment of the possible issues related to GPD polarimetry is of great importance in the light of its use in future instruments such as eXTP (Zhang et al. 2019). It was indeed during its calibration phase for which (and for the first time) polarized halos were noticed around unpolarized calibration sources, spurring an investigation into the origin of this effect.
Here, we illustrate the origin of this polarization leakage for the first time, showing that it is fundamentally related to errors in determining the photon absorption point at the track-reconstruction stage (a key part of the GPD-based approach) and, in particular, on the correlation of this error with the estimated EVPA. We developed a mathematical formalism that allows us to model the effect for generic sources, evaluating the range of validity of this model correction and presenting a comparison both with real data and more sophisticated Monte Carlo simulations. We have shown that the approach provides a reliable estimate of the effect, even if for a proper data cleaning, a more robust Montecarlo is likely to be necessary. By adopting the Mueller matrix formalism, we were able to apply our results to complex extended sources. A more complex approach, capable of handling non-circular PSFs, is in development.
While for isolated point sources, this polarization leakage can lead to radially polarized halos with a polarized fraction as high as 40%, the effect on extended source may be much smaller, depending on the intensity gradients. In general, for isolated point sources, this effect is of no concern as long as the regions used for the analysis are sufficiently large and/or centered on the source. For extended sources, the level of polarization due to polarization leakage depends mostly on how compact the source is (in comparison with the PSF) and on the level of the true intrinsic polarization. The worst case is that of a weak extended source close to a bright point source, in the case of which the latter’s halo can dominate the signal – it is then necessary to perform a careful subtraction for a valid polarization measurement. A python script to evaluate this effect optimized for IXPE has been released together with the ixpeobssim package (Baldini et al. 2022). We note that the accuracy of the formalism is sufficient to get an estimate of the effect, but not to perform a proper data cleaning.
It is clear that the level of this problem depends on the magnitude of the position mislocalization and its correlation with the EVPA. For the default IXPE track “moments analysis” (Bellazzini et al. 2002), the effect can be quite substantial, as we have shown. For other track analysis schemes, the effect will differ for the same events. For example, preliminary analysis of a neural net track measurement scheme (‘NN analysis’), indicates that the effect is ~3× smaller, but still present (Kitaguchi et al. 2019; Moriakov et al. 2020; Peirson et al. 2021; Peirson & Romani 2021). However any reconstruction algorithm will have some inaccuracy in determining the impact point, so this effect is likely to always be present in GPD-based polarimetric observations.
Acknowledgements
N.B. was supported by the INAF MiniGrant “PWNnumpol – Numerical Studies of Pulsar Wind Nebulae in The Light of IXPE”.
Appendix A Generalization of the linear formalism
The formalism we developed in Sect. 4.2 is based on the assumption that the displacement between the true interaction point, Pi and the reconstructed one, Pr, is purely along the direction, n, of the reconstructed polarization plane (the photo-electron track). As a consequence, the determination of the reconstructed polarization plane is independent of the offset of the interaction point with respect to its true position (i.e., measuring correctly – or not – the interaction point does not change the reconstructed direction of the polarization plane). This is not generally true. The tracks can have a quite complex geometry and overall the offset will have both a component along the reconstructed polarization plane (longitudinal) and one orthogonal to it (transverse). This implies not only that the offset is intrinsically 2D (as opposed to the 1D displacement assumption), but that even the reconstructed polarization plane might be different if we correctly locate the impact point or not. Ideally, the polarization plane should be the tangent plane to the track axis in the impact point. As can be seen from Fig. A.1, the tangent plane to a track axis can vary depending where the impact point is located. On top of this, the rotation of the inferred polarization plane might depend not just on the offset but also on the track shape. This means that photons having all the same polarization properties, if the impact point is correctly reconstructed in Pi, will show different polarization properties when reconstructed in Pr. In this sense, we cannot establish a one to one correspondence between the polarization at Pi and that at Pr – so, it is necessary to resort to statistical arguments.
 |
Fig. A.1 Schematic representation of the way spatial offset and the reconstruction of the polarization plane might be related. The red and purple curves represent two tracks originating from events having the same true impact point, Pi, and being wrongly reconstructed at the track end in the same point, Pr; also, ϕi is the polarization plane that would have been reconstructed as tangent to both tracks if the impacts points would have been correctly identified and ϕr1 and ϕr2 are the polarization planes reconstructed as tangent of the tracks in the point, Pr. |
In order to generalize the formalism, we assume that the chance an event reconstructed in Pr originates in Pi is higher if the reconstructed polarization plane in Pr and it is aligned with the direction, Pi − Pr – than if it were orthogonal. As a consequence, if the distribution of the polarisation planes in the true impact points Pi is uniform, then we expect that in the reconstructed point Pr, there ought to be an excess of photons with a reconstructed polarization plane in the aligned direction:
![$ {{\cal F}_{\rm{r}}} = \left( \phi \right){{\cal F}_i}\left( \phi \right){{\left[ {{\cal A}\left( {\delta l} \right) + {\cal B}\left( {\delta l} \right)\cos \left( {2\left( {\phi - {\phi _{{\rm{ir}}}}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{\cal A}\left( {\delta l} \right) + {\cal B}\left( {\delta l} \right)\cos \left( {2\left( {\phi - {\phi _{{\rm{ir}}}}} \right)} \right)} \right]} {{{2\pi = {{\cal F}_i}\left( \phi \right)\left[ {{\cal A}\left( {\delta l} \right) + {\cal B}\left( {\delta l} \right)\cos \left( {2\phi } \right)\cos \left( {2{\phi _{{\rm{ir}}}}} \right) + {\cal B}\left( {\delta l} \right)\sin \left( {2\phi } \right)\sin \left( {2{\phi _{{\rm{ir}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{2\pi = {{\cal F}_i}\left( \phi \right)\left[ {{\cal A}\left( {\delta l} \right) + {\cal B}\left( {\delta l} \right)\cos \left( {2\phi } \right)\cos \left( {2{\phi _{{\rm{ir}}}}} \right) + {\cal B}\left( {\delta l} \right)\sin \left( {2\phi } \right)\sin \left( {2{\phi _{{\rm{ir}}}}} \right)} \right]} {2\pi ,}}} \right. \kern-\nulldelimiterspace} {2\pi ,}}}}} \right. \kern-\nulldelimiterspace} {{{2\pi = {{\cal F}_i}\left( \phi \right)\left[ {{\cal A}\left( {\delta l} \right) + {\cal B}\left( {\delta l} \right)\cos \left( {2\phi } \right)\cos \left( {2{\phi _{{\rm{ir}}}}} \right) + {\cal B}\left( {\delta l} \right)\sin \left( {2\phi } \right)\sin \left( {2{\phi _{{\rm{ir}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{2\pi = {{\cal F}_i}\left( \phi \right)\left[ {{\cal A}\left( {\delta l} \right) + {\cal B}\left( {\delta l} \right)\cos \left( {2\phi } \right)\cos \left( {2{\phi _{{\rm{ir}}}}} \right) + {\cal B}\left( {\delta l} \right)\sin \left( {2\phi } \right)\sin \left( {2{\phi _{{\rm{ir}}}}} \right)} \right]} {2\pi ,}}} \right. \kern-\nulldelimiterspace} {2\pi ,}}}} $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq47.png) (A.1)
(A.1)
where ℱ(ϕ) is the distribution function of reconstructed polarization planes in the true impact point Pi and 𝒜(δl) represents the average (over polarization angle) chance an event is erroneously reconstructed at a distance δl = dist(Pr, Pi) from its true impact point, while ℬ(δl) (always < 𝒜(δl)) accounts for the fact that the displacement chance is higher for event with a reconstructed polarization plane aligned with the direction Pi − Pr, corresponding to an angle ϕir. Then, ℱr(ϕ) is the distribution of events reconstructed in Pr but originating in Pi. In Eq. A.1, we have assumed that the anisotropy in the distribution of the polarization planes can be described by a quadrupolar term. In general, the full description might be more complex, however, any higher harmonics, will have no effect of the determination of Stokes parameters and for this reason, we neglect it here.
We proceed as described earlier in this work, assuming ℱi(ϕ) is constant (unpolarized source). Then ℱi is just the intensity at the point Pi. Assuming a point source of intensity, Isrc, located at the origin of a reference frame and a geometrical PSF 𝒫g(r) dependent only on distance from the origin, then we have:
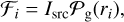 (A.2)
(A.2)
where 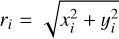 and Pi = (xi, yi). In terms of the quantities measured at the reconstructed impact point, Pr = (xr, yr) = (xi − δx, yi − δy), we can approximate it as:
and Pi = (xi, yi). In terms of the quantities measured at the reconstructed impact point, Pr = (xr, yr) = (xi − δx, yi − δy), we can approximate it as:
![$ \matrix{ {{{\cal F}_i} = {I_{{\rm{src}}}}\left[ {{P_{\rm{g}}}\left( {{r_r}} \right) + {{\partial {P_{\rm{g}}}} \over {\partial x}}\delta x + {{\partial {P_{\rm{g}}}} \over {\partial y}}\delta y + {1 \over 2}{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {x^2}}}\delta {x^2} + {1 \over 2}{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {y^2}}}\delta {y^2} + {{{\partial ^2}{P_{\rm{g}}}} \over {\partial x\partial y}}\partial x\partial y + {1 \over 6}{{{\partial ^3}{P_{\rm{g}}}} \over {\partial {x^3}}}\delta {x^3} + } \right.{1 \over 6}{{{\partial ^3}{P_{\rm{g}}}} \over {\partial {y^3}}}\delta {y^3} + {1 \over 2}{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {x^2}\partial y}}\delta {x^2}xy + } \cr {\left. { + {1 \over 2}{{{\partial ^2}{P_{\rm{g}}}} \over {\partial x\partial {y^2}}}\delta x\partial {y^2} + {1 \over {24}}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {x^4}}}\delta {x^4} + {1 \over {24}}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {y^4}}}\delta {y^4} + {1 \over 6}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {x^3}\partial y}}\delta {x^3}\delta y + {1 \over 6}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial x\partial {y^3}}}\delta x\delta {y^3} + {1 \over 4}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial x\partial {y^2}}}\delta {x^2}\delta {y^2}} \right] + {\cal O}\left( {\delta {l^3}} \right),} \cr } $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq50.png) (A.3)
(A.3)
where derivatives are taken at Pr. With respect to the previous case, here we need to take derivatives up to the 4fourth order. On the other hand, we have:
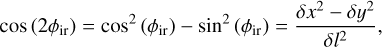 (A.4)
(A.4)
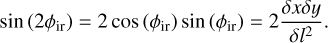 (A.5)
(A.5)
where the geometrical PSF 𝒫g and all its derivatives are evaluated in Pr. We note, moreover, that the anisotropy enters always through the term ℬ(δl)/δl2. It is reasonable to expect that for δl = 0, we have ℬ(δl) = 0, implying that when the impact point is correctly reconstructed, the distribution of the polarization planes of an unpolarized source has no preferential direction (but see (Rankin et al. 2022) for a discussion on spurious modulation). Then, symmetry considerations require that in the limit δl → 0, we have ℬ(δl) ∝ δl2. We can then introduce a regularized distribution for the anisotropy 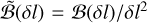 (noting, however, that this regularization is ultimately not necessary, given that potentially diverging terms eventually cancel each other out).
(noting, however, that this regularization is ultimately not necessary, given that potentially diverging terms eventually cancel each other out).
Given that 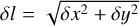 , the terms with odd powers in δx and/or δy are canceled out and only even terms remain. We can then define the following even moments related to the 𝒜(δl) distribution:
, the terms with odd powers in δx and/or δy are canceled out and only even terms remain. We can then define the following even moments related to the 𝒜(δl) distribution:
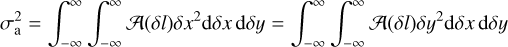 (A.7)
(A.7)
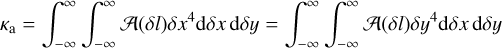 (A.8)
(A.8)
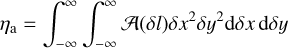 (A.9)
(A.9)
and of the 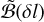 distribution:
distribution:
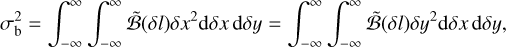 (A.10)
(A.10)
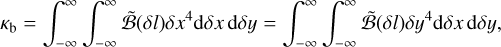 (A.11)
(A.11)
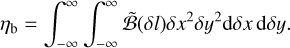 (A.12)
(A.12)
Now, using the following relation between cartesian and polar coordinates δx = δl cos θ and δx = δl sin θ, we can show that:
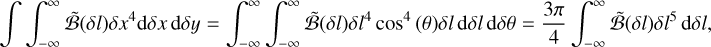 (A.13)
(A.13)
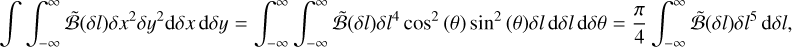 (A.14)
(A.14)
which show that κ = 3η. This leads to:
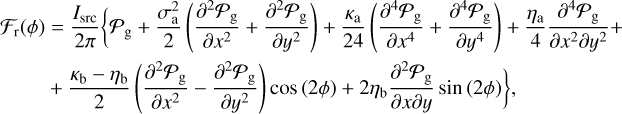 (A.15)
(A.15)
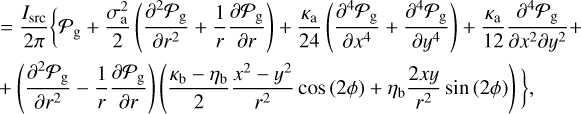 (A.16)
(A.16)
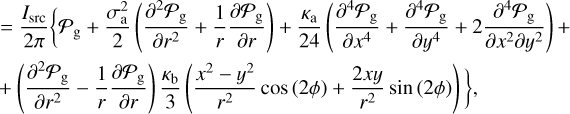 (A.17)
(A.17)
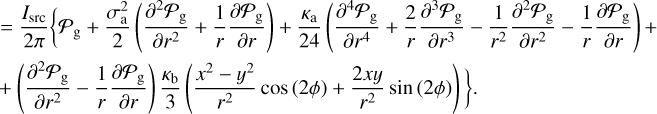 (A.18)
(A.18)
At this point we can proceed as before, defining values of the Stokes parameters at the same point Pr = (x, y) as:
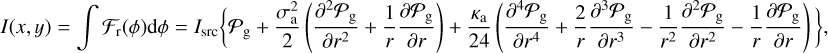 (A.19)
(A.19)
We can immediately see that for the effective PSF on intensity, apart from a higher order curvature term in κa, the functional form is identical to our previous simplified derivation with the simple exchange 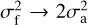 . For the PSF of the other Stokes parameter, which encodes the radial profile of polarization induced by an incorrect reconstruction of the track, again the functional form is identical to our previous simplified derivation with the simple exchange
. For the PSF of the other Stokes parameter, which encodes the radial profile of polarization induced by an incorrect reconstruction of the track, again the functional form is identical to our previous simplified derivation with the simple exchange 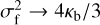 . In particular, if we assumes maximal anisotropy ℬ(δl) = 𝒜(δl), then, to a first-order in variance, e can show that
. In particular, if we assumes maximal anisotropy ℬ(δl) = 𝒜(δl), then, to a first-order in variance, e can show that 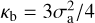 , Thus, we recover the following:
, Thus, we recover the following:
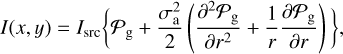 (A.22)
(A.22)
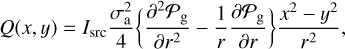 (A.23)
(A.23)
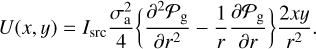 (A.24)
(A.24)
References
- Agostinelli, S., Allison, J., Amako, K., et al. 2003, Nucl. Instrum. Methods Phys. Res. A, 506, 250 [Google Scholar]
- Bachetti, M. 2016, Astron. Nachr., 337, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Baldini, L., Bucciantini, N., Lalla, N. D., et al. 2022, SoftwareX, 19, 101194 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, R., Angelini, F., Baldini, L., et al. 2002, Proceedings of SPIE - The International Society for Optical Engineering, 4843 [Google Scholar]
- Bellazzini, R., Angelini, F., Baldini, L., et al. 2006, Nucl. Instrum. Methods Phys. Res. A, 560, 425 [CrossRef] [Google Scholar]
- Bucciantini, N. 2018, Galaxies, 6, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, E., Soffitta, P., Bellazzini, R., et al. 2001, Nature, 411, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Di Lalla, N. 2019, PhD Thesis, https://etd.adm.unipi.it/t/etd-04042019-100412/ [Google Scholar]
- Fabiani, S., Costa, E., Del Monte, E., et al. 2014, ApJS, 212, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, H., Jiang, W., Minuti, M., et al. 2019, Exp. Astron., 47, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, C. A. 2017, AJ, 154, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, H. 2022, PASJ, 74, R1 [NASA ADS] [CrossRef] [Google Scholar]
- Kalemci, E. 2018, Eur. Phys. J. Plus, 133, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Kargaltsev, O., & Pavlov, G. G. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, American Institute of Physics Conference Series, 983, 171 [NASA ADS] [Google Scholar]
- Kitaguchi, T., Black, K., Enoto, T., et al. 2019, Nucl. Instrum. Methods Phys. Res. A, 942, 162389 [Google Scholar]
- Mereghetti, S., Pons, J. A., & Melatos, A. 2015, Space Sci. Rev., 191, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Moriakov, N., Samudre, A., Negro, M., et al. 2020, ApJ, submitted [arXiv: 2005.08126] [Google Scholar]
- Peirson, A. L., & Romani, R. W. 2021, ApJ, 920, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Peirson, A. L., Romani, R. W., Marshall, H. L., Steiner, J. F., & Baldini, L. 2021, Nucl. Instrum. Methods Phys. Res. A, 986, 164740 [Google Scholar]
- Rankin, J., Muleri, F., Tennant, A. F., et al. 2022, AJ, 163, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbatucci, L., & Salvat, F. 2016, Radiat. Phys. Chem., 121, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [Google Scholar]
- Singh, K. P. 2013, Bull. Astron. Soc. India, 41, 137 [NASA ADS] [Google Scholar]
- Soffitta, P., Baldini, L., Bellazzini, R., et al. 2003, Nucl. Instrum. Methods Phys. Res. A, 510, 170 [Google Scholar]
- Tinbergen, J. 1996, Astronomical Polarimetry [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. L. 2015, Rep. Progr. Phys., 78, 116901 [Google Scholar]
- Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
- Walter, R., & Ferrigno, C. 2017, in Handbook of Supernovae, eds. A. W. Alsabti, & P. Murdin, 1385 [CrossRef] [Google Scholar]
- Weisskopf, M. C., Silver, E. H., Kestenbaum, H. L., Long, K. S., & Novick, R. 1978, ApJ, 220, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Soffitta, P., Baldini, L., et al. 2022, J. Astron. Telescopes Instrum. Syst., 8, 026002 [NASA ADS] [Google Scholar]
- Zhang, S., Santangelo, A., Feroci, M., et al. 2019, Sci. China Phys. Mech. Astron., 62, 29502 [Google Scholar]
For ixpesim, see https://etd.adm.unipi.it/theses/available/etd-04042019-100412/
All Figures
 |
Fig. 1 Example of a photoelectron track generated by a 7 keV photon (left panel) and a 3.5 keV photon (right panel). The dashed lines and the black points represent respectively the simulated PE emission direction and X-ray impact point. The simulated photoelectron path is reported as well. Ionization charges created along the photoelectron path are reported as small cyan dots. The color scale, going from white to dark red, represents the amount of charge collected in each pixel. |
| In the text | |
 |
Fig. 2 Example of a wrongly reconstructed absorption point. The black dot is the real absorption point, the green one is the reconstructed absorption point and the blue one is the barycenter. Note: the reconstructed polarization plane (blues dashed line) differs from the true one (black dashed line) Colors have the same meaning as in Fig. 1. |
| In the text | |
 |
Fig. 3 Schematic picture of polarization leakagefoг an unpolarized source with a sharp edge. The light-blue region represents the portion of the GPD corresponding to the source. Four events, close to the edge of the source image, are represented with their respective PE tracks. The green dots represent the true absorption points and the blue segments are the reconstructed polarization planes of the original photons. On the left, all absorption points are correctly reconstructed in their true positions: all events are inside the edge and none remain outside (bottom panel represents the event count); there are as many PEs with tracks tangential as orthogonal to the edge so no net polarization is assigned to the source. On the right the absorption point of the track extending outside the source edge has been wrongly reconstructed at the end of the track (blue dot): there are less events reconstructed inside the edge and more outside (bottom panel represents the event count); there are more PEs reconstructed with tracks tangential than orthogonal to the edge inside the source region, while there are PE events with tracks orthogonal to the edge outside. This leads to a blurring of the edge and to a polarization pattern tangential inside the edge and orthogonal outside. |
| In the text | |
 |
Fig. 4 Schematic representation of the geometry involved in the absorption point displacement due to reconstruction errors. Here, Psrc is the location of the point source whence the photon come from; Pi is the true impact (absorption) point of the photon, displaced due to the mirror PSF, while the orange double-headed arrow represents the photo-electron direction, n; Pr is the reconstructed impact point displaced by an amount δx along the photo-electron direction plane. Then x−y are coordinate axes chosen such that x is parallel to the photo-electron direction plane, while ∆ϕ is the polar angle of the reconstructed impact point in the same reference frame, describing the azimuthal distribution of photons due to the mirror PSF. |
| In the text | |
 |
Fig. 5 Intensity (left), Stokes Q (center) and U (right) maps, for a uniform unpolarized disk of unitary surface brightness and radius equal to 15 arcses (upper panel) assuming for the geometrical PSF the one given by Fabiani et al. (2014) at 2.95 keV, and taking σf = 1 arcsec (recall that Q and U scales as |
| In the text | |
 |
Fig. 6 Comparison of the PSF computed with the linearized approach and fully nonlinear approach for various values of σf for an unpolarized point source (left). Comparison of the radial polarization as a function of distance from the source position computed with the linearized approach and fully nonlinear approach for the same values of σf (center). Elongation of the PSF for a fully (100%) polarized point source computed with the linearized approach and fully nonlinear approach (right). In all cases, 𝒫g(r) is given by the V11 PSF of ixpeobssim, and 𝒫f is assumed to be a 1D Gaussian. |
| In the text | |
 |
Fig. 7 Intensity profile (in various energy bands) of a point source, with photon index = −2 simulated with the GEANT4, and assuming the V11 ixpeobssim PSF as input geometrical PSF, compared both with the V11 PSF itself, and with the intensity profile computed with our fiducial nonlinear formalism for two different values of the variance σf (upper-left). Comparison of the profile of radial polarization (in various energy bands between the same GEANT4 simulation and our fiducial nonlinear formalism, where the σf = 5 case has been multiplied by a factor of 2 (upper-right). The same as the above is shown in the lower panels, but for Cygnus X-1 as observed by the IXPE satellite. |
| In the text | |
 |
Fig. 8 Maps of I, U and Q for a point source computed according to Eqs. (28)–(30) with functions 𝒢(r) and 𝒦(r), fitted on a GEANT4 simulation of an unpolarized point source (upper panels). The same is shown in the lower panels, but for functions 𝒢(r) and 𝒦(r) fitted on the Cygnus X-1 observation by the IXPE satellite. The reference frame is chosen such that Q is positive for polarization aligned along the x-axis. |
| In the text | |
 |
Fig. 9 Image in I, Q/I and U/I of the Crab nebula in the [2–8] keV band, assuming fully unpolarized radiation and computed using a full ixpeobssim plus GEANT4 simulation (upper panel). Data were reduced using a standard ixpeobssim data analysis tool. Gaussian smoothing was applied to reduce Poisson noise. The original source input file was the Chandra ObsId 16364. Lower rows show the same above, but computed by convolution of the Mueller matrix element with the intensity map of Chandra ObsId. In order, from the second to the fourth row, the functions 𝒢(r) and 𝒦(r) were derived as: nonlinear formalism (second row), fit of the results from a GEANT4 point source simulation (third row), and fit of the Cygnus X-1 data (forth row). The reference frame is chosen such that Q is positive for polarization aligned along the north-south direction. |
| In the text | |
 |
Fig. A.1 Schematic representation of the way spatial offset and the reconstruction of the polarization plane might be related. The red and purple curves represent two tracks originating from events having the same true impact point, Pi, and being wrongly reconstructed at the track end in the same point, Pr; also, ϕi is the polarization plane that would have been reconstructed as tangent to both tracks if the impacts points would have been correctly identified and ϕr1 and ϕr2 are the polarization planes reconstructed as tangent of the tracks in the point, Pr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$ {P_t}\left( {x,y} \right) = {P_g}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right] + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]\cos \left( {2\Delta \phi } \right) + 𝒪 \left( {\sigma _{\rm{f}}^4} \right), $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq12.png)
![$ \matrix{ {{P_{\rm{U}}}\left( {x,y} \right) = 2\int_0^{2\pi } {{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]} \sin\left( {2\phi } \right)\cos \left( {2\left( {{\phi _1} - \phi } \right)} \right){1 \over {2\pi }}{\rm{d}}\phi {\rm{ = }}{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]\sin \left( {2{\phi _1}} \right)} \cr { = {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_g}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_g}} \over {\partial r}}} \right]{{2xy} \over {{r^2}}},} \cr } $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq20.png)
![$ {P_{\rm{I}}}\left( {r\,\cos \left( {{\phi _1}} \right),r\,\sin \left( {{\phi _1}} \right)} \right) = {P_{\rm{g}}}\left( r \right) + {{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} + {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right] + {{{a_{{\rm{src}}}}} \over 2}{{\sigma _{\rm{f}}^2} \over 4}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {r^2}}} - {1 \over r}{{\partial {P_{\rm{g}}}} \over {\partial r}}} \right]\,\cos \left( {2\left( {{\phi _1} - {\phi _{\rm{o}}}} \right)} \right), $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq27.png)
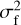
![$ \matrix{ {{{\cal F}_{\rm{r}}}\left( \phi \right) = {{{I_{{\rm{src}}}}} \over {2\pi }}\int_{ - \infty }^\infty {{\rm{d}}\delta x} \int_{ - \infty }^\infty {{\rm{d}}\delta y} \left\{ {{P_{\rm{g}}}{\cal A}\left( {\delta l} \right) + {\cal A}\left( {\delta l} \right)\left( {{{\partial {P_{\rm{g}}}} \over {\partial x}}\delta x + {{\partial {P_{\rm{g}}}} \over {\partial y}}\delta y} \right) + {1 \over 2}{\cal A}\left( {\delta l} \right)\left( {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {x^2}}}\delta {x^2} + {{{\partial ^2}{P_{\rm{g}}}} \over {\partial {y^2}}}\delta {y^2}} \right) + } \right.} \hfill \cr { + \left( {{P_{\rm{g}}}{\cal B}\left( {\delta l} \right){{\cos \left( {2\phi } \right)} \over {\delta {l^2}}}} \right)\left( {\delta {x^2} + \delta {y^2}} \right) + \left( {{\cal A}\left( {\delta l} \right){{{\partial ^2}{P_{\rm{g}}}} \over {\partial x\partial y}} + 2{P_{\rm{g}}}{{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}\sin \left( {2\phi } \right.} \right)\delta x\delta y + } \hfill \cr { + \left( {{{\cal A} \over 6}\left( {\delta l} \right){{{\partial ^3}{P_{\rm{g}}}} \over {\partial {x^3}}} + {{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}{{\partial {P_{\rm{g}}}} \over {\partial x}}\cos \left( {2\phi } \right)} \right)\delta {x^3} + \left( {{{{\cal A}\left( {\delta l} \right)} \over 6}{{{\partial ^3}{P_{\rm{g}}}} \over {\partial {y^3}}} - {{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}{{\partial {P_{\rm{g}}}} \over {\partial y}}} \right)\delta {y^3} + } \hfill \cr { + \left( {{{{\cal A}\left( {\delta l} \right)} \over 2}{{{\partial ^3}{P_{\rm{g}}}} \over {\partial {x^2}\partial y}} + {{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}\left[ {2{{\partial {P_{\rm{g}}}} \over {\partial x}}\sin \left( {2\phi } \right) + {{\partial {P_{\rm{g}}}} \over {\partial y}}\cos \left( {2\phi } \right)} \right]} \right)\delta {x^2}\delta y + } \hfill \cr { + \left( {{{{\cal A}\left( {\delta l} \right)} \over 2}{{{\partial ^3}{P_{\rm{g}}}} \over {\partial x\partial {y^2}}} + {{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}\left[ {2{{\partial {P_{\rm{g}}}} \over {\partial y}}\sin \left( {2\phi } \right) - {{\partial {P_{\rm{g}}}} \over {\partial x}}\cos \left( {2\phi } \right)} \right]} \right)\delta x\delta {y^2} + } \hfill \cr { + \left( {{{{\cal A}\left( {\delta l} \right)} \over {24}}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {x^4}}} + {{{\cal B}\left( {\delta l} \right)} \over {2\delta {l^2}}}{{{\partial ^2}{P_{\rm{g}}}} \over {\delta {x^2}}}\cos \left( {2\phi } \right)} \right)\delta {x^4} + \left( {{{{\cal A}\left( {\delta l} \right)} \over {24}}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {y^4}}} - {{{\cal B}\left( {\delta l} \right)} \over {2\delta {l^2}}}{{{\partial ^2}{P_{\rm{g}}}} \over {\delta {y^2}}}\cos \left( {2\phi } \right)} \right)\delta {y^4} + } \hfill \cr { + \left( {{{{\cal A}\left( {\delta l} \right)} \over 6}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {x^3}\partial y}} + {{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {x^2}}}\sin \left( {2\phi } \right) + {{{\partial ^2}{P_{\rm{g}}}} \over {\partial x\partial y}}\cos \left( {2\phi } \right)} \right]} \right)\delta {x^3}\delta y + } \hfill \cr { + \left( {{{{\cal A}\left( {\delta l} \right)} \over 6}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial x\partial {y^3}}} + {{{\cal B}\left( {\delta l} \right)} \over {\delta {l^2}}}\left[ {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {y^2}}}\sin \left( {2\phi } \right) - {{{\partial ^2}{P_{\rm{g}}}} \over {\partial x\partial y}}\cos \left( {2\phi } \right)} \right]} \right)\delta x\delta {y^3} + } \hfill \cr { + \left( {{{{\cal A}\left( {\delta l} \right)} \over 4}{{{\partial ^4}{P_{\rm{g}}}} \over {\partial {x^2}\partial {y^2}}} + {{{\cal B}\left( {\delta l} \right)} \over {2\delta {l^2}}}\left[ {4{{{\partial ^2}{P_{\rm{g}}}} \over {\partial x\partial y}}\sin \left( {2\phi } \right) + \left( {{{{\partial ^2}{P_{\rm{g}}}} \over {\partial {y^2}}} - {{{\partial ^2}{P_{\rm{g}}}} \over {\partial {x^2}}}} \right)\cos \left( {2\phi } \right)} \right]} \right)\delta {x^2}\delta {y^2},} \hfill \cr } $](/articles/aa/full_html/2023/04/aa45744-22/aa45744-22-eq53.png)