EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) L7 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number L7
Number of page(s) 14
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202245608
Published online 14 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

It has always been debated whether massive giant planets (4–13MJ) should be classified as planets or brown dwarfs (BDs; Chabrier et al. 2014; Spiegel et al. 2011; Schlaufman 2018). There are a few indirect ways to discriminate between massive giant planets and low-mass BDs. One is based on the deuterium burning mass limit, which states that, to be classified as a planet, an object should not be massive enough to sustain deuterium fusion at any point in its life. The upper mass limit for this deuterium fusion was calculated to be ≈13MJ for objects of solar metallicity (Boss et al. 2005), regardless of their formation channel. However, objects with less than 13MJ share a common “nature” with 13MJ objects, irrespective of what they have been called. That is why this definition, based on a clear-cut mass limit between BDs and planets, has caused disagreements (Chabrier et al. 2014), and various suggestions have been made to reshape it. The study by Spiegel et al. (2011) proposed that deuterium burning may vary from 11 to 16MJ, depending on the object’s helium and other metal content. Some other studies have recommended increasing the upper mass limit to ∼25MJ based on the “driest” region of the BD desert (Pont et al. 2005; Udry et al. 2010; Anderson et al. 2011). Hatzes & Rauer (2015) provided a new definition and proposed that objects in the 0.3–60MJ range be called giant gaseous planets because they follow a particular sequence in the mass-density diagram of all known planets, sub-stellar objects, and stars (see Fig. 1 of Hatzes & Rauer 2015). They do not see any abrupt changes in the mass–density diagram for objects in the 0.3–60MJ range and suggest that, irrespective of their formation scenarios, these objects should fall under the same general class of objects, that is to say, planets. However, the IAU recently proposed a working definition of exoplanets (Lecavelier des Etangs & Lissauer 2022) that states that, in addition to the 13MJ mass limit, the system should have a mass ratio with the central object below the L4/L5 instability (M/Mcentral < 2/(25 + 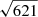) ≈ 1/25).

Some researchers favor using formation mechanisms to distinguish massive giant planets from BDs. Theoretically, two formation mechanisms dominate the literature: (i) core accretion (Schlaufman 2018; Pollack et al. 1996), which is generally followed by low-mass giant planets (MP < 4MJ), and (ii) disk instability (Boss 1997), which is generally favored by massive giant planets as well as low-mass BDs. However, the dominating mechanism for planet formation depends on the disk mass and host star metallicity conditions (i.e., their initial environmental conditions; Adibekyan 2019). Therefore, it is not clear how to trace the formation history of a planet from the current understanding, and this definition is also inadequate and problematic. Hence, a detailed characterization of more massive giant planets and low-mass BDs will enhance our knowledge of the processes involved in planet formation and offer more insight into the transition regions of these objects.

One frequently debated aspect of close-in massive giants or giant planets is whether they are formed at their present-day short orbits or migrated from farther out orbits (Batygin & Stevenson 2010; Baruteau et al. 2014). The common belief is that these planets form beyond the ice line and then migrate inward via various mechanisms to their present location. Migration of a planet to a close-in orbit occurs via torques from the protoplanetary disk (gas disk migration) or gravitational scattering due to another planet or star, that is, high-eccentricity tidal (HET) migration. Eventually, due to tidal forces, the orbit is circularized and shrunk (see Dawson & Johnson 2018, and references therein for a detailed review). Nevertheless, recent models suggest the in situ formation of close-in giant planets is also feasible (Batygin et al. 2016) and show that the inner boundary of short-period giant planets and their period-mass distribution could be consistent with predictions for in situ formation (Bailey & Batygin 2018). That is why which of these three scenarios predominates is still up for discussion, but a combination of these processes likely contributed to the current close-in giant planet population.

In this Letter we report the discovery of TOI-4603 b, a close-in massive giant planet in the overlapping mass region of BDs and planets. The subsequent sections discuss our observations, analysis, and results.

2. Observations

2.1. TESS observations

The Transiting Exoplanet Survey Satellite (TESS) observed the star TOI-4603 (HD 245134) in three sectors, 43, 44, and 45. All the observations were made with the two-minute cadence mode nearly continuously between September 16, 2021, and December 02, 2021 (∼74-day time span), with a gap of ∼5.5 days due to the data transferring from the spacecraft. Light curves were produced and analyzed for transit signals by the Science Processing Operations Center (SPOC; Jenkins et al. 2016), consisting of Simple Aperture Photometry (SAP) and Pre-search Data Conditioning Simple Aperture Photometry (PDCSAP; Smith et al. 2012; Stumpe et al. 2014) fluxes. These light curves are publicly available at the Mikulski Archive for Space Telescopes (MAST)1. The SPOC pipeline detected ten transits with a depth of ∼1020 ppm, an orbital period of ∼7.24 days, and a duration of ∼2.04 h. We adopted the median-normalized PDCSAP fluxes for further analysis, which we additionally detrended by fitting a high-order polynomial over out-of-transit data using the lightkurve package (Lightkurve Collaboration 2018). The normalized TESS light curve for TOI-4603 is shown in Fig. 1. The target pixel files (TPFs) of TOI-4603 generated with tpfplotter (Aller et al. 2020) for all the observing sectors can be found in Fig. B.6.

thumbnail Fig. 1.

Normalized PDCSAP light curve for TOI-4603 plotted with respect to time (upper panel) and to time in days from mid-transit (lower panel). The 2-min and 10-min binned data points are represented by blue and orange dots, respectively. The black line represents the best-fit transit model using EXOFASTv2 (see Sect. 3.3).

2.2. High resolution imaging

To assess the possible contamination of bound or unbound close companions on the derived planetary radii (Ciardi et al. 2015), we observed TOI-4603 with near-infrared adaptive optics (AO) imaging at Palomar Observatories. The observations of TOI-4603 were made with the Palomar High Angular Resolution Observer (PHARO) instrument (Hayward et al. 2001) behind the natural guide star AO system P3K (Dekany et al. 2013) on November 21, 2021, in a standard five-point quincunx dither pattern with steps of 5″ in the narrowband Brγ filter (λo = 2.1686; Δλ = 0.0326 μm). Each dither position was observed three times, offset in position from one another by 0.5″ for a total of 15 frames, with an integration time of 5.665 s per frame for total on-source times of 85 s. PHARO has a pixel scale of 0.025″ per pixel for a total field of view of ∼25″. The AO data were processed and analyzed with a custom set of IDL tools. The science frames were flat-fielded and sky-subtracted and then combined into a single image using an intra-pixel interpolation that conserves flux, shifts the individual dithered frames by the appropriate fractional pixels, and median-coadds the frames. The final resolutions of the combined dither were determined from the full width half maximum (FWHM) of the point spread functions: 0.117″. The sensitivities of the final combined AO image were determined by injecting simulated sources azimuthally around the primary target every 20° at separations of integer multiples of the central source’s FWHM (Furlan et al. 2017). The brightness of each injected source was scaled until standard aperture photometry detected it with 5σ significance. The resulting brightness of the injected sources relative to TOI-4603 set the contrast limits at that injection location. The final 5σ limit at each separation was determined from the average of all of the determined limits at that separation, and the uncertainty on the limit was set by the RMS dispersion of the azimuthal slices at a given radial distance. The final sensitivity curve for the Palomar data is shown in Fig. B.1; no additional stellar companions were detected.

2.2.1. Gaia assessment

The Gaia renormalized unit weight error (RUWE) is a metric similar to a reduced chi-square, where values ≲1.4 indicate that the Gaia astrometric solution is consistent with the star being single, whereas RUWE values ≳1.4 may indicate an astrometric excess noise, possibly caused by the presence of an unseen companion (e.g., Ziegler et al. 2020). TOI-4603 has a Gaia Early Data Release 3 (EDR3) RUWE value of 0.998, indicating that the astrometric fits are consistent with the single-star model.

2.3. Spectroscopy

2.3.1. Radial velocities with PARAS

Radial velocity (RV) observations were obtained using the PRL Advanced Radial velocity Abu-sky Search (PARAS) spectrograph coupled with the 1.2 m telescope at Physical Research Laboratory (PRL) at Gurushikhar Observatory, on Mount Abu, India. PARAS is a fiber-fed echelle spectrograph with a resolving power of R = 67 000 and a wavelength coverage of 380–690 nm. A total of 27 spectra were acquired between January 11, 2022, and November 02, 2022, using the simultaneous wavelength calibration mode with a uranium-argon (UAr) hollow cathode lamp as described in Chakraborty et al. (2014) and Sharma & Chakraborty (2021). The exposure time for all the spectra was 1800 s, leading to S/N per pixel of ∼9–18 at the blaze wavelength of 550 nm. More details on observations and data analysis can be found in Chakraborty et al. (2014). The reported uncertainties were measured as in Chaturvedi et al. (2016, 2018), and Khandelwal et al. (2022). All the RVs and their respective errors are listed in Table A.2.

2.3.2. Radial velocities with TRES

We obtained 13 observations between November 03, 2021, and September 16, 2022, using the Tillinghast Reflector Echelle Spectrograph (TRES; Fűrész 2008) on the 1.5 m Tillinghast Reflector telescope on Mount Hopkins, Arizona, USA. TRES is a fiber-fed echelle spectrograph with a resolving power of R = 44 000 that operates in the wavelength range 390–910 nm. The spectra were obtained in a sequence of three observations surrounded by ThAr calibration spectra, and then the medians were combined to remove cosmic rays. The average exposure time was 290 s, resulting in an average S/N per resolution element of 54.2. The spectra were extracted using the procedures outlined in Buchhave et al. (2010), and multi-order relative velocities were derived by cross-correlating the strongest S/N observed spectrum order by order against all of the remaining spectra. The RVs acquired with TRES spectra with their respective errors are listed in Table A.2.

3. Analysis

3.1. Spectroscopic parameters of TOI-4603

We used the stellar parameter classification tool (SPC; Buchhave et al. 2010, 2012, 2014) to derive stellar parameters from TRES spectra. It cross-correlates an observed spectrum against a grid of synthetic spectra based on Kurucz atmospheric models (Kurucz 1992). Using 12 of the 13 spectra that passed the quality flag based on the S/N, we derive Teff = 6243 ± 50 K, log g* of 3.94 ± 0.10 cgs, [m/H] of 0.22 ± 0.08 dex, and v sin i of 25.70 ± 0.50 km s−1.

We also obtained high S/N spectra (70 per resolution element at 550 nm) of the 1200 s with the Tautenburg Coude Echelle Spectrograph (TCES) installed at the 2 m Alfred Jensch Telescope in Thüringer Landessternwarte Tautenburg, Germany. The TCES is a slit spectrograph with a resolving power of R = 67 000 and a wavelength coverage of 470–740 nm. Details of the observations are provided in Guenther et al. (2009). The spectra were extracted using the IRAF and were used to compute stellar parameters with the zaspe package (Brahm et al. 2017). This yielded a Teff of 6273 ± 101 K, log g* of 3.73 ± 0.26 cgs, [Fe/H] of 0.34 ± 0.04 dex, and v sin i of 23.18 ± 0.37 km s−1 via a comparison against a grid of synthetic spectra generated from the ATLAS9 model atmospheres (Castelli et al. 2003). The stellar parameters acquired from TRES and TCES spectra are within the error bars.

Our analysis shows that TOI-4603 is a metal-rich, F-type sub-giant star. We also calculated the star’s rotation period by computing the generalized Lomb-Scargle (GLS) periodogram (Zechmeister & Kürster 2009) on the out-of-transit TESS PDCSAP light curves and find it to be 5.62 ± 0.02 days, which is comparable to the rotation period (assuming i = 90) derived using v sin i (Sect. 3.1) and stellar radii (Sect. 3.3). A less significant peak at ∼2.28 days was also observed in the periodogram, which may be quasi-periodic and related or unrelated to half of the rotational period signals. Pre-whitening the 5.62-day signal did not eliminate the 2.28-day signal, possibly suggesting it originated from another active region on the stellar disk. However, further analysis of the 2.28-day signal is beyond the scope of the current work.

We also inspected the star for solar-like oscillations. We first calculated the expected frequency of the maximum oscillation amplitude (vmax) using the above-calculated Teff and log g* using the seismic scaling relation (Lund et al. 2016), which yields vmax ≈ 700 μHz. Since this value is smaller than the Nyquist frequency for the 2-min (∼4166 μHz) cadence data, TESS photometric data are well suited for identifying the oscillations. We analyzed the oscillation signals using the lightkurve package and manually studied the power density spectra of the same TESS light curves, but could not detect any significant solar-like oscillations.

3.2. Periodogram analysis

Independent of photometry, we searched for periodic signals in RV data from both spectrographs, PARAS and TRES, using the GLS periodogram. These RVs were corrected for the instrumental offset prior to analysis. The periodogram is shown in panel 1 of Fig. B.2. We calculated the false alarm probability (FAP) of the signals using equations given in Zechmeister & Kürster (2009) and find the most significant signal at 7.24 days (marked with a vertical red line in Fig. B.2). This period is the same as estimated from transit data (see Sect. 2.1). The signal gives a FAP of 0.007% at 7.24 days using a bootstrap method over a narrow range centered on this period, robustly confirming the periodic signal in our RV data set. The other significant signals in the RV periodogram vanish after removing the 7.24-day periodic signal using the best-fit sinusoidal curve from the data sets (see the residual periodogram in panel 2). The spectral window function is shown in panel 3. As a diagnostic of the stellar activity indicator and stellar contamination from nearby stars, we computed the periodogram of bisectors (see panel 4) and find no statistically significant signal of stellar activity in the data sets.

3.3. Global modeling

We constrained the system parameters with simultaneous modeling and fitting of the RVs from PARAS and TRES and the TESS light curves using the publicly available EXOFASTv2 (Eastman et al. 2019) package. The software incorporates the differential evolution Markov chain Monte Carlo (MCMC) technique with the Bayesian approach to explore all the given parameter space.

To constrain the host star parameters, EXOFASTv2 uses a combination of (i) spectral energy distribution (SED; Stassun & Torres 2016) modeling, (ii) stellar evolutionary models, generally MESA isochrones and stellar tracks (MIST) isochrones (Choi et al. 2016; Dotter 2016), and (iii) the prior parameters. We performed SED fitting for TOI-4603 using the broadband photometry from Tycho BV (Høg et al. 2000), SDSS gri, APASS data release (DR) 9 BV (Henden et al. 2016), 2MASS JHK (Cutri et al. 2003), and ALL-WISE W1, W2, W3, and W4 (Cutri et al. 2021), as listed in Table A.1. We imposed Gaussian priors on the Teff and [Fe/H], determined from spectral analysis of the TCES spectra. Along with that, we also placed a Gaussian prior on the parallax from Gaia DR3 (Gaia Collaboration 2023) and enforced an upper limit on the V-band extinction of 1.59 from the Schlafly & Finkbeiner (2011) dust maps at the location of TOI-4603. The SED fitting uses Kurucz stellar atmospheric models (Kurucz 1979), and the resulting best-fit SED model with broadband photometry fluxes is shown in Fig. B.3. Within EXOFASTv2, the MIST evolutionary tracks are used to provide better estimates for the host star parameters. The most likely MIST evolutionary track from EXOFASTv2 provided the age of 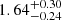Gyr (see Fig. B.4). The adopted stellar parameters are 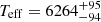K, 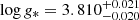dex, dex, M* = 1.765 ± 0.061 M⊙, and 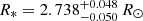. All the parameters are summarized in Table A.3 along with their 1σ uncertainty.

The simultaneous fitting of the RV and transit data was done by keeping all the parameters (such as b, i, Rp, aKω, and e) free and only providing starting values of P and Tc, given by the TESS QLP pipeline. The Mandel & Agol (2002) transit model was used for light curve fitting, and the RV data were modeled with a standard noncircular Keplerian orbit. We used the default quadratic limb-darkening law for the TESS passband, and the limb-darkening coefficients (u1 and u2) were calculated based on tables reported in Claret & Bloemen (2011) and Claret (2017). We used 42 chains and 50 000 steps for each MCMC fit, which were further diagnosed for convergence using built-in Gelman–Rubin statistics (Gelman & Rubin 1992; Ford 2006). The transit and RV data with their best-fit models using EXOFASTv2 are plotted in Figs. 1, 2, and B.5. We also fitted a long-term RV trend (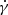) in the RV data and found it to be −0.14 ± 0.18 m s−1 day−1 (Table A.3), which may not be significant due to its relatively high uncertainty. All the planetary parameters obtained by EXOFASTv2 are reported in Table A.3.

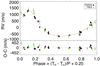thumbnail Fig. 2.

RVs obtained from PARAS and TRES plotted with respect to an orbital phase of ∼7.24 days. The best-fit RV model with EXOFASTv2 (see Sect. 3.3) is represented by the red line, and residuals between the best-fit model and the data are shown in the bottom panel.

4. Results and discussion

4.1. TOI-4603 b in context

We find the mass and radius of TOI-4603 b to be 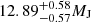and 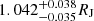, respectively, and find that it transits an F-type sub-giant star in an orbit of 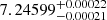days. The discovery of TOI-4603 b is a substantial contribution as it is in the overlapping mass region (11–16MJ; Spiegel et al. 2011) of massive giant planets and low-mass BDs based on the deuterium burning mass limit. As per the IAU definition for solar metallicity, the deuterium burning mass limit is 13MJ (Lecavelier des Etangs & Lissauer 2022). However, this limit depends on other factors, such as the abundance of helium and initial deuterium, and on the metallicity of the invoked model. For example, for three times the solar metallicity, 10% of initial deuterium can start burning at 11 MJ (Spiegel et al. 2011). Assuming the metallicity of TOI-4603 b to be the same as that of its parent star (i.e., 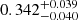dex), the companion here would have initiated deuterium fusion, thus not meeting its first criterion to be called a planet. However, according to the second criterion, TOI-4603 b has a mass ratio of 0.007, with the host below the L4/L5 instability (< 1/25), which is in favor of it being called an exoplanet. Finding the explicit nature of the astrophysical body in this mass range, whether it is a planet or a BD, can be an ambiguous task (see Schneider et al. 2011 for a detailed overview). Many in the field, including Spiegel et al. (2011, and references therein), do not consider the deuterium burning mass limit as a strict boundary for distinguishing planets and BDs. Some studies instead suggest as a criterion that the upper mass limit for a planet, in particular a gas-giant planet, should be 25MJ (Pont et al. 2005; Udry et al. 2010; Anderson et al. 2011) or, in some cases, 60MJ (Hatzes & Rauer 2015). Since TOI-4603 b, according to most of these definitions, qualifies as a gas giant, we would call it a planet here.

In Fig. 3 we present the mass versus density plot of transiting gas-giant planets and BDs that have a mass and radius with a precision better than 25% and reported mass ranges between 0.25MJ (lower mass limit for the gas giants from Dawson & Johnson 2018) and 85MJ (< 0.08 M⊙). To date, there are a total of 5310 confirmed exoplanets, out of which the masses of 1569 exoplanets have been determined2. Here we focus on the transiting giant planets (0.25–13 MJ), which leaves us with 477 transiting giant planets, including 35 massive giant planets (MP > 4MJ)3. In the figure we plot the MP = 13MJ the deuterium fusion mass limit for solar metallicity. As can be seen, there have only been three such close-in (a < 0.1 AU) transiting objects (HATS-70 b: Zhou et al. 2019 and XO-3 b: Johns-Krull et al. 2008) discovered in this mass range, including our work. This makes TOI-4603 b an important addition in the context of known giant planets.

thumbnail Fig. 3.

Planetary density as a function of planetary mass for transiting giant planets and BDs (0.25–85MJ). The shaded area represents the overlapping mass region of massive giant planets and BDs based on the deuterium burning limit, and the dotted lines are at MP = 13MJ and MP = 85MJ. The position of TOI-4603 b is denoted by the magenta dot.

4.2. Internal structure

We estimated the heavy element content of TOI-4603 b using the method described in Sarkis et al. (2021). Given the properties of TOI-4603 b, we estimated the planetary radius obtained with the evolution model completo21 (Mordasini et al. 2012) and compared it with the observed radius. We assumed that all the heavy elements are homogeneously mixed in the envelope and are modeled as water with the equation of state (EOS) of water ANEOS (Thompson 1990; Mordasini 2020). Similarly to Thorngren & Fortney (2018) and Komacek & Youdin (2017), we did not include a central core. The envelope was coupled with a semi-gray atmospheric model, and hydrogen and helium (He) were modeled with the SCvH EOS (Saumon et al. 1995) with a He mass fraction Y = 0.27. We used a Bayesian framework to infer the internal luminosity of the planet, which matches the planet’s radius given its mass and equilibrium temperature. The internal luminosity was governed by a linear uniform prior, and the content of heavy elements was informed by the Thorngren et al. (2016) relation. We find that the planetary radius is well reproduced with a fraction of heavy elements of 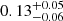. As noted in Sarkis et al. (2021), the prior on the internal luminosity has an effect on the final internal luminosity; however, the two values of heavy elements are compatible within 1σ. From this fraction of heavy elements in the envelope, we can derive the metal enrichment of the planet to be 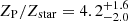(as done in Sect. 4.3 from Ulmer-Moll et al. 2022) and the total mass of heavy elements to be 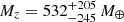. We include the posterior distribution of the fitted parameters in Appendix D.

TOI-4603b is a scientifically interesting object for studying the processes of planet formation at the transition between massive giant planets and BDs. Santos et al. (2017) proposed two populations of giant planets, with masses above and below ∼4MJ. Specifically, their finding suggests that the formation of lower-mass giant planets may be related to core accretion and that such planets have metal-rich hosts. In contrast, higher-mass planets may form through disk instability mechanisms and orbit stars with lower average metallicity values. Moreover, Schlaufman (2018) provided support to this theory by finding that planets with MP < 4MJ preferentially orbit metal-rich hosts, unlike planets with MP > 10MJ, which do not follow this trend. With its high metallicity ( dex), TOI-4603 b does not follow this trend and does not support the existence of any breakout point at 4MJ, as suggested by Adibekyan (2019). This demonstrates that, regardless of the metallicity of the host star, a massive giant planet can be formed via any process (Adibekyan 2019).

4.3. Eccentricity of TOI-4603 b and tidal circularization

The orbit of TOI-4603 b is found to be eccentric (e = 0.325 ± 0.020). Different processes, such as secular interactions, planet–planet scattering, planet–disk interactions, and high-eccentricity tidal migration, can explain the orbital evolution of giant planets (see Sect. 2 of Dawson & Johnson 2018 for more details). We plot the observed population of the transiting giant planets (0.25MJ < MP < 13MJ) in eccentricity and semimajor axis parameter space (similar to Dong et al. 2021) in Fig. 4 using the TEPcat database3. We show the region where planets could have undergone HET migration following the constant angular momentum tracks (shaded area). The boundary of this region is determined by the Roche limit and the tidal circularization timescale and is defined as a = 0.034–0.1 AU. The position of TOI-4603 b indicates that its orbit is undergoing HET migration.

thumbnail Fig. 4.

Orbital eccentricities of all the transiting giant planets (0.25MJ < M < 13MJ) plotted with respect to their semimajor axis (a) in AU. The data sets are taken from the TEPcat database (https://www.astro.keele.ac.uk/jkt/tepcat/), and planets whose eccentricities are known to a precision better than 25% are considered. The gray region represents the path of high-eccentricity migration with a range of 0.034–0.1 AU in the final semimajor axis and is set by the Roche limit and the circularization timescale. The giant planets are color-coded according to their host’s metallicity. Triangles represent planets with P < 3 days, diamonds 3 < P < 10 days, and circles P > 10 days. The position of TOI-4603 b is marked with an arrow.

Based on the giant planets’ eccentricity distribution (Fig. 4), planets with orbital periods between 3 and 10 days have a wider range of eccentricities (0.2 < e < 0.6) than those with shorter periods (e < 0.2). The most favorable explanation for these moderate eccentricities is HET migration, implying that these eccentric giant planets are in the process of tidal circularization. We also observe circular and eccentric giants at the same orbital periods because circular giant planets started their migration earlier than eccentric giant planets or have more efficient tidal dissipation effects. Some low eccentricities may be due to other formation channels, such as in situ formation or disk migration. Furthermore, most eccentric giant planets orbit metal-rich stars, whereas circular giant planets orbit both metal-poor and metal-rich stars (Fig. 4). Given the well-known correlation between the occurrence of giant planets and stellar metallicity, Dawson & Murray-Clay (2013) established that eccentric giant planets primarily orbit metal-rich stars. Their findings support HET migration via planet–planet gravitational interaction. TOI-4603 b, having an eccentric orbit and being a metallic host, is consistent with this trend. Moreover, Kervella et al. (2019) find that TOI-4603 has a widely separated (∼1.8 AU) BD companion (MP ≈ 20.52MJ) in its orbit. This BD companion may provide an explanation for this eccentricity. We also calculated the shortest tidal circularization timescale (τcir) to be 8.2 Gyr (for Q = 105; Adams & Laughlin 2006), greater than the star’s current age determined from this work. So, as per tidal evolutionary theory, the orbit of TOI-4603 b has not been circularized, which is consistent with our observations.

5. Summary and future prospects

This work presents the discovery and characterization of a transiting giant planet around the subgiant star TOI-4603 at an orbital period of 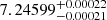days. It was initially identified as an exoplanet candidate using transit observations by NASA’s TESS mission. We complemented the TESS data with ground-based observations from the PARAS/PRL, TCES/TLS, TRES, and PHARO/Palomar instruments. Based on the global modeling of the TOI-4603 system, the host star is found to be a metal-rich ( dex), subgiant (log g*=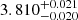 g cm−3), F-type ( 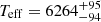K) star that has a mass, radius, and age of 1.765 ± 0.061 M⊙, 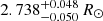, and 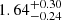Gyr, respectively. The planet TOI-4603 b has a mass of 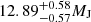, a radius of 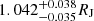, and an eccentricity of 0.325 ± 0.020 with an equilibrium temperature of 1677 ± 24 K. It is one of the most massive and densest transiting giant planets known to date and a valuable addition to the population of fewer than five known massive close-in giant planets in the high-mass planet and low-mass BD overlapping region (11MJ < MP < 16MJ). More such planets are required to understand the processes responsible for their formation.

TOI-4603 is a rapid rotator (v sin i = 23.18 ± 0.37 km s−1) and a relatively bright star (V = 9.2), well suited for study of the Rossiter–McLaughlin (RM) effect (Rossiter 1924; McLaughlin 1924) and helpful for measuring the projected stellar obliquity of planets. The calculated RM semi-amplitudes (Ohta et al. 2005) for the projected spin-orbit angle (λ) between 0° and 90° are 6.4 m s−1 and 31 m s−1. The detection of the RM effect for TOI-4603 is possible by observing precise RVs using moderate-sized telescopes (2.5–4 m aperture); for example, PARAS-2 (Chakraborty et al. 2018) at the 2.5 m telescope PRL is well suited for this work.

Acknowledgments

We acknowledge the generous support from PRL-DOS (Department of Space, Government of India) and the director of PRL for the PARAS spectrograph funding for the exoplanet discovery project and research grant for AK and SB. PC acknowledges the generous support from Deutsche Forschungsgemeinschaft (DFG) of the grant HA3279/11-1. We acknowledge the help from Kapil Kumar, Vishal Shah, and all the Mount-Abu, TLS, and Palomar observatory staff for their assistance during the observations. This work was also supported by the Thüringer Ministerium für Wirtschaft, Wissenschaft und Digitale Gesellschaft. This work has been carried out within the framework of the NCCR PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. We generously acknowledge Dr. Rafael Brahm for providing the grids to determine the spectroscopic parameters using zaspe. PC generously acknowledges Dr. Eike W. Guenther for his contribution in the spectroscopic observations from TCES. This research has made use of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. This research has made use of the Exoplanet Follow-up Observation Program (ExoFOP; DOI: 10.26134/ExoFOP5) website, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This paper includes data collected with the TESS mission, obtained from the MAST data archive at the Space Telescope Science Institute (STScI). This work has made use of the Transiting ExoPlanet catalogue (TEPcat) database. We would like to thank the anonymous referee for his/her numerous good suggestions which improved the quality of the paper.

References

  1. Adams, F. C., & Laughlin, G. 2006, ApJ, 649, 1004 [Google Scholar]
  2. Adibekyan, V. 2019, Geosciences, 9, 105 [Google Scholar]
  3. Aller, A., Lillo-Box, J., Jones, D., Miranda, L. F., & Barceló Forteza, S. 2020, A&A, 635, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Anderson, D. R., Collier Cameron, A., Hellier, C., et al. 2011, ApJ, 726, L19 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bailey, E., & Batygin, K. 2018, ApJ, 866, L2 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baruteau, C., Crida, A., Paardekooper, S. J., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 667 [Google Scholar]
  7. Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
  8. Batygin, K., Bodenheimer, P. H., & Laughlin, G. P. 2016, ApJ, 829, 114 [Google Scholar]
  9. Boss, A. P. 1997, Science, 276, 1836 [Google Scholar]
  10. Boss, A. P., Butler, R. P., Hubbard, W. B., et al. 2005, Proc. Int. Astron. Union, 1, 183 [CrossRef] [Google Scholar]
  11. Brahm, R., Jordán, A., Hartman, J., & Bakos, G. 2017, MNRAS, 467, 971 [NASA ADS] [Google Scholar]
  12. Buchhave, L. A., Bakos, G. Á., Hartman, J. D., et al. 2010, ApJ, 720, 1118 [NASA ADS] [CrossRef] [Google Scholar]
  13. Buchhave, L. A., Latham, D., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [CrossRef] [Google Scholar]
  14. Buchhave, L. A., Bizzarro, M., Latham, D. W., et al. 2014, Nature, 509, 593 [Google Scholar]
  15. Cannon, A. J., & Pickering, E. C. 1993, VizieR Online Data Catalog: III/135A [Google Scholar]
  16. Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, 210, A20 [Google Scholar]
  17. Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 619 [Google Scholar]
  18. Chakraborty, A., Mahadevan, S., Roy, A., et al. 2014, PASP, 126, 133 [CrossRef] [Google Scholar]
  19. Chakraborty, A., Thapa, N., Kumar, K., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, eds. C. J. Evans, L. Simard, & H. Takami, SPIE Conf. Ser., 10702, 107026G [NASA ADS] [Google Scholar]
  20. Chaturvedi, P., Chakraborty, A., Anandarao, B. G., Roy, A., & Mahadevan, S. 2016, MNRAS, 462, 554 [Google Scholar]
  21. Chaturvedi, P., Sharma, R., Chakraborty, A., Anandarao, B. G., & Prasad, N. J. S. S. V. 2018, AJ, 156, 27 [NASA ADS] [CrossRef] [Google Scholar]
  22. Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
  23. Ciardi, D. R., Beichman, C. A., Horch, E. P., & Howell, S. B. 2015, ApJ, 805, 16 [NASA ADS] [CrossRef] [Google Scholar]
  24. Claret, A. 2017, A&A, 600, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
  27. Cutri, R. M., Wright, E. L., Conrow, T., et al. 2021, VizieR Online Data Catalog: II/328 [Google Scholar]
  28. Dawson, R. I., & Johnson, J. A. 2018, ARA&A, 56, 175 [Google Scholar]
  29. Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [Google Scholar]
  30. Dekany, R., Roberts, J., Burruss, R., et al. 2013, ApJ, 776, 130 [CrossRef] [Google Scholar]
  31. Dong, J., Huang, C. X., Zhou, G., et al. 2021, ApJ, 920, L16 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
  33. Eastman, J. D., Rodriguez, J. E., Agol, E., et al. 2019, PASP, submitted [arXiv:1907.09480] [Google Scholar]
  34. Ford, E. B. 2006, ApJ, 642, 505 [Google Scholar]
  35. Fűrész, G. 2008, PhD Thesis, University of Szeged, Hungary [Google Scholar]
  36. Furlan, E., Ciardi, D. R., Everett, M. E., et al. 2017, AJ, 153, 71 [NASA ADS] [CrossRef] [Google Scholar]
  37. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, in press, https://doi.org/10.1051/0004-6361/202243940 [Google Scholar]
  39. Gelman, A., & Rubin, D. B. 1992, Statist. Sci., 7, 457 [NASA ADS] [Google Scholar]
  40. Guenther, E. W., Hartmann, M., Esposito, M., et al. 2009, A&A, 507, 1659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Hatzes, A. P., & Rauer, H. 2015, ApJ, 810, L25 [Google Scholar]
  42. Hayward, T. L., Brandl, B., Pirger, B., et al. 2001, PASP, 113, 105 [NASA ADS] [CrossRef] [Google Scholar]
  43. Henden, A. A., Templeton, M., Terrell, D., et al. 2016, VizieR Online Data Catalog: II/336 [Google Scholar]
  44. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
  45. Jenkins, J., Twicken, J., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [NASA ADS] [CrossRef] [Google Scholar]
  46. Johns-Krull, C. M., McCullough, P. R., Burke, C. J., et al. 2008, ApJ, 677, 657 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Khandelwal, A., Chaturvedi, P., Chakraborty, A., et al. 2022, MNRAS, 509, 3339 [NASA ADS] [Google Scholar]
  49. Komacek, T. D., & Youdin, A. N. 2017, ApJ, 844, 94 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kurucz, R. L. 1992, in The Stellar Populations of Galaxies, eds. B. Barbuy, & A. Renzini, 149, 225 [Google Scholar]
  52. Lecavelier des Etangs, A., & Lissauer, J. J. 2022, New Astron. Rev., 94 [Google Scholar]
  53. Lightkurve Collaboration (Cardoso, J. V. D. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
  54. Lund, M. N., Chaplin, W. J., Casagrande, L., et al. 2016, PASP, 128, 124204P [CrossRef] [Google Scholar]
  55. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [Google Scholar]
  56. McLaughlin, D. B. 1924, ApJ, 60, 22 [Google Scholar]
  57. Mordasini, C. 2020, A&A, 638, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Mordasini, C., Alibert, Y., Klahr, H., & Henning, T. 2012, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Ohta, Y., Taruya, A., & Suto, Y. 2005, ApJ, 622, 1118 [Google Scholar]
  60. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  61. Pont, F., Bouchy, F., Melo, C., et al. 2005, A&A, 438, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Rossiter, R. A. 1924, ApJ, 60, 15 [Google Scholar]
  63. Santos, N. C., Adibekyan, V., Figueira, P., et al. 2017, A&A, 603, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Sarkis, P., Mordasini, C., Henning, T., Marleau, G. D., & Mollière, P. 2021, A&A, 645, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
  66. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  67. Schlaufman, K. C. 2018, ApJ, 853, 37 [Google Scholar]
  68. Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Sharma, R., & Chakraborty, A. G. 2021, J. Astron. Telesc., Instrum. Syst., 7, 1 [NASA ADS] [CrossRef] [Google Scholar]
  70. Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [Google Scholar]
  71. Southworth, J. 2011, MNRAS, 417, 2166 [Google Scholar]
  72. Spiegel, D. S., Burrows, A., & Milsom, J. A. 2011, ApJ, 727, 57 [Google Scholar]
  73. Stassun, K. G., & Torres, G. 2016, ApJ, 831, L6 [NASA ADS] [CrossRef] [Google Scholar]
  74. Stassun, K. G., Oelkers, R. J., Pepper, J., et al. 2018, AJ, 156, 102 [Google Scholar]
  75. Stumpe, M. C., Smith, J. C., Catanzarite, J. H., et al. 2014, PASP, 126, 100 [Google Scholar]
  76. Thompson, S. L. 1990, Ann. Rev. Mat. Sci., 20, 245 [NASA ADS] [CrossRef] [Google Scholar]
  77. Thorngren, D. P., & Fortney, J. J. 2018, AJ, 155, 214 [Google Scholar]
  78. Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
  79. Udry, S. 2010, in In the Spirit of Lyot 2010, ed. A. Boccaletti, E11 [Google Scholar]
  80. Ulmer-Moll, S., Lendl, M., Gill, S., et al. 2022, A&A, 666, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
  82. Zhou, G., Bakos, G. Á., Bayliss, D., et al. 2019, AJ, 157, 31 [Google Scholar]
  83. Ziegler, C., Tokovinin, A., Briceño, C., et al. 2020, AJ, 159, 19 [Google Scholar]

Appendix A: Tables

Table A.1.

Basic stellar parameters for TOI-4603.

Table A.2.

RV measurements of TOI-4603.

Table A.3.

Priors along with median values and 68% confidence intervals for TOI-4603 from EXOFASTv2. The 𝒩 and 𝒰 represent the Gaussian and the uniform priors, respectively.

Appendix B: Figures

thumbnail Fig. B.1.

Palomar near-infrared AO imaging and sensitivity curves for TOI-4603 taken in the Brγ filter. The images were taken in good seeing conditions, and we reach a contrast of ∼7 magnitudes fainter than the host star within 0.″5. Inset: Image of the central portion of the data, centered on the star.

thumbnail Fig. B.2.

GLS periodogram for the RVs, residual RVs, window function, and bisector slope of TOI-4603, shown in panel s1, 2, 3, and 4 (upper to lower), respectively. The primary peak is seen at a period ≈7.24 days (vertical red line), consistent with the orbital period of the planetary candidate obtained from photometry. The FAP levels (dashed lines) of 0.1% for all the periodograms are shown in the legend of panel 1.

thumbnail Fig. B.3.

SED of TOI-4603.

thumbnail Fig. B.4.

Most likely MIST evolutionary track from EXOFASTv2 for TOI-4603, represented by a solid black line. The two dashed green lines show the evolutionary track of 1.58 M⊙ and 1.95 M⊙ (for 3σ limits).

thumbnail Fig. B.5.

RVs obtained from PARAS and TRES plotted with respect to time. The best-fit RV model with EXOFASTv2 (see Sect. 3.3) is represented by the red line, and residuals between the best-fit model and the data are shown in the bottom panel.

thumbnail Fig. B.6.

Target pixel file for TOI-4603 in sectors 43, 44, and 45 generated with tpfplotter (Aller et al. 2020). The squared region is the aperture mask used in the photometry, whereas the size of each individual dot is the magnitude contrast (Δm) from TOI-4603. The position of TOI-4603 is marked with a “1.”

Appendix C: Corner plot showing the covariances for all the fitted parameters for the TOI-4603 global fit

thumbnail Fig. C.1.

Corner plot showing the covariances for all the fitted parameters for the TOI-4603 global fit

Appendix D: Posterior distribution inferred for the interior modeling of TOI-4603 b

thumbnail Fig. D.1.

Posterior distribution inferred for the interior modeling of TOI-4603 b

All Tables

Table A.1.

Basic stellar parameters for TOI-4603.

In the text
Table A.2.

RV measurements of TOI-4603.

In the text
Table A.3.

Priors along with median values and 68% confidence intervals for TOI-4603 from EXOFASTv2. The 𝒩 and 𝒰 represent the Gaussian and the uniform priors, respectively.

In the text

All Figures

thumbnail Fig. 1.

Normalized PDCSAP light curve for TOI-4603 plotted with respect to time (upper panel) and to time in days from mid-transit (lower panel). The 2-min and 10-min binned data points are represented by blue and orange dots, respectively. The black line represents the best-fit transit model using EXOFASTv2 (see Sect. 3.3).
In the text
thumbnail Fig. 2.

RVs obtained from PARAS and TRES plotted with respect to an orbital phase of ∼7.24 days. The best-fit RV model with EXOFASTv2 (see Sect. 3.3) is represented by the red line, and residuals between the best-fit model and the data are shown in the bottom panel.
In the text
thumbnail Fig. 3.

Planetary density as a function of planetary mass for transiting giant planets and BDs (0.25–85MJ). The shaded area represents the overlapping mass region of massive giant planets and BDs based on the deuterium burning limit, and the dotted lines are at MP = 13MJ and MP = 85MJ. The position of TOI-4603 b is denoted by the magenta dot.
In the text
thumbnail Fig. 4.

Orbital eccentricities of all the transiting giant planets (0.25MJ < M < 13MJ) plotted with respect to their semimajor axis (a) in AU. The data sets are taken from the TEPcat database (https://www.astro.keele.ac.uk/jkt/tepcat/), and planets whose eccentricities are known to a precision better than 25% are considered. The gray region represents the path of high-eccentricity migration with a range of 0.034–0.1 AU in the final semimajor axis and is set by the Roche limit and the circularization timescale. The giant planets are color-coded according to their host’s metallicity. Triangles represent planets with P < 3 days, diamonds 3 < P < 10 days, and circles P > 10 days. The position of TOI-4603 b is marked with an arrow.
In the text
thumbnail Fig. B.1.

Palomar near-infrared AO imaging and sensitivity curves for TOI-4603 taken in the Brγ filter. The images were taken in good seeing conditions, and we reach a contrast of ∼7 magnitudes fainter than the host star within 0.″5. Inset: Image of the central portion of the data, centered on the star.
In the text
thumbnail Fig. B.2.

GLS periodogram for the RVs, residual RVs, window function, and bisector slope of TOI-4603, shown in panel s1, 2, 3, and 4 (upper to lower), respectively. The primary peak is seen at a period ≈7.24 days (vertical red line), consistent with the orbital period of the planetary candidate obtained from photometry. The FAP levels (dashed lines) of 0.1% for all the periodograms are shown in the legend of panel 1.
In the text
thumbnail Fig. B.3.

SED of TOI-4603.
In the text
thumbnail Fig. B.4.

Most likely MIST evolutionary track from EXOFASTv2 for TOI-4603, represented by a solid black line. The two dashed green lines show the evolutionary track of 1.58 M⊙ and 1.95 M⊙ (for 3σ limits).
In the text
thumbnail Fig. B.5.

RVs obtained from PARAS and TRES plotted with respect to time. The best-fit RV model with EXOFASTv2 (see Sect. 3.3) is represented by the red line, and residuals between the best-fit model and the data are shown in the bottom panel.
In the text
thumbnail Fig. B.6.

Target pixel file for TOI-4603 in sectors 43, 44, and 45 generated with tpfplotter (Aller et al. 2020). The squared region is the aperture mask used in the photometry, whereas the size of each individual dot is the magnitude contrast (Δm) from TOI-4603. The position of TOI-4603 is marked with a “1.”
In the text
thumbnail Fig. C.1.

Corner plot showing the covariances for all the fitted parameters for the TOI-4603 global fit
In the text
thumbnail Fig. D.1.

Posterior distribution inferred for the interior modeling of TOI-4603 b
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.