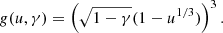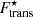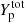| Issue |
A&A
Volume 672, April 2023
|
|
|---|---|---|
| Article Number | A160 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202245061 | |
| Published online | 14 April 2023 | |
The proto-neutron star inner crust in the liquid phase
1
Normandie Univ., ENSICAEN, UNICAEN, CNRS/IN2P3, LPC Caen, 14000 Caen, France
e-mail: dinh@lpccaen.in2p3.fr
2
Grand Accélérateur National d’Ions Lourds (GANIL), CEA/DRF – CNRS/IN2P3, Boulevard Henri Becquerel, 14076 Caen, France
Received:
26
September
2022
Accepted:
8
February
2023
Context. The crust of a neutron star is known to melt at a temperature that increases with increasing matter density, up to about 1010 K. At such high temperatures and beyond, the crustal ions are put into collective motion and the associated entropy contribution can affect both the thermodynamic properties and the composition of matter.
Aims. We studied the importance of this effect in different thermodynamic conditions relevant to the inner crust of the proto-neutron star, both at beta equilibrium and in the fixed-proton-fraction regime.
Methods. To this aim, we solved the hydrodynamic equations for an ion moving in an incompressible, irrotational, and non-viscous fluid, with different boundary conditions, thus leading to different prescriptions for the ion effective mass. We then employed a compressible liquid-drop approach in the one-component plasma approximation, including the renormalisation of the ion mass to account for the influence of the surrounding medium.
Results. We show that the cluster size is determined by the competition between the ion centre-of-mass motion and the interface properties, namely the Coulomb, surface, and curvature energies. In particular, including the translational free energy in the minimisation procedure can significantly reduce the optimal number of nucleons in the clusters and lead to an early dissolution of clusters in dense beta-equilibrated matter. On the other hand, we find that the impact of translational motion is reduced in scenarios where the proton fraction is assumed constant and is almost negligible on the inner-crust equation of state.
Conclusions. Our results show that the translational degrees of freedom affect the equilibrium composition of beta-equilibrated matter and the density and pressure of the crust-core transition in a non-negligible way, highlighting the importance of its inclusion when modelling the finite-temperature inner crust of the (proto-)neutron star.
Key words: dense matter / stars: neutron / equation of state / plasmas
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The inner crust of a neutron star (NS), a region of ≈1 km thickness laying outside the homogeneous nuclear-matter core of the star, is known to play a key role in several phenomena related to the physics of the whole star, particularly the cooling process (Newton et al. 2013; Horowitz et al. 2015; Lin et al. 2020) and its transport properties (see e.g. Schmitt & Shternin 2018 for a review). The inner crust is made of a periodic lattice of extremely exotic ions embedded in a highly relativistic electron gas; the nuclei are so neutron rich that the neutron eigenstates lay high in the continuum and constitute a superfluid neutron gas in which the nuclei are immersed. Because of this peculiar structure, the most realistic modelling of the NS inner crust available today is based on microscopic self-consistent Hartree-Fock (HF), Hartree-Fock+BCS, or Hartree-Fock-Bogoliubov (HFB) calculations (see e.g. Magierski & Heenen 2002; Baldo et al. 2007; Gögelein & Müther 2007; Grill et al. 2011; Shelley & Pastore 2020), or on the extended Thomas-Fermi plus Strutinski Integral method based on accurately calibrated functionals (see e.g. Pearson et al. 2018, 2020; Shelley & Pastore 2021; Pearson & Chamel 2022). These approaches allow a self-consistent treatment of the nucleonic states and the inclusion of pairing and shell effects. Some of the aforementioned works also allowed for extension to include the description of strongly deformed clusters at the edge of the crust-core transition, known as ‘pasta’ phases. These microscopic calculations usually employ effective functionals optimised on both experimental data, such as nuclear masses, and ab initio calculations of nuclear matter, and the residual model dependence can be accurately quantified with statistical tools (Pastore et al. 2017).
In finite-temperature phenomena, such as proto-NS cooling and NS mergers, where the temperature can easily exceed values of several 1010 K, the crust is expected to be made of a liquid multi-component plasma composed of different nuclear species in strong interaction with the neutron (and, at sufficiently high temperature, even the proton) gas (see e.g. Oertel et al. 2017; Burgio & Fantina 2018 for a review). In this regime, the Wigner-Seitz (WS) cell is not related to any lattice structure but only represents the smallest charge-neutral volume scale, where the ion translational motion should be accounted for. In particular, in the low-density, high-temperature nuclear statistical equilibrium limit, it is the competition between the translational and the mass term that determines the ion abundances, which are given by the stationary solution of the Saha equations (see e.g. Hillebrandt et al. 1984). This multi-component structure of the NS matter necessitates beyond-mean-field methods at a mesoscopic scale, which become computationally demanding for a full density functional treatment.
If we limit ourselves to moderate temperatures close to the crystallisation transition, kBTm ≈ 0.1 − 1 MeV (Haensel et al. 2007), with kB being the Boltzmann constant, Carreau et al. (2020b) showed that the cluster distribution is relatively narrow at least at the lowest densities in the inner crust, meaning that the one-component plasma (OCP) approximation can be justified (Burrows & Lattimer 1984). Still, in this temperature regime, the relative collective motion of the cluster and the nucleon fluid has to be included. Indeed, the melting process is mainly due to the competition between vibrational and translational degrees of freedom (Potekhin & Chabrier 2000; Haensel et al. 2007; Medin & Cumming 2010; Fantina et al. 2020; Carreau et al. 2020a), and these latter become more and more important with increasing temperature. However, accounting for the collective motion of the clusters in variational OCP approaches based on nucleonic degrees of freedom, such as the microscopic HFB, is not a straightforward task, particularly from a computational point of view.
Because of these difficulties and the intrinsic complexity of multi-component plasma calculations, since the pioneering work by Lattimer et al. (1985), most approaches to the finite-temperature crust employed the OCP approximation with cluster – rather than nucleon – degrees of freedom (see e.g. Avancini et al. 2009, 2017; Fantina et al. 2020; Carreau et al. 2020a). This same approximation is employed in most so-called ‘general-purpose’ equations of state currently used in supernova and merger simulations (Lattimer & Swesty 1991; Shen et al. 2011a,b; Schneider et al. 2017; see also Oertel et al. 2017; Burgio & Fantina 2018 for a review). In these formalisms, it is, in principle, straightforward to include translational degrees of freedom for the clusters. However, the translational term is often neglected (Avancini et al. 2009, 2017; Shen et al. 2011a) or excluded from the variational equation with respect to the cluster size (Lattimer & Swesty 1991; Schneider et al. 2017).
Indeed, evaluating the mobility of an ion in a fixed nucleon background is not a simple problem. Many works have been devoted to a similar issue, namely the mobility of superfluid neutrons in the ion rest frame in the case of a collective rotation of the solid crust. In this case, a non-dissipative drag due to Bragg scattering was predicted, the so-called ‘entrainment’ effect (Chamel 2005, 2006, 2012, 2017). This effect is due to the complex structure of the Fermi surface, originating from the neutron band structure generated by the periodic ion potential. The momentum transfer to the lattice of dripped neutrons lying in the energy bands imposed by the Bloch boundary conditions is found to lead to effective binding of the neutrons to the periodic structure. This would correspond to an increase in the effective mass of the clusters, even if the direction of the momentum transfer is still a matter of debate, with recent works reporting an ‘anti-entrainement’ with an increased neutron mobility and consequently a reduction of the ion effective mass (Kashiwaba & Nakatsukasa 2019; Sekizawa et al. 2022).
However, in the liquid phase, the situation is very different. The motion of the different clusters is fully uncorrelated, collective lattice effects are absent, and the Fermi surface of dripped neutrons is essentially spherical. The liquid phase problem closely resembles that of the fluid-dynamic flow of neutrons around impurities, as treated by different authors (Epstein 1988; Magierski & Bulgac 2004a,b; Martin & Urban 2016). In the hypothesis of an irrotational and incompressible flow, the local hydrodynamic equations admit an analytical solution, leading to a systematic reduction of the cluster effective mass. This can be explained given that the cluster, considered as a finite portion of nuclear matter at higher density with respect to the nucleon ‘gas’, is assumed to be permeable to the surrounding nuclear fluid. Therefore, in the frame of the cluster, the unbound neutrons counter-flow and the cluster effectively moves with a reduced speed. According to the hydrodynamical description, the ion inertia can be increased only if the nucleus is considered as an impermeable solid obstacle (Sedrakian 1996) displacing the neutron fluid in its motion and therefore leading to an effective drag, a picture that is difficult to reconcile with the microscopic treatment of nuclear dynamics (Negele 1982; Jin et al. 2021).
In this paper, we carry out a study of the effect of the inclusion of translational degrees of freedom on the equation of state and the composition of matter in the liquid phase in the density regime relevant to the inner crust of the (proto-)NS. We employed the formalism of Carreau et al. (2019, 2020a), Dinh Thi et al. (2021a,b), and Grams et al. (2022a) that, although not as microscopic as a full density functional treatment, was recently shown to provide results in good agreement with extended Thomas-Fermi calculations both at zero (Grams et al. 2022b) and finite temperature (Carreau et al. 2020a). This approach is extended here to include the possible presence of proton drip and to compute the exact numerical calculation of the Fermi integrals beyond the Sommerfeld approximation previously used in Carreau et al. (2020a). Our calculations were performed in two different conditions: (i) the beta-equilibrium and (ii) the fixed-proton-fraction case. The former situation is achieved in late (proto-)NS cooling stages, after tens of seconds from the birth of the hot proto-NS (Burrows & Lattimer 1986; Prakash et al. 1997; Yakovlev & Pethick 2004; Page et al. 2006). The second condition is of interest for astrophysical scenarios, either where the total proton fraction can be assumed to be roughly constant, as in some regions of the supernova collapsing core in the neutrino-trapped regime (e.g. Sato 1975; Bruenn 1985; see also Liebendörfer et al. 2005), or for the computation of general-purpose equations of state, where calculations are performed for given (fixed) values of density nB, temperature T, and total proton (or electron) fraction 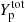 (see e.g. Lattimer & Swesty 1991; Shen et al. 2011b,a; Schneider et al. 2017; see also Oertel et al. 2017; Typel et al. 2015 for an overview of general-purpose equation-of-state computation). For this reasons, several studies have been devoted to calculations at finite temperature and fixed proton fraction (
(see e.g. Lattimer & Swesty 1991; Shen et al. 2011b,a; Schneider et al. 2017; see also Oertel et al. 2017; Typel et al. 2015 for an overview of general-purpose equation-of-state computation). For this reasons, several studies have been devoted to calculations at finite temperature and fixed proton fraction (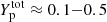 ), particularly for conditions relevant to supernova matter (e.g. Avancini et al. 2009, 2017; Newton & Stone 2009; Pais & Stone 2012; Pais et al. 2014; Ji et al. 2020).
), particularly for conditions relevant to supernova matter (e.g. Avancini et al. 2009, 2017; Newton & Stone 2009; Pais & Stone 2012; Pais et al. 2014; Ji et al. 2020).
The paper is organised as follows: In Sect. 2 we review the standard hydrodynamic calculation of ion motion and derive the expressions for the effective mass of an ion, treating the ion as a hard impenetrable sphere in Sect. 2.1 or as a permeable sphere in Sect. 2.2. We subsequently introduce our formalism for the proto-NS inner crust in Sect. 3. After outlining the expression of the bulk, Coulomb, surface, and curvature free-energy terms in Sects. 3.1 and 3.2, special attention is given to the derivation of the translational free energy in Sect. 3.3. In particular, we discuss the different modifications to the ideal-gas expression that have to be introduced in the dense medium. Results at beta equilibrium are presented in Sect. 4 while those in the fixed-proton-fraction scenario are shown in Sect. 5. Conclusions are given in Sect. 6.
2. Hydrodynamic approach of the ion motion
In the liquid phase we are interested in, the translational degrees of freedom of the ions should be accounted for. As discussed in Sect. 1, calculating the ion mobility in a nucleon background is not straightforward. If the effect of the nucleon background is neglected, the free energy corresponding to the translational motion reduces to the standard expression of an ideal gas (Haensel et al. 2007; see Sect. 3.3). However, densities in the NS crust are relatively high, particularly at the bottom of the crust, and therefore the in-medium effects cannot be ignored. In particular, the cluster bare mass Mi = (A − Z)mn + Zmp – where A and Z are the ion mass and proton number, respectively, and mn (mp) is the neutron (proton) mass – should be replaced by an effective mass 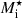 accounting for the modification of the free flow in a nuclear medium.
accounting for the modification of the free flow in a nuclear medium.
In this section, we review the derivation of the effective mass of the ion moving in an incompressible and irrotational fluid, within an ideal hydrodynamic approach, as already proposed in the literature for a different application (Epstein 1988; Sedrakian 1996; Magierski & Bulgac 2004a,b; Martin & Urban 2016; Chamel 2017). We present the solutions to the hydrodynamic equations with two different boundary conditions, which correspond to the assumptions that the ion is (i) an impenetrable hard sphere, and (ii) a permeable sphere.
Let us start by considering an ion – with density n(r) = ni for r < rN, where rN is the ion radius (therefore 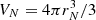 is the ion volume) – moving in a uniform background with density n(r) = ng = ngn + ngp for r > rN, where ngn (ngp) is the neutron (proton) component. The ion motion is sketched in Fig. 1: the ion centre-of-mass velocity u is directed along the z axis, with the ion centre of mass coinciding with the origin of the system of reference, that is,
is the ion volume) – moving in a uniform background with density n(r) = ng = ngn + ngp for r > rN, where ngn (ngp) is the neutron (proton) component. The ion motion is sketched in Fig. 1: the ion centre-of-mass velocity u is directed along the z axis, with the ion centre of mass coinciding with the origin of the system of reference, that is, 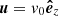 . As nuclear matter both inside and outside the ion is assumed to be incompressible and irrotational, there exists a velocity potential solution of the Laplace equation ∇2Φ(r) = 0 with v = ∇Φ, such that Φ(r) = Φin(r)+Φout(r), with Φin(r) and Φout(r) being the potential inside (r < rN) and outside (r > rN) the cluster, respectively.
. As nuclear matter both inside and outside the ion is assumed to be incompressible and irrotational, there exists a velocity potential solution of the Laplace equation ∇2Φ(r) = 0 with v = ∇Φ, such that Φ(r) = Φin(r)+Φout(r), with Φin(r) and Φout(r) being the potential inside (r < rN) and outside (r > rN) the cluster, respectively.
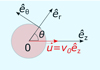 |
Fig. 1. Sketch of the motion of the ion (red sphere) in a uniform background, with the considered system of reference. |
Because of the azimuthal symmetry of the system, Φ(r) = Φ(r, θ), (see Fig. 1), the standard separable ansatz, Φ(r, θ) = R(r)Θ(θ), leads to the following general solution of the Laplace equation,
where k = {in, out}, Pl is the Legendre polynomial, and the coefficients of the series have to be determined from the boundary conditions. In the ion reference frame moving at speed u with respect to the crust, the general condition that the nucleon fluid should be asymptotically unaffected by the ion motion, that is limr → ∞v(r) = − u, implies l = 1 in Eq. (1) for the outer region, leading to:
independently of the conditions at the surface between the ion and the fluid.
2.1. Ion as an impenetrable hard sphere
Let us first consider the ion as an impenetrable hard sphere. In this case, the velocity potential Φin is fully determined by the condition that the velocity field is constant inside the ion, v(r < rN, θ) = u. Concerning Φout, the constants 𝒜out and ℬout in Eq. (2) are determined by imposing that in the crust reference frame, the nucleon fluid is at rest far from the ion, v(r → ∞, θ) = 0, and the sphere is impenetrable, meaning that the ion ‘pushes’ the external nucleon fluid along in the same direction of motion, that is, vr(r → rN, θ) = ur, where vr and ur are the radial components of v and u, respectively. This leads to the following expression for the potential field Φ:
The kinetic energy associated to the flow can therefore be calculated as
where ρb(r) is the local (baryonic) mass density, and the integral is extended to the total volume. Applying the divergence theorem, the kinetic energy reads
with ρb, i = Mi/VN being the mass density of the ion and ρb, g = mpngp + mnngn being that of the outside fluid. Defining γ ≡ ρb, g/ρb, i, we find
which reduces to 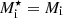 for nuclei in vacuum (γ = 0). Therefore, modelling the ion as an impenetrable hard sphere leads to an increase in the ion effective mass. Making the further approximation that the neutron and proton mass be equal, one retrieves Eq. (2.43) of Lattimer et al. (1985; although in the latter work the outside medium also includes alpha particles). Additionally, if there are no dripped protons, and therefore ng = ngn and γ = ngn/ni, one recovers the picture of the neutron fluid flowing around the cluster, as mentioned in Sedrakian (1996).
for nuclei in vacuum (γ = 0). Therefore, modelling the ion as an impenetrable hard sphere leads to an increase in the ion effective mass. Making the further approximation that the neutron and proton mass be equal, one retrieves Eq. (2.43) of Lattimer et al. (1985; although in the latter work the outside medium also includes alpha particles). Additionally, if there are no dripped protons, and therefore ng = ngn and γ = ngn/ni, one recovers the picture of the neutron fluid flowing around the cluster, as mentioned in Sedrakian (1996).
2.2. Ion as a permeable sphere
From the microscopic point of view, the cluster and the dripped nucleons are portions of the same fluid (nuclear matter) with different densities and proton-to-neutron ratios. One therefore expects that in the ion reference frame (at least a portion of) the nucleons in the cluster participate in the flow of the (external) fluid. This latter situation was studied by Magierski & Bulgac (2004a,b), who modelled the ion and the dripped neutrons as a single fluid and found that, as opposed to the hard-sphere image, a uniform flow of neutrons penetrates through the cluster. This latter is also an extreme picture, because we only expect the nucleons in the cluster to participate in the external flow if they are loosely bound. A more realistic picture would probably be intermediate between these latter two scenarios, whereby a fraction of neutrons in the cluster are able to ‘freely’ move with the external fluid (see also Fig. 7 in Martin & Urban 2016).
Let us use 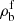 (nf) to denote the mass density (number density) of the neutrons that participate in the flow (therefore
(nf) to denote the mass density (number density) of the neutrons that participate in the flow (therefore 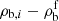 is the mass density of neutrons plus protons moving together in the cluster). The condition of the continuity of the current at the interface between the ion and the external fluid implies the following boundary condition to the velocity potential:
is the mass density of neutrons plus protons moving together in the cluster). The condition of the continuity of the current at the interface between the ion and the external fluid implies the following boundary condition to the velocity potential:
This means that we can consider only the l = 1 component in Eq. (1) for Φin. Additionally imposing the continuity of Φ at r = rN, that the medium is at rest at infinity (i.e., Φout → 0 for r → ∞), and the non-divergence of Φin at r = 0, the solution of the Laplace equation, Eq. (2), reads:
where we define 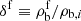 and γ ≡ ρb, g/ρb, i.
and γ ≡ ρb, g/ρb, i.
The kinetic energy associated to the flow is calculated using Eq. (4), yielding:
where we define the effective mass of the ion as:
As δf > 0, we can see that the effective mass of the cluster is reduced with respect to the bare mass; in other words, the cluster moves in the medium with a reduced speed. In the limiting δf = 0 case, corresponding to the situation where no neutrons participate in the external flow and all neutrons move with the protons in the cluster, one recovers Eq. (6).
Again assuming that the neutron and proton mass are equal and that the dripped-proton density is negligible leads to δf ≈ nf/ni and γ ≈ ngn/ni. Neglecting the possible contribution from proton unbound states appears to be a reasonable approximation at the relatively low temperatures considered in this work (see lower panels of Fig. 8).
In this approximation, and setting δf = 1, meaning that all neutrons in the cluster participate in the ‘free’ motion and the cluster is completely permeable to the flow of the outside fluid, one retrieves Eq. (12) of Magierski & Bulgac (2004b), which has the correct high-density physical limit, namely 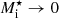 for γ → 1 (uniform homogeneous system),
for γ → 1 (uniform homogeneous system),
To precisely evaluate the effective mass, fully microscopic calculations of the dynamical properties of nuclei in a dense nuclear-matter medium would be needed. Nevertheless, we can evaluate the influence of the effective mass in two additional limiting cases:
-
The first considers that only neutrons in the continuum participate in the (collective) flow, as proposed by Carter et al. (2005). In this case, we can write
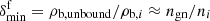 , leading to
, leading towhere we assume that the continuum contribution is homogeneous. It is interesting to note that here the effective mass is equal to the nucleus mass in the e-cluster representation proposed by Papakonstantinou et al. (2013) and Raduta et al. (2014). Although the prescription for continuum counting as ρb, unbound/ρb, i ≈ ngn/ni is rough, it is found to give an accurate estimation of the total number of unbound non-resonant states obtained from a microscopic HF (Papakonstantinou et al. 2013) or HFB (Chamel 2012; Martin & Urban 2016) calculation in the whole density region corresponding to the inner crust.
-
In the second limiting case, all neutrons in the cluster are considered to participate in the (external) flow, that is, δmax = ρb, in/ρb, i ≈ 1 − Z/A ≡ 1 − yp, leading to
The use of the different expressions for the ion effective mass in the translational free energy is presented in Sect. 3.3.
3. Model of the inner crust at finite temperature
In the OCP or single-nucleus approximation, the inner crust of a NS can be considered to be composed of identical WS cells, each of which includes a fully ionised ion characterised by mass number A and proton number Z, radius rN, and internal density ni. In the solid phase, the ion is located at the centre of the (body-centred cubic; bcc) cell of volume VWS and it is surrounded by uniform distributions of electrons, neutrons, and protons, whose densities are respectively denoted by ne, ngn, and ngp. In the liquid phase we are interested in, because of the OCP approximation, a WS volume can still be defined as the optimal volume centred on each (moving) ion, and is obtained from the condition of charge neutrality; see Eq. (16).
At a given thermodynamic condition, defined by the baryonic density nB and temperature T if beta equilibrium is assumed1, the total free-energy density of the system can be written as
where ℱe = ℱe(ne, T) is the electron gas free-energy density2, ℱg = ℱB(ng, δg, T)+mnc2ngn + mpc2ngp is the free-energy density of uniform nuclear matter (including the rest masses of nucleons) at baryonic density ng = ngn + ngp, isospin asymmetry 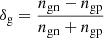 , and temperature T (see Sect. 3.1 for more details),
, and temperature T (see Sect. 3.1 for more details), 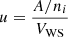 is the volume fraction of the cluster, and Fi is the cluster free energy, which includes the Coulomb interaction between the nucleus and the electron gas, as well as the residual interface interaction between the nucleus and the surrounding dilute nuclear-matter medium (see Sect. 3.2 for details). The excluded-volume term breaking the additivity of the free energy in Eq. (14), −uℱg, has also been shown to account for the subtraction of the gas states from the nuclear partition sum, which avoids double counting of unbound single-particle states (Gulminelli & Raduta 2015; Mallik & Gulminelli 2021).
is the volume fraction of the cluster, and Fi is the cluster free energy, which includes the Coulomb interaction between the nucleus and the electron gas, as well as the residual interface interaction between the nucleus and the surrounding dilute nuclear-matter medium (see Sect. 3.2 for details). The excluded-volume term breaking the additivity of the free energy in Eq. (14), −uℱg, has also been shown to account for the subtraction of the gas states from the nuclear partition sum, which avoids double counting of unbound single-particle states (Gulminelli & Raduta 2015; Mallik & Gulminelli 2021).
The total free-energy density ℱ in Eq. (14) was minimised under the two constraints coming from the conservation of the baryonic number and the charge neutrality:
where I = 1 − 2Z/A and np = Z/VWS. Two Lagrange multipliers, γ1 and γ2, were introduced, and the function to be minimised is expressed as
Minimising Ω with respect to ngn and ngp, we obtain the following expressions for γ1 and γ2:
in which μn and μp are respectively defined as
On the right-hand side of Eqs. (20) and (21), we can easily see that the first terms are the chemical potentials of the unbound nucleons, 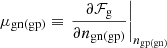 , while the last terms account for the in-medium modification induced by the Coulomb screening and the centre-of-mass translation.
, while the last terms account for the in-medium modification induced by the Coulomb screening and the centre-of-mass translation.
In order to describe the nuclear energetics, we employed a compressible liquid-drop (CLD) model approach, as in Carreau et al. (2019, 2020a), Dinh Thi et al. (2021a,b), which describes the ion as a cluster of nucleons in a leptodermous expansion. Considering the inner crust in the liquid phase, the collective degrees of freedom are translational, meaning that Fi in Eq. (14) can be written as:
where Mi = (A − Z)mn + Zmp is the total bare mass of the cluster, 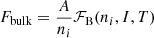 is the cluster bulk free energy, FCoul + surf + curv is the sum of the Coulomb, surface, and curvature energies, and the last term, Ftrans, accounts for the translational degree of freedom of the cluster. We discuss these terms in detail in the following sections.
is the cluster bulk free energy, FCoul + surf + curv is the sum of the Coulomb, surface, and curvature energies, and the last term, Ftrans, accounts for the translational degree of freedom of the cluster. We discuss these terms in detail in the following sections.
3.1. Nuclear matter free energy in the mean-field approximation
Computation of the cluster and the surrounding nuclear-matter bulk free-energy terms requires knowledge of the free-energy density of homogeneous nuclear matter ℱB(n, δ, T) at a total baryonic density3n = nn + np and isospin asymmetry δ = (nn − np)/n. To this aim, we used the self-consistent mean-field thermodynamics (Lattimer et al. 1985; Ducoin et al. 2007). In this approach, the free energy was decomposed into a ‘potential’ and a ‘kinetic’ part:
where the temperature dependence encoded in the term ℱkin is the same as in a system of independent quasi-particles with effective single-particle energies 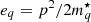 (p being the momentum and q = n, p labelling neutrons and protons) and with shifted effective chemical potentials
(p being the momentum and q = n, p labelling neutrons and protons) and with shifted effective chemical potentials 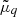 that account for the self-consistent interaction.
that account for the self-consistent interaction.
The terms ‘potential’ and ‘kinetic’ are put into quotes, because the kinetic term includes density-dependent neutron and proton effective masses 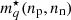 that physically arise from the non-locality of the effective nucleon–nucleon interaction. These effective masses lead to a deviation from the parabolic approximation to the symmetry energy (Li et al. 2021; Grams et al. 2022a), and a complex temperature dependence of the bulk term as discussed below, both for the dripped nucleons and for the nucleus. Beyond-mean-field effects may lead to an extra explicit temperature dependence of the potential term 𝒱. However, effects beyond the renormalisation of the nucleon effective mass were shown to be very small both in Brueckner-Hartree-Fock (Lu et al. 2019; Shang et al. 2020) and in many-body perturbation theory (Somasundaram et al. 2021), and are neglected in this work.
that physically arise from the non-locality of the effective nucleon–nucleon interaction. These effective masses lead to a deviation from the parabolic approximation to the symmetry energy (Li et al. 2021; Grams et al. 2022a), and a complex temperature dependence of the bulk term as discussed below, both for the dripped nucleons and for the nucleus. Beyond-mean-field effects may lead to an extra explicit temperature dependence of the potential term 𝒱. However, effects beyond the renormalisation of the nucleon effective mass were shown to be very small both in Brueckner-Hartree-Fock (Lu et al. 2019; Shang et al. 2020) and in many-body perturbation theory (Somasundaram et al. 2021), and are neglected in this work.
The density dependence of the ‘potential’ term was set to reproduce different nuclear functionals at zero temperature, covering the uncertainties of nuclear theory. To this aim, we employed the so-called meta-modelling approach proposed in Margueron et al. (2018a,b), where 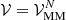 was expressed as a Taylor expansion truncated at order N around the saturation point (n = nsat, δ = 0). Margueron et al. (2018a) showed that different nucleonic energy functionals at zero temperature can be satisfactorily reproduced by truncating the expansion at order N = 4:
was expressed as a Taylor expansion truncated at order N around the saturation point (n = nsat, δ = 0). Margueron et al. (2018a) showed that different nucleonic energy functionals at zero temperature can be satisfactorily reproduced by truncating the expansion at order N = 4:
where x = (n − nsat)/(3nsat) and 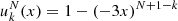 exp( − b(1 + 3x)), with b = 10ln(2) being a parameter governing the function at low densities. The factor
exp( − b(1 + 3x)), with b = 10ln(2) being a parameter governing the function at low densities. The factor 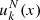 was introduced to ensure the convergence at the zero-density limit, while the parameters
was introduced to ensure the convergence at the zero-density limit, while the parameters 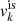 and
and 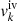 are linear combinations of the so-called nuclear matter empirical parameters, {nsat, Esat, sym, Lsym, Ksat, sym, Qsat, sym, Zsat, sym} (see Margueron et al. (2018a) for details). In this work, we mainly employ the BSk24 functional (Goriely et al. 2013) as an illustrative example, but we also consider the SLy4 (Chabanat et al. 1998a,b) and DD-MEδ (Roca-Maza et al. 2011) functionals to study the model dependence of the results (see Sect. 4). The numerical values of the nuclear matter empirical parameters of these models, including those ruling the density dependence of the nucleon effective masses, are listed in Table 1 of Dinh Thi et al. (2021a). These three interactions were selected because they all fulfill the basic constraints from nuclear theory, nuclear experiments, and NS observables, and at the same time they reasonably cover present uncertainties on the nucleonic energy functionals (Dinh Thi et al. 2021a,c).
are linear combinations of the so-called nuclear matter empirical parameters, {nsat, Esat, sym, Lsym, Ksat, sym, Qsat, sym, Zsat, sym} (see Margueron et al. (2018a) for details). In this work, we mainly employ the BSk24 functional (Goriely et al. 2013) as an illustrative example, but we also consider the SLy4 (Chabanat et al. 1998a,b) and DD-MEδ (Roca-Maza et al. 2011) functionals to study the model dependence of the results (see Sect. 4). The numerical values of the nuclear matter empirical parameters of these models, including those ruling the density dependence of the nucleon effective masses, are listed in Table 1 of Dinh Thi et al. (2021a). These three interactions were selected because they all fulfill the basic constraints from nuclear theory, nuclear experiments, and NS observables, and at the same time they reasonably cover present uncertainties on the nucleonic energy functionals (Dinh Thi et al. 2021a,c).
To evaluate the ℱkin(n, δ, T) term, we used the thermodynamic relation
where 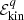 and
and 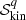 are the kinetic energy and entropy densities, respectively, of a system of independent particles with single-particle energy
are the kinetic energy and entropy densities, respectively, of a system of independent particles with single-particle energy 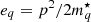 . The kinetic energy density corresponding to particles of type q at density nq (the density of the other species being noted as nq′) is given by:
. The kinetic energy density corresponding to particles of type q at density nq (the density of the other species being noted as nq′) is given by:
where ρ(eq) is the density of fermionic energy states,
ℏ is the Planck constant, 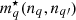 is the density-dependent nucleon effective mass,
is the density-dependent nucleon effective mass, 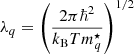 is the nucleon thermal wavelength, and F3/2 denotes the Fermi-Dirac integral:
is the nucleon thermal wavelength, and F3/2 denotes the Fermi-Dirac integral:
where j > −1. The system of equations is closed by the relation between the effective chemical potential 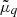 and the particle density nq:
and the particle density nq:
The entropy is defined from the partial grand canonical thermodynamic potential 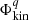 as:
as:
Using the expression of 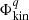 ,
,
we obtain:
Incorporating Eqs. (32) and (26) into Eq. (25), the final result for ℱkin reads:
Finite-temperature mean-field theory (Lattimer et al. 1985; Ducoin et al. 2007) implies that the free-energy density ℱkin given by Eq. (33) represents the correct ‘kinetic’ term entering Eq. (23), provided the following relation is imposed between the effective chemical potential 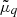 and the thermodynamic potential μq in Eqs. (20) and (21):
and the thermodynamic potential μq in Eqs. (20) and (21):
where the mean-field potential Uq is given by:
and the partial derivatives with respect to nn (np) are computed keeping np (nn) constant.
3.2. Coulomb, surface, and curvature energies
To model the inhomogeneities in the inner crust, in Eq. (22) the bulk free energy Fbulk was complemented by Coulomb, surface, and curvature contributions:
For the latter terms, we used the same expressions as in Carreau et al. (2019, 2020a), Dinh Thi et al. (2021a,b), which are reported here for completeness. The Coulomb term giving the electrostatic proton–proton, proton–electron, and electron–electron interaction energies, assuming a spherical geometry for the WS cell, reads:
where e is the elementary charge, and the function ηCoul(u) accounting for the electron screening is written as (Ravenhall et al. 1983a; Pethick & Ravenhall 1995)
Regarding the surface and curvature energies, we employ the expression of Lattimer & Swesty (1991), Maruyama et al. (2005), and Newton et al. (2013):
where d = 3, because here we only consider spherical nuclei, and σs and σc are the surface and curvature tensions. At zero temperature, we adopt the expressions of σs(I, T = 0) and σc(I, T = 0) from Ravenhall et al. (1983b), which are based on Thomas-Fermi calculations at extreme isospin asymmetries:
where yp = (1 − I)/2, and the parameters (σ0, σ0, c, bs, β, p) are optimised for each given bulk and effective mass functional in order to reproduce the experimental nuclear masses in the atomic mass evaluation (AME) 2016 (Wang et al. 2017).
At finite temperature, the surface tension is modified with respect to the case of zero temperature, and we use the following expression (Lattimer & Swesty 1991):
where
and Tc is the critical temperature given by Eq. (2.31) in Lattimer & Swesty (1991).
3.3. Translational energy
As the temperatures of interest in this work are above the melting point, clusters are expected to be in the liquid phase. As a result, it is necessary to account for their translational degrees of freedom.
If the effect of the fluid of dripped nucleons is neglected, the free energy corresponding to the translational motion reduces to the standard expression of an ideal gas (Haensel et al. 2007):
This expression is easily obtained considering a system of Ntot identical ions in a volume Vtot. In the thermodynamic limit, Ntot → ∞, Vtot → ∞, and Ntot/Vtot → 1/VWS. The partition function for the centre-of-mass motion of a non-relativistic classical particle can be written as
where 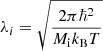 is the ion thermal wavelength, and gs = 2Ji + 1 is the ground-state spin degeneracy, which we set to unity independent of the ion species, because Ji = 0 for even–even nuclei, which are most abundant in the crust. This expression is valid in the non-degenerate Boltzmann limit, corresponding to
is the ion thermal wavelength, and gs = 2Ji + 1 is the ground-state spin degeneracy, which we set to unity independent of the ion species, because Ji = 0 for even–even nuclei, which are most abundant in the crust. This expression is valid in the non-degenerate Boltzmann limit, corresponding to 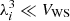 . For a system of Ntot identical and indistinguishable clusters, the total partition sum reads:
. For a system of Ntot identical and indistinguishable clusters, the total partition sum reads:
Using 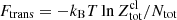 , Eq. (44) is immediately found. To check the validity of the non-degenerate limit for the calculation of the translational free energy, Eq. (44), we plot in Fig. 2 the ratio of the ion thermal wavelength,
, Eq. (44) is immediately found. To check the validity of the non-degenerate limit for the calculation of the translational free energy, Eq. (44), we plot in Fig. 2 the ratio of the ion thermal wavelength, 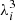 , to the WS cell volume as a function of the inner-crust baryon number density for the BSk24 model in beta equilibrium and for four different temperatures. We can see that, although the ratio
, to the WS cell volume as a function of the inner-crust baryon number density for the BSk24 model in beta equilibrium and for four different temperatures. We can see that, although the ratio 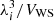 remains smaller than 1 throughout the inner crust, the non-degenerate Boltzmann limit tends to break at high densities and higher temperatures in the vicinity of the crust–core transition.
remains smaller than 1 throughout the inner crust, the non-degenerate Boltzmann limit tends to break at high densities and higher temperatures in the vicinity of the crust–core transition.
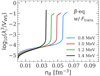 |
Fig. 2. Ratio (in logarithmic scale) of the ion thermal wavelength to the WS cell volume as a function of the baryonic density nB for the BSk24 model at four different temperatures: kBT = 0.8 MeV (blue line), kBT = 1.0 MeV (red line), kBT = 1.2 MeV (green line), and kBT = 1.4 MeV (black line). The results are obtained at beta equilibrium using the ideal-gas translational energy, Eq. (44). |
The derivation of Eq. (44) also shows that this expression is only valid in the limit of heavy ions, that is, those with Mi/mn ≫ 1, and if ions are considered as point-like particles moving in vacuum. The first of these conditions is well realised in the inner crust, but the latter two clearly become more doubtful as density increases. A first obvious correction to Eq. (44) that was considered in the literature since the first works on the finite-temperature crust (Lattimer et al. 1985; Lattimer & Swesty 1991) is to consider a reduced volume Vf for the centre-of-mass motion, in coherence with the excluded-volume approach of Eq. (14):
with rWS being the WS cell radius.
Moreover, in a proto-NS inner crust, nuclei are surrounded by a distribution of dripped protons and neutrons. At the bottom of the inner crust, the densities of these fluids are comparable to the nuclear internal density and, as a result, the cluster bare mass Mi should be replaced by an effective mass 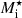 , accounting for the modification of the free flow in a nuclear medium.
, accounting for the modification of the free flow in a nuclear medium.
In Sect. 2 we present the derivation of the effective mass of the cluster moving in a uniform nucleon medium modelled as an ideal fluid, with different hypotheses as to the fluid properties of the cluster. Repeating the calculation of the translational partition sum of Eq. (45) – using either Eq. (5) or Eq. (9) for the thermal kinetic energy – leads to an expression identical to Eq. (44), with the substitution 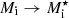 . Including both the corrections on the finite-size effect of nuclei and the effective mass, the translational free energy can be written as
. Including both the corrections on the finite-size effect of nuclei and the effective mass, the translational free energy can be written as
where 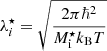 , with
, with 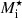 given by Eq. (10). For the latter term, we considered three cases:
given by Eq. (10). For the latter term, we considered three cases:
-
the limiting case δf = 0, leading to Eq. (6), corresponding to a solid cluster fully impermeable to the surrounding nuclear medium;
-
the limiting case δf = 1, corresponding to the single-fluid calculation by Magierski & Bulgac (2004b), Eq. (11);
-
the intermediate case
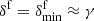 , leading to Eq. (12). We think that this latter case, which considers that the translational motion concerns protons, bound neutrons, and neutrons in unbound resonant states, while all neutrons occupying continuum states constitute the external fluid, is more realistic. Indeed, the mobility of the nucleons is given by their velocity flux at the Fermi surface (Carter et al. 2005). As such, this is only defined for ‘conduction’ nucleons with single-particle wave functions, which do not vanish at the WS boundary, that is, continuum states as defined in Papakonstantinou et al. (2013). Also, Gulminelli & Raduta (2015) showed that the factorization of the partition sum that is needed to theoretically obtain the extended nuclear statistical equilibrium models used to produce the general-purpose equation of state (Oertel et al. 2017; Typel et al. 2015; Raduta & Gulminelli 2019) is only possible if the cluster mass appearing in the translational part is the e-cluster mass, Ae = A(1 − ng/ni).
, leading to Eq. (12). We think that this latter case, which considers that the translational motion concerns protons, bound neutrons, and neutrons in unbound resonant states, while all neutrons occupying continuum states constitute the external fluid, is more realistic. Indeed, the mobility of the nucleons is given by their velocity flux at the Fermi surface (Carter et al. 2005). As such, this is only defined for ‘conduction’ nucleons with single-particle wave functions, which do not vanish at the WS boundary, that is, continuum states as defined in Papakonstantinou et al. (2013). Also, Gulminelli & Raduta (2015) showed that the factorization of the partition sum that is needed to theoretically obtain the extended nuclear statistical equilibrium models used to produce the general-purpose equation of state (Oertel et al. 2017; Typel et al. 2015; Raduta & Gulminelli 2019) is only possible if the cluster mass appearing in the translational part is the e-cluster mass, Ae = A(1 − ng/ni).
For comparison with Fig. 2, Fig. 3 shows the ratio of the ion thermal wavelength, 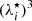 , to the WS cell volume VWS (top panels) as a function of the inner-crust baryonic density nB for the BSk24 model at beta equilibrium and at two different temperatures: 1.0 MeV (left panels) and 2.0 MeV (right panels). Three different prescriptions of
, to the WS cell volume VWS (top panels) as a function of the inner-crust baryonic density nB for the BSk24 model at beta equilibrium and at two different temperatures: 1.0 MeV (left panels) and 2.0 MeV (right panels). Three different prescriptions of 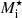 are considered, corresponding to the three listed cases of δf. We observe that, in this case, the ratio
are considered, corresponding to the three listed cases of δf. We observe that, in this case, the ratio 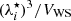 remains always ≪1 and smaller than that obtained in the ideal-gas case near the crust–core transition. This is due to the fact that in the ideal-gas case (taking Mi ≈ Amn), when the clusters dissolve near the crust–core transition point, A and VWS = Z/np become small (because of the sharp decrease in the cluster mass and proton number; see also Fig. 4 and related discussion), and therefore the ratio (λi)3/VWS is relatively large. On the other hand, when
remains always ≪1 and smaller than that obtained in the ideal-gas case near the crust–core transition. This is due to the fact that in the ideal-gas case (taking Mi ≈ Amn), when the clusters dissolve near the crust–core transition point, A and VWS = Z/np become small (because of the sharp decrease in the cluster mass and proton number; see also Fig. 4 and related discussion), and therefore the ratio (λi)3/VWS is relatively large. On the other hand, when 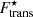 is used, the clusters remain large until high nB (see also Figs. 7 and 9), yielding a greater cluster mass and WS volume, resulting in a smaller thermal-wavelength-to-WS-cell-volume ratio. However, the ratio of
is used, the clusters remain large until high nB (see also Figs. 7 and 9), yielding a greater cluster mass and WS volume, resulting in a smaller thermal-wavelength-to-WS-cell-volume ratio. However, the ratio of 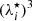 to the reduced volume Vf (bottom panels in Fig. 3) increases towards the crust–core transition, reaching ≈0.5 almost independently of the temperature and effective-mass estimation. This shows that the non-degenerate limit implicit in Eq. (48) is always a reasonable approximation, albeit less justified at the highest densities.
to the reduced volume Vf (bottom panels in Fig. 3) increases towards the crust–core transition, reaching ≈0.5 almost independently of the temperature and effective-mass estimation. This shows that the non-degenerate limit implicit in Eq. (48) is always a reasonable approximation, albeit less justified at the highest densities.
 |
Fig. 3. Ratio (in logarithmic scale) of the ion thermal wavelength to the WS cell volume (top panels) and to the reduced volume (bottom panels) as a function of the baryonic density nB for the BSk24 model, using three different prescriptions for the ion effective mass, at two different temperatures: kBT = 1 MeV (left panels) and kBT = 2.0 MeV (right panels). The results are obtained at beta equilibrium using the translational energy |
To investigate the effect of the translational free energy on the (proto-)NS inner-crust properties, we performed our calculations employing both the ideal-gas expression (see Eq. (44)), and the expression accounting for in-medium effects (see Eq. (48)). The corresponding results are discussed in the following sections.
4. Results at beta equilibrium
In this section, we discuss the impact of the translational free energy on the properties of the inner crust, assuming that beta equilibrium holds, which is believed to be the case in the proto-NS at moderate temperatures (see Oertel et al. 2017 and references therein). In this case, we minimised the function Ω defined in Eq. (17) with respect to the variational variables (rN, I, ni, np, ngn, ngp, ne). This resulted in the following system of equilibrium equations:
where Pg = μnngn + μpngp − ℱg is the pressure of the dripped nucleons, and μe = ∂ℱe/∂ne is the electron chemical potential. It is to be noted that, because of the definition of the chemical potentials μn and μp (see Eqs. (20) and (21)), the pressure term Pg is not just the pressure of a self-interacting nucleon gas but also includes in-medium effects. At each given (nB, T), this system of five coupled differential equations, Eqs. (49)–(53), was solved numerically together with the two constraints from the baryon number conservation, Eq. (15), and charge neutrality, Eq. (16), yielding the equilibrium composition.
We start by considering the standard ideal-gas expression for the translational motion, Eq. (44), while the excluded-volume and effective-mass corrections are addressed later in this section. To analyse the temperature dependence of the properties of the inner crust, we performed the calculations employing the energy-density functional BSk24 (Goriely et al. 2013) as an illustrative example at four selected temperature values: kBT = 0.8, 1.0, 1.2, and 1.4 MeV. Indeed, Carreau et al. (2020a), who calculated the melting temperature using the same BSk24 interaction model, showed that these temperatures are sufficiently high for the crust to be in the liquid phase. Figure 4 shows the evolution of the cluster mass number A (upper panel) and proton number Z (lower panel) with the baryonic number density nB for the chosen temperatures. We recall that, as we only consider spherical nuclei here, A is related to the variational variables rN and ni through the relation 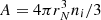 , and Z = A(1 − I)/2. To show the notable influence of the translational free energy Ftrans, Eq. (44), we show in Fig. 4 the results obtained including (solid lines) and neglecting (dashed lines) the Ftrans term in Eq. (22). Let us first discuss the case without Ftrans (dashed lines). In this case, Eq. (50) is equivalent to the equation of the Baym virial theorem (Baym et al. 1971), with an additional curvature term, ℱsurf + 2ℱcurv = 2ℱCoul. From this equation, the cluster mass number A can be deduced as
, and Z = A(1 − I)/2. To show the notable influence of the translational free energy Ftrans, Eq. (44), we show in Fig. 4 the results obtained including (solid lines) and neglecting (dashed lines) the Ftrans term in Eq. (22). Let us first discuss the case without Ftrans (dashed lines). In this case, Eq. (50) is equivalent to the equation of the Baym virial theorem (Baym et al. 1971), with an additional curvature term, ℱsurf + 2ℱcurv = 2ℱCoul. From this equation, the cluster mass number A can be deduced as
 |
Fig. 4. Cluster mass number A (upper panel) and proton number Z (lower panel) as a function of the baryonic density nB for the BSk24 model at four different temperatures: kBT = 0.8 MeV (blue lines), kBT = 1.0 MeV (red lines), kBT = 1.2 MeV (green lines), and kBT = 1.4 MeV (black lines). The solid (dashed) lines are obtained when the translational energy, defined by Eq. (44), is (not) included. |
This result is exact only if ℱcurv = 0. However, ℱcurv ≪ ℱsurf for all nuclei, and Eq. (54) provides a good approximation in the whole crust. As T increases, the surface tension decreases; see Eq. (42). Consequently, A decreases with temperature, as shown in the inset of the upper panel of Fig. 4. A similar behaviour is observed in Z. On the other hand, the denominator of the right-hand side of Eq. (54) is a decreasing function of the baryonic density nB. However, as nuclei become more neutron rich deeper in the crust, the surface tension σs(I, T) also decreases with nB. As a consequence, the trend of A versus nB cannot be straightforwardly deduced, and strongly depends on the detailed behaviour of σs, that is, on the nuclear model. From Fig. 4, one can see that for the considered temperatures and functional, the behaviour of the denominator prevails, hence the increase in cluster mass. For Z, this is not always the case because the isospin I also increases with nB. Taking into account the translational motion Ftrans (solid lines in Fig. 4) significantly reduces both the mass and proton numbers of the cluster. Specifically, at high densities, the cluster completely dissolves, that is, Z < 1. Analogously to the calculation without the translational term, the cluster size decreases with temperature. However, the density at which the transition from inhomogeneous to homogeneous matter occurs is much lower than that obtained without Ftrans. In particular, if we neglect (include) Ftrans, for all the considered temperatures, the crust–core transition occurs at around nCC ≈ 0.08 fm−3 (nCC ≈ 0.04 − 0.06 fm−3), as can be seen from Table 1.
Crust–core transition density, nCC, and pressure, PCC, for the BSk24 functional at different temperatures with (w/) and without (w/o) the inclusion of the translational free energy Ftrans.
To understand this behaviour, we observe that the size of the cluster is determined by the minimisation of the free energy per nucleon with respect to rN (or equivalently A), Eq. (50). From the definition of Fi in Eq. (22), Eq. (50) can be written as
This equation shows that we can have heavy or light clusters depending on the competition between fCoul + surf + curv, which favours the former (as we show above), and ftrans, which favours the latter. Indeed, it is easy to show that ftrans is minimised at
where C0 = ℏ3/gs(2π/mnkB)3/2.
Replacing realistic values for ni and u in Eq. (56), we find that A0 < 30 for temperatures equal to or above 1 MeV. This point is further illustrated in Fig. 5, in which we plot fCoul + surf + curv (teal dash-dotted lines), ftrans (violet dashed lines), and their sum (black solid lines) as a function of A at kBT = 1 MeV for two selected densities: nB = 0.04 fm−3 (upper panel) and nB = 0.05 fm−3 (lower panel). The other variables (I, ni, np, ngn, ngp, ne) are fixed to the values obtained from the minimisation at the given (nB, T). From this figure, we can see that, indeed, fCoul + surf + curv is minimised for large clusters (A > 100), whereas ftrans is minimised for very small ones, A ≈ 10. At higher density, as matter becomes more neutron rich, both the Coulomb and the surface energies per baryon decrease. Thus, the impact of the translational motion prevails. Moreover, ftrans clearly dominates at high temperatures. Consequently, the net effect is that the translational free energy is dominant at high temperatures and densities, as shown in Fig. 6. This explains why small clusters are found in this regime in Fig. 4 when the translational energy is accounted for in the minimisation procedure.
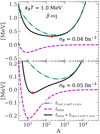 |
Fig. 5. Coulomb, surface, and curvature energies per nucleon, fCoul + surf + curv (teal dash-dotted lines), translational free energy per nucleon, ftrans (violet dashed lines), and their sum (black solid lines) as a function of A at kBT = 1 MeV and nB = 0.04 fm−3 (upper panel) and nB = 0.05 fm−3 (lower panel) for the BSk24 model. The red star in each panel indicates the solution for A from the minimisation. |
The surprising results of Figs. 4–6 are obtained using the oversimplified ideal-gas expression in Eq. (44), which is only justified at rather high temperature and relatively low density; see Fig. 2. One would expect the inclusion of the cluster effective mass and the reduction of the available volume for the translational motion to reduce the impact of the centre-of-mass motion. This is shown in Fig. 7, where the cluster mass number A and proton number Z are plotted as a function of baryonic number density nB for the BSk24 model at kBT = 1.0 MeV (left panels) and kBT = 2.0 MeV (right panels). For all the considered values of δf, including 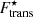 (Eq. (48)) still noticeably shrinks the size of the cluster with respect to the case where the collective degrees of freedom are neglected. However, the effect is not as dramatic as when the ideal-gas expression in Eq. (44) is used (see also Fig. 4). The latter is true both when
(Eq. (48)) still noticeably shrinks the size of the cluster with respect to the case where the collective degrees of freedom are neglected. However, the effect is not as dramatic as when the ideal-gas expression in Eq. (44) is used (see also Fig. 4). The latter is true both when 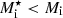 , that is, when δf > 0, and when
, that is, when δf > 0, and when 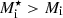 , that is, in the case where δf = 0. As one may expect, the influence of the translational free energy becomes larger with increasing temperature, as can be seen by comparing the left and right panels. The effect is also larger with decreasing δf. As already mentioned, among the three prescriptions of the ion effective mass discussed in Sect. 2, the most realistic one would be when all neutrons in the continuum states participate in the flow, that is, δf = γ. Therefore, in the following, we only show our results for this case, that is, we employ Eq. (12) in
, that is, in the case where δf = 0. As one may expect, the influence of the translational free energy becomes larger with increasing temperature, as can be seen by comparing the left and right panels. The effect is also larger with decreasing δf. As already mentioned, among the three prescriptions of the ion effective mass discussed in Sect. 2, the most realistic one would be when all neutrons in the continuum states participate in the flow, that is, δf = γ. Therefore, in the following, we only show our results for this case, that is, we employ Eq. (12) in 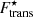 (Eq. (48)).
(Eq. (48)).
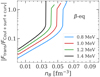 |
Fig. 6. Absolute value of the ratio of the translational free energy to the sum of surface, curvature, and Coulomb free energies as a function of the baryonic density nB for the BSk24 model at four different temperatures: kBT = 0.8 MeV (blue line), kBT = 1.0 MeV (red line), kBT = 1.2 MeV (green line), and kBT = 1.4 MeV (black line). |
Interestingly, in the case where δf = γ (green dash-dotted line in Fig. 7), we observe a transition to small proton-mass clusters, Z ∼ 2, at kBT = 2.0 MeV (right panels) and nB > 0.075 fm−3, and this configuration persists even at nB > 0.1 fm−3. As shown in Fig. 8, the neutron and proton cluster densities (solid lines), nin = ni(1 + I)/2 and nip = ni(1 − I)/2, of these light configurations are very similar to those of the surrounding homogeneous nuclear medium (dashed lines). From a physical point of view, these small-amplitude and small-wavelength inhomogeneities might correspond to correlations or resonant states that are expected to exist in nuclear matter but are not captured in the homogeneous matter mean-field approximation. However, in this density region, there is no clear distinction between inhomogeneous and homogeneous matter. Therefore, we identify this transition to low-Z clusters as the interface between the crust and the core.
 |
Fig. 7. Cluster mass number A (upper panels) and proton number Z (lower panels) as a function of the baryonic density nB for the BSk24 model at two different temperatures: kBT = 1.0 MeV (left panels) and kBT = 2.0 MeV (right panels). Different prescriptions for the translational free energy are considered. See text for details. |
 |
Fig. 8. Neutron (upper panels) and proton (lower panels) densities inside (solid lines) and outside (dashed lines) the cluster as a function of the baryonic density nB for the BSk24 model at two different temperatures: kBT = 1.0 MeV (left panels) and kBT = 2.0 MeV (right panels). The effective translational free energy |
In Fig. 9, we plot the cluster mass number A and proton number Z as a function of baryonic number density nB for three temperature values: kBT = 1.0 MeV (left panels), 1.5 MeV (middle panels), and 2.0 MeV (right panels) for the BSk24 (Goriely et al. 2013), (black lines), SLy4 (Chabanat et al. 1998a,b), (blue lines), and DD-MEδ (Roca-Maza et al. 2011), (orange lines) models. The A and Z obtained with (without) the translational energy 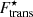 are shown with solid (dashed) lines. While the results are almost model-independent, they vary significantly with temperature. For all the considered models, with the most realistic expression that we consider in this work,
are shown with solid (dashed) lines. While the results are almost model-independent, they vary significantly with temperature. For all the considered models, with the most realistic expression that we consider in this work, 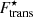 , at 1 MeV, very heavy clusters (A > 400) are favoured until the transition to the core, whereas at higher temperatures, the crust–core transition occurs at lower densities. The latter behaviour can be expected due to the increase of the translational degrees of freedom.
, at 1 MeV, very heavy clusters (A > 400) are favoured until the transition to the core, whereas at higher temperatures, the crust–core transition occurs at lower densities. The latter behaviour can be expected due to the increase of the translational degrees of freedom.
 |
Fig. 9. Cluster mass number A (upper panels) and proton number Z (lower panels) as a function of the baryonic density nB for the BSk24 (black lines), SLy4 (blue lines), and DD-MEδ (orange lines) models at three different temperatures: kBT = 1.0 MeV (left panels), kBT = 1.5 MeV (middle panels), and kBT = 2.0 MeV (right panels). The solid (dashed) lines are obtained with (without) the effective translational energy |
To better understand this finding, we notice that the mass number 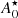 at which
at which 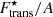 is minimised has the exact same functional form as in Eq. (56), that is
is minimised has the exact same functional form as in Eq. (56), that is
where
The behaviour of 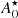 therefore depends on the competition between the T3/2 and the g(u, γ) factors. As nB increases, the ratio γ between the density outside and inside the ion increases and approaches 1 near the crust–core transition, thus reducing the effect of the translational term. If the volume fraction occupied by the ion u also increases (approaching 1), which is the case at relatively low temperatures, 1/g can be a very large number, and large clusters are still favoured even if the translational free energy is accounted for (see left panels of Fig. 9). However, at higher temperatures, that is kBT ≳ 1.5 MeV, we find that the translational effect dominates, and the cluster volume fraction decreases near the crust–core transition, which leads to the appearance of small clusters when
therefore depends on the competition between the T3/2 and the g(u, γ) factors. As nB increases, the ratio γ between the density outside and inside the ion increases and approaches 1 near the crust–core transition, thus reducing the effect of the translational term. If the volume fraction occupied by the ion u also increases (approaching 1), which is the case at relatively low temperatures, 1/g can be a very large number, and large clusters are still favoured even if the translational free energy is accounted for (see left panels of Fig. 9). However, at higher temperatures, that is kBT ≳ 1.5 MeV, we find that the translational effect dominates, and the cluster volume fraction decreases near the crust–core transition, which leads to the appearance of small clusters when 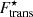 is included.
is included.
The impact of the excluded-volume approach on the transition from clusterised to homogeneous matter was also discussed by Typel (2016). This author noticed a strong increase (and even divergence) of the pressure, which resulted in the transition to uniform matter when the excluded-volume mechanism was implemented, and proposed a solution, namely a generalisation of the excluded-volume approach. In our case, this same divergence that is brought by the term (1 − u1/3)−3 in Eq. (57) is moderated by finite-temperature effects, yielding instead the appearance of lighter, essentially unbound clusters.
The effect of the modified translational free energy, 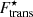 , on the compositions (A, Z) is significant at all densities in the proto-NS inner crust. Specifically, at the highest temperature considered, kBT = 2.0 MeV, the reduction in A and Z with respect to a calculation where the translational energy is neglected or excluded from the variational equation with respect to the cluster size, as in the works by Lattimer & Swesty (1991) and Shen et al. (2011a), is of the order of > 400 in A and > 20 in Z. Therefore, for calculations of the (liquid) inner crust where an accurate description of the composition is needed, we believe that the translational free energy should be taken into account. In contrast to the ideal-gas approximation, the inclusion of in-medium effects in the translational free energy does not lead to an early dissolution of the clusters, as can be seen by comparing Figs. 4 and 9. Instead, at all the considered temperatures, clusters are favoured over homogeneous nuclear matter up to nB ≳ 0.07 fm−3.
, on the compositions (A, Z) is significant at all densities in the proto-NS inner crust. Specifically, at the highest temperature considered, kBT = 2.0 MeV, the reduction in A and Z with respect to a calculation where the translational energy is neglected or excluded from the variational equation with respect to the cluster size, as in the works by Lattimer & Swesty (1991) and Shen et al. (2011a), is of the order of > 400 in A and > 20 in Z. Therefore, for calculations of the (liquid) inner crust where an accurate description of the composition is needed, we believe that the translational free energy should be taken into account. In contrast to the ideal-gas approximation, the inclusion of in-medium effects in the translational free energy does not lead to an early dissolution of the clusters, as can be seen by comparing Figs. 4 and 9. Instead, at all the considered temperatures, clusters are favoured over homogeneous nuclear matter up to nB ≳ 0.07 fm−3.
On the other hand, for most cases, the impact of the translational free-energy term is reduced on more global quantities like the equation of state. This is demonstrated in Fig. 10, where the total pressure P is plotted as a function of the baryon number density nB in the inner crust. We can see that, for all the considered models, including the in-medium modified translational free energy 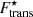 yields almost identical results to the case where it is not included; see the solid and dashed curves in Fig. 10, which are almost indistinguishable. The crust–core interface is indicated by green dots (violet squares) for the case where
yields almost identical results to the case where it is not included; see the solid and dashed curves in Fig. 10, which are almost indistinguishable. The crust–core interface is indicated by green dots (violet squares) for the case where 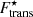 is (not) taken into account. The crust–core transition was determined by comparing the WS free-energy density of the inhomogeneous crust to that of homogeneous (or quasi-homogeneous) matter at beta equilibrium (see also Fig. 9). At kBT = 1.0 MeV (top panel), the translational degrees of freedom favour clusters over homogeneous matter by lowering the free-energy density of the system. Thus, the crust–core transition is moved to higher density (and pressure) when this term is accounted for. On the other hand, the situation is reversed for kBT = 1.5 MeV (middle panel) and 2.0 MeV (bottom panel). This is understood from the fact that the most favourable clusters decrease in size as the temperature increases, leading to a progressive ‘melting’ in the surrounding medium. Therefore, the resulting crust–core transition is very close to or even lower than that obtained when neglecting the translational-free-energy contribution. Values of the crust–core transition density and pressure are reported in Table 2.
is (not) taken into account. The crust–core transition was determined by comparing the WS free-energy density of the inhomogeneous crust to that of homogeneous (or quasi-homogeneous) matter at beta equilibrium (see also Fig. 9). At kBT = 1.0 MeV (top panel), the translational degrees of freedom favour clusters over homogeneous matter by lowering the free-energy density of the system. Thus, the crust–core transition is moved to higher density (and pressure) when this term is accounted for. On the other hand, the situation is reversed for kBT = 1.5 MeV (middle panel) and 2.0 MeV (bottom panel). This is understood from the fact that the most favourable clusters decrease in size as the temperature increases, leading to a progressive ‘melting’ in the surrounding medium. Therefore, the resulting crust–core transition is very close to or even lower than that obtained when neglecting the translational-free-energy contribution. Values of the crust–core transition density and pressure are reported in Table 2.
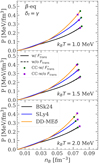 |
Fig. 10. Same as Fig. 9, but for pressure P vs. baryonic number density nB. The green dots (violet squares) mark the crust–core transition with (without) |
Crust–core transition density, nCC, and pressure, PCC, for the BSk24, SLy4, and DD-MEδ models at different temperatures with (w/) and without (w/o) the inclusion of the translational free energy 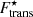 for the case δf = γ.
for the case δf = γ.
5. Results at fixed total proton fraction
At a fixed total proton fraction 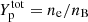 , Eq. (49) associated to beta equilibrium no longer holds, and the equilibrium state of matter for each given thermodynamic condition (nB, T,
, Eq. (49) associated to beta equilibrium no longer holds, and the equilibrium state of matter for each given thermodynamic condition (nB, T, 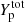 ) is determined by solving the system of four variational equations, Eqs. (50)–(53), together with the equations of baryon number conservation, Eq. (15), and charge neutrality, Eq. (16).
) is determined by solving the system of four variational equations, Eqs. (50)–(53), together with the equations of baryon number conservation, Eq. (15), and charge neutrality, Eq. (16).
Figure 11 displays the cluster proton number Z as a function of nB at kBT = 3.0 MeV (upper panel) and kBT = 4.0 MeV (lower panel) at two selected total proton fractions: 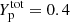 (red lines) and
(red lines) and 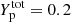 (green lines). Results are shown for the case where the translational free energy is neglected (dashed lines) and for the two different prescriptions for the translational-free-energy term considered in this work: Ftrans, Eq. (44), (solid lines), and
(green lines). Results are shown for the case where the translational free energy is neglected (dashed lines) and for the two different prescriptions for the translational-free-energy term considered in this work: Ftrans, Eq. (44), (solid lines), and 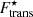 , Eq. (48), with δf = γ (dash-dotted lines). As in the beta-equilibrium case discussed in Sect. 4, both prescriptions, Ftrans and
, Eq. (48), with δf = γ (dash-dotted lines). As in the beta-equilibrium case discussed in Sect. 4, both prescriptions, Ftrans and 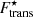 , have the effect of reducing the cluster size. In particular, this effect is greater at lower nB and
, have the effect of reducing the cluster size. In particular, this effect is greater at lower nB and 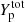 , and higher T. However, in the scenario where the proton fraction is fixed, the impact of the translational free energy is only slightly reduced when the in-medium corrections on the cluster volume and effective mass are taken into account, as can be seen by comparing the solid and the dash-dotted lines in Fig. 11.
, and higher T. However, in the scenario where the proton fraction is fixed, the impact of the translational free energy is only slightly reduced when the in-medium corrections on the cluster volume and effective mass are taken into account, as can be seen by comparing the solid and the dash-dotted lines in Fig. 11.
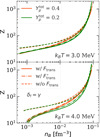 |
Fig. 11. Proton number Z as a function of the baryonic density nB for the BSk24 model at |
More strikingly, the role of the translational free energy is overall much less important than in the beta-equilibrium case. When the translational term is included, the clusters still survive up to around 0.1 fm−3, unlike in beta equilibrium (see Table 1 and Fig. 9). This can be understood by analysing the absolute ratio between the (ideal-gas) translational and the finite-size free energies, |Ftrans/FCoul + surf + curv|, shown in Fig. 12. Indeed, as already mentioned in Sect. 4, the cluster size results from the competition between these two terms. For the fixed proton fractions we consider, which are nevertheless higher than those obtained in beta equilibrium, the finite-size term dominates at all densities, and particularly at higher nB, higher 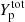 , and lower T, which explains the reduced impact of Ftrans in these regimes observed in Fig. 11. It is therefore natural to expect the effect of the translational free energy on the equation of state to remain negligible in the fixed-proton-fraction scenario as well, as can indeed be seen in Fig. 13.
, and lower T, which explains the reduced impact of Ftrans in these regimes observed in Fig. 11. It is therefore natural to expect the effect of the translational free energy on the equation of state to remain negligible in the fixed-proton-fraction scenario as well, as can indeed be seen in Fig. 13.
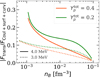 |
Fig. 12. Absolute value of the ratio of the translational energy to the sum of surface, curvature, and Coulombs energies as a function of the baryonic density nB for the BSk24 model at kBT = 4.0 MeV (solid lines) and kBT = 3.0 MeV (dotted lines), for |
6. Conclusions
In this work, we studied the influence of the translational degree of freedom in the liquid phase on the properties of finite-temperature ultra-dense stellar matter. To this aim, we derived different expressions for the effective mass of the ion moving in a uniform nucleon background using a hydrodynamical approach with different boundary conditions. This renormalisation of the ion mass to account for the in-medium effects was then included in the translational-free-energy contribution of the ion energetics. To calculate the latter, we employed a CLD model approach, in which the nuclear-matter properties were described using finite-temperature mean-field theory with nuclear energy-density functionals satisfying basic constraints from nuclear physics and astrophysics. Here, we optimised the surface parameters to reproduce the nuclear experimental masses consistently with the bulk energy. We performed this study at both beta equilibrium, as found in the proto-NS inner crusts close to the crystallisation transition, and at fixed proton fraction, which is relevant to the hot and dense matter found in supernovae.
Using a standard variational procedure, we show that the size of the clusters is determined by the competition between the motion of the centre-of-mass of the ion and the interface properties, namely, the Coulomb, surface, and curvature energies. Within the temperature range considered in this work (few 1010 K), the interface terms favour large clusters constituted of more than ≈100 nucleons, while the entropy gain associated to the translational motion is maximal for a gas-like composition of very small ions. Consequently, including the translational free energy in the variational theory can significantly reduce the number of nucleons in the clusters, especially at high temperatures.
However, the importance of this effect varies with the scenario. At beta equilibrium, considering the ions as an ideal gas, the inclusion of the translational free energy leads to a drastic reduction of the cluster proton and mass numbers already at temperatures as low as the crystallisation temperature. This implies an early dissolution of clusters in the dense medium, hence a very low crust–core transition density. We believe that this is an important result, because the translational degrees of freedom are typically neglected in the literature when modelling the finite-temperature crust for NS cooling simulations (Chamel et al. 2007; Fortin et al. 2010; Avancini et al. 2009, 2017; Nandi et al. 2021). A quantitative estimation of the effect will require a fully quantal microscopic description of the dynamical properties of nuclei in a dense fermionic environment. Such calculations are limited to the solid phase and moderate densities (Baiko et al. 2001), but could be in principle performed in the liquid phase similarly to in the work of Wlazłowski et al. (2016) and Sekizawa et al. (2022), with adapted boundary conditions.
Including the in-medium modification of the translational-free-energy expression resulting from considering that only neutrons in the continuum states participate in the flow, we obtain that, although the composition is strongly modified by the translational motion, the equation of state is just slightly affected. This unexpected influence of the translational entropy on the composition of matter is due to the fact that, in beta equilibrium, the proton fraction at high densities is very small, and the contribution from the Coulomb, surface, and curvature energies does not dominate the translational contribution. Conversely, if the total proton fraction is of the order of 0.2 or more, as typically found in supernova matter, the finite-size energies dominate, and the crust composition is less affected. Indeed, even at temperatures as high as kBT = 4 MeV, heavy clusters are still favoured close to the transition to homogeneous matter.
In supernova matter, neglecting the translational contribution in the variational treatment, as is done for instance in the popular equation of state by Lattimer & Swesty (1991), therefore appears to be justified. In this regime, the most questionable approximation is rather the OCP approximation, which we also used throughout this work. A comparison with a full MCP approach is in progress and will be presented in a separate paper.
Acknowledgments
This work has been partially supported by the IN2P3 Master Project NewMAC and the CNRS International Research Project (IRP) “Origine des éléments lourds dans l’univers: Astres Compacts et Nucléosynthèse (ACNu)”. We thank M. Antonelli for fruitful discussions.
References
- Avancini, S. S., Brito, L., Marinelli, J. R., et al. 2009, Phys. Rev. C, 79, 035804 [Google Scholar]
- Avancini, S. S., Ferreira, M., Pais, H., Providência, C., & Röpke, G. 2017, Phys. Rev. C, 95, 045804 [NASA ADS] [CrossRef] [Google Scholar]
- Baiko, D. A., Potekhin, A. Y., & Yakovlev, D. G. 2001, Phys. Rev. E, 64, 057402 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., Saperstein, E. E., & Tolokonnikov, S. V. 2007, Eur. Phys. J. A, 32, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Bethe, H. A., & Pethick, C. J. 1971, Nucl. Phys. A, 175, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Bruenn, S. W. 1985, ApJS, 58, 771 [Google Scholar]
- Burgio, G. F., & Fantina, A. F. 2018, Astrophys. Space Sci. Lib., 457, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., & Lattimer, J. M. 1984, ApJ, 285, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., & Lattimer, J. M. 1986, ApJ, 307, 178 [Google Scholar]
- Carreau, T., Gulminelli, F., & Margueron, J. 2019, Eur. Phys. J. A, 55, 188 [CrossRef] [Google Scholar]
- Carreau, T., Gulminelli, F., Chamel, N., Fantina, A. F., & Pearson, J. M. 2020a, A&A, 635, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carreau, T., Fantina, A. F., & Gulminelli, F. 2020b, A&A, 640, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, B., Chamel, N., & Haensel, P. 2005, Nucl. Phys. A, 748, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Chabanat, E., Bonche, P., Haensel, P., Meyer, J., & Schaeffer, R. 1998a, Nucl. Phys. A, 635, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Chabanat, E., Bonche, P., Haensel, P., Meyer, J., & Schaeffer, R. 1998b, Nucl. Phys. A, 643, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2005, Nucl. Phys. A, 747, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2006, Nucl. Phys. A, 773, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2012, Phys. Rev. C, 85, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2017, J. Low Temp. Phys., 189, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Naimi, S., Khan, E., & Margueron, J. 2007, Phys. Rev. C, 75, 055806 [NASA ADS] [CrossRef] [Google Scholar]
- Dinh Thi, H., Carreau, T., Fantina, A. F., & Gulminelli, F. 2021a, A&A, 654, A114 [CrossRef] [EDP Sciences] [Google Scholar]
- Dinh Thi, H., Fantina, A. F., & Gulminelli, F. 2021b, Eur. Phys. J. A, 57, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Dinh Thi, H., Mondal, C., & Gulminelli, F. 2021c, Universe, 7, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Ducoin, C., Chomaz, Ph., & Gulminelli, F. 2007, Nucl. Phys. A, 789, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, R. I. 1988, ApJ, 333, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Fantina, A. F., De Ridder, S., Chamel, N., & Gulminelli, F. 2020, A&A, 633, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortin, M., Grill, F., Margueron, J., Page, D., & Sandulescu, N. 2010, Phys. Rev. C, 82, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Gögelein, P., & Müther, H. 2007, Phys. Rev. C, 76, 024312 [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2013, Phys. Rev. C, 88, 024308 [NASA ADS] [CrossRef] [Google Scholar]
- Grams, G., Somasundaram, R., Margueron, J., & Reddy, S. 2022a, Phys. Rev. C, 105, 035806 [CrossRef] [Google Scholar]
- Grams, G., Margueron, J., Somasundaram, R., Chamel, N., & Goriely, S. 2022b, J. Phys. Conf. Ser., 2340, 012030 [CrossRef] [Google Scholar]
- Grill, F., Margueron, J., & Sandulescu, N. 2011, Phys. Rev. C, 84, 065801 [NASA ADS] [CrossRef] [Google Scholar]
- Gulminelli, F., & Raduta, Ad. R. 2015, Phys. Rev. C, 92, 055803 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1. Equation of State and structure (New York: Springer) [Google Scholar]
- Hillebrandt, W., Nomoto, K., & Wolff, R. G. 1984, A&A, 133, 175 [NASA ADS] [Google Scholar]
- Horowitz, C. J., Berry, D. K., Briggs, C. M., et al. 2015, Phys. Rev. Lett., 114, 031102 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, F., Hu, J., Bao, S., & Shen, H. 2020, Phys. Rev. C, 102, 015806 [CrossRef] [Google Scholar]
- Jin, S., Roche, K. J., Stetcu, I., Abdurrahman, I., & Bulgac, A. 2021, Comput. Phys. Commun., 269, 108130 [NASA ADS] [CrossRef] [Google Scholar]
- Kashiwaba, Y., & Nakatsukasa, T. 2019, Phys. Rev. C, 100, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Swesty, F. D. 1991, Nucl. Phys. A, 535, 331 [CrossRef] [Google Scholar]
- Lattimer, J. M., Pethick, C. J., Ravenhall, D. G., & Lamb, D. Q. 1985, Nucl. Phys. A, 432, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F., Lu, J.-J., Li, Z.-H., et al. 2021, Phys. Rev. C, 103, 024307 [Google Scholar]
- Liebendörfer, M., Rampp, M., Janka, H.-Th., & Mezzacappa, A. 2005, ApJ, 620, 840 [CrossRef] [Google Scholar]
- Lin, Z., Caplan, M. E., Horowitz, C. J., & Lunardini, C. 2020, Phys. Rev. C, 102, 045801 [CrossRef] [Google Scholar]
- Lu, J.-J., Li, Z.-H., Burgio, G. F., Figura, A., & Schulze, H.-J. 2019, Phys. Rev. C, 100, 054335 [NASA ADS] [CrossRef] [Google Scholar]
- Magierski, P., & Bulgac, A. 2004a, Nucl. Phys. A, 738, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Magierski, P., & Bulgac, A. 2004b, Acta Phys. Polon. B, 35, 1203 [NASA ADS] [Google Scholar]
- Magierski, P., & Heenen, P.-H. 2002, Phys. Rev. C, 65, 045804 [NASA ADS] [CrossRef] [Google Scholar]
- Mallik, S., & Gulminelli, F. 2021, Phys. Rev. C, 103, 015803 [Google Scholar]
- Margueron, J., Hoffmann Casali, R., & Gulminelli, F. 2018a, Phys. Rev. C, 97, 025805 [NASA ADS] [CrossRef] [Google Scholar]
- Margueron, J., Hoffmann Casali, R., & Gulminelli, F. 2018b, Phys. Rev. C, 97, 025806 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N., & Urban, M. 2016, Phys. Rev. C, 94, 065801 [NASA ADS] [CrossRef] [Google Scholar]
- Maruyama, T., Tatsumi, T., Voskresensky, D. N., Tanigawa, T., & Chiba, S. 2005, Phys. Rev. C, 72, 015802 [NASA ADS] [CrossRef] [Google Scholar]
- Medin, Z., & Cumming, A. 2010, Phys. Rev. E, 81, 036107 [Google Scholar]
- Nandi, R., Mukhopadhyay, S., & Banik, S. 2021, Phys. Rev. C, 104, 025803 [NASA ADS] [CrossRef] [Google Scholar]
- Negele, J. W. 1982, Rev. Mod. Phys., 54, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Newton, W. G., & Stone, J. R. 2009, Phys. Rev. C, 79, 055801 [NASA ADS] [CrossRef] [Google Scholar]
- Newton, W. G., Gearheart, M., & Li, B.-A. 2013, ApJS, 204, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Oertel, M., Hempel, M., Klähn, T., & Typel, S. 2017, Rev. Mod. Phys., 89, 015007 [Google Scholar]
- Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Pais, H., & Stone, J. R. 2012, Phys. Rev. Lett., 109, 151101 [Google Scholar]
- Pais, H., Newton, W. G., & Stone, J. R. 2014, Phys. Rev. C, 90, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Papakonstantinou, P., Margueron, J., Gulminelli, F., & Raduta, Ad. R. 2013, Phys. Rev. C, 88, 045805 [NASA ADS] [CrossRef] [Google Scholar]
- Pastore, A., Shelley, M., Baroni, S., & Diget, C. A. 2017, J. Phys. G, 44, 094003 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., & Chamel, N. 2022, Phys. Rev. C, 105, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Chamel, N., Potekhin, A. Y., et al. 2018, MNRAS, 481, 2994 [NASA ADS] [Google Scholar]
- Pearson, J. M., Chamel, N., & Potekhin, A. Y. 2020, Phys. Rev. C, 101, 015802 [NASA ADS] [CrossRef] [Google Scholar]
- Pethick, C. J., & Ravenhall, D. G. 1995, Ann. Rev. Nucl. Part. Sci., 45, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2000, Phys. Rev. E, 62, 8554 [NASA ADS] [CrossRef] [Google Scholar]
- Prakash, M., Bombaci, I., Prakash, M., et al. 1997, Phys. Rep., 280, 1 [Google Scholar]
- Raduta, Ad. R., & Gulminelli, F. 2019, Nucl. Phys. A, 983, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Raduta, Ad. R., Aymard, F., & Gulminelli, F. 2014, Eur. Phys. J. A, 50, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Ravenhall, D. G., Pethick, C. J., & Wilson, J. R. 1983a, Phys. Rev. Lett., 50, 2066 [NASA ADS] [CrossRef] [Google Scholar]
- Ravenhall, D. G., Pethick, C. H., & Lattimer, J. M. 1983b, Nucl. Phys. A, 407, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Roca-Maza, X., Viñas, X., Centelles, M., Ring, P., & Schuck, P. 2011, Phys. Rev. C, 84, 054309 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, K. 1975, Progr. Theor. Phys., 54, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, A., & Shternin, P. 2018, Astrophys. Space Sci. Lib., 457, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, A. S., Roberts, L. F., & Ott, C. D. 2017, Phys. Rev. C, 96, 065802 [Google Scholar]
- Sedrakian, A. D. 1996, Astrophys. Space Sci., 236, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Sekizawa, K., Kobayashi, S., & Matsuo, M. 2022, Phys. Rev. C, 105, 045807 [CrossRef] [Google Scholar]
- Shang, X. L., Li, A., Miao, Z. Q., Burgio, G. F., & Schulze, H.-J. 2020, Phys. Rev. C, 101, 065801 [NASA ADS] [CrossRef] [Google Scholar]
- Shelley, M., & Pastore, A. 2020, Universe, 6, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Shelley, M., & Pastore, A. 2021, Phys. Rev. C, 103, 035807 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, H., Toki, H., Oyamatsu, K., & Sumiyoshi, K. 2011a, ApJS, 197, 20 [CrossRef] [Google Scholar]
- Shen, G., Horowitz, C. J., & Teige, S. 2011b, Phys. Rev. C, 83, 035802 [NASA ADS] [CrossRef] [Google Scholar]
- Somasundaram, R., Drischler, C., Tews, I., & Margueron, J. 2021, Phys. Rev. C, 103, 045803 [NASA ADS] [CrossRef] [Google Scholar]
- Typel, S. 2016, Eur. Phys. J. A, 52, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Typel, S., Oertel, M., & Klähn, T. 2015, Phys. Part. Nuclei, 46, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Audi, G., Kondev, F. G., et al. 2017, Chin. Phys. C, 41, 030003 [NASA ADS] [CrossRef] [Google Scholar]
- Wlazłowski, G., Sekizawa, K., Magierski, P., Bulgac, A., & McNeil Forbes, M. 2016, Phys. Rev. Lett., 117, 232701 [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Crust–core transition density, nCC, and pressure, PCC, for the BSk24 functional at different temperatures with (w/) and without (w/o) the inclusion of the translational free energy Ftrans.
Crust–core transition density, nCC, and pressure, PCC, for the BSk24, SLy4, and DD-MEδ models at different temperatures with (w/) and without (w/o) the inclusion of the translational free energy  for the case δf = γ.
for the case δf = γ.
All Figures
 |
Fig. 1. Sketch of the motion of the ion (red sphere) in a uniform background, with the considered system of reference. |
| In the text | |
 |
Fig. 2. Ratio (in logarithmic scale) of the ion thermal wavelength to the WS cell volume as a function of the baryonic density nB for the BSk24 model at four different temperatures: kBT = 0.8 MeV (blue line), kBT = 1.0 MeV (red line), kBT = 1.2 MeV (green line), and kBT = 1.4 MeV (black line). The results are obtained at beta equilibrium using the ideal-gas translational energy, Eq. (44). |
| In the text | |
 |
Fig. 3. Ratio (in logarithmic scale) of the ion thermal wavelength to the WS cell volume (top panels) and to the reduced volume (bottom panels) as a function of the baryonic density nB for the BSk24 model, using three different prescriptions for the ion effective mass, at two different temperatures: kBT = 1 MeV (left panels) and kBT = 2.0 MeV (right panels). The results are obtained at beta equilibrium using the translational energy |
| In the text | |
 |
Fig. 4. Cluster mass number A (upper panel) and proton number Z (lower panel) as a function of the baryonic density nB for the BSk24 model at four different temperatures: kBT = 0.8 MeV (blue lines), kBT = 1.0 MeV (red lines), kBT = 1.2 MeV (green lines), and kBT = 1.4 MeV (black lines). The solid (dashed) lines are obtained when the translational energy, defined by Eq. (44), is (not) included. |
| In the text | |
 |
Fig. 5. Coulomb, surface, and curvature energies per nucleon, fCoul + surf + curv (teal dash-dotted lines), translational free energy per nucleon, ftrans (violet dashed lines), and their sum (black solid lines) as a function of A at kBT = 1 MeV and nB = 0.04 fm−3 (upper panel) and nB = 0.05 fm−3 (lower panel) for the BSk24 model. The red star in each panel indicates the solution for A from the minimisation. |
| In the text | |
 |
Fig. 6. Absolute value of the ratio of the translational free energy to the sum of surface, curvature, and Coulomb free energies as a function of the baryonic density nB for the BSk24 model at four different temperatures: kBT = 0.8 MeV (blue line), kBT = 1.0 MeV (red line), kBT = 1.2 MeV (green line), and kBT = 1.4 MeV (black line). |
| In the text | |
 |
Fig. 7. Cluster mass number A (upper panels) and proton number Z (lower panels) as a function of the baryonic density nB for the BSk24 model at two different temperatures: kBT = 1.0 MeV (left panels) and kBT = 2.0 MeV (right panels). Different prescriptions for the translational free energy are considered. See text for details. |
| In the text | |
 |
Fig. 8. Neutron (upper panels) and proton (lower panels) densities inside (solid lines) and outside (dashed lines) the cluster as a function of the baryonic density nB for the BSk24 model at two different temperatures: kBT = 1.0 MeV (left panels) and kBT = 2.0 MeV (right panels). The effective translational free energy |
| In the text | |
 |
Fig. 9. Cluster mass number A (upper panels) and proton number Z (lower panels) as a function of the baryonic density nB for the BSk24 (black lines), SLy4 (blue lines), and DD-MEδ (orange lines) models at three different temperatures: kBT = 1.0 MeV (left panels), kBT = 1.5 MeV (middle panels), and kBT = 2.0 MeV (right panels). The solid (dashed) lines are obtained with (without) the effective translational energy |
| In the text | |
 |
Fig. 10. Same as Fig. 9, but for pressure P vs. baryonic number density nB. The green dots (violet squares) mark the crust–core transition with (without) |
| In the text | |
 |
Fig. 11. Proton number Z as a function of the baryonic density nB for the BSk24 model at |
| In the text | |
 |
Fig. 12. Absolute value of the ratio of the translational energy to the sum of surface, curvature, and Coulombs energies as a function of the baryonic density nB for the BSk24 model at kBT = 4.0 MeV (solid lines) and kBT = 3.0 MeV (dotted lines), for |
| In the text | |
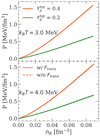 |
Fig. 13. Same as in Fig. 11 but for pressure P vs. baryonic number density nB. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



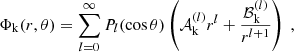
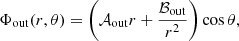
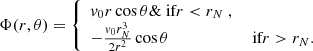
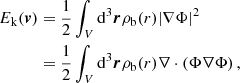
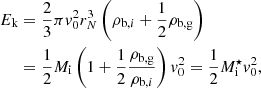
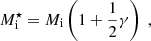
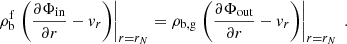
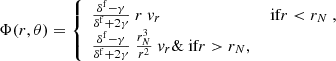
![$$ \begin{aligned} E_{\rm k}(\boldsymbol{v}) = \frac{1}{2} M_{\rm i} { v}_0^2 \left[ 1 - \delta ^\mathrm{f} + \frac{(\delta ^\mathrm{f}-\gamma )^2}{\delta ^\mathrm{f} + 2\gamma } \right] = \frac{1}{2} M_{\rm i}^\star { v}_0^2, \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq18.gif)
![$$ \begin{aligned} M_{\rm i}^{\star } = M_{\rm i} \left[ 1 - \delta ^\mathrm{f} + \frac{(\delta ^\mathrm{f}-\gamma )^2}{\delta ^\mathrm{f} + 2\gamma } \right] \ . \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq19.gif)
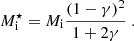
![$$ \begin{aligned} M^\star _{\mathrm{i}}&= M_{\mathrm{i}} \left[ 1 - \delta ^\mathrm{f}_{\rm min} + \frac{(\delta ^\mathrm{f}_{\rm min}-\gamma )^2}{\delta ^\mathrm{f}_{\rm min} + 2\gamma } \right] \nonumber \\&\approx M_{\rm i} \left(1- \frac{n_{\mathrm{gn}}}{n_i} \right) \ , \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq23.gif)
![$$ \begin{aligned} M^\star _{\mathrm{i}}&= M_{\mathrm{i}} \left[ 1 - \delta ^\mathrm{f}_{\rm max} + \frac{(\delta ^\mathrm{f}_{\rm max}-\gamma )^2}{\delta ^\mathrm{f}_{\rm max} + 2\gamma } \right] \nonumber \\&\approx M_{\rm i} \left[ { y}_{\rm p} + \frac{(1-{ y}_{\rm p}-n_{\mathrm{gn}}/n_i)^2}{1-{ y}_{\rm p} + 2 n_{\mathrm{gn}}/n_i} \right] \ . \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq24.gif)
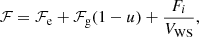
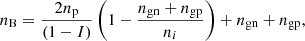
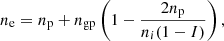
![$$ \begin{aligned} \Omega&= \frac{2n_{\rm p}}{1-I}\frac{F_i}{A}+ \left[ 1 - \frac{2n_{\rm p}}{(1-I)n_i}\right]\mathcal{F} _{\rm g} + \mathcal{F} _{\rm e} \nonumber \\&\quad + \gamma _1 \left[n_{\rm B} - \frac{2n_{\rm p}}{1-I}\left(1 - \frac{n_{\mathrm{gn}} + n_{\mathrm{gp}}}{n_i}\right) - n_{\mathrm{gn}} -n_{\mathrm{gp}}\right] \nonumber \\&\quad + \gamma _2 \left[n_{\rm e} - n_{\rm p} - n_{\mathrm{gp}}\left(1- \frac{2n_{\rm p}}{n_i (1-I)}\right)\right]. \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq30.gif)
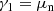
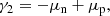
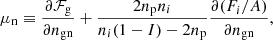
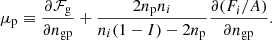
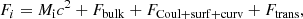
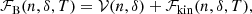
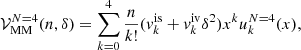
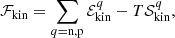
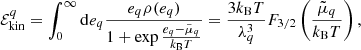
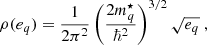
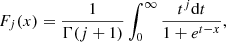
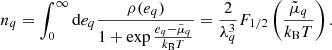
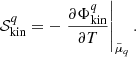
![$$ \begin{aligned} \Phi ^{{q}}_{\rm kin}&= -k_{\rm B} T\int _0^{\infty } \ln \left[1 + \exp {\left(-\frac{e_{{q}} - \tilde{\mu }_{{q}}}{k_{\rm B} T}\right)}\right]\rho (e_{{q}})\mathrm{d}e_{{q}}\nonumber \\&=-\frac{2}{3}\mathcal{E} ^{q}_{\rm kin} \ , \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq62.gif)
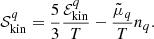
![$$ \begin{aligned} \mathcal{F} _{\rm kin} = \sum _{q = \mathrm{n,p}} \left[ { \frac{-2 k_{\rm B} T}{\lambda _{q}^3}F_{3/2}\left(\frac{\tilde{\mu }_{{q}}}{k_{\rm B} T}\right) + n_q \tilde{\mu }_{{q}}} \right]. \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq64.gif)
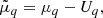
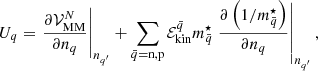
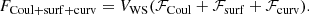
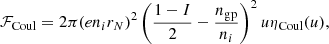
![$$ \begin{aligned} \eta _{\rm Coul}(u) =\frac{1}{5}\left[ u+ 2 \left( 1- \frac{3}{2}u^{1/3} \right) \right]. \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq70.gif)
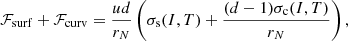
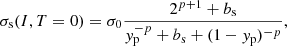
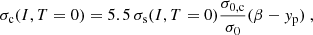
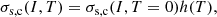
![$$ \begin{aligned} h(T) = {\left\{ \begin{array}{ll} 0&\text{ if} T > T_{\rm c} \ , \\ \left[1 -\left(\frac{T}{T_{\rm c}}\right)^2\right]^2&\text{ if} T \le T_{\rm c} , \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq75.gif)
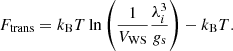
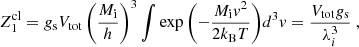
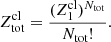
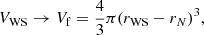
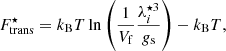
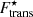
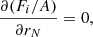
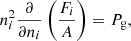
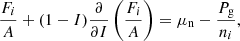
![$$ \begin{aligned}&2\left[ \frac{\partial }{\partial I}\left(\frac{F_i}{A}\right) - \frac{n_{\rm p}}{1-I} \frac{\partial }{\partial n_{\rm p}}\left(\frac{F_i}{A}\right) \right] =\mu _{\rm n} - \mu _{\rm p}, \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq101.gif)
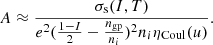
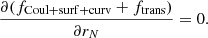
![$$ \begin{aligned} A \approx A_0 = \exp \left[ \frac{2}{5}\ln \left(C_0\frac{n_i u}{T^{3/2}}\right) + \frac{3}{5}\right] \ , \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq105.gif)
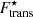
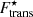
![$$ \begin{aligned} {A}_0^\star = \exp \left[ \frac{2}{5}\ln \left(C_0\frac{n_i u}{T^{3/2}g(u,\gamma )}\right) + \frac{3}{5}\right], \end{aligned} $$](/articles/aa/full_html/2023/04/aa45061-22/aa45061-22-eq116.gif)